Как найти множество истинности высказывательной формы

Содержание

1. Высказывания
   и высказывательные формы.

2. Конъюнкция
   и дизъюнкция высказываний.

3. Конъюнкция
   и дизъюнкция высказывательных форм.

Основная
литература 7,
9, 10, 11, 16, 30, 31, 32, 33, 34;

Дополнительная
литература 17,
18, 30, 39, 52, 63, 66, 78, 86

Введение.
Изучая реальные процессы, математика
описывает их, используя как естественный
словесный язык, так и свой символический.
Описание строится при помощи предложений.
Но чтобы математические знания были
достоверными, правильно отражали
окружающую нас реальность, эти предложения
должны быть истинными.

Но
как узнать, истинное или ложное знание
заключено в том или ином математическом
предложении? На этот и другие вопросы,
с ним связанные, отвечает раздел
«математические предложения». А сейчас
только заметим, что каждое математическое
предложение характеризуется содержанием
и логической формулой (структурой),
причем содержание неразрывно связано
с формой, и нельзя осмыслить первое, не
понимая второго. В связи с этим изучение
математических предложений будет в
основном связано с раскрытием логической
структуры математических предложений.

1.
Высказывания и высказывательные формы

Относительно
понятий и отношений между ними можно
высказывать различные суждения. Языковой
формой суждений являются повествовательные
предложения. Например, в начальном курсе
математики можно встретить такие
предложения:

1. число
   10-четное;

2. 2+58;

3. х+5=8;

4. В
   числе 15 один десяток и 5 единиц;

5. От
   перестановки множителей произведение
   не изменяется;

6. Некоторые
   числа делятся на 3.

Видим,
что предложения, используемые в
математике, могут быть записаны как на
естественном (русском) языке, так и на
математическом, с использованием
символов. Далее, о предложениях 1, 4, 5 и
6 можно сказать, что они несут верную
информацию, а предложение 2 – ложную.
Относительно предложения х+5=8 вообще
сказать нельзя истинно оно или ложно.
Взгляд на предложение с позиции – истину
или ложь оно нам сообщает – привел к
понятию высказывания.

Определение.
Высказыванием
в математике называют предложение,
относительно которого имеет смысл
вопрос: истинно оно или ложно.

Например,
предложения 1, 2, 4, 5 и 6 приведенные выше,
есть высказывания, причем предложения
1, 4, 5 и 6 – истинные, 2 – ложное.

Высказывания
принято обозначать прописными буквами
латинского алфавита: А, В, С, …, Z.
Если высказывание А истинно, то записывают:
А – «и», если же высказывание А – ложно,
то пишут: А – «л».

«Истина»
и «ложь» называются значениями истинности
высказывания.
Каждое высказывание либо истинно, либо
ложно, быть одновременно тем и другим
оно не может.

Предложение
х+5=8 не является высказыванием, так как
о нем нельзя сказать: истинно оно или
ложно. Однако при подстановке конкретных
значений переменной х оно обращается
в высказывание: истинное или ложное.
Например,
если
х=2, то 2+5=8- ложное высказывание, а при
х=3 оно обращается в истинное высказывание
3+5=8. Предложение х+5=8 называется
высказывательной
формой.
Оно порождает множество высказываний
одной и той же формы.

По
числу переменных, входящих в высказывательную
форму, различают одноместные, двухместные
и т.д. высказывательные формы и обозначают:
А(х), А(х,у) и т.д. Например, х+5=8 – одноместная
высказывательная форма, а предложение
«Прямая х параллельна прямой у» –
двухместная.

Следует
иметь в виду, что в высказывательной
форме переменные могут содержаться
неявно. Например, в предложениях: «число
четное», «две прямые пересекаются»
переменных нет, но они подразумеваются:
«Число х – четное», «Две прямые х и у
пересекаются».

Задание
высказывательной формы, как правило,
предполагает и задание того множества,
из которого выбираются значения
переменной (переменных), входящей в
высказывательную форму. Это множество
называется областью определения
высказывательной формы. Например,
неравенство х 
5 можно рассматривать на множестве
натуральных чисел, а можно считать, что
значение переменной х выбирается из
множества действительных чисел. Тогда
в первом случае областью определения
неравенства х 
5 будет множество натуральных чисел, а
во втором – множество действительных
чисел.

Дадим
определение одноместной высказывательной
формы (понятие высказывательной формы,
содержащей две и более переменных,
определяется аналогично).

Определение.
Одноместной
высказывательной формой,
заданной на множестве Х, называется
предложение с переменной, которое
обращается в высказывание при подстановке
в него значений переменной из множества
Х.

Среди
всех возможных значений переменной нас
в первую очередь интересуют те, которые
обращают высказывательную форму в
истинное высказывание. Множество
таких значений переменных называют
множеством истинности высказывательной
формы.

Например,
множество истинности высказывательной
формы х5,
заданной на множестве действительных
чисел, будет промежуток (5;).
Множество истинности высказывательной
формы х+5=8, заданной на множестве целых
неотрицательных чисел, состоит из одного
числа 3.

Условимся
обозначать множество истинности
высказывательной формы буквой Т. Тогда,
согласно, определению всегда Т 
Х.

Предложения
(высказывания и высказывательные формы),
которые мы рассматривали, были простыми,
но можно привести примеры суждений,
языковой формой которых будут сложные
предложения. Например: «Если треугольник
равнобедренный, то углы при основании
в нем равны». Естественно возникает
вопрос: как определить значение истинности
таких высказываний и находить множество
истинности таких высказывательных
форм?

Чтобы
ответить на эти вопросы, необходимо
познакомится с некоторыми логическими
понятиями.

В
логике считают, что из двух данных
предложений можно образовать новые
предложения, используя для этого союзы
«и», «или», «если…, то…», «тогда и только
тогда, когда» и др. С помощью частицы
«не» или словосочетания «неверно, что»
можно из данного предложения получить
новое.

Слова
«и», «или», «если …, то…», «тогда и только
тогда, когда», а также частицу «не»
(слова «неверно, что») называются
логическими
связками.
Предложения, образованные из других
предложений с помощью логических связок,
называют составными.
Предложения, не являющиеся составными,
называют элементарными.

Приведем
примеры составных предложений:

1. Число
   28 четное и делится на 7.

Это
предложение образованно из двух
элементарных: «число 28 четное», «число
28 делится на 7» с помощью логической
связки «и».

1. Число
   х меньше или равно 8.

Это
предложение образовано из двух
элементарных: «число х меньше 8», «число
х равно 8» с помощью логической связки
«или».

1. число
   14 не делится на 4.

Это
составное высказывание образовано из
предложения «число 14 делится на 4» с
помощью частицы «не».

Обратим
внимание на то, что все три предложения,
являясь с логической точки зрения
составными, по своей грамматической
структуре – простые. Не всегда, но так
бывает: простое предложение по своей
логической структуре может быть
составным.

А
как определять значение истинности
составного высказывания? Например,
истинно или ложно высказывание: «число
28 делится на 7 и на 9»? Элементарное
высказывание «число 28 делится на 7»,
входящее в составное, истинное – это
известно из начального курса математики.
Второе элементарное высказывание «число
28 делится на 9» – ложное (и это нам
известно). А каким будет в этом случае
значение истинности составного
высказывания, образованного из этих
высказываний с помощью союза «и»?
Ответить на этот вопрос можно, если
знать смысл этого союза. Но так как
составные высказывания образуются с
помощью и других логических связок, то
возникает необходимость в уточнении
их смысла.

Кроме
того, уточнение смысла используемых в
математике связок обусловлено их
неоднозначным толкованием в обычной
речи, что может привести к неоднозначному
ответу при нахождении значения истинности
составных высказываний.

Итак,
значение истинности элементарного
высказывания определяют, исходя из его
содержания с опорой на известные знания.
Чтобы определить значение истинности
составного высказывания, надо знать
смысл логических связок, с помощью
которых оно образовано из элементарных,
и уметь выявлять логическую структуру
высказывания.

Для
выявления логической структуры составного
предложения нужно установить:

1. из
   каких элементарных предложений
   образованно данное составное предложение;

2. с
   помощью каких логических связок оно
   образовано.

Выявим,
например,
логическую
структуру предложения «Если углы
вертикальные, то они равны». Оно состоит
из двух элементарных предложений:
предложения А – «углы вертикальные» и
предложения В – «углы равны». Соединены
они в одно составное предложение с
помощью логической связки «если …,
то…». Говорят, что данное составное
предложение имеет логическую структуру
(форму): «если А, то В».

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Математические предложения

План

• Высказывания и высказывательные формы.

• Значение истинности высказываний и высказывательных форм. Простые и составные высказывания и высказывательные формы. Логическая структура составного предложения.
• Значение истинности высказываний и высказывательных форм.
• Простые и составные высказывания и высказывательные формы.
• Логическая структура составного предложения.
• Конъюнкция и дизъюнкция высказываний Таблица истинности высказываний. Конъюнкция и дизъюнкция высказывательных форм.
• Таблица истинности высказываний.
• Конъюнкция и дизъюнкция высказывательных форм.
• Высказывания с кванторами. Квантор общности и значение истинности. Квантор существования и значение истинности.
• Квантор общности и значение истинности.
• Квантор существования и значение истинности.
• Отрицание высказываний и высказывательных форм.
• Отношения следования и равносильности.
• Структура и виды теорем. Теорема, правила, формулы Виды теорем. Закон контрпозиции
• Теорема, правила, формулы
• Виды теорем.
• Закон контрпозиции
• Основные выводы

Рассмотрим некоторые предложения

• «1 + 9 = 20 – 10. Это равенство»
• 37 + 6  37
• 20 + 8  20
• «некоторые числа делятся на 5»
• 5 + x = 9

Определим истинны ли они или ложные

Предложения 1,2,4 – истинные

Предложение 3 – ложное

Предложение 5 – нельзя указать истинное оно или ложное

высказывания

Высказывательная форма

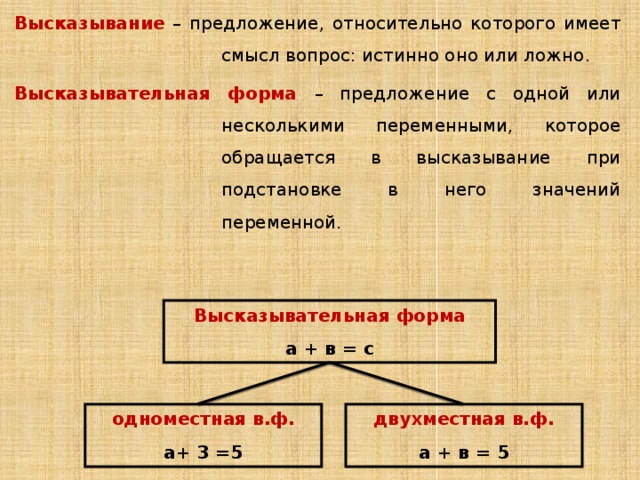
Высказывание – предложение, относительно которого имеет смысл вопрос: истинно оно или ложно.

Высказывательная форма – предложение с одной или несколькими переменными, которое обращается в высказывание при подстановке в него значений переменной.

Высказывательная форма

а + в = с

одноместная в.ф.

двухместная в.ф.

а+ 3 =5

а + в = 5

Обозначения : А – «И» – высказывание А – истинно

В – «Л» – высказывание В – ложно

«И», «Л» – значения истинности высказывания

Множество истинности высказывательной формы – это значения переменной, которые обращают высказывательную форму в истинное высказывание.

Пример: определить множество истинности высказывательной формы x  6, если а) x  N

б) x  Z в) x  R

• Множество истинности – {1,2,3,4,5}
• Множество истинности – {0,1,2,3,4,5}
• Множество истинности – {-  ; 6}

Выше рассмотренные предложения – простые или элементарные предложения.

Из двух простых предложений можно составить новые предложения с помощью союзов «и», «или»…

Логическая связка – «и», «или», «если,…то», «не», «тогда и только тогда, когда».

Составные предложения – это предложения, образованные из элементарных с помощью логических связок.

Для определения логической структуры составного предложения необходимо установить :

• Из каких элементарных предложений оно образовано;
• С помощью, каких логических связок оно образовано.

Пример : 1) x ≥7 – это составная высказывательная форма.

Логическая структура : « А или В »

Элементарные высказывательные формы – А – «x  7»

В – «x = 7»

Логическая связка – «или»

2) «если треугольник равнобедренный, то углы при основании в нем равны» – это составное высказывание.

Логическая структура : « Если А, то В »

Элементарные предложения :

А – «треугольник равнобедренный»

В – «углы при основании равны»

Логические связки : «Если ……, то».

«Число 25 четное и делится на 5»

Логическая структура – « А и В »

Элементарные высказывательные формы –

А – «25 – четное число»

В – «25 – делится на 5»

Логическая связка – « и »

Проблема : «Как определить значение истинности составных предложений?»

Составное высказывание вида «А и В» называют конъюнкцией (лат. «соединение»), обозначают А  В .

Определение. Конъюнкцией высказываний А и В называется высказывание А  В, которое истинно, когда оба высказывания истинны, и ложно, когда хотя бы одно из высказываний ложно.

Пример : А – «Л»  А  В – «Л» (по определению)

В – «И»

Составные высказывания вида «А или В» называют дизъюнкцией (лат. «разделение»), обозначают А  В.

Определение. Дизъюнкцией высказываний А и В называется высказывание А  В, которое истинно, когда истинно хотя бы одно из высказываний, и ложно, когда оба высказывания ложны.

Пример: «Число 25 делится на 5 или на 3».

А – «25 делится на 5»

В – «25 делится на 3»

Логическая связка – или

Логическая структура – А  В

А – «И»  – А  В «И» (по определению)

В – «Л»

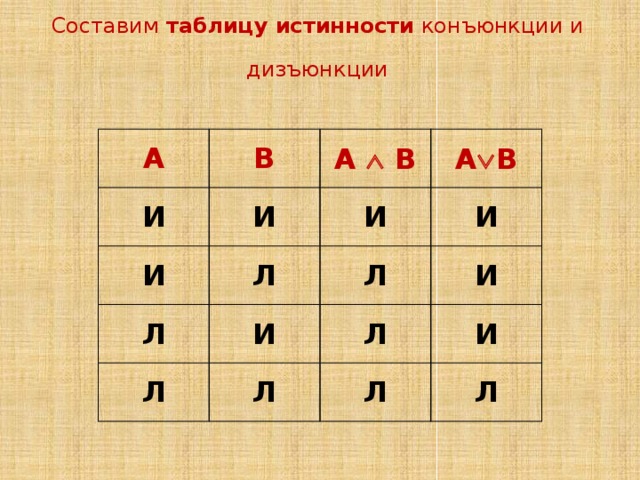
Составим таблицу истинности конъюнкции и дизъюнкции

А

В

И

И

И

А  В

Л

Л

И

А  В

И

И

Л

Л

И

Л

Л

И

Л

Л

Конъюнкцию одноместных высказывательных форм обозначают:

А(х)  В(х)

Высказывательная форма А(х)  В(х) обращается в истинное высказывание, если обращаются в истинное высказывание обе высказывательные формы А(х) и В(х) при значениях х из области определения Х.

Пример : х + 3  13 А(х) – х+3  13

3х  15 В(х) – 3х  15

Логическая структура А(х)  В(х)

х  10

х  5

5

10

Ответ: А(х)  В(х) – «И» при х  (5;10).

Дизъюнкцию одноместных высказывательных форм обозначают:

А(х)  В(х)

Высказывательная форма А(х)  В(х) обращается в истинное высказывание, при тех значениях х из области определения Х, при которых обращается в истинное высказывание хотя бы одна из высказывательных форм.

Пример: (х + 7) (х – 4) = 0

Произведение равно нулю, когда один из множителей равен нулю.

А(х) – х + 7=0

В(х) – х – 4 =0

Логическая структура: А(х)  В(х)

х +7=0 или х – 4 =0

х = – 7 х=4

Ответ. А(х )  В(х) – И при х  (-7;4).

Квантор существования – это выражения «существует», «некоторые», «найдется», «есть», «хотя бы один».

Обозначение :  х – «существует х»

(  х) Ах – «существует такое значение х, что А(х) – истинное высказывание».

Истинность высказывания с квантором существования устанавливается при помощи конкретного примера , а ложность – доказывается.

Пример: «Некоторые прямоугольные треугольники являются равносторонними».

Высказывание содержит квантор существования – «некоторые» и оно – «Л». Это необходимо доказать.

В равностороннем треугольнике все углы по 60  , а в прямоугольном один из углов – 90  . Следовательно, ни один прямоугольный треугольник не может быть равносторонним.

Квантор общности – это выражения «всякий», «любой», «каждый» и «все».

Обозначение :  х – для всякого х.

(  х) А(х) – «для всякого х предложения А(х ) – истинное высказывание».

Истинность высказывания с квантором общности устанавливается путем доказательства , а ложность – контрпример.

  Пример: «Всякое натуральное число делится на 2 » высказывание содержит квантор общности – «всякое и оно – Л, т.к. «3 не делится на 2» – контрпример.

В математике часто приходится строить предложения в которых что – либо отрицается.

Пример: «15 – простое число» А – Л

Построим отрицание высказывания: «неверно, что 15 простое число» – И

Обозначение: Ā

Читают: «Не А» или «Неверно, что А».

Определение. Отрицанием высказывания А называется высказывание Ā, которое ложно, если высказывание А истинно, и истинно, если высказывание А- ложно.

А

И

Ā

Л

Л

И

Отрицании конъюнкции и дизъюнкции

Законы де Моргана

Чтобы построить отрицание конъюнкции (дизъюнкции), достаточно заменить отрицаниями составляющие её высказывания, а союз «и» («или») заменить союзом «или» («и»).

  Пример: «Число 15 – нечетное и делится на 5».

Построить отрицание высказывания.

Решение

А  В – И

• способ. А  В – «Неверно, что 15 – нечетное число и делится на 5». А  В – Л  оно является отрицанием высказывания А.
• способ. Воспользуемся законом де Моргана

•  

«Число 15 – четное или не делится на 5» – Л

Отрицание высказываний с кванторами

Отрицание высказывания с квантором можно построить двумя способами:

• перед высказыванием ставится слова «неверно что»;
• квантор общности (существования) заменяется квантором существования (общности), а предложение, стоящее после квантора заменяется его отрицанием.

Пример: Построить отрицание высказываний

• А–«Всякий многоугольник является четырехугольником» – Л – высказывание с квантором общности.

• способ. Ā – «Неверно, что всякий многоугольник является четырехугольником» – И

А – Л  Ā построено верно

Ā – И

• способ . Ā – «Некоторые многоугольники не являются четырехугольниками» – И

А – Л  Ā построено верно

Ā – И

• А – «Некоторые свойства квадрата присущие прямоугольнику» – И – высказывание с квантором существования .

• способ. Ā – «Неверно, что некоторые свойства квадрата присущи прямоугольнику».

А – И  Ā построен верно

Ā – Л

• способ. Ā – «Всякое свойство квадрата не присуще прямоугольнику» – Л

А – И

Ā– Л

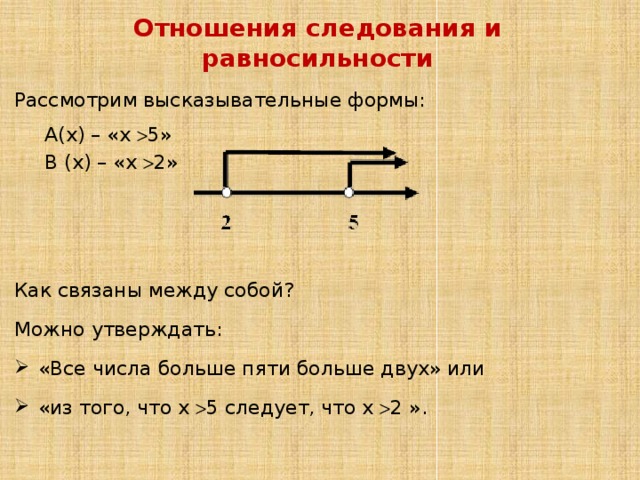
Отношения следования и равносильности

Рассмотрим высказывательные формы:

А(х) – «х  5»

В (х) – «х  2»

Как связаны между собой?

Можно утверждать:

• «Все числа больше пяти больше двух» или
• «из того, что х  5 следует, что х  2 ».

Определение. Высказывательная форма В (х) следует из высказывательной S формы А (х), если В (х) обращается в истинное высказывание при всех тех значениях х, при которых А (х) истинна.

Обозначение: А(х)  В(х)

Читают:

• Из А(х) следует В;
• Всякое А(х) есть В(х);
• Если А (х), то В(х);
• В(х)есть следствие А(х);
• А(х) – достаточное условие для В (х)
• В(х) – необходимое условие для А(х)
• Как установить истинность предложения А(х)  В(х)?

Его можно сформулировать в виде:

« Всякое А(х) есть В(х)»

Имеет место высказывание с квантором общности, значит истинность устанавливается путем доказательства, а ложность – контрпример.

Рассмотрим высказывания:

А(х) – «треугольник равнобедренный»

В(х) – «Углы при основании треугольника равны »

А(х)  В (х) – И

«Если в треугольнике углы при основании равны, то он равнобедренный» – И

Говорят: предложения А(х) и В(х) – равносильны.

Определение. Предложения А(х) и В(х) равносильны, если из предложения А(х) следует предложения В(х), а из предложения В(х) следует предложение А(х).

Обозначение: А(х)  В(х)

Читают:

• А(х) равносильно В(х)
• А(х) тогда и только тогда, когда В(х)
• А(х) – необходимое и достаточное условие В(х)
• В(х) – необходимое и достаточное условие А(х)

Теорема – это высказывание, истинность которого устанавливается путем доказательства.

•  

Логическая структура теоремы:

А  В, где А и В – высказывательные формы с одной или несколькими переменными.

Предложение А – условие теоремы ;

В – заключение.

Теорема. Если а – любое число и n, k – натуральные числа, то справедливо равенство

Для удобства использования теоремой её формулируют в виде правила.

•  

Правило. При умножении степеней с одинаковыми основаниями, основания оставляют прежним. А показатели степеней складывают.

Пусть дана теорема:

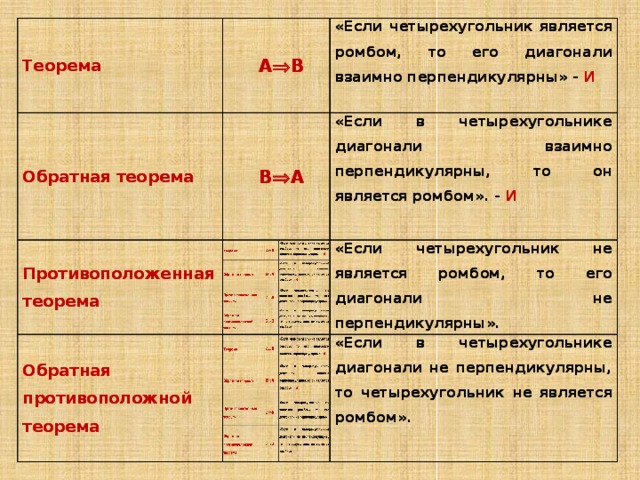
Теорема

Теорема

А  В

Обратная теорема

Обратная теорема

А  В

В  А

Противоположенная теорема

Противоположенная теорема

В  А

«Если четырехугольник является ромбом, то его диагонали взаимно перпендикулярны» – И

«Если четырехугольник является ромбом, то его диагонали взаимно перпендикулярны» – И

Обратная противоположной теорема

Обратная противоположной теорема

«Если в четырехугольнике диагонали взаимно перпендикулярны, то он является ромбом». – И

«Если в четырехугольнике диагонали взаимно перпендикулярны, то он является ромбом». – И

«Если четырехугольник не является ромбом, то его диагонали не перпендикулярны».

«Если четырехугольник не является ромбом, то его диагонали не перпендикулярны».

«Если в четырехугольнике диагонали не перпендикулярны, то четырехугольник не является ромбом».

«Если в четырехугольнике диагонали не перпендикулярны, то четырехугольник не является ромбом».

•  

Закон контрапозиции

т.е. всегда когда истинна данная теорема, будет истинна и теорема обратная противоположенной.

Вопросы для самоконтроля

• Сформулируйте разницу между высказыванием и высказывательной формой.
• Как определить логическую структуру составного предложения?
• Сформулируйте различие между конъюнкцией и дизъюнкцией.
• Как определяется истинность конъюнкции и дизъюнкции высказываний и высказывательных форм?
• Сформулируйте правила определения истинности высказываний с кванторами.
• Где используется закон де Моргана?
• Каким образом можно построить отрицание высказываний с кванторами?
• В каких случаях используют отношение логического следования и равносильности между предложениями?
• В чем отличие теоремы от правила?
• Какова логическая структура различных видов теорем?
• Каким законом связаны различные виды теорем?

Задания для практической работы

Стойлова Л.П. Математика: Учебное пособие для студентов средних педагогических учебных заведений «Академия», 1998.

§ 3, п.16 № 4,5,6,8

п.17 № 1,2,3,5,

п. 18 № 3,4

п. 20 № 5,6,7,9,10

п. 21 № 2,3,4,8

п.22№ 2,5,9,12

п.23 №2,5,6

Обновлено: 18.05.2023

Правило отрицания высказываний с кванторами: $$ mathrm< overline<(forall x)A(x)>=(exists x)overline, overline<(exists x)A(x)>=(forall x)overline > $$

п.2. Конъюнкция

Конъюнкция двух высказываний – это высказывание, которое будет истинным, если истинны оба исходных высказывания; а во всех остальных случаях – будет ложным.
Конъюнкция является логическим умножением.

С точки зрения операций над множествами, конъюнкция аналогична пересечению двух множеств (см. §10 справочника для 8 класса).

С точки зрения записи условий, конъюнкция аналогична системе с фигурной скобкой.

п.3. Дизъюнкция

Дизъюнкция двух высказываний – это высказывание, которое будет ложным, если ложны оба исходных высказывания; а во всех остальных случаях – будет истинным.
Дизъюнкция является логическим сложением.

С точки зрения операций над множествами, дизъюнкция аналогична объединению двух множеств (см. §10 справочника для 8 класса).

С точки зрения записи условий, дизъюнкция аналогична совокупности с квадратной скобкой. Например, запись (mathrm<(x^2-1geq 0)vee left(xgt frac12right)>) аналогична совокупности $$ left[ begin < l >mathrm & \ mathrm & endright. Leftrightarrow xleq -1 cup xgtfrac12 $$

п.4. Импликация

Импликация двух высказываний – это высказывание, которое будет ложным, если первое высказывание истинно, а второе ложно; а во всех остальных случаях – будет истинным.

п.5. Эквиваленция

Эквиваленция двух высказываний – это высказывание, которое будет истинным только при совпадении истинности обоих высказываний; а при несовпадении – будет ложным.

п.6. Законы де Моргана

Докажем эквивалентность с помощью таблиц истинности:

Мы видим, что итоговые столбцы слева и справа полностью совпадают.
Значит, высказывания эквивалентны.

Докажем эквивалентность с помощью таблиц истинности:

Высказывания слева и справа эквивалентны.

Высказывания называются эквивалентными (равносильными) , если соответствующие значения каждого из них совпадают в таблице истинности.

п.7. Алгоритм доказательства эквивалентности высказываний с помощью таблиц истинности

Например:
Докажем следующее свойство:

Отрицание импликации эквивалентно конъюнкции посылки и отрицания заключения: $$ mathrm< overline=A wedgeoverline > $$

Изучая реальные процессы, математика описывает их, используя как естественный словесный язык, так и свой символический. Описание строится при помощи предложений. Но чтобы математические знания правильно отражали окружающую нас реальность, эти предложения должны быть истинными.

Каждое математическое предложение характеризуется содержанием и логической формой (структурой), причем содержание неразрывно связано с формой, и нельзя осмыслить первое, не понимая второго.

1. Высказывания и высказывательные формы

Относительно понятий и отношений между ними можно высказывать различные суждения. Языковой формой суждений являются повествовательные предложения. Например, в начальном курсе математики можно встретить такие предложения:

1) число 12 – четное;

4) В числе 15 один десяток и 5 единиц;

5) От перестановки множителей произведение не изменяется;

6) Некоторые числа делятся на 3.

Видим, что предложения, используя в математике, могут быть записаны как на естественном (русском) языке, так и на математическом, с использованием символов. Далее, о предложениях 1, 4, 5 и 6 можно сказать, что они несут верную информацию, а предложение 2 – ложную. Относительно предложения х + 5 = 8 вообще нельзя сказать: истинное оно или ложное. Взгляд на предложение с позиции – истину или ложь оно нам сообщает – привел к понятию высказывания.

Определение. Высказыванием в математике называют предложение, относительно которого имеет смысл вопрос: истинно оно или ложно.

Например, предложения 1, 2, 4, 5 и 6 – высказывания, причем предложения 1, 4, 5 и 6 – истинные, а 2 – ложное.

Предложение х + 5 = 8 не является высказыванием, так как о нем нельзя сказать: истинно оно или ложно. Однако при подстановке конкретных значений переменной х оно обращается в высказывание: истинное или ложное. Предложение х + 5 = 8 называется высказывательной формой. Оно порождает множество высказываний одной и той же формы.

Определение. Одноместной высказывательной формой, заданной на множестве Х, называется предложение с переменной, которое обращается в высказывание при подстановке в него значений переменной из множества Х.

Множество Х – множество, из которого выбираются значения переменной.

Среди всех возможных значений переменной нас в первую очередь интересуют те, которые обращают высказывательную форму в истинное высказывание. Множество таких значений переменных называют множеством истинности высказывательной формы. Например, множеством истинности высказывательной формы х > 5, заданной на множестве действительных чисел, будет промежуток (5; ∞). Множество истинности высказывательной формы х + 5 = 8, заданной на множестве целых неотрицательных чисел, состоит из одного числа 3.

Условимся обозначать множество истинности высказывательной формы буквой Т. Тогда, согласно определению, всегда Т⊂Х.

Чтобы ответить на эти вопросы, необходимо познакомиться с некоторыми логическими понятиями.

Приведем примеры составных предложений.

1) Число 28 четное и делится на 7.

2) Число х меньше или равно 8.

3) Число 14 не делится на 4.

Эти предложения, являясь с логической точки зрения составными, по своей грамматической структуре – простые.

Для этого нужно установить:

1) из каких элементарных предложений образовано данное составное предложение;

2) с помощью каких логических связок оно образовано.

1. Конъюнкция и дизъюнкция высказываний

Определение.Конъюнкцией высказываний А и В называется высказывание А∧В, которое истинно, когда оба высказывания истинны, и ложно, когда хотя бы одно из высказываний ложно.

Определение конъюнкции можно записать с помощью таблицы, называемой таблицей истинности.

А	В	А∧В
и	и	и
и	л	л
л	и	л
л	л	л

Определение. Дизъюнкцией высказываний А и В называется высказывание А∨В, которое истинно, когда истинно хотя бы одно из этих высказываний, и ложно, когда оба высказывания ложны.

Образование составного высказывания с помощью логической связки называется логической операцией.

Определения конъюнкции и дизъюнкции можно обобщить на t составляющих их высказываний.

Конъюнкцией t высказываний называется предложение вида А₁ ∧ А₂ ∧…∧ Аt, которое истинно тогда и только тогда, когда истинны все составляющие его высказывания

Дизъюнкцией t высказываний называется предложение вида А₁ ∨ А₂ ∨…∨ Аt, которое ложно тогда и только тогда, когда ложны все составляющие его высказывания

1. Конъюнкция и дизъюнкция высказывательных форм

В математике рассматривают не только конъюнкцию и дизъюнкцию высказываний, но и выполняют соответствующие операции над высказывательными формами.

Конъюнкциюодноместных высказывательных форм А(х) и В(х), заданных на множестве Х, обозначают А(х) ∧ В(х). С появлением этого предложения возникает вопрос, как найти его множество истинности, зная множества истинности высказывательных форм А(х) и В(х). Другими словами, при каких значениях х из области определения Х высказывательная форма А(х) ∧ В(х) обращается в истинное высказывание? Очевидно, что это возможно при тех и только тех значениях х, при которых обращаются в истинное высказывание обе высказывательные формы А(х) и В(х). Если обозначить ТА – множество истинности предложения А(х), ТВ – множество истинности предложения В(х), а множество истинности их конъюнкции Т А∧В, то, по всей видимости, Т А∧В = ТА ∩ ТВ.

Докажем это равенство.

1. Пусть а – произвольный элемент множества Х и известно, что а ∈ Т А∧В. По определению множества истинности это означает, что высказывательная форма А(х) ∧ В(х) обращается в истинное высказывание при х = а, т.е. высказывание А(а) ∧ В(а) истинно. Так как данное высказывание конъюнкция, то получаем, что каждое из высказываний А(а) и В(а) также истинно. Это означает, что а ∈ Т А и а ∈ ТВ. Следовательно, по определению пересечения множеств, а ∈ ТА ∩ ТВ. Таким образом, мы показали, что Т А∧В ⊂ ТА ∩ ТВ.

2. Докажем обратное утверждение. Пусть а – произвольный элемент множества Х и известно, что а ∈ ТА ∩ ТВ. По определению пересечения множества это означает, что а ∈ Т А и а ∈ ТВ, откуда получаем, что А(а) и В(а) – истинные высказывания, поэтому конъюнкция высказываний А(а) ∧ В(а) также будет истинна. А это означает, что элемент а принадлежит множеству истинности высказывательной формы А(х) ∧ В(х), т.е.

а ∈ Т А∧В. Таким образом, мы доказали, что ТА ∩ ТВ ⊂ Т А∧В.

Из 1 и 2 в силу определения равных множеств вытекает справедливость равенства

Т А∧В = ТА ∩ ТВ, что и требовалось доказать.

Заметим, что полученное правило справедливо и для высказывательных форм, содержащих более одной переменной.

Дизъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х, обозначают А(х) ∨ В(х), Это предложение будет обращаться в истинное высказывание при тех и только тех значениях х из области определения Х, при которых обращается в истинное высказывание хотя бы одна из высказывательных форм, т.е.

Т А∨В = ТА ∪ ТВ. Доказательство этого равенства аналогично рассмотренному выше.

Приведем пример. Решим уравнение (х – 2) • (х + 5) = 0. Известно, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Это означает, что данное уравнение равносильно дизъюнкции: х – 2 = 0 ∨ х + 5 = 0 и поэтому множество его решений может быть найдено как объединение множеств решения первого и второго уравнений, т.е ∪ =.

Заметим, что дизъюнкцию уравнений (неравенств) называют также совокупностью.

Рассматривая конъюнкцию и дизъюнкцию высказывательных форм, мы установили их тесную связь с пересечением и объединением множеств.

А∩В = , А∪В = , причем каждое свойство представляет собой высказывательную форму.

1. Решение задач на распознавание объектов

С введением понятия конъюнкции и дизъюнкции высказывательных форм появились условия для рассмотрения вопросов, связанных с решением определенного вида задач, так называемых задач на распознавание объектов.

В задачах на распознавание объектов требуется ответить на вопрос: принадлежит тот или иной объект объему данного понятия или не принадлежит.

Решают такие задачи, используя определение соответствующего понятия. При этом важно понимать, что если понятие а определено через родовое понятие с и видовое отличие Р, то его объем А можно представить в таком виде: А = Эта запись показывает, что характеристическое свойство элементов, принадлежащих объему понятия а, представляет собой конъюнкцию двух свойств:

1) принадлежности объекта х объему С родового понятия (х ∈С);

Луч ВD на рисунке а) не является биссектрисой угла АВС, поскольку он не делит данный угол пополам. Луч ВD на рисунке б) является биссектрисой угла АВС, поскольку он делит данный угол пополам и выходит из вершины угла.

Если видовое отличие представляет собой конъюнкцию свойств, т.е. Р = Р₁∧Р₂∧…∧Рn, то распознавание проводится по следующему правилу: проверяют поочередно наличие у объекта каждого из свойств Р₁, Р₂, …, Рn; если окажется, что он не обладает каким-либо из этих свойств, то проверку прекращают и делают вывод о том, что объект не обладает свойством Р; если же окажется, что все свойства Р₁, Р₂, …, Рn присущи данному объекту, то заключают, что объект обладает свойством Р.

Если видовое отличие представляет собой дизъюнкцию свойств, т.е. Р = Р₁∨Р₂∨…∨Рn, то распознавание проводится по следующему правилу: проверка проводится до тех пор, пока не будет установлено, что хотя бы одно из свойств присуще данному объекту, на основании чего заключают, что объект обладает свойством Р. Если окажется, что он не обладает ни одним из свойств Р₁, Р₂, …, Рn, то проверку прекращают и делают вывод о том, что объект не обладает свойством Р.

В математике рассматривают не только конъюнкцию и дизъюнкцию высказываний, но и выполняют соответствующие операции над высказывательными формами (предикатами).

Пусть на множестве Х заданы две высказывательные формы А(х) и В(х).

Конъюнкцией высказывательных форм А(х) и В(х), заданных на множестве Х, называется высказывательная форма А(х) В(х), заданная на том же множестве Х, истинная при тех значениях х Х, при которых обе формы А(х) и В(х) истинны одновременно.

Например, конъюнкцией высказывательных форм А(х): «х>2 и В(х): «х 2 и х а и х

Таким образом, нестрогое неравенство вида х≥а (х≤а) является дизъюнкцией неравенства х>а (х

Если Т_А – множество истинности высказывательной формы А(х), хÎХ, а Т_В – множество истинности высказывательной формы В(х), хÎХ, то множеством истинности Т_{А В} высказывательной формы А(х) В(х), хÎХ, является объединение множеств истинности данных высказывательных форм А(х) и В(х), т.е. Т_{А В} = Т_А Т_В.

Выясним, как строить отрицание конъюнкции и дизъюнкции высказывательных форм А(х) и В(х), заданных на множестве Х. Используя законы де Моргана, рассмотренные и доказанные в пункте 2.3 настоящего пособия, а именно: =`А `B, =`А `B,сформулируем правило построения отрицания конъюнкции А(х) ÙВ(х) и дизъюнкции А(х) В(х) высказывательных форм, заданных на множестве Х.

Рассмотрим примеры образования отрицаний конъюнкции и дизъюнкции высказывательных форм.

т.е. дополнение множества истинности конъюнкции высказывательных форм А(х) и В(х) равно объединению дополнений к множествам истинности каждой высказывательной формы.

т.е. дополнение множества истинности конъюнкции высказывательных форм А(х) и В(х) равно объединению дополнений к множествам истинности каждой высказывательной формы.

Свидетельство и скидка на обучение каждому участнику

Зарегистрироваться 15–17 марта 2022 г.

Лекция 8. Конъюнкция и дизъюнкция высказываний.

Для задания таких связок удобно записывать таблицы истинности:

Согласно определению, конъюнкция двух элементарных высказываний истинна только в том случае, когда истинны оба высказывания, ее образующие (строка 1), и ложна в любом другом случае (строка2,3,4).

КОНЪЮНКЦИЯ А = истинна только тогда, когда Петя любит физику, а математику не любит. В остальных трех случаях, т.е. когда Петя:

не любит математику и не любит физику,

любит математику и физику,

любит математику, но не любит физику

высказывание А В ложно.

Таблица истинности для дизъюнкции имеет вид:

Дизъюнкция А VВ = будет истинной, если на первом уроке будет литература (вторая строка таблицы истинности) или математика (третья строка таблицы истинности), и ложной, если на первом уроке будет любой другой предмет или если урока вообще не будет (четвертая строка таблицы истинности).

Согласно Единой спортивной квалификации и высказывание А, и высказывание В истинны, следовательно, и дизъюнкция их истинна (1-я строка таблицы истинности).

Задания для самостоятельной работы по теме:

Определите значение истинности следующих высказываний:

2. Составьте 2-4 сложных высказывания на конъюнкцию, определите их истинность.

3. Определите значение истинности высказываний А,В, если:

4. Сформулируйте и запишите в виде конъюнкции условие истинности каждого предложения

(а, в ϵ R ): а) а×в≠0; б) а÷в=0; в) а 2 + в 2 = 0;

Определите значение истинности следующих высказываний:

5. Составьте 2-4 сложных высказывания на дизъюнкцию, определите их истинность.

6. Определите значение истинности высказываний С и D, если:

7. Сформулируйте и запишите в виде дизъюнкции условие истинности каждого предложения (а, в ϵ R ):а) а × в = 0, б) >2.

Математическая логика — это раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.

Алгебра высказываний

Логические операции

Операции над высказываниями задают в виде таблиц, называемых таблицами истинности.

Отрицание высказывания

Конъюнкция высказываний

Дизъюнкция высказываний

В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.

Импликация высказываний

Эквивалентность высказываний

Если в выражении присутствуют арифметические операции, операции сравнения и логические операции, то порядок старшинства операций следующий:

• • сначала выполняются арифметические операции (порядок старшинства арифметических операций: первыми выполняются все операции умножения и деления, потом операции сложения и вычитания);
• • затем — операции и операции сравнения (в том порядке, в каком они встречаются в выражении):
• • наконец, логические операции, причем первой везде выполняется операция отрицания, затем конъюнкции, потом дизъюнкции и т. д.

Использование различных операций позволяет в удобной аналитической форме задавать различные множества.

Например, множество точек А, заштрихованное на рис. 1.16, может быть задано следующей формулой:

Система операций называется полной, если всякая формула эквивалентна некоторой формуле, в которую входят только операции из системы . Система введенных пяти операций (отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности) полная, хотя вообще говоря, избыточна, так как одни логические операции могут быть выражены через другие. Например, импликация и эквивалентность можно выразить через отрицание, конъюнкцию и дизъюнкцию следующим образом:

Булевы функции

выражает функцию от переменных А, В и С.

Наиболее важные тождественно истинные формулы получили название Основные законы математической логики.

Основные законы математической логики

1.Коммутативность

2.Ассоциативность

3.Дистрибутивность

4.Законы де Моргана

5.Закон поглощения

6.Закон идемпотентности

8.Закон противоречия

9.Закон исключения третьего

10.Закон двойного отрицания

Пример:

Упростить выражение, используя тождественны преобразования

Существует бесконечное множество тавтологий. Некоторы из них легли в основу методов доказательства.

Основные методы доказательств

При построении любой теории выделяется некоторый набор высказываний, так называемых аксиом, истинность которых постулируется. Из аксиом чисто логическим путем может был установлена истинность некоторых других высказываний называемых теоремами. Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством. Высказывание, которое можно доказать, называется теоремой.

Формально каждая теорема может быть выражена в форме импликации где посылка А называется условием теоремы, а следствие В — заключением. Теорема верна, если выражающая ее импликация тождественно истинна, т. е. является тавтологией. Тавтологии рассматривают как некоторые логически истинные схемы рассуждений. В этой связи тавтологии играют роль законов, определяющих построение правильных умозаключений. Существует бесконечное множество тавтологий. Некоторые из них легли в основу методов доказательства. Основные методы доказательств.

Метод цепочек импликаций

Метод цепочек импликаций состоит в том, что из посылки А страивается цепочка из -импликаций, последним высказыванием в которой является заключение теоремы В, т. е.

В основе этого метода лежит закон цепного высказывания или закон силлогизма

Метод от противного

Метод необходимого и достаточного

а) доказывается, что если имеет место А, то справедливо В (В необходимо для А);

б) если имеет место В, то имеет место и А (В достаточно для А).

Доказательство таким методом базируется на законе тавтологии:

Алгебра предикатов

Предикатом заданным на множествах

Рассмотрим примеры, одноместный предикат на множестве комплексных чисел, при этом, например, если истинное высказывание, а

Логические операции над предикатами

Отрицание предиката

Пусть предикат задан на множествах Предикат называется отрицанием предиката тогда и только тогда, если при одних и тех же кортежах высказывание истинно, когда ложно и наоборот. Обозначение

Конъюнкция предикатов

Пусть на множествах заданы два — местных предиката и . Конъюнкцией этих предикатов называется предикат

который истинен для одних и тех же кортежей только тогда, когда оба предиката — и и истинны.

Дизъюнкция предикатов

Импликация предикатов

Эквивалентность предикатов

Квантор существования

Квантор существования есть операция, которая предикат превращает в высказывание: «существует хотя бы один

Кванторы обладают свойствами, являющимися аналогами законов де Моргана:

Переход от или называется квантификацией или связыванием переменной . Связанная переменная фактически не является переменной, т. е. переход от или от не меняет истинности выражений. Навешивание переменной на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных

Связывая обе переменные данного предиката, получим высказывания:

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Читайте также:

  

• Прощание с елкой в детском саду сценарий

  

• Переселенческая политика это кратко

  

• Итоги рейтингования детских садов воронежской области в 2021 году

  

• Виды готовности ребенка старшего дошкольного возраста к школьному обучению по логиновой

  

• Понятие замкнутого круга расходов кратко

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Высказывание и высказывательные формы

• 

  2 слайд

  План:
  1. Высказывания и высказывательные формы (предикат)
  2. Конъюнкция и дизъюнкция высказываний
  Математические предложения
  Изучая реальные процессы, математика описывает их, используя как естественный словесный язык, так и свой символический. Описание строится при помощи предложений. Но чтобы математические знания правильно отражали окружающую нас реальность, эти предложения должны быть истинными.
  Каждое математическое предложение характеризуется содержанием и логической формой (структурой), причем содержание неразрывно связано с формой, и нельзя осмыслить первое, не понимая второго.

• 

  3 слайд

  1. Высказывания и высказывательные формы

  Относительно понятий и отношений между ними можно высказывать различные суждения. Языковой формой суждений являются повествовательные предложения. Например, в начальном курсе математики можно встретить такие предложения:
  1) число 12 – четное;
  2) 2 + 5 > 8;
  3) х + 5 = 8;
  4) В числе 15 один десяток и 5 единиц;
  5) От перестановки множителей произведение не изменяется;
  6) Некоторые числа делятся на 3.

• 

  4 слайд

  Видим, что предложения, используя в математике, могут быть записаны как на естественном (русском) языке, так и на математическом, с использованием символов. Далее, о предложениях 1, 4, 5 и 6 можно сказать, что они несут верную информацию, а предложение 2 – ложную. Относительно предложения х + 5 = 8 вообще нельзя сказать: истинное оно или ложное. Взгляд на предложение с позиции – истину или ложь оно нам сообщает – привел к понятию высказывания.
  Определение. Высказыванием в математике называют предложение, относительно которого имеет смысл вопрос: истинно оно или ложно.

• 

  5 слайд

  Например, предложения 1, 2, 4, 5 и 6 – высказывания, причем предложения 1, 4, 5 и 6 – истинные, а 2 – ложное.
  Высказывания принято обозначать прописными буквами латинского алфавита: А, В, С, …, Z. Если высказывание А истинно, то записывают: А – «и», если же высказывание А – ложно, то пишут: А – «л».
  «Истина» и «ложь» называются значениями истинности высказывания. Каждое высказывание либо истинно, либо ложно, быть одновременно тем и другим оно не может.

• 

  6 слайд

  Предложение х + 5 = 8 не является высказыванием, так как о нем нельзя сказать: истинно оно или ложно. Однако при подстановке конкретных значений переменной х оно обращается в высказывание: истинное или ложное. Предложение х + 5 = 8 называется высказывательной формой. Оно порождает множество высказываний одной и той же формы.
  По числу переменных, входящих в высказывательную форму, различают одноместные, двухместные и т.д. высказывательные формы и обозначают: А(х), А(х, у) и т.д. Например, предложение «Прямая х параллельна прямой у» – двухместная.
  Определение. Одноместной высказывательной формой, заданной на множестве Х, называется предложение с переменной, которое обращается в высказывание при подстановке в него значений переменной из множества Х.
  Множество Х – множество, из которого выбираются значения переменной.

• 

  7 слайд

  Среди всех возможных значений переменной нас в первую очередь интересуют те, которые обращают высказывательную форму в истинное высказывание. Множество таких значений переменных называют множеством истинности высказывательной формы. Например, множеством истинности высказывательной формы х > 5, заданной на множестве действительных чисел, будет промежуток (5; ∞). Множество истинности высказывательной формы х + 5 = 8, заданной на множестве целых неотрицательных чисел, состоит из одного числа 3.
  Условимся обозначать множество истинности высказывательной формы буквой Т. Тогда, согласно определению, всегда Т⊂Х.

• 

  8 слайд

  Предложения, которые мы рассматривали, были простыми, но можно привести примеры суждений, языковой формой которых будут сложные предложения. Например: «Если треугольник равнобедренный, то углы при основании в нем равны». Естественно возникает вопрос: как определить значение истинности таких высказываний и находить множество истинности таких высказывательных форм?
  Чтобы ответить на эти вопросы, необходимо познакомиться с некоторыми логическими понятиями.
  В логике считают, что из двух данных предложений можно образовать новые предложения, используя для этого союзы «и», «или», «если… , то», «тогда и только тогда, когда», а также частица «не» или словосочетание «неверно, что». Слова «и», «или», «если…, то», «тогда и только тогда, когда», а также частица «не» называют логическими связками. Предложения, образованные из других предложений с помощью логических связок, называют составными. Предложения, не являющиеся составными, называют элементарными.

• 

  9 слайд

  Приведем примеры составных предложений.
  1) Число 28 четное и делится на 7.
  2) Число х меньше или равно 8.
  3) Число 14 не делится на 4.
  Эти предложения, являясь с логической точки зрения составными, по своей грамматической структуре – простые.
  Как определить значение истинности составного высказывания, например, «число 28 делится на 7 и на 9»? Значение истинности высказываний определяется с помощью определенных правил. Но для этого нужно уметь выявлять логическую структуру высказывания.
  Для этого нужно установить:
  1) из каких элементарных предложений образовано данное составное предложение;
  2) с помощью каких логических связок оно образовано.

• 

  10 слайд

  2. Конъюнкция и дизъюнкция высказываний

  Определение.Конъюнкцией высказываний А и В называется высказывание А∧В, которое истинно, когда оба высказывания истинны, и ложно, когда хотя бы одно из высказываний ложно.
  Обозначают А∧В (читают: «А и В»).
  Определение конъюнкции можно записать с помощью таблицы, называемой таблицей истинности.

• 

• 

  12 слайд

  Используя данное определение, найдем значение истинности высказывания «число 28 делится на 7 и на 9», которое, как было установлено раньше, состоит из двух элементарных высказываний, соединенных союзом «и», т.е. является конъюнкцией.. Так как первое высказывание истинно, а второе ложно, то, согласно определению конъюнкции, высказывание «число 28 делится на 7 и на 9» будет ложным.

• 

  13 слайд

  Определение. Дизъюнкцией высказываний А и В называется высказывание А∨В, которое истинно, когда истинно хотя бы одно из этих высказываний, и ложно, когда оба высказывания ложны.
  Высказывание образовано с помощью союза «или»: А∨В (читают А или В).
  Используя данное определение, найдем значение истинности высказывания «число 28 делится на 7 или на 9». Так как это предложение является дизъюнкцией двух высказываний, одно из которых истинно, то, согласно определению дизъюнкции, высказывание «число 28 делится на 7 и на 9» будет истинным.
  В математике союз «или» используется как неразделительный.
  Образование составного высказывания с помощью логической связки называется логической операцией.

• 

  14 слайд

  Выполнить упражнения

• 

  15 слайд

  Выполните упражнения
  7.В следующих составных предложениях выделите составляющие их элементарные предложения и логические связки:

• 

  16 слайд

  Выполните упражнения

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 256 832 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»

• Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»

• Курс профессиональной переподготовки «Организация логистической деятельности на транспорте»

• Курс повышения квалификации «Экономика: инструменты контроллинга»

• Курс повышения квалификации «Финансы: управление структурой капитала»

• Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»

• Курс повышения квалификации «Мировая экономика и международные экономические отношения»

• Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»

• Курс профессиональной переподготовки «Уголовно-правовые дисциплины: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»

• Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»

• Курс профессиональной переподготовки «Управление качеством»