Как найти множество натуральных чисел - Сайт, где вы сможете решить свои вопросы

Множества чисел бывают конечными или бесконечными и их принято обозначать большими буквами A, B, …, а их элементы – маленькими буквами, например, x, y, z,….

Что такое множество чисел

Термин множества чисел можно описать, как совокупность, объединение, набор некоторых объектов произвольной природы – элементы множества. Например, множество книг в библиотеке, множество студентов факультета, множество парных чисел, множество точек заданного отрезка и т. п.

Если элемент принадлежит множеству , тогда пишут , если же элемент не принадлежит множеству , тогда пишут, что или .

Множества, в которых нет ни одного элемента, называется пустым множеством и обозначается .

Рассмотрим несколько важных операций:

1. Два множества и называются равными (обозначают ), если они состоят из одинаковых элементов.

2. Множество называется подмножным множеством , если каждый элемент множества есть элементом множества .

Это обозначается так: и читается содержится в или в находится . Очевидно, что пустое множество входит в любое множество .

Например, если множество состоит из элементов обозначают:

= {}), а в = {} тогда .

3. Множества элементов , которые принадлежат множеству или множеству , или и , называется объединением этих множеств и обозначается .

4. Множества элементов , которые принадлежат двум множествам и называется пересечением множеств и и обозначается

Если, например, и – это множества точек, что принадлежат двум фигурам соответственно, тогда схематически на рис. 1 изображены их объединения в случаях а) и б). На рис. 2 изображено пересечение множеств и .

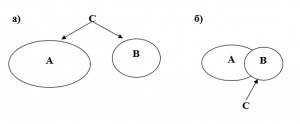
Рис. 1

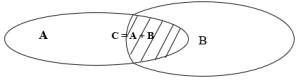
Рис. 2

5. Разницей множеств A и называется множество , что содержит те элементы , которые не есть элементами множества (см. рис. 3).

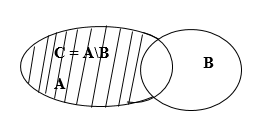
Рис. 3

Виды чисел

Существует 7 видов чисел:

1. Натуральные – ;

2. натуральные числа, в которые включается нуль – $N_{0}$ ;

3. целые числа – ;

а) целые положительные числа – $Z^{+}$ ;

б) целые отрицательные числа – $Z^{-}$ ;

4. рациональные числа – ;

5. иррациональные числа

6. Действительные числа – ;

7. Комплексные числа – .

Рассмотрим каждый вид числа более подробно:

1. Натуральные числа всегда используются при естественном счёте или перечислении предметов, вернее при их нумерации, то есть “первый”, “второй”, “третий”. Описывается множество натуральных чисел так:

= {1, 2, 3, …, }.

2. Натуральные числа, в которые включён нуль используются для обозначения количества предметов:

= {0, 1, 2, 3, …}

3. Целые числа – это числа, в которые входят натуральные числа с положительным и отрицательным знаками:

а) целые положительные числа (обозначаются $Z^{+}$ ) и пишутся: $Z^{+} = N =$ {1, 2, 3, …};

б) целые отрицательные числа (обозначаются $Z^{-}$ ) и пишутся: $Z^{-} = N$ {…, -3, -2, -1};

$Z = Z^{-}cup {0}cup{Z^{+}}$ = {…, -3, -2, -1, 0, 1, 2, 3, …}.

4. Рациональные числа – числа, которые представляются в виде обыкновенной дроби , где и – целые числа, а . Рациональные числа обозначаются латинской большой буквой :

= {}. Если переводить в десятичную дробь, тогда рациональное число может представляться конечной и бесконечной дробью.

5. Иррациональные числа – вещественное число, которое не рациональное и не может представляться в виде десятичной дроби.

6 Действительные числа или вещественные – это числа, в которых объединяются рациональные и иррациональные числа ().

7. Комплексные числа – это числа, в которых содержится – мнимая единица:

= { и }.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Подробнее

Примеры решения задач

Задача

Записать множество , если , причём = {2, 4, 6, 8, 10, 12}, = {3, 6, 9, 12}.

Решение

есть не что иное, как объединение множеств и , то есть, множество будет состоять из элементов, принадлежащих как множеству , так и множеству : = {2, 3, 4, 6, 8, 9, 10, 12}.

Ответ

Множество состоит из элементов, которые принадлежат двум множествам и .

Задача

Все студенты курса изучают разные иностранные языки. Значит, из них, 91 студент изучает английский язык, ещё 96 студентов изучают немецкий язык, 94 студента изучают исключительно французский язык, 36 студентов изучают не только английский, но и немецкий языки, ещё 32 студента изучают английский и французский языки, а 10 студентов занимаются изучением всех языков без исключения.

Вопрос: сколько студентов занимаются изучением немецкого и французского языков, если всего на курсе по списку 189 студентов?

Решение

Итак, для начала введём обозначения:

– множество всех студентов, которые находятся на данном курсе;

$A_{1}$ – множество студентов, которые изучают только английский язык;

$A_{2}$ – множество студентов, которые занимаются изучением немецкого языка;

$A_{3}$ – множество студентов, изучающих исключительно французский язык;

$A_{12}$ – множество студентов, которые изучают, как английский, так и немецкий язык;

$A_{13}$ – множество студентов, изучающие английский и французский языки;

$A_{23}$ – множество студентов, которіе изучают немецкий и французский язіки;

$A_{123}$ – множество студентов, которые изучают абсолютно все языки;

– количество элементов множества .

По условию задачи:

$|A| = 189, |A_{1}| = 91, |A_{3}| = 94, |A_{12}| = 36, |A_{23}| = 32, |A_{23}| = x.$

Найдём – количество студентов, которые изучают немецкий и французский языки. Согласно вышеописанному обозначению, у нас получается:

$A_{12} = A_{1}cup{A_{2}}$ , $A_{13} = A_{1}cup{A_{3}}$ , $A_{23} = A_{2}cup{A_{3}}$ , $A_{123} = A_{1}cup{A_2}cup{A_{3}}$ .

Из методов включения и исключения следует, что

$|A| = |A_{1}| + |A_{2}| + |A_{3}}| - |A_{1}cup{A_{2}}| - |A_{1}cup{A_{3}}| - |A_{2}cup{A_{3}}| - |A_{1}cup{A_{2}}cup{A_{3}}| =\ = |A_{1}| + |A_{2}| + |A_{3}| - |A_{12}| - |A_{13}| - |A_{23} + A_{123}|$ .

Ответ

студента занимаются изучением немецкого и французского языков.

Источник

Первое
числовое множество, с которым сталкиваются
учащиеся еще начальных классов –
множество натуральных чисел. В математике
существует два способа его построения.
Количественные
натуральные числа отождествляются
с мощностью непустого конечного множества
(построение по Кантору), порядковые
натуральные
числа построены на основе аксиом Пеано:

Натуральным
числом называются элементы непустого
конечного множества N,
в котором существует отношение
«непосредственно следует за» и
выполняются аксиомы:

1.
Существует натуральное число единица,
не следующее ни за каким натуральным
числом.

2. За
каждым натуральным числом следует одно
и только одно натуральное число.

3.
Всякое натуральное число, кроме единицы,
следует за одним и только одним
натуральным числом.

4.
Пусть М подмножество множества N. Если
1
,
и из допущения, что натуральное число
пМ следует, что М принадлежит и п (число,
непосредственно следующее за п), тоM
N.

В
школьном курсе математики на
наглядно-интуитивной основе представлены
оба эти способа: каждое новое число
появляется из анализа количества
предметов, представленных на рисунках,
а далее довольно четко выясняется и
упорядоченность, и дискретность
множества натуральных чисел.

Термин
«натуральное число» ввел римский автор
Боэций (475 – 524). Систематическое изучение
натуральных чисел начинается в 5-м
классе. Основная цель темы «Натуральные
числа» – обобщение и закрепление тех
сведений о множестве натуральных чисел,
которые получены учащимися еще в
начальной школе. Особое внимание
уделяется позиционной записи любого
натурального числа, выполнению
поразрядного сравнения натуральных
чисел. Вводятся символы = , >, <.

При
изучении арифметических операций над
натуральными числами учителю
необходимо достаточно отчетливо
представлять себе различие
в требованиях к технике вычислений, к
обоснованию этой техники и теории
операций. К
технике вычислений
надо предъявлять самые жесткие требования
– это основа (фундамент) всей вычислительной
культуры учащихся. Твердого обоснования
техники выполнения операций требовать
не следует. Достаточно, если учащиеся
будут выполнять эти операции и
пользоваться их свойствами («на» –
сложение или вычитание, «в» – умножение
или деление). Наиболее дифференцированно
приходится подходить к теории
самих операций.

Понятие
сложения вообще
не определяется и считается интуитивно
ясным из опыта предшествующего
обучения. Хотя понятие вычитания
тоже
интуитивно ясно учащимся, но относительно
него вводится строгое
определение, которое
остается неизменным для всех числовых
и даже нечисловых множеств (вычесть из
числа а
число в
– это значит найти такое число с, которое,
будучи сложенным с числом в,
даст число а).
Операция умножения
вводится
специальным
определением, справедливым
лишь на множестве

N ( а *
в = а+а+…+а).
Деление
опять
строго определяется ( а:в = с <=> с*в =
а).

в
раз

Хотя
глава и называется «Натуральные числа»,
фактически же в ней изучаются целые
неотрицательные числа. И здесь ученики
должны твердо усвоить двоякий смысл
термина «нуль» (нуль – цифра и нуль –
число). Поэтому необходимо научиться
оперировать с нулем : 0+а = а; а+0 = а; 0*а =
0; а*0 = 0; 0:а = 0; обоснование невозможности
деления на нуль в учебнике Н.Я. Виленкина
проводится на основании определения
операции деления: а:0 = х <=> х*0 = а, что
неверно, 0:0 = х <=> х*0 = 0, но в качестве
х можно взять любое число.

Лучшему
усвоению учащимися множества натуральных
чисел способствует изучение некоторых
вопросов делимости. По отношению
делимости на данное натуральное
число n
множество N разбивается на два
непересекающихся класса: натуральные
числа, делящиеся на n
и натуральные числа, не делящиеся на n.
По числу делителей – {простые},
{составные}, {1}. Рассматриваются признаки
делимости на 2, 3, 5, 9, 10 и деление с остатком.

В результате
изучения натуральных чисел у учащихся
на наглядно-интуитивной основе должно
быть сформировано:

знание
свойств натуральных чисел (множество
N – бесконечно, дискретно, упорядоченно,
ограничено снизу);
понимание
того факта, что операция умножения на
N не определяется;
определение
операции
вычитание,
умножение и деление;
умение работать
с числами 0 и 1.

Теоретический
материал в учебниках излагается в виде
фрагментов, а затем идет решение задач
и примеров.

В учебнике 5-го
класса приводятся определения следующих
понятий:

– натуральное
число, десятичная запись числа, миллиард,

– координатный
луч,

– сумма, разность,
произведение двух натуральных чисел,

– числовое выражение,

–
делитель числа, кратные числа,

– совершенное
число, простое число, дружественные
числа.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Введем понятие множества натуральных чисел. Начнем со следующего, используя число 1, названное единицей, построим некоторое подмножество множества следующим образом: обозначим сумму символом 2 и назовем его числом «два» ; обозначим сумму символом 3 и назовем его числом «три» ; аналогично определяем последовательно числа, называемые «четыре», «пять», и т.д. и обозначаемые символами и т.д.

Элементы множества

называются натуральными числами. Множество всех натуральных чисел обозначают через .

Обозначим через произвольно фиксированное натуральное число число называется числом, непосредственно следующим за числом , а само — непосредственно предшествующим числу .

Свойства натуральных чисел

Множество натуральных чисел обладает следующим свойством.

Если множество таково, что: ; ; следует, что , то

В самом деле, по условию 2) поэтому, согласно свойству 3) и и и т.д. Но любое натуральное число получается из 1 последовательным переходом от предыдущего натурального числа к последующему, поэтому , т.е. .

Итак, имеем и . По определению это означает, что .

Из свойства 2 следует так называемый принцип доказательства методом математической индукции.

Если имеется множество утверждений, каждому из которых соответствует натуральное число (его номер) и если доказано, что:

1) справедливо утверждение с номером 1;

2) из справедливости утверждения с произвольным номером следует справедливость утверждения с номером , то тем самым доказана справедливость всех рассматриваемых утверждений.

Операции натуральными числами

Операция сложения. Пусть — произвольное натуральное число. Если — какое-нибудь число из , то

Так, по индукции определяется операция, называемая сложением натуральных чисел. Например,

Операция умножения. Пусть — произвольное натуральное число. Если — какое-нибудь число из , то

Так, по индукции определяется операция, называемая умножением натуральных чисел. Например,

Для любых из и

В самом деле, при формула справедлива согласно аксиоме 2.5. Пусть равенство верно при . Покажем, что она справедлива при

$[(a_1 + a_2 +...+a_{k+1})b = [(a_1 +...+a_k) + a_{k+1}]b =]$

$[= (a_1 +...+a_k)b + a_{k+1}b = a_1b +...+ a_kb + a_{k+1}b.]$

В частности если , то

Множество целых чисел

Натуральные числа, им противоположные и нуль называются целыми числами.

Множество всех целых чисел обозначается через .

Множество рациональных чисел

Частные , где называются рациональными числами (от лат. — отношение). Множество всех рациональных чисел обозначается через .

Множество иррациональных чисел

Действительные числа, не являющиеся рациональными, называются иррациональными (от лат. — неразумный, от — отрицательная приставка к — число не являющееся рациональным. Множество всех иррациональных чисел обозначается через .

Таким образом,

Число , умноженное раз на себя, называется n-й степенью числа и обозначается через . Таким образом,

$[x^nstackrel{def}{=}underbrace{ x cdot x cdot ... cdot x}_{n};;;;;(1.5)]$

Число в степени называется основанием степени, а — показателем степени.

Для любых и полагают

$[x^0 stackrel{def}{=} 1, x^{-n} stackrel{def}{=}frac{1}{x^n} ;;;;;(1.6)]$

( не определяется).

Если то

$[x^m cdot x^n = x^{m+n}, {(x^n)}^m = x^{nm} ;;;;;(1.7)]$

для любого при и и для любого и при и .

$[x^mcdot x^n ={m} underbrace {xcdot x cdot ...cdot x}_{n} =underbrace{ x cdot x cdot ... cdot x}_{m+n} =x^{m+n}]$

$[x^mcdot x^n = x^0cdot x^n=1cdot x^n=x^n=x^{0+n}=x^{m+n};]$

$[x^mcdot x^n = x^mcdot x^0=x^mcdot 1=x^m=x^{m+0}=x^{m+n};]$

Пусть причем тогда

$[x^m cdot x^n = frac {1}{x^p} cdot x^n = frac {1}{x^p} cdot underbrace{ x cdot x cdot ... cdot x}_{p} underbrace{ x cdot x cdot ... cdot x}_{n-p } =]$

$[= {1}{x^p}cdot x^pcdot x^{n-p}=1cdot x^{n-p}=x^{n-p}=x^{n+m}.]$

Если же то в соответствии с 4.4

$[x^m cdot x^n = frac{1}{x^p} cdot x^n = frac{1}{x^n cdot x^{p-n}} cdot x^n = frac{1}{x^n} cdot frac{1}{x^{p-n}} cdot x^n = frac{1}{x^{p-n}} =]$

$[=frac{1}{x^{-m-n}} = x^{m+n}.]$

— аналогично)

Полагая и используя снова 4.4, получим:

$[x^m cdot x^n = frac{1}{x^p} cdot frac{1}{x^q} = frac{1}{x^p cdot x^q} = frac{1}{x^{p+q}} = frac{1}{x^{-m-n}} = x^{m+n}.]$

4.6. Если то

Действительно,

Источник

Множеством называют математическую единицу, которая подчиняется определенным правилам и законам. Оно обладает различными функциями и свойствами. Если элементами в нем являются числа, то речь идет о числовом множестве. Множества чисел могут быть конечными и бесконечными. Для их обозначения применяются большие буквы A, В…., элементы множеств обозначаются маленькими буквами, такими как x, y, z,….

Что такое множество чисел?

Математический термин «множество» можно охарактеризовать как отдельную совокупность, набор или объединение. Его элементами в теории могут быть различные объекты произвольной природы. К примеру, термин множество можно применить к большому количеству книг в библиотеке, товаров на полках магазина, студентов университета и т.д. В математике используются такие понятия, как множество точек отрезка заданной длины или множество парных чисел.

Для их математического обозначения используется определенный метод. В случае, когда какой-то элемент [x] принадлежит множеству A, тогда, тогда следует записывать [x in(A)], если же ситуация обратная и элемент [y] не принадлежит множеству A, то правильно будет записать [y notin(A)] или [y bar{in}(A)].

Если в множестве нет ни одного элемента, то его принято называть пустым множеством. Оно обозначается [phi].

Для того, чтобы понять суть числовых множеств, рассмотрим несколько важных характеристик:

Два отдельных множества A и B будут называть равными и обозначаться A=B в том случае, если составляющие их элементы полностью идентичные.
Множество A будет называться подмножным множеством B в случае, когда каждый из элементов множества A является элементом второго множества B. В этой случае используются следующее обозначение [A subset(B)]. Оно читается как A содержится в B, либо в B находится A.Очевидным является тот факт, что абсолютно в любое множество входит пустое множество [emptyset subset A]. Приведем пример. Если в состав множества A входят элементы 1, 2, 3, 4, 5, 6, 7, 8, 9, то оно записывается в виде: A={1, 2, 3, 4, 5, 6, 7, 8, 9}, а в B={2,3 ,5 ,7,9} тогда [B subset(A)].
Объединением множеств называют случаи, когда множества элементов C, принадлежащих множеству A либо множеству B, или одновременно A и B. Обозначается объединение множеств следующим образом: [C=cup(B)].
Пересечением множеств A и B в математике называют множества элементов C, принадлежащих сразу двум множествам A и B. Обозначается пересечение так: [C=A cap(B)].

В случае, если A и B — это два множества точек, которые принадлежат двум геометрическим фигурам соответственно, тогда варианты их объединения будут выглядеть следующим образом:

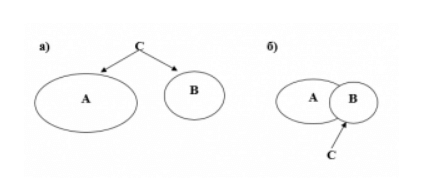
Если произойдет пересечение множеств A и B, то выглядеть это будет так:

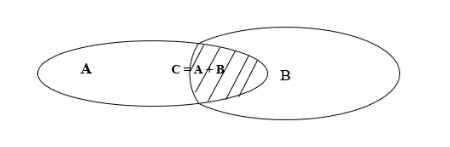
Разницей множеств A и B принято называть отдельное множество C = A | B, которое содержит все элементы A, которые не являются элементами, принадлежащими множеству B.

Нет времени решать самому?

Наши эксперты помогут!

Виды чисел

В математике все числа разделяются на 7 разных видов:

натуральные – N;
натуральные, включающие нуль – N_{0};
целые – Z;
- целые отрицательные – Z^{-};
- целые положительные – Z^{+};
иррациональные;
рациональные – Q;
комплексные – C;
действительные – R.

Рассмотрим более подробно каждый из перечисленных видов чисел:

Основным отличием натуральных чисел является то, что они применяются при перечислении различных предметов или естественном счете. Проще говоря, при нумерации – «первый», «второй», «третий», «четвертый» и т.п. Множество натуральных чисел описывается следующим образом: N={1,2,3,4,5, ….}.

Натуральными числами, включающими нуль обозначаются определенные количества каких-либо предметов: N={0,1,2,3,4,5…}.

Целыми называют числа, входящие в числа с отрицательными и положительными знаками:

обозначение целых отрицательных чисел выглядит следующим образом: Z^{- }и пишется Z^{-}=N={…,-5,-4,-3,-2,-1};

целые положительные числа в свою очередь обозначаются Z^{+} и записывается Z^{+}=N={1,2,3,4,5…}.

[begin{gathered}
Z=Z^{{-}} cup{O} cupleft{Z^{{+}}right}= \
{ldots-5,-4,-3,-2,-1,0,1,2,3,4,5 ldots}
end{gathered}]

Иррациональными называют вещественные числа, которые на являются рациональными и не могут никогда представляться в виде десятичных дробей.

Рациональными называют те числа, которые можно представить в виде обыкновенной дроби, имеющей вид m/n, где m и n — это целые числа, а [n neq{0}]. Для обозначения рациональных чисел в математике используется большая буква Q.

[Q=left{x mid x=frac{m}{n}, m in{Z}, n in{Z}, n neq{O}right}]

При переводе в десятичную дробь каждое рациональное число может представляться в виде бесконечной или конечной дроби.

Комплексными принято называть числа, в которых содержится мнимая единица i.

[C={mathrm{x}+i y / mathrm{x} in{R} u y in{R}}]

Действительные числа также называют вещественными. В них объединяются два вида чисел: рациональные (R) и иррациональные.

Примеры задач по определению множества чисел

Примеры

Необходимо записать множество D

при условии, что [D=A cup{B}], при этом [A={4,6,8,10,12},
B={6,9,12}].

Решение:

Исходя из условия [D=A cup{B}] можно сделать вывод, что это объединение множеств A и B.
Значит в множество D должны быть включены все элементы, которые присутствуют в обоих множествах
A и B. [D={4,6,8,9,10,12}].

Ответ: В множество D входят все элементы, принадлежащие двум множествам A и B.

Все студенты на курсе занимаются изучением разных иностранных языков. При этом английский язык изучают 90
студентов, а немецкий – 95 человек. Французский язык выбрали для изучения 93 человека, а одновременно
английский и немецкий – 35 студентов. 10 человек изучают все языки без исключения. Нужно узнать, сколько
студентов занимаются изучением немецкого и французского языков, если по списку на курсе

Решение

Решение задачи следует начать с введения некоторых обозначений, которые будут являться примерами множества
чисел.

A – множество студентов, которые проходят обучение на данном курсе;

A_{1} – множество студентов, изучающих исключительно английский язык;

A_{2} – множество студентов, специализирующихся на изучении немецкого языка;

A_{3} – множество студентов, которые изучают только французский;

A_{12} – множество человек, изучающих два языка (английский и немецкий);

A_{13} – множество человек, которые учат английский и французский языки;

A_{23} – множество студентов, изучающих все языки на курсе.

|B| — количество всех элементов, относящихся к множеству B.

Согласно условиям задачи, получаем выражение:

[|A|=185,left|A_{{1}}right|=90,left|A_{{3}}right|=93,left|A_{{12}}right|=35,left|A_{{23}}right|=31,left|A_{{23}}right|=x]

Далее необходимо найти x – количество человек на курсе, которые занимаются изучением французского и
немецкого
языка. Учитывая вышеописанные обозначения, приходим к следующему результату:

[A_{{12}}=A_{{1}} cupleft{A_{{2}}right}, A_{{13}}=A_{{1}} cupleft{A_{{3}}right},
A_{{23}}=\A_{{2}} cupleft{A_{{3}}right}, A_{{123}}=A_{{1}} cupleft{A_{2}right}
cupleft{A_{{3}}right}]

Применяя методы включения и исключения, приходим к выводу, что:

[|A|=left|A_{{1}}+right| A_{{2}} mid+\left|A_{{3}}-right| A_{{1}}
cupleft{A_{{2}}right}|-| A_{{1}} cupleft{A_{{3}}right}-mid
A_{{2}}\left.cupleft{A_{{3}}right}-left|A_{{1}} cupleft{A_{{2}}right} cupright|
A_{{3}}right}=\left|A_{{1}}right|+left|A_{{2}}right|+left|A_{{3}}right|-left|A_{{12}}right|-left|A_{{13}}right|-\left|A_{{23}}+A_{{123}}right|]

[185=90+95+93-35-31-x+10\185=222-x\x=37]

Ответ: 37 студентов на курсе изучают одновременно немецкий и французский языки.

Источник

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A₁, A₂ и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a₁, a₂ и т. д.

Границы совокупности обозначаются фигурными скобками { }.

Пример:

А = {а, в, с, у} – А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:

Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.

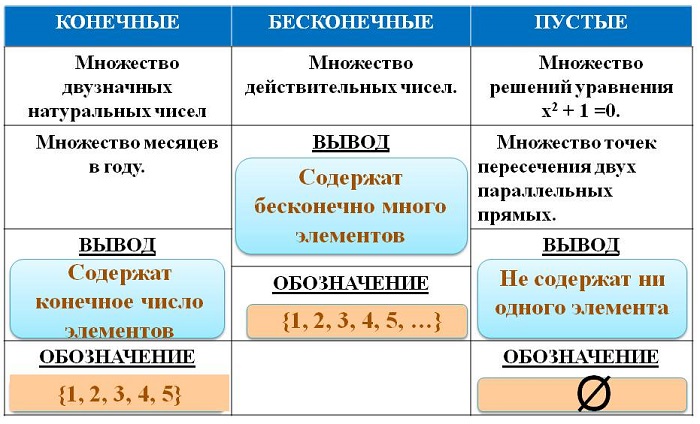
Выделяют три вида множеств:

конечные – совокупности, имеющие максимальный и минимальный предел (например, отрезок);
бесконечные – не являющиеся конечными (например, числовые);
пустые (обозначаются Ø) – не имеющие элементов.

Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком – ⊆.

Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

Множество натуральных чисел

К совокупности натуральных чисел (N) относятся цифры, используемые при счете – от 1 до бесконечности.

Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы – каждое следующее число больше предыдущего на единицу.

N = {9, 11, 13, 15……}.

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Z = {-112, -60, -25, 0, 36, 58, 256}.

Следовательно, N – подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.

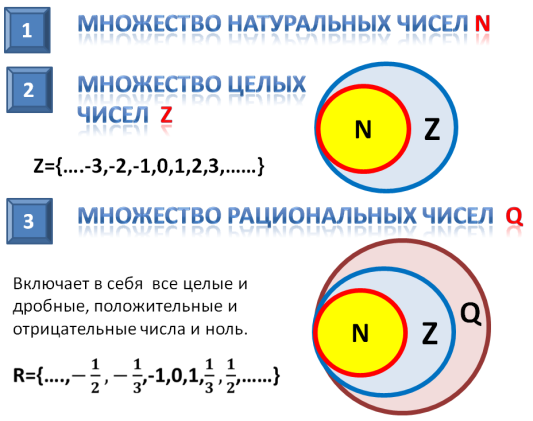
Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Q={-½; 0; ½, 5; 10}.

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

5 = 5/1 = 10/2 = 25/5;

0,45 = 45/100 = 9/20.

Следовательно, N и Z являются подмножествами Q.

Операции над множествами

Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

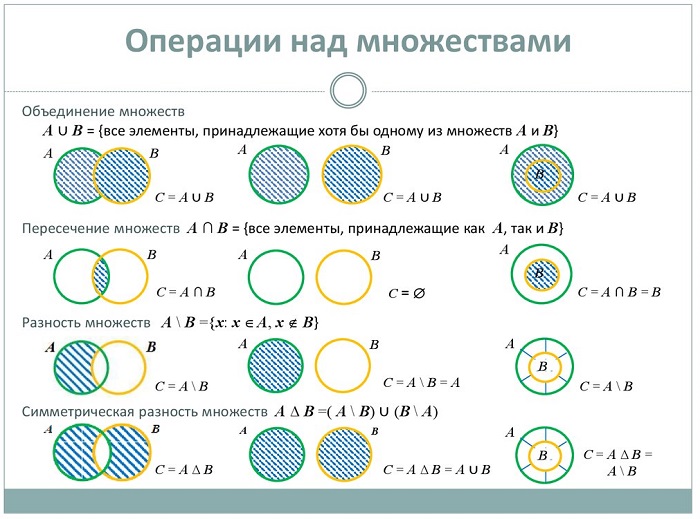
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.

Пример: В = {1, 6, 17} и С = {2, 13, 18}, В ∪ С= {1, 2, 6, 13, 17, 18}.

Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.

Пример: В = {36, 42, 53, 64} и С = {32, 42, 55, 66}, В ∩ С = {42}.

Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.

Пример: В = {12, 14, 16, 18} и С = {13, 14, 15, 17}, В / С = {14}.

В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.

Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:

Объединение

Пересечение

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.

Свойства операций над множествами

Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:

умножения S ∩ D = D ∩ S;
сложения S ∪ D = D ∪ S.

Ассоциативность – сочетательные законы:

умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).

Дистрибутивность – законы распределения:

умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).

Транзитивность – законы включения:

если S ⊆ Fи F ⊆ J, то S ⊆ J;
если S ⊆ F и F ⊆ S, то S = F.

Идемпотентность объединения и пересечения:

S ∩ S = S;
S ∪ S = S.

О других свойствах операций можно узнать из картинки:

Счетные и несчетные множества

Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

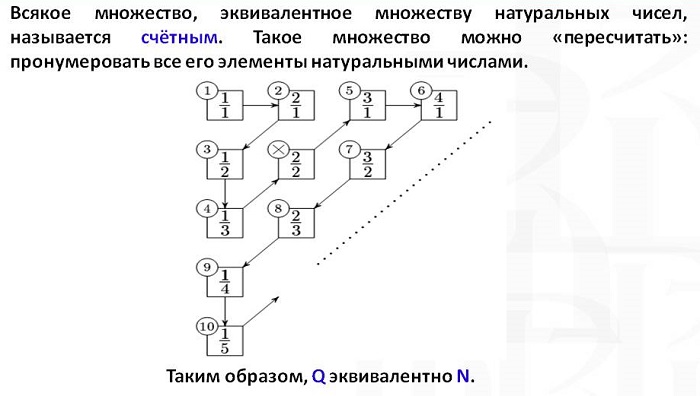
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

В случае, когда бесконечное множество равномощно натуральному ряду чисел, оно называется счетным, а если оно не равномощно – несчетным. Другими словами, счетная единица – это совокупность, которую мы можем представить в виде последовательности чисел по порядковым номерам.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.

Теория множеств – достаточно широкая тема, которая требует глубокого изучения. Она затрагивает начальный курс математики, изучается в среднем звене школьной программы по алгебре. Высшая математика, математический анализ, логика – рассматривают законы, теоремы, аксиомы множеств, на которых основаны фундаментальные знания науки.

Источник

Что такое множество чисел

Виды чисел

Примеры решения задач

Свойства натуральных чисел

Операции натуральными числами

Множество целых чисел

Множество рациональных чисел

Множество иррациональных чисел

Что такое множество чисел?

Виды чисел

Примеры задач по определению множества чисел

Что такое множество в математике и как оно обозначается

Множество натуральных чисел

Множество целых чисел

Множество рациональных чисел

Операции над множествами

Объединение

Пересечение

Дополнение

Свойства операций над множествами

Счетные и несчетные множества

Вам также может понравиться

Спина колесом как исправить у ребенка

Как найти все фото человека в интернете

Как решить задачу найти стоимость

Добавить комментарий Отменить ответ