Как найти множество предельных точек множества

Начнём с определения предельной точки множества. Пусть $%A$% — множество точек (скажем, на прямой, или на плоскости), и $%a$% — некоторая точка. Она может как принадлежать множеству $%A$%, так и не принадлежать. Для начала рассмотрим и опишем случай, когда точка $%a$% не является предельной точкой множества $%A$%. Тогда станет понятно, в каких случаях она ей является.

Допустим, что вблизи $%a$% нет других точек множества $%A$% за исключением, может быть, самой точки $%a$%, если она принадлежит $%A$%. Тогда точку $%a$% можно окружить маленькой окрестностью, в которой других точек множества не имеется. Эта окрестность задаётся числом $%varepsilon > 0$%: на прямой это будет интервал $%(a-varepsilon,a+varepsilon)$%. В этой окрестности нет точек множества $%A$% помимо точки $%a$% (а если $%anotin A$%, то и вообще ничего нет из $%A$%). В случае, если это имеет место, и $%ain A$%, такую точку называют изолированной точкой множества. Это легко представить себе наглядно: вот точка множества, а все остальные где-то “поодаль”.

Теперь рассмотрим противоположную ситуацию и опишем её словесно. Удобно исключить точку $%a$% из окрестности, чтобы не делать лишних оговорок. Тогда у нас получится множество $%(a-varepsilon,a)cup(a,a+varepsilon)$%. Оно называется проколотой окрестностью точки $%a$%. В более общем случае, если $%cal U$% обозначало какую-то окрестность точки, проколотая её окрестность будет иметь вид $%{cal U}setminus{a}$%. Иногда то же самое обозначают с “кружочком” над $%cal U$%, давая понять, что точка $%a$% этой проколотой окрестности не принадлежит.

Так вот, если мы посмотрим на определение изолированной точки, то у неё имеется проколотая окрестность, в которой нет точек множества $%A$%. И теперь, если точка $%a$% таким свойством не обладает, то в любой (сколь угодно малой) её проколотой окрестности найдётся хотя бы одна точка множества $%A$%. На наглядном уровне это означает, что в $%A$% есть точки, подходящие к $%a$% всё ближе и ближе.

Пример: $%A=[0;1)$%. Точка $%a=1$% будет предельной точкой множества $%A$%. В данном случае множеством всех предельных точек множества $%A$% будет отрезок $%[0;1]$%.

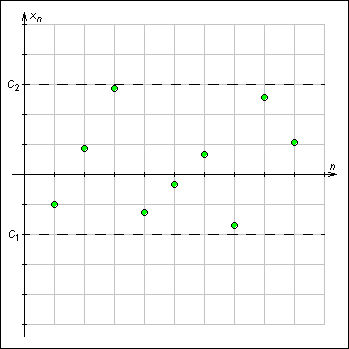
Теперь о понятиях lim sup и lim inf. С самого начала важно заметить, что эти понятия даются уже не для множества, как было выше, а для последовательности. То есть у нас есть произвольная бесконечная числовая последовательность $%a_n$%, где $%nge1$%. Объясним понятие верхнего предела этой последовательности, то есть первого из понятий. Второе будет ему аналогичным. В литературе на русском языке для верхнего предела принято использовать обозначение $%varlimsuplimits_{ntoinfty}a_n$%.

Рассмотрим несколько случаев. Первый: последовательность $%a_n$% не ограничена сверху. В этом случае верхнего предела у последовательности не существует. Иногда при этом говорят, что он равен $%+infty$%. То есть это простой случай.

Допустим теперь, что последовательность ограничена сверху, то есть множество её членов (не она сама!) имеет верхнюю грань. Заметим, что в этом случае множество также имеет и точную верхнюю грань. Пока это не нужно, но чуть позже потребуется для одного замечания. А сейчас рассмотрим второй лёгкий случай: когда наша последовательность является сходящейся, то есть имеет предел (обычный lim). Тогда он и будет верхним пределом.

Осталось рассмотреть случай, когда последовательность ограничена сверху, но предела не имеет. Типовой пример на этот счёт: 1, 2, 1, 2, … . Сама эта последовательность ни к чему не стремится, но в ней выделяются две подпоследовательности (постоянные), одна из которых стремится 1, а другая к 2. Если мы рассмотрели все такие случаи, то можно выбрать максимальное значение пределов сходящихся подпоследовательностей, и как раз оно будет верхним пределом (это к вопросу о том, как находить).

Пример, рассмотренный выше, можно чуть усложнить, беря вместо чередующихся 1 и 2 что-то вроде 1+3/n и 2-1/n. Понятно, что эти подпоследовательности будут стремиться к тем же числам (1 и 2 соответственно), и верхний предел останется равен 2. К слову сказать, нижний предел здесь будет равен 1, по тому же принципу.

Обобщим сказанное. Последовательность может не иметь предела, но какие-то её подпоследовательности могут иметь предел, то есть к каким-то числам стремиться. Надо выявить все такие случаи, и изучить, каким будет множество, как это говорят, частичных пределов последовательности (то есть пределов её подпоследовательностей). Если среди них есть наибольший, то он будет верхним пределом.

Тонкости, детали и прочее см. в учебниках или здесь. Я хочу в конце отметить, что верхний предел последовательности — это в общем случае не то же самое, что sup множества её членов. Например, последовательность $%a_n=(-1)^n/n$%, то есть -1, 1/2, -1/3, 1/4, … стремится к нулю. То есть её предел равен 0, и таковы же значения верхнего и нижнего пределов. При этом sup членов этой последовательности равен 1/2 (он же max), а inf равен -1 (он же совпадает с min).

Предельные, граничные точки.

Граничная
точка множества – точка
пространства, любая (открытая) окрестность
которой содержит как точки, принадлежащие
рассматриваемому множеству, так и не
принадлежащие ему точки (точки его
дополнения).

Граничная точка множества
может как принадлежать, так и не
принадлежать этому множеству.

Пример
1

Для
множества точек

где
n –
натуральное число, граничными служат
все эти точки и, кроме того, число 0.

Пример
2

Граничными
точками интервала (а;
b)
служат его концы – точки а
и b.

Пример
3

Для
множества рациональных чисел из отрезка
[0; 1] граничными служат вообще все точки
этого отрезка – как рациональные, так
и иррациональные. 

Пример
4

Для
множества точек М(х;
у)
плоскости, координаты которых удовлетворяют
условию

 граничными
являются точки двух концентрических
окружностей с центром в точке О(0;
0) и радиусами r
и R.
Если в условии заменить строгие
неравенства нестрогими, ответ не
изменится.

Точка
метрического пространства

называется
предельной
точкой
множества

,
если любая её окрестность содержит
бесконечно много точек из M.
Предельная точка может принадлежать,
а может и не принадлежать M.
Например, если M —
множество рациональных точек отрезка
[0;1],
то каждая точка этого отрезка является
предельной точкой множества M.

Открытые и замкнутые множества

Множество
M
на прямой называется открытым,
если каждая его точка сожержится в этом
множестве вместе с некоторым интервалом.
Замкнутым
называется
множество, содержащее все свои предельные
точки (т. е. такие, что любой интервал,
содержащий эту точку, пересекается со
множеством еще хотя бы по одной точке).
Например, отрезок является замкнутым
множеством, но не является открытым, а
интервал, наоборот, является открытым
множеством, но не является замкнутым.
Бывают множества, которые не являются
ни открытыми, ни замкнутыми (например,
полуинтервал). Существуют два множества,
которые одновременно и замкнутые, и
открытые – это пустое и все Z
(докажите, что других нет). Легко видеть,
что если M
открыто, то [M]
(или Z
M
– дополнение к множеству M
до Z)
замкнуто. Действительно, если [M]
не замкнуто, то оно не содержит какую-то
свою предельную точку m.
Но тогда m

M,
причем каждый интервал, содержащий m,
пересекается с множеством [M],
т. е. имеет точку, не лежащую в M,
а это противоречит тому, что M
– открытое. Аналогично, тоже прямо из
определения, доказывается, что если M
замкнуто, то [M]
открыто (проверьте!).

Теперь
докажем следующую важную теорему.

Теорема.
Любое открытое множество M можно
представить в виде объединения интервалов
с рациональными концами (т. е. с концами
в рациональных точках).

3) Понятие функции, график функции, способы задания, классификация.

Понятие
функции

Функция —
математическое понятие, отражающее
связь между элементами множеств. Можно
сказать, что функция это «закон», по
которому каждому элементу одного
множества (называемому областью
определения) ставится
в соответствие некоторый элемент другого
множества (называемого областью
значений).

Числовая функция —
это функция, области определения и
значений которой являются подмножествами
числовых множеств — как правило,
множества вещественных чисел

или
множества комплексных чисел

.

График
функции

Графиком
функции называется совокупность всех
точек на плоскости, прямоугольные
координаты которых х и у удовлетворяют
уравнению y=f(x). Горизонтальную ось Ох
называют осью абсцисс, вертикальную
ось Оу – осью ординат. Графическое
изображение функции имеет важное
значение для её изучения. На графике
функции часто непосредственно видны
такие её особенности, которые можно
было бы установить лишь путём длительных
вычислений. Если между величинами х и
у существует функциональная связь, то
безразлично, какую из этих величин
считать аргументом, а какую – функцией.

Существуют
разные способы задания функций.

1.
Аналитический
способ.

Аналитический
способ – это наиболее часто встречающийся
способ задания функции.

Заключается
он в том, что функция задается формулой,
устанавливающей, какие операции нужно
произвести над х, чтобы найти у. Например

.

Рассмотрим
первый пример –

.
Здесь значению x = 1 соответствует

,
значению x = 3 соответствует

и
т. д.

Функция может быть задана на
разных частях множества X разными
функциями.

Например:

Во
всех ранее приведенных примерах
аналитического способа задания, функция
была задана явно. То есть, справа стояла
переменная y, а справа формула от
переменной х. Однако, при аналитическом
способе задания, функция может быть
задана и неявно.

Например

.
Здесь, если мы задаем переменной x
значение, то, чтобы найти значение
переменной у (значение функции), мы
должны решить уравнение. Например, для
первой заданной функции при х = 3, будем
решать уравнение:

.
То есть, значение функции при х = 3 равно
-4/3.

При аналитическом
способе задания, функция может быть
задана параметрически – это, когда х и
у выражены через некоторый параметр t.
Например,

Здесь
при t = 2, x = 2, y = 4. То есть, значение функции
при х = 2 равно 4.

2. Графический
способ.

При
графическом способе вводится прямоугольная
система координат и в этой системе
координат изображается множество точек
с координатами (x,y). При этом

.
Пример:

3.
Табличный
способ.

Табличный
способ наиболее удобен, когда множество
Х конечно. При этом способе составляется
таблица, в которой каждому элементу из
множества Х, ставится в соответствие
число Y.

Пример:

4)
Последовательность
в R.
Определение предела. Критерий Коши о
сходимости числовой последовательности.

Числовые
последовательности

Последовательностью
называется множество чисел, перенумерованных
с помощью натуральных чисел и расставленных
в порядке возрастания их номеров
x₁,x₂,…x_n

Числа
x₁,x₂,…,x_n
— называются элементами
последовательности, символ x_n
— общим
элементом,
а число n — его номером. Сокращенно
последовательность обозначается
символом {x_n}.

Предел
последовательности

Окрестностью
точки x₀
называется любой интервал, содержащий
эту точку.

δ
— окрестностью точки
x₀
U_δ
(x₀)
называется интервал длиной 2δ с центром
в этой точке.

Определение
предела последовательности

Число
а называется пределом
последовательности {x_n},
если для любого ε > 0 найдется номер n₀
= n₀(ε)
∈
N такой, что для всех номеров n > n₀
выполняется неравенство |x_n
— a| <ε

Число
b называется пределом последовательности
{x_n}=x₁,
x₂,…,
x_n
(lim {x_n}
= b; n→∞)

Последовательность
{x_n},
имеющая конечный предел а, называется
сходящейся.

Последовательность,
имеющая бесконечный предел или вообще
не имеющая предела, называется расходящейся

Свойства
сходящихся последовательностей

Теорема
1.

Сходящаяся
последовательность имеет только один
предел.

Теормера
О сходимости подпоследовательности

Теорема
Об арифметических действиях над
сходящимися последовательностями

Теорема
8 Критерий Коши сходимости последовательности

Для
того чтобы последовательность {x_n}
сходилась, необходимо и достаточно,
чтобы ∀ε
>0 ∃номер
n₀
такой, что ∀n
> n₀
и
любого p∈N
выполнялось неравенство |x_n+p
–
x_n|
<ε

Если
предел последовательности равен нулю,
то ее называют бесконечно
малой

Теорема
Вейерштрасса.
Всякая
монотонная и ограниченная последовательность
имеет предел

Последовательность

называется
возрастающей,
если для любого

выполняется
неравенство

xn + 1 > xn.

Последовательность

называется
убывающей,
если для любого

выполняется
неравенство

xn + 1 < xn.

Если
в этих определениях неравенство будет
нестрогим, то последовательности будут
называться соответственно неубывающей
и невозрастающей.

Возрастающие
и убывающие последовательности называют
строго
монотонными.
Неубывающие и невозрастающие
последовательности называют монотонными.

Последовательность
{x_n}
называется ограниченной
снизу
(сверху), если существует такое число
C, что все члены последовательности
удовлетворяют условию x_n ≥ C
(x_n ≤ C).
Последовательность, ограниченную как
сверху, так и снизу,
называют ограниченной.

Рисунок 1.1.2.1. Последовательность называют ограниченной, если C1 ≤ xn ≤ C2.

Геометрически
ограниченность последовательности
означает, что все ее значения лежат на
некотором отрезке.

Можно
показать, что если последовательность
имеет предел, то она ограничена.

Заметим,
что не всякая ограниченная последовательность
является сходящейся. Примером расходящейся
ограниченной последовательности может
служить последовательность {x_n}:
x_n = (–1)ⁿ.

Теорема
( Критерий Коши ). Для того, чтобы
последовательность {x_n}
сходилась, необходимо и достаточно
чтобы она была фундаментальной.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Преде́льная то́чка множества в общей топологии — это такая точка, любая проколотая окрестность которой пересекается с этим множеством.

Определение и типы предельных точек[править | править код]

Точка называется предельной точкой подмножества в топологическом пространстве , если всякая проколотая окрестность точки имеет с непустое пересечение.

Точка называется точкой накопления подмножества , если всякая окрестность точки имеет с бесконечное число общих точек. Для T₁-пространств (то есть пространств, у которых все точки (одноточечные множества) замкнуты), понятия предельная точка и точка накопления равносильны.

Точка называется точкой конденсации подмножества , если всякая окрестность точки содержит несчётное множество точек .

Точка называется точкой полного накопления подмножества , если для всякой окрестности точки мощность пересечения равна мощности множества .

Связанные понятия и свойства[править | править код]

(В частности, поскольку отрезок прямой компактен, то он счётно компактен. Следовательно, всякое бесконечное ограниченное подмножество прямой имеет хотя бы одну предельную точку.)

• Замкнутое множество в хаусдорфовом пространстве называется совершенным, если каждая его точка является предельной (то есть, если множество не содержит изолированных точек). Примерами совершенных множеств могут служить отрезок прямой, множество Кантора.

Примеры[править | править код]

Предельная точка числового множества[править | править код]

В частности, предельной точкой числового множества, имеющего бесконечное число элементов, называется точка числовой прямой, в любой окрестности которой содержится бесконечно много элементов этого множества. Также можно считать предельной точкой такого множества , если из некоторых его элементов можно составить бесконечно большую последовательность с попарно различными отрицательными элементами. Если же можно составить бесконечно большую последовательность с попарно различными положительными элементами, то можно считать предельной точкой ^[1].

Верхняя предельная точка числового множества — это наибольшая из его предельных точек.

Нижняя предельная точка числового множества — это наименьшая из его предельных точек.

Свойства[править | править код]

• Из элементов любого ограниченного числового множества, имеющего бесконечное число элементов, можно выделить сходящуюся последовательность, элементы которой попарно различны.

Предельная точка числовой последовательности[править | править код]

Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности^[1].

 — предельная точка последовательности

Наибольшая предельная точка последовательности называется её верхним пределом, а наименьшая предельная точка — нижним пределом.

Иногда во множество возможных предельных точек включают «» и «». Так, если из последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой отрицательны, то говорят, что «» является предельной точкой этой последовательности. Если же из последовательности можно выделить бесконечно большую подпоследовательность с исключительно положительными элементами, то говорят, что «» является её предельной точкой^[1]. При этом, разумеется, у последовательности могут быть и другие предельные точки.

Свойства[править | править код]

Примеры[править | править код]

Предельная точка направления[править | править код]

Пусть  — направление элементов топологического пространства . Тогда называется предельной точкой направления, если для любой окрестности точки и для любого найдётся индекс такой что и

Свойства[править | править код]

• Точка является предельной точкой направления тогда и только тогда, когда существует поднаправление, сходящееся к этой точке.
  • В частности, точка является предельной точкой последовательности тогда и только тогда, когда существует поднаправление, сходящееся к этой точке.
  • Если каждая точка топологического пространства обладает счётной базой, то в предыдущем пункте можно говорить о подпоследовательностях.

Примеры[править | править код]

Пусть  — направлено по возрастанию. У направления существует единственная предельная точка в топологическом пространстве .

См. также[править | править код]

• Изолированная точка

Примечания[править | править код]

Литература[править | править код]

• Энгелькинг, Р. Общая топология. — М.: Мир, 1986. — 752 с.
• Л.В. Канторович, Г.П. Акилов. Функциональный анализ. — М.: Наука, 1984. — 752 с.

Ограниченность числовых множеств, их точные границы. Предельные точки числовых множеств.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Пусть $X -$ произвольное непустое множество действительных чисел. Число $M=max X$ называется наибольшим (максимальным) элементом множества $X,$ если $Min X$ и для всякого $xin X$ выполняется неравенство $xleq M$. Аналогично определяется понятие наименьшего (минимального) элемента $m=min X$ множества $X.$

Множество $X$ называется ограниченным сверху, если существует действительное число $a$ такое, что $xleq a$ для всех $xin X.$ Всякое число, обладающее этим свойством, называется верхней гранью множества $X.$ Для заданного ограниченного сверху множества $X$ множество всех его верхних граней имеет наименьший элемент, который называется точной верхней гранью множества $X$ и обозначается символом $sup X.$ Очевидно $sup X=max X$ тогда и только тогда когда $sup Xin X.$

Аналогично определяются понятия ограниченного снизу множества, нижней грани и точной нижней грани множества $X.$ Последняя обозначается символом $inf X.$

Множество $X,$ ограниченное снизу и сверху, называется ограниченным.

Пусть $xsubset R.$ Число $x_0in R$ называется предельной точкой множества X, если любая окрестность точки $x_0$ содержит точку из множества $X,$ отличную от $x_0,$ то есть для $$forallvarepsilon>0,,exists yin X, yneq x_0: |y-x_0|<varepsilon.$$

Сама точка $x_0$ может принадлежать, а может и не принадлежать множеству $X$.

Примеры.

1.73. Пусть $X=left{1, frac{1}{2}, frac{1}{3}, frac{1}{n}right}.$ 

а) Указать наименьший и наибольший элементы этого множества, если они существуют.

б) Каковы множества верхних и нижних граней для множества $X.$ Найти $sup X$ и $inf X.$

Решение.

а) Данное множество имеет наибольший элемент $M=1$ поскольку для всех элементов множества $xin X $ выполняется неравенство $xleq 1$ и при этом $1in X.$

Наименьшего элемента заданное множество не имеет, так как для любого элемента $x_n=frac{1}{n}in X$ всегда найдется элемент $x_{n+1}=frac{1}{n+1}in X$ для которого выполняется неравенство  $x_{n+1}leq x_n.$

б) Поскольку для всех элементов $x$ множества $X$ выполняется неравенство $xleq 1,$ причем $1in X,$ то множество верхних граней для множества $X$ это множество $[1, +infty)$ c наименьшим элементом равным $1.$ Таким образом, $sup X=1.$

Наименьшего элемента множества $X$ не существует. Очевидно, что для всех элементов $x$ множества $X$ выполняется $xgeq 0, $ то есть множество $X$ ограничено снизу. Покажем, что $0$ является предельным значением множества $X.$ Действительно, для любого $varepsilon>0$ можно найти натуральное число $$n>frac{1}{varepsilon},,Rightarrow,,frac{1}{n}<varepsilon,quadfrac{1}{n}in X.$$ Таким образом, множество нижних граней для $X$ это множество $(-infty, 0]$ c наибольшим элементом равным $0.$ Отсюда находим $inf X=0.$

Ответ: $M=1,$ наименьшего элемента не существует, $[1, +infty),$ $(-infty, 0],$ $sup X=1,$ $inf X=0.$

1.74. Для множества $X=left{xin R|,, x=frac{1}{2^n},,, nin Nright}$ найти $max X, ,, min X,$ $sup X$ и $inf X$ если они существуют.

Решение.

Запишем множество $X$ в виде 

$$X=left{xin R|,, x=frac{1}{2^n},,, nin Nright}=left{frac{1}{2},frac{1}{4}, frac{1}{8}, .., frac{1}{2^n},…right}$$ 

Данное множество имеет наибольший элемент $M=frac{1}{2}$ поскольку для всех элементов множества $xin X $ выполняется неравенство $xleq frac{1}{2}.$ При этом $frac{1}{2}in X.$

Наименьшего элемента заданное множество не имеет, так как для любого элемента $x_n=frac{1}{2^n}in X$ всегда найдется элемент $x_{n+1}=frac{1}{2^{n+1}}in X$ для которого выполняется неравенство  $x_{n+1}leq x_n.$

Поскольку для всех элементов $x$ множества $X$ выполняется неравенство $xleq frac{1}{2},$ причем $frac{1}{2}in X,$ то множество верхних граней для множества $X$ это множество $left[frac{1}{2}, +inftyright)$ c наименьшим элементом равным $frac{1}{2}.$ Таким образом, $sup X=frac{1}{2}.$

Наименьшего элемента множества $X$ не существует. Очевидно, что для всех элементов $x$ множества $X$ выполняется $xgeq 0, $ то есть множество $X$ ограничено снизу. Покажем, что $0$ является предельным значением множества $X.$ Действительно, для любого $varepsilon>0$ можно найти натуральное число $$n>log_2frac{1}{varepsilon},,Rightarrow 2^n>frac{1}{varepsilon}Rightarrow,,frac{1}{2^n}<varepsilon,quadfrac{1}{2^n}in X.$$Таким образом, множество нижних граней для $X$ это множество $(-infty, 0]$ c наибольшим элементом равным $0.$ Отсюда находим $inf X=0.$

Ответ: $M=frac{1}{2},$ наименьшего элемента не существует $sup X=frac{1}{2},$ $inf X=0.$

1.80. Пусть $Xsubset R -$ произвольное ограниченное множество. Доказать, что множество $-X={x|,, -xin X}$ так же ограничено и справедливы равенства $$sup (-X)=-inf X,qquad inf (-X)=-sup X.$$

Доказательство.

Так как множество $X$ ограничено, то оно ограничено сверху и снизу, а значит существуют соответственно, числа $a$ и $b$ такие, что $forall xin X, ,,  aleq xleq b. $ Отсюда, решая неравенство видно, что для элементов $-x$ верно неравенство $-bleq -xleq -a.$ То есть множество $-X={x|,, -xin X}$ также является ограниченным.

Пусть $a=inf X.$ Тогда из неравенства $-xleq -a$ получаем $-xleq -inf X.$

Если $ain X,$ то $-ain -X.$ В этом случае очевидно, что $$-a=sup(-X)Rightarrow sup(-X)=-inf X.$$

Если $anotin X,$ то $-anotin -X.$ Покажем, что $-a$ это наименьшй элемент принадлежащий множеству верхних граней. Действительно, пусть существует элемент $cneq a, ,,-cnotin -X,$ такой что для всех $-xin -X$ $-xleq -cleq -a.$ Тогда $cnotin X$ и віполняется неравенство $aleq cleq x.$ Следовательно, $aneq inf X.$ Получили противоречие. Таким образом, $$-a=sup(-X)Rightarrow sup(-X)=-inf X.$$

Аналогично доказывается, что $inf (-X)=-sup X.$

Что и требовалось доказать.

Домашнее задание.

1.75. Для множества $X=[-1, , 1]$ найти $max X, ,, min X,$ $sup X$ и $inf X$ если они существуют.

Ответ: $1,, -1,, 1,, -1.$ 

1.76. Для множества $X=left{xin Z|,, -5leq x <0right}$ найти $max X, ,, min X,$ $sup X$ и $inf X$ если они существуют.

Ответ: Не существует, $-5,, 0,, -5.$

1.81. Пусть $X,,, Ysubset R -$ произвольные ограниченные сверху множества. Доказать, что множество $X+Y={zin R|,, z=x+y,|,, xin X,, yin Y}$ ограничено сверху и справедливы равенства $$sup (X+Y)=sup X+sup Y.$$