Как найти множество задания функции

Зачастую в рамках решения задач по тригонометрии нам приходится искать множество значений функции на области определения или отрезке. Например, такой поиск нужно делать, если приходится решать разные типы неравенств, при оценке выражений и др.

В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми можно вычислить область значения и область определения функции, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графически. Прочитав эту статью, вы получите исчерпывающее представление о том, что такое область значения функции.

Начнем с базовых определений.

Определение 1

Множество значений функции y = f(x) – это множество всех значений на некотором интервале x, которые данная функция принимает при переборе всех значений x∈X.

Определение 2

Область значений функции y=f(x) – это множество всех ее значений, которые она может принять при переборе значений x из области x∈(f).

Область значений некоторой функции обычно принято называть и обозначать E(f).

Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.

Важно также различать область значений и область допустимых значений переменной x для выражения в правой части y=f(x). Область допустимых значений x для выражения f(x) и будет областью определения данной функции.

Ниже приводится иллюстрация, на которой показаны некоторые примеры, как построить графики функций и их построение. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.

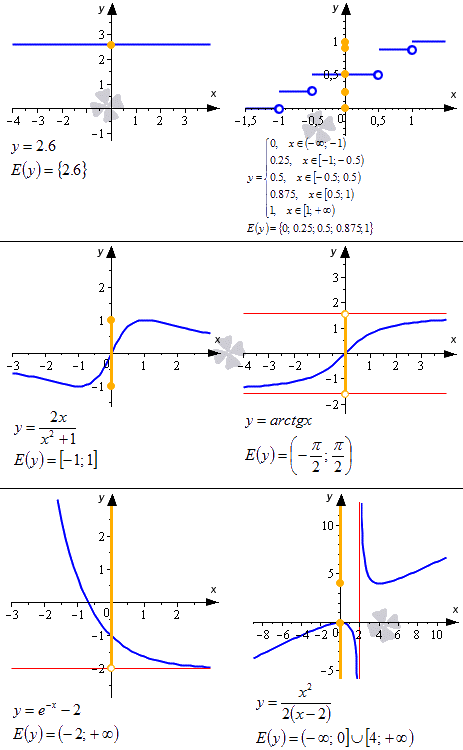
Как найти область значения функции? Очевидно, что область или множество значений функции можно найти или получить при проецировании графика функции на ось Oy. При этом она может представлять собой как одно число, так и множество чисел, отрезок, интервал, открытый луч, объединение числовых промежутков и др.

Рассмотрим основные способы, как определить область значения функции.

Первый этап – определить тип функции. Функция может быть квадратичной, а также содержать дроби и корни.

Начнем с определения множества значений непрерывной функции y = f(x) на некотором отрезке, обозначенном [a; b]. Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего maxx∈a; bf(x) и наименьшего значения minx∈a; bf(x). Значит, у нас получится отрезок minx∈a; bf(x); maxx∈a; bf(x), в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.

Возьмем задачу, в которой нужно определить область значений арксинуса.

Пример 1

Условие: найдите область значений y = arcsin x.

Решение

В общем случае область определения арксинуса располагается на отрезке [-1; 1]. Нам надо определить наибольшее и наименьшее значение указанной функции на нем.

y’ = arcsin x’=11-x2

Мы знаем, что производная функции будет положительной для всех значений x, расположенных в интервале [-1; 1], то есть на протяжении всей области определения функция арксинуса будет возрастать. Значит, самое маленькое значение она примет при x, равном -1, а самое большое – при x, равном 1.

minx∈-1; 1arcsin x=arcsin-1=-π2maxx∈-1; 1arcsin x=arcsin 1=π2

Таким образом, область значений функции арксинус будет равна E(arcsin x)=-π2; π2.

Ответ: E(arcsin x)=-π2; π2

Пример 2

Условие: вычислите область значений y=x4-5×3+6×2 на заданном отрезке [1; 4].

Решение

Как найти значение функции? Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.

Для определения точек экстремума надо произвести следующие вычисления:

y’=x4-5×3+6×2’=4×3+15×2+12x=x4x2-15x+12y’=0⇔x(4×2-15x+12)=0x1=0∉1; 4 или 4×2-15x+12=0D=-152-4·4·12=33×2=15-338≈1.16∈1; 4; x3=15+338≈2.59∈1; 4

Теперь найдем значения заданной функции в концах отрезка и точках x2=15-338; x3=15+338:

y(1)=14-5·13+6·12=2y15-338=15-3384-5·15-3383+6·15-3382==117+16533512≈2.08y15+338=15+3384-5·15+3383+6·15+3382==117-16533512≈-1.62y(4)=44-5·43+6·42=32

Как найти множество значений функции? Значит, множество значений функции будет определяться отрезком 117-16533512; 32.

Ответ: 117-16533512; 32.

Перейдем к нахождению множества значений непрерывной функции y = f(x) в промежутках (a; b), причем a; +∞, -∞; b, -∞; +∞.

Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведение функции в заданных условиях. Для этого у нас есть все необходимые данные.

Пример 3

Условие: вычислите область значений функции y=1×2-4 на интервале (-2; 2).

Решение

Определяем наибольшее и наименьшее значение функции на заданном отрезке

y’=1×2-4’=-2x(x2-4)2y’=0⇔-2x(x2-4)2=0⇔x=0∈(-2; 2)

У нас получилось максимальное значение, равное 0, поскольку именно в этой точке происходит перемена знака функции и график переходит к убыванию. См. на иллюстрацию:

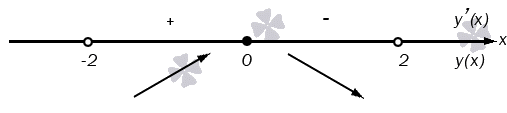
То есть, y(0)=102-4=-14 будет максимальным значением функции.

Теперь определим поведение функции при таком x, который стремится к -2 с правой стороны и к +2 с левой стороны. Иными словами, найдем односторонние пределы:

limx→-2+01×2-4=limx→-2+01(x-2)(x+2)==1-2+0-2-2+0+2=-14·1+0=-∞limx→2+01×2-4=limx→2+01(x-2)(x+2)==12-0-22-0+2=14·1-0=-∞

У нас получилось, что значения функции будут возрастать от минус бесконечности до -14 тогда, когда аргумент изменяется в пределах от -2 до 0. А когда аргумент меняется от 0 до 2, значения функции убывают к минус бесконечности. Следовательно, множеством значений заданной функции на нужном нам интервале будет (-∞; -14].

Ответ: (-∞; -14].

Пример 4

Условие: укажите множество значений y=tg x на заданном интервале -π2; π2.

Решение

Нам известно, что в общем случае производная тангенса в -π2; π2 будет положительной, то есть функция будет возрастать. Теперь определим, как ведет себя функция в заданных границах:

limx→π2+0tg x=tg-π2+0=-∞limx→π2-0tg x=tgπ2-0=+∞

Мы получили рост значений функции от минус бесконечности к плюс бесконечности при изменении аргумента от -π2 до π2,и можно сказать, что множеством решений данной функции будет множество всех действительных чисел.

Ответ: -∞; +∞.

Пример 5

Условие: определите, какова область значений функции натурального логарифма y = ln x.

Решение

Нам известно, что данная функция является определенной при положительных значениях аргумента D(y)=0; +∞. Производная на заданном интервале будет положительной: y’=ln x’=1x. Значит, на нем происходит возрастание функции. Далее нам нужно определить односторонний предел для того случая, когда аргумент стремится к 0 (в правой части), и когда x стремится к бесконечности:

limx→0+0ln x=ln(0+0)=-∞limx→∞ln x=ln+∞=+∞

Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.

Ответ: множество всех действительных чисел – область значений функции натурального логарифма.

Пример 6

Условие: определите, какова область значений функции y=9×2+1.

Решение

Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:

y’=9×2+1’=-18x(x2+1)2y’=0⇔x=0y’≤0⇔x≥0y’≥0⇔x≤0

В итоге мы определили, что данная функция будет убывать, если x≥0; возрастать, если x≤0; она имеет точку максимума y(0)=902+1=9 при переменной, равной 0.

Посмотрим, как же ведет себя функция на бесконечности:

limx→-∞9×2+1=9-∞2+1=9·1+∞=+0limx→+∞9×2+1=9+∞2+1=9·1+∞=+0

Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.

Подведем итоги: когда аргумент изменяется от минус бесконечности до нуля, то значения функции возрастают от 0 до 9. Когда значения аргумента меняются от 0 до плюс бесконечности, соответствующие значения функции будут убывать от 9 до 0. Мы отобразили это на рисунке:

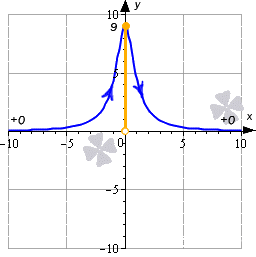
На нем видно, что областью значений функции будет интервал E(y)=(0; 9]

Ответ: E(y)=(0; 9]

Если нам надо определить множество значений функции y = f(x) на промежутках [a; b), (a; b], [a; +∞), (-∞; b], то нам понадобится провести точно такие же исследования. Эти случаи мы пока не будем разбирать: далее они нам еще встретятся в задачах.

А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.

Пример 7

Условие: определите, какой будет область значений y=xx-2.

Решение

Поскольку знаменатель функции не должен быть обращен в 0, то D(y)=-∞; 2∪2; +∞.

Начнем с определения множества значений функции на первом отрезке -∞; 2, который представляет из себя открытый луч. Мы знаем, что функция на нем будет убывать, то есть производная данной функции будет отрицательной.

limx→2-0xx-2=2-02-0-2=2-0=-∞limx→-∞xx-2=limx→-∞x-2+2x-2=limx→-∞1+2x-2=1+2-∞-2=1-0

Тогда в тех случаях, когда аргумент изменяется по направлению к минус бесконечности, значения функции будут асимптотически приближаться к 1. Если же значения x меняются от минус бесконечности до 2, то значения будут убывать от 1 до минус бесконечности, т.е. функция на этом отрезке примет значения из интервала -∞; 1. Единицу мы исключаем из наших рассуждений, поскольку значения функции ее не достигают, а лишь асимптотически приближаются к ней.

Для открытого луча 2; +∞ производим точно такие же действия. Функция на нем также является убывающей:

limx→2+0xx-2=2+02+0-2=2+0=+∞limx→+∞xx-2=limx→+∞x-2+2x-2=limx→+∞1+2x-2=1+2+∞-2=1+0

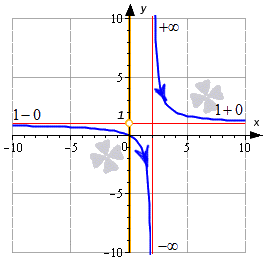
Значения функции на данном отрезке определяются множеством 1; +∞. Значит, нужная нам область значений функции, заданной в условии, будет объединением множеств -∞; 1 и 1; +∞.

Ответ: E(y)=-∞; 1∪1; +∞.

Это можно увидеть на графике:

Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.

Пример 8

Условие: определите область значений синуса y = sin x.

Решение

Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0; 2π и смотрим, каким будет множество значений на нем.

y’=(sin x)’=cos xy’=0⇔cos x=0⇔x=π2+πk, k∈Z

В рамках 0; 2π у функции будут точки экстремума π2 и x=3π2. Подсчитаем, чему будут равны значения функции в них, а также на границах отрезка, после чего выберем самое большое и самое маленькое значение.

y(0)=sin 0=0yπ2=sin π2=1y3π2=sin3π2=-1y(2π)=sin(2π)=0⇔minx∈0; 2πsin x=sin3π2=-1, maxx∈0; 2πsin x=sinπ2=1

Ответ: E(sin x)=-1; 1.

Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения (или указать). Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.

Пример 9

Условие: определите область значения y=3arccosx3+5π7-4.

Решение

Нам известно, что отрезок от 0 до пи есть область значений арккосинуса. Иными словами, E(arccos x)=0; π или 0≤arccos x≤π. Мы можем получить функцию arccosx3+5π7 из арккосинуса, сдвинув и растянув ее вдоль оси Ox, но такие преобразования нам ничего не дадут. Значит, 0≤arccosx3+5π7≤π.

Функция 3arccosx3+5π7 может быть получена из арккосинуса arccosx3+5π7 с помощью растяжения вдоль оси ординат, т.е. 0≤3arccosx3+5π7≤3π. Финалом преобразований является сдвиг вдоль оси Oy на 4 значения. В итоге получаем двойное неравенство:

0-4≤3arccosx3+5π7-4≤3π-4⇔-4≤3arccosx3+5π7-4≤3π-4

Мы получили, что нужная нам область значений будет равна E(y)=-4; 3π-4.

Ответ: E(y)=-4; 3π-4.

Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.

Пример 10

Условие: вычислите, какова будет область значений функции y=22x-1+3.

Решение

Перепишем функцию, заданную в условии, как y=2·(2x-1)-12+3. Для степенной функции y=x-12 область значений будет определена на промежутке 0; +∞, т.е. x-12>0. В таком случае:

2x-1-12>0⇒2·(2x-1)-12>0⇒2·(2x-1)-12+3>3

Значит, E(y)=3; +∞.

Ответ: E(y)=3; +∞.

Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.

Пример 11

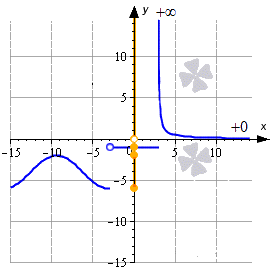
Условие: дана функция y=2sinx2-4, x≤-3-1, -3<x≤31x-3, x>3. Вычислите область ее значений.

Решение

Данная функция является определенной для всех значений x. Проведем ее анализ на непрерывность при значениях аргумента, равных -3 и 3:

limx→-3-0f(x)=limx→-32sinx2-4=2sin-32-4=-2sin32-4limx→-3+0f(x)=limx→-3(1)=-1⇒limx→-3-0f(x)≠limx→-3+0f(x)

Имеем неустранимый разрыв первого рода при значении аргумента -3. При приближении к нему значения функции стремятся к -2sin32-4, а при стремлении x к -3 с правой стороны значения будут стремиться к -1.

limx→3-0f(x)=limx→3-0(-1)=1limx→3+0f(x)=limx→3+01x-3=+∞

Имеем неустранимый разрыв второго рода в точке 3. Когда функция стремится к нему, ее значения приближаются к -1, при стремлении к той же точке справа – к минус бесконечности.

Значит, вся область определения данной функции является разбитой на 3 интервала (-∞; -3], (-3; 3], (3; +∞).

На первом из них у нас получилась функция y=2sinx2-4. Поскольку -1≤sin x≤1, получаем:

-1≤sinx2<1⇒-2≤2sinx2≤2⇒-6≤2sinx2-4≤-2

Значит, на данном промежутке (-∞; -3] множество значении функции – [-6;2].

На полуинтервале (-3; 3] получилась постоянная функция y =-1. Следовательно, все множество ее значений в данном случае будет сводится к одному числу -1.

На втором промежутке 3; +∞ у нас есть функция y=1x-3. Она является убывающей, потому что y’=-1(x-3)2<0. Она будет убывать от плюс бесконечности до 0, но самого 0 не достигнет, потому что:

limx→3+01x-3=13+0-3=1+0=+∞limx→+∞1x-3=1+∞-3=1+∞+0

Значит, множество значений исходной функции при x > 3 представляет собой множество 0; +∞. Теперь объединим полученные результаты: E(y)=-6; -2∪-1∪0; +∞.

Ответ: E(y)=-6; -2∪-1∪0; +∞.

Решение показано на графике:

Пример 12

Условие: есть функция y=x2-3ex. Определите множество ее значений.

Решение

Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:

y’=x2-3ex’=2xex-ex(x2-3)e2x=-x2+2x+3ex=-(x+1)(x-3)ex

Мы знаем, что производная обратится в 0, если x=-1 и x=3. Поместим эти две точки на ось и выясним, какие знаки будет иметь производная на получившихся интервалах.

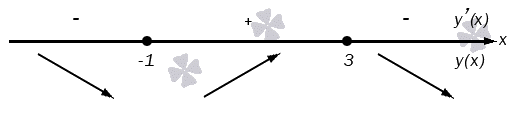
Функция будет убывать на (-∞; -1]∪[3; +∞) и возрастать на [-1; 3]. Точкой минимума будет -1, максимума –3.

Теперь найдем соответствующие значения функции:

y(-1)=-12-3e-1=-2ey(3)=32-3e3=6e-3

Посмотрим на поведение функции на бесконечности:

limx→-∞x2-3ex=-∞2-3e-∞=+∞+0=+∞limx→+∞x2-3ex=+∞2-3e+∞=+∞+∞==limx→+∞x2-3’ex’=limx→+∞2xex=+∞+∞==limx→+∞2x'(ex)’=2limx→+∞1ex=2·1+∞=+0

Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.

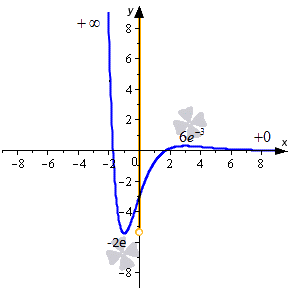
На нем видно, что значения функции будут убывать от плюс бесконечности до -2e тогда, когда аргумент меняется от минус бесконечности до -1. Если же он изменяется от 3 до плюс бесконечности, то значения будут убывать от 6e-3 до 0, но при этом 0 достигнут не будет.

Таким образом, E(y)=[-2e; +∞).

Ответ: E(y)=[-2e; +∞)

Источник

Загрузить PDF

Множество значений (область значений) функции — все значения, которые принимает функция в ее области определения. Другими словами, это те значения у, которые вы получаете при подстановке всех возможных значений х. Все возможные значения х и называются областью определения функции. Выполните следующие действия для нахождения множества значений функции.

1

Запишите функцию. Например: f(x) = 3x² + 6x -2. Подставив x в уравнение, мы сможем найти значение y. Эта квадратичная функция, и ее график — парабола.
2
Найдите вершину параболы. Если вам дана линейная функция или любая другая с переменной в нечетной степени, например, f(x) = 6x³+2x + 7, пропустите этот шаг. Но если вам дана квадратичная функция или любая другая с переменной х в четной степени, нужно найти вершину графика этой функции. Для этого используйте формулу х=-b/2a. В функции 3x² + 6x -2 a = 3, b = 6, c = -2. Вычисляем: х = -6/(2*3)= -1.
- Теперь подставьте х= -1 в функцию, чтобы найти у. f(-1) = 3*(-1)² + 6*(-1) -2 = 3 – 6 -2 = -5.
- Координаты вершины параболы (-1,-5). Нанесите ее на координатную плоскость. Точка лежит в третьем квадранте координатной плоскости.
3
Найдите еще несколько точек на графике. Для этого подставьте в функцию несколько других значений х. Так как член x² положительный, то парабола будет направлена вверх. Для подстраховки подставим в функцию несколько значений x, чтобы узнать, какие значения y они дают.
- f(-2) = 3(-2)² + 6(-2) -2 = -2. первая точка на параболе (-2, -2)
- f(0) = 3(0)² + 6(0) -2 = -2. Вторая точка на параболе (0,-2)
- f(1) = 3(1)² + 6(1) -2 = 7. Третья точка на параболе (1, 7).
4

Найдите множество значений функции на графике. Найдите наименьшее значение у на графике. Эта вершина параболы, где у=-5. Так как парабола лежит выше вершины, то множество значений функции y ≥ -5.

Реклама

1

Найдите минимум функции. Вычислите наименьшее значение у. Допустим, минимум функции у=-3. Это значение может становиться все меньше и меньше, вплоть до бесконечности, так что минимум функции не имеет заданной минимальной точки.
2

Найдите максимум функции. Допустим, максимум функции у= 10. Как и в случае с минимумом, максимум функции не имеет заданной максимальной точки.
3
Запишите множество значений. Таким образом, множество значений функции лежит в диапазоне от -3 до +10. Запишите множество значений функции как: -3 ≤ f(x) ≤ 10
- Но, допустим, минимум функции у=-3, а ее максимум — бесконечность (график функции уходит бесконечно вверх). Тогда множество значений функции: f(x) ≥ -3.
- С другой стороны, если максимум функции у=10, а минимум — бесконечность (график функции уходит бесконечно вниз), то множество значений функции: f(x) ≤ 10.
Реклама

1

Запишите множество координат. Из множества координат можно определить его область значения и область определения. Допустим, дано множество координат: {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}.^[1]
2

Перечислите значения у. Чтобы найти область значений множества, просто запишите все значения у: {-3, 6, -1, 6, 3}.^[2]
3

Удалите все повторяющиеся значения у. В нашем примере удалите “6”: {-3, -1, 6, 3}.^[3]
4

Запишите область значений в порядке возрастания. Областью значений множества координат {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} будет {-3, -1, 3, 6}.^[4]
5

Убедитесь, что множество координат дано для функции. Чтобы это было так, каждому одному значению х должно соответствовать одно значение у. Например, множество координат {(2, 3) (2, 4) (6, 9)} дано не для функции, потому что одному значению х=2 соответствуют два разных значения у: у=3 и у=4.^[5]

Реклама

1

Прочитайте задачу. «Ольга продает билеты в театр по 500 рублей за билет. Общая вырученная сумма за проданные билеты является функцией от количества проданных билетов. Какова область значений этой функции?»
2
Запишите задачу как функцию. В этом случае М — общая вырученная сумма за проданные билеты, а t — количество проданных билетов. Так как один билет стоит 500 рублей, надо умножить количество проданных билетов на 500, чтобы найти вырученную сумму. Таким образом, функция может быть записана в виде M(t) = 500t.
- Например, если она продаст 2 билета, нужно умножить 2 на 500 — в итоге получим 1000 рублей, вырученных за проданные билеты.
3

Найдите область определения. Для нахождения области значений вы должны сначала найти область определения. Это все возможные значения t. В нашем примере Ольга может продать 0 или больше билетов, — она не может продать отрицательное число билетов. Поскольку мы не знаем количество мест в театре, можно предположить, что теоретически она может продать бесконечное число билетов. И она может продавать только целые билеты (она не может продать, например, 1/2 билета). Таким образом, область определения функции t = любое неотрицательное целое число.
4
Найдите область значений. Это возможное количество денег, которые Ольга выручит от продажи билетов. Если вы знаете, что область определения функции — любое неотрицательное целое число, а функция имеет вид: М(t) = 5t, то вы можете найти вырученную сумму, подставив в функцию любое неотрицательное целое число (вместо t). Например, если она продаст 5 билетов, то М(5) = 5*500 = 2500 рублей. Если она продаст 100 билетов, то М(100) = 500 х 100 = 50000 рублей. Таким образом, область значений функции — любые неотрицательные целые числа, кратные пятистам.
- Это означает, что любое неотрицательное целое число, которое делится на 500, является значением у (вырученная сумма) нашей функции.
Реклама

Советы

В более сложных случаях лучше сначала чертить график, используя область определения, и только потом находить область значений.
Посмотрите, можете ли вы найти обратную функцию. Область определения обратной функции равна области значений исходной функции.
Проверьте, повторяется ли функция. Любая функция, которая повторяется вдоль оси x, будет иметь ту же область значений для всей функции. Например, область значений для f(x) = sin(x) будет составлять от -1 до 1.

Об этой статье

Эту страницу просматривали 453 100 раз.

Была ли эта статья полезной?

Источник

КАК НАЙТИ МНОЖЕСТВО ЗНАЧЕНИЙ
ФУНКЦИИ

Сильвестров
В.В.

д.ф.-м.н.,
профессор кафедры
естественнонаучных дисциплин

Чувашского
республиканского института образования

Единый государственный
экзамен (ЕГЭ) внес новое веяние в
экзаменационные задания по математике.
Наряду с задачами традиционного
характера, предлагающимися на выпускных
экзаменах за курс средней школы и
вступительных экзаменах в вузы, задания
ЕГЭ неизменно содержат 2-3 задачи на
нахождение множества значений функции
или сводящиеся к ним задачи. Такие задачи
вызывают у учащихся немалые затруднения,
и особенно, если требуется оформление
решения с обоснованием всех моментов.

В данной статье на
конкретных примерах раскрываются методы
нахождения множества значений функции.
Более подробно с этими методами, теорией
и типовыми примерами можно ознакомиться
по книге [1].

Приведем свойства непрерывных,
монотонных и дифференцируемых функций,
наиболее часто используемые при
нахождении множества значений функции.

Если функция

непрерывна на отрезке

и

– ее наименьшее и наибольшее значения
на этом отрезке, то множество значений
функции

на

есть отрезок

Если

непрерывная и возрастающая
функция на отрезке
,
то множество значений функции на этом
отрезке есть отрезок
.
При этом каждое значение

функция принимает ровно при одном
значении
,
т.е. уравнение

имеет единственный корень
на отрезке
.
Если

– непрерывная и убывающая функция на
отрезке
,
то ее множество значений на

есть отрезок
.

Если функция непрерывна
на отрезке

и дифференцируема (имеет
производную) в интервале

то наибольшее и наименьшее
значения функции на этом отрезке
существуют и достигаются либо на концах
отрезка, либо в критических точках
функции, расположенных на отрезке.

К основным методам и
приемам нахождения множества значений
функции относятся:

последовательное нахождение
значений сложных аргументов функции;
метод оценок;
использование свойств непрерывности
и монотонности функции;
использование производной;
графический метод;
метод введения параметра;
метод обратной функции.

Рассмотрим эти методы на конкретных
примерах.

Пример 1.
Найдите область значений

функции

Решим пример методом
последовательного нахождения значений
сложных аргументов функции.

Так как

принимает все неотрицательные
значения, и только их, то

Обозначим

Тогда

где

Функция

определена лишь при

поэтому ее множество значений при

совпадает с множеством значений функции
на промежутке (0; 10], где функция
непрерывна и возрастает. При

она стремится к
,
а при

принимает значение 1. Следовательно,
множество значений

на (0; 10] есть луч

Тем самым,
.
Тогда у функции

область значений
.

Через сложный аргумент
z
исходная функция выражается
формулой

где
.
Эта функция определена при

поэтому множество значений функции у
при

совпадает с ее множеством значений при
.
На промежутке (0; 2] функция

непрерывна и убывает. Так
как логарифмирование по основанию 0,1
меняет характер монотонности, то у
– непрерывная и возрастающая
функция на (0; 2]. При

дробь

стремится к
,
значит, функция у
стремится к
.
При

она равна

Следовательно, множество значений
функции у при

есть луч
.
Это и есть

Ответ:
.

Пример 2.
Найдите область значений

функции

Решим пример методом
оценок.

Из неравенств

складывая второе и
последнее по частям, получим

При

и

функция принимает значения

и

Эта функция, как линейная комбинация
непрерывных функций

и

непрерывна на всей числовой оси, поэтому
она принимает все значения с (– 7) до
7 включительно, причем только их, так
как в силу неравенств

другие значения у нее
невозможны.

Ответ:
.

Наиболее распространенная
ошибка при нахождении множества значений
функции методом оценок состоит в
следующем. На основании полученных
оценок, например, неравенств

делается ошибочно заключение,
что множество значений функции есть
отрезок [А; В],
в то время, как такое заключение
можно сделать лишь тогда, когда функция
непрерывна на рассматриваемом промежутке
и на нем имеются точки, в которых функция
принимает значения А
и В (достигает
нижней А и
верхней В
границы оценки). В общем
случае оценка

лишь означает, что множество
значений функции на рассматриваемом
промежутке принадлежит
отрезку [А; В],
и вовсе не означает, что оно
совпадает со
всем отрезком [А; В].
Например, функция

как и функция в примере 2, удовлетворяет
неравенствам

Однако нет таких значений
x,
при которых функция принимала бы значения
(– 7) и 7, поэтому на основании неравенств

можно лишь утверждать о
принадлежности множества значений
функции отрезку
.
На самом деле,
,
что найдем в следующем примере, используя
производную.

Пример 3.

Решение. По формуле синуса
тройного угла

Обозначим

Тогда

Так как

принимает все значения с
(– 1) до 1 включительно, и только их,
то область значений функции у
совпадает с множеством
значений функции

на отрезке
.

На этом отрезке функция

дифференцируема, так как ее
производная

существует при всех
.
Из уравнения

находим критические точки функции

которые принадлежат отрезку
.
В этих точках и на концах отрезка

Так как

то

и по свойству дифференцируемой функции
наименьшее значение функции

на отрезке

равно
,
а наибольшее значение равно
.
На отрезке

функция
,
как многочлен, непрерывна
(это следует также из дифференцируемости
функции), поэтому ее множество значений
на этом отрезке есть и область значений
.

Ответ:
.

Пример 4.
Найдите множество значений
функции

на отрезке
.

Решим пример, используя
свойство непрерывности и
монотонности функции.

На отрезке

функция

а значит, и функция

убывают и непрерывны. Кроме того,

так как

для всех х.
Так как

имеет другой характер монотонности,
чем t,
и

то функция

непрерывна, возрастает и положительна
при
.
Функция

непрерывна и возрастает на
всей числовой оси, в частности, и на
отрезке
,
где она, кроме того, положительна.
Следовательно, функция

как произведение двух непрерывных,
возрастающих и положительных функций

и
,
также непрерывна и возрастает на отрезке
,
поэтому искомое множество значений
функции

есть отрезок

Ответ:
.

Задача нахождения области
(множества) значений функции

тесно связана с вопросом о разрешимости
уравнения

Действительно, число а
является одним из значений
функции

тогда и только тогда, когда
найдется хотя бы одно значение аргумента
х такое,
что

Последнее означает, что
уравнение

имеет хотя бы один корень х.
Следовательно, область
значений

функции

совпадает с множеством значений параметра
а, для которых уравнение

имеет хотя бы один корень.

Пример 5.

Решение. Найдем множество
значений параметра а,
для которых уравнение

имеет хотя бы один корень.

При

уравнение является линейным

с ненулевым коэффициентом при неизвестной
x,
поэтому имеет решение.

При

уравнение является квадратным,
поэтому оно разрешимо тогда и только
тогда, когда его дискриминант

Так как точка

принадлежит заштрихованному отрезку,
то искомым множеством значений параметра
а, значит, и
областью значений

будет весь этот отрезок.

Ответ:
.

Как продолжение метода
введения параметра
можно рассматривать метод обратной
функции, для нахождения
которой надо решать относительно х
уравнение

считая у
параметром. Если это уравнение
имеет единственное решение

то область
значений

исходной функции

совпадает с областью
определения
обратной
функции

Пример 6.

Решение. Найдем обратную
функцию

из уравнения

Теперь найдем область
определения
:

Так как

то

Ответ:

При нахождении множества
значений функции во многих случаях
помогает схематический график функции.

Пример 7.
Из уравнения

нашли всевозможные у
через х.
Найдите множество всех
значений, которые может принимать у.

Решим пример графически.

В системе координат Оху
построим график уравнения

Им будет окружность
радиуса 2 с центром в точке (0; 1). С
другой стороны, этот график представляет
собой совокупность графиков всевозможных
функций у,
определяемых из заданного
уравнения, поэтому у
может принимать все те
значения, которые являются координатами
проекций точек графика на ось Оу.
Из рисунка видно, что искомое
множество есть отрезок
.

Ответ:
.

Пример 8.
Найдите все те значения функции

каждое из которых она принимает только
при одном значении аргумента х
(ровно один раз).

Решение. По свойствам
степеней
.
Обозначим

Тогда

Так как

и

– возрастающая
функция на числовой оси, то различным
значениям х
соответствуют различные
положительные значения t,
поэтому задача равносильна
задаче нахождения таких значений а
функции

каждое из которых она принимает ровно
при одном положительном значении
аргумента t.

Последнее означает, что
график функции

при

(часть параболы с вершиной в точке

ветви которой направлены вверх) и
прямая

имеют единственную общую
точку (пересечения или касания). Из
рисунка, на котором изображены нужные
нам часть параболы и прямые, видно,
что указанному условию удовлетворяют
значения

Это и есть искомые значения функции
у.

Ответ:

Приведенные примеры не
исчерпывают все многообразие задач,
связанных с нахождением множества
значений функции. Большое число таких
задач, с решениями и без них, имеется в
книге [1]. Приведем некоторые из них,
рекомендуя читателям самостоятельно
решить их.

А1. Найдите области (множества)
значений функций:

1) 2) 3)

4) 5) 6) 7) .

А2. Найдите наименьшее
значение функции

A3. Найдите наибольшее
значение функции

Bl.
Найдите области (множества) значений
функций:

1) 2)

3) 4)

В2. Найдите наименьшее
целое значение функции

В3. Найдите наибольшее
целое значение функции

В4. Найдите наименьшее
значение функции

на отрезке

С1. Найдите области
(множества) значений функций:

1) ;

С2. Найдите все целые
значения функции

СЗ. Найдите все те
значения функции

каждое из которых функция принимает
только при одном значении х.

С4. Найдите все
неотрицательные значения параметра с,
при которых уравнение

не имеет корней.

Ответы:

А1. 1) [– 5; 5]; 2)
[2; 3]; 3)

4)
5)

6)

7)

А2. – 3.

A3. 8.

В1. 1) [1; 3]; 2) [– 2; – 1];
3) [1/3; 27]; 4)

В2. – 3.

ВЗ. – 5.

В4. 0,4.

С1. 1) [– 5; 2,5]; 2)
3)
[– 0,5; 2,5].

С2. 3; 4; 5; 6; 7; 8.

С3.

С4. [0; 16).

ЛИТЕРАТУРА

1.
Сильвестров В.В. Множество значений
функции. Чебоксары: Изд-во ЧГУ, 2004. 64 с.

Источник

subjects:mathematics:множество_значений_функции

Содержание

Математика ( Справочник )

- Множество значений функции

Нахождение множества значений функции

Обозначения

D(f) — те значения, которые может принимать аргумент, т.е. область определения функции.
E(f) — те значения, которые может принимать функция, т.е. множество значений функции.

Способы нахождения областей значений функций.

последовательное нахождение значений сложных аргументов функции;
метод оценок/границ;
использование свойств непрерывности и монотонности функции;
использование производной;
использование наибольшего и наименьшего значений функции;
графический метод;
метод введения параметра;
метод обратной функции.

Рассмотрим некоторые из них.

Используя производную

Общий подход к нахождению множества значений непрерывной функции f(x) заключается в нахождении наибольшего и наименьшего значения функции f(x) в области ее определения (или в доказательстве того, что одно из них или оба не существуют).

В случае, если нужно найти множества значений функции на отрезке:

найти производную данной функции f ‘(x);
найти критические точки функции f(x) и выбрать те из них, которые принадлежат данному отрезку;
вычислить значения функции на концах отрезка и в выбранных критических точках;
среди найденных значений выбрать наименьшее и наибольшее значения;
Множество значений функции заключить между этими значениями.

Если областью определения функции является интервал, то используется та же схема, но вместо значений на концах используются пределы функции при стремлении аргумента к концам интервала. Значения пределов из не входят в множество значений.

Метод границ/оценок

Для нахождения множества значений функции сначала находят множество значений аргумента, а затем отыскивают соответствующие наименьше и наибольшее значения функции функции. Используя неравенства – определяют границы.

Суть состоит в оценке непрерывной функции снизу и сверху и в доказательстве достижения функцией нижней и верхней границы оценок. При этом совпадение множества значений функции с промежутком от нижней границы оценки до верхней обуславливается непрерывностью функции и отсутствием у неё других значений.

Свойства непрерывной функции

Другой вариант заключается в преобразовании функции в непрерывную монотонную, тогда используя свойства неравенств оценивают множество значений вновь полученной функции.

Последовательное нахождение значений сложных аргументов функции

Основан на последовательном отыскании множества значений промежуточных функций, из которых составлена функция

Области значений основных элементарных функций

Функция	Множество значений
$y = kx+ b$	E(y) = (-∞;+∞)
$y = x^{2n}$	E(y) = [0;+∞)
$y = x^{2n +1}$	E(y) = (-∞;+∞)
$y = k/x$	E(y) = (-∞;0)u(0;+∞)
$y = x^{frac{1}{2n}}$	E(y) = [0;+∞)
$y = x^{frac{1}{2n+1}}$	E(y) = (-∞;+∞)
$y = a^{x}$	E(y) = (0;+∞)
$y = log_{a}{x}$	E(y) = (-∞;+∞)
$y = sin{x}$	E(y) = [-1;1]
$y = cos{x}$	E(y) = [-1;1]
$y = {rm tg}, x$	E(y) = (-∞;+∞)
$y = {rm ctg}, x$	E(y) = (-∞;+∞)
$y = arcsin{x}$	E(y) = [-π/2; π/2]
$y = arccos{x}$	E(y) = [0; π]
$y = {rm arctg}, x$	E(y) = (-π/2; π/2)
$y = {rm arcctg}, x$	E(y) = (0; π)

Примеры

Найдите множество значений функции:

Используя производную

НЕ используя производную

Найдите наибольшее и наименьшее значения функции:

$f(x)=sin^{2}{x}+cos{x}-frac{1}{2}$

Используя метод границ/оценок

$y=5-4sin{x}$

$y=cos{7x}+5cos{x}$

$f(x)=1+2sin^{2}{x}$

$$
\ -1leqsin{x}leq 1
\ 0leqsin^{2}{x}leq 1
\ 0leq2sin^{2}{x}leq 2
\ 1leq1+2sin^{2}{x}leq 3
$$
Ответ: E(f) = [1; 3].

$f(x)=3-2^{3+{rm tg}^{2}, x}$

$$
\ -infty < {rm tg}, x < +infty
\ 0 leq {rm tg}^{2}, x < +infty
\ 3 leq 3+{rm tg}^{2}, x < +infty
\ 2^{3} leq 2^{3+{rm tg}^{2}, x} < +infty
\ -infty < -2^{3+{rm tg}^{2}, x} leq -8
\ -infty < 3-2^{3+{rm tg}^{2}, x} leq -5
$$
Ответ: E(f) = (–∞; -5].

$f(x)=2+sqrt{16-lg^{2}{x}}$

$$
\ -infty < lg{x} < +infty
\ 0 leq lg^{2}{x} < +infty
\ -infty < -lg^{2}{x} leq 0
\ -infty < 16-lg^{2}{x} leq 16
\ 0 leq sqrt{16-lg^{2}{x}} leq 4
\ 2 leq 2+sqrt{16-lg^{2}{x}} leq 6
$$
Ответ: E(f) = [2; 6].

$f(x)=sqrt{2-x}+sqrt{2+x}$

$y=sin{x}+cos{x}$

Используя непрерывную функцию

Иные

Использованная литература

Статьи:

Область значения функций в задачах ЕГЭ, Минюк Ирина Борисовна
Советы по нахождению множества значений функции, Беляева И., Федорова С.
Нахождение множества значений функции
Как решать задачи по математике на вступительных экзаменах, И.И.Мельников, И.Н.Сергеев

Общая информация

У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.

Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.

В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.

Основные понятия

Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».

Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.

Например, нужно найти область значений квадратичной функции y = 3x² — 2x — 1. Следует записать уравнение 3x² — 2x — 1 = 0. Ордината вычисляется таким образом: y0 = -D / 4a = -[b² — 4ac] / 4a = -[(-2)^2 — 4 * 3 * (-1)] / (4 * 3) = -16 / 12 = -4/3. Если коэффициент а>0, то ветви параболы направлены вверх. Следовательно, E (y) = (-4/3;+бесконечность).

Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.

Типы функций

Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:

(-бесконечность;+бесконечность): y =kx + b, y = x^(2n+1), y = x^(1/(2n+1)), y = log (x) с основанием а, y = tg (x) и y = ctg (x).
[0;+бесконечность): y = x^(2n), y = x^(1/(2n)) и y = a^x.
(-бесконечность;0] U [0;+бесконечность) только для y = k / x (гипербола).
[-1;1]: y = sin (x) и y = cos (x).
[0;Pi]: y = arccos (x) и arcsin (x).
[-Pi/2;Pi/2]: y = arctg (x) и arcsin (x).

Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.

Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.

Важные свойства

Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:

В случае, когда функция f (x) является непрерывной, и наблюдается ее возрастание или убывание на отрезке [a;b], то множество значений — интервал [f (a);f (b)].
Если y = f (x) обладает непрерывностью на промежутке [a;b], и существует некоторое минимальное m и максимальное М ее значения, то множеством ее значений является интервал [m;M].
При непрерывности и дифференцируемости функции на промежутке [a;b], она имеет минимальное и максимальное значения на данном промежутке.

Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.

Методы нахождения

Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:

Отдельное нахождение значений элементов сложной функции.
Оценочный.
Учет непрерывности и монотонности.
Взятие производной.
Использование max и min функции.

Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.

Для каждого элемента

Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:

Выполнить необходимые преобразования — упростить выражение.
Разбить выражение на элементы.
Выполнить поиск E (f) для каждого элемента.
Произвести замену.
Анализ.
Результат решения.

Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:

Упростить (выделить квадрат): y = log0.5 (4 — 2 * 3^x — 9^x) = log0.5 [5 — (1 — 2 * 3^x — 9^x)] = log0.5 [5 — (3^x + 1)].
Разбить на элементарные функции: y = 3^x, y = 3^x + 1, y = [-(3^x + 1)]^2 и y = [5 — (3^x + 1)]^2.
Определить для каждого элемента E (f): E (3^x) = (0;+бесконечность), E (3^x + 1) = (1;+бесконечность), E ([-(3^x + 1)]^2) = (-бесконечность;-1) и E ([5 — (3^x + 1)]^2) = (-бесконечность;4).
Произвести замену: t = 5 — (3^x + 1)]^2 (-бесконечность <= t <=4).
Анализ: поскольку E (f) на луче (-бесконечность;4) совпадает с интервалом (0;4), то функция непрерывна и убывает. Необходимо отметить, что интервал (0;4) получен при пересечении луча (-бесконечность;4) с областью определения функции логарифмического типа (0;+бесконечность). На интервале (0;4) эта функция непрерывна и убывает. Если t>0, то она стремится к бесконечности. Когда t = 4, ее значение равно -2.
Результат решения — искомый интервал: E (f) = (-2;+бесконечность).

Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.

Оценочный способ

Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:

Доказать непрерывность.
Составить неравенство или неравенства для нескольких функций.
Узнать оценку.
Записать интервал.

Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:

Функция вида y = cos (x) является непрерывной.
Неравенства: -1<=cos (7x)?1 и -5<=5 * cos (x)?5.
Оценка получает при объединении неравенств: -6<=y?6. При значениях независимой переменной x = Pi и x = 0 функция принимает значения -6 и 6 соответственно (нижняя и верхняя границы). Функция состоит из двух элементов, следовательно, она является линейной и непрерывной.
Интервал: E (y) = [-6;6].

Метод позволяет найти решение без использования дополнительных вычислений. Но при его использовании легко ошибиться.

Учет непрерывности и монотонности

Одним из простых способов решения, который специалисты рекомендуют новичкам, является метод учета непрерывности и монотонности. Для этого существует специальный алгоритм:

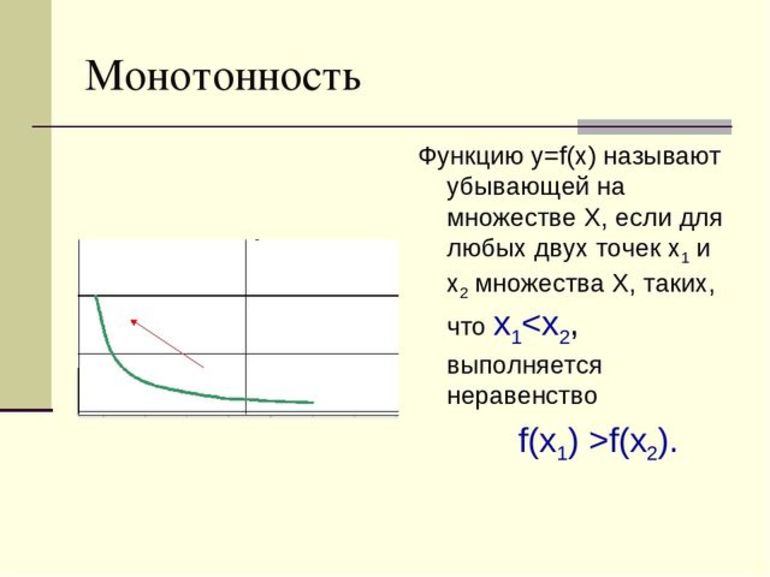
Упростить выражение.
Выполнить замену при необходимости.
Найти вершину графика.
Определить промежуток.
Вычислить максимальное и минимальное значения.
Записать E (f).

Например, существует некоторая функция y = cos (2x) + 2cos (x). Необходимо найти ее E. Искать следует по алгоритму решения методом учета монотонности и непрерывности:

Упростить (по формуле двойного угла): y = 2 * (cos (x))^2 + 2cosx — 1.
Замена t = cos (x): y = 2 * t² + 2 * t — 1 = 2 * (t + 0,5)^2 — 1,5.
Показательная функция является параболой. Она монотонна, непрерывна и имеет вершину по оси ОУ -1,5. Промежуток, который рассматривается — [-1;1], поскольку E (cos (x)) = [-1;1].
Минимальное значение равно -1,5, так как ветви направлены вверх. Максимальное на промежутке [-1;1] – MAX (y) = 3. Для его нахождения нужно построить график параболы y = 2 * (t + 0,5)^2 — 1,5.
Искомый интервал — E (cos (2x) + 2cos (x)) = [-1,5;3].

Чтобы построить график параболы, нужно найти ее вершину и точки пересечения с осью абсцисс. Последние находятся при решении уравнения 2 * (t + 0,5)^2 — 1,5 = 0. Однако существует способ намного проще. Для этого следует привести выражение к виду 2 * (t + 0,5)^2 = 1,5. Отсюда t = – 0,5. Следовательно, координаты вершины — (-0,5;-1,5). Корни уравнения при его решении: t1 = -[(1 + (3)^0.5)] / 2 и t2 = -[(1 — (3)^0.5)] / 2.

Производная, min и max

Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:

Найти производную.
Анализ.
Указать MAX (f) и MIN (f).
Запись интервала в формате (MIN (f);MAX (f)).

Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:

Производная: y’ = [arcsin (x)]’ = 1 / [(1 — x²)^0.5].
Функция возрастает на интервале (-1;1).
Минимум и максимум на отрезке (-1;1): MIN (arcsin (-1)) = -Pi/2 MAX (arcsin (1)) = Pi/2.
Интервал: E (arcsin (x)) = [-Pi/2;Pi/2].

В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:

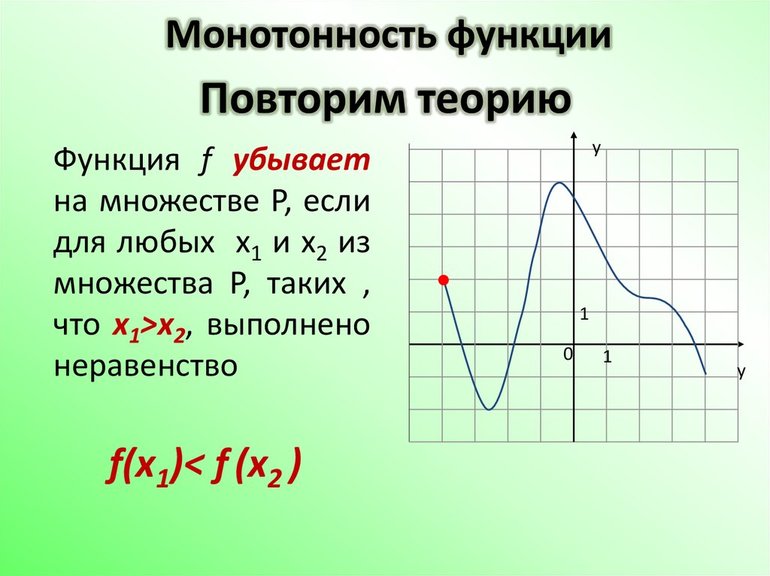
Производная: y’ = [sin (x)]’ = cos (x).
Период функции равен 2Pi. Следует взять отрезок [0;2Pi]. Для нахождения множества значений на нем нужно приравнять производную функции к 0, т. е. cos (x) = 0. Найти х = Pi/2 + Pi * к, где «к» принадлежит Z. Точки экстремума равны Pi/2 и 3Pi/2.
Минимум и максимум на отрезке [0;2Pi): MIN ([sin (3Pi/2)]) = -1 и MAX ([sin (3Pi/2)]) = 1.
E (sin (x)) = [-1;1].

Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.

Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.

Источник

Советы

Об этой статье