Как найти множество заданных предикатов

Гусева
А.И. Дискретная
математика: Математическая логика

Лекции 14-15

Исчисление
предикатов

Основные понятия

Одноместным предикатом P(x)
называется всякая функция одного
переменного, аргумент который х
определен на некотором множестве М,
а значение функции определены на
множестве {0,1}[1].

Множество М, на котором задан
предикат, называется областью
определения предиката.

Множество I_p,
на котором предикат принимает только
истинные значения, называется областью
истинности предиката P(x).

Предикат P(x)
называется тождественно истинным
(тождественно ложным) на множестве
М, если I_p=М
(I_p=0).

N-местным
предикатом Q(x₁,
x₂,…,x_n)
называется всякая функция n
переменных, определенная на множестве
и принимающая значение на множестве
{0,1}.

Предикат P(x)
является следствием Q(x)
()
, если

Предикаты P(x)
и Q(x)
равносильны (),
если
,
т.е. они являются следствием друг друга.

Логические операции над предикатами

Так как предикаты принимают значения
0 и 1, к ним можно применять все операции
алгебры высказываний. Пусть на некотором
множестве М заданы два предиката P(x)
и Q(x).

Конъюнкцией двух предикатов
P(x)
и Q(x)
называется новый предикат
,
который равен 1 при тех и только при тех
значениях
,
при которых каждый из предикатов
принимает значение «истина», и принимает
значение «ложь» во всех остальных
случаях.

Очевидно, что областью истинностью
предиката

является
.

Дизъюнкцией двух предикатов
P(x)
и Q(x)
называется новый предикат
,
который равен 0 при тех и только при тех
значениях
,
при которых каждый из предикатов
принимает значение «ложь», и принимает
значение «истина» во всех остальных
случаях.

Очевидно, что областью истинностью
предиката

является
.

Отрицанием предиката P(x)
называется новый предикат
,
который равен 0 при всех значениях
,
при которых P(x)
равен значению «истина», и равен 1 при
всех значениях
,
при которых P(x)
равен значению «ложь».

Очевидно, что областью истинностью
предиката

является
.

Импликацией предикатов P(x)
и Q(x)
называется новый предикат
,
который равен 0 при тех и только при тех
значениях
,
при которых P(x)
принимает значение «истина», а Q(x)
– значение «ложь», и принимает значение
«истина» во всех остальных случаях.

Очевидно, что областью истинностью
предиката

является
.

Задача 1

Заданы предикаты
,
и

на множестве натуральных чисел N:
:
«число Х делится на 5»

:
«число Х четное».

Найти область истинности предикатов

,

,

.

Решение

Так как I_p
= {5, 10, 15, 20, …. 5n,
..} и I_Q
= {2, 4, 6, 8, 10, … 2n,
..}, то

={10,
20, …,20n,..},

={2,
4, 5, 6, 8, 10, … 2n,5n,
..},

={5,
10, 15,… ,5n,
..}
{1, 3, 5, … 2n-1,
..}= {1, 3, 5, 7, 9, 10, … 2n-1,5n,
..}.

Задача 2

Задан
предикат
:>0
на
множестве рациональных чисел R.
Найти
область истинности предиката
.

Решение

Найдем область, на которой данный
предикат может быть определен. Поскольку
знаменатель дроби не может быть равен
0, то
.
Для того, чтобы наша дробь была
положительной, необходимо, чтобы знаки
числителя и знаменателя совпадали:

Отсюда

Кванторные
операции над предикатами

Задан предикат,
определенный на множестве М.
Если а – некий элемент из
множества М, то его подстановка
вместо х в предикат,
превращает этот предикат в высказывание

.

В логике предикатов существуют две
кванторные операции, которые превращают
одноместный предикат в высказывание и
связывают переменные.

Пусть задан предикат,
определенный на множестве М.

Тогда под выражением
понимаем
высказывание, истинное тогда и только
тогда, когда

истинен для каждого элемента х
из М, и ложное в противном
случае. Это высказывание не зависит от
х, его словесное выражение
выглядит так «Для любого х

истинно». Символ

называется квантором всеобщности.

Переменная х в предикате

свободна, в высказывании

переменная х связана квантором
всеобщности.

Под выражением
понимаем
высказывание, истинное тогда и только
тогда, когда существует элемент х
из М, для которого

истинен, и ложное в противном
случае. Это высказывание не зависит от
х, его словесное выражение
выглядит так «Существует х, для
которого

истинно». Символ

называется квантором существования.

Переменная х в предикате

свободна, в высказывании

переменная х связана квантором
существования.

Кванторные
операции применяются и к многоместным
предикатам.

Например, применение кванторной операции

к двухместному предикату, превращает
его в одноместный, зависящий только от
переменной y.

Рассмотрим предикат
,
определенный на множестве M={a₁,
a₂,…,a_n}.
Если

тождественно истинен, то истинными
будут высказывания
….
При этом истинными будут выказывание


и конъюнкция
.
Если найдется хотя бы один элемент
a_j
из М, на котором
,
то ложными будут высказывания

и конъюнкция
.
Следовательно, существует равносильность

Рассмотрим предикат
,
определенный на множестве M={a₁,
a₂,…,a_n}.
Если

тождественно ложен, то ложными будут
высказывания
….
При этом ложными будут выказывание


и дизъюнкция
.
Если найдется хотя бы один элемент
a_j
из М, на котором
,
то истинными будут высказывания

и дизъюнкция
.
Следовательно, существует равносильность

Таким
образом, кванторные операции можно
трактовать, как обобщение дизъюнкции
и конъюнкции на случай бесконечных
множеств.

Исчисление предикатов

Исчисление предикатов – это формальная
теория, в которой определены следующие
компоненты [2].

Алфавит:

связки основные

вспомогательные

служебные символы ( , )

кванторы всеобщности

существования

предметные константы a,
b,…a₁,
b₁,

переменные x,y,….x₁,y₁

предметные предикаты P,
Q, R,
….

функторы f,
g, h,….

Формулы: (определены в нотации
Бэкуса-Наура)

<формула> ::=
<атом> ││<формула>
<формула>
│

<переменная>
<формула> │
<переменная><формула>

<атом> ::=
<предикат>( <список термов> )

<список
термов> ::= <терм> │<терм> , <список
термов>

<терм> ::=
<константа> │<переменная> │<функтор>
(<список термов> )

Аксиомы:

Кроме того, выполняется любая система
аксиом исчисления высказываний.

Правила вывода:

,
,

Исчисление предикатов, в котором кванторы
могут связывать только предметные
переменные, но не предикаты или функторы,
называется исчислением первого
порядка.

Исчисления, в которых кванторы связывают
не только предметные переменные, но и
предикаты, функторы и т.д., называются
исчислениями высших порядков.

Равносильные формулы

Рассмотрим основные равносильности
исчисления предикатов. Их можно разбить
на четыре группы [1,3].

1. Равносильности для двойственности

2. Равносильности для конъюнкции и
квантора всеобщности

3. Равносильности для дизъюнкции и
квантора существования

4. Вынесение константы

Задача 3

Доказать равносильность.

Решение

Если предикаты P(x)
и Q(x)
тождественно истинны, то тождественно
истинен предикат
,
а поэтому, будут истинны высказывания

т.е. обе части равносильности принимают
значение истина.

В случае, если один из предикатов,
например,
,
( а как следствие
)
будет не тождественно истинен, то ложными
будут

Предваренная нормальная
форма

Говорят, что формула исчисления предикатов
имеет нормальную форму, если она содержит
только операции конъюнкция, дизъюнкция
и кванторные операции, а оперция отрицания
отнесена к элементарным формулам.

Например, приведение формулы к нормальной
форме выглядит следующим образом.

Среди нормальных форм выделяют
предваренные нормальные формы (ПНФ), в
которых кванторные операции либо
полностью отсутствуют, либо они
используются после всех операций алгебры
логики.

Например, приведем рассматриваемую
формулу к ПНФ

=

=

А для формулы необходимы следующие
преобразования.

Теорема

Всякая
формула исчисления предикатов может
быть приведена к предваренной нормальной
форме

Общезначимость и
выполнимость

Формула А выполнима в области
М, если существуют значения
переменных, входящих в эту формулу и
отнесенных к области М, при
которых формула принимает истинные
значения.

Формула А выполнима, если
существует область, на которой она
выполнима.

Формула А тождественно истинна в
области М, если она принимает
истинные значения для всех значений
переменных, входящих в эту формулу и
отнесенных к этой области.

Формула А тождественно ложна в
области М, если она принимает ложные
значения для всех значений переменных,
входящих в эту формулу и отнесенных к
этой области.

Формула А общезначима, если она
тождественно истинна во всякой области.

Разрешимость

Проблема разрешимости для исчисления
предикатов ставится стандартно:
существует ли алгоритм, позволяющий
для любой формулы установить, является
ли она общезначимой, выполнимой или
тождественно ложной?

Ответ на этот вопрос для бесконечных
областей дает теорема Черча.

Теорема Черча

Проблема
разрешимости исчисления предикатов в
общем виде неразрешима

Очевидно, что проблема разрешимости
для конечных областей разрешима.

Литература

1. Лихтарникова
   Л.М., Сукачева Т.Г. Математическая
   логика/Курс лекций. – СПб.: Издательство
   «Лань», 1998.-288с

2. .Новиков Ф.А.
   Дискретная математика для программистов.
   – СПб.: Питер, 2001. – 304с

3. Горбатов В.А.
   Фундаментальные основы дискретной
   математики. – М.: Наука. Физматлит,
   1999.-544с

Соседние файлы в папке ДМ_К1

• #

  10.05.2014205.31 Кб291.doc

• #

  10.05.2014198.66 Кб3710.doc

• #
• #
• #

  10.05.2014158.21 Кб942.doc

• #

  10.05.2014144.9 Кб473.doc
• #

  10.05.2014123.39 Кб244.doc

• #

  10.05.2014127.49 Кб235.doc

• #

  10.05.2014119.81 Кб246.doc

Логика предикатов

Предикаты вслед за высказываниями являются следующим важным предметом, исследуемым математической логикой. Понятие предиката обобщает понятие высказывания, а теория предикатов представляет собой более тонкий инструмент, по сравнению с теорией высказываний, для изучения закономерностей процессов умозаключения и логического следования, составляющих предмет математической логики. В настоящей главе рассматриваются основы теории предикатов.

Понятие предиката

В высказывании все четко: это — конкретное утверждение о конкретных объектах — истинное или ложное. Предикат — предложение, похожее на высказывание, но все же им не являющееся: о нем нельзя судить, истинно оно или ложно. Дадим точное определение.

Определение 18.1. Определенным на множествах n-местным предикатом называется предложение, содержащее переменных , превращающееся в высказывание при подстановке вместо этих переменных любых конкретных элементов из множеств соответственно.

Для n-местного предиката будем использовать обозначение . Переменные называют предметными, а элементы множеств , которые эти переменные пробегают, — конкретными предметами. Всякий n-местный предикат , определенный на множествах , представляет собой функцию п аргументов, заданную на указанных множествах и принимающую значения в множестве всех высказываний. Поэтому предикат называют также функцией-высказыванием.

Рассмотрим пример. Предложение “Река впадает в озеро Байкал” является одноместным предикатом, определенным над множеством всех названий рек. Подставив вместо предметной переменной название “Баргузин”, получим высказывание “Река Баргузин впадает в озеро Байкал”. Это высказывание истинно. Подставив вместо предметной переменной название “Днепр”, получим ложное высказывание “Река Днепр впадает в озеро Байкал”.

Другой пример. Предложение (выражение) “” является двухместным предикатом, заданным над множествами . Множества, на которых задан двухместный предикат, совпадают (говорят, что “двухместный предикат задан на множестве “). Пара действительных чисел 2, 2 превращает данный предикат в истинное высказывание: ““, а пара чисел 2, 3 — в ложное: ““.

Отметим еще один подход к понятию предиката. Как отмечалось, предикат , определенный на множествах , превращается в конкретное высказывание , если вместо предметных переменных подставить в него конкретные предметы (элементы ) из множеств соответственно. Это высказывание может быть либо истинным, либо ложным, т. е. его логическое значение равно 1 или 0. Следовательно, данный предикат определяет функцию аргументов, заданную на множествах принимающую значение в двухэлементном множестве . Иногда эту функцию и называют предикатом.

---

Классификация предикатов

Определение 18.2. Предикат , заданный на множествах , называется:

а) тождественно истинным, если при любой подстановке вместо переменных любых конкретных предметов из множеств соответственно он превращается в истинное высказывание ;

б) тождественно ложным, если при любой подстановке вместо переменных любых конкретных предметов из множеств соответственно он превращается в ложное высказывание;

в) выполнимым (опровержимым), если существует по меньшей мере один набор конкретных предметов из множеств соответственно, при подстановке которых вместо соответствующих предметных переменных в предикат последний превратится в истинное (ложное) высказывание .

Приведем примеры предикатов.

Одноместный предикат “Город расположен на берегу реки Волги”, определенный на множестве названий городов, является выполнимым, потому что существуют города, названия которых превращают данный предикат в истинное высказывание, или, иначе, удовлетворяют этому предикату (например, Ульяновск, Саратов и т. д.). Но данный предикат не будет тождественно истинным, потому что существуют города, названия которых превращают его в ложное высказывание, или, иначе, не удовлетворяют этому предикату (например, Прага, Якутск и т.д.). Этот же предикат являет собой пример опровержимого, но не тождественно ложного предиката (продумайте!).

В другом примере одноместный предикат ““, определенный на множестве действительных чисел, тождественно истинный. Наконец, двухместный предикат ““, заданный также на множестве действительных чисел, является тождественно ложным предикатом, потому что любая пара действительных чисел превращает его в ложное высказывание (не удовлетворяет ему).

Отметим некоторые достаточно очевидные закономерности взаимосвязей между предикатами различных типов (рекомендуется осмыслить их):

1) каждый тождественно истинный предикат является выполнимым, но обратное неверно;
2) каждый тождественно ложный предикат является опровержимым, но обратное неверно;
3) каждый не тождественно истинный предикат будет опровержимым, но, вообще говоря, не будет тождественно ложным;
4) каждый не тождественно ложный предикат будет выполнимым, но, вообще говоря, не будет тождественно истинным.

---

Множество истинности предиката

Определение 18.3. Множеством истинности предиката , заданного на множествах , называется совокупность всех упорядоченных n-систем , в которых , таких, что данный предикат обращается в истинное высказывание при подстановке . Это множество будем обозначать . Таким образом,

Множество истинности “-местного предиката представляет собой n-арное отношение между элементами множеств . Если предикат — одноместный, заданный над множеством , то его множество истинности является подмножеством множества .

Например, множеством истинности двухместного предиката “Точка принадлежит прямой “, заданного на множестве всех точек плоскости и на множестве всех прямых этой плоскости, является бинарное отношение принадлежности (инцидентности) между точками и прямыми плоскости. Другой пример. Множество истинности двухместного предиката , заданного на множестве , есть множество всех таких пар действительных чисел, которые являются координатами точек плоскости, образующими окружность с центром в начале координат и радиуса 3. Наконец, если “” — одноместный предикат над , то , или .

В терминах множества истинности легко выразить понятия, связанные с классификацией предикатов (определение 18.2). В самом деле, n-местный предикат , заданный на множествах , будет:

а) тождественно истинным тогда и только тогда, когда ;
б) тождественно ложным тогда и только тогда, когда ;
в) выполнимым тогда и только тогда, когда ;
г) опровержимым тогда и только тогда, когда .

На языке множеств истинности еще более отчетливо проясняются закономерности взаимосвязей между предикатами различных типов, отмеченные в конце предыдущего пункта. Проанализируйте их еще раз.

---

Равносильность и следование предикатов

Определение 18.4. Два n-местных предиката и , заданных над одними и теми же множествами , называются равносильными, если набор предметов (элементов) превращает первый предикат в истинное высказывание в том и только в том случае, когда этот набор предметов превращает второй предикат в истинное высказывание .

Другими словами (на языке множеств истинности), предикаты и равносильны тогда и только тогда, когда их множества истинности совпадают. .

Утверждение о равносильности двух предикатов и символически будем записывать так: . Отношение равносильности предикатов является отношением эквивалентности, так что совокупность всех n-местных предикатов, определенных на множествах , распадается на непересекающиеся классы равносильных предикатов (все они определяют одну и ту же функцию, заданную на множествах и принимающую значения в двухэлементном множестве ). Переход от предиката к равносильному ему предикату называется равносильным преобразованием первого. Это понятие очень важно для школьной математики, потому что изучаемые в ней уравнения и неравенства представляют собой частные виды предикатов. Решение уравнения и неравенства есть поиск их множеств истинности. При таком поиске мы проделываем над уравнением и неравенством различные преобразования, и здесь важно, чтобы эти преобразования были равносильными, т. е. чтобы найденное множество оказалось бы множеством истинности именно исходного уравнения или неравенства. Аналогична ситуация при решении систем уравнений или неравенств.

Рассмотрим простой пример. Пусть требуется решить уравнение (найти множество истинности предиката): . Преобразуем его равносильным образом:

Ответ: — множество всех решений данного уравнения (множество истинности данного предиката).

Отметим следующее немаловажное обстоятельство: может быть так, что два предиката равносильны, если их рассматривать над одним множеством, и неравносильны, если их рассматривать над другим (в частности, объемлющим первое) множеством. Такова, например, ситуация с предикатами: и .

---

Определение 18.5. Предикат , заданный над множествами , называется следствием предиката , заданного над теми же множествами, если он превращается в истинное высказывание на всех тех наборах значений предметных переменных из соответствующих множеств, на которых в истинное высказывание превращается предикат .

Другими словами (в терминах множеств истинности), можно сказать, что предикат является следствием предиката тогда и только тогда, когда .

Утверждение о том, что предикат является следствием предиката , будем символически записывать так: .

Например, одноместный предикат, определенный на множестве натуральных чисел, “ делится на 3″ является следствием одноместного предиката, определенного на том же множестве, “ делится на 6″. Из двух предикатов, упомянутых перед последним определением, первый будет следствием второго, если считать, что оба предиката заданы на множестве целых чисел.

Язык множеств истинности позволяет установить взаимосвязь между понятиями равносильности и следования предикатов: два предиката, определенные на одних и тех же множествах, равносильны тогда и только тогда, когда каждый из них является следствием другого. Кроме того, этот же язык дает возможность без труда установить следующие простые теоремы.

Теорема 18.6. Каждые два тождественно истинных (тождественно ложных) предиката, заданных на одних и тех же множествах, равносильны. Обратно, всякий предикат, равносильный тождественно истинному (тождественно ложному) предикату, сам является тождественно истинным (тождественно ложным) предикатом.

Теорема 18.7. Каждый тождественно истинный n-местный предикат является следствием любого другого n-местного предиката, определенного на тех же множествах. Каждый n-местный предикат является следствием любого тождественно ложного n-местного предиката, определенного на тех же множествах.

Теорема 18.8. Пусть и — два n-местных предиката, определенные на одних и тех же множествах, такие, что есть следствие . Тогда:

а) если тождественно истинный (выполнимый), то и тождественно истинный (выполнимый);

б) если тождественно ложный (опровержимый), то и тождественно ложный (опровержимый).

Доказательство теоремы 18.8:

а) Поскольку , поэтому . Если теперь тождественно истинный предикат, то

(где — множества, на которых определены n-местные предикаты и ).

Но . Поэтому , а, значит, предикат — тождественно истинный предикат. Если же — выполнимый предикат, то . Но . Тогда и — выполнимый предикат.

б) Пусть — тождественно ложный предикат. Тогда . Но , поэтому . Следовательно, предикат — тождественно ложный. Наконец, пусть — опровержимый предикат. Тогда . Поскольку, кроме того,

и , то .

Следовательно, предикат — опровержимый.

Отыщите самостоятельно в настоящем и предыдущем пунктах данной лекции утверждения, обосновывающие остальные сформулированные теоремы.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Рассмотрим повествовательное предложение «Число X Меньше 3». Это предложение не является высказыванием. Если заменить в нём переменную X На конкретное число, то получим высказывание – истинное или ложное в зависимости от значения X.

Определение. Предикатом называется предложение с одной или несколькими переменными, обращающееся в Высказывание при подстановке вместо переменных их значений.

Предикаты обозначаются прописными латинскими буквами с приписанной переменной. Предикат записывается в квадратных скобках.

Например, .

Областью определения D(P) предиката называется множество значений переменной , при которых предикат имеет смысл.

Например, запись Р(X), D(P) означает предикат одной переменной X, Определённый на множестве D(P).

Областью истинности предиката называется множество значений переменной , при которых предикат обращается в Истинное высказывание.

К предикатам, определённым На одном и том же множестве, применяются логические операции, определённые в пункте 1.2. Кроме них используются две дополнительные логические операции Связывания переменных кванторами.

1. Символическая запись означает высказывание «для всех » или «для каждого », истинное тогда и только тогда, когда предикат принимает истинное значение для Каждого элемента множества D(P).

Символ называется Квантором всеобщности, а переменная – Связанной этим квантором.

2. Символическая запись означает высказывание «существует , для которого » или «найдётся хотя бы одно , такое что», истинное тогда и только тогда, когда предикат принимает истинное значение Хотя бы для одного элемента множества D(P).

Символ называется Квантором существования, а переменная – Связанной этим квантором.

Символическая запись означает высказывание «существует единственный элемент , для которого », истинное тогда и только тогда, когда предикат принимает истинное значение Только для одного элемента множества D(P).

Например: высказывание «Произведение любых двух последовательных натуральных чисел кратно числу два» записывается в символьной форме с использованием квантора всеобщности так: (в математике запись «» означает, что число A делится на число B без остатка).

Предикат двух переменных и обозначается символом.

Например: если и – действительные числа, обозначает предикат , то высказывание читается так: для любого действительного числа существует единственное действительное число такое, что . Это истинное высказывание, так как для любого действительного числа существует единственное действительное число , при котором .

С помощью логических операций и скобок формируются формулы алгебры предикатов. Все равносильности алгебры высказываний, сформулированные в теореме 1.1, справедливы для формул алгебры предикатов. Для упрощения записи формул устанавливается следующий порядок выполнения логических операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.

Теорема 1.4. При вынесении квантора из-под знака отрицания высказывания квантор изменяется на двойственный, а операция отрицания переходит на предикат:

и .

Пример. Найти множество истинности предиката , определенного на множестве действительных чисел.

Решение. По условию, . Для ответа на вопрос задачи нужно найти множество решений квадратного неравенства: . Значит, .□

Определение. Предикат называется Выполнимым на множестве, если он обращается в истинное высказывание Хотя бы при одном значении переменной.

Например, на множестве действительных чисел предикат является выполнимым.

Определение. Предикат называется Тождеством на множестве, если он обращается в истинное высказывание при Всех значениях переменной.

Например, на множестве действительных чисел предикат является тождеством.

Определение. Предикат называется Невыполнимым на множестве, если он обращается в ложное высказывание при Всех значениях переменной.

Например, на множестве действительных чисел предикат является невыполнимым.

Задачи и упражнения

1.16. Выберите среди следующих предложений предикаты.

1) Здравствуйте, Петя!

2) Число 5 является корнем уравнения .

3) .

4) Сколько граммов в одном килограмме?

5) X2 + y2.

6) .

7) Число 6 делится на 2 и на 3.

1.17. Запишите следующие высказывания в символьной форме с использованием предикатов и кванторов. Определите истинностные значения высказываний с кванторами:

1) любое натуральное число больше 3;

1.19. Выберите среди заданных высказываний правильную запись высказывания «Всякое действительное число не меньше самого себя»:

1) ;

2) ;

3) ;

4).

1.20. Укажите, какие из следующих предикатов выполнимы на множестве действительных чисел:

1) ;

2) ;

3) ;

4) .

1.21. Укажите, какие из следующих предикатов являются тождествами на множестве действительных чисел:

1) ;

2) ;

3) ;

4) .

1.22. Приведите примеры значений параметра , при которых каждый из заданных предикатов, определенных на множестве действительных чисел, является тождеством:

1) ;

2) ;

3) ;

4) .

1.23. Найдите и изобразите на числовой плоскости область истинности следующих предикатов:

1) ;

2) ;

3) ;

4) ;

5) .

< Предыдущая		Следующая >

ЧАСТЬ III. ЛОГИКА ПРЕДИКАТОВ
§1. Понятие предиката. Множество истинности предиката. Равносильные предикаты. Классификация предикатов.
Рассмотрим предложения, содержащие переменную : 1) – простое число, 2) , 3) , 4) – город на Волге.
Высказываниями эти предложения не являются, так как о них мы не можем сказать, истинны они или ложны. Однако из этих предложений можно получить высказывания, придавая переменной те или иные значения из некоторого множества. Например, если в предложении 1) заменить переменную конкретными значениями из множества натуральных чисел, то получим высказывания. При получим ложное высказывание «- простое число», при получим истинное высказывание « – простое число» и так далее.
Такие предложения с одной переменной называются одноместными предикатами.
Определение. Одноместным предикатом, определенном на множестве , называется предложение с переменной, обращающееся в высказывание при подстановке вместо этой переменной конкретных элементов (предметов) из множества .
Множество называется множеством определения данного предиката.
Конкретные одноместные предикаты, заданные на множестве , будем обозначать , ,…. Одноместные предикатные переменные, заданные на множестве , будем обозначать , ,… .
В приведенных примерах множества определения предикатов таковы: 1) , 2) , 3) , 4) множество всех названий городов.
Определение. Множеством истинности предиката называется подмножество множества , состоящее из элементов, при подстановке которых в данный предикат он обращается в истинное высказывание.
Множество истинности предиката будем обозначать . .
В приведенных выше примерах множества истинности предикатов таковы 1) множество простых чисел, 2) , 3) множество четных целых чисел, 4) множество названий городов на Волге.
Определение. Два предиката и , заданные на одном и том же множестве называются равносильными, если их множества истинности совпадают.
Тот факт, что предикаты и , заданные на множестве , равносильны будем обозначать .
Пример. : «», ,
: «»,.
, .
Значит, .
Определение. Предикат , заданный на множестве , называется тождественно истинным (ложным), если при любой подстановке вместо переменной любого конкретного предмета из множества , он превращается в истинное (ложное) высказывание .
Определение. Предикат , заданный на множестве , называется выполнимым (опровержимым), если существует хотя бы один конкретный предмет , при подстановке которого вместо переменной в предикат , он превращается в истинное (ложное) высказывание.
Примеры. Предикат : «», тождественно истинный и одновременно выполнимый.
Предикат : «», тождественно ложный и одновременно опровержимый.
Предикат : «», выполнимый и одновременно опровержимый.
Обобщением понятия одноместного предиката является понятие многоместно предиката.
Определение. – местным предикатом, определенным на множестве называется предложение, содержащее (предметных) переменных и обращающееся в высказывание при подстановке вместо этих переменных конкретных элементов (предметов) из множеств соответственно.
– местные предикаты будем обозначать
,
Приведем примеры многоместных предикатов:
: «», .
: «»,.
: «Прямая проходит через точки и », , где есть множество прямых плоскости, есть множество точек плоскости.
: «Река впадает в море », где – множество названий рек, – множество названий морей.
Упражнения.
1.1. Найдите множества истинности следующих предикатов, заданных на множестве .
1) ,
2) ,
3) двузначное число кратно 10, ,
4) , .
Решение.
1) решая неравенство , получаем , .
2) учитывая, что а если , получаем .
3) .
4) Областью допустимых значений уравнения является множество . На этом множестве данное уравнение равносильно уравнению , которому удовлетворяет любое действительное число из множества . Следовательно, .
1.2. Выяснить, равносильны ли предикаты, если их последовательно рассматривать заданными на множестве действительных чисел , затем на множестве рациональных чисел , на множестве целых чисел , на множестве натуральных чисел .
1) : «», : «».
2) : «», : « ».
3) : «», : «».
4) : «», : «».
Решение.
1) На множестве действительных чисел множество истинности предиката , а предиката , значит и не равносильны.
На множестве рациональных чисел , , значит и не равносильны. .
На множестве целых чисел , , значит .
На множестве натуральных чисел , , значит .
2) На множестве , , значит и не равносильны на множестве .
Отсюда видим, что данные предикаты не равносильны на множестве и равносильны на множестве .
3) На множестве , поэтому и не равносильны на множестве .
Отсюда видим, что данные предикаты не равносильны на множеств и равносильны на множествах , .
4) На множестве , , поэтому и не равносильны на множестве .
Отсюда видим, что данные предикаты не равносильны на множествах и равносильны на множестве .
1.3. Среди предикатов укажите тождественно истинные, тождественно ложные, выполнимые.
1) : «», ,
2) : «», ,
3) : «», .
Решение.
1) , значит предикат тождественно истинный,
2) , значит предикат тождественно ложный,
3) , значит предикат выполнимый.
§2 Логические операции над предикатами
Предикаты, так же, как высказывания принимают два значения и , поэтому к ним применимы все операции алгебры высказываний.
Рассмотрим логические операции над одноместными предикатами.
Пусть предикаты и заданы на некотором множестве .
Определение. Конъюнкцией предикатов и , заданных на множестве , называется предикат , заданный на множестве , который обращается в истинное высказывание при тех и только тех из , при которых оба предиката и обращаются в истинные высказывания.
Пример. Рассмотрим предикаты : «», , и : «», . Тогда : «», , то есть : «», .
Аналогично определяются дизъюнкция предикатов , , отрицание предиката , .
Определение. Импликацией предикатов и , заданных на множестве , называется предикат , заданный на множестве , который обращается в ложное высказывание при тех и только тех из , при которых предикат принимает значение «истина», а предикат – значение «ложь».
Пример. Рассмотрим предикаты : «Число », , : «Число – натуральное», . : «Если число , то – натуральное число», . .
Определение. Эквиваленцией предикатов и , заданных на множестве , называется предикат , заданный на множестве , который обращается в истинное высказывание при тех и только тех из , при которых предикаты и одновременно либо истинны, либо ложны.
Пример. Для предикатов , , рассмотренных в предыдущем примере, получаем : «Число тогда и только тогда, когда число натуральное», .
.
Свойства логических операций над предикатами получаются из свойств логических операций над высказываниями.
Пусть , , – произвольные предикаты, заданные на множестве , тогда
1. .
2. .
3.
Остальные равносильности 4-10 получаются из соответствующих равносильностей алгебры высказываний.
1о .
2о .
3о .
Можно показать, что для любых предикатов и , заданных на множестве
(1), (2), (3).
Тогда, учитывая равносильности 1о и 2о, получаем
(4)
(5).
Изобразим множества истинности конъюнкции, дизъюнкции, отрицания, импликации и эквиваленции указанных предикатов с помощью кругов Эйлера-Венна.
Аналогично определяются операции над – местными предикатами.
Упражнения.
2.1. Пусть даны предикаты : «», : «», . Найдите множества истинности предикатов , , , , , , .
Решение.
Так как , , то, учитывая равенства (1) – (5), получаем
2.2. Изобразите на координатной плоскости множества истинности предикатов:
1) «» «», 4) «» «»,
2) «» «», 5) «» «».
3) «» «»,
Решение.
1) Множеством истинности указанного предиката является пересечение множеств истинности предикатов «» и «». (рис.1)
2) Множеством истинности указанного предиката является объединение множеств истинности предикатов «» и «». (рис.2)
рис.1 рис.2
3)Учитывая, что предикат
(«» «»)(«» «»),
получаем, что множеством истинности указанного предиката является объединение множеств истинности предикатов «» и «». (рис.3)
4) Учитывая, что предикат
(«» «)(«» «»),
получаем, что множеством истинности указанного предиката является объединение множеств истинности предикатов «» и «». (рис.4)
5) Учитывая, что предикат («» «»)(« «») («» «»), получаем, что множеством истинности указанного предиката является пересечение множеств истинности предикатов, рассмотренных в пунктах 3 и 4. (рис.5)
рис.3 рис. 4
рис. 5
§3 Кванторные операции над предикатами.
Специфика, природы предикатов позволяет ввести над ними такие операции, которые не имеют аналогов среди операций над высказываниями.
Известно, что для превращения одноместного предиката в высказывание нужно подставить вместо переменной какой-либо предмет из множества определения предиката. Имеется еще один способ для такого превращения – это применение к предикату операций связывания квантором общности или квантором существования. Поясним сказанное на примере.
Пусть на множестве задан предикат «- простое число». Поставим перед предикатом слово «всякое». Получим: «Всякое натуральное число – простое» – ложное высказывание. Поставим перед предикатом слово «существует». Получим: «Существует натуральное число , являющееся простым» – истинное высказывание.
Определение. Операцией связывания квантором общности по переменной одноместного предиката , заданного на множестве , называется логическая операция, обращающая предикат в высказывание, которое истинно в том и только том случае, когда предикат , тождественно истинен.
Обозначают: . Читают: «Для всех из истинно ». Вместо слова «все» можно встретить слова: «каждое», «любое», «всякое». Символ – это перевернутая латинская буква , первая в немецком слове «alle» – все.
Определение. Операцией связывания квантором существования по переменной одноместного предиката, заданного на множестве , называется логическая операция, обращающая предикат в высказывание, которое ложно тогда и только тогда, когда предикат , тождественно ложен.
Обозначают: . Читают: «Существует такое из , что истинно . Вместо слова «существует» употребляют слова: « найдется», «хотя бы для одного». Символ – это перевернутая латинская буква – первая в немецком слове «existieren» – существовать.
Переменную в предикате , называют свободной (ей можно давать различные значения из ), а в высказываниях , переменную называют связанной соответственно квантором , квантором .
Можно доказать, что для кванторов , справедливы равносильности (законы де Моргана для кванторов)
(1)
(2).
Равносильность (1) говорит о том, что высказывание: «Неверно, что для всех истинно » равносильно высказыванию: «Существует , такой, что истинно ».
Равносильность (2) говорит о том, что высказывание: «Не существует , при котором истинно » равносильно высказыванию: «Для всех будет истинно ».
Примеры.
1. «- простое число», . Высказывание: « Неверно, что любое натуральное число простое» равносильно высказыванию: Существует натуральное число , не являющееся простым».
(,) «- простое число»
(,) «- не простое число»
2. : , . Высказывание: « Неверно, что существует действительное число , такое, что «» равносильно высказыванию: «Ни одно действительное число не удовлетворяет равенству ». .
Кванторные операции можно применять к – местному предикату; в результате получится – местный предикат, в котором одна из переменных будет связанной, а остальные – свободными. К полученному – местному предикату можно применять кванторные операции по одной из оставшихся свободными переменных, в результате получим – местный предикат и так далее.
Упражнения.
3.1. Для предикатов «» и «», определенных на множестве , установите, какие из высказываний , , , истинны, а какие ложны.
Решение.
Так как при любом действительном , то предикат , тождественно истинный, по определению кванторов и высказывания , – истинные. Корнями квадратного трехчлена являются числа и , поэтому . Значит, предикат , не тождественно истинный и не тождественно ложный, по определению кванторов и высказывание ложное, а высказывание истинное.
3.2. Каждый из предикатов «», «», заданных на множестве обратить в высказывание; а) подставляя место свободной переменной какое-либо значение из множества определения; б) применяя к предикатам операции связывания кванторами , по свободной переменой.
Решение.
В предикате «» переменная – свободная, а – связанная. Обозначим этот предикат . При получаем «» – истинное высказывание. При получаем «» – ложное высказывание. Следовательно, предикат , не тождественно истинный и не тождественно ложный.
Применяя к предикату кванторные операции получаем: «» – ложное высказывание.
«» – истинное высказывание.
В предикате «» переменная – свободная, а – связанная. Обозначим этот предикат . При получаем «» – ложное высказывание. При получаем «» – ложное высказывание. Легко видеть, что предикат , тождественно ложный.
Применяя к предикату , кванторные операции, получаем: «» – ложное высказывание.
«» – ложное высказывание.
3.3. К предикату «» , применить операции связывания кванторами , по переменным и . Рассмотреть всевозможные высказывания, получающиеся при этом.
Решение.
Применение кванторных операций к предикату «» приводит а восьми возможным высказываниям:
1) «» – «Для любых действительных и выполняется равенство » Ложное высказывание.
2) «» – «Существует действительное число такое, что квадрат любого действительного числа равен ». Ложное высказывание.
3) «» – «Для любого действительного числа существует действительное число такое, что ». Ложное высказывание.
4) «» – «Существуют действительные числа и такие, что » Истинное высказывание.
5) «» – «Для любых действительных чисел и выполняется равенство » Ложное высказывание.
6) «» – « Существует действительное число такое, что любое действительное число равно ». Ложное высказывание.
7) «» – « Для любого действительного числа существует действительное число такое, что ». Истинное высказывание.
8) «» – «Существуют действительные числа и такие, что ». Истинное высказывание.
Из этого примера видим, что в общем случае изменение порядка следования разноименных кванторов изменяется смысл высказывания, а значит и его значение (например, высказывания и ).
§4 Логическое следствие. Необходимые, достаточные условия. Условия необходимые и достаточные.
Пусть предикаты и заданы на множестве .
Определение. Предикат , заданный на множестве , называется логическим следствием предиката , заданного на том же множестве , если он превращается в истинное высказывание при всех тех значениях предметной переменной , при которых в истинное высказывание превращается предикат . В этом случае предикат называют необходимым условием для предиката , а предикат называют достаточным условием для предиката .
Из определения логического следствия видим, что предикат является логическим следствием предиката тогда и только тогда, когда .
Теорема. Предикат , является логическим следствием предиката , тогда и только тогда, когда предикат , является тождественно истинным.
Это значит, что всякую тождественно истинную импликацию можно сформулировать, используя термины «необходимо», «достаточно».
«Для того, чтобы предикат был истинным необходимо, чтобы предикат был истинным».
«Для того, чтобы предикат был истинным достаточно, чтобы был истинным предикат ».
Отметим, что термин «необходимое условие» часто заменяют словами: «только в том случае», «только тогда», «требуется», а термин «достаточное условие» заменяют словами: «тогда, когда», «в том случае, если».
Пусть каждый из предикатов , и , является логическим следствием другого, следовательно тождественно истинными являются импликации
(1) , ,
(2) , .
В этом случае каждый из предикатов является для другого необходимым и достаточным условием, а тождественная истинность импликаций (1) и (2) означает, что тождественно истинной будет эквиваленция , .
Этот факт читают так:
«Для того, чтобы было истинно необходимо и достаточно, чтобы было истинно », или
« истинно тогда и только тогда, когда истинно », или
« истинно в том и только в том случае, когда истинно ».
Пример. Рассмотрим предикаты:
: «- ромб», : «- параллелограмм», , где – множество четырехугольников плоскости.
(3) Предикат , :
«Если четырехугольник – ромб, то четырехугольник – параллелограмм» тождественно истинный. Следовательно, предикат есть логическое следствие предиката , а значит – предикат «четырехугольник – параллелограмм» есть необходимое условие для предиката «четырехугольник – ромб», а предикат «четырехугольник – ромб» есть достаточное условие для предиката «четырехугольник – параллелограмм».
Используя термины «необходимое условие», «достаточное условие» импликацию (3) можно выразить так:
«Для того, чтобы четырехугольник был ромбом, необходимо, чтобы четырехугольник был параллелограммом». Иначе: «Четырехугольник ромб только тогда, когда он параллелограмм».
«Для того, чтобы четырехугольник был параллелограммом, достаточно, чтобы четырехугольник был ромбом». Иначе: «Четырехугольник параллелограмм тогда, когда он ромб».
Таким образом, необходимое условие представляет собой то требование, которое непременно должно быть выполнено для справедливости условия . Однако справедливость не гарантирует справедливости условия , то есть не является достаточным условием для .
Упражнения.
4.1.Определите, является ли один из предикатов, заданных на множестве действительных чисел, логическим следствием другого:
1) : «», : «».
2) : «», : «».
Решение.
1) , .
Видим, что предикат обращается в истинное высказывание при всех тех значениях , при которых второй предикат превращается в истинное высказывание, или , поэтому предикат есть логическое следствие предиката .
2) ,
, поэтому предикат есть логическое следствие предиката .
4.2. Используя слова 1) если…., то…, 2) необходимо, 3) достаточно, 4) тогда, когда, 5) только тогда, когда, 6) те, которые, 7) только те, которые, 8) содержатся, 9) всякие, сформулируйте утверждения «Равные фигуры равновелики».
Решение.
1. Если фигуры равны, то они равновелики.
2. Для того, чтобы фигуры были равны, необходимо, чтобы они были равновелики.
3. Для того, чтобы фигуры были равновелики, достаточно, чтобы они были равны.
4. Фигуры равновелики тогда, когда они равны.
5. Фигуры равны только тогда, когда они равновелики.
6. Те фигуры равновелики, которые равны.
7. Только те фигуры равны, которые равновелики.
8. Равные фигуры содержатся среди равновеликих.
9. Всякие равные фигуры равновелики.
§5 Формулы логики предикатов. Классификация формул логики предикатов.
Понятие формулы логики предикатов вводится аналогично понятию формулы алгебры высказываний. Сначала зададим алфавит символов, из которых будут составляться формулы:
1.предметные переменные ;
2. переменные высказывания ;
3. – местные предикатные переменные , … с указанием числа свободных мест в них;
4. символы логических операций: ;
5. кванторы: ;
6. – скобки.
Для обозначения формул логики предикатов будем использовать большие буквы латинского алфавита .
Определение формулы логики предикатов.
1. Каждое переменной высказывание есть формула.
2. Если – – местная предикатная переменная, то есть формула, в которой все переменные свободны.
3. Если и – формулы, и если предметные переменные, входящие одновременно в обе эти формулы свободны в каждой их них, то , , , , также являются формулами. При этом предметны переменные, свободные (связанные) хотя бы в одной из формул , , являются свободными (связанными) и в новых формулах.
4. Если – формула, – предметная переменная, входящая в свободно, то , также являются формулами, в которых переменная связанная, а все остальные предметные переменные, входящие в формулу свободно или связанно, остаются и в новых формулах соответственно такими же.
5. Никаких других формул логики предикатов, кроме получающихся согласно пунктам 1- 4, нет.
Как и в алгебре высказываний, договоримся внешние скобки у формулы не писать.
Примеры формул.
1.
2. , .
3. , .
4. , .
5.
.
Выражение формулой не является, так как в формуле переменная связанная, а в формуле переменная свободная.
Если в формулу логики предикатов вместо каждой предикатной переменной подставить конкретный предикат, определенный на некотором множестве , то формула превратится в конкретный предикат, заданный на множестве . Если теперь вместо предметных переменных подставить конкретные предметы из множества , то полученный предикат, а в конечном итоге – исходная формула, превратится в конкретной высказывание.
Пример 1.
Рассмотрим формулу . В качестве множества возьмем множество , а) вместо предикатной переменной подставим конкретный предикат: «». Тогда данная формула превращается в высказывание «» – «для любого натурального числа существует большее него натуральное число ». Истинное высказывание.
б) Вместо предикатной переменой поставим конкретный предикат «». Получим высказывание «» – для любого натурального числа существует меньшее него натуральное число ». Ложное высказывание.
Классификация формул логики предикатов.
Определение. Формула логики предикатов называется выполнимой (опровержимой) на множестве , если при некоторой подстановке вместо предикатных переменных конкретных предикатов, заданных на множестве , она превращается в выполнимый (опровержимый) предикат.
Формула примера 1 является как выполнимой, так и опровержимой на множестве .
Определение. Формула логики предикатов называется тождественно истинной (тождественно ложной) на множестве , если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на множестве , она превращается в тождественно истинный (тождественно ложный) предикат.
Пример 2.
Рассмотрим формулу .
а) В качестве множества возьмем одноэлементное множество. При любой подстановке в эту формулу вместо переменного предиката любого конкретного предиката , заданного на множестве , высказывание ; одновременно будут либо истинными, либо ложными, а их импликация будет истинным высказыванием. Следовательно, данная формула является тождественно истинной на одноэлементном множестве .
б) Пусть . Вместо переменного предиката подставим в данную формулу конкретный предикат «». Получим высказывание «»«», которое является ложным.
Следовательно, данная формула не является тождественно истинной на множестве . Видим, что эта формула опровержимая на множестве . Легко показать, что данная формула выполнимая на множестве .
Определение. Формула логики предикатов называется общезначимой или тавтологией (тождественно ложной или противоречием), если при всякой подстановке вместо предикатных переменных, заданных на каких угодно множествах, она превращается в тождественно истинный (тождественно ложный) предикат.
Тот факт, что формула является тавтологией обозначают ╞ .
Из определений видим, что формула из примера 2 не является ни тавтологией, ни противоречием.
Пример 3. ╞ .
Пример 4. ╞.
Докажем, что формула из примера 3 является тавтологией. Действительно, допустим противное: пусть существует конкретный предикат , заданный на некотором множестве , при подстановке которого в рассматриваемую формулу она превращается в предикат (от переменной ) не являющийся тождественно истинным. Это означает, что существует предмет такой, что высказывание ложное. По определению импликации получаем, что высказывание – ложное, а высказывание истинное. Из истинности последнего высказывания и определения квантора общности следует, что предикат , тождественно истинный, а значит высказывание истинное. Полученное противоречие означает, что формула тавтология.
Аналогично доказывается, что формула из примера 4 является тавтологией.
§6 Применение логики предикатов
I. Прямая, обратная и противоположная теоремы.
Многие математические теоремы, словесная формулировка которых включает слова «если…, то…», имеют строение, выраженное формулой , предикат , называется условием теоремы, а предикат , называется заключением теоремы.
Пример.
Теорема 1. Если четырехугольник прямоугольник, то его диагонали равны.
Условие теоремы – предикат: «Четырехугольник – прямоугольник», заключение теоремы – предикат: «Диагонали четырехугольника равны», , где – множество четырехугольников плоскости.
Пусть – запись истинной теоремы. Тогда по определению квантора общности предикат , тождественно истинный, следовательно, предикат является логическим следствием предиката . Поэтому заключение теоремы является необходимым условием для условия теоремы , а условие теоремы является достаточным условием для её заключения . Иногда вместо слов «необходимое условие», «достаточное условие» употребляют соответственно слова: «необходимый признак», «достаточный признак».
Из теоремы 1 видим, что равенство диагоналей четырехугольника есть необходимый (но не достаточный) признак прямоугольника.
Теорема 2. Если в квадратной матрице две строки равны, то её определитель равен .
Видим, что равенство двух строк квадратной матрицы есть достаточный (но не необходимый) признак равенства определители квадратной матрицы.
Пусть дана теорема вида , (1) назовем эту теорему прямой.
Определения.
Теорему вида (2) называют обратной данной.
Теорему вида (3) называют противоположной прямой.
Теорему вида (4) называют противоположной обратной или обратной противоположной.
Можно доказать, что равносильны теоремы прямая и противоположная обратной , а так же равносильны обратная и противоположная теоремы .
На основании равносильности теорем (1) и (4) вместо доказательства прямой теоремы можно доказывать равносильную ей противоположную обратной. Этот метод доказательства теорем называется методом доказательства от противного.
Если условие или заключение теоремы представляют собой конъюнкцию или дизъюнкцию, либо содержат кванторные операции, то при составлении противоположной теоремы и противоположной обратной следует учитывать соответствующие законы де Моргана.
( ,).
Иногда конъюнкция или дизъюнкция, кванторные операции в формулировке теоремы присутствуют неявно, «замаскировано». Поэтому, чтобы правильно сформулировать теорему противоположную и противоположную обратной, нужно сначала тщательно проанализировать прямую теорему и выявить подразумеваемые конъюнкции или дизъюнкции, либо кванторные операции (если таковые имеются).
Пример.
Теорема 3. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Условие и заключение этой теоремы представляют собой дизъюнкции высказываний
«» «» «»
«» «» «».
Теорема 3 читается так: «Если один из углов треугольника прямой, то квадрат одной из сторон треугольника равен сумме квадратов двух других его сторон» (истинная теорема).
Обратная теорема: «Если квадрат одной из сторон треугольника равен сумме квадратов двух других его сторон, то этот треугольник прямоугольный» (истинная теорема).
Противоположная теорема: «Если треугольник не прямоугольный, то квадрат ни одной из сторон этого треугольника не равен сумме квадратов двух других его сторон» (истинная теорема).
Сформулируем обратную и противоположную и противоположную обратной теоремы для теоремы 2. Условие этой теоремы содержит квантор существования. Теорема 2 читается так: «Если в квадратной матрице хотя бы (существуют) две строки равны, то её определитель равен » (истинная теорема).
Обратная теорема. «Если определитель квадратной матрицы равен , то хотя бы две строки этой матрицы равны» (ложная теорема).
Противоположная теорема. «Если все строки квадратной матрицы попарно различны, то её определитель отличен от » (ложная теорема).
Противоположная обратной. «Если определитель квадратной матрицы отличен от нуля, то все её строки попарно различны» (истинная теорема).
Из приведенных примеров видим, что одновременно истинны теорема 3 и обратная к ней, истинна теорема 2, но обратная к ней ложна.
В случае, когда одновременно истинны прямая и обратная теоремы, то каждый из предикатов и является для другого необходимым и достаточным условием.
В этом случае обе теоремы
и
могут быть записаны в виде
.
Для теоремы 3 и обратной к ней получаем: «Для того, чтобы треугольник был прямоугольным необходимо и достаточно, чтобы квадрат одной из сторон этого треугольника был равен сумме квадратов двух других его сторон».
Упражнения.
6.1. Следующие теоремы сформулируйте, используя термины: «необходимо», «достаточно». Для данных теорем сформулируйте обратную, противоположную. Укажите, какие из них истинны, какие ложны.
1) Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник – параллелограмм.
2) Формула алгебры высказываний является тождественно истинной, если каждый множитель ее КНФ содержит хотя бы одну пару слагаемых, из которых одно является отрицанием другого.
Решение.
1) «Для того, чтобы в четырехугольнике две противоположные стороны были равны и параллельны, необходимо, чтобы этот четырехугольник был параллелограммом».
«Для того, чтобы четырехугольник был параллелограммом, достаточно, чтобы две противоположные стороны этого четырехугольника были равны и параллельны».
Обратная теорема. «Если четырехугольник параллелограмм, то две его противоположные стороны равны и параллельны» (истинная теорема).
Противоположная теорема. «Если в четырехугольнике никакие две противоположные стороны не равны или не параллельны, то этот четырехугольник не параллелограмм» (истинная теорема).
2) «Для того, чтобы формула алгебры высказываний была тождественно истинной необходимо, чтобы каждый множитель ее КНФ содержал хотя бы одну пару слагаемых, из которых одно является отрицанием другого.
«Для того чтобы каждый множитель КНФ формулы алгебры высказываний содержал хотя бы одну пару слагаемых, из которых одно есть отрицание другого, достаточно, чтобы эта формула была тожественно истинной.
Обратная теорема. «Если каждый множитель КНФ формулы алгебры высказываний содержит хотя бы одну пару слагаемых, из которых одно есть отрицание другого, то эта формула является тождественно истинной» (истинная теорема).
Противоположная теорема: «Если формула алгебры высказываний не является тождественно истинной, то хотя бы один множитель ее КНФ не содержит ни одной пары слагаемых, из которых одно является отрицанием другого» (истинная теорема).
II. Запись на языке логики предикатов определений и построение их отрицаний.
Язык логики предикатов удобен для записи математических предложений. Он дает возможность записывать формулировки различных определений, строить их отрицания.
При построении отрицаний определений часто используются следующие равносильности логики предикатов:
.
Рассмотрим некоторые примеры.
6. Пусть действительная функция от действительного аргумента, определенная на множестве .
Определение функции, периодической на множестве .
«Функция называется периодической на множестве , если существует действительное, отличное от , число такое, что для любых из множества определения числа и так же принадлежат множеству и при этом выполняется равенство ».
«Функция периодическая на множестве »
Отрицание этого определения записывается так:
«Функция не является периодической на множестве »
то есть «Функция не является периодической на множестве , если для любого действительного, отличного от , числа найдется такое, что или или ».
2. Определение точки максимума функции , определенной и непрерывной на множестве : «Точка из области определения функции называется точкой максимума функции , если существует положительное действительное число , такое что для всех , отличных от и удовлетворяющих неравенству , выполняется неравенство ».
Записывается так:
«Точка является точкой максимума функции »
Утверждение: «Точка не является точкой максимума функции » означает
, то есть «точка не является точкой максимума функции , если или для любого положительного действительного числа найдется из , отличное от , такое что , а ».
3. Определение функции непрерывной в точке .
«Функция называется непрерывной в точке , если для любого положительного числа найдется положительное число такое, что для всех , для которых выполняется неравенство ».
На языке логики предикатов записывается так:
«Функция непрерывна в точке »
.
Утверждение
«Функция не является непрерывной в точке » означает: , то есть «Функция не является непрерывной в точке , если существует положительное число , такое, что для любого найдется из , такое, что , а ».
4. Определение функции, непрерывной на интервале : «Функция называется непрерывной на , если она непрерывна в любой точке этого интервала».
На языке логики предикатов записывается так:
«Функция непрерывна на »
.
Утверждение «Функция не является непрерывной на », означает:
, то есть
«Функция не является непрерывной на , если существует , для которого найдется положительное , такое, что для любого найдется из , такое, что , а ».

Определение. Предикатом называется повествовательное предложение, содержащее предметные переменные, определённые на соответствующих мно- жествах; при замене переменных конкретными значениями (элементами) этих множеств предложение обращается в высказывание, т. е. принимает значение «истинно» или «ложно».

Определение. Предикатом называется функция P : M ⁿ → B , где B = { 0,1 } , M – любое множество, 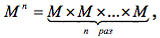т. е. функция P , сопоставляющая вектору (x₁ , x₂ ,…, x_n ) значения 0 или 1.

Множество M называется предметной областью предиката P ,

x₁ , x₂ ,…, x_n – предметные переменные,

P – предикатный символ,

n – местность предиката,

декартово произведение M × M × … × M область определения предиката P .

Обозначение: P (x₁ , x₂ ,…, x_n– n – местный предикат, заданный на множестве M .

Определение. Областью истинности предиката P называется подмножество I_p ⊆ Mⁿ его предметной области, на элементах которого значения предиката равны 1.

Область истинности предиката, выраженного предикатной формулой, определяется областями истинности составляющих и применяемыми в формуле операциями: I_PvQ = I_P ∪ I_Q, I_{P ∧ Q} = I_P ∩ I_Q , I_P→Q = I_P ∪ I_Q, I _P = I_P .

Задача 3.1. Найти область истинности предиката

P ( X, Y ) = (( X + Y ) – нечётно ) ∨ (( X – Y ) делятся на 3) , где X = {1;3;6;7}, Y = {2;4;5}.

Решение.

Составим таблицы истинности для предикатов P₁ ( X, Y ) = (( X + Y) – нечётно), P₂( X, Y ) = (( X – Y ) – делятся на 3) , P = P₁ ∨ P₂.

I_P = I _P1∨P2 = I_P1 ∪ I_P2 = {(1,2), (1,4), (3,2), (3,4), (6,5), (7,2), (7,4)} ∪ {(1,4), (7,4)} = {(1,2), (1,4), (3,2), (3,4), (6,4), (7,2), (7,4)}.
Ответ: I_P = {(1,2), (1,4), (3,2), (3,4), (6,4), (7,2), (7,4)}.

Задача 3.2. Найти область истинности предиката

P ( X ) = (( число 3 не делитель x ) → ( x ≤ 6 ))

на множестве однозначных натуральных чисел.

Решение.

Определим области истинности предикатов P₁ = {число 3 не не делитель x},

P₂ = {x ≤ 6}, P = P₁→ P₂ .

I_P1 = {1,2,4,5,7,8}, I_P2 = {1,2,3,4,5,6}, I_P = I_P1→P2 = I_P1 = {1,2,3,4,5,6,9}.

Ответ: I _P = {1,2,3,4,5,6,9}.

Задачи для самостоятельного решения

Найти область истинности предиката

1. P ( X, Y ) = ((( X – Y ) – нечетно ) ∧ ( min ( X, Y)  – четно )), где X = {2;5;6;8};
2. P ( X ,Y ) = (( X + Y )) – делится на 3) → (( X + Y ) > 5), где X = {2;5;6;8}, Y = {3;6;9};
3. P ( X, Y ) = ((( X – Y ) – нечётно ) ∧ ( |Y-X| ≤ 1 )), где X = {5;8;9}, Y = {4;7;8;10};
4. P ( X, Y ) = (( X – Y ) – чётно ) ∨ (( X + Y ) – делится на 3), где X = {5;8;9}, Y = {4;7;8;10};
5. P ( X ) = (( число 3 делитель x ) ∨ ( x ≤ 6 )), заданного на множестве однозначных натуральных чисел;
6. P ( X ) = ((( число 3 делитель x ) ∧ ( x > 6 )), заданного на множестве однозначных натуральных чисел;
7. P ( X ) = (( x ≥ 3 ) ∧ ( x ≤ 10 )), заданного на множестве всех действительных чисел;
8. P ( X ) = (( x² ≤ 4 ) ∧ ( x -1 ≥ 1 )), заданного на множестве всех действительных чисел;
9. P ( X ) = (( x ≤ 0 ) ∧ ( x² – 2x ≤ 0 )), заданного на множестве всех действительных чисел;
10. P ( X ) = (( x³ – 6x² +11x – 6 = 0 ) ∧ ( x² – 4x + 3 = 0 )),заданного на множестве всех действительных чисел.