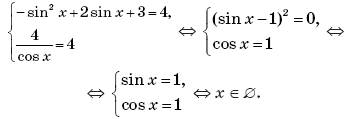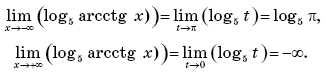Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Функцией, заданной на множестве $X$ и принимающей значения из множества $Y$ называют некую закономерность, по которой каждому элементу из множества $X$ соответствует лишь один и только один элемент из множества $Y$.
Из этого определения следует, что множество (область) значений функции — это те значения функции $y(x)$, которые она может принимать соответственно области её определения. Теперь перейдём к следующему определению.
Определение 2
Область (множество) значений функции на некотором рассматриваемом отрезке — это интервал значений, которые функция принимает на этом рассматриваемом отрезке.
Чаще всего в учебной литературе встречается термин «множество значений функции». Кратко его обозначают $E(f)$.
Как определить область значения функции
Для определения множества значений функции пользуются графическим методом, методом поисков минимума и максимума, вычислением производной и другими.
Определение множества значений функции графическим методом
Графический метод подразумевает построение графика функции и изучение этого графика. Этот метод наиболее удобен, если не известна какая-либо закономерность изменения функции $f(x)$, а есть только набор произвольных точек или собственно сам график.
Пример 1
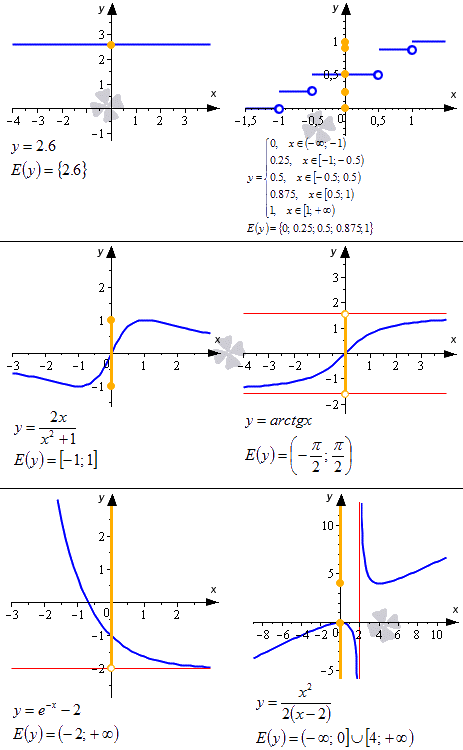
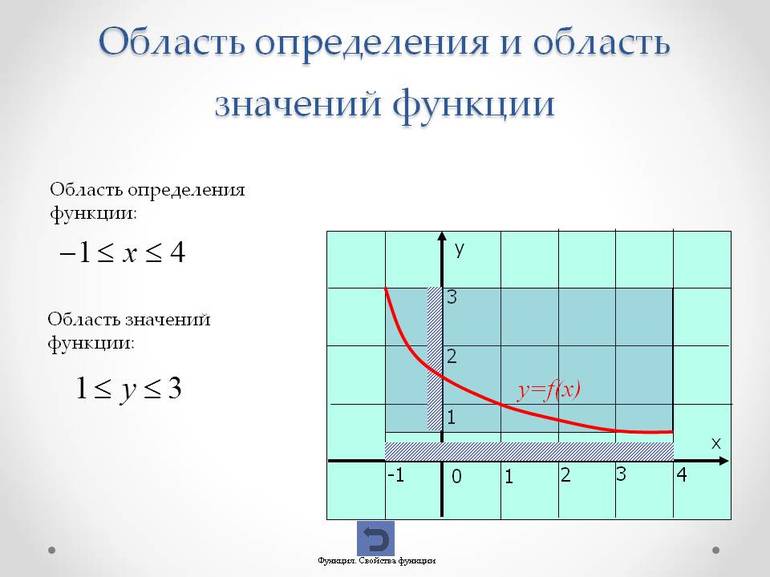
Рисунок 1. Определение множества значений функции графическим методом
На данном рисунке область значений функции $y=f(x)$ равна $E(y)=3$, так как на протяжении всего отрезка функция $y$ не меняет своего значения и всегда равна $3$, тогда как область определения функции $D(y)=[0;3.5]$.
Скобки в данном случае для области определения функции необходимо использовать квадратные, так как обе точки закрашены, то есть включены в отрезок. В случае если точки не закрашены, они не включаются в отрезок и тогда применяются круглые скобки.
«Множество значений функции» 👇
Метод нахождения области значения функции через производную
Метод нахождения области значения функции через производную состоит в том, чтобы сначала оценить область её определения (то есть определить те значения, которые может принимать аргумент $x$, а затем осуществить процедуру нахождения самой производной. После этого осуществляют поиск значений $x$, при которых производная функции равна нулю и при которых производная не существует.
Рассмотрим пример нахождения области значений функции через производную.
Пример 2
Дана функция $f(x)=sqrt{16-x^2}$. Найдите область её значений.
Сначала определяем, какие значения может принимать $x$ для существования функции.
При значении $x^2>16$ под корнем получается отрицательное число, а это значит, что область определения функции от $[-4;4]$ включительно.
Теперь найдём производную функции:
$(sqrt{16-x^2})’=-frac{x}{sqrt{16-x^2}}$
Если в знаменателе производной нуль, то производной не существует, в данном случае это условие выполняется при $x=±4$.
Приравниваем производную к нулю и находим значения $x$. Производная данной функции принимает нулевое значение при $x=0$. Теперь подставляем найденные значения производной в нашу функцию, и получаем, что наименьшее значение функции — это $f(4)$ и $f(-4)$, при этих значениях функция равна нулю, а наибольшее значение $f(x)$ — при $x=0$, в этой точке функция равна $16$.
Метод поиска минимума и максимума
Метод поиска минимума и максимума основан на том, чтобы найти максимальное и и минимальное значение, которые функция принимает на изучаемой области.
Пример 3
Определите область значений функции:
$y=6-4sinx$
Проанализируем данную функцию. Так как минимальное значение синуса равно минус единице, а а максимальное — единице, то подставив эти значения получаем, что $max(f(x))=10$ при $x=frac{3π}{2}$, а минимум $min(f(x))=2$ при $x=frac{π}{2}$. Следовательно, множество значений, которые может принимать данная функция — $E(x)=[2;10]$.
Разница между областью значения и областью определения функции
Стоит обратить внимание, что область значений функции — не одно и то же с термином «область определения функции».
Определение 3
Область определения функции $D(y)$ — это диапазон таких значений переменной $x$, при которых существует функция $y(x)$.
Например, рассмотрим функцию $y(x)=x^2$. В данном случае область определения этой функции будет множеством вещественных (действительных) чисел $mathbb{R}$, а сама функция будет принимать значения только положительных действительных чисел $mathbb{R}^+$, так как вещественное число, возведённое в квадрат, не может давать отрицательное значение. То есть, в этом примере множество значений функции — это множество положительных вещественных чисел $mathbb{R}^+$.
Также имеют место случаи, когда область определения функции совпадает с областью значений.
В качестве иллюстрации можно рассмотреть функцию $y(x)=2x$. За аргумент $x$ данная функция может принимать любое действительное число из множества $mathbb{R}$, а значения, которые будет принимать сама функция — это удвоенные числа из множества всех действительных чисел. То есть, в данном случае областью значений $E(y)$ будет также всё множество вещественных чисел $mathbb{R}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
subjects:mathematics:множество_значений_функции
Содержание
Математика ( Справочник )
-
-
Множество значений функции
-
Нахождение множества значений функции
Обозначения
-
D(f) — те значения, которые может принимать аргумент, т.е. область определения функции.
-
E(f) — те значения, которые может принимать функция, т.е. множество значений функции.
Способы нахождения областей значений функций.
-
последовательное нахождение значений сложных аргументов функции;
-
метод оценок/границ;
-
использование свойств непрерывности и монотонности функции;
-
использование производной;
-
использование наибольшего и наименьшего значений функции;
-
графический метод;
-
метод введения параметра;
-
метод обратной функции.
Рассмотрим некоторые из них.
Используя производную
Общий подход к нахождению множества значений непрерывной функции f(x) заключается в нахождении наибольшего и наименьшего значения функции f(x) в области ее определения (или в доказательстве того, что одно из них или оба не существуют).
В случае, если нужно найти множества значений функции на отрезке:
-
найти производную данной функции f ‘(x);
-
найти критические точки функции f(x) и выбрать те из них, которые принадлежат данному отрезку;
-
вычислить значения функции на концах отрезка и в выбранных критических точках;
-
среди найденных значений выбрать наименьшее и наибольшее значения;
-
Множество значений функции заключить между этими значениями.
Если областью определения функции является интервал, то используется та же схема, но вместо значений на концах используются пределы функции при стремлении аргумента к концам интервала. Значения пределов из не входят в множество значений.
Метод границ/оценок
Для нахождения множества значений функции сначала находят множество значений аргумента, а затем отыскивают соответствующие наименьше и наибольшее значения функции функции. Используя неравенства – определяют границы.
Суть состоит в оценке непрерывной функции снизу и сверху и в доказательстве достижения функцией нижней и верхней границы оценок. При этом совпадение множества значений функции с промежутком от нижней границы оценки до верхней обуславливается непрерывностью функции и отсутствием у неё других значений.
Свойства непрерывной функции
Другой вариант заключается в преобразовании функции в непрерывную монотонную, тогда используя свойства неравенств оценивают множество значений вновь полученной функции.
Последовательное нахождение значений сложных аргументов функции
Основан на последовательном отыскании множества значений промежуточных функций, из которых составлена функция
Области значений основных элементарных функций
| Функция | Множество значений |
|---|---|
| $y = kx+ b$ | E(y) = (-∞;+∞) |
| $y = x^{2n}$ | E(y) = [0;+∞) |
| $y = x^{2n +1}$ | E(y) = (-∞;+∞) |
| $y = k/x$ | E(y) = (-∞;0)u(0;+∞) |
| $y = x^{frac{1}{2n}}$ | E(y) = [0;+∞) |
| $y = x^{frac{1}{2n+1}}$ | E(y) = (-∞;+∞) |
| $y = a^{x}$ | E(y) = (0;+∞) |
| $y = log_{a}{x}$ | E(y) = (-∞;+∞) |
| $y = sin{x}$ | E(y) = [-1;1] |
| $y = cos{x}$ | E(y) = [-1;1] |
| $y = {rm tg}, x$ | E(y) = (-∞;+∞) |
| $y = {rm ctg}, x$ | E(y) = (-∞;+∞) |
| $y = arcsin{x}$ | E(y) = [-π/2; π/2] |
| $y = arccos{x}$ | E(y) = [0; π] |
| $y = {rm arctg}, x$ | E(y) = (-π/2; π/2) |
| $y = {rm arcctg}, x$ | E(y) = (0; π) |
Примеры
Найдите множество значений функции:
Используя производную
НЕ используя производную
Найдите наибольшее и наименьшее значения функции:
$f(x)=sin^{2}{x}+cos{x}-frac{1}{2}$
Используя метод границ/оценок
$y=5-4sin{x}$
$y=cos{7x}+5cos{x}$
$f(x)=1+2sin^{2}{x}$
$$
\ -1leqsin{x}leq 1
\ 0leqsin^{2}{x}leq 1
\ 0leq2sin^{2}{x}leq 2
\ 1leq1+2sin^{2}{x}leq 3
$$
Ответ: E(f) = [1; 3].
$f(x)=3-2^{3+{rm tg}^{2}, x}$
$$
\ -infty < {rm tg}, x < +infty
\ 0 leq {rm tg}^{2}, x < +infty
\ 3 leq 3+{rm tg}^{2}, x < +infty
\ 2^{3} leq 2^{3+{rm tg}^{2}, x} < +infty
\ -infty < -2^{3+{rm tg}^{2}, x} leq -8
\ -infty < 3-2^{3+{rm tg}^{2}, x} leq -5
$$
Ответ: E(f) = (–∞; -5].
$f(x)=2+sqrt{16-lg^{2}{x}}$
$$
\ -infty < lg{x} < +infty
\ 0 leq lg^{2}{x} < +infty
\ -infty < -lg^{2}{x} leq 0
\ -infty < 16-lg^{2}{x} leq 16
\ 0 leq sqrt{16-lg^{2}{x}} leq 4
\ 2 leq 2+sqrt{16-lg^{2}{x}} leq 6
$$
Ответ: E(f) = [2; 6].
$f(x)=sqrt{2-x}+sqrt{2+x}$
$y=sin{x}+cos{x}$
Используя непрерывную функцию
Иные
Использованная литература
Статьи:
-
Область значения функций в задачах ЕГЭ, Минюк Ирина Борисовна
-
Советы по нахождению множества значений функции, Беляева И., Федорова С.
-
Нахождение множества значений функции
-
Как решать задачи по математике на вступительных экзаменах, И.И.Мельников, И.Н.Сергеев
Рекомендуем
· Последние изменения: 2018/09/19 21:14 —
¶
Зачастую в рамках решения задач по тригонометрии нам приходится искать множество значений функции на области определения или отрезке. Например, такой поиск нужно делать, если приходится решать разные типы неравенств, при оценке выражений и др.
В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми можно вычислить область значения и область определения функции, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графически. Прочитав эту статью, вы получите исчерпывающее представление о том, что такое область значения функции.
Начнем с базовых определений.
Множество значений функции y = f(x) – это множество всех значений на некотором интервале x, которые данная функция принимает при переборе всех значений x∈X.
Область значений функции y=f(x) – это множество всех ее значений, которые она может принять при переборе значений x из области x∈(f).
Область значений некоторой функции обычно принято называть и обозначать E(f).
Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.
Важно также различать область значений и область допустимых значений переменной x для выражения в правой части y=f(x). Область допустимых значений x для выражения f(x) и будет областью определения данной функции.
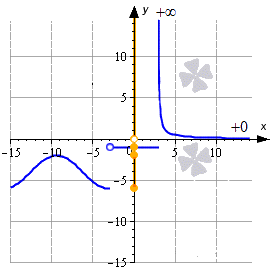
Ниже приводится иллюстрация, на которой показаны некоторые примеры, как построить графики функций и их построение. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.
Как найти область значения функции? Очевидно, что область или множество значений функции можно найти или получить при проецировании графика функции на ось Oy. При этом она может представлять собой как одно число, так и множество чисел, отрезок, интервал, открытый луч, объединение числовых промежутков и др.
Рассмотрим основные способы, как определить область значения функции.
Первый этап – определить тип функции. Функция может быть квадратичной, а также содержать дроби и корни.
Начнем с определения множества значений непрерывной функции y = f(x) на некотором отрезке, обозначенном [a; b]. Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего maxx∈a; bf(x) и наименьшего значения minx∈a; bf(x). Значит, у нас получится отрезок minx∈a; bf(x); maxx∈a; bf(x), в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.
Возьмем задачу, в которой нужно определить область значений арксинуса.
Условие: найдите область значений y = arcsin x.
Решение
В общем случае область определения арксинуса располагается на отрезке [-1; 1]. Нам надо определить наибольшее и наименьшее значение указанной функции на нем.
y’ = arcsin x’=11-x2
Мы знаем, что производная функции будет положительной для всех значений x, расположенных в интервале [-1; 1], то есть на протяжении всей области определения функция арксинуса будет возрастать. Значит, самое маленькое значение она примет при x, равном -1, а самое большое – при x, равном 1.
minx∈-1; 1arcsin x=arcsin-1=-π2maxx∈-1; 1arcsin x=arcsin 1=π2
Таким образом, область значений функции арксинус будет равна E(arcsin x)=-π2; π2.
Ответ: E(arcsin x)=-π2; π2
Условие: вычислите область значений y=x4-5×3+6×2 на заданном отрезке [1; 4].
Решение
Как найти значение функции? Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.
Для определения точек экстремума надо произвести следующие вычисления:
y’=x4-5×3+6×2’=4×3+15×2+12x=x4x2-15x+12y’=0⇔x(4×2-15x+12)=0x1=0∉1; 4 или 4×2-15x+12=0D=-152-4·4·12=33×2=15-338≈1.16∈1; 4; x3=15+338≈2.59∈1; 4
Теперь найдем значения заданной функции в концах отрезка и точках x2=15-338; x3=15+338:
y(1)=14-5·13+6·12=2y15-338=15-3384-5·15-3383+6·15-3382==117+16533512≈2.08y15+338=15+3384-5·15+3383+6·15+3382==117-16533512≈-1.62y(4)=44-5·43+6·42=32
Как найти множество значений функции? Значит, множество значений функции будет определяться отрезком 117-16533512; 32.
Ответ: 117-16533512; 32.
Перейдем к нахождению множества значений непрерывной функции y = f(x) в промежутках (a; b), причем a; +∞, -∞; b, -∞; +∞.
Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведение функции в заданных условиях. Для этого у нас есть все необходимые данные.
Условие: вычислите область значений функции y=1×2-4 на интервале (-2; 2).
Решение
Определяем наибольшее и наименьшее значение функции на заданном отрезке
y’=1×2-4’=-2x(x2-4)2y’=0⇔-2x(x2-4)2=0⇔x=0∈(-2; 2)
У нас получилось максимальное значение, равное 0, поскольку именно в этой точке происходит перемена знака функции и график переходит к убыванию. См. на иллюстрацию:
То есть, y(0)=102-4=-14 будет максимальным значением функции.
Теперь определим поведение функции при таком x, который стремится к -2 с правой стороны и к +2 с левой стороны. Иными словами, найдем односторонние пределы:
limx→-2+01×2-4=limx→-2+01(x-2)(x+2)==1-2+0-2-2+0+2=-14·1+0=-∞limx→2+01×2-4=limx→2+01(x-2)(x+2)==12-0-22-0+2=14·1-0=-∞
У нас получилось, что значения функции будут возрастать от минус бесконечности до -14 тогда, когда аргумент изменяется в пределах от -2 до 0. А когда аргумент меняется от 0 до 2, значения функции убывают к минус бесконечности. Следовательно, множеством значений заданной функции на нужном нам интервале будет (-∞; -14].
Ответ: (-∞; -14].
Условие: укажите множество значений y=tg x на заданном интервале -π2; π2.
Решение
Нам известно, что в общем случае производная тангенса в -π2; π2 будет положительной, то есть функция будет возрастать. Теперь определим, как ведет себя функция в заданных границах:
limx→π2+0tg x=tg-π2+0=-∞limx→π2-0tg x=tgπ2-0=+∞
Мы получили рост значений функции от минус бесконечности к плюс бесконечности при изменении аргумента от -π2 до π2,и можно сказать, что множеством решений данной функции будет множество всех действительных чисел.
Ответ: -∞; +∞.
Условие: определите, какова область значений функции натурального логарифма y = ln x.
Решение
Нам известно, что данная функция является определенной при положительных значениях аргумента D(y)=0; +∞. Производная на заданном интервале будет положительной: y’=ln x’=1x. Значит, на нем происходит возрастание функции. Далее нам нужно определить односторонний предел для того случая, когда аргумент стремится к 0 (в правой части), и когда x стремится к бесконечности:
limx→0+0ln x=ln(0+0)=-∞limx→∞ln x=ln+∞=+∞
Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.
Ответ: множество всех действительных чисел – область значений функции натурального логарифма.
Условие: определите, какова область значений функции y=9×2+1.
Решение
Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:
y’=9×2+1’=-18x(x2+1)2y’=0⇔x=0y’≤0⇔x≥0y’≥0⇔x≤0
В итоге мы определили, что данная функция будет убывать, если x≥0; возрастать, если x≤0; она имеет точку максимума y(0)=902+1=9 при переменной, равной 0.
Посмотрим, как же ведет себя функция на бесконечности:
limx→-∞9×2+1=9-∞2+1=9·1+∞=+0limx→+∞9×2+1=9+∞2+1=9·1+∞=+0
Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.
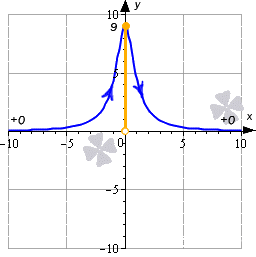
Подведем итоги: когда аргумент изменяется от минус бесконечности до нуля, то значения функции возрастают от 0 до 9. Когда значения аргумента меняются от 0 до плюс бесконечности, соответствующие значения функции будут убывать от 9 до 0. Мы отобразили это на рисунке:
На нем видно, что областью значений функции будет интервал E(y)=(0; 9]
Ответ: E(y)=(0; 9]
Если нам надо определить множество значений функции y = f(x) на промежутках [a; b), (a; b], [a; +∞), (-∞; b], то нам понадобится провести точно такие же исследования. Эти случаи мы пока не будем разбирать: далее они нам еще встретятся в задачах.
А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.
Условие: определите, какой будет область значений y=xx-2.
Решение
Поскольку знаменатель функции не должен быть обращен в 0, то D(y)=-∞; 2∪2; +∞.
Начнем с определения множества значений функции на первом отрезке -∞; 2, который представляет из себя открытый луч. Мы знаем, что функция на нем будет убывать, то есть производная данной функции будет отрицательной.
limx→2-0xx-2=2-02-0-2=2-0=-∞limx→-∞xx-2=limx→-∞x-2+2x-2=limx→-∞1+2x-2=1+2-∞-2=1-0
Тогда в тех случаях, когда аргумент изменяется по направлению к минус бесконечности, значения функции будут асимптотически приближаться к 1. Если же значения x меняются от минус бесконечности до 2, то значения будут убывать от 1 до минус бесконечности, т.е. функция на этом отрезке примет значения из интервала -∞; 1. Единицу мы исключаем из наших рассуждений, поскольку значения функции ее не достигают, а лишь асимптотически приближаются к ней.
Для открытого луча 2; +∞ производим точно такие же действия. Функция на нем также является убывающей:
limx→2+0xx-2=2+02+0-2=2+0=+∞limx→+∞xx-2=limx→+∞x-2+2x-2=limx→+∞1+2x-2=1+2+∞-2=1+0
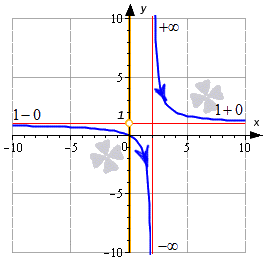
Значения функции на данном отрезке определяются множеством 1; +∞. Значит, нужная нам область значений функции, заданной в условии, будет объединением множеств -∞; 1 и 1; +∞.
Ответ: E(y)=-∞; 1∪1; +∞.
Это можно увидеть на графике:
Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.
Условие: определите область значений синуса y = sin x.
Решение
Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0; 2π и смотрим, каким будет множество значений на нем.
y’=(sin x)’=cos xy’=0⇔cos x=0⇔x=π2+πk, k∈Z
В рамках 0; 2π у функции будут точки экстремума π2 и x=3π2. Подсчитаем, чему будут равны значения функции в них, а также на границах отрезка, после чего выберем самое большое и самое маленькое значение.
y(0)=sin 0=0yπ2=sin π2=1y3π2=sin3π2=-1y(2π)=sin(2π)=0⇔minx∈0; 2πsin x=sin3π2=-1, maxx∈0; 2πsin x=sinπ2=1
Ответ: E(sin x)=-1; 1.
Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения (или указать). Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.
Условие: определите область значения y=3arccosx3+5π7-4.
Решение
Нам известно, что отрезок от 0 до пи есть область значений арккосинуса. Иными словами, E(arccos x)=0; π или 0≤arccos x≤π. Мы можем получить функцию arccosx3+5π7 из арккосинуса, сдвинув и растянув ее вдоль оси Ox, но такие преобразования нам ничего не дадут. Значит, 0≤arccosx3+5π7≤π.
Функция 3arccosx3+5π7 может быть получена из арккосинуса arccosx3+5π7 с помощью растяжения вдоль оси ординат, т.е. 0≤3arccosx3+5π7≤3π. Финалом преобразований является сдвиг вдоль оси Oy на 4 значения. В итоге получаем двойное неравенство:
0-4≤3arccosx3+5π7-4≤3π-4⇔-4≤3arccosx3+5π7-4≤3π-4
Мы получили, что нужная нам область значений будет равна E(y)=-4; 3π-4.
Ответ: E(y)=-4; 3π-4.
Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.
Условие: вычислите, какова будет область значений функции y=22x-1+3.
Решение
Перепишем функцию, заданную в условии, как y=2·(2x-1)-12+3. Для степенной функции y=x-12 область значений будет определена на промежутке 0; +∞, т.е. x-12>0. В таком случае:
2x-1-12>0⇒2·(2x-1)-12>0⇒2·(2x-1)-12+3>3
Значит, E(y)=3; +∞.
Ответ: E(y)=3; +∞.
Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.
Условие: дана функция y=2sinx2-4, x≤-3-1, -3<x≤31x-3, x>3. Вычислите область ее значений.
Решение
Данная функция является определенной для всех значений x. Проведем ее анализ на непрерывность при значениях аргумента, равных -3 и 3:
limx→-3-0f(x)=limx→-32sinx2-4=2sin-32-4=-2sin32-4limx→-3+0f(x)=limx→-3(1)=-1⇒limx→-3-0f(x)≠limx→-3+0f(x)
Имеем неустранимый разрыв первого рода при значении аргумента -3. При приближении к нему значения функции стремятся к -2sin32-4, а при стремлении x к -3 с правой стороны значения будут стремиться к -1.
limx→3-0f(x)=limx→3-0(-1)=1limx→3+0f(x)=limx→3+01x-3=+∞
Имеем неустранимый разрыв второго рода в точке 3. Когда функция стремится к нему, ее значения приближаются к -1, при стремлении к той же точке справа – к минус бесконечности.
Значит, вся область определения данной функции является разбитой на 3 интервала (-∞; -3], (-3; 3], (3; +∞).
На первом из них у нас получилась функция y=2sinx2-4. Поскольку -1≤sin x≤1, получаем:
-1≤sinx2<1⇒-2≤2sinx2≤2⇒-6≤2sinx2-4≤-2
Значит, на данном промежутке (-∞; -3] множество значении функции – [-6;2].
На полуинтервале (-3; 3] получилась постоянная функция y =-1. Следовательно, все множество ее значений в данном случае будет сводится к одному числу -1.
На втором промежутке 3; +∞ у нас есть функция y=1x-3. Она является убывающей, потому что y’=-1(x-3)2<0. Она будет убывать от плюс бесконечности до 0, но самого 0 не достигнет, потому что:
limx→3+01x-3=13+0-3=1+0=+∞limx→+∞1x-3=1+∞-3=1+∞+0
Значит, множество значений исходной функции при x > 3 представляет собой множество 0; +∞. Теперь объединим полученные результаты: E(y)=-6; -2∪-1∪0; +∞.
Ответ: E(y)=-6; -2∪-1∪0; +∞.
Решение показано на графике:
Условие: есть функция y=x2-3ex. Определите множество ее значений.
Решение
Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:
y’=x2-3ex’=2xex-ex(x2-3)e2x=-x2+2x+3ex=-(x+1)(x-3)ex
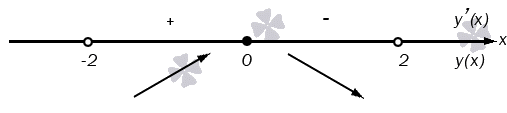
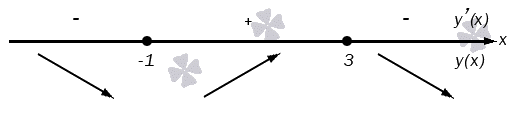
Мы знаем, что производная обратится в 0, если x=-1 и x=3. Поместим эти две точки на ось и выясним, какие знаки будет иметь производная на получившихся интервалах.
Функция будет убывать на (-∞; -1]∪[3; +∞) и возрастать на [-1; 3]. Точкой минимума будет -1, максимума –3.
Теперь найдем соответствующие значения функции:
y(-1)=-12-3e-1=-2ey(3)=32-3e3=6e-3
Посмотрим на поведение функции на бесконечности:
limx→-∞x2-3ex=-∞2-3e-∞=+∞+0=+∞limx→+∞x2-3ex=+∞2-3e+∞=+∞+∞==limx→+∞x2-3’ex’=limx→+∞2xex=+∞+∞==limx→+∞2x'(ex)’=2limx→+∞1ex=2·1+∞=+0
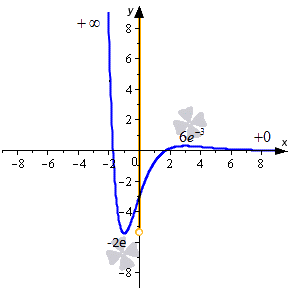
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.
На нем видно, что значения функции будут убывать от плюс бесконечности до -2e тогда, когда аргумент меняется от минус бесконечности до -1. Если же он изменяется от 3 до плюс бесконечности, то значения будут убывать от 6e-3 до 0, но при этом 0 достигнут не будет.
Таким образом, E(y)=[-2e; +∞).
Ответ: E(y)=[-2e; +∞)
Тема урока «Множество значений функции в задачах ЕГЭ»
Сегодня на уроке мы обратимся к одному из основных понятий
математики — понятию функции; более детально рассмотрим одно из свойств
функции — множество ее значений.
Ход урока
Учитель. Решая задачи, мы
замечаем, что подчас именно нахождение множества значений функции ставит нас в
затруднительные ситуации. Почему? Казалось бы, изучая функцию с 7-го класса, мы
знаем о ней достаточно много. Поэтому у нас есть все основания сделать
упреждающий ход. Давайте сегодня сами «поиграем» с множеством значений функции,
чтобы снять многие вопросы этой темы на предстоящем экзамене.
Множества значений элементарных функций
Учитель. Для начала необходимо
повторить графики, уравнения и множества значений основных элементарных функций
на всей области определения.
На экран проецируются графики функций: линейной,
квадратичной, дробно-рациональной, тригонометрических, показательной и
логарифмической, для каждой из них устно определяется множество значений.
Обратите внимание учащихся на то, что у линейной функции E(f) = R или
одно число, у дробно-линейной
Это наша азбука. Присоединив к ней наши знания о
преобразованиях графиков: параллельный перенос, растяжение, сжатие, отражение,
мы сможем решить задачи первой части ЕГЭ и даже чуть сложнее.
Проверим это.
Самостоятельная работа
Условия задач и системы координат напечатаны для каждого
ученика.
1. Найдите множество значений функции на всей области
определения:
а) y = 3 sin х ;
б) y = 7 – 2х
;
в) y = –arccos (x + 5):
г) y = | arctg
x |;
д)
2. Найдите множество значений функции y = x2 на промежутке J, если:
а) J = [2; 3];
б) J = [–1; 5).
3. Задайте функцию аналитически (уравнением), если
множество ее значений:
1) E(f(x)) = (–∞;
2] и f(x) — функция
а) квадратичная,
б) логарифмическая,
в) показательная;
2) E(f(x)) = R{7}.
При обсуждении задания 2 самостоятельной работы
обратите внимание учащихся на то, что, в случае монотонности и непрерывности
функции y = f(x) на заданном промежутке [a; b],
множество ее значений — промежуток, концами которого являются
значения f(a) и f(b).
Варианты ответов к заданию 3.
1.
а) y = –x2 + 2 , y = –(x
+ 18)2 + 2,
y = a(x – xв)2
+ 2 при а < 0.
б) y = –| log8 x | + 2,
в) y = –| 3x – 7 | + 2, y =
–5| x | + 3.
2.
а)
б)
в) y = 12 – 5x, где x
≠ 1 .
Нахождение множества значений функции с помощью производной
Учитель. В 10-м классе мы
знакомились с алгоритмом нахождения экстремумов непрерывной на отрезке функции и
отыскания ее множества значений, не опираясь на график функции. Вспомните, как
мы это делали? (С помощью производной.) Давайте вспомним этот алгоритм.
1. Убедиться, что функция y = f(x) определена и непрерывна на отрезке J = [a; b].
2. Найти значения функции на концах отрезка: f(a) и f(b).
Замечание. Если мы знаем, что функция непрерывна и монотонна на J, то можно сразу дать ответ: E(f) = [f(a); f(b)] или E(f) = [f(b); f(а)].
3. Найти производную, а затем критические точки xk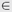
4. Найти значения функции в критических точках f(xk).
5. Сравнить значения функции f(a), f(b) и f(xk), выбрать наибольшее и наименьшее значения функции и дать ответ: E(f)= [fнаим; fнаиб].
Задачи на применение данного алгоритма встречаются в
вариантах ЕГЭ. Так, например, в 2008 году была предложена такая задача. Вам
предстоит решить ее дома.
Задание С1. Найдите наибольшее значение функции
f (x) = (0,5x + 1)4 – 50(0,5x
+ 1)2
при | x + 1| ≤ 3.
Условия домашних задач распечатаны для каждого ученика .
Нахождение множества значений сложной функции
Учитель. Основную часть нашего
урока составят нестандартные задачи, содержащие сложные функции, производные от
которых являются очень сложными выражениями. Да и графики этих функций нам
неизвестны. Поэтому для решения мы будем использовать определение сложной
функции, то есть зависимость между переменными в порядке их вложенности в данную
функцию, и оценку их области значений (промежутка изменения их значений). Задачи
такого вида встречаются во второй части ЕГЭ. Обратимся к примерам.
Задание 1. Для функций y = f(x)
и y = g(x) записать сложную функцию y = f(g(x))
и найти ее множество значений:
а) f(x) = –x2 + 2x +
3, g(x) = sin x;
б) f(x) = –x2 + 2x +
3, g(x) = log7 x;
в) g(x) = x2 + 1;
г)
Решение. а) Сложная функция имеет вид: y = –sin2 x + 2sin x + 3.
Вводя промежуточный аргумент t, мы можем записать эту
функцию так:
y = –t2 + 2t + 3, где t =
sin x.
У внутренней функции t = sin x аргумент
принимает любые значения, а множество ее значений — отрезок [–1; 1].
Таким образом, для внешней функции
y = –t2 +2t + 3 мы узнали промежуток изменения значений ее аргумента t:
t [–1; 1].
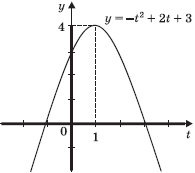
Обратимся к графику функции
y = –t2 +2t + 3.
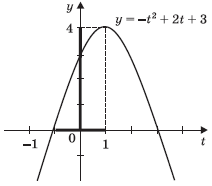
Замечаем, что квадратичная функция при t
[–1; 1] принимает
наименьшее и наибольшее значения на его концах: yнаим = y(–1)
= 0 и yнаиб = y(1) = 4. А так как эта функция
непрерывна на отрезке [–1; 1], то она принимает и все значения между ними.
Ответ: y [0; 4].
б) Композиция этих функций приводит нас к сложной функции
которая после введения промежуточного аргумента, может быть представлена так:
y = –t2 + 2t + 3, где t =
log7 x,
У функции t = log7 x
x (0; +∞), t
(–∞;
+∞).
У функции y = –t2 + 2t + 3
(см. график) аргумент t принимает любые значения, а сама квадратичная
функция принимает все значения не больше 4.
Ответ: y (–∞; 4].
в) Сложная функция имеет следующий вид:
Вводя промежуточный аргумент, получаем:
где t = x2 + 1.
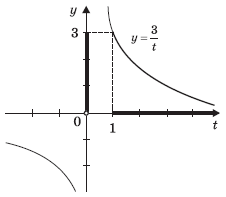
Так как для внутренней функции x
R,
а t [1; +∞),
то по графику функции нетрудно видеть, что множеством значений будет промежуток
(0; 3].
Ответ: y (0; 3].
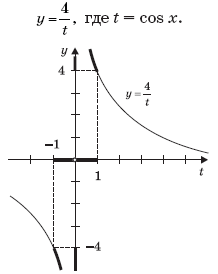
г) Композиция двух данных функций дает нам сложную функцию
которая может быть записана как
Заметим, что
Значит, при
где k
Z, t
[–1; 0)
(0; 1].
Нарисовав график функции видим, что при этих значениях t
y (–∞; –4]
[4; +∞).
Ответ: y (–∞; –4]
c [4; +∞).
— Kакая из четырех композиций более сложная и почему?
Четвертая: функция имеет точки разрыва 2-го рода, в которых
имеются вертикальные асимптоты.
— Какая из четырех композиций более простая и почему?
Первая данная квадратичная функция непрерывна и монотонна на
данном промежутке .
Итак, мы познакомились с иным алгоритмом нахождения множества
значений сложной функции:
1. Разложить сложную функцию на составляющие ее элементарные функции.
2. Оценить множества значений этих функций в порядке их вложенности в сложную функцию.
Дома вы попробуете решить эту же задачу, но для
функции y = g(f(x)) (поменяете порядок вложенности
функций).
Учитель. Данные задачи имеют красивое логическое
продолжение. Любое уравнение (неравенство) — это две функции, соединенные знаком
равенства (неравенства). Зная области значений этих функций, мы можем их
сравнить. И если мы увидим, что эти области, границы которых параллельны оси
Ох, не имеют общих точек, то их графики не пересекаются. А это значит, что
исходное уравнение не имеет решений. Возможны и другие интересные случаи.
Метод оценки при решении уравнений и неравенств
Метод решения уравнений (неравенств), при котором
сравниваются множества значений функций, стоящих в левой и правой частях
уравнения (неравенства), называют методом оценки.
Задание 2. Учитывая найденные множества значений функций
из задания 1, составьте такие уравнения и неравенства, которые решаются методом
оценки, и объясните их решение.
Варианты ответов:
1)
Сравнивая множества значений функций из левой и правой частей
уравнения, замечаем, что они имеют только один общий элемент — число 4. То есть
решениями этого уравнения могут быть только те значения x, при которых
обе функции будут принимать значение равное 4.
— Как вы думаете: сколько решений может иметь уравнение в
этом случае?
Возможны любые варианты : ни одного, одно,
два, … и сколько угодно.
Потребуем выполнения этого необходимого условия от каждой
функции и получим систему двух уравнений:
2) — x — любое число, кроме
где k
Z.
3) — не имеет решений.
4) — не имеет корней.
5) — не имеет решений.
6) — x — любое число, кроме
где k
Z.
Можно выбрать и нестрогие знаки неравенств.
В вариантах ЕГЭ во второй и третьей частях встречаются
задачи, которые решаются методом оценки. Вот одно из таких заданий из вариантов
ЕГЭ 2008 года.
Задание В8. Решите уравнение
Рассмотрите его решение дома.
Свойство монотонности сложной функции
Учитель. В ходе урока вы,
надеюсь, заметили, что если данная функция монотонна и непрерывна, то поиск
области ее значений упрощается. Остановимся на свойстве монотонности сложной
функции подробнее.
— От каких данных может зависеть монотонность?
От монотонности входящих в нее функций.
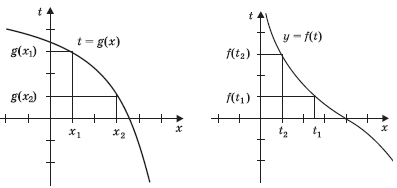
Задание 3. Докажите, что если функция t = g(x) —
непрерывна и убывает на некотором промежутке J, а функция y = f(t)
также непрерывна и убывает на промежутке J1, причем из того,
что x J,
следует, что t J1, то сложная функция y = f(g(x))
есть функция возрастающая на J.
Доказательство. Так как функции t = g(x)
и y = f(t) — убывающие, то каждое свое значение они
принимают ровно один раз и большему значению аргумента соответствует меньшее
значение функции. А тогда для любых x1 и x2
из J и для t1 = g(x1) и t2
= g(x2) из J1 имеем:
для g(x): (x1 < x2
g(x1)
> g(x2)) (x1 < x2
t1
> t2),
для f(t): t1 > t2
f(t1)
< f(t2).
Видим, что для любых x1 и x2
из J
(x1 < x2
f(t1)
< f(t2))
Û (x1 < x2
f(g(x1)) > f(g(x2))).
То есть функция y = f(g(x)) —
возрастает на J. Что и требовалось доказать.
Аналогично можно доказать, что
- композиция двух возрастающих функций — функция
возрастающая, - композиция двух функций различных монотонностей — убывающая
функция.
Посмотрим на примере, как приведенные выше свойства упрощают
решение задач.
Задание 4. Найдите множество значений функции у
= log5 (arcctg x) на J, если
а) J = [–1; 4] ;
б) на всей области определения.
Решение. Вначале исследуем данную функцию на
монотонность. Функция t = arcctg x — непрерывная и убывающая на
R и множество ее значений (0; π).
Функция y = log5 t определена на промежутке (0;
π), непрерывна и возрастает
на нем. Значит, данная сложная функция убывает на множестве R. И
она, как композиция двух непрерывных функций, будет непрерывна на R.
Решим задачу «а».
Так как функция непрерывна на всей числовой оси, то она
непрерывна и на любой ее части, в частности, на данном отрезке. А тогда она на
этом отрезке имеет наименьшее и наибольшее значения и принимает все значения
между ними:
f (4) = log5 arcctg 4.
— Какое из полученных значений больше? Почему? И каким же
будет множество значений?
Ответ:
Решим задачу «б».
Ответ: у (–∞; log5
π) на всей области
определения.
Задача с параметром
Теперь попробуем составить и решить несложное уравнение с
параметром вида f(x) = a, где f(x) — та же
функция, что и в задании 4.
Задание 5. Определите количество корней уравнения log5
(arcctg x) = а для каждого значения параметра а.
Решение. Как мы уже показали в задании 4, функция у
= log5 (arcctg x) — убывает и непрерывна на R и
принимает значения меньше log5 π.
Этих сведений достаточно, чтобы дать ответ.
Ответ: если а < log5
π, то уравнение имеет
единственный корень;
если а ≥ log5 π, то
корней нет.
Учитель. Сегодня мы рассмотрели задачи, связанные с
нахождением множества значений функции. На этом пути мы открыли для себя новый
метод решения уравнений и неравенств — метод оценки, поэтому нахождение
множества значений функции стало средством решения задач более высокого уровня.
При этом мы увидели, как конструируются такие задачи и как свойства монотонности
функции облегчают их решение.
И мне хочется надеяться, что та логика, которая связала рассмотренные сегодня
задачи, вас поразила или хотя бы удивила. Иначе и быть не может: восхождение на
новую вершину никого не оставляет равнодушным! Мы замечаем и ценим красивые
картины, скульптуры и т.д. Но и в математике есть своя красота, притягивающая и
завораживающая — красота логики. Математики говорят, что красивое решение — это,
как правило, правильное решение, и это не просто фраза. Теперь Вам самим
предстоит находить такие решения и один из путей к ним мы указали сегодня. Удачи
вам! И помните: дорогу осилит идущий!
Баженова В.
Общая информация
У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.
Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.
В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.
Основные понятия
Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».
Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.
Например, нужно найти область значений квадратичной функции y = 3x 2 — 2x — 1. Следует записать уравнение 3x 2 — 2x — 1 = 0. Ордината вычисляется таким образом: y0 = -D / 4a = -[b 2 — 4ac] / 4a = -[(-2)^2 — 4 * 3 * (-1)] / (4 * 3) = -16 / 12 = -4/3. Если коэффициент а>0, то ветви параболы направлены вверх. Следовательно, E (y) = (-4/3;+бесконечность).
Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.
Типы функций
Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:
- (-бесконечность;+бесконечность): y =kx + b, y = x^(2n+1), y = x^(1/(2n+1)), y = log (x) с основанием а, y = tg (x) и y = ctg (x).
- [0;+бесконечность): y = x^(2n), y = x^(1/(2n)) и y = a^x.
- (-бесконечность;0] U [0;+бесконечность) только для y = k / x (гипербола).
- [-1;1]: y = sin (x) и y = cos (x).
- [0;Pi]: y = arccos (x) и arcsin (x).
- [-Pi/2;Pi/2]: y = arctg (x) и arcsin (x).
Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.
Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.
Важные свойства
Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:
- В случае, когда функция f (x) является непрерывной, и наблюдается ее возрастание или убывание на отрезке [a;b], то множество значений — интервал [f (a);f (b)].
- Если y = f (x) обладает непрерывностью на промежутке [a;b], и существует некоторое минимальное m и максимальное М ее значения, то множеством ее значений является интервал [m;M].
- При непрерывности и дифференцируемости функции на промежутке [a;b], она имеет минимальное и максимальное значения на данном промежутке.
Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.
Методы нахождения
Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:
- Отдельное нахождение значений элементов сложной функции.
- Оценочный.
- Учет непрерывности и монотонности.
- Взятие производной.
- Использование max и min функции.
Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.
Для каждого элемента
Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:
- Выполнить необходимые преобразования — упростить выражение.
- Разбить выражение на элементы.
- Выполнить поиск E (f) для каждого элемента.
- Произвести замену.
- Анализ.
- Результат решения.
Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:
- Упростить (выделить квадрат): y = log0.5 (4 — 2 * 3^x — 9^x) = log0.5 [5 — (1 — 2 * 3^x — 9^x)] = log0.5 [5 — (3^x + 1)].
- Разбить на элементарные функции: y = 3^x, y = 3^x + 1, y = [-(3^x + 1)]^2 и y = [5 — (3^x + 1)]^2.
- Определить для каждого элемента E (f): E (3^x) = (0;+бесконечность), E (3^x + 1) = (1;+бесконечность), E ([-(3^x + 1)]^2) = (-бесконечность;-1) и E ([5 — (3^x + 1)]^2) = (-бесконечность;4).
- Произвести замену: t = 5 — (3^x + 1)]^2 (-бесконечность <= t <=4).
- Анализ: поскольку E (f) на луче (-бесконечность;4) совпадает с интервалом (0;4), то функция непрерывна и убывает. Необходимо отметить, что интервал (0;4) получен при пересечении луча (-бесконечность;4) с областью определения функции логарифмического типа (0;+бесконечность). На интервале (0;4) эта функция непрерывна и убывает. Если t>0, то она стремится к бесконечности. Когда t = 4, ее значение равно -2.
- Результат решения — искомый интервал: E (f) = (-2;+бесконечность).
Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.
Оценочный способ
Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:
- Доказать непрерывность.
- Составить неравенство или неравенства для нескольких функций.
- Узнать оценку.
- Записать интервал.
Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:
- Функция вида y = cos (x) является непрерывной.
- Неравенства: -1<=cos (7x)?1 и -5<=5 * cos (x)?5.
- Оценка получает при объединении неравенств: -6<=y?6. При значениях независимой переменной x = Pi и x = 0 функция принимает значения -6 и 6 соответственно (нижняя и верхняя границы). Функция состоит из двух элементов, следовательно, она является линейной и непрерывной.
- Интервал: E (y) = [-6;6].
Метод позволяет найти решение без использования дополнительных вычислений. Но при его использовании легко ошибиться.
Учет непрерывности и монотонности
Одним из простых способов решения, который специалисты рекомендуют новичкам, является метод учета непрерывности и монотонности. Для этого существует специальный алгоритм:
- Упростить выражение.
- Выполнить замену при необходимости.
- Найти вершину графика.
- Определить промежуток.
- Вычислить максимальное и минимальное значения.
- Записать E (f).
Например, существует некоторая функция y = cos (2x) + 2cos (x). Необходимо найти ее E. Искать следует по алгоритму решения методом учета монотонности и непрерывности:
- Упростить (по формуле двойного угла): y = 2 * (cos (x))^2 + 2cosx — 1.
- Замена t = cos (x): y = 2 * t 2 + 2 * t — 1 = 2 * (t + 0,5)^2 — 1,5.
- Показательная функция является параболой. Она монотонна, непрерывна и имеет вершину по оси ОУ -1,5. Промежуток, который рассматривается — [-1;1], поскольку E (cos (x)) = [-1;1].
- Минимальное значение равно -1,5, так как ветви направлены вверх. Максимальное на промежутке [-1;1] – MAX (y) = 3. Для его нахождения нужно построить график параболы y = 2 * (t + 0,5)^2 — 1,5.
- Искомый интервал — E (cos (2x) + 2cos (x)) = [-1,5;3].
Чтобы построить график параболы, нужно найти ее вершину и точки пересечения с осью абсцисс. Последние находятся при решении уравнения 2 * (t + 0,5)^2 — 1,5 = 0. Однако существует способ намного проще. Для этого следует привести выражение к виду 2 * (t + 0,5)^2 = 1,5. Отсюда t = – 0,5. Следовательно, координаты вершины — (-0,5;-1,5). Корни уравнения при его решении: t1 = -[(1 + (3)^0.5)] / 2 и t2 = -[(1 — (3)^0.5)] / 2.
Производная, min и max
Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:
- Найти производную.
- Анализ.
- Указать MAX (f) и MIN (f).
- Запись интервала в формате (MIN (f);MAX (f)).
Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:
- Производная: y’ = [arcsin (x)]’ = 1 / [(1 — x 2 )^0.5].
- Функция возрастает на интервале (-1;1).
- Минимум и максимум на отрезке (-1;1): MIN (arcsin (-1)) = -Pi/2 MAX (arcsin (1)) = Pi/2.
- Интервал: E (arcsin (x)) = [-Pi/2;Pi/2].
В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:
- Производная: y’ = [sin (x)]’ = cos (x).
- Период функции равен 2Pi. Следует взять отрезок [0;2Pi]. Для нахождения множества значений на нем нужно приравнять производную функции к 0, т. е. cos (x) = 0. Найти х = Pi/2 + Pi * к, где «к» принадлежит Z. Точки экстремума равны Pi/2 и 3Pi/2.
- Минимум и максимум на отрезке [0;2Pi): MIN ([sin (3Pi/2)]) = -1 и MAX ([sin (3Pi/2)]) = 1.
- E (sin (x)) = [-1;1].
Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.
Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.