- Функция, обратная данной
- Алгоритм вывода формулы функции, обратной данной
- Свойства взаимно обратных функций
- Примеры
Функция, обратная данной
По определению (см. §34 справочника для 7 класса)
Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Пусть некоторое соответствие задано таблицей:
|
x |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
Множество значений X = {-4;-3;…;4} отображается в множество значений Y = {-2;-1,5;…;2}: $X xrightarrow{f} Y$. При этом каждому значению x соответствует единственное значение y, т.е., данное соответствие f является функцией.
С другой стороны, мы можем рассмотреть обратное отображение $Y xrightarrow{g} X$, заданное той же таблицей. При этом каждому значению y соответствует единственное значение x, т.е., обратное соответствие $g = f^{-1}$ также является функцией.
Функцию $f: X xrightarrow{f} Y$ с областью определения X и областью значений Y называют обратимой, если обратное ей соответствие $g: Y xrightarrow{g} g X$ также является фунцией.
Если функция f обратима, то обратное ей соответствие $g = f^{-1}$ называют обратной функцией к f.
Например: аналитическое выражение для функции $X xrightarrow{f} Y$, заданной таблицей $y = f(x) = frac{x}{2}$. Обратное соответствие $Y xrightarrow{g} X$ также является функцией x = g(y) = 2y.
Функция g – обратная функция к f.
В общем случае формулы функций записывают в виде y(x). При такой записи, функции $y = frac{x}{2}$ и y=2x являются взаимно обратными.
Алгоритм вывода формулы функции, обратной данной
На входе: множества X и Y, для которых оба соответствия $X xrightarrow{f} Y$ и $Y xrightarrow{g} X$ являются функциями.
Шаг 1. В формуле для исходной функции заменить обозначения аргумента и значения: $x rightarrow y$, $y rightarrow x$.
Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.
Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.
Например:
1) Пусть исходная функция $y = frac{x}{2}$
Шаг 1. Меняем аргумент и значение: $x = frac{y}{2}$
Шаг 2. Находим y из полученной формулы: y = 2x – искомая обратная функция
Шаг 3. Ограничений на x и y нет
2) Пусть исходная функция y = -2x+3
Шаг 1. Меняем аргумент и значение: x = -2y+3
Шаг 2. Находим y из полученной формулы: $y = frac{-x+3}{2}$ – искомая обратная функция
Шаг 3. Ограничений на x и y нет
3) Пусть исходная функция $y = sqrt{x+1}$
Шаг 1. Меняем аргумент и значение: $x = sqrt{y+1}$
Шаг 2. Находим y из полученной формулы: $y = x^2-1$ – искомая обратная функция
Шаг 3. На исходную функцию накладываются ограничения
на $x:x+1 ge 0 Rightarrow x ge -1$, на $y:y ge 0$
Тогда исходная функция определяется на множествах $y ge -1$, $x ge 0$
4) Пусть исходная функция $y = 2x^2+1$
Шаг 1. Меняем аргумент и значение: $x = 2y^2+1$
Шаг 2. Находим y из полученной формулы: $y = sqrt{frac{x-1}{2}}$ – искомая обратная функция
Шаг 3. На обратную функцию накладываются ограничения
на $x:x-1 ge 0 Rightarrow x ge 1$, на $y:y ge 0$
Тогда исходная функция определяется на множествах $y ge 1$, $x ge 0$
Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.
Свойства взаимно обратных функций
Пусть f и g – взаимно обратные функции. Тогда:
1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.
2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.
3. Если f – нечётная, то и g – нечётная.
4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.
5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.
Например:
Графики пар взаимно обратных функций, найденных выше:
Примеры
Пример 1. Задайте формулой функцию, обратную данной.
а) y = 5x-4
Меняем аргумент и значение: x = 5y-4
Получаем: $y = frac{x+4}{5}$ – искомая обратная функция
б) y = -3x+2
Меняем аргумент и значение: x = -3y+2
Получаем: $y = frac{-x+2}{3}$ – искомая обратная функция
в) y = 4x+1, где $-1 le x le 5$
Меняем аргумент и значение: x = 4y+1
Получаем: $y = frac{x-1}{4}$
Требуем, чтобы: $-1 le y le 5 Rightarrow -1 le frac{x-1}{4} le 5 Rightarrow -4 le x-1 le 20 Rightarrow -3 le x le 21$
Итак, искомая обратная функция: $y = frac{x-1}{4}$, где -3 $le x le 21$
г) $y=- frac{1}{2} x+7$, где $2 le x le 9$
Меняем аргумент и значение: $x=-frac{1}{2} y+7$
Получаем: y = 2(-x+7) = -2x+14
Требуем, чтобы: $2 le y le 9 Rightarrow 2 le -2x+14 le 9 Rightarrow -12 le -2x le -5 Rightarrow$
$6 ge x ge 2,5 Rightarrow 2,5 le x le 6$
$y = -2x+14,где 2,5 le x le 6$ – искомая обратная функция
Пример 2. Найдите функцию, обратную данной.
Постройте график исходной и обратной функции в одной системе координат.
|
а) $y=x^2,x le 0$ Обратная функция $x = y^2 Rightarrow y = pm sqrt{x}$ При этом $y le 0$ Поэтому выбираем $y = – sqrt{x}$ – искомая обратная функция |
 |
|
б) y = x-3, $-1 le x le 4$ Обратная функция $x = y-3 Rightarrow y = x+3$ При этом $-1 le y le 4 Rightarrow -1 le x+3 le 4$ $Rightarrow -4 le x le 1$ y = x+3, $-4 le x le 1$ – искомая обратная функция |
 |
|
в) $y = frac{1}{x+1} $ Обратная функция $x = frac{1}{y+1} Rightarrow y = frac{1}{x} -1$ |
 |
|
г) $y = 1+ sqrt{x-3}$ Область определения: $x ge 3$ Область значений: $y ge 1$ Обратная функция: $x = 1+ sqrt{y-3} Rightarrow y = (x-1)^2+3$ Область определения: $x ge 1$ Область значений: $y ge 3$ |
 |
Понятие функции является одним из основных в математике. Оно вводится следующим образом.
Пусть заданы два множества (X) и (Y). Если каждому элементу (x) из множества (X) поставлен в соответствие элемент (y=f(x)) множества (Y), то говорят, что на множестве (X) задана функция (f). При этом элемент (x) называется независимой переменной, а элемент (y) − зависимой переменной. В случае, когда (x и y) являются действительными числами, функцию (y=f(x)) можно представить в виде графика в декартовой системе координат (Oxy).
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции, то есть по оси абсцисс откладываются значения переменной (x), а по оси ординат откладываются значения переменной (y).
Область определения функции (D(y)) – это множество всех допустимых значений аргумента (x), при которых выражение, стоящее в правой части уравнения функции (y=f(x)), имеет смысл. Другими словами, это область допустимых значений выражения (f(x)).
Чтобы по графику функции (y=f(x)) найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений (x), на которых существует график функции.
Пример 1. Найти область определения функции: (y=sqrt{4x-x^3}).
Решение: Поскольку квадратный корень можно извлекать только из неотрицательных чисел, то область определения данной функции задается неравенством (4x-x^3ge0 Leftrightarrow x^3-4xle0 Rightarrow x(x-2)(x+2)le0).
Решая это неравенство с помощью метода интервалов, получим: (xin (-infty; -] cup [0;2]).
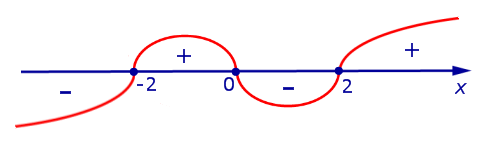
Ответ: (xin (-infty; -] cup [0;2]).
Множество значений функции (E(y)) – это множество всех значений, которые может принимать зависимая переменная (y).
Чтобы по графику функции (y=f(x)) найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений (y), на которых существует график функции.
Пример 2. Найти множество значений функции: (y = x^2 + 6x + 8).
Решение: Поскольку (y=x^2+6x+8=x^2+6x+9-1=(x+3)^2-1ge-1) и для каждого числа (yge-1) существуют решения уравнения (x^2 + 6x + 8 = y), определяемые формулой (x_{1,2}=-3pm sqrt{y+1}), то множеством значений функции ( y = x^2 + 6x + 8) будет множество ([-1;+infty)).
Ответ: (yin [-1;+infty)).
Обратная функция
Пусть задана функция (y=f(x)). Чтобы найти обратную для нее функцию, надо из уравнения (y=f(x)) выразить переменную (x) через (y) и затем поменять переменные местами. Обратную функцию часто обозначают в виде (y=f^{−1}(x)). Исходная и обратная функции симметричны относительно прямой (y=x).

Чтобы для данной функции (y = f(x)) найти обратную, надо:
- В соотношении (y = f(x)) заменить (x) на (y), а (y) на (x): (x = f(y)).
- В полученном выражении (x=f(y)) выразить (y) через ( x).
Например, (y=3x-8: x=3y-8 Rightarrow 3y=x+8 Rightarrow y=frac{x+8}3).
Свойства взаимно обратных функций
Тождества. Пусть (f) и (g) – взаимно обратные функции. Это означает, что равенства (y = f(x)) и (x = g(y)) равносильны. Подставим одно из этих равенств в другое. Получим два тождества: (f(g(y)) = y) и (g(f(x)) = x).
Область определения. Пусть (f) и (g) – взаимно обратные функции. Область определения функции (f) совпадает с областью значений функции (g), и наоборот, область значений функции (f) совпадает с областью определения функции (g).
Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное верно и для убывающих функций.
Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой (y = x).
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Для самостоятельной работы студентов
По дисциплине: МАТЕМАТИКА (включая алгебру и начала математического анализа; геометрию)
Тема: «Обратные функции»
Специальность: 34.02.01 Сестринское дело Курс: 1
(базовой подготовки)
Купино
2020
Рассмотрено на заседании предметной цикловой
Методической комиссии по общеобразовательным дисциплинам,
общему гуманитарному и социально-экономическому, математическому и
естественно-научному циклу
Протокол № _____ от «_____» _________20____г.
Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.
Купино
2020 г
Пояснительная записка к методическому пособию
Методическое пособие предназначено для повторения теоретических и практических знаний по теме.
Цель пособия – повторить понятияобратной функции, определять вид и строить график обратной функции, находить ее область определения и область значений и подготовится к занятию по теме «Обратные функции».
Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения, свойства и формулы по теме: Обратные функции, тест для самоконтроля и ключи к тесту.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Обратные функции
Определение обратной функции
Пусть функция ![]() строго монотонная (возрастающая или убывающая) и непрерывная на области определения
строго монотонная (возрастающая или убывающая) и непрерывная на области определения ![]() , область значений этой функции
, область значений этой функции ![]() , тогда на интервале
, тогда на интервале ![]() определена непрерывная строго монотонная функция
определена непрерывная строго монотонная функция ![]() с областью значений
с областью значений ![]() , которая является обратной для
, которая является обратной для ![]() .
.
Другими словами, об обратной функции ![]() для функции
для функции ![]() на конкретном промежутке имеет смысл говорить, если на этом интервале
на конкретном промежутке имеет смысл говорить, если на этом интервале ![]() либо возрастает, либо убывает.
либо возрастает, либо убывает.
Функции f и g называют взаимно обратными.
Зачем вообще рассматривать понятие обратных функций?
Это вызвано задачей решения уравнений ![]() . Решения как раз и записываются через обратные функции.
. Решения как раз и записываются через обратные функции.
Примеры нахождения взаимнообратных функций.
Например, требуется решить уравнение ![]() .
.
Решениями являются точки 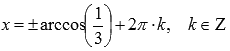 .
.
Функции косинус и арккосинус как раз являются обратными на области определения.
Рассмотрим несколько примеров нахождения обратных функций.
Начнем с линейных взаимнообратных функций.
Пример.
Найти функцию обратную для ![]() .
.
Решение.
Областью определения и областью значений этой функции является все множество действительных чисел. Выразим x через y (другими словами, решим уравнение ![]() относительно x ).
относительно x ).
![]() – это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать
– это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать ![]() .
.
Таким образом, ![]() и
и ![]() – взаимно обратные функции.
– взаимно обратные функции.
Приведем графическую иллюстрацию взаимно обратных линейных функций.
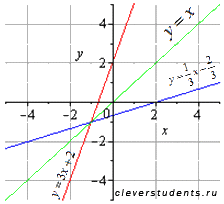
Очевидно, что графики симметричны относительно прямой y=x (биссектрисы первого и третьего квадрантов). Это одно из свойств взаимно обратных функций, о которых речь пойдет ниже.
Теперь рассмотрим пример нахождения логарифмической функции, обратной к заданной показательной функции.
Пример.
Найти функцию обратную для ![]() .
.
Решение.
Областью определения этой функции является все множество действительных чисел, областью значений является интервал ![]() . Выразим x через y(другими словами, решим уравнение
. Выразим x через y(другими словами, решим уравнение ![]() относительно x).
относительно x).
![]() – это и есть обратная функция. Переставив буквы x и y , имеем
– это и есть обратная функция. Переставив буквы x и y , имеем ![]() .
.
Таким образом, ![]() и
и ![]() – показательная и логарифмическая функции есть взаимно обратные функции на области определения.
– показательная и логарифмическая функции есть взаимно обратные функции на области определения.
График взаимно обратных показательной и логарифмической функций.
Свойства взаимно обратных функций
Перечислим свойства взаимно обратных функций ![]() и
и ![]() .
.
-
и
.
-
Из первого свойства видно, что область определения функции
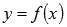 совпадает с областью значений функции
совпадает с областью значений функции 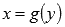 и наоборот.
и наоборот. -
Графики взаимно обратных функций симметричны относительно прямой y=x.
-
Если
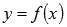 возрастает, то и
возрастает, то и 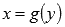 возрастает, если
возрастает, если 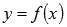 убывает, то и
убывает, то и 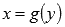 убывает.
убывает.
Замечание по свойству 1).
Рекомендуем ОЧЕНЬ ВНИМАТЕЛЬНО относиться к области определения и области значений функций.
Например: и
– взаимно обратные функции. По первому свойству имеем
. Это равенство верно только для положительных y , для отрицательных y логарифм не определен. Так что не спешите с записями вида
, а если уж так написали, то следует добавить фразу «при положительных y».
Равенство в свою очередь верно для любых действительных x.
Надеемся, Вы уловили этот тонкий момент.
Особенно аккуратными надо быть с тригонометрическими и обратными тригонометрическими функциями.
К примеру, , так как область значений арксинуса , а
в нее не попадает.
Правильно будет
В свою очередь есть верное равенство.
То есть при
и
при
.
Графики основных элементарных взаимно обратных функций
-
Взаимно обратные степенные функции, графики.
Для степенной функции при
обратной является также степенная функция
Если заменить буквы, то получим пару взаимно обратных функций
и
Графики для положительных а и отрицательных а.
-
Взаимно обратные показательная и логарифмическая функции
и
, графики.
Подразумеваем, что а положительное и не равное единице число.
Графики для и для
-
Взаимно обратные тригонометрические и обратные тригонометрические функции.
График главной ветви синуса и арксинуса (светлая область).
График главной ветви косинуса и арккосинуса (светлая область).
График главной ветви тангенса и арктангенса (светлая область).
График главной ветви котангенса и арккотангенса (светлая область).
Если Вам потребуются обратные функции для ветвей тригонометрических функций, отличных от главных, то соответствующую обратную тригонометрическую функцию нужно будет сдвинуть вдоль оси ординат на необходимое количество периодов.
Например, если Вам потребуется обратная функция для ветви тангенса на промежутке (эта ветвь получается из главной ветви сдвигом на величину
вдоль оси ох ), то ей будет являться ветвь арктангенса, сдвинутая вдоль оси oy на
.
Пока на этом закончим с обратными функциями.
Тест по теме: Обратные функции
1. Как называют функция y = f(х), если она принимает каждое своё значение только при одном значении х?
2. Найдите функцию, обратную к функции у = 5х + 2.
Варианты ответов
-
у = 0,2 (х – 2)
-
у = 0,5 (х – 2)
-
у = 0,2 (2 + х)
-
у = (х – 2)2
3. Является ли монотонная функция обратимой?
Варианты ответов
-
является
-
не является
4.Укажите, какие из перечисленных функций являются обратимыми.
Варианты ответов
-
у = 5х + 2
-
у = х2
-
у = х5
-
у = х3 + 1
5.Укажите истинные утверждения.
Если g(x) – функция, обратная к функции f(x), то и f(x) – функция, обратная к g(x), при этом …
Варианты ответов
-
область определения обратной функции совпадает со множеством значений исходной функции
-
множество значений обратной функции совпадает с областью определения исходной функции
-
область определения обратной функции совпадает с областью определения исходной функции
-
множество значений обратной функции совпадает со множеством значений исходной функции
6.Найдите область значений функции, обратной для f(x) = 4 – 3x.
Варианты ответов
-
(-∞;+∞)
-
(0;+∞)
-
(-∞;4)
-
[3;4]
-
[-4;-3]
7.Найдите область определения и область значения функции, обратной данной у = 7х – 5.
Варианты ответов
-
D(y) = (-∞;+∞)
-
E(y) = (-∞;+∞)
-
D(y) = (-5;+∞)
-
E(y) = (-∞;5)
-
D(y) = (-7;+∞)
-
E(y) = (-5;7)
8.Укажите номер рисунка, на котором изображен график обратной функции к функции у = х2, при х є [0;+∞).
9.Сопоставьте функции и обратные к ним.
Варианты ответов
-
y=x+53
-
y=x3
-
y=x2
10.Какое значение принимает обратная функция при х = 6 к функции у = 2х – 4.
Эталоны ответов теста по теме: Обратные функции
1. Как называют функция y = f(х), если она принимает каждое своё значение только при одном значении х? Ответ обратимая
2. Найдите функцию, обратную к функции у = 5х + 2.
Варианты ответов
-
у = 0,2 (х – 2)
-
у = 0,5 (х – 2)
-
у = 0,2 (2 + х)
-
у = (х – 2)2
3. Является ли монотонная функция обратимой?
Варианты ответов
-
является
-
не является
4.Укажите, какие из перечисленных функций являются обратимыми.
Варианты ответов
-
у = 5х + 2
-
у = х2
-
у = х5
-
у = х3 + 1
5.Укажите истинные утверждения.
Если g(x) – функция, обратная к функции f(x), то и f(x) – функция, обратная к g(x), при этом …
Варианты ответов
-
область определения обратной функции совпадает со множеством значений исходной функции
-
множество значений обратной функции совпадает с областью определения исходной функции
-
область определения обратной функции совпадает с областью определения исходной функции
-
множество значений обратной функции совпадает со множеством значений исходной функции
6.Найдите область значений функции, обратной для f(x) = 4 – 3x.
Варианты ответов
-
(-∞;+∞)
-
(0;+∞)
-
(-∞;4)
-
[3;4]
-
[-4;-3]
7.Найдите область определения и область значения функции, обратной данной у = 7х – 5.
Варианты ответов
-
D(y) = (-∞;+∞)
-
E(y) = (-∞;+∞)
-
D(y) = (-5;+∞)
-
E(y) = (-∞;5)
-
D(y) = (-7;+∞)
-
E(y) = (-5;7)
8.Укажите номер рисунка, на котором изображен график обратной функции к функции у = х2, при х є [0;+∞).
Ответ 4
9.Сопоставьте функции и обратные к ним.
Варианты ответов
-
y=x+53
-
y=x3
-
y=x2
10.Какое значение принимает обратная функция при х = 6 к функции у = 2х – 4. Ответ 5
Критерии оценивания тестовых заданий
10 вопросов 5 (отлично) (10-9 ответов)
10 вопросов 4 (хорошо) (8 ответов)
10 вопросов 3 (удов) (7 ответов)
Литература
-
Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М.: 2018
-
Башмаков М.И. Сборник задач: учеб. пособие (базовый уровень). 11 кл. – М.: 2012
Интернет-ресурсы
-
http://school-collection.edu.ru – Электронный учебник «Математика в
школе, XXI век».
-
http://fcior.edu.ru – информационные, тренировочные и контрольные материалы.
-
www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов
Обратная функция
-
Рассмотрим
две функции,

и
 ,
,
графики которых изображены, соответственно,
на рисунках 1 и 2. Функция
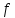
обладает следующим свойством: каждое
свое значение функция принимает только
при одном
значении
аргумента. То есть, если
 ,
,
то
уравнение
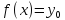
имеет единственное решение
 .
.
В геометрической интерпретации это
означает, что параллельная
оси абсцисс прямая

пересекает
график функции
ровно в одной точке.
Определение
1.
Если функция

каждое свое значение принимает только
при одном
значении
аргумента, то эта функция называется
обратимой. Иначе можно сказать, что
разным значениям аргумента соответствуют
разные значения функции
 .
.

Функция

таким свойством не обладает. Например,
отмеченное на рисунке 2 значение функции

принимается при разных значениях
аргумента,
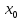
и
 ,
,
то есть

и
 .
.
Другими словами, уравнение

имеет при данном значении

два корня. Прямая,
параллельная оси абсцисс, может
пересечь
график этой функции
более чем в одной точке.
Свойство
функции

принимать каждое свое значение только
при одном
значении
аргумента, то есть быть обратимой,
позволяет определить новую функцию. А
именно функцию, которая ставит в
соответствие значению

то единственное
значение
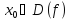 ,
,
при котором
 .
.
То есть ставит числу

в соответствие единственный корень
уравнения
 .
.
Назовем эту функцию обратной к функции
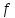
и
обозначим буквой
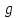 .
.
Таким образом,
 .
.
Отметим,
что в
отличие от
функции
 ,
,
для функции

задать таким же способом обратную
функцию не удастся, поскольку уравнение

может иметь несколько корней.
Дадим
определение обратной фукции.
Определение
2.
Пусть задана обратимая функция
 .
.
Функция
 ,
,
определенная на множестве
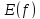 ,
,
и ставящая в соответствие числу

число
 ),
),
такое, что
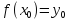 ,
,
называется обратной к функции
 .
.
-
Найдем
обратную функцию к функции
 .
.
Область определения функции
 ,
,
отрезок
 ,
,
обозначим буквой
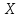 ,
,
то есть

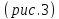 .
.
Множество значений функции

составляет отрезок
 ,
,
обозначенный буквой
 ,
,
то есть


Функция

числу из промежутка
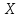
ставит в соответствие корень квадратный
из этого числа, например,
 .
.
Функция

является обратимой, поскольку разным
значениям ее аргумента соответствуют
разные значения функции.
Обратная
функция

определена на промежутке

и произвольному числу

ставит в соответствие число
 ,
,
которое определяется условием
 ,
,
то есть равенством

(рис.4). Выражаем из этого равенства
 ,
,
возведя обе части равенства в квадрат,
 .
.
Таким образом, функция

произвольному числу
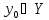
ставит в соответствие число
 ,
,
равное
 .
.
Значит, для каждого
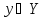
имеем
 ,
,
то есть
 .
.
Независимой
переменной, то есть аргументом обратной
функции
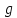 ,
,
является переменная
 ,
,
а зависимой – переменная
 .
.
То есть, в сравнении с функцией
 ,
,
переменные поменялись ролями. Если
теперь переменные обозначить традиционным
образом, а именно, буквой х – аргумент
функции
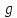 ,
,
а зависимую переменную – буквой
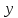 ,
,
то функция

примет вид
 .
.
Таким образом, мы нашли, что квадратичная
функция
 ,
,
заданная на отрезке
 ,
,
является обратной к функции
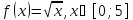 ..
..
Множество значений обратной функции –
отрезок
 .
.
График
обратной функции

мы можем изобразить в той же системе
координат, что и график
 .
.
Для этого отрезок
 ,
,
составляющий область определения
функции

нужно отложить на оси ординат, поскольку
на этой оси располагаются значения
аргумента функции. Точки графика функции

имеют координаты
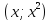 ,
,
при этом

(рис.5).

На
рисунке 5 показано, что области определения
и множества значений функций

«меняются местами»:
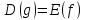
и
 .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
