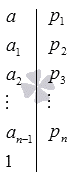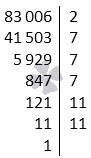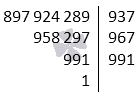Как найти множители трехзначного числа

Как найти множители трехзначного числа

Формат:
Кратко
Подробно
В столбик

Онлайн калькулятор раскладывает число в произведение простых множителей.
Для вычислений используется длинная арифметика, поэтому можно легко
разложить на множители даже большие числа.

Что такое разложение числа на множители?

Любое натуральное число n > 1 можно представить в виде
произведения простых чисел. Это представление называется разложением
числа n на простые множители.

Натуральное число n называется делителем целого числа m, если для подходящего целого числа k верно
равенство m = n cdot k. В этом случае говорят, что m делится на n или что число m кратно
числу n.

Простым числом называют натуральное число p ge 2, делящееся только на себя и на единицу. Составным
числом называют число, имеющее больше двух различных делителей (любое натуральное число m, не равное 1,
имеет как минимум два делителя: 1 и |m|). Например, числа 2, 3, 5, 7, 11 – простые, а числа 9 = 3cdot 3, 26 = 2cdot 13 – составные.

Основная теорема арифметики. Любое натуральное число n, большее единицы, можно
разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования
сомножителей.

Как разложить число на множители?

В школе на уроках математики разложение числа на множители обычно записывают столбиком в две колонки. Делается это
так: в левую колонку выписываем исходное число, затем

  • Берём самое маленькое простое число — 2 и по признакам
    делимости или обычным делением проверяем, делится ли исходное число на 2.
  • Если делится, то в правую колонку выписываем 2. Далее делим исходное число на 2 и записываем результат в левую
    колонку под исходным числом.
  • Если не делится, то берём следующее простое число — 3.

Повторяем эти шаги, при этом работаем уже с последним числом в левой колонке и с текущим простым числом. Разложение
заканчивается, когда в левой колонке будет записано число 1.

Чтобы лучше понять алгоритм, разберём несколько примеров.

Пример. Разложить на множители число 84.

Решение. Записываем число 84 в левую колонку:

Берём первое простое число — два и проверяем, делится ли 84 на 2. Так как 84 оканчивается на 4, а 4 делится на 2,
то и 84 делится на 2 по признаку делимости. Записываем 2 в
правую колонку. 84:2 = 42, число 42 записываем в левую колонку. Получили вот что:

Теперь работаем уже с числом 42. Число 42 делится на 2, поэтому записываем 2 в правую колонку, 42:2 = 21, число
21 записываем в левую колонку.

Число 21 на 2 не делится, поэтому проверяем его делимость на следующее простое число — 3. Число 21 делится на 3,
21:3 = 7. Записали 3 в правую колонку, 7 — в левую. Получили

Число 7 — простое число, поэтому в правой колонке записываем 7, в левую пишем 1. В итоге получили:

Всё, число разложено!

В результате в правой колонке оказались записаны все простые множители числа 84. То есть 84=2∙2∙3∙7.

Онлайн калькулятор для разложения числа на множители

Программа раскладывает числа на множители методом
перебора делителей. Для вычислений используется длинная арифметика, поэтому раскладывать можно даже большие
числа. Однако если число простое или имеет большие простые делители, разложение его на множители занимает
продолжительное время.

Источник


Загрузить PDF


Загрузить PDF

Множители – числа, которые при перемножении дают исходное число. То есть любое число есть результат произведения его множителей. Умение раскладывать числа на множители – один из основных математических навыков, который необходим не только в математике, но и в других науках.

  1. Изображение с названием Factor a Number Step 1

    1

    Запишите целое число. Это число, не являющееся обыкновенной или десятичной дробью.

    • Рассмотрим число 12.

  2. Изображение с названием Factor a Number Step 2

    2

    Найти два числа, которые при перемножении дадут данное число. Любое целое число можно записать в виде произведения двух других чисел. Даже простое число можно записать как произведение 1 и самого числа.

    • В нашем примере у числа 12 есть несколько множителей: 12*1; 6*2; 3*4. Таким образом, вы можем заявить, что множителями числа 12 являются числа 1, 2, 3, 4, 6, 12. Рассмотрим пару множителей 6 и 2.
    • Четные числа легко разложить на множители, так как множителем любого четного числа является 2. 4 = 2*2, 26 = 13*2 и т.д.

  3. Изображение с названием Factor a Number Step 3

    3

    Если возможно, разложите на множители найденные множители. Когда вы нашли все множители числа, определите, можно ли разложить их на множители.

    • В нашем примере мы разложили 12 на 2*6. Обратите внимание, что 6 можно разложить на множители: 3*2 = 6. Таким образом, вы можете заявить, что 12 = 2*(3*2).

  4. Изображение с названием Factor a Number Step 4

    4

    Если множителями являются простые числа, то дальше можете не продолжать. Простые числа – это числа, которые делятся только на себя или на 1. Например, 2, 3, 5, 7, 11, 13 или 17 – простые числа.

    • В нашем примере вы разложили 12 на 2*(2*3). 2, 2, 3 – это простые числа. Их можно разложить на множители, например, 2=2*1 и 3=3*1, но это не имеет смысла (по крайней мере в большинстве задач).

  5. Изображение с названием Factor a Number Step 5

    5

    Отрицательные числа раскладываются на множители аналогичным образом. Единственным отличием является необходимость учесть знаки множителей, чтобы при их перемножении получить отрицательное число.

    • Например, разложим на множители число -60.
      • -60 = -10*6
      • -60 = (-5*2)*6
      • -60 = (-5*2)*(3*2)
      • -60 = -5*2*3*2. Обратите внимание, что при разложении на множители отрицательного числа количество отрицательных множителей должно быть нечетным. Например, вы можете разложить число -60 и так: -5*2*-3*-2.

    Реклама

  1. Изображение с названием Factor a Number Step 6

    1

    Разложить на множители большое число – нелегкая задача. Большинство людей затрудняются раскладывать четырех- или пятизначные числа. Для упрощения процесса запишите число над двумя колонками.

    • Разложим на множители число 6552.

  2. Изображение с названием Factor a Number Step 7

    2

    Разделите данное число на наименьший простой делитель (кроме 1), на который данное число делится без остатка. Запишите этот делитель в левой колонке, а в правой колонке запишите результат деления. Как отмечалось выше, четные числа легко раскладывать на множители, так как их наименьшим простым множителем всегда будет число 2 (у нечетных чисел наименьшие простые множители различны).

    • В нашем примере число 6552 – четное, поэтому 2 является его наименьшим простым множителем. 6552 ÷ 2 = 3276. В левой колонке запишите 2, а в правой – 3276.

  3. Изображение с названием Factor a Number Step 8

    3

    Далее разделите число в правой колонке на наименьший простой делитель (кроме 1), на который данное число делится без остатка. Запишите этот делитель в левой колонке, а в правой колонке запишите результат деления (продолжите этот процесс до тех пор, пока в правой колонке не останется 1).

    • В нашем примере: 3276 ÷ 2 = 1638. В левой колонке запишите 2, а в правой – 1638. Далее: 1638 ÷ 2 = 819. В левой колонке запишите 2, а в правой – 819.

  4. Изображение с названием Factor a Number Step 9

    4

    Вы получили нечетное число; для таких чисел найти наименьший простой делитель сложнее. Если вы получили нечетное число, попробуйте разделить его на наименьшие простые нечетные числа: 3, 5, 7, 11.

    • В нашем примере вы получили нечетное число 819. Разделите его на 3: 819 ÷ 3 = 273. В левой колонке запишите 3, а в правой – 273.
    • При подборе делителей опробуйте все простые числа вплоть до квадратного корня из наибольшего делителя, который вы нашли. Если ни один делитель не делит число нацело, то вы, скорее всего, получили простое число и можете прекратить вычисления.

  5. Изображение с названием Factor a Number Step 10

    5

    Продолжите процесс деления чисел на простые делители до тех пор, пока в правой колонке не останется 1 (если в правой колонке вы получили простое число, разделите его само на себя, чтобы получить 1).

    • Продолжим вычисления в нашем примере:
      • Разделите на 3: 273 ÷ 3 = 91. Остатка нет. В левой колонке запишите 3, а в правой – 91.
      • Разделите на 3. 91 делится на 3 с остатком, поэтому разделите на 5. 91 делится на 5 с остатком, поэтому разделите на 7: 91 ÷ 7 = 13. Остатка нет. В левой колонке запишите 7, а в правой – 13.
      • Разделите на 7. 13 делится на 7 с остатком, поэтому разделите на 11. 13 делится на 11 с остатком, поэтому разделите на 13: 13 ÷ 13 = 1. Остатка нет. В левой колонке запишите 13, а в правой – 1. Ваши вычисления закончены.

  6. Изображение с названием Factor a Number Step 11

    6

    В левой колонке представлены простые множители исходного числа. Другими словами, при перемножении всех чисел из левой колонки вы получите число, записанное над колонками. Если один множитель появляется в списке множителей несколько раз, используйте показатели степени для его обозначения. В нашем примере в списке множителей 2 появляется 4 раза; запишите эти множители как 24, а не как 2*2*2*2.

    • В нашем примере 6552 = 23× 32 × 7 × 13. Вы разложили число 6552 на простые множители (порядок множителей в этой записи не имеет значения).

    Реклама

Советы

  • Также важным является понятие простого числа – это число, которое имеет только два множителя: 1 и само себя. 3 – простое число, потому что его простые множители 1 и 3. С другой стороны, 4 имеет 2 в качестве простого множителя. Число, которое не является простым, называется составным . (1 – число, которое считается ни простым, ни составным – это особый случай.)
  • Наименьшие простые числа: 2, 3, 5, 7, 11, 13, 17, 19 и 23.
  • Поймите, что одно число является множителем другого, большего числа, если оно “делит его полностью”, то есть без остатка. Например, 6 является множителем 24, потому что 24 ÷ 6 = 4 (без остатка). С другой стороны , 6 не является множителем 25.
  • Если цифры в числе при их сложении делятся на 3 , то 3 является множителем этого числа. (819 = 8 +1 +9 = 18, 1 +8 = 9. Три – множитель девяти, так что 3 является множителем и 819.)
  • Помните, что мы рассматривали только “натуральные числа” – 1, 2, 3, 4, 5 … Мы не рассматривали отрицательные числа или дроби, которые могут быть описаны в других статьях.
  • Некоторые числа могут быть разложены более быстрыми способами, но этот метод работает каждый раз и, как дополнительный бонус, в ответе дает простые множители в порядке их возрастания.

Реклама

Предупреждения

  • Не делайте лишней работы. После того, как вы убрали неподходящий множитель, вы не должны рассматривать его далее. После того, как мы решили, что 2 не является множителем 819, нам не надо рассматривать 2 дальше в процессе вычисления.

Реклама

Что вам понадобится

  • Бумага
  • Карандаш и ластик
  • Калькулятор (по желанию)

Об этой статье

Эту страницу просматривали 71 089 раз.

Была ли эта статья полезной?

Источник

Разложить число на простые множители онлайн

Разложить число на простые множители значит представить это число в виде произведения простых чисел. Любое составное натуральное число можно представить единственным образом в виде произведения простых чисел, если не учитывать порядка записей простых множителей.

Алгоритм разложения чисел на простые множители

Проводим вертикальную черту

Слева от черты пишем число

Справа от черты пишем простой делитель этого числа

Слева записываем число которое образовалось в результате деления

Продолжаем процесс пока слева не останется 1

Рассмотрим пример

Разложим число 36

Проводим черту, записываем 36 слева. Самым маленьким простым делителем числа 36 является 2. Делим 36/2 = 18. 18 записываем под числом 36. Далее повторяем. Самым маленьким делителем числа 18 является 2. Дилим 18/2 = 9. 9 записываем под числом 18. Опять повторяем. Самым маленьким простым множителем числа 9 является 3. Делим 9/3 получается 3. Тройку записываем под 9. Тройка это простое число у которого делить только 3 и 1. Записываем 3 напротив тройки. Делим 3/3 = 1. 1 записывам под 3. Разложение закончено.

Целое положительное число называется простым, если оно делится только на 1 и на само себя.

Целое положительное число называется составным, если у него есть хоть один делитель, отличный от 1 и самого себя.

Таблица составных чисел

4 6 8 9 10 12 14 15 16 18
20 21 22 24 25 26 27 28 30 32
33 34 35 36 38 39 40 42 44 45
46 48 49 50 51 52 54 55 56 57
58 60 62 63 64 65 66 68 69 70
72 74 75 76 77 78 80 81 82 84
85 86 87 88 90 91 92 93 94 95
96 98 99 100 102 104 105 106 108 110
111 112 114 115 116 117 118 119 120 121
122 123 124 125 126 128 129 130 132 133
134 135 136 138 140 141 142 143 144 145
146 147 148 150 152 153 154 155 156 158
159 160 161 162 164 165 166 168 169 170
171 172 174 175 176 177 178 180 182 183
184 185 186 187 188 189 190 192 194 195
196 198 200 201 202 203 204 205 206 207
208 209 210 212 213 214 215 216 217 218
219 220 221 222 224 225 226 228 230 231
232 234 235 236 237 238 240 242 243 244
245 246 247 248 249 250 252 253 254 255
256 258 259 260 261 262 264 265 266 267
268 270 272 273 274 275 276 278 279 280
282 284 285 286 287 288 289 290 291 292
294 295 296 297 298 299 300 301 302 303

Таблица простых чисел до 1000

2 3 5 7 11 13 17 19
23 29 31 37 41 43 47 53
59 61 67 71 73 79 83 89
97 101 103 107 109 113 127 131
137 139 149 151 157 163 167 173
179 181 191 193 197 199 211 223
227 229 233 239 241 251 257 263
269 271 277 281 283 293 307 311
313 317 331 337 347 349 353 359
367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457
461 463 467 479 487 491 499 503
509 521 523 541 547 557 563 569
571 577 587 593 599 601 607 613
617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719
727 733 739 743 751 757 761 769
773 787 797 809 811 821 823 827
829 839 853 857 859 863 877 881
883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997

Похожие калькуляторы

Источник

Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.

Что значит разложить число на простые множители?

Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида 2·7·7·23 имеем, что у нас 4 простых множителя в виде 2,7,7,23.

Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа 30, тогда получим 2,3,5. Запись примет вид 30=2·3·5. Не исключено, что множители могут повторяться. Такое число как 144 имеет 144=2·2·2·2·3·3.

Не все числа предрасположены к разложению. Числа, которые больше 1 и являются целыми можно разложить на множители. Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.

При z, относящемуся к целым числам, представляется  в виде произведения а и b, где z делится на а и на b. Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше 1, то его разложение на множители p1, p2, …, pn принимает вид a=p1, p2, …, pn. Разложение предполагается в единственном варианте.

Каноническое разложение числа на простые множители

При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p1, который встречается s1 раз и так далее pn – sn раз. Таким образом разложение примет вид a=p1s1·a=p1s1·p2s2·…·pnsn. Эта запись имеет название канонического разложения числа на простые множители.

При разложении числа 609840 получим, что 609 840=2·2·2·2·3·3·5·7·11·11,его канонический вид будет 609 840=24·32·5·7·112. При помощи канонического разложения можно найти все делители числа и их количество.

Алгоритм разложения числа на простые множители

Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида p1, p2, …,pn чисел a, a1, a2, …, an-1, это дает возможность получить a=p1·a1, где a1=a:p1, a=p1·a1=p1·p2·a2, где a2=a1:p2, …, a=p1·p2·…·pn·an, где an=an-1:pn. При получении an=1, то равенство a=p1·p2·…·pn  получим искомое разложение числа а на простые множители. Заметим, что p1≤p2≤p3≤…≤pn.

Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа z. При взятии простых чисел 2,3,5,11 и так далее, причем на них делим число z. Так как z не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше z.  Видно, что не существуют делителей z, тогда понятно, что z является простым числом.

Пример 1

Рассмотрим на примере числа 87.  При его делении на 2 имеем, что 87:2=43  с остатком равным 1. Отсюда следует, что 2 делителем не может являться, деление должно производиться нацело. При делении на 3 получим, что 87:3=29. Отсюда вывод – 3 является наименьшим простым делителем числа 87.

При разложении на простые множители необходимо пользоваться таблицей простых чисел, где a.  При разложении 95 следует использовать около 10 простых чисел, а при 846653 около 1000.

Рассмотрим алгоритм разложения на простые множители:

  • нахождение наименьшего множителя при делителе p1 числа a по формуле a1=a:p1, когда a1=1, тогда а является простым числом и включено в разложение на множители, когда не равняется 1, тогда a=p1·a1 и следуем к пункту, находящемуся ниже;
  • нахождение простого делителя p2 числа a1 при помощи последовательного перебора простых чисел, используя a2=a1:p2, когда a2=1, тогда разложение примет вид a=p1·p2, когда a2=1, тогда a=p1·p2·a2, причем производим переход к следующему шагу;
  • перебор простых чисел и нахождение простого делителя p3 числа a2 по формуле a3=a2:p3, когда a3=1, тогда получим, что a=p1·p2·p3, когда не равняется 1, тогда a=p1·p2·p3·a3 и производим переход к следующему шагу;
  • производится нахождение простого делителя pn числа an-1 при помощи перебора простых чисел с pn-1, а также an=an-1:pn, где an=1, шаг является завершающим, в итоге получаем, что a=p1·p2·…·pn.

Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.

Алгоритм разложения числа на простые множители

Полученный алгоритм можно применять при помощи разложения чисел на простые множители.

Примеры разложения на простые множители

Во время разложения на простые множители следует придерживаться основного алгоритма.

Пример 2

Произвести разложение числа 78 на простые множители.

Решение

Для того, чтобы найти наименьший простой делитель, необходимо перебрать все простые числа, имеющиеся в 78. То есть 78:2=39. Деление без остатка, значит это первый простой делитель, который обозначим как p1. Получаем, что a1=a:p1=78:2=39. Пришли к равенству вида a=p1·a1, где 78=2·39. Тогда a1=39, то есть следует перейти к следующему шагу.

Остановимся на нахождении простого делителя p2 числа a1=39. Следует перебрать простые числа, то есть 39:2=19 (ост. 1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39:3=13. Значит, что p2=3 является наименьшим простым делителем 39 по a2=a1:p2=39:3=13. Получим равенство вида a=p1·p2·a2 в виде 78=2·3·13. Имеем, что a2=13 не равно 1, тогда следует переходит дальше.

Наименьший простой делитель числа a2=13 ищется при помощи перебора чисел, начиная с 3. Получим, что 13:3=4 (ост. 1). Отсюда видно, что 13 не делится на 5,7,11, потому как 13:5=2 (ост. 3), 13:7=1 (ост. 6) и 13:11=1 (ост. 2). Видно, что 13 является простым числом. По формуле выглядит так: a3=a2:p3=13:13=1. Получили, что a3=1, что означает завершение алгоритма. Теперь множители записываются в виде 78=2·3·13(a=p1·p2·p3).

Примеры разложения на простые множители

Ответ: 78=2·3·13.

Пример 3

Разложить число 83 006 на простые множители.

Решение

Первый шаг предусматривает разложение на простые множители p1=2 и a1=a:p1=83 006:2=41 503, где 83 006=2·41 503.

Второй шаг предполагает, что 2, 3 и 5 не простые делители для числа a1=41 503, а 7 простой делитель, потому как 41 503:7=5 929. Получаем, что p2=7, a2=a1:p2=41 503:7=5 929. Очевидно, что 83 006=2·7·5 929.

Нахождение наименьшего простого делителя p4 к числу a3=847 равняется 7. Видно, что a4=a3:p4=847:7=121, поэтому 83 006=2·7·7·7·121.

Для нахождения простого делителя числа a4=121 используем число 11, то есть p5=11. Тогда получим выражение вида a5=a4:p5=121:11=11, и 83 006=2·7·7·7·11·11.

Для числа a5=11 число p6=11 является наименьшим простым делителем. Отсюда a6=a5:p6=11:11=1. Тогда a6=1. Это указывает на завершение алгоритма. Множители запишутся в виде 83 006=2·7·7·7·11·11.

Каноническая запись ответа примет вид 83 006=2·73·112.

Примеры разложения на простые множители

Ответ: 83 006=2·7·7·7·11·11=2·73·112.

Пример 4

Произвести разложение числа 897 924 289 на множители.

Решение

Для нахождения первого простого множителя произвести перебор простых чисел, начиная с 2. Конец перебора приходится на число 937. Тогда p1=937, a1=a:p1=897 924 289:937=958 297 и 897 924 289=937·958 297.

Второй шаг алгоритма заключается в переборе  меньших простых чисел. То есть начинаем с числа 937.  Число 967 можно считать простым, потому как оно является простым делителем числа a1=958 297. Отсюда получаем, что p2=967, то a2=a1:p1=958 297:967=991 и 897 924 289=937·967·991.

Третий шаг говорит о том, что 991 является простым числом, так как не имеет ни одного простого делителя, который не превосходит 991. Примерное значение подкоренного выражения имеет вид 991<402. Иначе запишем как 991<402. Отсюда видно, что p3=991 и a3=a2:p3=991:991=1. Получим, что разложение числа 897 924 289 на простые множители получается как  897 924 289=937·967·991.

Примеры разложения на простые множители

Ответ: 897 924 289=937·967·991.

Использование признаков делимости для разложения на простые множители

Чтобы разложить число на простые множители, нужно придерживаться алгоритма. Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.

Пример 5

Если необходимо произвести разложение на множители 10, то по таблице видно: 2·5=10. Получившиеся числа 2 и 5 являются простыми, поэтому они являются простыми множителями для числа 10.

Пример 6

Если необходимо произвести разложение числа 48, то  по таблице видно: 48=6·8. Но 6 и 8 – это не простые множители, так как их можно еще разложить как 6=2·3 и 8=2·4. Тогда полное разложение отсюда получается как 48=6·8=2·3·2·4. Каноническая запись примет вид 48=24·3.

Пример 7

При разложении числа 3400 можно пользоваться признаками делимости. В данном случае актуальны признаки делимости на 10 и на 100. Отсюда получаем, что 3 400=34·100, где 100 можно разделить на 10, то есть записать в виде 100=10·10, а значит, что 3 400=34·10·10. Основываясь на признаке делимости получаем, что 3 400=34·10·10=2·17·2·5·2·5. Все множители простые. Каноническое разложение принимает вид 3 400=23·52·17.

Когда мы находим простые множители, необходимо использовать признаки делимости и таблицу умножения. Если представить число 75 в виде произведения множителей, то необходимо учитывать правило делимости на 5. Получим, что 75=5·15, причем 15=3·5. То есть искомое разложение пример вид произведения 75=5·3·5.

Источник

Разложение числа на простые множители

  1. Главная
  2. /
  3. Математика
  4. /
  5. Арифметика
  6. /
  7. Разложение числа на простые множители

Чтобы разложить число на простые множители воспользуйтесь нашим онлайн сервисом:

Просто введите число и получите результат.

Как разложить число на простые множители

Для того чтобы разложить число на простые множители нужно, для начала, поделить его на 2. Если число разделится на 2 без остатка, то 2 – это первый множитель. Далее полученный результат опять делим на 2, если число разделится на 2 без остатка, то второй множитель тоже 2. Если же при делении получается остаток, то пробуем делим на 3, 4, … n, до тех пор число не разделится без остатка. Далее рассмотрим пример из которого станет всё понятно.

Пример

К примеру разложим число 40 на простые множители:

  • 40 ÷ 2 = 20 (первый множитель 2)
  • 20 ÷ 2 = 10 (второй множитель 2)
  • 10 ÷ 2 = 5 (третий множитель 2)
  • 5 ÷ 2 = 2.5 (тут появился остаток, значит делим на 3)
  • 5 ÷ 3 = 1.66
  • 5 ÷ 4 = 1.25
  • 5 ÷ 5 = 1 (последний множитель 5)

Получаем простые множители числа 40: 2⋅2⋅2⋅5

Если число делится без остатка только на 1 и на само себя, то оно является простым числом. Такое число нельзя разложить на простые множители.

Разложить число на простые множители в столбик

Удобнее всего раскладывать числа на простые множества столбиком. Для примера опять разложим число 40:

40 2
20 2
10 2
5 5
1

Получаем: 2 ⋅ 2 ⋅ 2 ⋅ 5 = 40

Ещё несколько примеров:

Разложим число 15:

15 3
5 5
1

3 ⋅ 5 = 15

Разложим число 77:

77 7
11 11
1

7 ⋅ 11 = 77

Разложим число 195:

195 3
65 5
13 13
1

3 ⋅ 5 ⋅ 13 = 195

См. также

Источник

Добавить комментарий