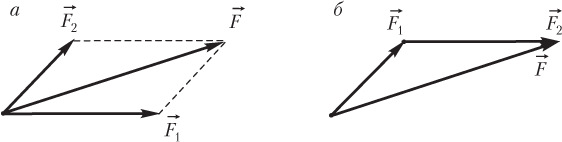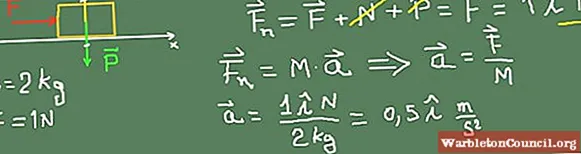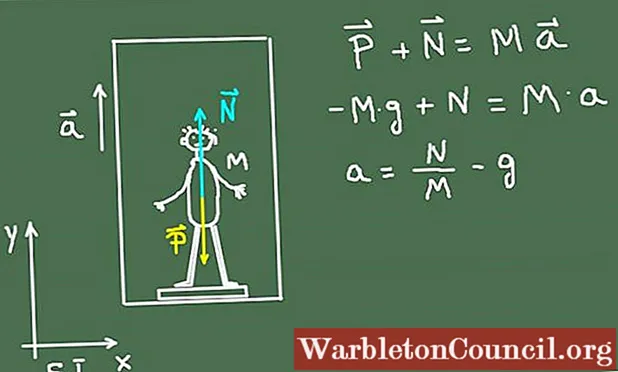Формула модуля равнодействующей силы в физике
Формула модуля равнодействующей силы
На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.
Формула равнодействующей всех сил
Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(1right).]
Формула (1) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.
Складывают векторы, используя правило треугольника (рис.1)
правило параллелограмма (рис.2).
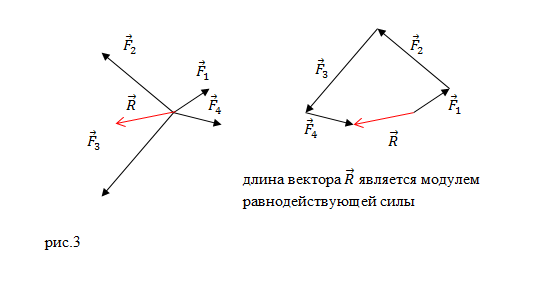
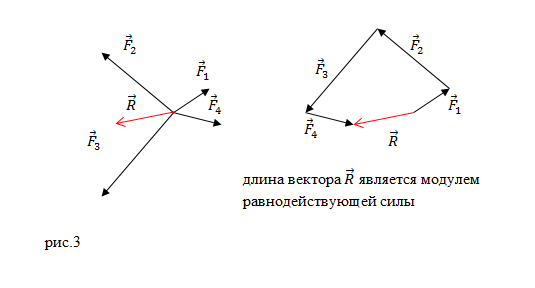
или многоугольника (рис.3):
Второй закон Ньютона и формула модуля равнодействующей
Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:
[overline{F}=sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(2right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач с решением
Пример 1
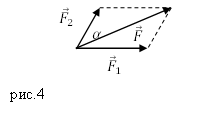
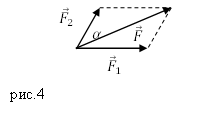
Задание. К материальной точке приложены силы, направленные под углом $alpha =60{}^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?
Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline{F}$ найдем, применяя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{40}^2+{20}^2+2cdot 40cdot 20{cos (60{}^circ ) }}approx 52,92 left(Нright).]
Ответ. $F=52,92$ Н
Пример 2
Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A{cos (omega t)(м) }$, где $s$ – путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?
Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:
[overline{F}=moverline{a}left(2.1right).]
Следовательно, модуль силы можно найти как:
[F=ma left(2.2right).]
Ускорение точки будем искать, используя связь между ним и перемещением точки:
[a=frac{d^2s}{dt^2}left(2.3right).]
Первая производная от $s$ по времени равна:
[frac{ds}{dt}=frac{d}{dt}(A{cos (omega t))=-Aomega {rm sin}?(omega t) (м) }left(frac{м}{с}right)(2.4);;]
вторая производная:
[frac{d^2s}{dt^2}=-A{omega }^2{cos left(omega tright) } left(frac{м}{с^2}right)(2.5).]
Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:
[F=mA{omega }^2{cos left(omega tright) }left(Нright).]
Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:
[F_{max}=mA{omega }^2 left(Нright).]
Ответ. $F=mA{omega }^2{cos left(omega tright) }left(Нright); F_{max}=mA{omega }^2 left(Нright)$
Читать дальше: формула периода колебаний математического маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Модель – сила
Cтраница 1
Модель силы, по второму закону Ньютона, определяется тремя главными количественными сторонами: величиной ( интенсивностью), направлением действия и точкой приложения. Такому определению силы полностью отвечает образ вектора, равного по длине выраженной в масштабе величине силы, приложенного в дайной точке и направленного в сторону действия силы.
[1]
В этой модели силы притяжения обычной материв уравновешены силами гравитац.
[2]
В таких моделях силы тяжести приводят к образованию языков растворителя в верхней части пласта.
[3]
Разумеется, отсутствие в модели сил межмолекулярного взаимодействия ограничивает применимость такой модели областью сильноразбавленных растворов полимеров. Однако очевидно, что аналогичные конформации образуются как в расплавах полимеров, так и в полимерах, находящихся в каучукоподоб-ном состоянии.
[4]
Настоящие результаты представляют собой первую попытку систематической корреляции параметров модели сил Лоренца с материальными свойствами реального сверхпроводника NbsSn, имеющего высокое критическое магнитное поле и высокую критическую плотность тока.
[5]
Это значит, что величина DAA A почти не зависит от выбора модели сил взаимодействия и потенциальной функции. Крйме того, это объясняет, почему критерий Шмидта для газов при низких давлениях почти не зависит от температуры.
[6]
Это значит, что отношение Ри и ц почти не зависит от выбора модели сил взаимодействия и потенциальной функции. Кроме того, это объясняет, почему критерий Шмидта для газов при низком давлении почти не зависит от температуры.
[7]
Если при неустановившейся стадии ползучести феноменологические приближения ( так называемая теория истощения) и более современные теории, связанные с моделями сил Пайерлса, пересечения леса и поперечного скольжения, относятся к временной функции течения, то для второй стадии процесса основные закономерности связаны с зависимостью минимальной скорости ползучести от напряжения.
[8]
Полученные выводы, особенно последние три из них, представляют определенный новый момент, поскольку они не могут быть получены из моделей внутримолекулярных сил, использующихся в настоящее время при конформационном анализе в органической химии, и в какой-то степени противоречат этим моделям. Безусловно, полученные заключения требуют дальнейшей экспериментальной проверки и подтверждения. Но ясно также, что проблему поворотной изомерии органических молекул с сопряженными двойными связями нельзя рассматривать без подробного изучения свойств простейших молекул этого класса и эта последняя задача актуальна и важна.
[9]
Однако в обычном газе, когда частицы находятся близко одна от другой, межмолекулярная сила довольно велика; следовательно, модель жестких столкновений, хотя и весьма грубая, при описании существенных особенностей системы оказывается точнее модели непрерывно распределенной слабой силы.
[10]
Чтобы получить среднюю конформацию иона полиэлектролита, необходимо знать только среднюю величину каждого угла у. Так как эти величины не зависят друг от друга и поскольку вследствие ограничений модели силы электростатистического взаимодействия между каждой парой статистических элементов одинаковы, каждый из ( а – 1) углов будет иметь одну и ту же среднюю величину.
[11]
Например, для определения средней проводимости на бумаге вырезают зону, содержащую выработки с известными водопритоками и ограниченную замкнутой гидроизогипсой с заданным напором вдоль нее или другими контурами с известными граничными условиями. Проводимость моделируемой зоны рассчитывают исходя из замеренной на модели силы тока. При наличии на отдельных участках вертикальных перетоков или дополнительного инфильтрационного питания целесообразно использовать комбинированные модели из электропроводной бумаги с дополнительными переменными сопротивлениями, дискретно присоединенными к бумажной модели [14], или же двумерные численные модели.
[12]
Объем настоящей книги не позволяет привести все наиболее важные таблицы значений. По этой причине приводятся лишь коэффициенты разложения, необходимые для расчета некоторых весьма полезных величин, определение которых на основе прямого табулирования результатов невозможно. В виде исключения таблицы приведены только в тех случаях, когда оригинальные работы опубликованы в малодоступных изданиях. Все модели удобно разделить на две категории: модели центральных сил и модели сил, зависящих от ориентации частиц.
[13]
Простые жидкости – это жидкости, построенные из атомов со сферически симметричным потенциалом взаимодействия. Понятие о простых жидкостях является естественным развитием этой модели, которая и в теории жидкости не утратила своего познавательного значения. Модель жестких сфер учитывае-существенное свойство молекул – непроницаемость; добавление к этот модели сил притяжения создает модель простой жидкости, учитывающей второе существенное свойство молекул – притяжение, благодаря чемй образуется жидкость и твердое тело. Вследствие относительной простоты модели простой жидкости ее статистическая теория наиболее развита.
[14]
Постепенно, впрочем, в психологические объяснения вводятся социальные параметры. Подмечается, что предприниматели относительно чаще являются выходцами из больших семей. Играет роль и характер самой семьи. Например, довольно оригинальный портрет предпринимателя как маргинала и нон-конформиста нарисован в реактивной модели психодинамических сил, складывающих личность предпринимателя.
[15]
Страницы:
1
2
Модель силы для уравновешивания системы из двух грузов на трех пружинах
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
Новосибирский государственный технический университет
Факультет: АВТФ
Кафедра вычислительной техники
Расчетно-графическая работа
по дисциплине «Основы теории управления»
Модель силы для уравновешивания системы из двух грузов на трех пружинах
Выполнил: Ряшинцев А.С.
Группа: АМ-610
Преподаватель: Воевода А.А.
Новосибирск 2008
Содержание
Введение
. Математическое моделирование объектов. Принципы получения и использования математических моделей
.1 Использование математических моделей
.2 Построение математической модели объекта в виде системы дифференциальных уравнений
. Передаточная функция системы
. Синтез устройства управления
.1 Алгебраический метод синтеза
. Критерии устойчивости
.1 Проверка на устойчивость по критерию Найквиста
.2 Проверка на устойчивость по критерию Гурвица
Вывод
Список литературы
Введение
Цель работы
Построение и исследование математической модели системы из двух грузов, подвешенных на пружинах. Провести синтез регулятора для исследуемой системы по ЛАЧХ и исследование системы с регулятором.
Техническое задание
Объект управления – Система из двух грузов на трех пружинах
В заданной работе с помощью силы F2 необходимо уравновесить x2
1. Математическое моделирование объектов, Принципы получения и использования математических моделей
Математизация изучаемых объектов состоит не в том, чтобы исключить из процесса познания эксперимент и наблюдение. Смысл математизации состоит в том, чтобы из точно сформулированных предпосылок выводить и прогнозировать то, что часто недоступно непосредственному наблюдению. Когда речь идет о еще не созданном техническом объекте, такое наблюдение вообще невозможно. Для того чтобы изучить физическую систему, используя метод математического моделирования, мы заменяем ее абстрактной системой – математической моделью – с теми же соотношениями, и наша задача становится чисто математической. Математическая постановка задачи имеет ряд серьезных достоинств.
Во-первых, она позволяет на принципиально иной основе провести предпроектное исследование системы и, используя соответствующий аналитический аппарат, выполнить с приемлемой для практики точностью сложные технические расчеты. Во-вторых, реализуя построенную математическую модель на ЭВМ, имеется возможность многократно и в широком диапазоне изменять входные параметры и условия функционирования проектируемой системы и, тем самым, заменить натурные испытания и эксперименты на физических моделях так называемым “вычислительным” экспериментом на ЭВМ.
Есть еще два важных свойства метода математического моделирования. Одно из них состоит в том, что с помощью этого метода системы и процессы, имеющие разное физическое содержание, часто могут быть исследованы на базе одинаковых математических моделей. В качестве такого примера в таблице приведены различные системы (в том числе и немеханические), которые описываются одинаковыми математическими моделями, отличающимися лишь постоянными параметрами. Если для механических систем (в таблице – это 1, 2, 3, 4) математические модели выражаются через обобщенные перемещения и ускорения (х, х, ф, ф, а, ä), то последняя система (5) представляет собой электрический контур, в котором емкость конденсатора обозначена С, его заряд в момент времени t – q(t) и индуктивность катушки – L.
Другая особенность метода математического моделирования состоит в том, что построение математических моделей не требует всеобъемлющей информации о проектируемом объекте. Достаточно знать только формы движения (поведения) системы и характер связей между ее составными частями. Например, при исследовании системы 3 (см. таблицу) совершенно безразлично, какие опоры имеет поступательно движущаяся масса m1 – опоры скольжения или опоры качения, имеет ли она колесный или гусеничный движитель или каким типом соединения масса m1 связана с массой m2 (нужно только знать характер движения массы m1 относительно массы m2). Точно так же для системы 2 не имеют значения особенности конструкции упругих опор, что представляет собой тело, опирающееся на эти опоры (корпус или кузов машины, платформу и др.). Важно только знать формы движения тела, полученные под воздействием каких-то внешних факторов. Никаких других сведений для построения математической модели не требуется.
Прежде чем практическая задача становится объектом математического исследования, она должна пройти довольно длительный путь. Для этого, прежде всего, нужно четко сформулировать цели исследования, изучить и проанализировать необходимую исходную информацию и соответствующим образом ее обработать, установить наиболее существенные факторы, которые должны быть учтены при построении модели, и факторы, которыми можно пренебречь. Последнее позволит получить математическую модель, поддающуюся либо аналитическому решению, либо требующую небольших затрат машинного времени при реализации модели на ЭВМ.
Упрощая математическую модель явления, исследователь как бы очерчивает границы ее применимости. Выводы, полученные в результате реализации такой модели, уже не будут справедливы за пределами этих границ. В противном случае мы можем прийти к совершенно искаженному толкованию изучаемого явления.
Математическая модель – это условный образ исследуемого объекта – совокупность соотношений (уравнений, неравенств, формул, графических образов или логических условий), связывающих характеристики процесса с параметрами объекта (системы), исходными данными и начальными условиями.
Математическое моделирование – это процесс исследования системы с помощью математических моделей. Оно включает в себя не только построение математической модели системы, но и ее предварительное изучение, выделение наиболее существенных характеристик системы, экспериментальный и теоретический анализ модели, ее решения, сопоставление результатов решения с известными данными о системе, корректировку модели и т. д.
Построение математической модели сводится к получению соотношений, описывающих интересующие характеристики системы в функции ее параметров, внешних возмущений и начальных условий. Для одних систем могут быть использованы типовые математические схемы, для других требуется построить оригинальную математическую модель.
.1 Использование математических моделей
Математическая модель может быть задана по-разному. В одних случаях – это набор отдельных характеристик исследуемой системы xj(t) (j = 1, 2, …, r), отражающих те или иные свойства системы. Эти характеристики выражаются через соответствующие параметры системы в виде аналитических зависимостей. В других – это формулы как результат решения этих уравнений или эксперимента (эмпирические модели). Однако на практике, говоря о математической модели системы, чаще всего имеют в виду первоначальную математическую модель, получаемую непосредственно в результате формализации рассматриваемой системы. Например, для динамической системы – это записанные в общем виде дифференциальные уравнения движения, которые затем решают аналитически или реализуют на ЭВМ. При использовании аналитических методов такую математическую модель необходимо преобразовать и привести к виду, удобному для интегрирования. Конечный результат этих действий обычно – построение явных формул для искомых величин.
Теперь опишем параметры и характеристики заданной системы:
Масса 1-ого и 2-ого грузов – m1, m2
Координаты грузов – х1, х2, х3
Силы (воздействия), приводящие систему в движение – F1, F2 , F3
Коэффициенты упругости пружин – k1, k2, k3
Перейдем к построению математической модели объекта управления в виде системы ДУ.
1.2 Построение математической модели объекта в виде системы дифференциальных уравнений
1) Рассмотрим механическую систему, состоящую из 1-ой пружины, закрепленной с одного конца, и груза массой m, прикрепленного к свободному концу пружины. Будем считать, что груз может двигаться только в направлении оси пружины (например, движение происходит вдоль стержня).
Построим математическую модель этой системы. Будем описывать состояние системы расстоянием x от центра груза до его положения равновесия. Опишем взаимодействие пружины и груза с помощью закона Гука (F = ? kx) после чего воспользуемся вторым законом Ньютона, чтобы выразить его в форме ДУ:
где означает вторую производную от x по времени:
Полученное уравнение описывает математическую модель рассмотренной физической системы.
) Рассмотрим систему из груза m1 и двух пружинок k1,k2.При приложении к грузу силы F2, добавляется воздействие, которое происходит через пружины, соединяющий груз и вершину модели.
х1 х2
m1F2
Аналогичным образом можем записать:
) Рассмотрим систему из груза m2 и двух пружинок k1,k3 .При приложении к грузу силы F3, добавляется воздействие, которое происходит через пружины, соединяющий груз и вершину модели.
F3
Аналогичным образом можем записать:
) Рассмотрим систему из двух грузов m1, m2 и трёх пружинок, при воздействии на каждый груз силы, получаем систему уравнений, составленную из уравнений из п.2, п.3
(1) – это уравнение соединения 3 пружин.
У нас:
Подставим эти силы в уравнение (1). Получаем:
Перейдем от дифференциальных уравнений к линейным при помощи преобразования Лапласа для этого введем вместо второй производной:
,
,
Эта система была получена из системы из п.4 путем подстановки в эту систему найденного значения .
Здесь мы выражаем переменные и путем деления правой части на
,
,
Дальше мы выносим в правой части уравнения и как общие множители
Далее приводим подобные члены, получим окончательную систему уравнений
Структурная схема исследуемой системы:
Мы имеем нескорректированную систему.
2. Передаточная функция системы
Пусть коэффициенты упругости для пружин равны по 1, то есть: k1 =1,k2 =1,k3 = 1 . И пусть тогда массы грузов тоже будет по единице: m1 =1, m2 = 1. Это все нужно для упрощения структурной схемы. Так как в заданной работе с помощью силы F2 необходимо уравновесить х2 , то получим следующий вид нашей исследуемой системы:
Тогда при заданных значениях мы переходим от системы:
К системе:
Упрощенная структурная схема исследуемой системы:
Построим графики сигналов на входе и выходе нескорректированной разомкнутой системы
3. Синтез устройства управления
Передаточная функция исследуемого объекта:
[A,B,C,D]=linmod(‘R3’);
sys=tf(ss(A,B,C,D))function:^2 + 0.6^4 – 8.326e-017 s^3 + 1.2 s^2 – 4.825e-017 s + 0.2
Так как коэффициенты при и очень малы, мы примем их равными 0. Составим передаточную функцию:
Здесь два слагаемых приближенно равны
: 8.326e-017 s^3 , 4.825e-017 s
Перейдем к построению ЛАЧХ (амплитудно-частотная характеристика) и ФЧХ (фазово-частотная характеристика).
bode(sys)
step (sys)
impulse(sys)
rlocus(sys.num{1},sys.den{1}
Мы не видим возможности применить метод синтеза УУ по ЛАЧХ.
3.1 Алгебраический метод синтеза
Замкнутая скорректированная система с УУ
Разработаем регулятор со степенью на 1 меньше, то есть 3 степени:
Произведём расчет регулятора с помощью корней ХПЗС скорректированной системы. ХПЗС скорректированной системы равен:
ХПЗС имеет вид:
Произведём подстановку в ХПЗС всех чисел и переменных
Необходимо, чтобы система была устойчива, поэтому корни ХПЗС должны лежать в левой полуплоскости. Приведем многочлен к виду , у которого все корни равны -1, т.е. лежат в левой полуплоскости.
Получим выражение:
Нужно найти значения y3, y2, y1, y0, x3, x2, x1, x0:
[ 1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
.2 0 1 0 1 0 0 0
1.2 0 1 0 1 0 0
.2 0 1.2 0 0.6 0 1 0
0.2 0 1.2 0 0.6 0 1
0 0.2 0 0 0 0.6 0
0 0 0.2 0 0 0 0.6];
A = [1 7 21 35 35 21 7 1]; = B’;
X = inv(A)*B
Результаты:
= 1.0000 7.0000 42.2000 7.4000-22.4000 19.2000 -2.4000 -0.8000
Регулятор имеет вид:
Структурная схема замкнутой скорректированной системы
Сигнал на выходе скорректированной замкнутой системы
Устройство управления приводит систему к устойчивому состоянию за 14 интервалов
Теперь построим графики переходных процессов в системе c регулятором
математический устройство управление система
bode(sys)
(sys)
impulse(sys)
rlocus(sys.num{1},sys.den{1})
4. Критерии устойчивости
Необходимое условие устойчивости
Необходимое и достаточное условие устойчивости – отрицательность действительных частей корней характеристического уравнения или, что идентично, эти корни должны располагаться слева от мнимой оси.
В этих формулировках изложен не только признак устойчивости, но и дан, в сущности, метод исследования устойчивости: необходимо найти корни характеристического уравнения и проверить, лежат ли они в левой полуплоскости или нет. Однако такой метод совершенно неадекватен задаче исследования в силу следующих причин.
. Задача определения корней характеристического уравнения просто решается только для уравнений первого и второго порядка; для всех других случаев приходится пользоваться различными приближенными, сравнительно громоздкими методами.
. Для определения устойчивости необходимо знать только знаки корней, поэтому определение корней представляет ненужную трудоемкую работу. Между тем не получают общих формул, по которым можно было бы судить о влиянии коэффициентов уравнений на устойчивость системы, но именно это влияние, в первую очередь, и интересует проектировщика системы автоматического регулирования.
Задача исследования часто ставится таким образом, что необходимо определить коэффициенты уравнений, при которых система была бы устойчива.
В распоряжении исследователя имеются методы, позволяющие судить об устойчивости системы по так называемым условиям устойчивости, не решая характеристического уравнения и не находя его корней. Первым таким условием, которое следует рассмотреть, является необходимое условие устойчивости.
Пусть характеристическое уравнение n-й степени имеет корни s1, s2, …, sn. Тогда это уравнение можно записать следующим образом
(s – s1) (s – s2) … (s – sn) = 0. (6.26)
Если система устойчива, то корни должны быть либо действительными отрицательными, либо комплексно-сопряженными с отрицательной действительной частью.
Пусть s1 = –?, ? > 0, тогда s – s1 = s + ? > 0.
Пусть s2,3 = –? ± i ?, ? > 0, тогда
(s – s2) (s – s3) = (s + ? – i ?) (s + ? + i ?) = (s + ?)2 + ?2 > 0.
Отсюда следует, что после раскрытия скобок все коэффициенты уравнения будут положительны.
Из этих рассуждений следует, что, когда хоть один из коэффициентов характеристического уравнения отрицателен, то система неустойчива.
Если все коэффициенты характеристического полинома ai > 0, то любое действительное положительное значение s, подставленное в уравнение, не может обратить его в нуль и, следовательно, не является корнем характеристического уравнения. Поэтому при ai > 0 невозможно появление нарастающих экспонент, характеризующих апериодическую неустойчивость, т.е. апериодическая неустойчивость невозможна. Однако может возникнуть колебательная неустойчивость, т.е. появление в решении составляющих в виде колебаний с нарастающей амплитудой. Это возникает, когда существуют комплексно-сопряженные корни с положительной действительной частью. Поэтому условие положительности коэффициентов при порядке системы больше двух является необходимым условием, но не достаточным, а для уравнений первого и второго порядка это условие является и достаточным.
4.1 Проверка на устойчивость по критерию Найквиста
Формулировка критерия Найквиста: для устойчивости замкнутой системы необходимо и достаточно чтобы амплитудно – фазовая характеристика устойчивой разомкнутой системы при изменении от0 до не охватывала точку с координатами {-1, j0}.
1 – устойчивая система
2 – неустойчивая система
Рис. 4. Частотные характеристики, иллюстрирующие критерий Найквиста
Разомкнутая система может быть неустойчива, но это не означает, что неустойчивой будет и замкнутая. В этом случае меняется формулировка критерия Найквиста: для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика неустойчивой разомкнутой системы при изменении от 0 до охватывала точку с координатами {-1, j0} в положительном направлении r/2 раз, где r число корней характеристического уравнения разомкнутой системы с положительной вещественной частью.
Имеем Объект:
Имеем Регулятор:
Устойчивая разомкнутая система:
Wраз=WpWo
= tf([-22.4 19.2 -15.84 10.72 -1.44 -0.48],
[1 7 43.4 15.8 50.84 10.28 8.44 1.48])
nyquist(A)
Вывод: График не охватывает точку [-1;j0] значит, устойчива замкнутая система.
4.2 Проверка на устойчивость по критерию Гурвица
Это алгебраический критерий, который предполагает рассмотрение характеристического уравнения в стандартной форме:
Из его коэффициентов по следующему правилу составляется матрица Гурвица:
на главной диагонали сверху вниз выписываются по порядку коэффициенты характеристического уравнения от anдо a1включительно. В каждом столбце вниз от диагонали записывают коэффициенты при возрастающих степенях оператора p, вверх – при убывающих степенях p. Недостающие элементы в столбцах дополняются нулями.
(4.13)
H = n x n
Приведем без доказательства критерий Гурвица.
Формулировка критерия. Для устойчивости линейной системы необходимо и достаточно, чтобы все n определителей, получаемых из матрицы Гурвица H, были положительны.
(4.14)
Здесь
Условие, при котором система находится на границе устойчивости, согласно критерию Гурвица, имеет вид:
Характеристическое уравнение:
Все коэффициенты характеристического уравнения положительны – значит, выполняется необходимое условия устойчивости по критерию Гурвица
Если произведение крайних меньше произведения средних – выполняется достаточное условие по критерию Гурвицу и система будет устойчива.
1.48*1<7*8.44
истинно
*8.44<43.4*10.28
истинно
.4*10.18<15.8*50.84
истинно
Все условия выполнились, значит, система устойчива.
Выводы по работе
В проделанной работе мы определили, что Устройство управления (УУ) имеет передаточную функцию
и приводит систему к устойчивому состоянию. Проверяли систему на устойчивость разными критериями: Найквиста, Гурвица; увидели, что по этим критериям система устойчива.
Список литературы
1. Востриков А.С., Французова Г.А. Теория автоматического управления. Линейные системы: Учебное пособие. – Новосибирск: НГТУ, 1997.
. Ту Ю. Современная теория управления. – М.: Машиностроение, 1971.
. Солодовников В.В., Плотников В.Н., Яковлев А.В. Основы теории и элементы систем автоматического регулирования. – М.: Машиностроение, 1985.
. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. – М.:Наука, 1974.
5.Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления с примерами на языке MATLAB. – СПб.:Наука, 1999.
Содержание
- Формула равнодействующей всех сил
- Второй закон Ньютона и формула модуля равнодействующей
- Примеры задач с решением
- О причинах изменений
- Сложение сил
- Задачи
- Что мы узнали?
На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.
Формула равнодействующей всех сил
Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.
Складывают векторы, используя правило треугольника (рис.1)
правило параллелограмма (рис.2).
или многоугольника (рис.3):
Второй закон Ньютона и формула модуля равнодействующей
Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:
$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач с решением
Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?
Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:
Вычислим модуль равнодействующей силы:
[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Н
ight).]
Ответ. $F=52,92$ Н
Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?
Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:
Следовательно, модуль силы можно найти как:
Ускорение точки будем искать, используя связь между ним и перемещением точки:
Первая производная от $s$ по времени равна:
Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:
Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:
О причинах изменений
Классическая механика разделена на два раздела – кинематику, при помощи уравнений описывающую траекторию движения тел, и динамику, которая разбирается с причинами изменения положения объектов или самих объектов.
Причиной изменений выступает некоторая сила, которая есть мера действия на тело других тел или силовых полей (например, электромагнитное поле или гравитация). К примеру, сила упругости вызывает деформацию тела, сила тяжести – падение тел на Землю.
Сила – это векторная величина, то есть, ее действие – направленное. Модуль силы в общем случае пропорционален некоему коэффициенту (для деформации пружины – это ее жесткость), а также параметрам действия (масса, заряд).
Сложение сил
В случае, когда на тело действует n сил, говорят о равнодействующей силе, а формула второго закона Ньютона принимает вид:
$mvec a = sumlimits_^n vec F_i$.
Рис. 1. Равнодействующая сил.
Поскольку F – векторная величина, сумма сил называется геометрической (или векторной). Такое сложение выполняется по правилу треугольника или параллелограмма, либо по компонентам. Поясним каждый метод на примере. Для этого запишем формулу равнодействующей силы в общем виде:
$F = sumlimits_^n vec F_i$
А силу $F_i$ представим в виде:
Тогда суммой двух сил будет новый вектор $F_ = (F_ + F_, F_ + F_, F_ + F_)$.
Рис. 2. Покомпонентное сложение векторов.
Абсолютное значение равнодействующей можно рассчитать так:
Теперь дадим строгое определение: равнодействующая сила есть векторная сумма всех сил, оказывающих влияние на тело.
Разберем правила треугольника и параллелограмма. Графически это выглядит так:
Рис. 3. Правило треугольника и параллелограмма.
Внешне они кажутся различными, но когда доходит до вычислений, сводятся к нахождению третьей стороны треугольника (или, что тоже самое, диагонали параллелограмма) по теореме косинусов.
Если сил больше двух, иногда удобней пользоваться правилом многоугольника. По своей сути – это всё тот же треугольник, только повторенный на одном рисунке некоторое количество раз. В случае, если по итогу контур получился замкнутым, общее действие сил равно нулю и тело покоится.
Задачи
- На ящик, размещенный в центре декартовой прямоугольной системы координат, действуют две силы: $F_1 = (5, 0)$ и $F_2 = (3, 3)$. Рассчитать равнодействующую двумя методами: по правилу треугольника и при помощи покомпонентного сложения векторов.
Решение
Равнодействующей силой будет векторная сумма $F_1$ и $F_2$.
$vec F = vec F_1 + vec F_2 = (5+3, 0+3) = (8, 3)$
Абсолютное значение равнодействующей силы:
Теперь получим тоже значение при помощи правила треугольника. Для этого сначала найдем абсолютные значения $F_1$ и $F_2$, а также угол между ними.
Угол между ними – 45˚, так как первая сила параллельна оси Оx, а вторая делит первую координатную плоскость пополам, то есть является биссектрисой прямоугольного угла.
Теперь, разместив вектора по правилу треугольника, рассчитаем по теореме косинусов равнодействующую:
- На машину действуют три силы: $F_1 = (-5, 0)$, $F_2 = (-2, 0)$, $F_1 = (7,0)$. Какова их равнодействующая?
Решение
Достаточно сложить иксовые компоненты векторов:
Что мы узнали?
В ходе урока было введено понятие равнодействующей сил и рассмотрены различные методы ее расчета, а также введена запись второго закона Ньютона для общего случая, когда количество сил неограниченно.
Силу, заменяющую собой действие на тело нескольких сил, называют равнодействующей ; равнодействующая сила равна векторной сумме сил, приложенных к данному телу:
F → = F → 1 + F → 2 + . + F → N ,
где F → 1 , F → 2 , . F → N — силы, приложенные к данному телу.
Равнодействующую двух сил удобно находить графически по правилу параллелограмма (рис. 2.14, а ) или треугольника (рис. 2.14, б ).
Для сложения нескольких сил (вычисления равнодействующей) используют следующий алгоритм :
1) вводят систему координат и записывают проекции всех сил на координатные оси:
F 1 x , F 2 x , . F Nx ,
F 1 y , F 2 y , . F Ny ;
2) вычисляют проекции равнодействующей как алгебраическую сумму проекций сил:
F x = F 1 x + F 2 x + . + F Nx ,
F y = F 1 y + F 2 y + . + F Ny ;
3) модуль равнодействующей вычисляют по формуле
F = F x 2 + F y 2 .
Рассмотрим частные случаи равнодействующей.
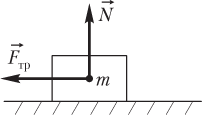
Силу взаимодействия тела с горизонтальной опорой , по которой может происходить движение тела, рассчитывают как равнодействующую силы трения и силы реакции опоры (рис. 2.15):
F → вз = F → тр + N → ,
ее модуль вычисляется по формуле
F вз = F тр 2 + N 2 ,
где F → тр — сила трения скольжения или покоя; N → — сила реакции опоры.
Частные случаи равнодействующей:
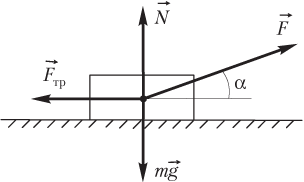
Силу взаимодействия тела с комбинированной опорой (например, креслом автомобиля, самолета и т.п.) рассчитывают как равнодействующую сил давления на вертикальную и горизонтальную части опоры (рис. 2.16):
F → вз = F → гор + F → верт ,
где F → гор — сила давления, действующая на тело со стороны горизонтальной части опоры (численно равная весу тела); F → верт — сила давления, действующая на тело со стороны вертикальной части опоры (численно равная силе инерции).
Частные случаи равнодействующей:
Равнодействующая силы тяжести и силы Архимеда называется подъемной силой (рис. 2.17):
F → под = F → А + m g → ,
ее модуль вычисляется по формуле
F под = F А − m g ,
где F → А — сила Архимеда (выталкивающая сила); m g → — сила тяжести.
Частные случаи равнодействующей:
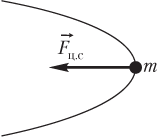
Если под влиянием нескольких сил тело равномерно движется по окружности, то равнодействующая всех приложенных к телу сил является центростремительной силой (рис. 2.18):
F → ц .с = F → 1 + F → 2 + . + F → N .
где F → 1 , F → 2 , . F → N — силы, приложенные к телу.
Модуль центростремительной силы, направленной по радиусу к центру окружности, может быть вычислен по одной из формул:
F ц .с = m v 2 R , F ц .с = m ω 2 R , F ц .с = m v ω ,
где m — масса тела; v — модуль линейной скорости тела; ω — величина угловой скорости; R — радиус окружности.
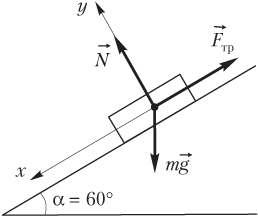
Пример 21. По дну водоема, наклоненному под углом 60° к горизонту, начинает скользить тело массой 10 кг, полностью находящееся в воде. Найти модуль равнодействующей всех сил, приложенных к телу, если между телом и дном водоема воды нет, а коэффициент трения составляет 0,15.
Решение. Так как между телом и дном водяная прослойка отсутствует, то сила Архимеда на тело не действует.
Искомой величиной является модуль векторной суммы всех сил, приложенных к телу:
F → = F → тр + m g → + N → ,
где N → — сила нормальной реакции опоры; m g → — сила тяжести; F → тр — сила трения. Указанные силы и система координат изображены на рисунке.
Вычисление модуля результирующей силы F проведем в соответствии с алгоритмом.
1. Определим проекции сил, приложенных к телу, на координатные оси:
проекция силы трения
F тр x = − F тр = − μ N ;
проекция силы тяжести
( m g ) x = m g sin 60 ° = 0,5 3 m g ;
проекция силы реакции опоры
проекция силы трения
проекция силы тяжести
( m g ) y = − m g cos 60 ° = − 0,5 m g ;
проекция силы реакции опоры
где m — масса тела; g — модуль ускорения свободного падения; µ — коэффициент трения.
2. Вычислим проекции равнодействующей на координатные оси, суммируя соответствующие проекции указанных сил:
F x = F тр x + ( m g ) x = − μ N + 0,5 3 m g ;
F y = ( m g ) y + N y = − 0,5 m g + N .
Движение по оси Oy отсутствует, т.е. F y = 0, или, в явном виде:
Отсюда следует, что
что позволяет получить формулу для расчета силы трения:
F тр = μ N = 0,5 μ m g .
3. Искомое значение равнодействующей:
F = F x 2 + F y 2 = | F x | = − 0,5 μ m g + 0,5 3 m g = 0,5 m g ( 3 − μ ) .
F = 0,5 ⋅ 10 ⋅ 10 ( 3 − 0,15 ) = 79 Н.
Пример 22. Тело массой 2,5 кг движется горизонтально под действием силы, равной 45 Н и направленной под углом 30° к горизонту. Определить величину силы взаимодействия тела с поверхностью, если коэффициент трения скольжения равен 0,5.
Решение. Силу взаимодействия тела и опоры найдем как равнодействующую силы трения F → тр и силы нормальной реакции опоры N → :
F → вз = F → тр + N → ,
модуль которой определяется формулой
F вз = F тр 2 + N 2 .
Силы, приложенные к телу, показаны на рисунке.
Модуль силы нормальной реакции опоры определяется формулой
N = m g − F sin 30 ° ,
а модуль силы трения скольжения —
где m — масса тела; g — модуль ускорения свободного падения; µ — коэффициент трения; F — модуль силы, вызывающей движение тела.
С учетом выражений для N и F тр формула для расчета искомой силы принимает вид:
F вз = ( μ N ) 2 + N 2 = N μ 2 + 1 = ( m g − F sin 30 ° ) μ 2 + 1 .
F вз = ( 2,5 ⋅ 10 − 45 ⋅ 0,5 ) ( 0,5 ) 2 + 1 ≈ 2,8 Н.
Пример 23. Во сколько раз изменится подъемная сила, если с аэростата сбросить балласт, равный половине его массы? Плотность воздуха считать равной 1,3 кг/м 3 , массу аэростата с балластом — 50 кг. Объем аэростата составляет 50 м 3 .
Решение. Подъемная сила, действующая на аэростат, является равнодействующей силы Архимеда F → А и силы тяжести m g → :
F → под = F → А + m g → ,
модуль которой определяется формулой
где F A = ρ возд gV — модуль силы Архимеда; ρ возд — плотность воздуха; g — модуль ускорения свободного падения; V — объем аэростата; m — масса аэростата (с балластом или без него).
Модуль подъемной силы может быть рассчитан по формулам:
- для аэростата с балластом
F под 1 = ρ возд g V − m 1 g ,
- для аэростата без балласта
F под 2 = ρ возд g V − m 2 g ,
где m 1 — масса аэростата с балластом; m 2 — масса аэростата без балласта.
Искомое отношение модулей подъемных сил составляет
F под 2 F под 1 = ρ возд V − m 2 ρ возд V − m 1 = 1,3 ⋅ 50 − 25 1,3 ⋅ 50 − 50 ≈ 2,7 .
Пример 24. Модуль равнодействующей всех сил, действующих на тело, равен 2,5 Н. Определить в градусах угол между векторами скорости и ускорения, если известно, что модуль скорости остается постоянным.
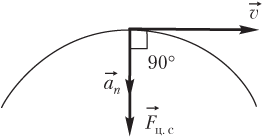
Решение. Скорость тела не изменяется по величине. Следовательно, тело обладает только нормальной составляющей ускорения a → n ≠ 0 . Такой случай реализуется при равномерном движении тела по окружности.
Равнодействующая всех сил, приложенных к телу, является центростремительной силой и показана на рисунке.
Векторы силы, скорости и ускорения имеют следующие направления:
- центростремительная сила F → ц .с направлена к центру окружности;
- вектор нормального ускорения a → n направлен так же, как и сила;
- вектор скорости v → направлен по касательной к траектории движения тела.
Следовательно, искомый угол между векторами скорости и ускорения равен 90°.
Содержание
- Объяснение и формулы
- Решенные упражнения
- Упражнение 1
- Решение
- Упражнение 2.
- Решение
- Приложения второго закона Ньютона
- Ускорение лифта
- Решение
- Баночка для майонеза
- Решение
- Опыты для детей
- Эксперимент 1
- Эксперимент 2
- Интересные статьи
- Ссылки
В второй закон Ньютона или фундаментальный закон динамики устанавливает, что если объект подвергается действию силы или набора сил, которые не отменяются, то объект будет ускоряться в направлении результирующей силы, причем это ускорение пропорционально интенсивности этой результирующей силы и обратно пропорциональна массе объекта.
да F чистая сила, M масса объекта и к При увеличении ускорения второй закон Ньютона математически будет выражен следующим образом:к = F / М или самым обычным способом F = M∙к
Объяснение и формулы
Как объяснялось выше, обычно второй закон выражается формулой:
F = M∙к
Как ускорение, так и сила должны измеряться в инерциальной системе отсчета. Обратите внимание, что масса является положительной величиной, поэтому ускорение указывает в том же направлении, что и результирующая сила.
Также обратите внимание, что когда результирующая сила равна нулю (F = 0) то и ускорение будет нулевым ( к = 0 ) пока M> 0. Этот результат полностью согласуется с первым законом Ньютона или законом инерции.
Первый закон Ньютона устанавливает инерциальные системы отсчета как системы, которые движутся с постоянной скоростью относительно свободной частицы. На практике и для наиболее распространенных приложений система отсчета, прикрепленная к земле, или любая другая система, которая движется с постоянной скоростью относительно нее, будет считаться инерционной.
Сила – это математическое выражение взаимодействия объекта с окружающей средой. Сила может быть постоянной величиной или изменяться со временем, положением и скоростью объекта.
Единицей измерения силы в Международной системе (СИ) является Ньютон (Н). Масса в (СИ) измеряется в (кг), а ускорение – в (м / с.2). Один ньютон силы – это сила, необходимая для ускорения объекта массой 1 кг со скоростью 1 м / с.2 .
Решенные упражнения
Упражнение 1
Объект массой m падает с определенной высоты и измеряется ускорение падения 9,8 м / с².
То же самое происходит с другим объектом с массой m ‘и другим с массой m’ ‘, а также с другим объектом. Результатом всегда является ускорение свободного падения, которое обозначается буквой g и равно 9,8 м / с². В этих экспериментах форма объекта и значение его массы таковы, что сила сопротивления воздуха незначительна.
Его просят найти модель силы притяжения Земли (известной как вес), которая согласуется с экспериментальными результатами.
Решение
Мы выбираем инерциальную систему отсчета (фиксированную относительно земли) с положительным направлением вертикальной оси X и вниз.
Единственная сила, действующая на массовый объект м притяжение земли, эта сила называется весом п, поскольку он направлен вниз, он положительный.
Ускорение, которое приобретает массовый объект. м как только он будет выпущен, это а = г , направленный вниз и положительный.
Мы предлагаем второй закон Ньютона.
P = m a
Какой будет модель P, при которой ускорение, предсказываемое вторым законом, будет равно g независимо от значения m? : Единственная альтернатива – P = m g всякий раз, когда m> 0.
м г = м а откуда мы очищаем: а = г
Мы заключаем, что вес, сила, с которой Земля притягивает объект, будет массой объекта, умноженной на ускорение свободного падения, и его направление вертикальное и направленное вниз.
P = м∙грамм
Упражнение 2.
Блок массой 2 кг опирается на абсолютно ровный и горизонтальный пол. Если к нему приложить силу 1 Н, то каково ускорение блока и какую скорость он будет иметь через 1 с.
Решение
Первым делом необходимо определить инерциальную систему координат. Один выбран с осью X на полу и осью Y перпендикулярно ему. Затем составляется силовая диаграмма, в которой размещаются силы, возникающие при взаимодействии блока с окружающей средой.
Сила N представляет собой нормаль, это вертикальная восходящая сила, которую поверхность пола оказывает на блок M. Известно, что N точно уравновешивает P, потому что блок не перемещается в вертикальном направлении.
F – горизонтальная сила, приложенная к блоку M, указывающая в положительном направлении оси X.
Чистая сила – это сумма всех сил, действующих на блок массы M. Мы складываем векторную сумму F, P и N. Поскольку P и N равны и противоположны, они компенсируют друг друга, а итоговая сила равна F.
Таким образом, результирующее ускорение будет отношением чистой силы к массе:
a = F / M = 1 Н / 2 кг = 0,5 м / с²
Поскольку блок запускается из состояния покоя через 1 секунду, его скорость изменится с 0 до 0,5 м / с.
Приложения второго закона Ньютона
Ускорение лифта
Мальчик измеряет свой вес весами. Полученное значение составляет 50 кг. Затем мальчик переносит груз к лифту своего дома, потому что он хочет измерить ускорение лифта. Результаты, полученные при запуске:
- Весы регистрируют вес 58 кг за 1,5 с.
- Затем снова отмерьте 50 кг.
Используя эти данные, рассчитайте ускорение лифта и его скорость.
Решение
Весы измеряют вес в единицах, называемыхkilogram_force. По определению kilogram_force – это сила, с которой планета Земля притягивает объект массой 1 кг.
Когда единственной силой, действующей на объект, является его вес, он приобретает ускорение 9,8 м / с². Таким образом, 1 кг_с равен 9,8 Н.
Вес п мальчика тогда 50 кг * 9,8 м / с² = 490 Н
Во время ускорения шкала проявляет силу N для мальчика 58 кг_с эквивалентно 58 кг * 9,8 м / с² = 568,4 Н.
Ускорение лифта будет определяться:
а = Н / М – г = 568,4 Н / 50 кг – 9,8 м / с² = 1,57 м / с²
Скорость, достигаемая лифтом через 1,5 с при ускорении 1,57 м / с², составляет:
v = а * т = 1,57 м / с² * 1,5 с = 2,36 м / с = 8,5 км / ч
На следующем рисунке представлена диаграмма сил, действующих на мальчика:
Баночка для майонеза
Мальчик передает своему брату банку с майонезом своему брату, который сидит на другом конце стола. Для этого он приводит его в движение так, что он развивает скорость 3 м / с. С того момента, как он уронил бутылку, пока она не остановилась на противоположном конце стола, ход составлял 1,5 м.
Определите значение силы трения, которое стол оказывает на бутылку, зная, что ее масса составляет 0,45 кг.
Решение
Сначала определим ускорение при торможении. Для этого воспользуемся следующей зависимостью, уже известной из равноускоренного прямолинейного движения:
Vf² = Vi² + 2 * a * d
где Vf конечная скорость, Увидел начальная скорость, к ускорение и d смещение.
Ускорение, полученное из предыдущего соотношения, равно, когда смещение бутылки было положительным.
а = (0 – 9 (м / с) ²) / (2 * 1,5 м) = -3 м / с²
Чистая сила, действующая на банку для майонеза, представляет собой силу трения, так как нормальный вес и вес банки уравновешивают: Fnet = Fr.
Fr = m * a = 0,45 кг * (-3 м / с²) = -1,35 Н = -0,14 кг-сила
Опыты для детей
Дети и взрослые могут проводить простые эксперименты, которые позволяют им убедиться, что второй закон Ньютона действительно работает в реальной жизни. Вот два очень интересных:
Эксперимент 1
Для простого эксперимента требуются весы для ванной и лифт. Возьмите гирю для ванной комнаты в лифт и запишите значения, которые она отмечает во время подъема, начала спуска и во время движения с постоянной скоростью. Рассчитайте ускорение лифта для каждого случая.
Эксперимент 2
- Возьмите игрушечную машинку с хорошо смазанными колесами.
- К концу прикрепите веревку.
- На краю стола прикрепите лентой карандаш или другой гладкий цилиндрический предмет, по которому будет проходить веревка.
- На другом конце веревки повесьте небольшую корзину, в которую вы поместите несколько монет или что-то, что будет служить грузом.
Схема эксперимента представлена ниже:
- Отпустите тележку и наблюдайте, как она ускоряется.
- Затем увеличьте массу тележки, поместив на нее монеты или что-то, что увеличивает ее массу.
- Скажите, увеличивается или уменьшается ускорение. Положите еще теста на тележку, посмотрите, как она разгонится, и закончите.
Затем тележку оставляют без лишнего веса и дают ей разогнаться. Затем на корзину помещается больший вес, чтобы увеличить силу, прилагаемую к тележке.
- Сравните ускорение с предыдущим случаем, укажите, увеличивается оно или уменьшается. Вы можете повторить добавление веса в корзину и наблюдать за ускорением тележки.
- Укажите, увеличивается или уменьшается.
- Проанализируйте свои результаты и скажите, согласны ли они со вторым законом Ньютона.
Интересные статьи
Примеры второго закона Ньютона.
Первый закон Ньютона.
Примеры второго закона Ньютона.
Ссылки
- Алонсо М., Финн Э. 1970. Том I физики: Механика. Fondo Educativo Interamericano S.A. 156-163.
- Хьюитт, П. 2012. Концептуальная физика. Издание пятое. 41-46.
- Янг, Хью. 2015. Университетская физика с современной физикой. 14-е изд. Пирсон. 108-115.