Загрузить PDF
Загрузить PDF
Среднее значение, медиана и мода — значения, которые часто используются в статистике и математике. Эти значения найти довольно легко, но их легко и перепутать. Мы расскажем, что они из себя представляют и как их найти.
-

1
Сложите все числа, которые вам даны. Допустим, вам даны числа 2, 3 и 4. Сложим их: 2 + 3 + 4 = 9.
-

2
Сосчитайте количество чисел. У нас есть три цифры.
-

3
Разделите сумму чисел на их количество. Берем 9, делим на 3. 9/3 = 3. Среднее значение в данном случае равно 3. Помните, что не всегда получается целое число.
Реклама
-

1
Запишите все числа, которые вам даны, в порядке возрастания. Например, нам даны числа: 4, 2, 8, 1, 15. Запишите их от меньшего к большему, вот так: 1, 2, 4, 8, 15.
-

2
Найдите два средних числа. Мы расскажем, как это сделать, если у вас имеется четное количество чисел, и как это сделать, если количество чисел нечетное:
- Если у вас нечетное количество чисел, вычеркните левое крайнее число, затем правое крайнее число и так далее. Один оставшийся номер и будет искомой медианой. Если вам дан ряд чисел 4, 7, 8, 11, 21, тогда 8 — медиана, так как 8 стоит посередине.
- Если у вас четное количество чисел, вычеркните по одному числу с каждой стороны, пока у вас не останется два числа посередине. Сложите их и разделите на два. Это и есть значение медианы. Если вам дан ряд чисел 1, 2, 5, 3, 7, 10, то два средних числа — это 5 и 3. Сложим 5 и 3, получим 8, разделим на два, получим 4. Это и есть медиана.
Реклама
-

1
Запишите все числа в ряд. Например, вам даны числа 2, 4, 5, 5, 4 и 5. Запишите их в порядке возрастания.
-

2
Найдите число, которое чаще всего встречается. В данном случае это 5. Если два числа встречаются одинаково часто, то этот ряд двухвершинный или бимодальный, а если больше — то мультимодальный.
Реклама
Советы
- Вам будет легче найти моду и медиану, если вы запишете числа в порядке возрастания.
Реклама
Об этой статье
Эту страницу просматривали 353 377 раз.
Была ли эта статья полезной?
В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

Иногда при работе с данными нужно описать множество значений каким-то одним числом. Например, при исследовании эффективности сотрудников, уровня вовлеченности в аккаунте, KPI или времени ответа на сообщения клиентов. В таких случаях используют меры центральной тенденции. Их можно называть проще — средние значения.
Но в зависимости от вводных данных, находить среднее значение нужно по-разному. Основной набор задач закрывается с использованием среднего арифметического, медианы и моды. Но если выбрать неверный способ — выводы будут необъективны, а результаты исследования нельзя будет признать действительными. Чтобы не допустить ошибку, нужно понимать особенности разных способов нахождения средних значений.

Cтратег, аналитик и контент-продюсер. Работает с агентством «Палиндром».

Как считать среднее арифметическое
Использовать среднее арифметическое стоит тогда, когда множество значений распределяются нормально ― это значит, что значения расположены симметрично относительно центра. Как выглядит нормальное распределение на графике и в таблице, можно посмотреть на примере:


Если данные распределяются как в примерах — вам повезло. Можно без лишних заморочек считать среднее арифметическое и быть уверенным, что выводы будут объективны. Однако, нормальное распределение на практике встречается крайне редко, поэтому среднее арифметическое в большинстве случаев лучше не использовать.
Как рассчитать
Сумму значений нужно поделить на их количество. Например, вы хотите узнать средний ER за 4 дня при нормальном распределении значений и без аномальных выбросов. Для этого считаем среднее арифметическое: складываем ER всех дней и делим полученное число на количество дней.

Если хотите автоматизировать вычисления и узнать среднее арифметическое для большого числа показателей — используйте Google Таблицы:
- Заполните таблицу данными.
- Щелкните по пустой ячейке, в которую хотите записать среднее арифметическое.
- Введите «=AVERAGE(» и выделите ряд чисел, для которых нужно вычислить среднее арифметическое. Нажмите «Enter» после ввода формулы.

Когда можно не использовать
Если данные распределены ненормально, то наши расчеты не будут отражать реальную картину. На ненормальность распределения указывают:
- Отсутствие симметрии в расположении значений.
- Наличие ярко выраженных выбросов.
Как пример ненормального распределения (с выбросами) можно рассматривать среднее время ответа на комментарии по неделям:

Если посчитать среднее значение для такого набора данных с помощью среднего арифметического, то получится завышенное число. В итоге наши выводы будут более позитивными, чем реальное положение дел. Еще стоит учитывать, что выбросы могут не только завышать среднее значение, но и занижать его. В таком случае вы получите более скромный показатель, который не будет соответствовать реальности.
Например, в группе «Золотое Яблоко» во ВКонтакте иногда публикуют конкурсные посты. Они набирают более высокие показатели вовлеченности чем обычные публикации. Если посчитать средний ER с учетом конкурсов, мы получим 0,37%, а без учета конкурсов — только 0,29%. Аналогичная ситуация с числом комментариев. С конкурсами в среднем получаем 917 комментариев, а без конкурсов — всего лишь 503. Очевидно, что из-за розыгрышей средние показатели вовлеченности завышаются. В этом случае конкурсные посты следует исключить из анализа, чтобы объективно оценить эффективность контента в группе.

Еще часто бывает так, что данных очень много, заметны явные выбросы, но на их обработку и исключение аномальных значений не хватит ни времени, ни терпения. Тем более нет гарантий, что исключив выбросы, вы получите нормальное распределение. В таком случае лучше подсчитать средние значения, используя медиану.
Как найти медиану и когда ее применять
Если вы имеете дело с ненормальным распределением или замечаете значительные выбросы — используйте медиану. Так можно получить более адекватное среднее значение, чем при использовании среднего арифметического. Чтобы понять, как работать с медианой, рассмотрим аналогичный пример с ненормальным распределением времени ответов на комментарии.

Ниже в таблице уже введены данные из графика и рассчитано среднее время ответа с помощью среднего арифметического и медианы. Из расчетов видна наглядная разница между средним арифметическим и медианой ― она составляет 17 минут. Такое различие появляется из-за низкого темпа работы на выходных и в нестандартных ситуациях, когда к ответу на сообщения нужно относиться с особой ответственностью (события конца февраля). Подобные выбросы сильно завышают среднее арифметическое, а вот на медиану они практически не влияют. Поэтому если хотите посчитать среднее значение избегая влияния выбросов, — используйте медиану. Такие данные будут без искажений.

Как рассчитать
Разберем на примере. В аккаунте опубликовали семь постов и они набрали разное количество комментариев: 35, 105, 2, 15, 2, 31, 1. Чтобы вычислить медиану, нужно пройти два этапа:
- Расположите числа в порядке возрастания. Итоговый ряд будет выглядеть так: 1, 2, 2, 15, 31, 35, 105.
- Найдите середину сформированного ряда. В центре стоит число 15 — его и нужно считать медианой.
Немного сложнее найти медиану, если вы работаете с четным количеством чисел. Например, вы собрали количество лайков на последних шести постах: 32, 48, 36, 201, 52, 12. Чтобы найти медиану, выполните три действия:
- Расставьте числа по возрастанию: 12, 32, 36, 48, 52, 201.
- Возьмите два из них, наиболее близких к центру. В нашем случае — это 36 и 48.
- Сложите два этих числа и разделите на два: (36 + 48) / 2 = 42. Результат и есть медиана.
Чтобы вычислять медиану быстрее и обрабатывать большие объемы данных — используйте Google Таблицы:
- Внесите данные в таблицу.
- Щелкните по свободной ячейке, в которую хотите записать медиану.
- Введите формулу «=MEDIAN(» и выделите ряд чисел, для которых нужно рассчитать медиану. Нажмите «Enter», чтобы все посчиталось.

Когда можно не использовать
Если данные распределены нормально и вы не видите заметных выбросов — медиану можно не использовать. В этом случае значение среднего арифметического будет очень близким к медиане. Можете выбрать любой способ нахождения среднего, с которым вам работать проще. Результат от этого сильно не изменится.
Что такое мода и где ее использовать
Мода ― это самое популярное/часто встречающееся значение. Например, стоит задача узнать, сколько комментариев чаще всего набирают посты в аккаунте. В этом случае можно не высчитывать среднее арифметическое или медиану ― лучше и проще использовать моду.
Еще пример. Нужно узнать, в какое время аудитория чаще всего взаимодействует с публикациями. Для этого можно посчитать данные вручную или использовать готовую таблицу из LiveDune (вкладка «Вовлеченность» ― таблица «Лучшее время для поста»). По ее данным ― больше всего реакций пользователи оставляют в среду в 16 часов. Это время и есть мода. Таким образом, если вам нужно найти самое популярное значение, а не классическое среднее — проще использовать моду.

Как рассчитать
Чтобы найти наиболее часто встречающееся значение в наборе данных, нужно посмотреть, какое число встречается в ряду чаще всех. Например, для ряда 5, 4, 2, 4, 7 ― модой будет число 4.
Иногда в ряде значений встречается несколько мод. Например, ряду 7, 7, 21, 2, 5, 5 свойственны две моды — 7 и 5. В этом случае совокупность чисел называется мультимодальной. Также поиск моды можно упростить с помощью Google Таблиц:
- Внесите значения в таблицу.
- Щелкните по ячейке, в которую хотите записать моду.
- Введите формулу «=MODE(» и выделите ряд чисел, для которых нужно вычислить моду. Нажмите «Enter».

Однако важно иметь в виду, что табличная функция выдает только самую меньшую моду. Поэтому будьте внимательны — можно упустить из виду несколько мод.
Когда использовать не стоит
Моду нет смысла использовать, если вас не просят найти самое популярное значение. Там, где надо найти классическое среднее значение, про моду лучше забыть.
Памятка по использованию
Среднее арифметическое
Как находим: сумма чисел / количество чисел.
Используем: если данные распределены нормально и нет ярких выбросов.
Не используем: если видим явные выбросы или ненормальное распределение.
Медиана
Как находим: располагаем числа в порядке возрастания и находим середину сформированного ряда.
Используем: если работаем с ненормальным распределением или видим выбросы.
Не используем: если выбросов нет и распределение нормальное.
Мода
Как находим: определяем значение, которое чаще всего встречается в ряду чисел.
Используем: если нужно найти не среднее, а самое популярное значение.
Не используем: если нужно найти классическое среднее значение.
Только важные новости в ежемесячной рассылке
Нажимая на кнопку, вы даете согласие на обработку персональных данных.

Подписывайся сейчас и получи гайд аудита Instagram аккаунта
Маркетинговые продукты LiveDune — 7 дней бесплатно
Наши продукты помогают оптимизировать работу в соцсетях и улучшать аккаунты с помощью глубокой аналитики

Анализ своих и чужих аккаунтов по 50+ метрикам в 6 соцсетях.
Оптимизация обработки сообщений: операторы, статистика, теги и др.
Автоматические отчеты по 6 соцсетям. Выгрузка в PDF, Excel, Google Slides.
Контроль за прогрессом выполнения KPI для аккаунтов Инстаграм.
Аудит Инстаграм аккаунтов с понятными выводами и советами.
Поможем отобрать «чистых» блогеров для эффективного сотрудничества.
Среднее арифметическое, мода и медиана
- Предмет, цели и методы математической статистики
- Метод выборочных исследований
- Средняя арифметическая, простая и взвешенная
- Мода и медиана
- Примеры
Предмет, цели и методы математической статистики
Начиная с XVIII века, в общем направлении статистических исследований начинает активно формироваться математическая статистика.
Математическая статистика – раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений.
В зависимости от предмета исследований математическая статистика делится на:
- статистику чисел;
- многомерный статистический анализ;
- анализ функций (процессов) и временных рядов;
- статистику объектов с нечисловыми характеристиками.
В зависимости от цели и методов исследований математическая статистика делится на: описательную статистику; теорию оценивания; теорию проверки гипотез.
| Описательная статистика | Теория оценивания | Теория проверки гипотез | |
| Цель | Обработка и систематизация эмпирических данных | Оценивание ненаблюдаемых данных и сигналов от объектов наблюдения на основе наблюдаемых данных | Обоснование предположений о виде распределения и свойствах случайной величины |
| Методы |
1. Наглядное представление в форме графиков и таблиц. 2. Количественное описание с помощью статистических показателей. |
1. Параметрические методы (наименьших квадратов, максимального правдоподобия и др.). 2. Непараметрические методы. |
1. Последовательный анализ. 2. Статистические критерии. |
Метод выборочных исследований
Статистика получила признание в различных областях человеческой деятельности благодаря заметной экономии времени и прочих ресурсов. Её основная идея: не нужно измерять всё, измерьте только часть всего и сделайте предположение об остальном.
«Всё» в статистике называется генеральной совокупностью.
«Часть всего», которую мы тщательно исследуем, называется выборкой.
Метод выборочных исследований – способ определения свойств группы объектов (генеральной совокупности) на основании статистического исследования её части (выборки).
Например, чтобы оценить средние размеры апельсина, который продаётся в магазине в декабре, необязательно денно и нощно мерить все апельсины во всех ящиках (сколько же для этого нужно времени и людей?!). Достаточно сделать выборку – мерить по одному апельсину из каждого ящика в течение месяца (тут уже и один человек справится).
Статистика предоставляет методику и оценки для того, чтобы правильно провести выборку и на основании знаний о среднем размере апельсина в выборке (выборочной средней) судить о средних размерах всех декабрьских апельсин (генеральной средней).
Средняя арифметическая, простая и взвешенная
Статистическое исследование опирается на собранные данные о каком-то признаке (рост, вес, возраст, доход и т.п.).
Варианта – полученное эмпирическое значение признака.
Вариационный ряд – совокупность собранных вариант.
Пусть мы сделали выборку, провели N измерений и получили x_1,x_2,…,x_N вариант.
Вариационный ряд, состоящий из отдельных вариант, называют дискретным.
Чтобы найти выборочную среднюю дискретного вариационного ряда, нужно вычислить среднюю арифметическую простую:
$$ x_{cp} = frac{1}{N} sum_{i=1}^N x_i ,i = overline{1,N} $$
Знак Σ означает «сумма», i – это индекс полученных вариант, который пробегает все значения, от 1 до N.
Например:
На протяжении четверти школьник получил такие оценки по алгебре: 5,4,3,5,4,4,5,4,3,5,5,4,3,5,4,4. Найдите среднюю оценку за четверть.
Считаем среднюю арифметическую простую:
$$ x_cp = frac{5+4+3+⋯+4}{16} ≈ 4,2 $$
Нетрудно заметить, что оценки повторяются, и вычисления можно упростить, если вместо сложения одинаковых оценок использовать умножение оценок на их количество.
Чтобы найти выборочную среднюю при повторяющихся вариантах, удобно вычислять среднюю арифметическую взвешенную:
$$ x_{cp} = frac{1}{N} sum_{i=1}^K x_i n_i , N = sum_{i=1}^K n_i , i = overline{1,K} $$
где K – количество групп с повторяющимися вариантами, $x_i$ – значение варианты в -й группе, $n_i$ – частота варианты $x_i$.
Например:
Рассматриваем тот же ряд оценок: 5,4,3,5,4,4,5,4,3,5,5,4,3,5,4,4 и составляем таблицу:
$$ x_cp = frac{3cdot3+4cdot7+5cdot6}{3+7+6} ≈ 4,2 $$
Вычисления заметно упростились.
Мода и медиана
Мода дискретного вариационного ряда – это варианта с максимальной частотой. Мод может быть несколько. Тогда говорят, что ряд мультимодальный.
В примере с оценками по алгебре мода $M_0 = 4$ – эта оценка встречается чаще всего, её частота равна 7.
Медиана дискретного вариационного ряда – это значение варианты посредине упорядоченного ряда.
Алгоритм:
-
Отсортировать ряд по возрастанию.
-
Если общее количество измерений N нечётное, найти m = $lceil frac{N}{2}rceil$ и округлить в сторону увеличения. $M_e = x_m$ – искомая медиана.
-
Если общее количество измерений N чётное, найти $m = frac{N}{2}$ и вычислить медиану как среднее $M_e = frac{x_m+x_{m+1}}{2}$.
В примере с оценками по алгебре N = 16 – четное. $m = frac{N}{2} = 8 $.
Сортируем ряд оценок по возрастанию: 3,3,3,4,4,4,4, 4,4, 4,5,5,5,5,5,5
$$ x_8 = 4, x_9 = 4 Rightarrow M_e = frac{4+4}{2} = 4 $$
Внимание!
Мода и медиана учитывают индивидуальные варианты и поэтому важны для характеристики вариационного ряда.
Особенное значение мода и медиана приобретают в рядах с выбросами – одиночными очень большими или очень малыми вариантами. В этом случае они оберегают от выводов на основании «средней температуры по больнице».
Примеры
Пример 1. В исследовании месячных доходов десяти человек были получены следующие данные: 200,100,300,300,1000,5000,100,200, 300,400 (дол.).
Найдите выборочную среднюю, моду и медиану.
Почему при оценке доходов мода и медиана предпочтительней выборочной средней?
Составим таблицу:
$x_i$, дол.
100
200
300
400
1000
5000
$sum$
$n_i$, чел.
2
2
3
1
1
1
10
$x_i n_i$
200
400
900
400
1000
5000
7900
Выборочная средняя:$ x_{cp} = frac{7900}{10} = 790$ (дол.)
Мода: $M_o$ = 300 (дол.) – максимальная частота 3
Медиана:
100, 100, 200, 200, 300, 300, 300, 400, 1000, 5000
$$ m = frac{10}{2} = 5, x_5 = x_6 = 300, M_e = frac{300+300}{2} = 300 (дол.) $$
Выборочная средняя не отражает доходов большей части людей в выборке, поскольку даже один человек с большими доходами может резко сместить оценку вправо. Мода и медиана хорошо отражают доходы большей части людей в выборке.
Пример 2. Исследовалось время решения задачи. В исследовании принимало участие 20 человек, из них двое задачу не решили. Время решения остальных участников:
$x_i$, мин
10
15
20
25
30
Найдите выборочную среднюю, моду и медиану.
При подборе задач для контрольной работы, сколько времени следует отвести на решение подобной задачи?
Проведём вычисления:
$x_i$
10
15
20
25
30
$sum$
$x_i n_i$
20
75
100
100
60
355
$$x_cp = frac{355}{18} ≈ 19,7 мин $$
В выборке 2 моды: $M_{o1}$ = 15 мин, $M_{o2}$ = 20 мин
Положение медианы: $m = frac{N}{2} = frac{18}{2} = 9, x_9 = x_10 = 20, Me = 20$ мин
Средняя, одна из мод и медиана равны 20 мин. Поэтому при составлении контрольной следует отвести на подобную задачу 20 мин.
Пример 3. работа по геометрии показала следующие результаты:
Найдите выборочную среднюю, моду и медиану.
Что вы можете сказать об уровне понимания материала?
Проведём вычисления:
$x_i n_i$
10
66
40
10
126
$$x_cp = frac{126}{39} ≈ 3,2$$
Мода: $M_o$ = 3 – эта оценка получена 22 раза
Положение медианы: $m = ⌈ frac{N}{2}⌉ = ⌈frac{39}{2}⌉ = 20, x_{20} = 3, Me = 3$
Средняя, мода и медиана равны 3.
Уровень понимания удовлетворительный, «на троечку».
План урока:
Понятие выборки и генеральной совокупности
Среднее арифметическое выборки
Упорядоченный ряд и таблица частот
Размах выборки
Мода выборки
Медиана выборки
Ошибки в статистике
Понятие выборки и генеральной совокупности
Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.
В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:

Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.

В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.
В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.

Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.
Среднее арифметическое выборки
Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.

Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=
= 349:20 = 17,45.
Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.
Упорядоченный ряд и таблица частот
В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Такую запись называют упорядоченным рядом данных.

Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:

При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,
2+3+1+1+2+2+1+2+2+1+1+2 = 20.
С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:
(12•2+13•3+14•1+15•1+16•2+17•2+18•1+19•2+20•2+21•1+24•1+25•2):20 =
(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.
Размах выборки
Следующий важная характеристика ряда данных – это размах выборки.

Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:
25 – 12 = 13,
так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.
Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:
(8+9+9+8+9):5 = 43:5 = 8,6;
(7+10+10+6+10):5 = 43:5 = 8,6.
Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен
9 – 8 = 1,
в то время как размах выборки второго спортсмена равен
10 – 6 = 4.
Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.

В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
1, 2, 3, 3, 3, 4, 5, 5, 5
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
6, 6, 7, 7, 8, 8.
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Медиана выборки
Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:

Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:


Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна
(17+17):2 = 34:2 = 17.
Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.
Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):
39, 41, 67, 36, 60, 58, 46, 44, 39, 69.
Найдем среднее арифметическое, размах, моду и медиану для этого ряда.
Решение. Сначала перепишем ряд в упорядоченном виде:
36, 39, 39, 41, 44, 46, 58, 60, 67, 69.
Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):
(36+39+39+41+44+46+58+60+67+69):10 =
= 499:10 = 49,9 кг.
Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен
69 – 36 = 33 кг.
В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.
В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно
(44+46):2 = 90:2 = 45 кг.
Поэтому и медиана ряда будет равна 45 кг.
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.
Распределение
случайной величины характеризуется
параметрами
распределения,
которые объединены в четыре группы
характеристик:
-
характеристики
положения, -
характеристики
рассеивания, -
характеристики
асимметрии, -
характеристики
эксцесса.
Естественно,
что параметры распределения определяются
только для данных, представленных либо
в интервальной шкале, либо в шкале
отношений.
Из
характеристик положения
рассмотрим моду, медиану и среднее
арифметическое значение. По-другому
эти параметры называются мерами
центральной тенденции.
Мода
(М0)
– наиболее часто встречающееся значение;
его называют также модальным значением.
Кроме модального значения используется
также понятие модального интервала –
так именуется интервал, куда попадает
наибольшее количество значений. Нередко
модальное значение оказывается как раз
в модальном интервале. Распределение
величины может быть унимодальным
и полимодальным:
если мода в распределении одна – то
распределение унимодальное, если более
– то полимодальное.
Среднее
арифметическое значение
Мх
рассчитывается по формуле:
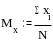
где
хi
– это сумма
всех значений случайной величины от
первого х1
до последнего xN,
а N
– это общее число значений случайной
величины.
Медиана
(Ме)
– это такое значение случайной величины,
которое делит упорядоченную
(в порядке возрастания или убывания
величины) выборку пополам, то есть справа
и слева от медианы находится равное
количество значений случайной величины.
При нечетном количестве измерений за
медиану принимается непосредственно
центральное значение, справа и слева
от него располагается по (n-1)/2
значений. Так, в выборке из 15 упорядоченных
значений это будет восьмое значение, а
в выборке из 23 значений – двенадцатое и
т.д.
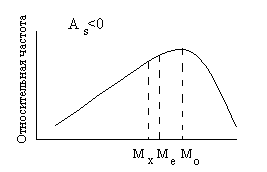
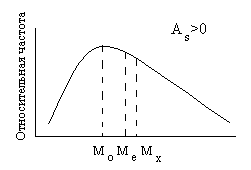
Рис.3.
Соотношение между мерами центральной
тенденции в асимметричном частотном
распределении.
Если
число значений случайной величины в
выборке четное, то медиана оказывается
между двумя значениями; в этом случае
значение медианы рассчитывается как
среднее между ними. На кривой распределения
значение медианы всегда располагается
между значениями моды и среднего
арифметического (рис.3).
Квантили
– это такие значения случайной величины,
которые делят распределение на равные
части. Есть несколько разновидностей
квантилей:
-
Квартили
делят распределение на 4 равных части
по 25%, соответственно квартилей три Q1,
Q2,
Q3. -
Квинтили
– их 4 (К1
….К4),
они делят распределение на 5 частей по
20% в каждой. -
Децили.
Девять децилей (D1
… D9)
делят распределение на 10 частей по 10%. -
Процентили
в количестве 99 (Р1….Р99)
делят распределение на 100 частей по 1%.
Все остальные
квантили можно выражать через процентили:
так, первый квинтиль – это двадцатый
процентиль или второй дециль. Второй
квартиль – это 50 процентиль, или пятый
дециль, или медиана.
Процентили
нельзя ни в коем случае путать с
процентными показателями. Процентные
показатели – это первичные показатели,
определяющие количество правильно
выполненных заданий, а процентиль –
показатель производный, указывающий
на долю от общего числа членов группы.
Первичный результат, который ниже любого
показателя в выборке получает нулевой
процентиль Ро,
а результат, превышающий все другие
показатели группы – получает процентильный
ранг 100 – Р100.
Эти процентили не означают ни нулевого,
ни 100-процентного выполнения теста.
Среди
характеристик рассеивания
рассмотрим:
-
размах
d -
дисперсию
2
или D -
среднеквадратическое
(стандартное) отклонение -
коэффициент
вариации V.
Размах
d
– это разность между максимальным и
минимальным значениями случайной
величины:
d
= хmax
– хmin
Дисперсия
2
(или D) характеризует разброс значений
случайной величины вокруг среднего
арифметического значения, т.е. насколько
плотно значения случайной величины
группируются вокруг среднего
арифметического Мх. Чем больше разброс,
тем сильнее варьируют результаты
испытуемых в данной группе, тем больше
различия между испытуемыми.
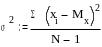
На первый взгляд
может показаться, что было бы проще
взять не квадрат значений отклонения
от среднего, а просто отклонения значений
от среднего. Но легко убедиться, что
сумма таких отклонений будет равна
нулю. Возведение же отклонений от
среднего в квадрат позволяет избежать
отрицательных чисел. На практике расчета
дисперсии наряду с указанной формулой
используется и расчет «способом моментов»
по формуле
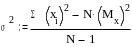
где
(xi)2
– сумма квадратов значений Х.
Дисперсия
имеет «квадратную размерность», то
есть, если какая-то величина измерена
в сантиметрах, то размерность дисперсии
– сантиметры в квадрате, а если в баллах
– то дисперсия – в «баллах в квадрате».
Это не всегда удобно, большую наглядность
в отношении разброса величины имеет
среднеквадратическое
или стандартное
отклонение
(греческая буква «сигма»). Размерность
этого параметра совпадает с размерностью
случайной величины.
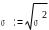
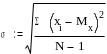
Среднеквадратическое
отклонение используется очень широко
в математической статистике. Малое
значение стандартного отклонения
указывает, что наблюдения хорошо
группируются около среднего арифметического
значения. Большое значение стандартного
отклонения говорит о том, что наблюдения
широко рассеяны относительно среднего
значения и имеют слабую тенденцию к
централизации.
Коэффициент
вариации
размерности не имеет, он служит для
сравнения вариативности, то есть
изменчивости случайных величин, имеющих
различную природу. Рассчитывается
коэффициент вариации по формуле:
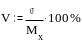
Если
коэффициент вариации меньше 40%, то
коэффициент вариации признается низким,
то есть изменчивость величины невелика.
Характеристики
асимметрии. В
случаях, когда по тем или иным причинам
более часто встречаются значения с
показателями ниже или выше среднего,
то появляются асимметричные распределения
величины. Основная мера асимметрии –
это коэффициент
асимметрии
As,
рассчитываемый по формуле:
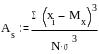
Коэффициент
асимметрии изменяется от минус до плюс
бесконечности. Асимметрия бывает
левосторонняя или положительная, если
As>0
(на рисунке 2 справа), и правосторонняя
или отрицательная, если коэффициент
асимметрии меньше 0 (слева на рис.2). При
левосторонней асимметрии чаше встречаются
значения по величине меньшие среднего
арифметического (то есть медиана, и мода
на графике находятся слева от среднего
арифметического), при правосторонней
асимметрии, соответственно, чаще
встречаются значения, по величине
превосходящие среднее арифметическое.
Для симметричных распределений
коэффициент асимметрии равен нулю,
мода, медиана и среднее арифметическое
совпадают между собой.
Характеристики
эксцесса: Коэффициент эксцесса
(или островершинности) рассчитывается
по формуле
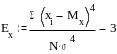
Распределения
с острой вершиной будут характеризоваться
положительным эксцессом, а сглаженные
либо с понижением в центральной части
– отрицательным. Пример расчета параметров
распределения приведен в таблице 2:
Таблица 2
Расчет параметров
распределения
-
Х
Отклонение от
среднего(Xi
– Mx)
(Xi
– Mx)
2(Xi
– Mx)
3(Xi
– Mx)
448
8
64
512
4096
47
7
49
343
2401
43
3
9
27
81
41
1
1
1
1
41
1
1
1
1
40
0
0
0
0
38
-2
2
-8
16
36
-4
16
-64
256
34
-6
36
-216
1296
32
-8
64
-512
4096
Х=400
Mx=40
(Xi
– Mx)
2 ==244
(Xi
– Mx)
3=84(Xi
– Mx)4==12244
Модальное
значение – 41, поскольку оно встречается
дважды. Медиана – 40.5 (пять чисел меньше
этой величины, пять больше). Среднее
арифметическое равно 400/10=40.
Дисперсия
2
=244/9=27.11
Стандартное
отклонение
=5.207.
Коэффициент
асимметрии As
= 0.011
Коэффициент
эксцесса Ex
= -1.334
При
работе на компьютере параметры
распределения можно рассчитать, используя
встроенные функции Microsoft
Excel.
Для этого надо войти в раздел «Анализ
данных» из меню «Сервис», где выбрать
подраздел «Описательная статистика».
На экране при этом высвечивается меню
«Описательная статистика», в котором
задаются входной интервал переменной
и выходной интервал для вывода результатов
расчета. Входной интервал переменной
задается через двоеточие, например
интервал «a1:a24»
включает в себя 24 значения переменной
в столбце A
с 1 по 24 ячейку. Можно рассчитывать
параметры распределения сразу нескольких
переменных, если они представляют собой
единый массив данных. Так, входной
интервал a1:c25
включает в себя три переменных по 25
значений в каждой: a1:a25,
b1:b25
и c1:c25.
Если в первой строке интервала находится
заголовок столбца (строки), то это следует
указать в специальном окошке меню. В
окне «Выходной интервал» следует указать
номер левой верхней ячейки выходного
интервала. Выходные данные включают
среднее
арифметическое значение, стандартную
ошибку среднего, медиану, моду, стандартное
отклонение, дисперсию выборки, коэффициенты
эксцесса и асимметрии, размах выборки
(обозначен как «Интервал»), минимальное
и максимальное значения («Минимум» и
«Максимум»), сумму всех значений и
количество значений переменных («Счет»).
Следует учесть, что в Microsoft
Excel
коэффициенты
асимметрии и эксцесса рассчитываются
по формулам,
несколько отличающимся от приведенных
выше.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
