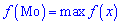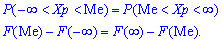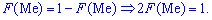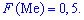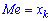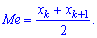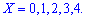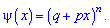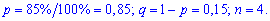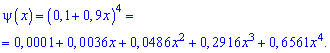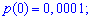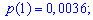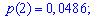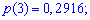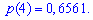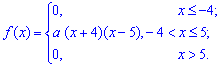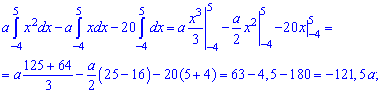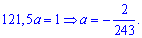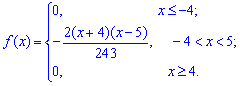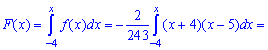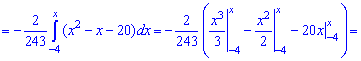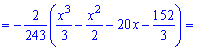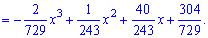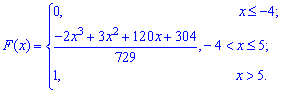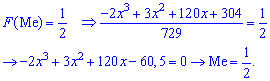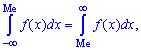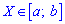Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
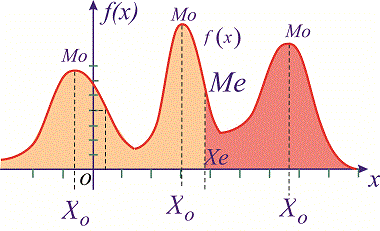
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике – мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
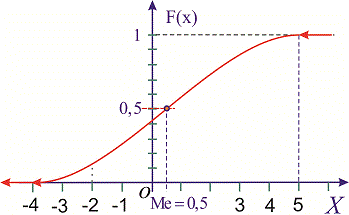
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Математическое ожидание случайной величины
Закон
распределения
полностью характеризует случайную
величину с вероятностной точки зрения.
Однако при решении многих практических
задач нет необходимости приводить весь
закон распределения случайной
величины,
достаточно указать некоторые величины,
называемые числовыми характеристиками,
назначение которых – это выражение
наиболее существенных особенностей
распределения. Для каждой случайной
величины необходимо знать некоторое
среднее значение, около которого
группируются ее возможные значения,
число, характеризующее степень
разбросанности этих значений относительно
среднего, а также некоторые другие
числовые характеристики.
Одной из
таких характеристик является математическое
ожидание случайной величины.
Определение
6. Математическое
ожидание –
это среднее значение случайной
величины.
Математическое ожидание
случайной величины обозначается
или
.
Если
случайная величина –
дискретная и принимает конечное число
значений, то
(8)
Если случайная
величина –
дискретная и принимает бесконечное, но
счетное число значений, то
(9)
Если случайная
величина –
непрерывная и принимает значения на
конечном промежутке ,
то
(10)
Если
случайная величина –
непрерывная и принимает значения на
всей числовой оси, то
(11)
Встречаются
случайные величины, для которых
математическое ожидание не существует,
так как ряд (9) или
интеграл (11)
расходятся, но такие случайные величины
встречаются редко.
Свойства
математического ожидания.
1. Математическое
ожидание константы равно этой
константе: ;
2. ;
3. ;
4. Определение
7. Две случайные
величины называются независимыми,
если закон распределения одной
из них
не меняется от того, какие возможные
значения приняла другая величина.
Если
случайные величины и
независимы,
то
;
5. =0.
Пример
9. Дан
ряд распределения дискретной случайной
величины :
|
|
2 |
|
4 |
|
|
0,2 |
0,4 |
0,4 |
Известно,
что математическое ожидание .
Найти .
Решение. Так
как дискретная случайная величина
принимает конечное число значений,
воспользуемся
формулой (8), получим
уравнение:
,
из
которого находим :
.
Пример
10. Закон
распределения непрерывной случайной
величины задан
с помощью плотности распределения:
Найти
математическое ожидание данной случайной
величины.
Решение. Так
как непрерывная случайная величина
принимает значения на конечном промежутке,
то для
вычисления математического
ожидания воспользуемся формулой (10),
получаем:
.
Вопрос. Случайная
величина принимает
только отрицательные значения.
Тогда равно:
а)
0;
б) 1;
в) отрицательному числу;
г)
числу из отрезка .



Мода и медиана случайной величины
Определение
8. Модой дискретной
случайной величины называется
ее значение ,
имеющее
наибольшую вероятность.
(13)
Графическим
представлением закона распределения
дискретной случайной величины является
многоугольник
распределения, тогда
мода – это точка, имеющая наибольшую
ординату.
Рис.7
Определение
9. Модой непрерывной
случайной величины называется точка
локального максимума плотности
распределения.
(14)
Рис.8
Мода может
не существовать, может иметь единственное
значение( тогда распределение случайной
величины
называется унимодальным),
может иметь множество значений( в этом
случае распределение называется
мультимодальным).
Определение
10. Медианой случайной
величины называется
такое ее значение ,
относительно
которого равновероятны
получение большего и получение меньшего
значения.
Если –
дискретная случайная величина, то –
это число на отрезке ,
для которого
(15)
Отрезок называется медианным.
Если –
непрерывная случайная величина, то
(16)
то есть медиана
– это корень уравнения:
(17)
Графически
медиана – это абсцисса точки, в которой
площадь под кривой распределения делится
пополам.
Рис.9
Если
распределение унимодальное и симметричное,
то математическое ожидание, мода и
медиана случайной
величины
совпадают.
Пример
11. Дан
ряд распределения дискретной случайной
величины :
|
|
2 |
4 |
6 |
8 |
|
|
0,4 |
0,2 |
0,1 |
0,3 |
Найти
моду и медиану случайной
величины.
Решение. Наибольшую
вероятность имеет значение ,
поэтому .
Так
как ,
а ,
то медианным отрезком является
отрезок ,
тогда
медианой является любое число из этого
отрезка.
Пример
12. Закон
распределения непрерывной случайной
величины задан
плотностью распределения:
Найти моду и
медиану случайной величины.
Решение. Кривой
распределения является парабола, ветви
которой направлены вниз, поэтому она
имеет точку
максимума, найдем
ее, для этого вычислим производную
функции :
.
Точка максимума является корнем
уравнения ,
получаем уравнение
,
из которого находим .
Так
как парабола симметрична относительно
прямой, проходящей через точку ,
параллельно оси ординат,
то распределение
– симметричное, поэтому .
Рис.10
Вопрос. Непрерывная
случайная величина принимает значения
на отрезке ,
распределение симметричное,
.
Тогда .


Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кроме математического ожидания и дисперсии в теории вероятностей применяется еще ряд числовых характеристик, в частности, мода и медиана случайной величины.
Модой Дискретной случайной величины X называется ее наиболее вероятное значение.
Модой непрерывной случайной величины X называется такое ее значение , при котором плотность распределения
Имеет максимум, т. е.
.
На рис. 3 и 4 показана мода для дискретной и непрерывной случайной величины.

Рис. 3 Рис. 4
Если многоугольник распределения (кривая распределения) имеет два или несколько максимумов, то распределение называется Двухмодальным или многомодальным.
Иногда встречаются распределения, которые имеют минимум, но не имеют максимум. Такие распределения называются Антимодальными.
Медианой непрерывной случайной величины X (обозначение:) называется такое ее значение
, для которого одинаково вероятно, окажется ли случайная величина
Меньше
или больше
, т. е.
. (9)
Геометрически вертикальная прямая , Проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две равные части (рис. 5). Каждая из этих площадей равна
, т. к. площадь, ограниченная кривой распределения, равна единице. Поэтому функция распределения в точке
равна
, т. е.
.
Рис. 5
Для дискретной случайной величины медиана обычно не определяется.
| < Предыдущая | Следующая > |
|---|
Для нахождения моды и медианы случайной величины необходимы хорошие умения интегрировать и знания следующего теоретического материала. Модой 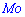
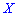
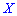
В зависимости от вида функции 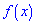
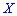
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой 
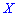
Графически мода и медиана изображенные на рисунке
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин 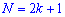
в случае четного количества 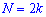
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины 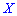
Решение. Случайной величина может принимать значения
Вероятности появления значений определяем по образующей функцией
Для заданной задачи входные величины принимают значения
Искомые вероятности входят множителями при степенях аргумента
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду 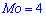
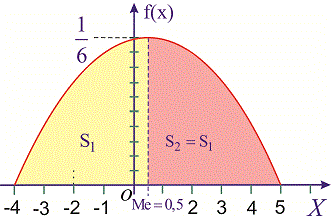
Пример 2. По заданной плотностью вероятностей
найти параметр 
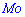
Решение. Применяя условие нормирования выполняем интегрирование
после того определяем параметр
Плотность вероятностей, учитывая найденное значение будет иметь вид
а ее график изображен на рисунке ниже
Из графика плотности вероятностей видим, что мода принимает значение 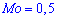

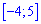
Функция распределения иметь следующий вид
а ее график будет иметь вид
Для определения медианы случайной величины 
Медиану 
для дискретной случайной величины из промежутка
Таким образом медиану 
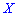
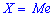
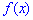
——————————-
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.
Мода непрерывной случайной величины
Предмет
Теория вероятностей
Разместил
🤓 violettakusu
👍 Проверено Автор24
то значение случайной величины, для которого плотность распределения вероятностей имеет максимум.
Научные статьи на тему «Мода непрерывной случайной величины»
Формулы статистических характеристик
right)=frac{a_1+a_2+ dots ,+a_n}{n}=frac{sumlimits^n_{i=1}{a_i}}{n}]
Пусть теперь дана непрерывно…
распределенная совокупность, тогда
Определение
Среднее арифметическое непрерывно распределенной…
случайной величины на отрезке $[a,b]$ называется величина $overline{{f(x)}_{left[a,bright]}}$ определенная…
a_n$, тогда
Определение
Среднее геометрическое совокупности $n$ чисел называется значение величины…
Мода
Определение
Мода — наиболее часто встречающееся значение данного множества.

Статья от экспертов
Рождение оптических вихрей при распространении поля с начальным дробным топологическим зарядом
Топологический заряд параксиального оптического вихря при распространении в свободном пространстве в общем случае не сохраняется, в отличие от орбитального углового момента, который сохраняется. В работе на примере Гауссова пучка с дробным топологическим зарядом в начальной плоскости показано численно, как меняется топологический заряд при распространении. Имеется четыре сценария эволюции оптического вихря с начальным дробным топологическим зарядом, в зависимости от близости дробного топологического заряда к целому чётному или нечётному числу. Для простых оптических вихрей (моды Лагерра–Гаусса или Бесселя–Гаусса) топологический заряд сохраняется и при распространении, и при слабом фазовом искажении. Экспериментально показано, что целый топологический заряд оптического вихря сохраняется при рассеянии на фазовом случайном экране вплоть до величины случайного искажения разности хода на половину длины волны. Поэтому при слабой турбулентности имеет смысл измерять топологический заряд, та…
Начальные и центральные моменты
Начальным моментом $k$-го порядка случайной величины $X$ называется математическое ожидание случайной…
Для непрерывной случайной величины $X$
[nu _{k} (X)=int limits _{-infty }^{+infty } x^{k} cdot…
Для непрерывной случайной величины $X$
[mu _{k} (X)=int limits _{-infty }^{+infty } (x-M(X))^{…
Если кривая плотности распределения непрерывной случайной величины такова, что справа от моды расположена…
Коэффициент асимметрии $S_{k} $ отрицателен, если «длинная часть» кривой распределения расположена слева от моды

Статья от экспертов
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек