Как найти моду питон

Mode of a data set is/are the member(s) that occur(s) most frequently in the set. If there are two members that appear most often with same number of times, then the data has two modes. This is called bimodal.

If there are more than 2 modes, then the data would be called multimodal. If all the members in the data set appear the same number of times, then the data set has no mode at all.

Following function modes() can work to find mode(s) in a given list of data:

import numpy as np; import pandas as pd

def modes(arr):
    df = pd.DataFrame(arr, columns=['Values'])
    dat = pd.crosstab(df['Values'], columns=['Freq'])
    if len(np.unique((dat['Freq']))) > 1:
        mode = list(dat.index[np.array(dat['Freq'] == max(dat['Freq']))])
        return mode
    else:
        print("There is NO mode in the data set")

Output:

# For a list of numbers in x as
In [1]: x = [2, 3, 4, 5, 7, 9, 8, 12, 2, 1, 1, 1, 3, 3, 2, 6, 12, 3, 7, 8, 9, 7, 12, 10, 10, 11, 12, 2]
In [2]: modes(x)
Out[2]: [2, 3, 12]
# For a list of repeated numbers in y as
In [3]: y = [2, 2, 3, 3, 4, 4, 10, 10]
In [4]: modes(y)
Out[4]: There is NO mode in the data set
# For a list of strings/characters in z as
In [5]: z = ['a', 'b', 'b', 'b', 'e', 'e', 'e', 'd', 'g', 'g', 'c', 'g', 'g', 'a', 'a', 'c', 'a']
In [6]: modes(z)
Out[6]: ['a', 'g']

If we do not want to import numpy or pandas to call any function from these packages, then to get this same output, modes() function can be written as:

def modes(arr):
    cnt = []
    for i in arr:
        cnt.append(arr.count(i))
    uniq_cnt = []
    for i in cnt:
        if i not in uniq_cnt:
            uniq_cnt.append(i)
    if len(uniq_cnt) > 1:
        m = []
        for i in list(range(len(cnt))):
            if cnt[i] == max(uniq_cnt):
                m.append(arr[i])
        mode = []
        for i in m:
            if i not in mode:
                mode.append(i)
        return mode
    else:
        print("There is NO mode in the data set")

Область статистики часто понимают неправильно, однако она играет важную роль в повседневной жизни. Корректно составленная статистика позволяет извлечь знания из неопределённого и сложного реального мира, однако при неправильном применении она может нанести вред или ввести в заблуждение. Для того, чтобы отличить правду от лжи, важно чётко понимать методы статистики и значение различных статистических измерений.

В этой статье мы поговорим о:

• определении статистики;
• описательной статистике:
  • мерах центральной тенденции;
  • мерах разброса.

Нам не понадобятся глубокие знания статистики, однако понадобится хотя бы минимальное знание Python. Если вы не встречались с циклами for и списками, будет лучше сначала ознакомиться с ними.

Не знаете с какой стороны подойти к Python? Тогда почитайте о том, с чего начать изучение Python.

Загружаем данные

Мы будем обсуждать статистику, используя реальные данные, взятые с платформы Kaggle из датасета Wine Reviews. Сами данные были извлечены с сайта Wine Enthusiast.

Предположим, вы — ученик сомелье. Вы нашли интересный датасет и хотели бы сравнить различные вина, воспользовавшись статистикой для описания данных и сделав для себя несколько выводов.

Код, представленный ниже, загружает датасет wine-data.csv в переменную wines в виде списка списков. В статье мы будем вести статистику на примере этой переменной:

import csv
with open("wine-data.csv", "r", encoding="latin-1") as f:
    wines = list(csv.reader(f))

Давайте посмотрим на первые пять строк данных, указанных в таблице, чтобы понять, с какими значениями мы работаем:

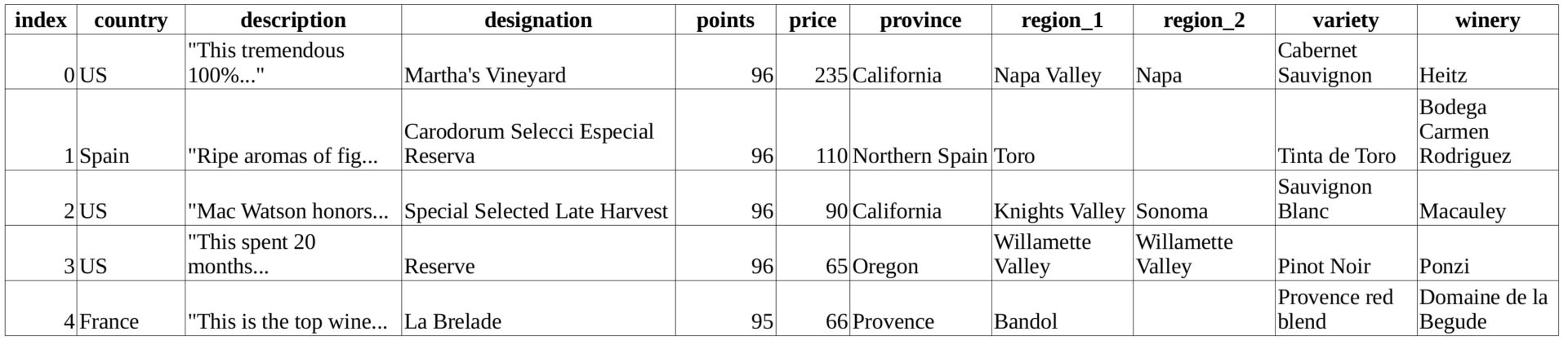
Что именно представляет собой статистика?

Это вопрос с подвохом. Статистика включает в себя много всего, поэтому попытка кратко описать её неизбежно приведёт к упущению некоторых деталей. Тем не менее нам нужно с чего-то начинать.

Область статистики можно рассматривать как научную среду для работы с данными. Это определение включает все задачи, связанные со сбором, анализом и интерпретацией данных. Также статистика может относиться к отдельным измерениям, которые представляют собой сводную информацию по данным или определенные их аспекты. В этой статье мы постараемся провести грань между научной областью статистики и непосредственными измерениями.

И первым шагом будет логичный вопрос: а что такое «данные»? К счастью, это определение дать проще. Данные — это совокупность наблюдений за миром, которая может иметь множество вариаций, от качественных до количественных. Исследователи собирают данные, полученные в ходе экспериментов, предприниматели собирают данные своих клиентов, а игровые компании собирают данные о поведении игроков

Эти примеры указывают на ещё один важный аспект: наблюдения обычно связаны с генеральной совокупностью, представляющей интерес. Возвращаясь к предыдущему примеру: исследователь может рассматривать группу пациентов с определённым состоянием. Для наших данных генеральной совокупностью будет набор отзывов о винах. Чётко определив генеральную совокупность, мы можем применить методы статистики и извлечь знания из полученных результатов.

Но почему нас интересуют генеральные совокупности? Полезно иметь возможность сравнивать и противопоставлять их, чтобы проверить наши идеи. Например, мы хотели бы узнать, что пациенты, получающие новое лечение, выздоравливают быстрее тех, кто получает плацебо, но кроме того мы хотели бы доказать это количественно. Здесь на помощь приходит статистика, которая предоставляет точный подход к данным и даёт возможность принимать решения, основанные на реальных событиях, а не на догадках.

Ключевые идеи:

• статистика — наука о данных;
• данные — набор наблюдений за интересующей нас генеральной совокупностью;
• статистика предоставляет конкретный способ сравнения генеральных совокупностей с помощью чисел, а не неоднозначных описаний.

Описательная статистика

Когда у нас есть набор наблюдений, полезно свести признаки наших данных в одно определение. Этим занимается описательная статистика. Как следует из названия, описательная статистика описывает конкретное свойство данных, которые она обобщает. Такую статистику можно разделить на две категории: меры центральной тенденции и меры разброса.

Меры центральной тенденции

Меры центральной тенденции — показатели, представляющие собой ответ на вопрос: «На что похожа середина данных?». Слово «середина» звучит неточно, так как существует множество определений для её описания. Далее мы обсудим, как каждая новая мера меняет наше определение «середины».

Среднее значение

Данная характеристика описывает среднее значение в наборе данных. Вычислить её довольно просто: сложите все значения и разделите полученную сумму на количество значений.

В случае со средним значением «серединой» датасета будет среднее арифметическое его значений. Среднее значение отражает типичный показатель в наборе данных. Если мы случайно выберем один из показателей, то, скорее всего, получим значение, близкое к среднему.

Вычислить среднее значение на Python просто. Давайте выясним, чему равна средняя оценка вина в нашем датасете:

# Извлекаем оценки из датасета
scores = [float(w[4]) for w in wines]

# Складываем все оценки
sum_score = sum(scores)

# Ищем количество оценок
num_score = len(scores)

# Считаем среднее значение
avg_score = sum_score/num_score

print(avg_score)  # выводит 87.8884184721394

Это среднее значение говорит нам, что «типичная» оценка в датасете равна примерно 87,8. Соответственно, большинство вин имеют высокий рейтинг, если предположить, что оценивают по шкале от 0 до 100. Тем не менее нужно учесть, что Wine Enthusiast не публикует отзывы с рейтингом ниже 80.

Есть разные типы среднего значения, но это — наиболее распространённая форма. Оно называется средним арифметическим, так как интересующие нас значения складываются.

Медиана

Следующая мера центральной тенденции, о которой пойдёт речь, — медиана. Медиана, как и среднее значение, нужна для определения типичного значения в наборе данных, но при этом не требует вычислений.

Чтобы найти медиану, данные нужно расположить в порядке возрастания. Медианой будет значение, которое совпадает с серединой набора данных. Если количество значений чётное, то берётся среднее двух значений, которые «окружают» середину.

Стандартной библиотекой Python не предусмотрен поиск медианы, но мы можем написать свою реализацию, следуя описанному алгоритму. Попробуем найти медиану цен на вина:

# Извлекаем цены
prices = [float(w[5]) for w in wines if w[5] != ""]

# Находим их количество
num_wines = len(prices)

# Сортируем в порядке возрастания
sorted_prices = sorted(prices)

# Ищем индекс среднего элемента
middle = (num_wines / 2) + 0.5

# Находим медиану
print(sorted_prices[middle])  # 24

Прим.перев. С версии Python 3.4 есть встроенный способ поиска медианного значения.

Медианная цена бутылки вина составляет 24$. Это предполагает, что как минимум у половины вин в датасете цена равна или ниже 24$. Неплохо! А что насчёт среднего значения? Учитывая, что и медиана, и среднее значение отражают типичное значение, можно предположить, что они должны быть примерно одинаковы:

print(sum(prices)/len(prices))  # 33.13

Средняя цена в 33,13$ на порядок выше медианной. Как это произошло? Разница между медианой и средним значением существует из-за робастности (выбросоустойчивости).

Проблема выбросов

Как вы помните, среднее значение можно найти, сложив все значения и разделив сумму на их количество, в то время как медиана ищется простой перестановкой значений. Если в данных есть выбросы — значения, которые гораздо выше или ниже остальных, — это может негативно повлиять на среднее значение. Таким образом, среднее значение не робастно, а медиана — напротив, выбросоустойчива.

Давайте взглянем на максимальную и минимальную цену в наших данных:

min_price = min(prices)
max_price = max(prices)
print(min_price, max_price)  # 4.0, 2300.0

Теперь мы знаем, что в данных есть выбросы. Выбросы могут отражать интересные события или ошибки в нашем наборе данных, поэтому важно уметь определять их наличие. Сравнение медианы и моды — один из способов определить наличие выбросов, хотя визуализация обычно позволяет сделать это быстрее.

Мода

Это последняя мера центральной тенденции, о которой пойдёт речь. Мода определяется как значение, которое наиболее часто встречается в наборе данных. Мода не так очевидно соответствует понятию «середины» как среднее значение или медиана, но это соответствие абсолютно обосновано: если значение появляется в данных неоднократно, оно приблизит среднее значение к моде. Чем чаще появляется значение, тем сильнее оно влияет на среднее. Таким образом, мода показывает наиболее значимый фактор, формирующий среднее значение.

Как и в случае с медианой, встроенной функции для поиска моды у Python нет. Зато мы можем вычислить её сами, посчитав количество повторений различных цен и выбрав самую частую:

# Создаём пустой словарь, в котором будем считать количество появлений цен
price_counts = {}
for p in prices:
    if p not in price_counts:
        counts[p] = 1
    else:
        counts[p] += 1

# Проходимся по словарю и ищем максимальное количество повторений
maxp = 0
mode_price = None
for k, v in counts.items():
    if maxp < v:
        maxp = v
        mode_price = k
print(mode_price, maxp)  # 20.0, 7860

Прим.перев. На самом деле, с версии Python 3.4 можно найти и моду.

Мода относительно близка к медиане, поэтому можно уверенно сказать, что и мода, и медиана отражают средние значения цен на вино.

Меры центральной тенденции полезны для описания среднего значения данных. Тем не менее они не показывают, насколько большой разброс присутствует в данных. Здесь на помощь приходят меры разброса данных.

Меры разброса данных

Меры разброса отвечают на вопрос: «Как сильно варьируются мои данные?». В мире существует не так много вещей, которые остаются в одном и том же состоянии при каждом наблюдении. Эта изменчивость делает мир нечётким и неопределённым, поэтому полезно иметь показатели, которые могут обобщить эту «нечёткость».

Размах

Наша первая мера разброса — размах. Из всех измерений, которые мы рассмотрим далее, его вычислить проще всего. Для этого нужно просто вычесть из наибольшего значения в наборе данных наименьшее.

Мы нашли максимальную и минимальную цены, когда искали медиану, поэтому сейчас можем использовать их:

price_range = max_price - min_price
print(price_range)  # 2296.0

Итак, размах равен 2296, но что это значит? Когда мы рассматриваем результаты различных измерений, очень важно делать это в контексте наших данных. Наша медианная цена была 24$, а размах равен 2296$. Размах на два порядка больше медианы, что указывает на сильный разброс данных. Возможно, будь у нас ещё один винный датасет, мы могли бы сравнить размахи, чтобы понять, как они отличаются. В ином случае сам по себе размах не слишком полезен.

Мы скорее хотели бы узнать, как сильно данные отличаются от типичного значения. Здесь нам помогут стандартное отклонение и дисперсия случайной величины.

Стандартное отклонение

Стандартное отклонение тоже является мерой разброса данных. Оно помогает узнать, как сильно данные отличаются от типичного значения. Иными словами, оно говорит о том, как сильно данные отличаются от среднего арифметического. Отношение к среднему арифметическому хорошо видно при расчёте отклонения:

Поговорим немного о строении уравнения. Как вы помните, среднее арифметическое рассчитывается путём сложения всех значений и деления на их количество. Уравнение стандартного отклонения похоже, но используется, чтобы найти, на сколько в среднем значения отклоняются от типичного, и включает дополнительную операцию с извлечением корня.

В некоторых источниках можно увидеть в качестве знаменателя n вместо n-1. Такие детали выходят за рамки нашей статьи, но знайте, что использование n-1 считается более корректным. Можете прочитать интуитивное объяснение коррекции Бесселя.

Мы хотим посчитать стандартное отклонение, чтобы более полно описать цены вин и их оценки, поэтому напишем свою функцию. Поиск кумулятивной суммы вручную выглядел бы довольно громоздко, но циклы for в Python всё упрощают. Мы пишем свою функцию, чтобы показать, что на Python легко заниматься такой статистикой. Тем не менее в библиотеке numpy тоже реализовано вычисление стандартного отклонения через функцию std:

def stdev(nums):
    diffs = 0
    avg = sum(nums)/len(nums)
    for n in nums:
        diffs += (n - avg)**(2)
    return (diffs/(len(nums)-1))**(0.5)

print(stdev(scores))  # 3.2223917589832167

print(stdev(prices))  # 36.32240385925089

Такие результаты вполне ожидаемы. Оценки варьируются от 80 до 100, поэтому можно предположить, что стандартное отклонение будет небольшим. С другой стороны, отклонение в ценах гораздо выше из-за выбросов. Чем больше стандартное отклонение, тем больше рассеяны данные вокруг среднего значения, и наоборот.

Далее мы увидим, что дисперсия тесно связана со стандартным отклонением.

Дисперсия

Часто стандартное отклонение и дисперсию связывают вместе и делают это не без причины. Вот уравнение дисперсии, ничего не напоминает?

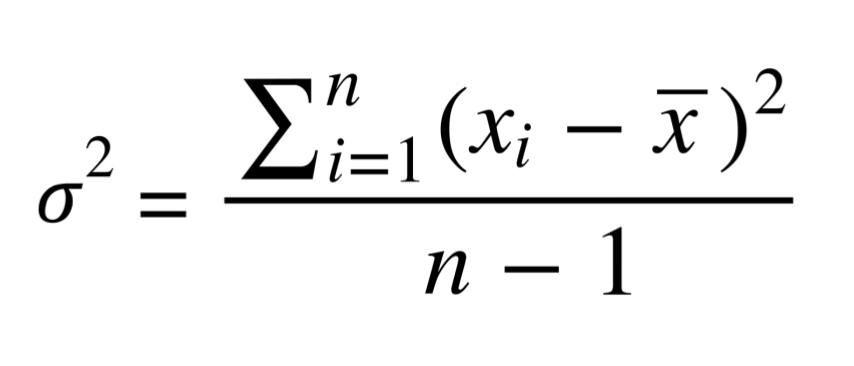
Дисперсия и стандартное отклонение — почти одно и то же! Дисперсия — просто квадрат стандартного отклонения. Более того, обе величины отражают одну и ту же вещь — меру разброса, хотя стоит отметить, что единицы измерения разные. В каких бы единицах ни измерялись ваши данные, единицы измерения отклонения будут такими же, а у дисперсии они будут возведены в квадрат.

Многие новички в статистике задают вопрос: «Зачем возводить отклонение в квадрат? Разве нельзя избавится от отрицательных слагаемых при помощи модуля?». Избавление от отрицательных значений — хорошая причина для возведения в квадрат, но не единственная. Как и на среднее значение, на дисперсию и стандартное отклонение влияют выбросы. Очень часто нас интересуют выбросы, поэтому возведение в квадрат позволяет выделить эту особенность. Если вы знакомы с математическим анализом, то поймете, что наличие экспоненциального выражения позволяет найти точку минимального отклонения.

Чаще всего при статистическом анализе нам понадобятся только среднее значение и стандартное отклонение, однако дисперсия по-прежнему важна в других академических областях. Меры центральной тенденции и разброса позволяют нам систематизировать данные и извлечь из них знания.

Ключевые идеи:

• описательная статистика используется для систематизации и количественного описания данных;
• среднее значение указывает на типичное значение в нашем наборе данных. Оно не робастно;
• медиана является центральным значением в ряду данных. Она робастна;
• мода — значение, которое появляется наиболее часто;
• размах — это разность между максимальным и минимальным значениями в наборе данных;
• дисперсия и стандартное отклонение являются средним расстоянием от среднего арифметического значения.

Перевод статьи «Basic Statistics in Python: Descriptive Statistics»

The mode of a set of data values is the value that appears most often. It is the value at which the data is most likely to be sampled. A mode of a continuous probability distribution is often considered to be any value x at which its probability density function has a local maximum value, so any peak is a mode.
Python is very robust when it comes to statistics and working with a set of a large range of values. The statistics module has a very large number of functions to work with very large data-sets. The mode() function is one of such methods. This function returns the robust measure of a central data point in a given range of data-sets.

Example : 

Given data-set is :  [1, 2, 3, 4, 4, 4, 4, 5, 6, 7, 7, 7, 8]
The mode of the given data-set is 4
Logic: 4 is the most occurring/ most common element from the given list 

Syntax :
mode([data-set])
Parameters : 
[data-set] which is a tuple, list or a iterator of 
real valued numbers as well as Strings.
Return type : 
Returns the most-common data point from discrete or nominal data.
Errors and Exceptions : 
Raises StatisticsError when data set is empty.

Code #1 : This piece will demonstrate mode() function through a simple example. 

Mode of given data set is 4

Code #2 : In this code we will be demonstrating the mode() function a various range of data-sets. 

Mode of data set 1 is 5
Mode of data set 2 is 1.3
Mode of data set 3 is 1/2
Mode of data set 4 is -2
Mode of data set 5 is black

Code #3 : In this piece of code will demonstrate when StatisticsError is raised 

Output 

Traceback (most recent call last):
  File "/home/38fbe95fe09d5f65aaa038e37aac20fa.py", line 20, in 
    print(statistics.mode(data1))
  File "/usr/lib/python3.5/statistics.py", line 474, in mode
    raise StatisticsError('no mode for empty data') from None
statistics.StatisticsError: no mode for empty data

NOTE: In newer versions of Python, like Python 3.8, the actual mathematical concept will be applied when there are multiple modes for a sequence, where, the smallest element is considered as a mode.

Say, for the above code, the frequencies of -1 and 1 are the same, however, -1 will be the mode, because of its smaller value.

Applications: The mode() is a statistics function and mostly used in Financial Sectors to compare values/prices with past details, calculate/predict probable future prices from a price distribution set. mean() is not used separately but along with two other pillars of statistics mean and median creates a very powerful tool that can be used to reveal any aspect of your data. 
 

Last Updated :
23 Aug, 2021

Like Article

Save Article

Среднее значение, медиана и мода являются фундаментальными темами статистики. Вы можете легко вычислить их в Python, с использованием внешних библиотек и без них.

Эти три меры являются основными Главная тенденция. Центральная тенденция позволяет нам узнать «нормальные» или «средние» значения набора данных. Если вы только начинаете заниматься наукой о данных, это руководство для вас.

К концу этого урока вы:

• Понимание понятия среднего, медианы и моды
• Уметь создавать свои собственные функции среднего, медианы и режима в Python.
• Используйте модуль статистики Python, чтобы быстро начать использовать эти измерения.

Если вам нужна загружаемая версия следующих упражнений, не стесняйтесь проверить Репозиторий GitHub.

Давайте рассмотрим различные способы вычисления среднего значения, медианы и моды.

иметь в виду или среднее арифметическое является наиболее часто используемой мерой центральной тенденции.

Помните, что центральная тенденция является типичным значением набора данных.

Набор данных — это набор данных, поэтому набор данных в Python может быть любой из следующих встроенных структур данных:

• Списки, кортежи и наборы: коллекция объектов
• Строки: набор символов
• Словарь: набор пар ключ-значение

Примечание. Хотя в Python есть и другие структуры данных, такие как очереди или стеки, мы будем использовать только встроенные.

Мы можем вычислить среднее значение, добавив все значения набора данных и разделив результат на количество значений. Например, если у нас есть следующий список чисел:

[1, 2, 3, 4, 5, 6]

Среднее значение будет 3,5, потому что сумма списка равна 21, а его длина равна 6. Двадцать один разделить на шесть равно 3,5. Вы можете выполнить этот расчет с помощью следующего расчета:

(1 + 2 + 3 + 4 + 5 + 6) / 6 = 21

В этом уроке мы будем использовать игроков баскетбольной команды в качестве примера данных.

Создание пользовательской функции среднего

Начнем с расчета среднего (среднего) возраста игроков баскетбольной команды. Название команды будет «Pythonic Machines».

pythonic_machine_ages = [19, 22, 34, 26, 32, 30, 24, 24]

def mean(dataset):
    return sum(dataset) / len(dataset)

print(mean(pythonic_machine_ages))

Разбираем этот код:

• «pythonic_machine_ages» — это список возрастов баскетболистов.
• Мы определяем функцию mean(), которая возвращает сумму данного набора данных, деленную на его длину.
  • Функция sum() возвращает общую сумму (по иронии судьбы) значений итерируемого объекта, в данном случае списка. Попробуйте передать набор данных в качестве аргумента, он вернет 211
  • Функция len() возвращает длину итерации, если вы передадите ей набор данных, вы получите 8
• Мы передаем возраст баскетбольной команды в функцию mean() и печатаем результат.

Если вы проверите вывод, вы получите:

26.375
# Because 211 / 8 = 26.375

Этот результат представляет собой средний возраст игроков баскетбольной команды. Обратите внимание, что число не появляется в наборе данных, но точно описывает возраст большинства игроков.

Использование mean() из статистического модуля Python

Вычисление показателей центральной тенденции является обычной операцией для большинства разработчиков. Это потому что Статистика Python модуль предоставляет различные функции для их расчета, а также другие основные темы статистики.

Поскольку это часть Стандартная библиотека Python вам не нужно будет устанавливать какой-либо внешний пакет с PIP.

Вот как вы используете этот модуль:

from statistics import mean

pythonic_machine_ages = [19, 22, 34, 26, 32, 30, 24, 24]

print(mean(pythonic_machine_ages))

В приведенном выше коде вам просто нужно импортировать функцию mean() из модуля статистики и передать ей набор данных в качестве аргумента. Это вернет тот же результат, что и пользовательская функция, которую мы определили в предыдущем разделе:

26.375

Теперь у вас есть кристально ясное понятие среднего, давайте продолжим измерение медианы.

Нахождение медианы в Python

медиана является средним значением отсортированного набора данных. Он используется — опять же — для предоставления «типичного» значения определенного Население.

В программировании мы можем определить медиану как значение, которое разделяет последовательность на две части — нижнюю половину и верхнюю половину.

Чтобы вычислить медиану, сначала нам нужно отсортировать набор данных. Мы могли бы сделать это с помощью алгоритмов сортировки или с помощью встроенной функции sorted(). Второй шаг — определить, является ли длина набора данных четной или нечетной. В зависимости от этого некоторые из следующих процессов:

• Нечетный: медиана — это среднее значение набора данных.
• Четное: медиана представляет собой сумму двух средних значений, деленную на два.

Продолжая работу с набором данных нашей баскетбольной команды, давайте рассчитаем средний рост игроков в сантиметрах:

[181, 187, 196, 196, 198,  203, 207, 211, 215]
# Since the dataset is odd, we select the middle value
median = 198

Как видите, поскольку длина набора данных нечетная, мы можем взять среднее значение в качестве медианы. Однако что произойдет, если игрок только что вышел на пенсию?

Нам нужно будет вычислить медиану, взяв два средних значения набора данных.

[181, 187, 196, 198, 203, 207, 211, 215] 
# We select the two middle values, and divide them by 2
median = (198 + 203) / 2
median = 200.5

Создание пользовательской медианной функции

Давайте реализуем описанную выше концепцию в функции Python.

Помните три шага, которые нам нужно выполнить, чтобы получить медиану набора данных:

• Сортировка набора данных: мы можем сделать это с помощью функции sorted()
• Определите, является ли он нечетным или четным: мы можем сделать это, получив длину набора данных и используя оператор по модулю (%)
• Верните медиану на основе каждого случая:
  • Нечетный: вернуть среднее значение
  • Даже: возвращает среднее значение двух средних значений.

Это приведет к следующей функции:

pythonic_machines_heights = [181, 187, 196, 196, 198, 203, 207, 211, 215]
after_retirement = [181, 187, 196, 198, 203, 207, 211, 215]

def median(dataset):
    data = sorted(dataset)
    index = len(data) // 2
    
    # If the dataset is odd  
    if len(dataset) % 2 != 0:
        return data[index]
    
    # If the dataset is even
    return (data[index - 1] + data[index]) / 2

Печать результата наших наборов данных:

print(median(pythonic_machines_heights))
print(median(after_retirement))

Выход:

198
200.5

Обратите внимание, как мы создаем переменную данных, которая указывает на отсортированную базу данных в начале функции. Хотя приведенные выше списки отсортированы, мы хотим создать повторно используемую функцию, поэтому набор данных будет сортироваться при каждом вызове функции.

Индекс сохраняет среднее значение — или верхне-среднее значение — набора данных с помощью оператора целочисленного деления. Например, если бы мы передавали список «pythonic_machine_heights», он имел бы значение 4.

Помните, что в Python индексы последовательности начинаются с нуля, потому что мы можем вернуть средний индекс списка с целочисленным делением.

Затем мы проверяем, является ли длина набора данных нечетной, сравнивая результат операции по модулю с любым значением, отличным от нуля. Если условие истинно, мы возвращаем средний элемент, например, со списком «pythonic_machine_heights»:

>>> pythonic_machine_heights[4]
# 198

С другой стороны, если набор данных четный, мы возвращаем сумму средних значений, деленную на два. Обратите внимание, что данные[index -1] дает нам нижнюю среднюю точку набора данных, а данные[index] дает нам верхнюю среднюю точку.

Использование median() из статистического модуля Python

Этот способ намного проще, потому что мы используем уже существующую функцию из модуля статистики.

Лично для меня, если бы что-то уже было определено, я бы использовал это из-за принципа DRY — Don’t Repeat Yourself (в данном случае — не повторять чужой код).

Вы можете вычислить медиану предыдущих наборов данных с помощью следующего кода:

from statistics import median

pythonic_machines_heights = [181, 187, 196, 196, 198, 203, 207, 211, 215]
after_retirement = [181, 187, 196, 198, 203, 207, 211, 215]

print(median(pythonic_machines_heights))
print(median(after_retirement))

Выход:

198
200.5

Вычисление режима в Python

Режим является наиболее часто встречающимся значением в наборе данных. Мы можем думать об этом как о «популярной» группе школы, которая может представлять собой стандарт для всех учащихся.

Примером режима могут быть ежедневные продажи в магазине техники. Режим этого набора данных будет самым продаваемым продуктом за определенный день.

['laptop', 'desktop', 'smartphone', 'laptop', 'laptop', 'headphones']

Как вы понимаете, режим приведенного выше набора данных — «ноутбук», потому что это наиболее часто встречающееся значение в списке.

Преимущество режима в том, что набор данных не должен быть числовым. Например, мы можем работать со строками.

Проанализируем продажи другого дня:

['mouse', 'camera', 'headphones', 'usb', 'headphones', 'mouse']

Приведенный выше набор данных имеет два режима: «мышь» и «наушники», потому что оба имеют частоту, равную двум. Это означает, что это мультимодальный набор данных.

Что, если мы не сможем найти моду в наборе данных, как показано ниже?

['usb', 'camera', 'smartphone', 'laptop', 'TV']

Это называется равномерное распределениепо сути, это означает, что в наборе данных нет моды.

Теперь, когда вы быстро разобрались с концепцией режима, давайте посчитаем его в Python.

Создание функции пользовательского режима

Мы можем думать о частоте значения как о паре ключ-значение, другими словами, как о словаре Python.

Повторяя аналогию с баскетболом, мы можем использовать два набора данных для работы: количество очков за игру и спонсорство кроссовок некоторых игроков.

Чтобы сначала найти моду, нам нужно создать словарь частот с каждым из значений, присутствующих в наборе данных, затем получить максимальную частоту и вернуть все элементы с этой частотой.

Переведем это в код:

points_per_game = [3, 15, 23, 42, 30, 10, 10, 12]
sponsorship = ['nike', 'adidas', 'nike', 'jordan',
               'jordan', 'rebook', 'under-armour', 'adidas']

def mode(dataset):
    frequency = {}

    for value in dataset:
        frequency[value] = frequency.get(value, 0) + 1

    most_frequent = max(frequency.values())

    modes = [key for key, value in frequency.items()
                      if value == most_frequent]

    return modes

Проверка результата с передачей двух списков в качестве аргументов:

print(mode(points_per_game))
print(mode(sponsorship))

Выход:

[10]
['nike', 'adidas', 'jordan']

Как видите, первый оператор печати дал нам один режим, а второй вернул несколько режимов.

Объяснение более глубокого кода выше:

• Объявляем частотный словарь
• Мы перебираем набор данных, чтобы создать гистограмма — статистический термин для набора счетчиков (или частот) —
  • Если ключ найден в словаре, то он добавляет единицу к значению
  • Если он не найден, мы создаем пару ключ-значение со значением один
• Переменная most_frequent хранит, по иронии судьбы, самое большое значение (не ключ) частотного словаря.
• Мы возвращаем переменную режимов, которая состоит из всех ключей в частотном словаре с наибольшей частотой.

Обратите внимание, как важно именовать переменные для написания читаемого кода.

Использование режима() и мультимода() из статистического модуля Python

И снова модуль статистики предоставляет нам быстрый способ выполнения основных операций со статистикой.

Мы можем использовать две функции: Режим() а также многомодовый().

from statistics import mode, multimode

points_per_game = [3, 15, 23, 42, 30, 10, 10, 12]
sponsorship = ['nike', 'adidas', 'nike', 'jordan',
               'jordan', 'rebook', 'under-armour', 'adidas']

Приведенный выше код импортирует обе функции и определяет наборы данных, с которыми мы работали.

Вот небольшое отличие: функция mode() возвращает первый обнаруженный режим, а multimode() возвращает список с наиболее часто встречающимися значениями в наборе данных.

Следовательно, мы можем сказать, что пользовательская функция, которую мы определили, на самом деле является функцией multimode().

print(mode(points_per_game))
print(mode(sponsorship))

Выход:

10
nike

Примечание. В Python 3.8 и более поздних версиях функция mode() возвращает первый найденный режим. Если у вас более старая версия, вы получите СтатистикаОшибка.

Использование функции multimode():

print(multimode(points_per_game))
print(multimode(sponsorship))

Выход:

[10]
['nike', 'adidas', 'jordan']

Подводить итоги

Поздравляем! Если вы дочитали до этого момента, вы научились вычислять среднее значение, медиану и моду, основные измерения центральной тенденции.

Хотя вы можете определить свои пользовательские функции для поиска среднего значения, медианы и моды, рекомендуется использовать модуль статистики, так как он является частью стандартной библиотеки, и вам не нужно ничего устанавливать, чтобы начать его использовать.

Затем прочитайте дружественное введение в анализ данных в Python.