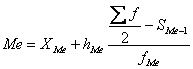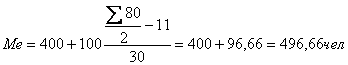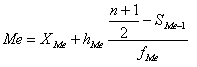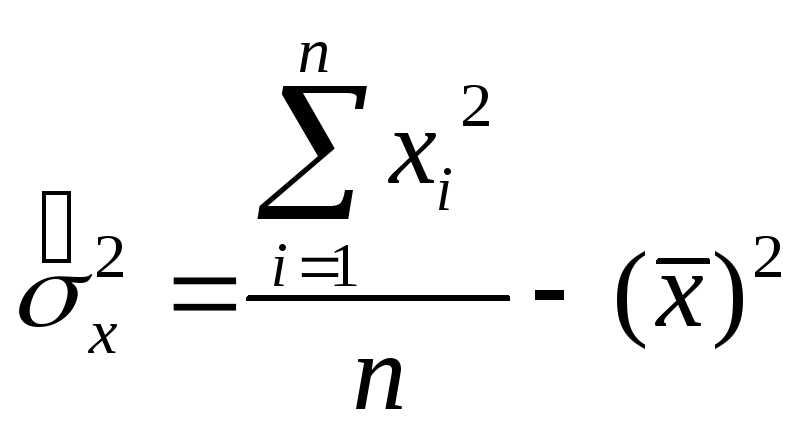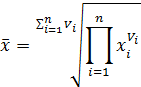ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4.
Расчёт структурных характеристик
вариационного ряда распределения.
Студент
должен:
знать:
– область применения и методику расчёта структурных
средних величин;
уметь:
– исчислять структурные средние величины;
– формулировать вывод по полученным результатам.
Методические указания
В
статистике исчисляются мода и медиана, которые относятся к структурным средним,
так как их величина зависит от строения статистической совокупности.
Расчёт моды
Модой называется значение признака
(варианта), чаще всеговстречающееся в изучаемой
совокупности. В дискретном ряду распределения модой будет варианта с наибольшей
частотой.
Например: Распределение проданной женской обуви по размерам характеризуется
следующим образом:
|
Размер |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
|
Количество |
8 |
19 |
34 |
108 |
72 |
51 |
6 |
2 |
В этом ряду
распределения модой является 37 размер,
т.е. Мо=37 размер.
Для
интервального ряда распределения мода определяется по формуле:
где ХMo –
нижняя граница модального интервала;
hMo – величина модального интервала;
fMo –
частота модального интервала;
fMo–1 и
fMo+1 – частота интервала соответственно
предшествующего модальному и следующего за ним.
Например:
Распределение рабочих по стажу работы характеризуется следующими данными.
|
Стаж работы, лет |
до 2 |
2-4 |
4-6 |
6-8 |
8-10 |
10 и более |
|
Число рабочих, чел. |
4 |
23 |
20 |
35 |
11 |
7 |
Определить моду
интервального ряда распределения.
Мода интервального ряда составляет
Мода всегда бывает
несколько неопределённой, т.к. она зависит от величины групп и точного
положения границ групп. Мода широко применяется в коммерческой практике при
изучении покупательского спроса, при регистрации цен и т.п.
Расчёт медианы
Медианой в статистике называется варианта,
расположенная в середине упорядоченного ряда данных, и которая делит
статистическую совокупность на две равные части так, что у одной половины
значения меньше медианы, а у другой половины – больше её. Для определения
медианы необходимо построить ранжированный ряд, т.е. ряд в порядке возрастания
или убывания индивидуальных значений признака.
В дискретном
упорядоченном ряду с нечётным числом членов медианой будет варианта,
расположенная в центре ряда.
Например: Стаж пяти рабочих составил 2, 4, 7, 9 и 10 лет. В таком ряду медиана-7
лет, т.е. Ме=7 лет
Если дискретный
упорядоченный ряд состоит из чётного числа членов, то медианой будет средняя
арифметическая из двух смежных вариант, стоящих в центре ряда.
Например: Стаж работы шести рабочих составил 1, 3, 4, 5, 10 и 11лет. В этом ряду
имеются две варианты, стоящие в центре ряда. Это варианты 4 и 5. Средняя
арифметическая из этих значений и будет медианой ряда
Чтобы определить медиану для
сгруппированных данных, необходимо считать накопленные частоты.
Например: По имеющимся данным определим медиану размера обуви
|
Размер обуви |
Количество проданных пар |
Сумма накопленных частот |
|
34 |
8 |
8 |
|
35 |
19 |
8+19=27 |
|
36 |
34 |
27+34=61 |
|
37 |
108 |
61+108=169 |
|
38 |
72 |
– |
|
39 |
51 |
– |
|
40 |
6 |
– |
|
41 |
2 |
– |
|
Итого |
300 |
Для
определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание
итога продолжается до получения накопленной суммы частот, превышающей половину суммы частот
ряда. В нашем примере сумма частот составила 300, её половина – 150. Накопленная
сумма частот получилась равной 169. Варианта, соответствующая этой сумме, т.е.
37 и есть медиана ряда.
Если
же сумма накопленных частот против одной из вариант равна точно половине суммы
частот ряда, то медиана определяется как средняя арифметическая этой варианты и
последующей.
Например: По имеющимся данным определим медиану заработной платы рабочих
|
Месячная заработная плата, тыс.руб. |
Число рабочих, чел. |
Сумма накопленных частот |
|
14,0 |
2 |
2 |
|
14,2 |
6 |
2+6=8 |
|
16,0 |
12 |
8+12=20 |
|
16,8 |
16 |
– |
|
18,0 |
4 |
– |
|
Итого: |
40 |
– |
Медиана будет равна:
Медиана
интервального вариационного ряда распределения определяется по формуле:
Где ХМе – нижняя граница медианного интервала;
hMe –
величина медианного интервала;
∑f
– сумма частот ряда;
fМе – частота медианного интервала;
Например: По имеющимся данным о распределении предприятий по численности
промышленно – производственного персонала рассчитать медиану в интервальном
вариационном ряду
|
Группы предприятий по численности ППП, чел. |
Число предприятий |
Сумма накопленных частот |
|
100-200 |
1 |
1 |
|
200-300 |
3 |
1+3=4 |
|
300-400 |
7 |
4+7=11 |
|
400-500 |
30 |
11+30=41 |
|
500-600 |
19 |
– |
|
600-700 |
15 |
– |
|
700-800 |
5 |
|
|
Итого: |
80 |
Определим, прежде всего,
медианный интервал. В данном примере сумма накопленных частот, превышающих половину
суммы всех значений ряда, соответствует интервалу 400-500.Это и есть медианный
интервал, т.е. интервал, в котором находится медиана ряда. Определим её
значение
Если же сумма накопленных частот
против одного из интервалов равна точно половине суммы частот ряда, то медиана
определяется по формуле:
где n – число
единиц в совокупности.
Например: По имеющимся данным о распределении предприятий по
численности промышленно – производственного персонала рассчитать медиану в
интервальном вариационном ряду
|
Группы предприятий по численности ППП, чел. |
Число предприятий |
Сумма накопленных частот |
|
100-200 |
1 |
1 |
|
200-300 |
3 |
1+3=4 |
|
300-400 |
6 |
4+6=10 |
|
400-500 |
30 |
10+30=40 |
|
500-600 |
20 |
40+20=60 |
|
600-700 |
15 |
– |
|
700-800 |
5 |
|
|
Итого: |
80 |
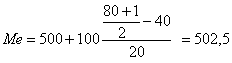
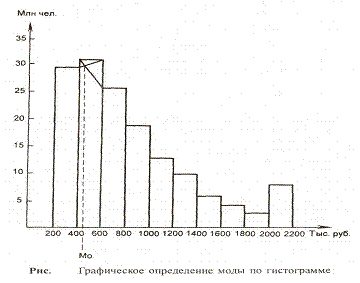
Моду и медиану в
интервальном ряду можно определить
графически:
моду
в дискретных рядах – по полигону распределения, моду в интервальных рядах – по
гистограмме распределения, а медиану – по кумуляте.
Мода интервального ряда распределения
определяется по гистограмме распределения определяют
следующим образом. Для этого выбирается самый высокий прямоугольник, который
является в данном случае модальным. Затем правую вершину модального
прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения.
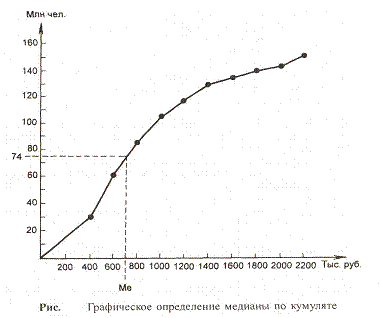
Медиана рассчитывается по
кумуляте. Для её определения из точки на шкале
накопленных частот (частостей), соответствующей 50%,
проводится прямая, параллельная оси абсцисс, до
пересечения с кумулятой. Затем из точки пересечения
указанной прямой с кумулятой опускается перпендикуляр
на ось абсцисс. Абсцисса точки пересечения является медианой.
Кроме моды и медианы в вариантных рядах могут быть
определены и другие структурные характеристики – квантили. Квантили
предназначены для более глубокого изучения структуры ряда распределения.
Квантиль – это значение
признака, занимающее определенное место в упорядоченной по данному признаку
совокупности. Различают следующие виды квантилей:
– квартили – значения признака, делящие упорядоченную
совокупность на четыре
равные части;
– децили
– значения признака, делящие упорядоченную совокупность на десять
равных частей;
– перцентели –
значения признака, делящие упорядоченную совокупность на сто равных частей.
Таким образом, для характеристики положения центра ряда распределения
можно использовать 3 показателя: среднее значение признака, мода, медиана. При выборе вида и формы конкретного показателя
центра распределения необходимо исходить из следующих рекомендаций:
–
для устойчивых социально-экономических
процессов в качестве показателя центра используют среднюю
арифметическую. Такие процессы характеризуются симметричными распределениями, в
которых ;
–
для неустойчивых процессов положение
центра распределения характеризуется с помощью Mo
или Me. Для асимметричных процессов предпочтительной
характеристикой центра распределения является медиана, поскольку занимает
положение между средней арифметической и модой.
Аннотация: Для получения более полной характеристики вариационного ряда помимо средней величины рассчитываются так называемые структурные показатели. К ним относятся мода, медиана, квартили, децили, перцентили, квартильные и децильные коэффициенты.
8.1. Мода
Мода (Мо) – это наиболее часто встречающееся значение признака, или иначе говоря, значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по-разному.
8.1.1. Определение моды в дискретных вариационных рядах
В дискретных вариационных рядах для определения моды не требуется специальных вычислений: значение признака, которому соответствует наибольшая частота, и будет значением моды.
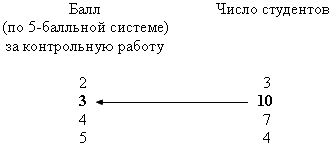
Пример 8.1. По представленным ниже результатам проведения контрольной работы по статистике определим моду.
Здесь наибольшая частота – 10, она принадлежит варианте со значением 3, значит, Мо = 3. Таким образом, самой распространенной оценкой, полученной студентами за контрольную работу, была “тройка”.
8.1.2. Определение моды в интервальных вариационных рядах с равными интервалами
Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем ведут расчет по формуле
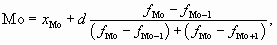
где хМо – нижняя граница модального интервала;
d – величина интервала;
fMo – частота модального интервала;
fMo – 1 – частота интервала, предшествующего модальному;
fMo + 1 – частота интервала, следующего за модальным.
Пример 8.2. Имеются данные по группе банков.
| Сумма выданных кредитов, млн ден. ед. | Количество банков |
|---|---|
| До 40 | 8 |
| 40-60 | 15 |
| 60-80 | 21 |
| 80-100 | 12 |
| 100-120 | 9 |
| 120-140 | 7 |
| 140 и выше | 4 |
| Итого | 77 |
Определим модальный размер выданных кредитов:
- модальным является интервал 60-80, так как ему соответствует наибольшая частота (21);
- нижняя граница модального интервала xМо = 60; величина интервала d = 20 (80 – 60 = 20);
- частота модального интервала fМо = 21; частота интервала, предшествующего модальному, fМо – 1 = 15; частота интервала, следующего за модальным, fМо + 1 = 12.
Подставив в формулу соответствующие величины, получим
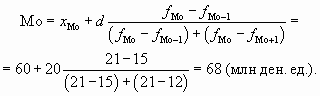
Определить модальное значение признака можно и по графику. Для этого в случае дискретных вариационных рядов строится полигон распределения. Напомним, что у него на оси абсцисс помещаются значения признака (варианты), а на оси ординат – соответствующие им частоты. Значение абсциссы, соответствующее наибольшей вершине полигона, будет значением моды.
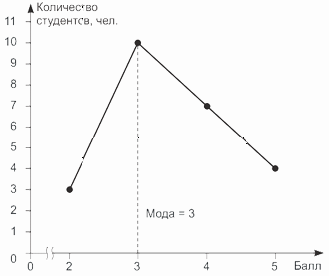
Пример 8.3. По результатам проведения контрольной работы по статистике, приведенным в примере 8.1, определим моду графическим способом.
Для этого построим полигон распределения и найдем абсциссу его вершины (рис. 8.1).
Рис.
8.1.
Определение моды по полигону распределения
Если имеется интервальный вариационный ряд с равными интервалами, то для определения моды строится гистограмма, у которой на оси абсцисс находятся значения границ интервалов, а на оси ординат – соответствующие интервалам частоты. На гистограмме модальный интервал будет иметь наибольшую высоту столбца. Затем надо провести линии, соединяющие вершины модального столбца с прилегающими вершинами соседних столбцов. Для нахождения значения моды из точки пересечения проведенных линий на ось абсцисс опускают перпендикуляр. Абсцисса точки пересечения будет значением моды. Продемонстрируем это на примере.
Пример 8.4. По данным о распределении банков по сумме выданных кредитов, приведенным в примере 8.2, определим моду графическим способом (рис. 8.2).
Рис.
8.2.
Определение моды по гистограмме распределения
Вариационный ряд может содержать несколько модальных значений. Чаще всего это происходит, когда в один ряд объединяют разнородные единицы наблюдения, которые желательно разделить на подгруппы и анализировать по отдельности. Вариационный ряд, имеющий одну моду, называется унимодальным, две – бимодальным, три и более – мультимодальным.
Дискретный вариационный ряд и его характеристики
- Классификация рядов распределения
- Дискретный вариационный ряд, полигон частот и кумулята
- Выборочная средняя, мода и медиана
- Степень асимметрии вариационного ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования дискретного вариационного ряда
- Примеры
п.1. Классификация рядов распределения
Статистический ряд распределения – это количественное распределение единиц совокупности на однородные группы по некоторому варьирующему признаку.
В зависимости от природы признака различают атрибутивные и вариационные ряды.
Атрибутивный ряд распределения построен на качественном признаке.
Вариационный ряд распределения построен на количественном признаке.
Например:
Качественными признаками, которые не поддаются измерению, являются: профессия, пол, национальность и т.п.
Количественными признаками, которые можно подсчитать или измерить, являются: количество людей в группе, число повторений в опыте, возраст, вес, рост, скорость, температура и т.п.
По упорядоченности вариационные ряды делятся на упорядоченные (ранжированные) и неупорядоченные. Упорядочить ряд можно по возрастанию или убыванию исследуемого признака.
По характеру непрерывности признака вариационные ряды делятся на дискретные и интервальные.
Например:
Дискретными признаками, которые принимают отдельные значения, являются: количество людей в группе, число детей в семье, количество домов, число опытов и т.п.
Непрерывными признаками, которые могут принимать любые значения в интервале, являются: возраст, вес, рост, скорость, температура и т.п.
Варианты – это отдельные значения признака, которые он принимает в вариационном ряду.
Частоты – это численности отдельных вариант.
Например:
Распределение учеников по оценкам за контрольную работу
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
В данном ряду признак – это оценка, варианты признака (x_i) – это множество {2;3;4;5}, частоты (f_i) – это количество учеников, получивших каждую из оценок.
п.2. Дискретный вариационный ряд, полигон частот и кумулята
Дискретный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся прерывно и принимающему конечное множество значений.
Общий вид дискретного вариационного ряда
| Варианты, (x_i) | (x_1) | (x_2) | … | (x_k) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k – число вариант исследуемого признака.
Тогда общее количество исходов (число единиц в совокупности): (N=sum_{i=1}^k f_i)
Полигон частот – это ломаная, которая соединяет точки ((x_i,f_i)).
Например:
| Для распределения учеников по оценкам из нашего примера получаем такой полигон: |  |
Относительная частота варианты (x_i) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$ Относительная частота (w_i) является эмпирической оценкой вероятности варианты (x_i) в исследуемом ряду.
Полигон относительных частот – это ломаная, которая соединяет точки ((x_i,w_i)).
Полигон относительных частот является эмпирическим законом распределения исследуемого признака.
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)).
Ступенчатая кривая (F(x_i)), построенная по точкам ((x_i,S_i)), является эмпирической функцией распределения исследуемого признака.
Например:
Проведем необходимые расчеты и построим полигон относительных частот, кумуляту и эмпирическую функцию распределения учеников по оценкам.
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
| (w_i) | 0,0909 | 0,4545 | 0,3030 | 0,1515 | 1 |
| (S_i) | 0,0909 | 0,4545 | 0,8485 | 1 | – |
Полигон относительных частот (эмпирический закон распределения)
Кумулята (красная ломаная) и эмпирическая функция распределения (ступенчатая синяя кривая).
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 2\ 0,0909, 2lt xleq 3\ 0,5455, 3lt xleq 4\ 0,8485, 4lt xleq 5\ 1, xgt 5 end{cases} $$
п.3. Выборочная средняя, мода и медиана
Выборочная средняя дискретного вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Мода дискретного вариационного ряда – это варианта с максимальной частотой: $$ M_o=x*, f(x*)=underset{i=overline{1,k}}{max}f_i $$ Мод может быть несколько. Тогда говорят, что ряд мультимодальный.
На полигоне частот мода – это абсцисса самой высокой точки.
Медиана дискретного вариационного ряда – это значение варианты посредине упорядоченного ряда.
Алгоритм:
1. Отсортировать ряд по возрастанию.
2а. Если общее количество измерений N нечётное, найти (m=lceilfrac N2rceil) и округлить в сторону увеличения. (M_e=x_m) – искомая медиана.
2б. Если общее количество измерений N чётное, найти (m=frac N2) и вычислить медиану как среднее (M_e=frac{x_m+x_{m+1}}{2}).
На графике кумуляты медиана – это абсцисса первой точки слева, ордината которой превысила 0,5.
Например:
1) Найдем выборочную среднюю для распределения учеников по оценкам:
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
| (x_if_i) | 6 | 45 | 40 | 25 | 116 |
$$ X_{cp}=frac{6+45+40+25}{33}=frac{116}{33}approx 3,5 $$ Средняя оценка за контрольную – 3,5.
2) Найдем моду. Максимальная частота – 15 человек – у троечников. Значит: (M_o=3).
3) Найдем медиану. Общее количество измерений N=33 – нечетное.
Находим: (m=lceilfrac N2rceil=17)
Смотрим на ряд слева направо. Сначала у нас идет 3 двоечника, затем 15 троечников.
Вместе их 18, и 17-й человек в ряду – троечник. Группа троечников является медианной: (M_e=3).
Также, медиану можно найти по графику кумуляты. (3;0,5455) – это первая слева точка, в которой ордината больше 0,5. Значит, медиана равна абсциссе этой точки, т.е. (M_e=3).
п.4. Степень асимметрии вариационного ряда
В рядах с асимметрией или выбросами выборочная средняя не отражает в полной мере особенности исследуемого признака. Типичный случай – значение среднего уровня доходов в странах с высоким индексом Джини, где 5% населения получает 95% доходов. Или анекдотичный случай со «средней температурой по больнице».
Поэтому, кроме средней, в статистическом исследовании всегда следует определять моду и медиану.
Мода, медиана и выборочная средняя совпадут, если вариационный ряд является симметричным: $$ X_{cp}=M_o=M_e $$ Если вершина распределения сдвинута влево и правая часть ветви длиннее левой (длинный правый хвост), такая асимметрия называется правосторонней. При правосторонней асимметрии: $$ M_olt M_elt X_{cp} $$ Если вершина распределения сдвинута вправо и левая часть ветви длиннее правой (длинный левый хвост), такая асимметрия называется левосторонней. При левосторонней асимметрии: $$ M_ogt M_egt X_{cp} $$ Для умеренно асимметричных рядов (по Пирсону) модуль разности между модой и средней не более 3 раз превышает модуль разности между медианой и средней: $$ frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}geq 3 $$
Например:
Для распределения учеников по оценкам мы получили (X_{cp}=3,5; M_o=3; M_e=3).
Т.к. средняя оказалась больше моды и медианы, наше распределение имеет правостороннюю асимметрию (что видно на полигоне частот – правый хвост длиннее).
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{0,5}{0,5}=1lt 3), т.е. распределение умеренно асимметрично.
п.5. Выборочная дисперсия и СКО
Выборочная дисперсия дискретного вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac{(x_1-X_{cp})^2 f_1+(x_2-X_{cp})^2 f_2+…+(x_k-X_{cp})^2 f_k}{N}=\ =frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
1) Найдем выборочную дисперсию для распределения учеников по оценкам:
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
| (x_i^2) | 4 | 9 | 16 | 25 | – |
| (x_i^2 f_i) | 12 | 135 | 160 | 125 | 432 |
$$ D=frac{12+135+160+125}{33}-3,5^2=frac{432}{33}-3,5^2approx 0,73 $$ 2) Значение СКО: (sigma=sqrt{D}approx 0,86)
п.6. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия дискретного вариационного ряда определяется как: begin{gather*} S^2=frac{1}{N-1}sum_{i=1}^k(x_i-X_{cp})^2 f_i=frac{N}{N-1}D end{gather*}
В теоретической статистике доказывается, что выборочная дисперсия D является смещенной оценкой дисперсии при распространении на генеральную совокупность.
А именно, выборочная дисперсия D всегда меньше математического ожидания для дисперсии генеральной совокупности.
Исправленная выборочная дисперсия S2 является несмещенной оценкой.
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Если показатель вариации V<33%, то выборка считается однородной, т.е. большинство полученных в ней вариант находятся недалеко от средней, и выборочная средняя хорошо характеризует среднюю генеральной совокупности.
В противном случае, выборка неоднородна. Варианты в выборке находятся далеко от средней, есть выбросы. А значит, и в генеральной совокупности они возможны. Т.е., распространять результаты выборки на генеральную совокупность нельзя.
Если исследуется не выборка, а вся генеральная совокупность, дисперсию «исправлять» не нужно.
Например:
Для распределения учеников по оценкам получаем:
1) Исправленная выборочная дисперсия $$ S^2=frac{N}{N-1}D=frac{33}{32}cdot 0,73approx 0,76 $$ 2) Стандартное отклонение $$ x=sqrt{S^2}approx 0,87 $$ 3) Коэффициент вариации: $$ V=frac{0,87}{3,5}cdot 100text{%}approx 24,8text{%}lt 33text{%} $$ Выборка является однородной.
Это означает, что согласно коэффициенту вариации полученные результаты контрольной работы можно рассматривать в качестве «типичных» и распространить их на генеральную совокупность, т.е. на всех школьников, которые будут писать эту работу.
п.7. Алгоритм исследования дискретного вариационного ряда
На входе: таблица с вариантами (x_i) и частотами (f_i, i=overline{1,k})
Шаг 1. Составить расчетную таблицу. Найти (w_i,S_i,x_if_i,x_i^2,x_i^2f_i)
Шаг 2. Построить полигон относительных частот (эмпирический закон распределения) и график кумуляты с эмпирической функцией распределения. Записать эмпирическую функцию распределения.
Шаг 3. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 4. Найти выборочную дисперсию и СКО.
Шаг 5. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.8. Примеры
Пример 1. На площадке фриланса была проведена выборка из 100 фрилансеров и подсчитано количество постоянных заказчиков, с которыми они работают.
В результате было получено следующее распределение:
| Число постоянных заказчиков | 0 | 1 | 2 | 3 | 4 | 5 |
| Число фрилансеров | 22 | 35 | 27 | 11 | 3 | 1 |
Исследуйте полученный вариационный ряд.
1) Вариационный ряд является дискретным.
Исследуемый признак – «число постоянных заказчиков».
Варианты признака (x_iinleft{0;1;..;5right}). Количество вариант k=6.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | ∑ |
| (f_i) | 23 | 35 | 27 | 11 | 3 | 1 | 100 |
| (w_i) | 0,23 | 0,35 | 0,27 | 0,11 | 0,03 | 0,01 | – |
| (S_i) | 0,23 | 0,58 | 0,85 | 0,96 | 0,99 | 1 | – |
| (x_if_i) | 0 | 35 | 54 | 33 | 12 | 5 | 139 |
| (x_i^2) | 0 | 1 | 4 | 9 | 16 | 25 | – |
| (x_i^2f_i) | 0 | 35 | 108 | 99 | 48 | 25 | 315 |
2) Полигон относительных частот (эмпирический закон распределения):
Кумулята и эмпирическая функция распределения:
$$ F(x)= begin{cases} 0, xleq 0\ 0,23, 0lt xleq 1\ 0,58, 1lt xleq 2\ 0,85, 2lt xleq 3\ 0,96, 3lt xleq 4\ 0,99, 4lt xleq 5\ 1, xgt 5 end{cases} $$ 3) Выборочная средняя: $$ X_{cp}=frac1Nsum_{i=1}^k x_if_i= frac{1}{100}cdot 139=1,39 $$ Мода (абсцисса самой высокой точки на полигоне частот): (M_0=1).
Медиана (абсцисса первой слева точки на кумуляте, где значение превысило 0,5): точка (1;0,58), (M_e=1).
(X_{cp}gt M_e=M_0) – распределение асимметрично, с правосторонней асимметрией.
При этом (frac{|M_0-X_{cp}|}{|M_e-X_{cp}|}=frac{0,39}{0,39}=1lt 3), т.е. распределение умеренно асимметрично.
4) Выборочная дисперсия: $$ D=frac1Nsum_{i=1}^k x_i^2f_i-X_{cp}^2=frac{1}{100}cdot 315-1,39^2=1,2179approx 1,218 $$ CKO: $$ sigma=sqrt{D}approx 1,104 $$
5) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{100}{99}cdot 1,218approx 1,230 $$ Стандартное отклонение выборки: $$ s=sqrt{S^2}approx 1,109 $$ Коэффициент вариации: $$ V=frac{s}{X_{cp}}cdot 100text{%}=frac{1,109}{1,39}cdot 100text{%}approx 79,8text{%}gt 33text{%} $$ Представленная выборка неоднородна. Полученное значение средней (X_{cp}=1,39) не может быть распространено на генеральную совокупность всех фрилансеров.
-
Вариационный ряд, полигон и гистограмма
Рядами
распределения
называются числовые ряды, характеризующие
структуру совокупности по некоторому
признаку. Ряд распределения может быть
получен в результате структурной
группировки. Ряд распределения,
образованный по количественному признаку
(вариационный
ряд), может
быть дискретным (признак принимает
ограниченное число возможных значений,
например 2,3,4,5) или интервальным (значения
признака выражены вещественными числами
или число возможных значений признака
достаточно велико).
Характеристиками
ряда являются:
xi
− варианта
(отдельное возможное численное значение
признака)
(i=1,k);
ni
− частота
(численность отдельных групп);
n
− общее число элементов совокупности;
qi
−
частость
(доля отдельных групп во всей совокупности).
Вариационный ряд
оформляется в виде таблицы, где в первой
графе указываются варианты (интервалы)
значений признака, а в следующих −
частота и частость.
Ряд распределения
в целом характеризует структуру
совокупности по данному признаку. Однако
могут использоваться и кумулятивные
ряды, т.е. ряды накопленных частот
(частостей).
Накопленная
частота (частость)
− это число (доля) элементов совокупности,
у которых значения признака не превышают
данного.
Обозначим
F(x)
− накопленная частота для данного
значения x;
G(x)
− накопленная частость для данного
значения x.
Эти характеристики
обладают следующими свойствами:
Рассмотрим
интервал с номером i
: [xi
xi+1]
Накопленная
частота на конец i-го
интервала определяется по формуле
Вариационный ряд
можно изобразить в виде графика.
Изображением
дискретного ряда является полигон.
При его построении по оси абсцисс
откладываются варианты (xi),
а по оси ординат − частоты или частости
− fi.
Затем точки с координатами (xi;fi)
последовательно соединяются отрезками
прямой.
Изображением
интервального ряда является гистограмма.
При ее построении по оси абсцисс
откладываются интервалы ряда. Над осью
абсцисс строится прямоугольник,
основанием которого является интервал,
а высотой − значение частоты или
частости.
Изображением ряда
накопленных частот является кумулята.
Накопленные частоты откладываются по
оси ординат для границ интервалов и
соединяются отрезками прямых.
Пример
1. Распределение
квартир дома по числу жителей приведено
в таблице. Построить полигон и кумуляту.
|
Число живущих в xi |
Число квартир (частота) ni |
Накопленная Fi |
|
1 |
2 |
2 |
|
2 |
3 |
5 |
|
3 |
10 |
15 |
|
4 |
23 |
38 |
|
5 |
9 |
47 |
|
6 |
2 |
49 |
|
7 |
1 |
50 |
|
ВСЕГО |
50 |
Пример
2. Распределение
банков по степени риска приведено в
таблице. Построить гистограмму и
кумуляту.
|
Степень |
Доля банков (частость) qi |
Накопленная Gi |
|
0-10 |
0,61 |
0,61 |
|
10-20 |
0,04 |
0,65 |
|
20-30 |
0,35 |
1,00 |
|
ВСЕГО |
1,00 |
-
СТАТИСТИЧЕСКИЕ
ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ
-
Средняя
арифметическая
-
для несгруппированных
данных

-
для сгруппированных
данных

где xi
−варианта
или середина интервалаi-й
группы;
ni
− частота i-й
группы;
k
− количество групп.
-
Медиана
Ме(x)
Медиана представляет
собой такое значение признака, которое
делит объем совокупности пополам в том
смысле, что число элементов совокупности
со значениями признака, меньшими медианы,
равно числу элементов совокупности со
значениями признака, большими медианы.
Численное значение
медианы можно определить по ряду
накопленных частот. Накопленная частота
для медианы равна половине объема
совокупности:
.
Для интервального
ряда сначала определяется интервал, в
котором будет находиться медиана. Само
же значение Ме(x)
может быть приближенно определено с
помощью интерполяции

где x0
− начало интервала, содержащего медиану;
− величина
интервала, содержащего медиану;
F(x0)
− накопленная частота на начало
интервала, содержащего медиану;
n
− объем совокупности;
n0
− частота
интервала, в котором расположена медиана.
-
Мода
Мо(Х) –
наиболее часто встречающееся значение
признака в совокупности.
Для дискретного
ряда это то значение признака, которому
соответствует наибольшая частота
распределения.
Для интервального
ряда вначале определяется интервал,
содержащий моду (с наибольшей частотой).
Затем приближенно вычисляется значение
моды по формуле
где х0
– начало
интервала, содержащего моду;
− величина
интервала;
n0
– частота интервала, в котором расположена
мода;
n–1
– частота интервала, предшествующего
модальному;
n1
– частота интервала, следующего за
модальным.
-
СТАТИСТИЧЕСКИЕ
ПОКАЗАТЕЛИ ВАРИАЦИИ
-
Выборочная
дисперсия
()
– это среднее
значение квадратов отклонений
индивидуальных значений признака от
средней величины:
– для несгруппированных
данных:

– для
сгруппированных данных

Если ряд интервальный,
то в качестве xi
берется середина i-го
интервала.
Более удобны
следующие формулы вычислений:
(для несгруппированных
данных)
(для сгруппированных
данных),
-
Среднее
квадратическое отклонение
()
представляет
собой квадратный корень из дисперсии
.
Этот показатель
является средним квадратическим
отклонений значений признака от средней.
-
Коэффициент
вариации
характеризует относительную величину
варьируемости признака в данной
совокупности (по отношению к среднему
значению)
.
Пример.
Имеются
сгруппированные данные по зарплате
|
Зарплата, |
Середина |
Частоты |
Накопленные |
|
8,6 |
9,0 |
2 |
2 |
|
9,4 |
9,8 |
6 |
8 |
|
10,2 |
10,6 |
15 |
23 |
|
11,0 |
11,4 |
23 |
46 |
|
11,8 |
12,2 |
25 |
71 |
|
12,6 |
13,0 |
17 |
88 |
|
13,4 |
13,8 |
7 |
95 |
|
14,2 |
14,6 |
5 |
100 |
|
Итого |
100 |
Найдем медиану.
В данном случае
.
Эта величина больше 46, но меньше 71,
следовательно, медиана находится в
интервале (11,8 – 12,6). Рассчитаем ее значение
Найдем
моду по этим данным. Мода находится в
том же интервале, так как максимальная
частота (25) приходится на этот интервал.
.
Средняя
арифметическая
.
Выборочная
дисперсия

Среднее квадратическое
отклонение
Коэффициент
вариации
%.
Задание 2.
-
На основе структурной
группировки по второму показателю,
полученной в задании 1, построить
гистограмму и кумуляту. -
Вычислить по
сгруппированным данным:
-
среднее
арифметическое; -
медиану и моду;
-
дисперсию и среднее
квадратическое отклонение; -
коэффициент
вариации.
-
АБСОЛЮТНЫЕ
И ОТНОСИТЕЛЬНЫЕ СТАТИСТИЧЕСКИЕ
ПОКАЗАТЕЛИ. ВЫЧИСЛЕНИЕ СРЕДНИХ ЗНАЧЕНИЙ
ОТНОСИТЕЛЬНЫХ ПОКАЗАТЕЛЕЙ.
Под абсолютными
показателями в статистике понимают
исходные показатели статистического
наблюдения (объем продукции, количество
населения и т. д.). Они могут быть как
моментными (на определенный момент
времени), так и интервальными (за
определенный период). Любая абсолютная
величина (показатель) имеет присущую
ей единицу измерения (штуки, килограммы,
метры и т. д.). Часто в качестве абсолютных
показателей используют стоимостные
показатели (в рублях).
Под относительными
показателями в статистике понимают
показатели, характеризующие соотношение
двух абсолютных показателей (ВНП на
душу населения, производительность
труда, себестоимость продукции и т. д.).
Различают
относительные величины структуры,
координации, динамики, сравнения и
интенсивности.
Относительные
величины структуры
показывают долю каждой группы в общей
численности совокупности. Их получают
путем деления численности каждой группы
на численность всей совокупности.
Относительные
величины координации
получают как соотношение между частями
одной совокупности. Например, это может
быть отношение числа мужчин к числу
женщин.
Относительные
величины динамики
– это результат сопоставления уровней
одного и того же показателя в разные
моменты или периоды времени. Например,
сопоставляя объем добычи нефти в России
в 2009 г. и 2008 г., получим относительную
величину динамики.
Относительные
величины сравнения
получают в результате сопоставления
двух одноименных показателей, относящихся
к разным совокупностям. Например, при
сравнении величины основных фондов
двух разных регионов.
Относительные
величины интенсивности
получают, сопоставляя разноименные
признаки одной совокупности. Например,
коэффициент рождаемости равен отношению
числа родившихся детей к числу жителей,
а себестоимость продукции равна отношению
полных затрат к объему выпуска продукции.
Для расчета средних
значений относительных величин
используются формулы различных взвешенных
средних в зависимости от экономического
смысла показателей. В статистике
используются различные виды средних
величин.
Наиболее часто
применяются следующие средние величины:
– средняя
арифметическая;
– средняя
гармоническая;
– средняя
геометрическая;
– средняя
квадратическая.
Все указанные
средние величины можно рассчитать по
общей формуле степенной
средней
Если
данные сгруппированы,
то
Последние две
формулы позволяют получить различные
виды средних при разных значениях m
(см. таблицу).
|
Вид |
m |
Формула |
Формула |
|
Гармоническая |
-1 |
|
|
|
Геометрическая |
|
|
|
|
Арифметическая |
1 |
|
|
|
Квадратическая |
2 |
|
|
Средняя
арифметическая, средняя гармоническая,
средняя геометрическая и средняя
квадратическая, рассчитанные для одних
и тех же исходных данных, отличаются
друг от друга. При этом всегда выполняется
следующее соотношение:
Приведем несколько
примеров использования средних взвешенных
зависимостей.
Пример
1. Найдем
средний коэффициент выполнения плана
по предприятиям отрасли.
Пусть
– план i–го
предприятия;
– относительный
показатель выполнения плана (в долях);
n
– число предприятий отрасли.
Тогда фактический
объем выпуска продукции составит
Плановый
объем выпуска продукции по отрасли
Средний
показатель выполнения плана по отрасли
Этот
показатель представляет собой
средневзвешенное арифметическое
показателей
с весами, соответствующими плану
производства – .
Пример
2. Найдем
среднюю скорость движения автомобиля,
если он проехал расстояние S1
со скоростью
v1,
а затем расстояние S2
со скоростью
v2.
Для нахождения средней скорости надо
разделить суммарное расстояние S1
+
S2 на
суммарное время, затраченное на этот
путь. Суммарное время в пути будет равно
Таким
образом, средняя скорость составит
В общем случае при
наличии n
участков с различной скоростью
Нетрудно видеть,
что средняя скорость представляет собой
средневзвешенное гармоническое из
скоростей на отдельных участках пути
с весами, равными длине участков пути.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мода и медиана
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Обратимся снова к нашему примеру со сборной по футболу:
Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?
Все верно, это число ( displaystyle 181), так как два игрока имеют рост ( displaystyle 181) см; рост же остальных игроков не повторяется.
Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.
Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).
Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.
Ну что, вернемся к нашей выборке футболистов?
Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!
Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).
Вот, что у меня получилось:
Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.
Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?
Все верно – игроков ( displaystyle 11), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.
Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас ( displaystyle 11), значит, по краям остается по пять чисел, а рост ( displaystyle 183) см будет медианой в нашей выборке.
Не так уж и сложно, правда?
Частота и относительная частота
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:
Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост ( 176)?
Все верно, один игрок. Таким образом, частота встречи игрока с ростом ( 176) в нашей выборке равна ( 1).
Сколько игроков имеет рост ( 178)? Да, опять же один игрок. Частота встречи игрока с ростом ( 178) в нашей выборке равна ( 1).
Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:
Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).
То есть в нашем примере: ( 1+1+1+2+1+1+1+1+1+1=11)
Перейдем к следующей характеристике – относительная частота.
Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем ( left( n=11 right)) .
Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:
А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.