Мода и медиана функции плотности распределения f(x)
Задача 5. Плотность распределения вероятностей случайной величины Х имеет вид

1. Найти:
а) параметр распределения С (в виде дроби);
а) математическое ожидание M(X);
б) дисперсию D(X) и среднее квадратическое отклонение σ(Х);
в) функцию распределения F(x) случайной величины X;
г) моду M0;
д) медиану Me;
е) вероятность осуществления неравенств ![]() и
и ![]() .
.
2. Построить графики функций f(x) и F(x). Изобразить на графике функции f(x) найденные характеристики и вероятности.
Решение находим с помощью калькулятора.
Случайная величина Х задана плотностью распределения f(x):
0, x ≤ 0
2•A(8/5-x), 0 < x < 8/5
0, x ≥ 8/5
Найдем параметр A из условия:


или
64/25*A-1 = 0
Откуда,
A = 25/64
Поскольку находили квадрат A, то ![]()
а) Математическое ожидание.


б) Дисперсия.


= -25/128•(8/5)4+5/12•(8/5)3 – (-25/128•04+5/12•03) – (8/15)2 = 32/225
Среднеквадратическое отклонение.
![]()
в) Функция распределения F(x) случайной величины X.



г) Мода M0.
Модой M0(X) называют то возможное значение X, при котором плотность распределения имеет максимум.
Построим график функции плотности распределения.

Как видим, максимум функции соответствует x = 0.
Mo( 0) = 2•25/64(8/5-0) = 5/4
д) Медиана Me.
Медианой Me(X) называют то возможное значение X, при котором ордината f(x) делит пополам площадь, ограниченную кривой распределения.
Необходимо найти такое x, при котором функция распределения равна ½.


Решая уравнение:
![]()
получаем:
![]()
![]()
Поскольку функция ограничена на интервале (0; 1,6), то искомое значение x = 0,46.
![]()
Построим график функции распределения.

е) Вероятность осуществления неравенств ![]() и
и ![]() .
.
![]()
![]()
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике – мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Чтобы использовать калькулятор среднее, медиана и мода, введите список чисел в соответствующее поле. Они не обязательно должны быть целыми числами. Разделите список пробелами, например: 1.5 1 2.5 1 2 8 3 6 2 2. Обратите внимание, что введенный список не должен быть отсортирован. Нажмите кнопку «Рассчитать», и отобразятся среднее, медиана и мода данного набора чисел. Обратите внимание, что мода будет выводить «Undefined», если числа не повторяются, и покажет наименьший режим, если два числа имеют одинаковую частоту. Для справки, этот примерный список имеет среднее значение 2,9, медиану 2 и моду 2.
.
Среднее— это сумма всех чисел в данном наборе, разделенная на их количество.
Медиана — число, характеризующее выборку набор чисел.
Мода — значение во множестве наблюдений, которое встречается наиболее часто. (Мода = типичность.) Иногда в совокупности встречается более чем одна мода (например: 6, 2, 6, 6, 8, 9, 9, 9, 0; мода — 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством.
Значение случайной
величины
![]() ,
,
принимаемое с наибольшей вероятностью,
называетсямодойи обозначается![]()
![]()
Мода называется
еще наивероятнейшим значениемслучайной величины.
Если эксперимент
описывается случайной величиной, то в
результате проведенной серии этого
эксперимента чаще всего встречается
мода случайной величины.
Медиана![]() является значением случайной величины
является значением случайной величины![]() .
.
Вероятность того, что случайная величина
принимает значение меньше медианы,
равна 0,5:
![]()
Не все дискретные
случайные величины имеют медиану.
Пример 1. Задан
закон распределения случайной величины
|
|
|
3 |
5 |
6 |
|
0,2 |
0,3 |
0,4 |
0,1 |
Найти моду и медиану
случайной величины
![]() .
.
Найдем моду:
![]() .
.
Тогда
![]() .
.
Для нахождения
медианы нужно рассмотреть
![]() ,
,
где![]() значения
значения
случайной величины![]() .
.
![]() .
.
Заметим, что
![]() .
.
Из данных закона
распределения случайной величины
![]()
![]()
![]()
![]() .
.
Тогда
![]() .
.
Нет необходимости находить![]() .
.
Пример 2. Задан
закон распределения случайной величины
|
|
0 |
1 |
|
0,9 |
0,1 |
Найти моду и медиану
случайной величины
![]() .
.
Значение 0 принимается с наибольшей
вероятностью
![]() .
.
Тогда
![]() .
.
Найдем медиану
![]()
![]() .
.
Нет значения
![]() случайной величины
случайной величины![]() ,
,
при котором![]() .
.
Поэтому случайная величина![]() медианы не имеет.
медианы не имеет.
3.6. Корреляционный момент. Коэффициент корреляции
Вводится величина,
характеризующая зависимость между
двумя случайными величинами. Задано
совместное распределение случайных
величин
![]() и
и![]()
![]() .
.
Корреляционным
моментомслучайных величин![]() и
и![]() (иликовариациеймежду
(иликовариациеймежду![]() и
и![]() )
)
называется число
![]()
Для дискретных
случайных величин
![]() и
и![]() имеем
имеем
![]() .
.
Непосредственно
из свойств математического ожидания
вытекают свойства ковариации:
-
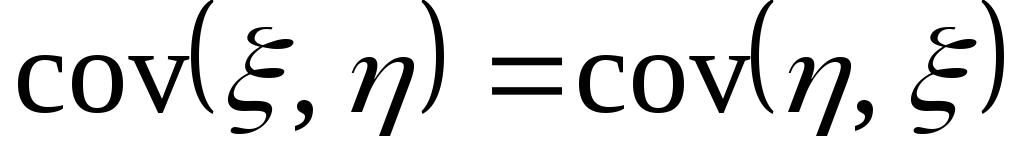 ;
; -
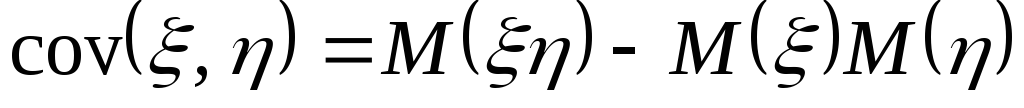 ;
;
Для дискретных
случайных величин имеем
![]() .
.
-
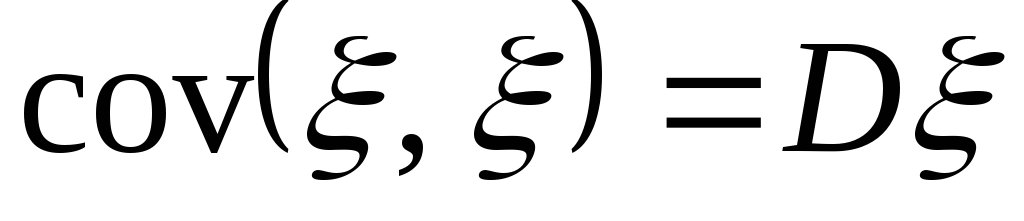 ;
; -
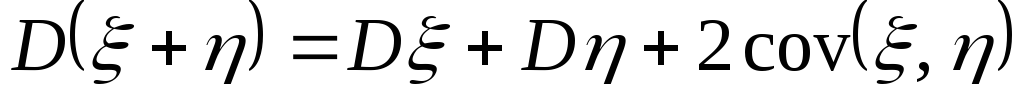 ;
; -
Если случайные
величины независимы, то их ковариация
равна нулю.
Обратное не верно.
Если
![]() ,
,
то случайные величины![]() и
и![]() могут быть как зависимыми, так и
могут быть как зависимыми, так и
независимыми.
Коэффициентом
корреляциимежду случайными величинами![]() и
и![]() называются число
называются число
![]() .
.
Приведем некоторые
свойства коэффициента корреляции.
Пусть
![]() и введем случайную величину
и введем случайную величину
![]() .
.
Знакоположительная
случайная величина
![]() имеет не отрицательное математическое
имеет не отрицательное математическое
ожидание:
![]() при любом
при любом
![]() .
.
Распишем
![]()
![]()
![]() .
.
Получаем квадратичное
неравенство
![]() ,
,
где
![]() ,
,![]() .
.
Неравенство
выполняется при любом
![]() ,
,
если дискриминант неположительный![]() .
.
Тогда
![]() ,
,
откуда
![]() .
.
Таким образом,
![]() .
.
-
Если
 и
и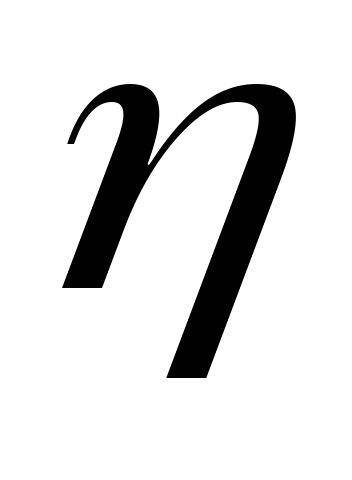 независимы, то
независимы, то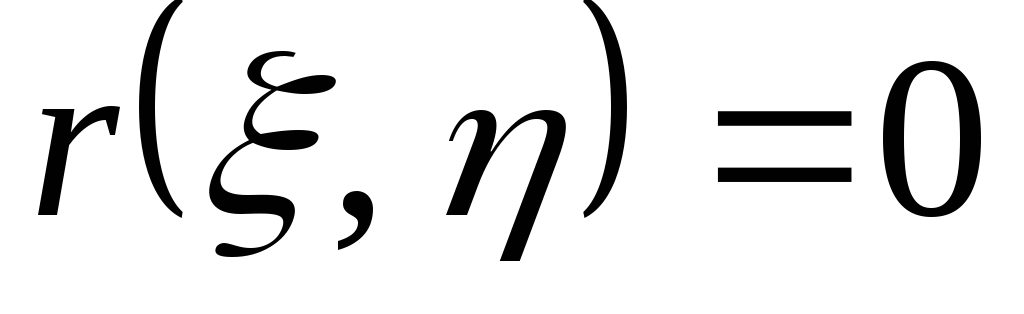 ,
,
что следует из свойства 5 ковариации. -
Коэффициент
корреляции равен
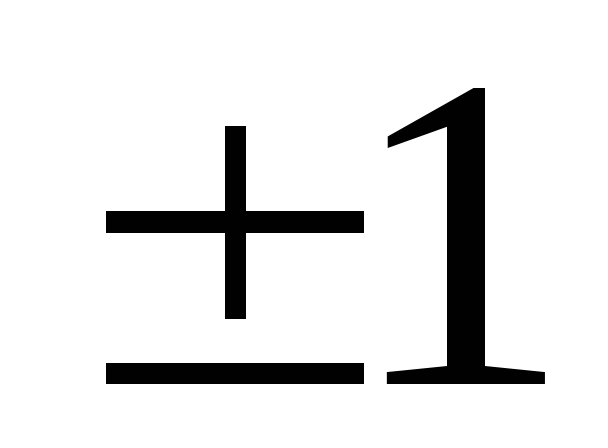 тогда и только тогда, когда случайные
тогда и только тогда, когда случайные
величины линейно зависимы
![]()
Пусть
![]() .
.
Тогда![]() и
и![]() ,
,
![]() .
.
Тогда
![]() .
.
Пусть
![]() .
.
Рассмотрим случайную
величину
![]() .
.
Найдем
![]()
![]() ,
,
![]() .
.
Из свойства
математического ожидания
![]() .
.
Тогда
![]() и
и
![]() .
.
Получим линейное
выражение
![]() через
через![]() .
.
Случай
![]() разбирается аналогично. Вводится
разбирается аналогично. Вводится
случайная величина![]() .
.
Пример 1. Задано
совместное распределение случайных
величин![]() и
и![]()
|
|
2 |
4 |
|
|
||
|
0 |
0,1 |
0,3 |
|
1 |
0,2 |
0,4 |
Найти
![]() .
.
Запишем распределения
случайных величин
![]() и
и![]()
-

0
1
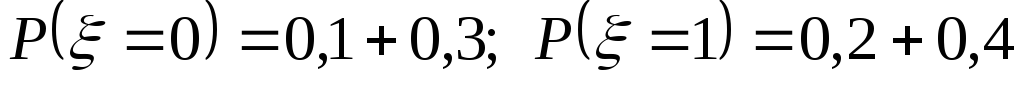 ;
;0,4
0,6
-
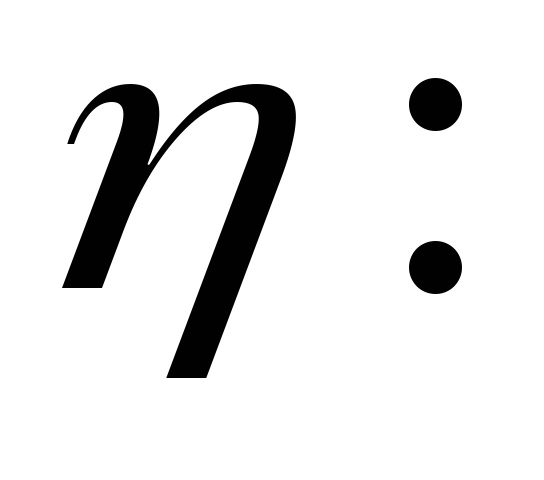
2
4
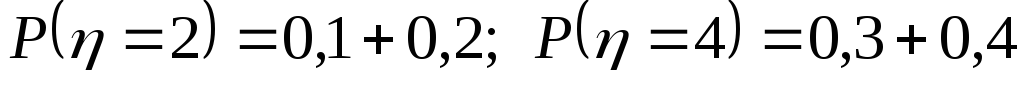 .
.0,3
0,7
Найдем основные
характеристики случайных величин
![]() и
и![]() :
:
![]() ;
;
![]() ;
;
![]()
![]() .
.
Используем формулу
![]() .
.
Найдем
![]() :
:
![]() .
.
Тогда
![]() и
и
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для нахождения моды и медианы случайной величины необходимы хорошие умения интегрировать и знания следующего теоретического материала. Модой 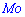 дискретной случайной величины
дискретной случайной величины 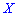 называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины
называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины 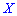 , которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
, которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
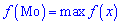
В зависимости от вида функции 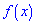 случайная величина
случайная величина 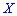 может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой  случайной величины
случайной величины 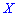 называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
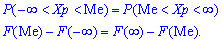
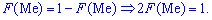
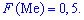
Графически мода и медиана изображенные на рисунке
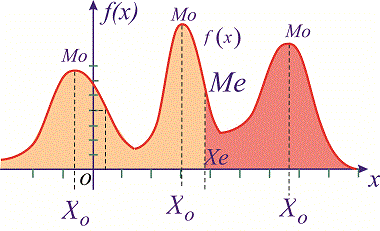
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин 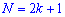 то медиана равна средней величине
то медиана равна средней величине
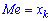
в случае четного количества 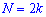 полусумме средних величин
полусумме средних величин
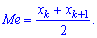
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины 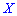 — количество дорожек, которые требуют уборки. Найти моду
— количество дорожек, которые требуют уборки. Найти моду 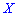 .
.
Решение. Случайной величина может принимать значения
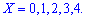
Вероятности появления значений определяем по образующей функцией
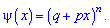
Для заданной задачи входные величины принимают значения
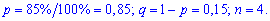
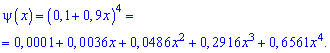
Искомые вероятности входят множителями при степенях аргумента
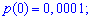
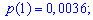
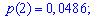
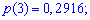
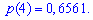
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду 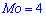 , как значение при максимальной вероятности. Получили одномодальное распределение
, как значение при максимальной вероятности. Получили одномодальное распределение
Пример 2. По заданной плотностью вероятностей
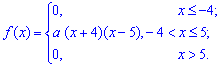
найти параметр  , плотность вероятностей
, плотность вероятностей 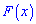 , моду
, моду 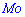 .
.
Решение. Применяя условие нормирования выполняем интегрирование
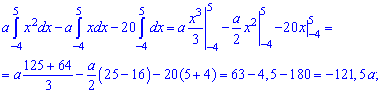
после того определяем параметр
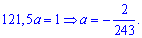
Плотность вероятностей, учитывая найденное значение будет иметь вид
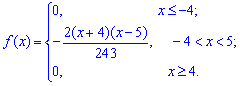
а ее график изображен на рисунке ниже
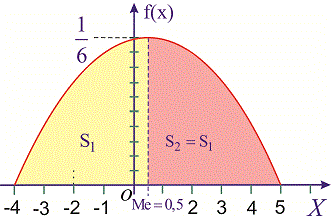
Из графика плотности вероятностей видим, что мода принимает значение 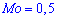 . Определим медиану
. Определим медиану  с помощью функции распределения вероятностей. Ее значение на промежутке
с помощью функции распределения вероятностей. Ее значение на промежутке 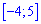 находим интегрированием
находим интегрированием
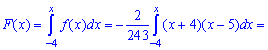
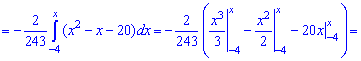
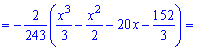
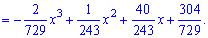
Функция распределения иметь следующий вид
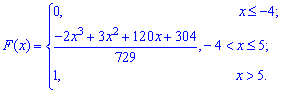
а ее график будет иметь вид
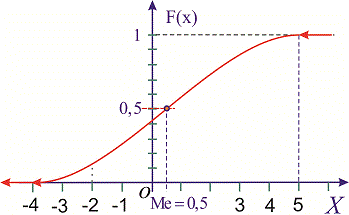
Для определения медианы случайной величины  применяем формулу
применяем формулу
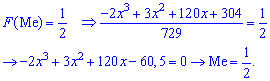
Медиану  можно найти с помощью плотности вероятностей
можно найти с помощью плотности вероятностей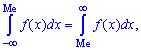
для дискретной случайной величины из промежутка 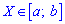
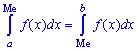
Таким образом медиану  — возможное значение случайной величины
— возможное значение случайной величины 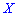 , при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости
, при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости 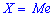 , делит площадь фигуры, ограниченной функцией плотности вероятностей
, делит площадь фигуры, ограниченной функцией плотности вероятностей 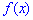 на две равные части.
на две равные части.
——————————-
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.

