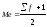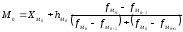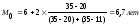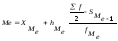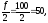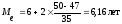Мода
и медиана –
особого рода средние, которые используются
для изучения структуры вариационного
ряда. Их иногда называют структурными
средними, в отличие от рассмотренных
ранее степенных средних.
Мода
– это величина признака (варианта),
которая чаще всего встречается в данной
совокупности, т.е. имеет наибольшую
частоту.
Мода
имеет большое практическое применение
и в ряде случаев только мода может дать
характеристику общественных явлений.
Медиана
– это варианта, которая находится в
середине упорядоченного вариационного
ряда.
Медиана
показывает количественную границу
значения варьирующего признака, которой
достигла половина единиц совокупности.
Применение медианы наряду со средней
или вместо нее целесообразно при наличии
в вариационном ряду открытых интервалов,
т.к. для вычисления медианы не требуется
условное установление границ отрытых
интервалов, и поэтому отсутствие сведений
о них не влияет на точность вычисления
медианы.
Медиану
применяют также тогда, когда показатели,
которые нужно использовать в качестве
весов, неизвестны. Медиану применяют
вместо средней арифметической при
статистических методах контроля качества
продукции. Сумма абсолютных отклонений
варианты от медианы меньше, чем от любого
другого числа.
Рассмотрим
расчет моды и медианы в дискретном
вариационном ряду:
|
Стаж, |
Число |
Накопленные |
|
1 |
2 |
2 |
|
3 |
4 |
6 |
|
4 |
5 |
(11) |
|
8 |
4 |
15 |
|
10 |
1 |
16 |
|
ИТОГО: |
16 |
– |
Определить моду и медиану.
Мода
Мо =
4 года, так как этому значению соответствует
наибольшая частота f
= 5.
Т.е.
наибольшее число рабочих имеют стаж 4
года.
Для
того, чтобы вычислить медиану, найдем
предварительно половину суммы частот.
Если сумма частот является числом
нечетным, то мы сначала прибавляем к
этой сумме единицу, а затем делим пополам:
Ме=16/2=8
Медианой
будет восьмая по счету варианта.
Для
того, чтобы найти, какая варианта будет
восьмой по номеру, будем накапливать
частоты до тех пор, пока не получим сумму
частот, равную или превышающую половину
суммы всех частот. Соответствующая
варианта и будет медианой.
Ме
= 4 года.
Т.е.
половина рабочих имеет стаж меньше
четырех лет, половина больше.
Если
сумма накопленных частот против одной
варианты равна половине сумме частот,
то медиана определяется как средняя
арифметическая этой варианты и
последующей.
Вычисление
моды и медианы в интервальном вариационном
ряду
Мода
в интервальном вариационном ряду
вычисляется по формуле
где ХМ0
– начальная
граница модального интервала,
hм0
– величина модального интервала,
fм0,
fм0-1,
fм0+1
– частота
соответственно модального интервала,
предшествующего модальному и последующего.
Модальным
называется такой интервал, которому
соответствует наибольшая частота.
Пример
1
|
Группы |
Число |
Накопленные |
|
1 |
2 |
3 |
|
До |
4 |
4 |
|
2-4 |
23 |
27 |
|
4-6 |
20 |
47 |
|
6-8 |
35 |
82 |
|
8-10 |
11 |
93 |
|
свыше |
7 |
100 |
|
ИТОГО: |
100 |
– |
Определить
моду и медиану.
Решение.
Модальный
интервал [6-8], т.к. ему соответствует
наибольшая частота f
= 35. Тогда:
Хм0=6,
fм0=35
hм0=2,
fм0-1=20
fм0+1=11
Вывод:
Наибольшее число рабочих имеет стаж
примерно 6,7 лет.
Для
интервального ряда Ме вычисляется по
следующей формуле:
где Хме
–
нижняя граница медиального интервала,
hме
– величина медиального интервала,
–
половина суммы частот,
fме
– частота медианного интервала,
Sме-1
–сумма
накопленных частот интервала,
предшествующего медианному.
Медианный
интервал – такой интервал, которому
соответствует кумулятивная частота,
равная или превышающая половину суммы
частот.
Определим
медиану для нашего примера.
Найдем:
т.к
82>50, то медианный интервал [6-8].
Тогда:
Хме
=6, fме
=35,
hме
=2, Sме-1=47,
Вывод: Половина рабочих имеет стаж
меньше 6,16 лет, а половина имеет стаж
больше, чем 6,16 лет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дискретный вариационный ряд и его характеристики
- Классификация рядов распределения
- Дискретный вариационный ряд, полигон частот и кумулята
- Выборочная средняя, мода и медиана
- Степень асимметрии вариационного ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования дискретного вариационного ряда
- Примеры
п.1. Классификация рядов распределения
Статистический ряд распределения – это количественное распределение единиц совокупности на однородные группы по некоторому варьирующему признаку.
В зависимости от природы признака различают атрибутивные и вариационные ряды.
Атрибутивный ряд распределения построен на качественном признаке.
Вариационный ряд распределения построен на количественном признаке.
Например:
Качественными признаками, которые не поддаются измерению, являются: профессия, пол, национальность и т.п.
Количественными признаками, которые можно подсчитать или измерить, являются: количество людей в группе, число повторений в опыте, возраст, вес, рост, скорость, температура и т.п.
По упорядоченности вариационные ряды делятся на упорядоченные (ранжированные) и неупорядоченные. Упорядочить ряд можно по возрастанию или убыванию исследуемого признака.
По характеру непрерывности признака вариационные ряды делятся на дискретные и интервальные.
Например:
Дискретными признаками, которые принимают отдельные значения, являются: количество людей в группе, число детей в семье, количество домов, число опытов и т.п.
Непрерывными признаками, которые могут принимать любые значения в интервале, являются: возраст, вес, рост, скорость, температура и т.п.
Варианты – это отдельные значения признака, которые он принимает в вариационном ряду.
Частоты – это численности отдельных вариант.
Например:
Распределение учеников по оценкам за контрольную работу
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
В данном ряду признак – это оценка, варианты признака (x_i) – это множество {2;3;4;5}, частоты (f_i) – это количество учеников, получивших каждую из оценок.
п.2. Дискретный вариационный ряд, полигон частот и кумулята
Дискретный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся прерывно и принимающему конечное множество значений.
Общий вид дискретного вариационного ряда
| Варианты, (x_i) | (x_1) | (x_2) | … | (x_k) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k – число вариант исследуемого признака.
Тогда общее количество исходов (число единиц в совокупности): (N=sum_{i=1}^k f_i)
Полигон частот – это ломаная, которая соединяет точки ((x_i,f_i)).
Например:
| Для распределения учеников по оценкам из нашего примера получаем такой полигон: |  |
Относительная частота варианты (x_i) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$ Относительная частота (w_i) является эмпирической оценкой вероятности варианты (x_i) в исследуемом ряду.
Полигон относительных частот – это ломаная, которая соединяет точки ((x_i,w_i)).
Полигон относительных частот является эмпирическим законом распределения исследуемого признака.
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)).
Ступенчатая кривая (F(x_i)), построенная по точкам ((x_i,S_i)), является эмпирической функцией распределения исследуемого признака.
Например:
Проведем необходимые расчеты и построим полигон относительных частот, кумуляту и эмпирическую функцию распределения учеников по оценкам.
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
| (w_i) | 0,0909 | 0,4545 | 0,3030 | 0,1515 | 1 |
| (S_i) | 0,0909 | 0,4545 | 0,8485 | 1 | – |
Полигон относительных частот (эмпирический закон распределения)
Кумулята (красная ломаная) и эмпирическая функция распределения (ступенчатая синяя кривая).
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 2\ 0,0909, 2lt xleq 3\ 0,5455, 3lt xleq 4\ 0,8485, 4lt xleq 5\ 1, xgt 5 end{cases} $$
п.3. Выборочная средняя, мода и медиана
Выборочная средняя дискретного вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Мода дискретного вариационного ряда – это варианта с максимальной частотой: $$ M_o=x*, f(x*)=underset{i=overline{1,k}}{max}f_i $$ Мод может быть несколько. Тогда говорят, что ряд мультимодальный.
На полигоне частот мода – это абсцисса самой высокой точки.
Медиана дискретного вариационного ряда – это значение варианты посредине упорядоченного ряда.
Алгоритм:
1. Отсортировать ряд по возрастанию.
2а. Если общее количество измерений N нечётное, найти (m=lceilfrac N2rceil) и округлить в сторону увеличения. (M_e=x_m) – искомая медиана.
2б. Если общее количество измерений N чётное, найти (m=frac N2) и вычислить медиану как среднее (M_e=frac{x_m+x_{m+1}}{2}).
На графике кумуляты медиана – это абсцисса первой точки слева, ордината которой превысила 0,5.
Например:
1) Найдем выборочную среднюю для распределения учеников по оценкам:
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
| (x_if_i) | 6 | 45 | 40 | 25 | 116 |
$$ X_{cp}=frac{6+45+40+25}{33}=frac{116}{33}approx 3,5 $$ Средняя оценка за контрольную – 3,5.
2) Найдем моду. Максимальная частота – 15 человек – у троечников. Значит: (M_o=3).
3) Найдем медиану. Общее количество измерений N=33 – нечетное.
Находим: (m=lceilfrac N2rceil=17)
Смотрим на ряд слева направо. Сначала у нас идет 3 двоечника, затем 15 троечников.
Вместе их 18, и 17-й человек в ряду – троечник. Группа троечников является медианной: (M_e=3).
Также, медиану можно найти по графику кумуляты. (3;0,5455) – это первая слева точка, в которой ордината больше 0,5. Значит, медиана равна абсциссе этой точки, т.е. (M_e=3).
п.4. Степень асимметрии вариационного ряда
В рядах с асимметрией или выбросами выборочная средняя не отражает в полной мере особенности исследуемого признака. Типичный случай – значение среднего уровня доходов в странах с высоким индексом Джини, где 5% населения получает 95% доходов. Или анекдотичный случай со «средней температурой по больнице».
Поэтому, кроме средней, в статистическом исследовании всегда следует определять моду и медиану.
Мода, медиана и выборочная средняя совпадут, если вариационный ряд является симметричным: $$ X_{cp}=M_o=M_e $$ Если вершина распределения сдвинута влево и правая часть ветви длиннее левой (длинный правый хвост), такая асимметрия называется правосторонней. При правосторонней асимметрии: $$ M_olt M_elt X_{cp} $$ Если вершина распределения сдвинута вправо и левая часть ветви длиннее правой (длинный левый хвост), такая асимметрия называется левосторонней. При левосторонней асимметрии: $$ M_ogt M_egt X_{cp} $$ Для умеренно асимметричных рядов (по Пирсону) модуль разности между модой и средней не более 3 раз превышает модуль разности между медианой и средней: $$ frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}geq 3 $$
Например:
Для распределения учеников по оценкам мы получили (X_{cp}=3,5; M_o=3; M_e=3).
Т.к. средняя оказалась больше моды и медианы, наше распределение имеет правостороннюю асимметрию (что видно на полигоне частот – правый хвост длиннее).
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{0,5}{0,5}=1lt 3), т.е. распределение умеренно асимметрично.
п.5. Выборочная дисперсия и СКО
Выборочная дисперсия дискретного вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac{(x_1-X_{cp})^2 f_1+(x_2-X_{cp})^2 f_2+…+(x_k-X_{cp})^2 f_k}{N}=\ =frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
1) Найдем выборочную дисперсию для распределения учеников по оценкам:
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
| (x_i^2) | 4 | 9 | 16 | 25 | – |
| (x_i^2 f_i) | 12 | 135 | 160 | 125 | 432 |
$$ D=frac{12+135+160+125}{33}-3,5^2=frac{432}{33}-3,5^2approx 0,73 $$ 2) Значение СКО: (sigma=sqrt{D}approx 0,86)
п.6. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия дискретного вариационного ряда определяется как: begin{gather*} S^2=frac{1}{N-1}sum_{i=1}^k(x_i-X_{cp})^2 f_i=frac{N}{N-1}D end{gather*}
В теоретической статистике доказывается, что выборочная дисперсия D является смещенной оценкой дисперсии при распространении на генеральную совокупность.
А именно, выборочная дисперсия D всегда меньше математического ожидания для дисперсии генеральной совокупности.
Исправленная выборочная дисперсия S2 является несмещенной оценкой.
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Если показатель вариации V<33%, то выборка считается однородной, т.е. большинство полученных в ней вариант находятся недалеко от средней, и выборочная средняя хорошо характеризует среднюю генеральной совокупности.
В противном случае, выборка неоднородна. Варианты в выборке находятся далеко от средней, есть выбросы. А значит, и в генеральной совокупности они возможны. Т.е., распространять результаты выборки на генеральную совокупность нельзя.
Если исследуется не выборка, а вся генеральная совокупность, дисперсию «исправлять» не нужно.
Например:
Для распределения учеников по оценкам получаем:
1) Исправленная выборочная дисперсия $$ S^2=frac{N}{N-1}D=frac{33}{32}cdot 0,73approx 0,76 $$ 2) Стандартное отклонение $$ x=sqrt{S^2}approx 0,87 $$ 3) Коэффициент вариации: $$ V=frac{0,87}{3,5}cdot 100text{%}approx 24,8text{%}lt 33text{%} $$ Выборка является однородной.
Это означает, что согласно коэффициенту вариации полученные результаты контрольной работы можно рассматривать в качестве «типичных» и распространить их на генеральную совокупность, т.е. на всех школьников, которые будут писать эту работу.
п.7. Алгоритм исследования дискретного вариационного ряда
На входе: таблица с вариантами (x_i) и частотами (f_i, i=overline{1,k})
Шаг 1. Составить расчетную таблицу. Найти (w_i,S_i,x_if_i,x_i^2,x_i^2f_i)
Шаг 2. Построить полигон относительных частот (эмпирический закон распределения) и график кумуляты с эмпирической функцией распределения. Записать эмпирическую функцию распределения.
Шаг 3. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 4. Найти выборочную дисперсию и СКО.
Шаг 5. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.8. Примеры
Пример 1. На площадке фриланса была проведена выборка из 100 фрилансеров и подсчитано количество постоянных заказчиков, с которыми они работают.
В результате было получено следующее распределение:
| Число постоянных заказчиков | 0 | 1 | 2 | 3 | 4 | 5 |
| Число фрилансеров | 22 | 35 | 27 | 11 | 3 | 1 |
Исследуйте полученный вариационный ряд.
1) Вариационный ряд является дискретным.
Исследуемый признак – «число постоянных заказчиков».
Варианты признака (x_iinleft{0;1;..;5right}). Количество вариант k=6.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | ∑ |
| (f_i) | 23 | 35 | 27 | 11 | 3 | 1 | 100 |
| (w_i) | 0,23 | 0,35 | 0,27 | 0,11 | 0,03 | 0,01 | – |
| (S_i) | 0,23 | 0,58 | 0,85 | 0,96 | 0,99 | 1 | – |
| (x_if_i) | 0 | 35 | 54 | 33 | 12 | 5 | 139 |
| (x_i^2) | 0 | 1 | 4 | 9 | 16 | 25 | – |
| (x_i^2f_i) | 0 | 35 | 108 | 99 | 48 | 25 | 315 |
2) Полигон относительных частот (эмпирический закон распределения):
Кумулята и эмпирическая функция распределения:
$$ F(x)= begin{cases} 0, xleq 0\ 0,23, 0lt xleq 1\ 0,58, 1lt xleq 2\ 0,85, 2lt xleq 3\ 0,96, 3lt xleq 4\ 0,99, 4lt xleq 5\ 1, xgt 5 end{cases} $$ 3) Выборочная средняя: $$ X_{cp}=frac1Nsum_{i=1}^k x_if_i= frac{1}{100}cdot 139=1,39 $$ Мода (абсцисса самой высокой точки на полигоне частот): (M_0=1).
Медиана (абсцисса первой слева точки на кумуляте, где значение превысило 0,5): точка (1;0,58), (M_e=1).
(X_{cp}gt M_e=M_0) – распределение асимметрично, с правосторонней асимметрией.
При этом (frac{|M_0-X_{cp}|}{|M_e-X_{cp}|}=frac{0,39}{0,39}=1lt 3), т.е. распределение умеренно асимметрично.
4) Выборочная дисперсия: $$ D=frac1Nsum_{i=1}^k x_i^2f_i-X_{cp}^2=frac{1}{100}cdot 315-1,39^2=1,2179approx 1,218 $$ CKO: $$ sigma=sqrt{D}approx 1,104 $$
5) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{100}{99}cdot 1,218approx 1,230 $$ Стандартное отклонение выборки: $$ s=sqrt{S^2}approx 1,109 $$ Коэффициент вариации: $$ V=frac{s}{X_{cp}}cdot 100text{%}=frac{1,109}{1,39}cdot 100text{%}approx 79,8text{%}gt 33text{%} $$ Представленная выборка неоднородна. Полученное значение средней (X_{cp}=1,39) не может быть распространено на генеральную совокупность всех фрилансеров.
8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:
(8.16 – формула Моды)
где хо – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1– частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:

где хо – нижняя граница медианного интервала;
NМе– порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число
семей |
Накоп-
ленные частоты |
в % к итогу |
| До 5000 | 600 | 600 | 6 |
| 5000-6000 | 700 | 1300
(600+700) |
13 |
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 )
(1300+1700) |
30 |
| 7000-8000
(хо) |
2500
(fМо) (fМе) |
5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 |
| 9000-10000 | 1500 | 9200 | 92 |
| Свыше 10000 | 800 | 10000 | 100 |
| Итого | 10000 | – | – |
Пример вычисления Моды. Найдем моду по формуле (8.16) см. обозначения в таблице, а h = 8000-7000=1000, т.е. получаем:
Пример вычисления Моды
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):
Пример вычисления Медианы
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Пример .СРЕДНИЙ, МЕДИАННЫЙ И МОДАЛЬНЫЙ УРОВЕНЬ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ ЦЕЛОМ ПО РОССИИ И ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ЗА 2013 год см. по ссылке. Источник: оценка на основании данных выборочного обследования бюджетов домашних хозяйств и макроэкономического показателя денежных доходов населения
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если Мо<Ме<Х – имеет место правосторонняя асимметрия.
При Х<Ме<Мо следует сделать вывод о левосторонней асимметрии ряда.
Средние величины (арифметическая, гармоническая, геометрическая, квадратическая) см. по ссылке
Оценка статьи:
Загрузка…
К структурным средним значениям выборки относят моду и медиану.
Мода 
Для интервального вариационного ряда:

где 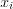

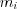



Медиана 
Для дискретного вариационного ряда:
1) если 

где 

2) если 

где 



Для интервального вариационного ряда:

где 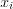





Пример 1. Найдите моду и медиану статистического распределения:

























Решение. Расположим значения признака в порядке возрастания:

























1. Мода: 

2. Медиану найдем по формуле 11.7, так как 

Ответ: 

Пример 2. Найдите моду и медиану дискретного вариационного ряда:
Решение. 1. Мода: 

2. Медиану найдем по формуле 11.8, так как 

Ответ: 

Пример 3. Найдите моду и медиану интервального вариационного ряда:
Решение. 1. Моду найдем по формуле 11.6 Модальный интервал: 






2. Медиану найдем по формуле 11.9.
Найдем накопленные частоты:
Медианный интервал: 






Ответ: 

1. Чтобы найти медиану дискретного вариационного ряда, варианты необходимо расположить в порядке возрастания.
2. Если объем выборки равен