|
Как найти модуль перемещения тела (формула)?
Общая формула для всех видов движения по которой можно найти модуль перемещения выглядит так. s = x-x0, где х0 – начальная координата, х – координата через промежуток времени, за которое совершено перемещение. Для более простых видов перемещения есть частные формулы. Для равномерного прямолинейного движения x = x0 + vt, где м – скорость тела. Для равноускоренного прямолинейного движения x = x0 + v0t + (a t^2)/2. система выбрала этот ответ лучшим
Zolotynka 6 месяцев назад Прежде чем писать/запоминать формулу, давайте разберемся, что представляет собой само понятие перемещения тела – это разница между двумя положениями объекта. Далее: это векторная величина, потому что у нее также есть направление – от начальной позиции к финальной. Формула перемещения выглядит следующим образом: Sx = x – x0. __ Перемещение не обязательно всегда положительно, оно также может быть нулевым или отрицательным. Знаете ответ? |
В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться!

Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.
Сила и модуль силы
В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.
Что такое модуль силы?
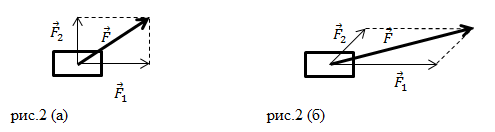
Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.
Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.
Модуль равнодействующих двух сил определяется по формулам:
- F=F1 + F2 (в случае сил с одинаковым направлением)
- F=F1 – F2 (силы с разным направлением)
Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.
Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).
Что это модуль скорости?

Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.
Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.
Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:
v = S/t = (x – x0)/t.
Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.
Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:
- Вычисляется скорость v21 на базе закона сложения скоростей v2 = v21 + v1, а значит v21 = v2 – v1.
- Определяется модуль скорости тела согласно теореме Пифагора.
Модуль импульса и модуль оси
Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается? Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.
Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее. Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Скорость равномерного прямолинейного движения прямо пропорциональна перемещению тела и обратно пропорциональна значению времени этого перемещения.
v→=s→t.
Можно выразить перемещение из этой формулы, умножив обе части на значение времени: s→=v→⋅t.
О направлении векторов этих величин относительно друг друга можно судить, в частности, по уравнениям, записанным в векторной форме.
Проекция перемещения на ось (OX) рассчитывается по формуле
sx=vxt
, где (upsilon_x) — проекция скорости на ось (OX) принимает положительное значение, если направление перемещения совпадает с направлением оси (OX); принимает отрицательное значение, если перемещение противоположно направлено относительно оси (OX).
Если при решении задач направление движения не влияет на смысл условия и ход решения задачи, то направление векторных величин можно не учитывать. Тогда говорят о модулях величин, то есть их размере без учёта направления: (|vec{s}|=|vec{upsilon}|cdot t) можно заменить на s=vt.
При прямолинейном равномерном движении модуль перемещения равен пройденному пути: (|vec{s}|=s), если направление скорости совпадает с направлением вектора перемещения.
На рисунке представлена зависимость (v(t)) для равномерного движения.

Формула для расчета модуля перемещения: s=v1⋅t1.
Однако произведение v1⋅t1, т.е. скорости на промежуток времени, численно равно площади (S) закрашенной фигуры (в данном случае прямоугольника).
Это наблюдение позволяет сделать вывод; что при прямолинейном равномерном движении модуль перемещения численно равен площади прямоугольника, которые образуется между графиком скорости и осью времени. При этом необходимо учитывать моменты времени: начало наблюдения за объектом и конец наблюдения. В данном случае начало наблюдения соответствует точке (O,) а конец наблюдения — точке t1.
Можно говорить о равенстве пройденного пути и площади под графиком скорости.
Обновлено: 23.05.2023
То-же, что и в математике – величину вектора, без учёта направления!
В физике обычно используется модуль вектора. Других применений модуля я не припоминаю. Модуль вектора, по сути это длина вектора, т. е. его абсолютная величина. Например если говорится что на тело действует сила F = 10 Н, это означает что модуль силы – т. е. ее абсолютная величина равна 10 Ньютон. При этом не указано направление действия силы. Ведь сила – это вектор, и имеет определенное направление. Обычно в физике для изучаемой системы выбирается система координат. И в этой системе координат сила может быть направлена как в положительном направлении, так и в отрицательном. В уравнения динамики в таком случае сила входит с соответствующим знаком. А вот число, стоящее после знака и есть модуль силы – т. е. ее величина.

2. Архит. Исходная единица измерения, устанавливаемая для данного архитектурного сооружения, служащая мерилом для придания соразмерности отдельным частям здания.
3. Тех. Часть прибора или конструкции, собранная из типовых деталей и имеющая многоцелевое применение.
[От лат. modulus — мера]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Модуль — функционально завершённый узел радиоэлектронной аппаратуры, оформленный конструктивно как самостоятельный продукт. См. также: унификация.
Модуль (космонавтика) — автономно управляемая часть космического корабля (например, модуль МКС).
Модуль — предварительно заданная величина, размер, кратным которому принимаются остальные размеры при разработке или при оценке проекта здания.
Модуль — шаг сетки, основа композиции полос и разворотов в модульной системе вёрстки.
Модуль — произведение длины между перпендикулярами, ширины и высоты борта судна в судостроении.
Модуль (реклама) — размеры графики для печатной рекламы.
Модуль зубчатого колеса — основной параметр зубчатой передачи.
Модуль (программирование) — функционально законченный фрагмент программы, оформленный в виде отдельного файла с исходным кодом или поименованной непрерывной её части.
Исполнимый модуль — файл, содержащий программу в виде, в котором она может быть исполнена компьютером.
Объектный модуль — файл с промежуточным представлением отдельного модуля программы, полученный в результате обработки исходного кода компилятором.
Модуль ядра — объект, содержащий код, который расширяет функциональность запущенного или т. н. базового ядра ОС.
Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.
Сила и модуль силы
В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.
Что такое модуль силы?

Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.
Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.
Модуль равнодействующих двух сил определяется по формулам:
- F=F1 + F2 (в случае сил с одинаковым направлением)
- F=F1 – F2 (силы с разным направлением)
Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.
Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).
Что это модуль скорости?

Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.
Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.
Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:
v = S/t = (x – x0)/t.
Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.
Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:
- Вычисляется скорость v21 на базе закона сложения скоростей v2 = v21 + v1, а значит v21 = v2 – v1.
- Определяется модуль скорости тела согласно теореме Пифагора.
Модуль импульса и модуль оси
Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается? Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.
Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее. Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.
В 7 классе вы узнали, что равномерным движением называют такое движение, при котором за равные интервалы времени тело проходит равные части пути (см. § 1-ж). Например, если поезд ежечасно проезжает 60 км, ежеминутно проезжает 1 км и так далее, то движение равномерное. Итак, скорость равномерного движения:
υ – скорость равномерного движения, м/с
l – пройденный телом путь, м
Δ t – интервал времени движения, с
Поскольку пройденный путь и интервал времени – скалярные величины, то скорость равномерного движения является скаляром тоже. То есть, имея только числовое значение, она ничего не говорит нам о пространственном направлении изучаемого движения.
Обратим внимание: если движение является не только равномерным, но и прямолинейным, то путь тела равен модулю перемещения. Поэтому, пользуясь аналогией с предыдущей формулой, в физике определяют скорость равномерного прямолинейного движения:
– скорость равнопрямолинейного движения, м/с
– перемещение тела, м
Δ t – интервал времени движения, с
Поскольку перемещение – векторная величина, то скорость равномерного прямолинейного движения является вектором тоже, то есть величиной, имеющей не только числовое значение, но и пространственное направление.
Из геометрии мы знаем, что в результате произведения вектора на положительный скаляр получается новый вектор, направление которого совпадает с направлением исходного, а модуль равен произведению модуля исходного вектора на скаляр. Последняя формула – пример произведения вектора s на положительный скаляр ¹/ Δ t. Поэтому направление скорости равномерного прямолинейного движения всегда совпадает с направлением перемещения.
- При равномерном движении тело проходит равные части пути .
- Скорость равномерного движения находят делением пройденного пути на .
- Скорость равномерного движения является скалярной величиной, так как .
- Являться скалярной величиной – значит не давать информации .
- Модуль перемещения тела совпадает с пройденным путём, .
- Формулу для скорости равнопрямолинейного движения вводят, .
- Делением перемещения тела на интервал времени движения находят .
- Подобно перемещению, вектором является и .
- Являться вектором – значит быть .
- Поскольку скаляр ¹/ Δ t положителен, то .
Задача 1. Минутная стрелка часов-курантов на Спасской башне Кремля имеет длину 327 см. Найдите скорость движения её конца-указателя.
Решение. Поскольку конец стрелки движется по окружности циферблата, траектория движения является криволинейной. Наряду с этим движение является равномерным, так как за любые равные интервалы времени, например, за каждую минуту, конец стрелки проходит равные части пути (деления на циферблате, равные друг другу по всей длине окружности).
Поэтому мы применяем формулу из первой рамки в начале параграфа:
| υ = | . l . | = | 2 π R | ≈ | 2 · 3,14 · 327 см | ≈ | 2054 см | ≈ 34 см/мин |
| Δ t | Δ t | 60 мин | 60 мин |
Задача 2. Турист прошёл на север 3 км, затратив на это 45 минут, а затем повернул на восток и прошёл ещё 4 км, затратив на это 1 час. За какое время он прошёл бы из начальной в конечную точку маршрута, двигаясь прямолинейно с таким же модулем скорости, как и прежде?
Решение. Часть этой задачи мы уже решили в § 12-в, поэтому знаем, что расстояние между начальной и конечной точками равно 5 км. Но какова скорость туриста? Сначала найдём модули скоростей на обоих этапах:
| υ 1 = | . s 1 . | = | 3 км | = 4 км/ч | ; | υ 2 = | . s 2 . | = | 4 км | = 4 км/ч |
| Δ t 1 | 0,75 ч | Δ t 2 | 1 ч |
| υ = | . s . | ⇒ | Δ t | = | . s . | = | 5 км | = 1,25 ч | = 1 час 15 мин |
| Δ t | υ | 4 км/ч |
- Траектория конца стрелки криволинейна, .
- Наряду с непрямолинейностью траектории конца стрелки, его .
- Равномерность этого движения мы обосновываем тем, что .
- Поскольку движение равномерно, но непрямолинейно, .
- Конец стрелки ежеминутно передвигается на .
- Как должен идти турист по условию задачи?
- После первой пары вычислений мы обнаруживаем: .
- Поскольку модули скоростей равны, то их .
- При отсутствии какого термина задача будет не решаема?
- Если движение туриста непрямолинейно, то будет невозможно .
Основываясь на определении скорости, мы можем утверждать, что скорость является вектором. Она непосредственно выражается через вектор-перемещения, отнесенный к промежутку времени, и должна обладать всеми свойствами вектора перемещения.
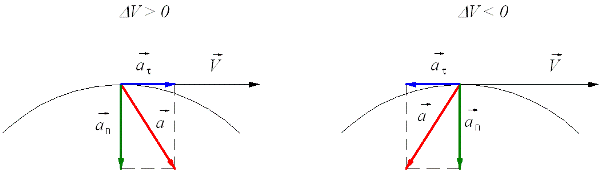
Направление вектора скорости, так же как направление физически малого вектора перемещения, определяется по чертежу траектории. В этом можно наглядно убедиться на простых примерах.
Если к вращающемуся точильному камню прикоснуться железной пластинкой, то снимаемые им опилки приобретут скорость тех точек камня, к которым прикасалась пластинка, и затем улетят в направлении вектора этой скорости. Все точки камня движутся по окружностям. Во время опыта хорошо видно, что отрывающиеся раскаленные частички-опилки уходят по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек вращающегося точильного камня.
Обратите внимание на то, как расположены выходные трубы у кожуха центробежного водяного насоса или у сепаратора для молока. В этих машинах частицы жидкости заставляют двигаться по окружностям и затем дают им возможность выйти в отверстие, расположенное в направлении вектора той скорости, которую они имеют в момент выхода. Направление вектора скорости в этот момент совпадает с направлением касательной к траектории движения частиц жидкости. И выходная труба тоже направлена по этой касательной.
Точно так же обеспечивают выход частиц в современных ускорителях электронов и протонов при ядерных исследованиях.
Итак, мы убедились, что направление вектора скорости определяется по траектории движения тела. Вектор скорости всегда направлен вдоль касательной к траектории в той точке, через которую проходит движущееся тело.
Для того чтобы определить, в какую сторону вдоль касательной направлен вектор скорости и каков его модуль, нужно обратиться к закону движения. Допустим, что закон движения задан графиком, показанным на рис. 1.54. Возьмем приращение длины пути соответствующее малому вектору по которому определяется вектор скорости. Вспомним, что Знак указывает
направление движения по траектории, а следовательно, определяет ориентировку вектора скорости вдоль касательной. Очевидно, что через модуль этого приращения длины пути будет определяться модуль скорости.
Таким образом, модуль вектора скорости и ориентировку вектора скорости вдоль касательной к траектории можно определить из соотношения
Здесь является алгебраической величиной, знак которой указывает, в какую сторону по касательной к траектории направлен вектор скорости.
Итак, мы убедились, что модуль вектора скорости может быть найден по графику закона движения. Отношение определяет угол наклона а касательной на этом графике. Наклон касательной на графике закона движения будет тем больше, чем больше т. е. чем больше в выбранный момент скорость движения.
Еще раз обратим внимание на то, что для полного определения скорости требуется одновременное знание траектории и закона движения. Чертеж траектории позволяет определить направление скорости, а график закона движения — ее модуль и знак.
Если теперь мы обратимся снова к определению механического движения, то убедимся в том, что после введения понятия скорости для полного описания любого движения больше ничего не требуется. Используя понятия радиус-вектора, вектора перемещения, вектора скорости, длины пути, траектории и закона движения, можно получить ответы на все вопросы, связанные с определением особенностей любого движения. Все эти понятия взаимосвязаны друг с другом, причем знание траектории и закона движения позволяет найти любую из этих величин.

Разберем сегодня, что значит модуль числа, как считать модуль и как обозначается модуль в математике. А также его свойства и, конечно же, примеры.
О чем эта статья:
Определение модуля числа
Алгебра дает четкое определение модуля числа. Модуль числа в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Знак модуля: |a| = OA.
Разберем на примере:
Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.
Число 3 (длину отрезка OB) называют модулем числа −3.
Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.
Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
2. Модуль положительного числа равен самому числу.
3. Модуль отрицательного числа равен противоположному числу.
4. Модуль нуля равен нулю.
5. Противоположные числа имеют равные модули.
6. Модуль произведения равен произведению модулей этих чисел.
−(a · b), когда a · b
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.
Нарисуем числовую прямую и отобразим это на ней.
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
Решим уравнение: |х| = 5.
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
Когда у нас есть два числа a и b, то их разность |a – b| равна расстоянию между ними на числовой прямой или длине отрезка АВ.
Расстояние от точки a до точки b равно расстоянию от точки b до точки a, тогда |a – b| = |b – a|.
Решим уравнение: |a – 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.
Уравнение имеет два решения: −1 и 7. Мы из 3 вычли 4 – и это один ответ, а также к 3 мы прибавили 4 – и это второй ответ.
Решим неравенство: |a + 7|
График функции
График функции равен y = |х|.
Для x > 0 имеем y = x.
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
В контрольной работе или на ЕГЭ может встретиться задачка, в которой нужно вычислить √ a 2 , где a – некоторое число или выражение.
При этом, √ a 2 = |a|.
По определению арифметического квадратного корня √ a 2 — это такое неотрицательное число, квадрат которого равен a 2 .
Оно равно a при а > 0 и −а, при а
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.
Читайте также:
- К п победоносцев биография кратко
- Культура киевской руси ix xii вв кратко
- Коуз экономист биография кратко
- Рецензия на фильм форсаж кратко
- Опираясь на текст расскажите о колядках кратко
Сила Ампера — сила, которая действует на проводник с током, помещенный в магнитное поле.
Модуль силы Ампера обозначается как FA. Единица измерения — Ньютон (Н).
Математически модуль силы Ампера определяется как произведение модуля вектора магнитной индукции B, силы тока I, длины проводника l и синуса угла α между условным направлением тока и вектором магнитной индукции:
FA=BIlsinα
Максимальное значение сила Ампера принимает, когда ток в проводнике направлен перпендикулярно вектору магнитной индукции, так как sin90°=1. И сила Ампера отсутствует совсем, если ток в проводнике направлен относительно вектора магнитной индукции вдоль одной линии. В этом случае угол между ними равен 0, а sin0°=1.
Пример №1. Максимальная сила, действующая в однородном магнитном поле на проводник с током длиной 10 см, равна 0,02 Н. Сила тока в проводнике равна 8 А. Найдите модуль вектора магнитной индукции этого поля.
10 см = 0,1 м
Так как речь идет о максимальной силе, действующей на проводник с током, тоsinα при этом равен 1 (проводник с током расположен перпендикулярно вектору магнитной индукции).
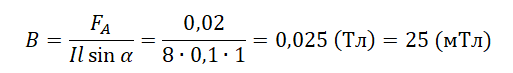
Определение направления силы Ампера
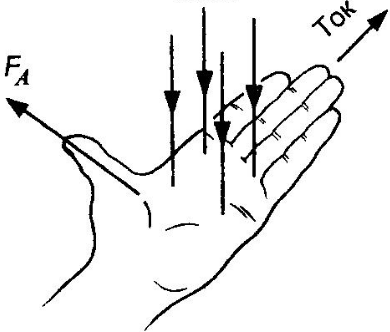
Направление вектора силы Ампера определяется правилом левой руки.
Правило левой руки
Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции →B входила в ладонь, то отогнутый на 90 градусов большой палец покажет направление силы, действующий на отрезок проводника (направление силы Ампера).
Пример №2. В однородном магнитном поле находится рамка, по которой начинает течь ток (см. рисунок). Какое направление (вверх, вниз, влево, вправо, от наблюдателя, наблюдателю) имеет сила, действующая на нижнюю сторону рамки?
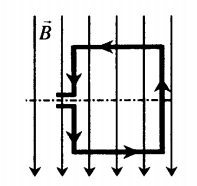
Так как в нижней стороне рамки ток направлен вправо, то четыре пальца левой руки нужно направить вправо. Саму левую руку при этом нужно расположить перпендикулярно плоскости рисунка ладонью вверх, чтобы в нее входили линии вектора магнитной индукции. Если отогнуть большой палец на прямой угол, то он покажет направление силы Ампера, действующей на нижнюю часть рамки. В данном случае она направлена в сторону от наблюдателя.
Работа силы Ампера
Проводники, на которые действует сила Ампера, могут перемещаться под действием этой силы. В этом случае говорят, что сила Ампера совершает работу. Из курса механики вспомним, что работа равна:
A=Fscosα
F — сила, совершающая работу, s — перемещение, совершенное телом под действием этой силы, α — угол между вектором силы и вектором перемещения.
Отсюда работа, совершаемая силой Ампера, равна:
A=FAscosα=BIlsinβscosα
α — угол между вектором силы и вектором перемещения, β — угол между условным направлением тока и вектором магнитной индукции.
Пример №3. Проводник длиной l = 0,15 м перпендикулярен вектору магнитной индукции однородного магнитного поля, модуль которого B = 0,4 Тл. Сила тока в проводнике I = 8 А. Найдите работу, которая была совершена при перемещении проводника на 0,025 м по направлению действия силы Ампера.
Так как проводник расположен перпендикулярно вектору магнитной индукции, и поле однородно, то синус угла между ними равен «1». Так как направление перемещение проводника совпадает с направлением действия силы Ампера, то косинус угла между ними тоже равен «1». Поэтому формула для вычисления работы силы Ампера принимает вид:
A=BIls
Подставим известные данные:
A=0,4·8·0,15·0,025=0,012 (Дж)=12 (мДж)
Задание EF17704
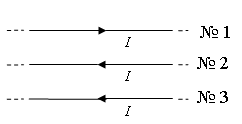 Как направлена сила Ампера, действующая на проводник № 3 со стороны двух других (см. рисунок), если все проводники тонкие, лежат в одной плоскости и параллельны друг другу? По проводникам идёт одинаковый ток силой I.
Как направлена сила Ампера, действующая на проводник № 3 со стороны двух других (см. рисунок), если все проводники тонкие, лежат в одной плоскости и параллельны друг другу? По проводникам идёт одинаковый ток силой I.
а) вверх
б) вниз
в) к нам
г) от нас
Алгоритм решения
1.Определить направление вектора результирующей магнитной индукции первого и второго проводников в любой точке третьего проводника.
2.Используя правило левой руки, определить направление силы Ампера, действующей на третий проводник со стороны первых двух проводников.
Решение
На третьем проводнике выберем произвольную точку и определим, в какую сторону в ней направлен результирующий вектор →B, равный геометрической сумме векторов магнитной индукции первого и второго проводников (→B1и →B2). Применим правило буравчика. Мысленно сопоставим острие буравчика с направлением тока в первом проводнике. Тогда направление вращения его ручки покажем, что силовые линии вокруг проводника 1 направляются относительно плоскости рисунка против хода часовой стрелки. Ток во втором проводнике направлен противоположно току в первом. Следовательно, его силовые линии направлены относительно плоскости рисунка по часовой стрелке.
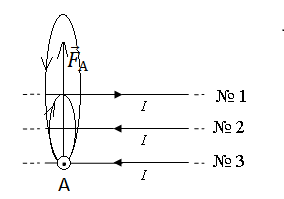
В точке А вектор →B1 направлен в сторону от наблюдателя, а вектор →B2— к наблюдателю. Так как второй проводник расположен ближе к третьему, создаваемое им магнитное поле в точке А более сильное (силы тока во всех проводниках равны по условию задачи). Следовательно, результирующий вектор →B направлен к наблюдателю.
Теперь применим правило левой руки. Расположим ее так, чтобы четыре пальца были направлены в сторону течения тока в третьем проводнике. Ладонь расположим так, чтобы результирующий вектор →B входил в ладонь. Теперь отставим большой палец на 90 градусов. Относительно рисунка он покажет «вверх». Следовательно, сила Ампера →FА, действующая на третий проводник, направлена вверх.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18417
Чему равна сила Ампера, действующая на стальной прямой проводник с током длиной 10 см и площадью поперечного сечения 2⋅10–2 мм2 , если напряжение на нём 2,4 В, а модуль вектора магнитной индукции 1 Тл? Вектор магнитной индукции перпендикулярен проводнику. Удельное сопротивление стали 0,12 Ом⋅мм2/м.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения силы Ампера.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Длина проводника: l = 10 см.
• Площадь поперечного сечения проводника: S = 2⋅10–2 мм2.
• Напряжение в проводнике: U = 2,4 В.
• Модуль вектора магнитной индукции: B = 1 Тл.
• Удельное сопротивление стали: r = 0,12 Ом⋅мм2/м.
• Угол между проводником с током и вектором магнитной индукции: α = 90о.
10 см = 0,1 м
Сила Ампера определяется формулой:
FA=BIlsinα
Так как α = 90о, синус равен 1. Тогда сила Ампера равна:
FA=BIl
Силу тока можно выразить из закона Ома:
I=UR
Сопротивление проводника вычисляется по формуле:
R=rlS
Тогда сила тока равна:
I=USrl
Конечная формула для силы Ампера принимает вид:
FA=BlUSrl=BUSr=1·2,4·2·10−20,12=0,4 (Н)
Ответ: 0,4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17725
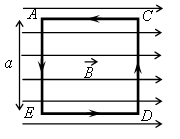 На непроводящей горизонтальной поверхности стола лежит жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата AСDЕ со стороной a(см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции B которого перпендикулярен сторонам AE и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
На непроводящей горизонтальной поверхности стола лежит жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата AСDЕ со стороной a(см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции B которого перпендикулярен сторонам AE и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?
Алгоритм решения
1.Сделать список известных данных.
2.Определить, при каком условии рамка с током будет вращаться вокруг стороны CD.
3.Выполнить решение в общем виде.
Решение
По условию задачи известными данными являются:
• Сторона квадратной рамки с током: a.
• Вектор магнитной индукции однородного горизонтального магнитного поля, в котором лежит рамка: B.
Пусть по рамке течёт ток I. На стороны АЕ и CD будут действовать силы Ампера:
FA1=FA2=IaB
Для того чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз. Момент силы Ампера относительно оси, проходящей через сторону CD:
MA=Ia2B
Момент силы тяжести относительно оси CD:
Mmg=−12mga
Чтобы рамка с током оторвалась от горизонтальной поверхности, нужно чтобы суммарный момент сил был больше нуля:
MA+Mmg>0
Так как момент силы тяжести относительно оси CD отрицательный, это неравенство можно записать в виде:
Ia2B>12mga
Отсюда выразим силу тока:
I>mga2a2B
I>mg2aB
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10.8k
