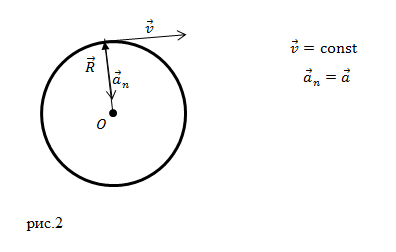Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 апреля 2021 года; проверки требуют 3 правки.
Разложение ускорения 



Центростреми́тельное (норма́льное) ускоре́ние — составляющая ускорения тела, характеризующая быстроту изменения направления вектора скорости (вторая составляющая, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, с чем и связан термин.
Обозначается символом, выбранным для ускорения, с добавлением значка «нормальное»: 

Пример движения с ненулевым центростремительным ускорением — движение по окружности (в таком случае 
В классической механике нормальное ускорение вызывается компонентами сил, направленными ортогонально вектору скорости. Например, движение космического объекта на орбите характеризуется центростремительным ускорением, вызванным гравитацией. Составляющая суммы сил, обусловливающая наличие нормального ускорения, называется центростремительной силой. Связанное понятие для неинерциальных систем отсчёта — центробежная сила.
Осестремительное ускорение, рассматриваемое в случаях вращения тела вокруг оси, в проекции на плоскость, перпендикулярную оси, предстаёт как центростремительное.
Общая формула[править | править код]
Нормальное ускорение 
или (с использованием соотношения 
,
где 


Выражения могут быть переписаны в векторном виде:
.
Здесь 
Эти формулы применимы как к частной ситуации равномерного движения (



Вывод формулы[править | править код]
Для разложения ускорения на тангенциальное и нормальное можно продифференцировать по времени вектор скорости, представленный в виде 

.
Здесь первое слагаемое — тангенциальное ускорение, а второе — нормальное ускорение. Через 






Равенство 














О радиусе кривизны[править | править код]
Вычисление радиуса кривизны и координат центра кривизны траектории является математической задачей (см. Кривизна). Если кривая задана уравнением 


,
а положение центра кривизны — по формулам[2]
.
Единичный вектор нормали в таком случае составит (

.
Если известна зависимость радиус-вектора материальной точки от времени 
,
где 


Мотивация, замечания[править | править код]
То, что разложение вектора ускорения на компоненты — одну вдоль касательной к траектории (тангенциальное ускорение) и другую ортогональную ей (нормальное ускорение) — может быть удобным и полезным, довольно очевидно само по себе. При движении с постоянной по модулю скоростью тангенциальная составляющая становится равной нулю, то есть в этом важном частном случае остается только нормальная составляющая. Кроме того, каждая из этих составляющих имеет ярко выраженные собственные свойства и структуру, и нормальное ускорение содержит в структуре своей формулы достаточно важное и нетривиальное геометрическое наполнение. Крайне важен также частный случай движения по окружности.
Абсолютная величина тангенциального ускорения зависит только от путевого ускорения, совпадая с его абсолютной величиной, в отличие от абсолютной величины нормального ускорения, которая от путевого ускорения не зависит, зато зависит от путевой скорости.
История понятия[править | править код]
Первым правильные формулы для центростремительного ускорения (или центробежной силы) получил, по-видимому, Гюйгенс. Практически с этого времени рассмотрение центростремительного ускорения входит в обычную технику решения механических задач.
Несколько позже эти формулы сыграли существенную роль в открытии закона всемирного тяготения (формула центростремительного ускорения использовалась для получения закона зависимости гравитационной силы от расстояния до источника гравитации, исходя из выведенного из наблюдений третьего закона Кеплера).
К XIX веку рассмотрение центростремительного ускорения становится уже совершенно рутинным как для чистой науки, так и для инженерных приложений.
См. также[править | править код]
- Тангенциальное ускорение
- Кривизна кривой
- Центробежная сила
Примечания[править | править код]
- ↑ Как видно из формулы, при движении с постоянной путевой скоростью — тангенциальное ускорение попросту равно нулю.
- ↑ 1 2 Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», c. 368-370.
Формула центростремительного ускорения в физике
Формула центростремительного ускорения
Определение и формула центростремительного ускорения
Определение
Центростремительным ускорением называют компоненту полного ускорения материальной точки, движущейся по криволинейной траектории,
которая определяет быстроту изменения направления вектора скорости.
Другой компонентой полного ускорения является тангенциальное ускорение, оно отвечает за изменение величины скорости. Обозначают центростремительное ускорение, обычно ${overline{a}}_n$. Центростремительное ускорение еще называют нормальным.
Центростремительное ускорение равно:
[{overline{a}}_n=frac{v^2}{r^2}overline{r }=frac{v^2}{r}{overline{e}}_rleft(1right),]
где ${overline{e}}_r=frac{overline{r }}{r}$ – единичный вектор, который направлен от центра кривизны траектории к рассматриваемой точке; $r$ – радиус кривизны траектории в месте нахождения материальной точки в рассматриваемый момент времени.
Первым верные формулы для вычисления центростремительного ускорения получил Х. Гюйгенс.
Единицей измерения центростремительного ускорения в Международной системе единиц является метр, деленный на секунду в квадрате:
[left[a_nright]=frac{м}{с^2}.]
Формула центростремительного ускорения при равномерном движении точки по окружности
Рассмотрим равномерное движение материальной точки по окружности. При таком перемещении величина скорости материальной точки неизменна ($v=const$). Но это не означает, что полное ускорение материальной точки при таком виде движения равно нулю. Вектор мгновенной скорости направлен по касательной к окружности, по которой перемещается точка. Следовательно, в этом движении скорость постоянно изменяет свое направление. Отсюда следует, что точка имеет ускорение.
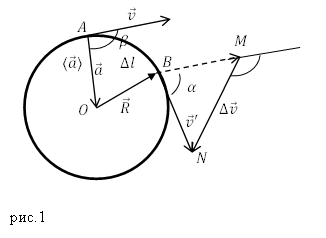
Рассмотрим точки A и B которые лежат на траектории движения частицы. Вектор изменения скорости для точек A и B найдем как:
[Delta overline{v}={overline{v}}’-overline{v}left(2right).]
Если время, затрачиваемое на движение от точки A до точки B, стремится к нулю, то дуга AB мало не отличается от хорды AB. Треугольники AOB и BMN подобны, получим:
[frac{Delta v}{v}=frac{Delta l}{R}=alpha left(3right).]
Величину модуля среднего ускорения определяют как:
[leftlangle arightrangle =frac{Delta v}{Delta t}=frac{vDelta l}{RDelta t}left(4right).]
Перейдем к пределу при $Delta tto 0 $ от $leftlangle arightrangle $в формуле (4):
[a={mathop{lim }_{Delta tto 0} leftlangle arightrangle }={mathop{lim }_{Delta tto 0} frac{vDelta l}{rDelta t}=frac{v}{R} }mathop{{rm lim}}_{Delta tto 0}frac{Delta l}{Delta t}=frac{v}{R}v=frac{v^2}{R}left(5right).]
Вектор среднего ускорения составляет с вектором скорости угол равный:
[beta =frac{pi +alpha }{2}left(6right).]
При $Delta tto 0 $ угол $alpha to 0.$ Получается, что вектор мгновенного ускорения составляет с вектором скорости угол $frac{pi }{2}$.
И так, что материальная точка, равномерно движущаяся по окружности, обладает ускорением, которое направленно к центру окружности (${overline{a}}_nbot overline{v}$), его величина равна скорости в квадрате, деленной на радиус окружности:
[a_n=frac{v^2}{R}={omega }^2R left(7right),]
где $omega $ – угловая скорость движения материальной точки ($v=omega cdot R$). В векторном виде формулу для центростремительного ускорения можно записать, опираясь на (7) как:
[{overline{a}}_n=-{omega }^2overline{R} left(8right),]
где $overline{R}$ – радиус-вектор, равный по длине радиусу дуги окружности, направленный от центра кривизны к местоположению рассматриваемой материальной точки.
Примеры задач с решением
Пример 1
Задание. Векторное уравнение $overline{r}left(tright)=overline{i}{cos left(omega tright)+overline{j}{sin left(omega tright) } }$, где $omega =2 frac{рад}{с},$ описывает движение материальной точки. По какой траектории движется данная точка? Чему равен модуль ее центростремительного ускорения? Считайте, что все величины в системе СИ.
Решение. Рассмотрим уравнение движения точки:
[overline{r}left(tright)=overline{i}{cos left(omega tright)+overline{j}{sin (omega t) } } left(1.1right).]
В декартовой системе координат это уравнение эквивалентно системе уравнений:
[left{ begin{array}{c}
x={cos left(omega tright);; } \
y={sin left(omega tright) } end{array}
left(1.2right).right.]
Для того, чтобы понять по какой траектории движется точка нам следует исключить время из уравнений системы (1.2). Для этого возведем оба уравнение в квадрат и сложим их:
[x^2+y^2={cos}^2left(omega tright)+{sin}^2left(omega tright)=1 left(1.3right).]
Из уравнения (1.3) мы видим, что траекторией движения точки является окружность (рис.2) радиуса $R=1$ м.
Для того чтобы найти центростремительное ускорение воспользуемся формулой:
[a_n=frac{v^2}{R}left(1.4right).]
Модуль скорости определим используя систему уравнений (1.2). Найдем компоненты скорости, которые равны:
[left{ begin{array}{c}
v_x=frac{dx}{dt}=-omega {sin left(omega tright) }, \
v_y=frac{dy}{dt}=omega {{cos left(omega tright) } , } end{array}
right.left(1.5right).]
Квадрат модуля скорости будет равен:
[v^2=v^2_x+v^2_y={omega }^2left(1.6right).]
Из того, какой получился модуль скорости (1.6), мы видим, что наша точка движется по окружности равномерно, следовательно, центростремительное ускорение будет совпадать с полным ускорением.
Подставим $v^2$ из (1.6) в формулу (1.4), имеем:
[a_n=frac{{omega }^2}{R}.]
Вычислим $a_n$:
$a_n=frac{4}{1}=4 left(frac{м}{с^2}right).$
Ответ. 1) Окружность; 2) $a_n=4 frac{м}{с^2}$
Пример 2
Задание. Каково центростремительное ускорение точек на ободе диска в момент времени, равный $t=2$c,
если диск вращается в соответствии с уравнением: $varphi (t)=3+2t^3$? Радиус диска равен $R=0,{rm 1}$ м.
Решение. Центростремительное ускорение точек диска будем искать, применяя формулу:
[a_n={omega }^2Rleft(2.1right).]
Угловую скорость найдем, используя уравнение $varphi (t)=3+2t^3$ как:
[omega =frac{dvarphi }{dt}=6t^2. ]
При $t=2 $c угловая скорость равна:
[omega left(t=2right)=24 left(frac{рад}{с}right).]
Можно вычислить центростремительное ускорение по формуле (2.1):
[a_n={24}^2cdot 0,1=57,6 left(frac{м}{с^2}right).]
Ответ. $a_n=57,6frac{м}{с^2}$
Читать дальше: формула циклической частоты колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение точки, движущейся по окружности
Полное ускорение точки, движущейся по окружности, складывается из двух составляющих:
- тангенциального ускорения, направленного по касательной к данной окружности;
- центростремительного ускорения, направленного по радиусу от точки к центру окружности.
Замечание 1
Тангенциальное ускорение отражает изменение величины скорости движения, центростремительное, называемое также нормальным и обозначаемое обычно как $a_n$, – измерение направления вектора скорости.
Центростремительное ускорение
Формула для расчета центростремительного ускорения:
$a_n = frac{v^2}{R}$,
где $v$ – мгновенная скорость, $R$ – радиус кривизны траектории.
Выразив мгновенную скорость из угловой как
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
$v = omega cdot R$
и подставив в формулу, найдем центростремительное ускорение как
$a_n = frac{(omega cdot R)^2}{R} = omega^2 cdot R$
Основы теории о центростремительном ускорении заложил голландский физик Христиан Гюйгенс (1629 — 1695 гг.). В своем сочинении “Маятниковые часы” он не только изложил инженерные расчеты, необходимые для изготовления хронометров, но и сформулировал физические законы циклического движения. В частности, Гюйгенс открыл зависимость периодичности колебаний маятника от длины подвеса, описал явление изохронности ввел понятие центробежной силы и центростремительного ускорения. Это дало толчок не только прикладной механике, но и развитию теории о движении небесных тел, повлиявшей, в частности, на научные взгляды Исаака Ньютона.
Особенностью кругового движения является то, что даже если точка движется по окружности со скоростью неизменной величины (тангенциальное ускорение равно нулю), ее суммарное ускорение не равно нулю, поскольку направление вектора скорости всё время меняется. В этом заключается физический смысл центростремительного ускорения.
«Формула центростремительного ускорения в физике» 👇
Геометрически центростремительное ускорение можно выразить следующим образом. Рассмотрим окружность, по которой движется точка.
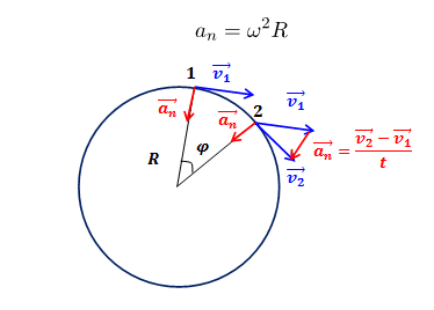
Рисунок 1. Центростремительное ускорение. Автор24 — интернет-биржа студенческих работ
Выберем в качестве ее начального положения верхнюю точку. При этом вектор мгновенной скорости $vec{v_1}$ будет направлен горизонтально. Когда точка пройдет некоторую дугу, вектор мгновенной скорости $vec{v_2}$ окажется наклоненным к первому под углом $varphi$, который равен пройденному угловому расстоянию. Таким образом, центростремительный вектор окажется основанием равнобедренного треугольника с углом при вершине $varphi$ и стороной $bar{v_A} = bar{v_B}$. Обозначим длину основания этого треугольника как $Delta v$. Подобный треугольник со стороной $R$ мы видим внутри окружности. Его вершина соответствует ее центру. Приняв, что при достаточно малом $varphi$ длины дуги и хорды между точками $A$ и $B$ приблизительно совпадают, найдем из подобия треугольников, что
$frac{R}{v cdot Delta t} approx frac{v}{Delta v}$,
где $v cdot Delta t$ – путь, пройденный точкой по дуге, почти совпадающей с хордой.
Формулу можно преобразовать следующим образом:
$frac{Delta v}{Delta t} approx frac{v^2}{R}$
Учитывая малое пройденное угловое расстояние (при $Delta t$ стремящемся к нулю), можно считать вектор $vec{Delta v}$ направленным к центру окружности. Следовательно,
$vec{a_n} = frac{Delta vec{v}}{Delta t}; Delta t to 0; a_n = frac{v^2}{R}$
Замечание 2
Хорошим способом представить себе центростремительное ускорение является конкретный пример. Центростремительное ускорение Земли, вращающейся вокруг своей оси, составляет $0,03 м/с^2$. Это значит, что в его отсутствие почва “уходила бы у нас из под ног” со скоростью 3 см/с.
Пример 1
Велосипедист едет по дороге со скоростью 10 м/с. Какое центростремительное ускорение точки обода колеса, если его радиус 35 см?
Подставим в формулу центростремительного ускорения числовые значения:
$a_n = frac{{10}^2}{0,35} = 285 m/c^2$
Ответ: 285 метров в секунду.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Движение по окружности – простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
∆l=R∆φ
Если угол поворота мал, то ∆l≈∆s.
Проиллюстрируем сказанное:
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω, то есть скорости изменения угла поворота.
Угловая скорость в данной точке траектории – предел отношения углового перемещения ∆φ к промежутку времени ∆t, за которое оно произошло. ∆t→0.
ω=∆φ∆t, ∆t→0.
Единица измерения угловой скорости – радиан в секунду (радс).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
ω=vR
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
an=∆v→∆t, ∆t→0
Модуль центростремительного ускорения можно вычислить по формуле:
an=v2R=ω2R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v→ за малый промежуток времени ∆t. ∆v→=vB→-vA→.
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a→=∆v→∆t, ∆t→0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что OAAB=BCCD.
Если значение угла ∆φ мало, расстояние AB=∆s≈v·∆t. Принимая во внимание, что OA=R и CD=∆v для рассмотренных выше подобных треугольников получим:
Rv∆t=v∆v или ∆v∆t=v2R
При ∆φ→0, направление вектора ∆v→=vB→-vA→ приближается к направлению на центр окружности. Принимая, что ∆t→0, получаем:
a→=an→=∆v→∆t; ∆t→0; an→=v2R.
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
an→=-ω2R→.
Здесь R→ – радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов – нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
aτ=∆vτ∆t; ∆t→0
Здесь ∆vτ=v2-v1 – изменение модуля скорости за промежуток ∆t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие vx и vy.
Если движение равномерное, величины vx и vy а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T=2πRv=2πω
Что такое центростремительное ускорение
Центростремительное ускорение — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.
Центростремительное ускорение, которое также называют нормальным ускорением, всегда направлено к центру окружности, по которой движется точка.
Чему равно центростремительное ускорение
Модуль центростремительного ускорения определяется формулой:
[a_{n}=frac{v^{2}}{R}]
Модуль an остается постоянным, однако направление вектора an все время меняется, поэтому движение по окружности не является равноускоренным.
Центростремительное ускорение также можно определить через угловую скорость:
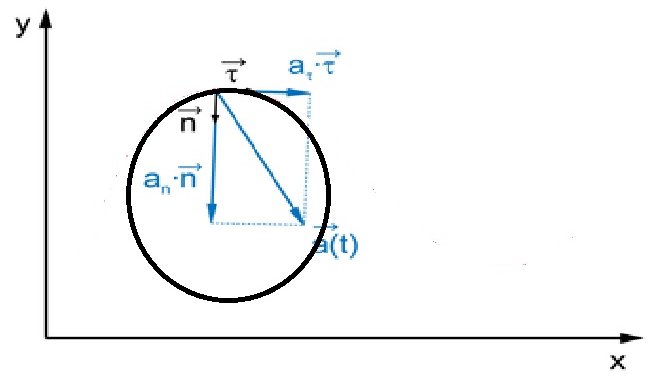
В общем случае ускорение движущейся по окружности точки можно представить в виде двух составляющих – нормальной и тангенциальной. Первая составляющая направлена по касательной к траектории, вторая по радиусу непосредственно к центру круга. Всё это можно представить в виде формулы:
[mathbf{a}=mathbf{d} v / d t=(d v / d t) * boldsymbol{tau}+v *(d tau / d t)=(mathrm{dv} / mathrm{dt}) * boldsymbol{tau}+left(mathrm{v}^{2} / mathrm{R}right) * mathbf{n}]
Где R – радиус окружности, n – единичный вектор нормали к траектории.
Тангенциальное ускорение
Это ускорение (dv/dt) * τ, оно характеризует изменение скорости по величине за единицу времени и является её производной. В системе СИ тангенциальное ускорение измеряется в м/c2. Оно может быть, как положительным, так и отрицательным. При положительных значениях тангенциального ускорения модуль скорости движущейся по окружности точки возрастает и движение именуют ускоренным. При отрицательных значениях величина скорости понижается и движение называют замедленным. Если тангенциальное ускорение постоянно, то к словам ускоренный и замедленный добавляется приставка «равно».
Нет времени решать самому?
Наши эксперты помогут!
Нормальное или центростремительное ускорение
Это вторая составляющая разложенного нами движения (v2/R)*n. Обозначим её как an Поясним, откуда взялись квадрат скорости, радиус и n.
Одновременно умножаем и делим v * (dτ/dt) на стремящийся к нулю элемент длины траектории, т. е. v*(dτ/dl)(dl/dt). Последний множитель в этом выражении есть скорость, его можно записать как v *(dτ/dl)*v. Отсюда v2*(dτ/dl). dl допустимо представить как R*dϕ. dϕ здесь есть малый угол поворота вокруг центра окружности.
n = dϕ/dτ. Это ясно из геометрических соображений. Δτ = τ ′- τ есть разность единичных касательных векторов в рассматриваемой нами точке (τ) и бесконечно близкой к ней точке (τ ′). По величине она равна 2sin(dϕ/2). Здесь dϕ есть угол между τ и τ ′. Эта разность в рассматриваемой точке имеет направление к нормали n под углом dϕ/2. Из-за малости dϕ становится возможным совпадение его с вектором нормали n. Также из-за малости dϕ синус допустимо разложить в ряд Тейлора. В результате всего этого мы приходим к тому, что Δτ = Δϕ * n. Для бесконечно малых это выражение переходит в dτ = dϕ * n.
Мгновенную скорость можно выразить соотношением v =ω*R. После этого формула центростремительного ускорения приобретает у нас вид an = (ω*R)2/R = ω2*R.
Теперь о том, в чем измеряется центростремительное ускорение в физике. Хотя некоторым может показаться странным, но меряется оно, также как и тангенциальное ускорение в метрах на секунду квадрат, т. е. м/c2.
Первым (или одним из первых), кто стал пользоваться понятием центростремительного ускорения, был по-видимому Христиан Гюйгенс. Именно с его времени понятие нормального ускорения в физике начали повсеместно применять при решении самых разных механических задач.
Примеры решения задач
Примеры
Задача №1.
Поезд движется со скоростью 54 километра в час по закруглению, радиус которого равен 1 километру.
Найти чему равно его центростремительное ускорение.
Дано:
Радиус R = 1 км = 1000 м.
Скорость v = 54 км/ч = 15 м/с.
Найти нужно нормальное ускорение [a_{n}].
Решение:
Формула центростремительного ускорения в физике нам известна [a_{n}=v^{2} / R]. Подставляем в неё наши
числовые значения и находим [a_{n}=(15 м/с)^{2} / 1000=0,225 м/
с^{2}].
Ответ: [a_{n}=0,225 м/с^{2}].
Задача №2.
Тело движется по траектории радиусом 5 метров с угловой скоростью 0,3 радиан в секунду. Требуется найти его
центростремительное ускорение.
Дано:
Радиус R = 5 м.
Угловая скорость [omega=0,3 text { рад/с }]
Найти центростремительное ускорение [a_{n}].
Решение:
Опять подставляем числовые значения, но уже в формулу [a_{n}=omega^{2} * R].
[a_{n}=5^{2 *} 0,3=0,45 м/с^{2}].
Ответ: [a_{n}] равно [0,45 м/с^{2}]
Задача №3.
Диск вращается вокруг неподвижной оси. Угол поворота диска изменяется в соответствие с уравнением ϕ = 5t+7.
Нужно вычислить, чему равно центростремительное ускорение очки диска, расположенной на расстоянии R от оси
вращения равном 0,5 м на 4 секунду от времени начала вращения.
Дано:
Радиус R = 0,5 м.
Время t = 4 c.
Закон движения ϕ = 5t+7 .
Найти [a_{n}].
Решение:
Формула центростремительного ускорения, включающая угловую скорость [a_{n}=omega^{2 *} R].
Угловую скорость можно найти по формуле [omega=d phi / d t].
Подставляем вместо ϕ уравнение изменения угла поворота [omega=d(5 t+7) / d t].
Производная этого выражения равна 10t.
Теперь нужно подставить вместо t конкретное числовое значение, т.е. 4 секунды.
Получаем [a_{n}=10 * 4=40 м/с^{2}].
Ответ: [a_{n}] точки на диске равно [40 м/с^{2}].