Как найти модуль индукционного тока

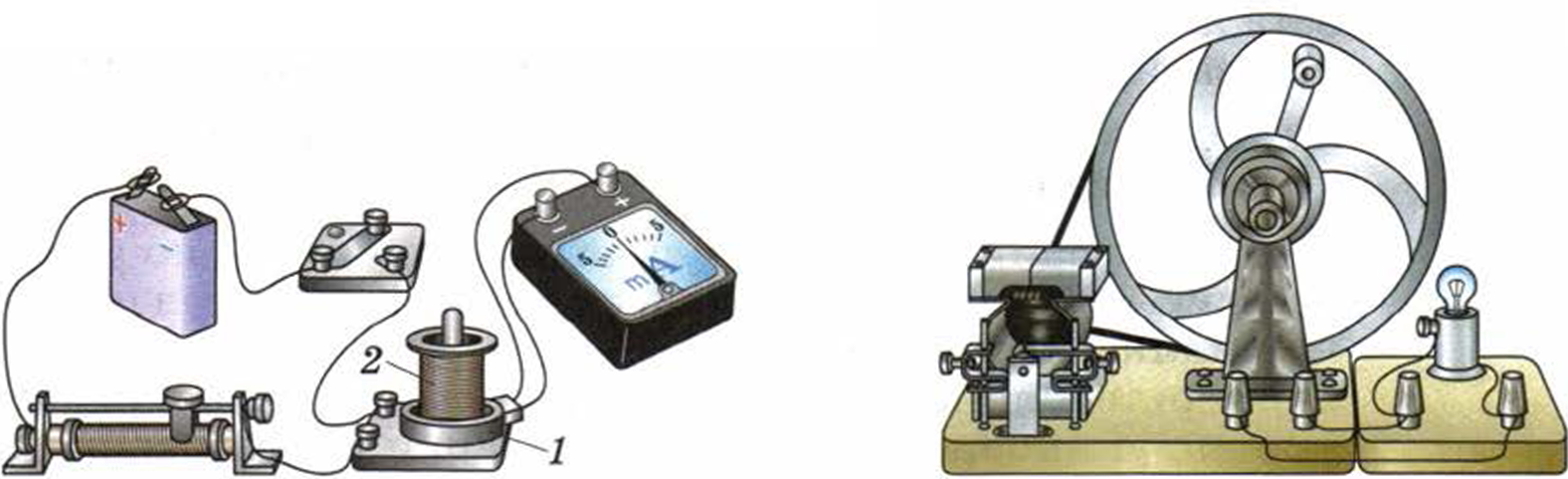
Цель работы: Изучить явление электромагнитной индукции.
Оборудование: Миллиамперметр, катушка-моток, магнит дугообразный, источник питания, катушка с железным сердечником от разборного электромагнита, реостат, ключ, провода соединительные, модель генератора электрического тока (одна на класс).
Указания к работе:
1.    Подключите катушку-моток к зажимам миллиамперметра.
2.    Наблюдая за показаниями миллиамперметра, подводите один из полюсов магнита к катушке, потом на несколько секунд остановите магнит, а затем вновь приближайте его к катушке, вдвигая в неё (рис. 196). Запишите, возникал ли в катушке индукционный ток во время движения магнита относительно катушки; во время его остановки.

 Запишите, менялся ли магнитный поток Ф, пронизывающий катушку, во время движения магнита; во время его остановки.
4.     На основании ваших ответов на предыдущий вопрос сделайте и запишите вывод о том, при каком условии в катушке возникал индукционный ток.
5.     Почему при приближении магнита к катушке магнитный поток, пронизывающий эту катушку, менялся? (Для ответа на этот вопрос вспомните, во-первых, от каких величин зависит магнитный поток Ф и, во-вторых, одинаков
ли модуль вектора индукции В магнитного поля постоянного магнита вблизи этого магнита и вдали от него.)
6.     О направлении тока в катушке можно судить по тому, в какую сторону от нулевого деления отклоняется стрелка миллиамперметра.
Проверьте, одинаковым или различным будет направление индукционного тока в катушке при приближении к ней и удалении от неё одного и того же полюса магнита.

 4.      Приближайте полюс магнита к катушке с такой скоростью, чтобы стрелка миллиамперметра отклонялась не более чем на половину предельного значения его шкалы.
Повторите тот же опыт, но при большей скорости движения магнита, чем в первом случае.
При большей или меньшей скорости движения магнита относительно катушки магнитный поток Ф, пронизывающий эту катушку, менялся быстрее?
При быстром или медленном изменении магнитного потока сквозь катушку сила тока в ней была больше?
На основании вашего ответа на последний вопрос сделайте и запишите вывод о том, как зависит модуль силы индукционного тока, возникающего в катушке, от скорости изменения магнитного потока Ф, пронизывающего этукатушку.
5.      Соберите установку для опыта по рисунку 197.
6.      Проверьте, возникает ли в катушке-мотке 1 индукционный ток в следующих случаях:
а) при замыкании и размыкании цепи, в которую включена катушка 2;
б) при протекании через катушку 2 постоянного тока;
в) при увеличении и уменьшении силы тока, протекающего через катушку 2, путём перемещения в соответствующую сторону движка реостата.
10. В каких из перечисленных в пункте 9 случаев меняется магнитный поток, пронизывающий катушку 1? Почему он меняется?
11. Пронаблюдайте возникновение электрического тока в модели генератора (рис. 198). Объясните, почему в рамке, вращающейся в магнитном поле, возникает индукционный ток.
  Рис. 196

  Рис. 197                                                                               Рис. 198

Индукционные силы

ИНДУКЦИОННЫЕ СИЛЫ — это одна из трех составляющих сил межмолекулярного взаимодействия (силы Ван-дер-Ваальса). Индукционно-динамические силы возникают между полярной и неполярной молекулами — под действием поля полярной молекулы соседняя приобретает индуцированный дипольный момент. Правило индуцирования (наведения) силы соответственно работает для замкнутого проводника, находящегося под воздействием изменяющегося магнитного поля. Возникающая в этом случае электродвижущая сила заставляет заряды двигаться в определенном направлении. Возникает индукционный ток.

Сила индукционного тока

Сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром проводника. Направление индукционного тока определяет правило Ленца: свое магнитное поле противодействует изменению внешнего магнитного потока. Модуль силы рассчитывается по формуле, предварительно найдя ЭДС индукции из закона Фарадея.

Модуль силы индукционного тока в катушке

Представляет особый интерес изучение индукционного тока в катушках индуктивности. Изучая по приборам возникающий (индуцированный изменяющимся магнитным полем магнита или электромагнита) в катушке ток, установили, что он зависит от:

• скорости изменения магнитного поля,
• количества витков катушки (большее число витков соответствует большему значению индуктируемой ЭДС).

Индукционно-динамические силы

Индукционно-динамические системы находят широкое применение на практике в качестве быстродействующих приводов различных устройств. В частности, индукционно-динамические двигатели применяются для создания импульсных механических воздействий на нагрузку и используются при сейсморазведочных работах и при разработке промышленных технологий, требующих применения импульсных механических воздействий. Например, индукционно-динамический привод применяется в ударных устройствах с регулируемым механическим воздействием на рабочее тело при клепке, формовке деталей и в других случаях.

Источник

1. Подключим катушку-моток к зажимам миллиамперметра.

2. Введем один из полюсов магнита в катушку, а затем на несколько секунд остановим магнит. Запишите, возникал ли в катушке индукционный ток: а) во время движения магнита относительно катушки; б) во время его остановки._______________________________________

3. Запишите, менялся ли магнитный поток Ф, пронизывающий катушку: а) во время движения магнита; б) во время его остановки.____________________________________________________

4. Сформулируйте, при каком условии в катушке возникал индукционный ток _________________

______________________________________________________________________________________ 5. Введите один из полюсов магнита в катушку, а затем с такой же скоростью удалите.

а) Запишите, каким будет направление индукционного тока. ______________________________

б) Запишите, каким будет модуль индукционного тока. ___________________________________

6. Повторите опыт, но при большей скорости движения магнита.

а) Запишите, каким будет направление индукционного тока. ______________________________

б) Запишите, каким будет модуль индукционного тока. ___________________________________

7. Запишите, как скорость движения магнита влияет: а) На величину изменения магнитного потока.____________________________________________________________________________

б) На модуль индукционного тока. ____________________________________________________

8. Сформулируйте, как зависит модуль силы индукционного тока от скорости изменения магнитного потока.__________________________________________________________________

9. Соберите установку для опыта по рисунку.

10. Проверьте, возникает ли в катушке-мотке 1 индукционный ток при: а) замыкании и размыкании цепи, в которую включена катушка 2; б) протекании через 2 постоянного тока; в) изменении силы тока реостатом._______________________________________________________

11. Запишите, в каких из перечисленных случаев: а) менялся магнитный поток, пронизывающий катушку 1; б) возникал индукционный ток в катушке 1.___________________________________

Источник

Физика

Возникновение ЭДС приводит к появлению в проводящем контуре индукционного тока , сила которого определяется по формуле

где ℰ i — ЭДС индукции, возникающая в контуре; R — сопротивление контура.

При протекании индукционного тока в контуре выделяется теплота , количество которой определяется одним из выражений:

Q i = I i 2 R t , Q i = ℰ i 2 t R , Q i = I i | ℰ i | t ,

где I i — сила индукционного тока в контуре; R — сопротивление контура; t — время; ℰ i — ЭДС индукции, возникающая в контуре.

Мощность индукционного тока вычисляется по одной из формул:

P i = I i 2 R , P i = ℰ i 2 R , P i = I i | ℰ i | ,

где I i — сила индукционного тока в контуре; R — сопротивление контура; ℰ i — ЭДС индукции, возникающая в контуре.

При протекании индукционного тока в проводящем контуре через площадь поперечного сечения проводника переносится заряд , величина которого вычисляется по формуле

где I i — сила индукционного тока в контуре; Δ t — интервал времени, в течение которого по контуру течет индукционный ток.

Пример 21. Кольцо, изготовленное из проволоки с удельным сопротивлением 50,0 ⋅ 10 −10 Ом ⋅ м, находится в однородном магнитном поле с индукцией 250 мТл. Длина проволоки равна 1,57 м, а площадь ее поперечного сечения составляет 0,100 мм 2 . Какой максимальный заряд пройдет по кольцу при выключении поля?

Решение . Появление ЭДС индукции в кольце вызвано изменением потока вектора индукции, пронизывающего плоскость кольца, при выключении магнитного поля.

Поток индукции магнитного поля через площадь кольца определяется формулами:

• до выключения магнитного поля

Ф 1 = B 1 S cos α,

где B 1 — первоначальное значение модуля индукции магнитного поля, B 1 = 250 мТл; S — площадь кольца; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости кольца;

• после выключения магнитного поля

Ф 2 = B 2 S cos α = 0,

где B 2 — значение модуля индукции после выключения магнитного поля, B 2 = 0.

Изменение потока вектора индукции магнитного поля определяется разностью

∆Ф = Ф 2 − Ф 1 = −Ф 1 ,

или, с учетом явного вида Ф 1 ,

∆Ф = − B 1 S cos α.

Среднее значение ЭДС индукции, возникающей в кольце при выключении поля,

| ℰ i | = | Δ Ф Δ t | = | − B 1 S cos α Δ t | = B 1 S | cos α | Δ t ,

где ∆ t — интервал времени, за который происходит выключение поля.

Наличие ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = B 1 S | cos α | R Δ t ,

где R — сопротивление кольца.

При протекании индукционного тока по кольцу переносится индукционный заряд

q i = I i Δ t = B 1 S | cos α | R .

Максимальному значению заряда соответствует максимальное значение функции косинус (cos α = 1):

q i max = I i Δ t = B 1 S R .

Полученная формула определяет максимальное значение заряда, который пройдет по кольцу при выключении поля.

Однако для расчета заряда необходимо получить выражения, которые позволят найти площадь кольца и его сопротивление.

Площадь кольца — площадь круга радиусом r , периметр которого определяется формулой длины окружности и совпадает с длиной проволоки, из которой изготовлено кольцо:

где l — длина проволоки, l = 1,57 м.

Отсюда следует, что радиус кольца определяется отношением

S = π r 2 = π l 2 4 π 2 = l 2 4 π .

Сопротивление кольца задается формулой

где ρ — удельное сопротивление материала проволоки, ρ = 50,0 × × 10 −10 Ом ⋅ м; S 0 — площадь поперечного сечения проволоки, S 0 = = 0,100 мм 2 .

Подставим полученные выражения для площади кольца и его сопротивления в формулу, определяющую искомый заряд:

q i max = B 1 l 2 S 0 4 π ρ l = B 1 l S 0 4 π ρ .

q i max = 250 ⋅ 10 − 3 ⋅ 1,57 ⋅ 0,100 ⋅ 10 − 6 4 ⋅ 3,14 ⋅ 50,0 ⋅ 10 − 10 = 0,625 Кл = 625 мКл .

При выключении поля по кольцу проходит заряд, равный 625 мКл.

Пример 22. Контур площадью 2,0 м 2 и сопротивлением 15 мОм находится в однородном магнитном поле, индукция которого возрастает на 0,30 мТл в секунду. Найти максимально возможную мощность индукционного тока в контуре.

Решение . Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость контура, при изменении индукции магнитного поля с течением времени.

Изменение потока вектора индукции магнитного поля определяется разностью

где ∆ B — изменение модуля индукции магнитного поля за выбранный интервал времени; S — площадь, ограниченная контуром, S = 2,0 м 2 ; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости контура.

Среднее значение ЭДС индукции, возникающей в контуре, при изменении индукции магнитного поля:

| ℰ i | = | Δ Ф Δ t | = | Δ B S cos α Δ t | = Δ B S | cos α | Δ t ,

где ∆ B /∆ t — скорость изменения модуля вектора индукции магнитного поля с течением времени, ∆ B /∆ t = 0,30 мТл/с.

Появление ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = Δ B S | cos α | R Δ t ,

где R — сопротивление контура.

Мощность индукционного тока

P i = I i 2 R = ( Δ B Δ t ) 2 S 2 R cos 2 α R 2 = ( Δ B Δ t ) 2 S 2 cos 2 α R .

Максимальному значению мощности индукционного тока соответствует максимальное значение функции косинус (cos α = 1):

P i max = ( Δ B Δ t ) 2 S 2 R .

P i max = ( 0,30 ⋅ 10 − 3 ) 2 ( 2,0 ) 2 15 ⋅ 10 − 3 = 24 ⋅ 10 − 6 Вт = 24 мкВт .

Максимальная мощность индукционного тока в данном контуре равна 24 мкВт.

Источник

Как найти модуль индукционного тока

Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока , пронизывающего контур.

Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный , создается магнитным полем с индукцией , пронизывающим по направлению нормали плоский контур площадью :

Эта формула носит название закона Фарадея .

Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца .

Рис. 1.20.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.

Правило Ленца отражает тот экспериментальный факт, что и всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.

1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле перпендикулярное плоскости контура. Пусть одна из сторон контура длиной скользит со скоростью по двум другим сторонам (рис. 1.20.3).

На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен

Работа силы _Л на пути равна

В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для можно придать привычный вид. За время Δ площадь контура изменяется на Δ = υΔ. Изменение магнитного потока за это время равно ΔΦ = υΔ. Следовательно,

Для того, чтобы установить знак в формуле, связывающей _инд и нужно выбрать согласованные между собой по правилу правого буравчика направление нормали и положительное направление обхода контура как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.

Если сопротивление всей цепи равно , то по ней будет протекать индукционный ток, равный _инд = _инд/. За время Δ на сопротивлении выделится джоулево тепло

Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера . Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен _A = . Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δ эта работа равна

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение . Полная работа силы Лоренца равна нулю . Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным . Его называют вихревым электрическим полем . Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 г.

Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково , но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Источник

Индукционные силы

ИНДУКЦИОННЫЕ СИЛЫ — это одна из трех составляющих сил межмолекулярного взаимодействия (силы Ван-дер-Ваальса). Индукционно-динамические силы возникают между полярной и неполярной молекулами — под действием поля полярной молекулы соседняя приобретает индуцированный дипольный момент. Правило индуцирования (наведения) силы соответственно работает для замкнутого проводника, находящегося под воздействием изменяющегося магнитного поля. Возникающая в этом случае электродвижущая сила заставляет заряды двигаться в определенном направлении. Возникает индукционный ток.

Сила индукционного тока

Сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром проводника. Направление индукционного тока определяет правило Ленца: свое магнитное поле противодействует изменению внешнего магнитного потока. Модуль силы рассчитывается по формуле, предварительно найдя ЭДС индукции из закона Фарадея.

Модуль силы индукционного тока в катушке

Представляет особый интерес изучение индукционного тока в катушках индуктивности. Изучая по приборам возникающий (индуцированный изменяющимся магнитным полем магнита или электромагнита) в катушке ток, установили, что он зависит от:

• скорости изменения магнитного поля,
• количества витков катушки (большее число витков соответствует большему значению индуктируемой ЭДС).

Индукционно-динамические силы

Индукционно-динамические системы находят широкое применение на практике в качестве быстродействующих приводов различных устройств. В частности, индукционно-динамические двигатели применяются для создания импульсных механических воздействий на нагрузку и используются при сейсморазведочных работах и при разработке промышленных технологий, требующих применения импульсных механических воздействий. Например, индукционно-динамический привод применяется в ударных устройствах с регулируемым механическим воздействием на рабочее тело при клепке, формовке деталей и в других случаях.

Найти силу индукционного тока

1. Учесть, что индукционный ток всегда имеет направление, которое препятствует изменению внешнего магнитного потока. То есть знак ЭДС индукции противоположен знаку изменения магнитного поля. Это позволит избавиться от модуля.
2. Применить формулу закона Ома для полной цепи.

Электричество, магнетизм и оптика.

Поток вектора магнитной индукции,

закон электромагнитной индукции Фарадея,

индуктивность, энергия магнитного поля катушки с током,

колебательный контур,

законы отражения и преломления света, ход лучей в линзе

В. З. Шапиро

Задание 15 ЕГЭ по физике – это темы «Электромагнитная индукция», «Электромагнитные колебания и волны». Это задание относится к базовому уровню сложности. Задачи носят, в основном, расчетный характер. Их решение основывается на знаниях закона электромагнитной индукции, правила Ленца, понятия индуктивности, самоиндукции, энергии магнитного поля, закономерностях электромагнитных колебаний.

1. На рисунке приведён график зависимости силы тока I от времени t в электрической цепи, содержащей катушку, индуктивность которой 2мГн. Определите модуль ЭДС самоиндукции в катушке в интервале времени от 15 до 20 с.

Ответ: ___________________________ мкВ.

Необходимая теория: Самоиндукция

Для решения задачи надо воспользоваться формулой, определяющей ЭДС самоиндукции.

 знак «минус» в этой формуле учитывает направление индукционного тока, которое определяется по правилу Ленца. Но так как по условию требуется определить модуль ЭДС самоиндукции, то в расчетах этот знак «минус» можно опустить. Так как ток в интервале времени от 15 до 20 с меняется на 20 мА, то эти значения будут определять расчет модуля ЭДС самоиндукции.

(мкВ).

Ответ: 8 мкВ.

Секрет решения. Безусловно, решение подобной задачи требует знаний соответствующей формулы. Но именно в этой теме важно глубокое понимание взаимного превращения электрического и магнитных полей. Ключевым моментом является понятие «изменение» магнитного поля, приводящее к появлению электрического поля. В данном случае теоретические знания происходящих процессов первичны, конечно же, они должны быть подкреплены необходимыми формулами.

Как всегда, следует обратить внимание на единицы измерения. Расчеты – только в системе СИ, ответ в тех единицах измерения, которые требуются по условию.

2. Энергия магнитного поля катушки с током равна 0,32 Дж. Индуктивность катушки равна 10 мГн. Какова сила тока в катушке?

Ответ: ___________________________ А.

Необходимая теория: Самоиндукция

Энергию магнитного поля можно рассчитать по формуле:

(1), где L – индуктивность катушки, I – сила тока в катушке. Выразим силу тока из формулы (1).

 Проведем расчет  (А).

Ответ: 8 А.

Секрет решения. Метод аналогий является одним из основных методов познания. Энергию магнитного поля можно сравнить с кинетической энергией движущегося тела. Индуктивность контура (катушки) аналогична массе тела,  сила тока – скорости, тогда известная формула для  поможет понять, вывести и запомнить формулу для энергии магнитного поля

Этот метод применим и при решении задач. Например, колебательное движение поплавка в воде аналогично колебанию груза на пружине.

3. Колебательный контур состоит из конденсатора емкостью C и катушки индуктивностью L. Во сколько раз увеличится период собственных колебаний контура, если его индуктивность увеличить в 10 раз, а емкость уменьшить в 2,5 раза?

Ответ: в __________________________ раз(а).

Необходимая теория:  Электромагнитные колебания

Период электромагнитных колебаний рассчитывается согласно формуле Томсона

Здесь необходимо рассмотреть два случая.

  (1);

  (2).

Разделив (2) на (1) получим 

Ответ: в 2 раза.

Секрет решения. Для первой части ЕГЭ подобная задача является очень распространенной. Единая формула для двух случаев, в которых изменения могут быть прописаны текстом, заданы графиком или даже схемой.

В этой схеме при переводе ключа из положения 1 в положение 2 емкость конденсатора увеличивается в 4 раза. Соответственно, период возрастает в 2 раза.

Электромагнитная индукция

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ​( S )​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​( B )​, площади поверхности ​( S )​, пронизываемой данным потоком, и косинуса угла ​( alpha )​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ​( Phi )​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​( alpha )​ магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​( N )​ витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​( R )​:

При движении проводника длиной ​( l )​ со скоростью ​( v )​ в постоянном однородном магнитном поле с индукцией ​( vec{B} )​ ЭДС электромагнитной индукции равна:

где ​( alpha )​ – угол между векторами ​( vec{B} )​ и ( vec{v} ).

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​( varepsilon_{is} )​, возникающая в катушке с индуктивностью ​( L )​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ​( Phi )​ через контур из этого проводника пропорционален модулю индукции ​( vec{B} )​ магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ​( L )​ между силой тока ​( I )​ в контуре и магнитным потоком ​( Phi )​, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• закона электромагнитной индукции;
• ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

6. Решение проверить.