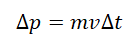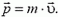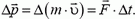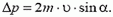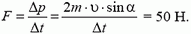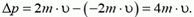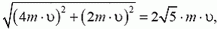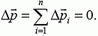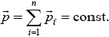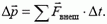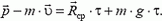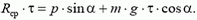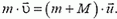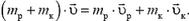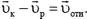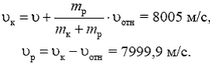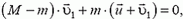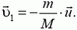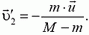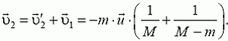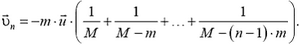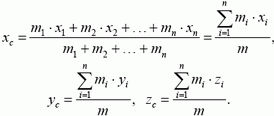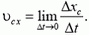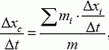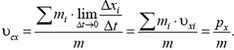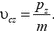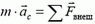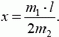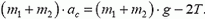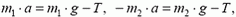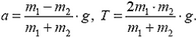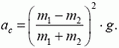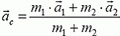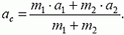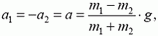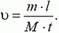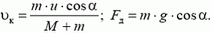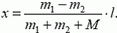Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: |
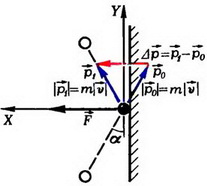
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730

Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520

. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
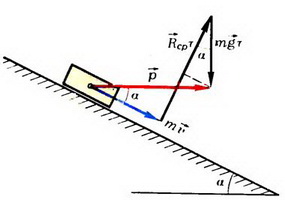
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20k
iSopromat.ru
Пример решения задачи по определению импульса сил, действующих, за определенное время, на материальную точку заданной массы, движущуюся по окружности с постоянной скоростью.
Задача
Материальная точка массой m=10 г движется по окружности с постоянной скоростью 40 см/с.
Найти импульс сил, действующих на точку за время прохождения точкой половины окружности (рисунок 2.3).
Импульс тела, закон сохранения импульса
теория по физике 🧲 законы сохранения
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p 1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
Изменение импульса тела
∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар
Конечный импульс тела:
Модуль изменения импульса тела равен модулю его начального импульса:
Абсолютно упругий удар
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Пуля пробила стенку
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:
Радиус-вектор тела повернул на 180 градусов
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Угол падения равен углу отражения:
Модуль изменения импульса в этом случае определяется формулой:
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:
Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:
Так как угол α = 90 о , вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Материальная точка массой 1 кг равномерно движется по окружности со скоростью 10 м/с. Найти изменение импульса за одну четверть периода; половину периода; период
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,061
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
[spoiler title=”источники:”]
http://www.soloby.ru/309399/%D0%BC%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F-%D1%80%D0%B0%D0%B2%D0%BD%D0%BE%D0%BC%D0%B5%D1%80%D0%BD%D0%BE-%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D0%B8-%D1%81%D0%BA%D0%BE%D1%80%D0%BE%D1%81%D1%82%D1%8C%D1%8E-%D0%B8%D0%B7%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
[/spoiler]
Предположим, что нам дан график зависимости равнодействующей силы, приложенной к какому-то объекту, от времени.
Допустим, что этот график описывает изменение равнодействующей силы, приводящей в движение маленький кораблик на радиоуправлении массой 2.5 килограмма, который мы запустили плавать в спокойную речку.
В задаче требуется найти скорость тела через 7 секунд после начала движения (в самом начале оно покоилось).
Как же мы будем работать? Во-первых, мы найдем изменение импульса на трех ключевых участках, хорошо видных на рисунке.
Потом через импульс мы узнаем скорость кораблика в интересующий нас момент времени (мы сможем это сделать, так как знаем массу тела и его начальную скорость, которая равна нулю):
varDelta{vec{p}}=vec{p}-vec{p}_0
varDelta{vec{p}}=mvec{v}-mvec{v}_0
varDelta{vec{p}}=mvec{v}
vec{v}=dfrac{varDelta{vec{p}}}{m}
Начнем с того, что найдем изменение импульса в промежутке от 0 до 3 секунд. Для этого нам достаточно найти площадь прямоугольника, находящегося под графиком на этом участке. Почему так? Изменение импульса равно произведению суммы приложенных к телу сил и времени, в течение которого они действовали:
varDelta{vec{p}}=varSigma{vec{F}}varDelta{t}
Если теперь взглянуть на график, можно заметить, что модуль этого произведения совпадает с площадью нашего прямоугольника.
Итак, модуль изменения импульса на первом участке равен:
varDelta{p}=S_Box=ab=4thickspaceН×3thickspaceс=12thickspaceН⋅с
Равнодействующая сила действовала в положительном направлении, поэтому и изменение импульса будет положительно:
varDelta{vec{p}}_1=12thickspaceН⋅с
Используя графический способ нахождения модуля изменения импульса, найдем его и на двух других участках:
varDelta{p}_2=dfrac{1}{2}×4thickspaceН×2thickspaceс=4thickspaceН⋅с
varDelta{p}_3=dfrac{1}{2}×2thickspaceН×1thickspaceс=1thickspaceН⋅с
Добавим направления:
varDelta{vec{p}}_2=4thickspaceН⋅с
varDelta{vec{p}}_3=-,1thickspaceН⋅с
Найдем суммарное изменение импульса:
varDelta{vec{p}}=varDelta{vec{p}}_1+varDelta{vec{p}}_2+varDelta{vec{p}}_3
varDelta{vec{p}}=12thickspaceН⋅с+4thickspaceН⋅с-1thickspaceН⋅с
varDelta{vec{p}}=15thickspaceН⋅с
Осталось узнать скорость кораблика через 7 секунд после начала движения:
vec{v}=dfrac{varDelta{vec{p}}}{m}=dfrac{15thickspaceН⋅с}{2.5thickspaceкг}=6thickspaceм/с
Гольдфарб Н., Новиков В. Импульс тела и системы тел // Квант. — 1977. — № 12. — С. 52-58.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Понятие импульса (количества движения) было впервые введено в механику Ньютоном. Напомним, что под импульсом материальной точки (тела) понимается векторная величина 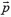
Наряду с понятием импульса тела используется понятие импульса силы. Импульс силы специального обозначения не имеет. В частном случае, когда действующая на тело сила постоянна, импульс силы по определению равен произведению силы на время ее действия: 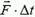
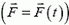
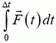
Используя понятие импульса тела и импульса силы, первый и второй законы Ньютона можно сформулировать следующим образом.
Первый закон Ньютона: существуют системы отсчета, в которых сохраняется неизменным импульс тела, если на него не действуют другие тела или действия других тел компенсируются.
Второй закон Ньютона: в инерциальных системах отсчета изменение импульса тела равно импульсу приложенной к телу силы, то есть
В отличие от привычной галилеевской формы второго закона: 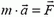
Подчеркнем, что импульс, приобретаемый телом, зависит не только от действующей на тело силы, но и от продолжительности ее действия. Это можно проиллюстрировать, например, на опыте с выдергиванием листа бумаги из-под бутылки — мы оставим ее стоящей практически неподвижно, если сделаем это рывком (рис. 1). Сила трения скольжения, действующая на бутылку в течение очень малого промежутка времени, то есть небольшой импульс силы, вызывает соответственно малое изменение импульса бутылки.
Рис. 1.
Второй закон Ньютона (в «импульсной» форме) дает возможность по изменению импульса тела определить импульс силы, действующей на данное тело, и среднее значение силы за время ее действия. В качестве примера рассмотрим такую задачу.
Задача 1. Мячик массой 50 г ударяет в гладкую вертикальную стенку под углом 30° к ней, имея к моменту удара скорость 20 м/с, и упруго отражается. Определить среднюю силу, действующую на мячик во время удара, если соударение мячика со стенкой длится 0,02 с.
На мячик во время удара действуют две силы — сила 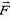
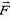
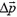
Следовательно, со стороны стенки на мячик действует сила 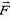
По третьему закону Ньютона мячик действует на стенку с такой же по абсолютной величине силой.
Сравним теперь абсолютные значения импульсов сил 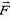
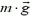
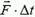
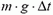
Мы видим, что 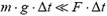
Рис. 2.
Импульс замечателен тем, что под действием одной и той же силы он изменяется одинаково у всех тел, независимо от их массы, если только время действия силы одинаково. Разберем следующую задачу.
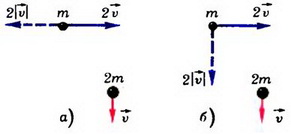
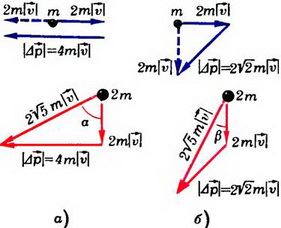
Задача 2. Две частицы массами m и 2m движутся во взаимно перпендикулярных направлениях со скоростями соответственно 2
Рис. 3.
Изменение импульсов обеих частиц одно и то же: на них одинаковое время действовали одинаковые силы. В случае а) модуль изменения импульса первой частицы равен
Вектор 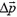
модуль скорости равен 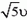

Аналогично найдем, что в случае б) модуль изменения импульса первой частицы равен 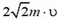
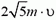
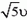
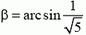
Рис. 4.
Когда мы переходим к системе взаимодействующих тел (частиц), то оказывается, что полный импульс системы — геометрическая сумма импульсов взаимодействующих тел — обладает замечательным свойством сохраняться во времени. Этот закон сохранения импульса является прямым следствием второго и третьего законов Ньютона. В учебнике «Физика 8» этот закон выведен для случая двух взаимодействующих тел, образующих замкнутую систему (эти тела не взаимодействуют ни с какими другими телами). Легко обобщить этот вывод на замкнутую систему, состоящую из произвольного числа n тел. Покажем это.
Согласно второму закону Ньютона изменение импульса i-гo тела системы за малый промежуток времени Δt равно сумме импульсов сил взаимодействия его со всеми другими телами системы:
Изменение полного импульса системы 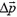
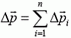
В соответствии с третьим законом Ньютона силы взаимодействия между телами системы попарно одинаковы по абсолютной величине и противоположны по направлению: 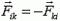
Но если изменение некой величины за произвольный малый промежуток времени Δt равно нулю, то сама эта величина неизменна во времени:
Таким образом, изменение импульса любого из тел, составляющих замкнутую систему, компенсируется противоположным изменением в других частях системы. Иными словами, импульсы тел замкнутой системы могут как угодно изменяться, но сумма их остается постоянной во времени. Если же система не замкнута, то есть на тела системы действуют не только внутренние, но и внешние силы, то, рассуждая подобным образом, придем к выводу, что приращение полного импульса системы за промежуток времени Δt будет равно сумме импульсов внешних сил за тот же промежуток времени:
Импульс системы могут изменить только внешние силы.
Если 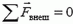
Рассмотрим теперь несколько конкретных задач.
Задача 3. Орудие массы m соскальзывает по гладкой наклонной плоскости, составляющей угол α с горизонтом. В момент, когда скорость орудия равна 
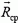
Начальный импульс системы тел орудие — снаряд равен 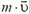
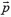
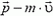
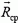
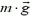
Рис. 5.
Представим это соотношение графически (рис. 6). Из рисунка сразу видно, что искомое значение 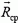
Рис. 6.
Импульс — величина векторная, поэтому закон сохранения импульса можно применять к каждой из его проекций на оси координат. Иначе говоря, если сохраняется 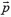
В случае, когда сумма внешних сил не равна нулю, но проекция этой суммы на некоторое направление — нуль, проекция полного импульса на это же направление сохраняется неизменной. Например, при движении системы в поле силы тяжести сохраняется проекция ее импульса на любое горизонтальное направление.
З
адача 4. Горизонтально летящая пуля попадает в деревянный брусок, подвешенный на очень длинном шнуре, и застревает в бруске, сообщив ему скорость u = 0,5 м/с. Определить скорость пули перед ударом. Масса пули m = 15 г, масса бруска М = 6 кг.
Торможение пули в бруске — сложный процесс, но для решения задачи нет никакой необходимости вникать в его детали. Так как в направлении скорости пули до удара и скорости бруска после застревания пули (подвес очень длинный, поэтому скорость бруска горизонтальна) не действуют внешние силы, то можно применить закон сохранения импульса:
Отсюда скорость пули
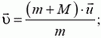
В реальных условиях — в условиях земного притяжения — не существует замкнутых систем, если не включать в них Землю. Однако, если взаимодействие между телами системы много сильнее, чем их взаимодействие с Землей, то можно с большой точностью применять закон сохранения импульса. Так можно поступать, например, при всех кратковременных процессах: взрывах, столкновениях и т. п. (см. например, задачу 1).
Задача 5. Третья ступень ракеты состоит из ракеты-носителя массой mp = 500 кг и головного конуса массой mк = 10 кг. Между ними помещена сжатая пружина. При испытаниях на Земле пружина сообщила конусу скорость υ = 5,1 м/с по отношению к ракете-носителю. Каковы будут скорости конуса υк и ракеты-носителя υp, если их отделение произойдет на орбите при движении со скоростью υ = 8000 м/с?
Согласно закону сохранения импульса
Кроме того,
Из этих двух соотношений получим
Эту задачу можно решать и в системе отсчета, движущейся со скоростью 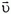
Закон сохранения импульса лежит в основе реактивного движения. Струя газа, вырывающаяся из ракеты, уносит импульс. Этот импульс должен быть скомпенсирован таким же по модулю изменением импульса оставшейся части системы ракета-газ.
Задача 6. Из ракеты массой М выбрасываются продукты сгорания порциями одной и той же массы m со скоростью 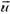
Пусть 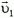
где 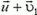
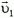
Найдем теперь скорость 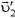
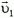
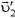
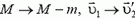
Тогда 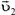
Продолжая этот процесс дальше, нетрудно получить
Закону сохранения импульса можно придать другую форму, упрощающую решение многих задач, если ввести понятие центра масс (центра инерции) системы. Координаты центра масс (точки с) по определению связаны с массами и координатами частиц, составляющих систему, следующими соотношениями:
Следует заметить, что центр масс системы в однородном поле тяжести совпадает с центром тяжести.
Для выяснения физического смысла центра масс вычислим его скорость 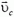
В этой формуле
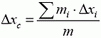
поэтому
Точно так же найдем, что
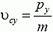
Отсюда следует, что
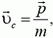
— полный импульс системы равен произведению массы системы на скорость ее центра масс.
Центр масс (центр инерции) системы, таким образом, приобретает смысл точки, скорость которой равна скорости движения системы как целого. Если 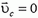
С помощью формулы 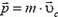
— ускорение центра инерции определяется равнодействующей всех внешних сил, приложенных к системе.
Рассмотрим такие задачи.
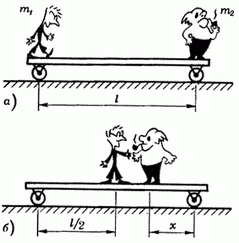
3адача 7. На концах однородной платформы длиной l находятся два человека, массы которых 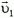
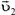
Рис. 7.
Найдем координаты центра масс системы в начальный и конечный моменты и приравняем их (поскольку центр масс остался на том же месте). Примем за начало координат точку, где в начальный момент находился человек массой m1. Тогда
(здесь М — масса платформы). Отсюда
Очевидно, что если m1 > 2m2, то x > l — задача теряет смысл.
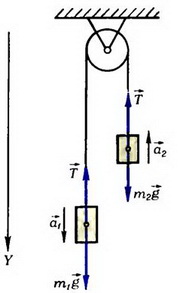
Задача 8. На нити, перекинутой через невесомый блок, подвешены два груза, массы которых m1 и m2 (рис. 8). Найти ускорение центра масс этой системы, если m1 > m2.
Рис. 8.
Система, состоящая из грузов, нити и блока, незамкнутая. Извне на систему действуют силы тяжести грузов 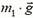
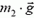
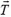
Силу 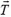
откуда
Подставив полученное значение 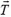
Задачу можно решить и по-другому. Непосредственно из определения центра масс следует, что
(здесь 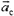
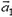
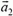
Учитывая, что
получим
Упражнения
1. Два человека стоят на коньках на расстоянии l друг от друга. Один из них бросает мяч массы m, другой подхватывает его через промежуток времени t. С какой скоростью начнет скользить человек, бросавший мяч, если его масса М?
2. По клину с углом при основании α, который может двигаться по гладкому горизонтальному столу, движется заводной игрушечный автомобиль с постоянной по отношению к клину скоростью 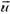
3. Гимнаст массой М, имея при себе груз массой m, прыгает под углом α к горизонту с начальной скоростью 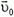
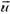
4. Снаряд выброшен орудием с начальной скоростью 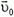
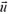
5. Лодка массой М неподвижно стоит в озере. На корме и на носу лодки на расстоянии l друг от друга находятся рыболовы массами m1 и m2 (m1 > m2). Рыболовы меняются местами. На сколько переместится при этом лодка? Сопротивлением воды пренебречь.
6. На краю покоящегося плота массой М стоят n мальчиков, масса каждого из которых равна m. Найти скорость плота после того, как мальчики спрыгнут с одной и той же горизонтальной скоростью и относительно плота: а) одновременно; б) поочередно. В каком случае скорость плота будет больше? Сопротивлением воды пренебречь.
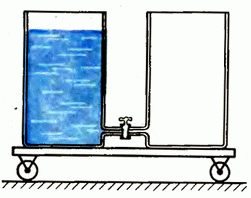
7. На тележке стоят два бака, соединенных между собой трубкой с краном. Один из них наполнен водой (рис. 9). При открывании крана вода переливается в другой бак. Описать характер движения тележки.
Рис. 9.
Ответы
1.
2.
3. 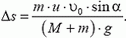
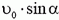
4. 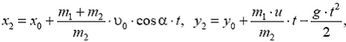
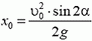
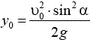
5.
6. а) 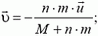
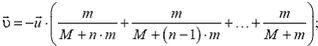
7. Положение центра масс системы не может измениться под действием внутренних сил. Поэтому вначале тележка должна двигаться в сторону, противоположную движению воды. После того, как уровни в баках окончательно сравняются, движение тележки прекратится.
Закон
сохранения импульса
1.
Два
тела движутся по взаимно
перпендикулярным
пересекающимся прямым,
как показано на рисунке.
Модуль
импульса первого тела равен
,
а второго тела равен
.
Чему равен модуль импульса
системы этих тел после их абсолютно
неупругого удара?
1)
2)
3)
4)
Решение.
В
системе не действует никаких
внешних сил, следовательно
выполняется закон сохранения
импульса. Вектор полного
импульса системы есть сумма
векторов
и
.
Так как эти вектора перпендикулярны,
то модуль импульса системы
равен по теореме Пифагора
.
Правильный
ответ: 2.
Ответ:
2
401
2
2.
Система
состоит из двух тел a
и b.
На рисунке стрелками в
заданном масштабе указаны
импульсы этих тел.
Чему
по модулю равен импульс всей
системы?
1)
2)
3)
4)
Решение.
Используя
масштаб рисунка, определим
модули импульсов тел a
и b.
Из рисунка видно, что
и
.
Импульс всей системы равен
.
Так как вектора
и
перпендикулярны,
то модуль импульса всей системы
равен
.
Правильный
ответ: 4.
Ответ:
4
402
4
3.
Система
состоит из двух тел a
и b.
На рисунке стрелками в
заданном масштабе указаны
импульсы этих тел.
Чему
по модулю равен импульс всей
системы?
1)
2)
3)
4)
Решение.

способ:
Сложим
импульсы по правилу
треугольника, суммарный
импульс обозначен на рисунке
красной стрелкой. Видно, что его
длина равна 4 клеткам, следовательно,
импульс системы по модулю
равен
.
Второй
способ (более длинный и менее
удачный):
Используя
масштаб рисунка, определим
модули импульсов тел a
и b.
Из рисунка видно, что
.
Импульс
всей системы равен
.
Так как вектора
и
перпендикулярны,
то модуль импульса всей системы
равен
.
Правильный
ответ: 2.
Ответ:
2
403
2
4.
Система
состоит из двух тел 1 и 2, массы
которых равны 0,5 кг и 2 кг. На
рисунке стрелками в заданном
масштабе указаны скорости
этих тел.
Чему
равен импульс всей системы по
модулю?
1)
2)
3)
4)
Решение.
Используя
масштаб рисунка, определим
величины скоростей тел:
и
.
Вычислим модули импульсов
тел:
и
.
Импульс
всей системы равен
.
Так как вектора
и
перпендикулярны,
то модуль импульса всей системы
равен
.
Правильный
ответ: 1.
Ответ:
1
404
1
5.
Кубик
массой m
движется по гладкому столу
со скоростью
и
налетает на покоящийся
кубик такой же массы. После удара кубики
движутся как единое целое без
вращений, при этом:
1)
скорость кубиков равна
2)
импульс кубиков равен
3)
импульс кубиков равен
4)
кинетическая энергия
кубиков равна
Решение.
На
систему не действует никаких
внешних сил, следовательно
выполняется закон сохранения
импульса. До столкновения
один кубик скользил со скоростью
,
а второй — покоился,
значит полный импульс системы
по модулю был равен
.
Таким
он останется и после столкновения.
Следовательно, утверждение
2 верно. Покажем, что утверждения
1 и 4 ложны. Используя закон
сохранения импульса,
найдем скорость
совместного
движения кубиков после
столкновения:
.
Следовательно скорость
кубиков
,
а не
.
Далее, находим их кинетическую
энергию:
.
Правильный
ответ: 2.
Ответ:
2
405
2
6.
Маятник
массой m
проходит точку равновесия
со скоростью
.
Через половину периода
колебаний он проходит
точку равновесия, двигаясь
в противоположном
направлении с такой же по
модулю скоростью
.
Чему равен модуль изменения
импульса маятника за это
время?
1)
2)
3)
4)
Решение.
Через
половину периода
проекция скорости маятника
меняется на противоположную
и становится равной
.
Следовательно, модуль
изменения импульса
маятника за это время равен
.
Правильный
ответ: 3.
Ответ:
3
406
3
7.
Маятник
массой m
проходит точку равновесия
со скоростью
.
Через четверть периода
колебаний он достигает
точки максимального удаления
от точки равновесия. Чему равен
модуль изменения импульса
маятника за это время?
1)
2)
3)
4)
Решение.
Через
четверть периода, когда
маятник достигает точки
максимального удаления,
его скорость обращается
в ноль. Следовательно, модуль
изменения импульса
маятника за это время равен
.
Правильный
ответ: 2.
Ответ:
2
407
2
8.
Груз
массой m
на пружине, совершая свободные
колебания, проходит
положение равновесия
со скоростью
.
Через половину периода
колебаний он проходит
положение равновесия,
двигаясь в противоположном
направлении с такой же по
модулю скоростью
.
Чему равен модуль изменения
кинетической энергии
груза за это время?
1)
2)
3)
4)
Решение.
Поскольку
кинетическая энергия тела
зависит только от величины
его скорости, но не от ее
направления, а, по условию,
через половину периода
модуль скорости не изменяется,
заключаем, что модуль
изменения кинетической
энергии за это время равен нулю.
Правильный
ответ: 4.
Ответ:
4
408
4
9.
Груз
массой m
на пружине, совершая свободные
колебания, проходит
положение равновесия
со скоростью
.
Через четверть периода
колебаний он достигает
положения максимального
удаления от положения
равновесия. Чему равен модуль
изменения кинетической
энергии груза за это время?
1)
2)
3)
4)
Решение.
Через
четверть периода, когда
маятник достигает
положения максимального
отклонения, его скорость
обращается в ноль. Таким
образом, модуль изменения
кинетической энергии за
это время равен
.
Правильный
ответ: 3.
Ответ:
3
409
3
10.
Если
при увеличении модуля
скорости материальной
точки величина ее импульса
увеличилась в 4 раза, то при этом
кинетическая энергия
1)
увеличилась в 2 раза
2)
увеличилась в 4 раза
3)
увеличилась в 16 раз
4)
уменьшилась в 4 раза
Решение.
Импульс
материальной точки
пропорционален скорости,
а кинетическая энергия —
квадрату скорости:
.
Таким
образом, увеличение
импульса материальной
точки в 4 раза соответствует
увеличению энергии в 16 раз.
Правильный
ответ: 3.
Ответ:
3
414
3
11..
Танк движется со скоростью
,
а грузовик со скоростью
.
Масса танка
.
Отношение величины
импульса танка к величине
импульса грузовика равно
2,25. Масса грузовика равна
1)
1 500 кг
2)
3 000 кг
3)
4 000 кг
4)
8 000 кг
Решение.
Импульс
танка равен
.
Импульс грузовика равен
где
M —
искомая масса. По условию,
.
Таким образом, для массы грузовика
имеем
.
Правильный
ответ: 3
Ответ:
3
416
3
12.
Поезд
движется со скоростью
,
а теплоход со скоростью
.
Масса поезда
.
Отношение модуля импульса
поезда к модулю импульса
теплохода равно 5. Масса
теплохода равна
1)
20 тонн
2)
50 тонн
3)
100 тонн
4)
200 тонн
Решение.
Импульс
поезда равен
.
Импульс теплохода равен
где
M —
искомая масса. По условию,
.
Таким образом, для массы грузовика
имеем
.
Правильный
ответ: 2.
Ответ:
2
417
2
13.
Самолет
летит со скоростью
,
а вертолет со скоростью
.
Масса самолета
.
Отношение импульса
самолета к импульсу
вертолета равно 1,5. Масса
вертолета равна
1)
1 500 кг
2)
3 000 кг
3)
4 000 кг
4)
8 000 кг
Решение.
Импульс
самолета равен
.
Импульс вертолета равен
где
M —
искомая масса. По условию,
.
Таким образом, для массы вертолета
имеем
.
Правильный
ответ: 3. Нcdot м
Ответ:
3
418
3
14.
Автомобиль
движется со скоростью
,
а мотоцикл со скоростью
.
Масса мотоцикла
.
Отношение импульса
автомобиля к импульсу
мотоцикла равно 1,5. Масса
автомобиля равна
1)
1 500 кг
2)
3 000 кг
3)
4 000 кг
4)
8 000 кг
Решение.
Импульс
автомобиля равен
,
где M —
искомая масса. Импульс мотоцикла
равен
.
По условию,
.
Таким образом, для массы автомобиля
имеем
.
Правильный
ответ: 1.
Ответ:
1
419
1
15.
Масса
грузовика
,
масса легкового автомобиля
.
Грузовик движется со
скоростью
.
Отношение величины
импульса грузовика к
величине импульса
автомобиля равно 2,5. Скорость
легкового автомобиля
равна
1)
2)
3)
4)
Решение.
Импульс
грузовика равен
.
Импульс легкового автомобиля
равен
,
где u —
искомая скорость. По условию,
.
Таким образом, для скорости
легкового автомобиля
имеем
.
Правильный
ответ: 4.
Ответ:
4
420
4
16.
Две
тележки движутся навстречу
друг другу с одинаковыми по
модулю скоростями
.
Массы тележек m
и 2m.
Какой будет скорость движения
тележек после их абсолютно
неупругого столкновения?
1)
2)
3)
4)
Решение.
Для
тележек выполняется
закон сохранения импульса,
поскольку на систему не
действует никаких внешних
сил в горизонтально
направлении:
.
Отсюда
находим скорость тележек
после абсолютно неупругого
удара:
.
Правильный
ответ: 4.
Ответ:
4
421
4
17.
Охотник
массой 60 кг, стоящий на
гладком льду, стреляет из ружья
в горизонтальном направлении.
Масса заряда 0,03 кг. Скорость
дробинок при выстреле
.
Какова скорость охотника
после выстрела?
1)
2)
3)
4)
Решение.
Для
охотника с ружьем выполняется
закон сохранения импульса,
поскольку на эту систему не
действует никаких внешних
сил в горизонтальном
направлении:
.
Отсюда
находим скорость охотника
после выстрела:
.
Правильный
ответ: 2.
Ответ:
2
422
2
18.
Тело
движется по прямой в одном
направлении. Под действием
постоянной силы за 3 с импульс
тела изменился на
.
Каков модуль силы?
1)
0,5 Н
2)
2 Н
3)
9 Н
4)
18 Н
Решение.
Сила,
изменение импульса под
действием этой силы и интервал
времени, в течение которого
произошло изменение,
связаны согласно второму
закону Ньютона, соотношением
.
Отсюда
находим модуль силы
.
Правильный
ответ: 2.
Ответ:
2
423
2
19..
Отношение массы грузовика
к массе легкового автомобиля
.
Каково отношение их
скоростей
,
если отношение импульса
грузовика к импульсу
легкового автомобиля
равно 3?
1)
1
2)
2
3)
3
4)
5
Решение.
Импульс
грузовика равен
.
Импульс легкового
автомобиля —
По
условию,
.
Таким образом, отношение
скоростей равно
.
Правильный
ответ: 1.
Ответ:
1
424
1
20.
Тело
движется по прямой. Под действием
постоянной силы величиной
2 Н за 3 с модуль импульса
тела увеличился и стал равен
.
Первоначальный импульс
тела равен
1)
2)
3)
4)
Решение.
Сила,
изменение импульса под
действием этой силы и интервал
времени, в течение которого
произошло изменение,
связаны согласно второму
закону Ньютона, соотношением
Следовательно,
.
Таким
образом, первоначальный
импульс был равен
.
Правильный
ответ: 1.
Ответ:
1
425
1
21.
Два
шара массами m
и 2m
движутся по одной прямой со
скоростями, равными
соответственно
и
.
Первый шар движется за вторым
и, догнав, прилипает к нему.
Чему равен суммарный импульс
шаров после удара?
1)
2)
3)
4)
Решение.
Для
шаров выполняется закон
сохранения импульса,
поскольку на систему не
действует никаких внешних
сил в горизонтально
направлении:
.