Как найти модуль изменения потенциальной энергии

Задания

Версия для печати и копирования в MS Word

Подтемы раздела

№3 статика. гидростатика. механические колебания и волны. импульс. законы сохранения в механике

.01Давление

.02Гидростатика. Сила Архимеда

.03Момент силы, механическое равновесие тела

.04Механические колебания

.05Волны

.06Импульс

.07Закон сохранения импульса и изменения импульса

.08Работа силы

.09Кинетическая энергия

.10Потенциальная энергия силы тяжести и пружины

.11Закон сохранения энергии и изменения энергии

.12Мощность. КПД. Энергия

Энергия – важнейшее понятие и термин в механике. Что такое энергия, и что она значит? Существует множество определений, и вот одно из них.

Что такое энергия?

Энергия в физике – это способность тела совершать работу. 

Кинетическая энергия

Что такое кинетическая энергия?

Рассмотрим тело, которое двигалось под действием каких-то сил, изменило свою скорость с v1→ до v2→. В этом случае силы, действующие на тело, совершили определенную работу A. 

Работа всех сил, действующих на тело, равна работе равнодействующей силы. 

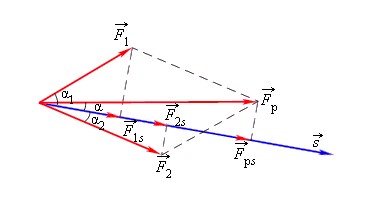
Fр→=F1→+F2→

A=F1·s·cosα1+F2·s·cosα2=Fрcosα.

Как находить связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила F→, направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы F→, v→, a→, s→ совпадают по направлению и их можно рассматривать как алгебраические величины. 

Работа силы F→ равна A=Fs. Перемещение тела выражается формулой s=v22-v122a. Отсюда:

A=Fs=F·v22-v122a=ma·v22-v122a

A=mv22-mv122=mv222-mv122.

Если вычислять, то работа, совершенная силой, пропорционально изменению квадрата скорости тела. 

Теорема о кинетической энергии

Вновь будем работать с рассмотренным примером и сформулируем теорему о кинетической энергии тела.

Таким образом, кинетическая энергия тела массы m, движущегося со скоростью v→, будет измеряться (при измерении) и равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.

A=mv22=EK.

Чтобы остановить тело, нужно совершить работу 

A=-mv22=-EK

Потенциальная энергия

Что будет означать или обозначать кинетическая энергия?

Кинетическая энергия – это энергия движения. Наряду с кинетической энергией есть еще такой вид энергии как потенциальная энергия, то есть энергия взаимодействия тел, которая будет вычисляться и зависеть от их положения. Кинетическая и потенциальная энергии рассматриваются параллельно.

Формула потенциальной энергии:

E пот = m * g * h

Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциал-я энергия. Когда тело движется и падает вниз под действием силы тяжести (притяжения), эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.

Вообще о потенциально энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.

Примеры консервативных сил: сила тяжести, сила упругости.

Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу. 

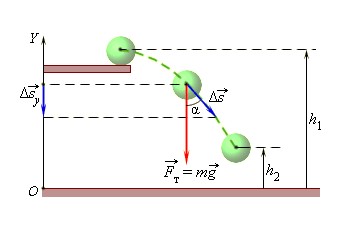
Рассмотрим вычисление на примере, когда шар переместился из точки с высотой h1 в точку с высотой h2. 

При этом сила тяжести совершила работу, равную 

A=-mg(h2-h1)=-(mgh2-mgh1).

Эта работа равна изменению величины mgh, взятому с противоположным знаком. 

Величина ЕП=mgh – потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальную энергию тела можно не рассчитывать: она равна нулю.

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

A=-(EП2-EП1).

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.

EП=-GmMr.

Здесь G – гравитационная постоянная, M – масса Земли.

Потенциальная энергия пружины

Представим, что в первом случае мы взяли пружину и удлинили ее на величину x. Во втором случае мы сначала удлинили пружину на 2x, а затем уменьшили на x. В обоих случаях пружина оказалась растянута на x, но это было сделано разными способами. 

При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна

Aупр=-A=-kx22.

Величина Eупр=kx22 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.

Если перед вами часто поднимается вопрос определения и характеристики энергии, как явления, вам стоит подумать о сохранении описанной выше информации.

1. Определение потенциальной энергии

В предыдущем параграфе мы говорили о работе, которую может совершить тело за счет уменьшения своей скорости, а теперь нас будет интересовать работа, которую может совершить тело или система тел вследствие изменения положения тел.

Рассмотрим примеры.

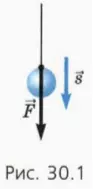
Работа поднятого груза. Когда подвешенный на тросе груз равномерно движется вниз, он действует на трос силой, направленной тоже вниз (рис. 30.1).

Эта сила обусловлена силой тяжести: она совершает работу, действуя на груз, а груз совершает работу, действуя на трос.

Итак, благодаря действию силы тяжести груз может совершить работу при движении вниз.

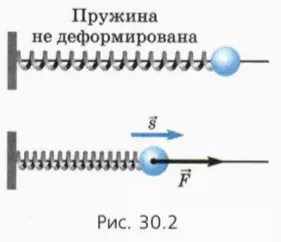
Работа пружины. Когда деформация пружины уменьшается, пружина действует на тело силой упругости, направленной так же, как перемещение тела (рис. 30.2). При этом пружина совершает положительную работу.

Итак, деформированная пружина может совершить работу при возвращении в недеформированное состояние.

В рассмотренных примерах работу совершают силы тяготения и силы упругости. Как мы уже знаем, общая важная особенность этих сил состоит в том, что при движении по замкнутой траектории (когда тело возвращается в начальное положение) работа этих сил равна нулю. (Такие силы называют консервативными. Если между телами замкнутой системы действуют только консервативные силы, то, как мы увидим далее, механическая энергия системы сохраняется («консервируется»).)

Благодаря этому для системы тел, взаимодействующих посредством сил тяготения и упругости, можно определить потенциальную энергию как величину, характеризующую способность системы тел совершать работу и зависящую только от взаимного положения тел.

Потенциальная энергия системы тел характеризует ее способность совершать работу вследствие изменения взаимного положения взаимодействующих тел.

Если система тел совершает положительную работу, потенциальная энергия системы уменьшается. А если система тел совершает отрицательную работу, ее потенциальная энергия увеличивается. При этом

изменение потенциальной энергии системы тел равно работе сил упругости и тяготения, действующих со стороны тел системы, взятой со знаком минус:

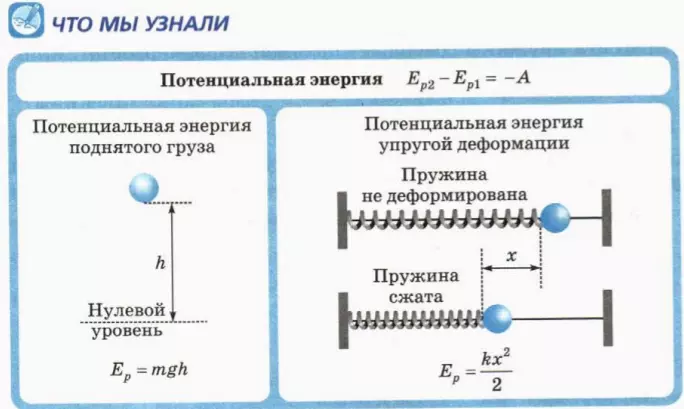
E_p2 – E_p1 = –A     (1)

Здесь E_p1 и E_p2 обозначают начальную и конечную потенциальную энергию системы тел.

(Мы приводим определение потенциальной энергии, применимое к механическим явлениям. В дальнейшем мы расширим и уточним это определение.)

? 1. Как изменяется потенциальная энергия системы «камень + Земля», когда камень движется вверх? вниз? Объясните свои ответы.

? 2. Как изменяется потенциальная энергия пружины, когда деформация уменьшается? увеличивается? Объясните свои ответы.

Нулевой уровень потенциальной энергии. Из формулы (1) следует, что физический смысл имеет только изменение потенциальной энергии: оно измеряется работой, совершенной телами системы.

Поэтому нулевой уровень потенциальной энергии (состояние системы, которому сопоставляется нулевое значение потенциальной энергии) выбирают так, чтобы упростить расчеты.

2. Потенциальная энергия поднятого груза

Когда груз массой m равномерно перемещается вертикально вниз на расстояние h, он совершает положительную работу mgh, потому что он действует на опору или поднес направленной вниз силой (весом груза), равной силе тяжести.

Следовательно, при уменьшении высоты груза на h потенциальная энергия груза уменьшается на mgh. (Важно понимать, что это потенциальная энергия системы взаимодействующих тел – груза и Земли.) Если сопоставить нулевой уровень потенциальной энергии наинизшему положению груза, то

потенциальная энергия груза массой m, поднятого на высоту h, выражается формулой

E_p = mgh. (2)

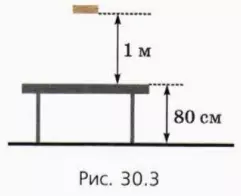
? 3. Брусок массой 200 г поднят на высоту 1 м над поверхностью стола высотой 80 см (рис. 30.3).

а) Чему равна потенциальная энергия бруска, если за нулевой уровень потенциальной энергии бруска принять уровень стола? уровень пола?
б) Чему равно изменение потенциальной энергии бруска при его падении на стол, если за нулевой уровень потенциальной энергии бруска принять уровень стола? уровень пола?

Эти примеры подтверждают, что имеет значение только изменение потенциальной энергии. Оно измеряется работой, совершенной телом или системой тел, и не зависит от выбора нулевого уровня потенциальной энергии.

3. Потенциальная энергия упругой деформации

При возвращении в недеформированное состояние сила упругости пружины совершает положительную работу

A = (kx²)/2.

При этом потенциальная энергия пружины уменьшается на такую же величину. Если нулевому уровню потенциальной энергии сопоставить состояние недеформированной пружины, то

потенциальная энергия деформированной пружины жесткостью k выражается формулой

Ep = (kx²)/2,     (3)

где x – деформация пружины.

Потенциальную энергию, выражаемую формулой (3), называют также потенциальной энергией упругой деформации. Она зависит от квадрата деформации. Поэтому потенциальная энергия сжатой пружины равна потенциальной энергии растянутой пружины, если модуль деформации пружины в обоих случаях один и тот же.

? 4. В начальном состоянии пружина жесткостью 200 Н/м сжата на 1 см. Как изменилась потенциальная энергия пружины, если в конечном состоянии:
а) пружина не деформирована?
б) сжата на 2 см?
в) растянута на 1 см?
г) растянута на 2 см?

? 5. Шар массой 200 г подвешен к пружине жесткостью 100 Н/м и находится в равновесии, Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка.
а) На какую высоту подняли шар?
б) Как изменилась потенциальная энергия шара за время, в течение которого он возвращался в положение равновесия?
в) Как изменилась за то же время потенциальная энергия пружины?
г) Как изменилась за то же время потенциальная энергия системы «шар + Земля + пружина»?

Дополнительные вопросы и задания

6. С высоты 20 м над поверхностью земли свободно без начальной скорости падает камень массой 300 г. За нулевой уровень потенциальной энергии камня примите уровень земли.
а) Чему равна потенциальная энергия камня в начальный момент?
б) Чему равна потенциальная энергия камня через 1 с после начала движения?
в) Через какое время после начала движения потенциальная энергия камня уменьшилась в 2 раза по сравнению с ее начальным значением?

7. Шар массой 1 кг брошен с поверхности земли с начальной скоростью 20 м/с под углом 30º к горизонту. Считайте, что сопротивлением воздуха при движении шара можно пренебречь.
а) До какой максимальной высоты поднялся шар?
б) Как изменилась потенциальная энергия шара за время подъема?

8. По реке с постоянной скоростью плывет плот. Как изменяется со временем:
а) кинетическая энергия плота?
б) потенциальная энергия плота?

9. Когда сжатую пружину сжали еще на 2 см, ее потенциальная энергия увеличилась в 9 раз.
а) Во сколько раз модуль конечной деформации пружины больше, чем модуль начальной деформации?
б) Чему равен модуль начальной деформации пружины?

10. Две пружины жесткостью 100 Н/м и 400 Н/м соединены последовательно. Систему соединенных пружин растянули на 5 см.
а) Чему равна деформация более мягкой пружины?
б) Чему равна деформация более жесткой пружины?
в) Потенциальная энергия упругой деформации какой пружины больше, и во сколько раз?