Модуль и аргумент комплексного числа
Пусть задано комплексное число $ z = a+bi $.
| Формула |
| Модуль комплексного числа равен корню квадратному из суммы квадратов мнимой и действительной части и находится по формуле: $$ |z| = sqrt{a^2 + b^2} $$ |
Если комплексное число состоит только из действительной части $ z = a $, то его модуль равен $ |z| = |a| $.
Стоит заметить, что модуль комплексных чисел всегда неотрицательный $ |z| ge 0 $ и равен нулю $ |z| = 0 $, только в случае $ z = 0 $.
| Формула |
Аргумент комплексного числа обозначается $ varphi = arg z $ и зависит от полуплоскости, в которой лежат числа $a,b$:
|
Введите комплексное число
Пример 1 Пример 2 Правила ввода
| Пример 1 |
| Найти модуль и аргумент комплексного числа $ z = 3 – 4i $. |
| Решение |
|
Комплексное число состоит из действительной и мнимой части: $$ a = Re z = 3 $$ $$ b = Im z = -4 $$ Применяя формулу вычисления модуля получаем: $$ |z| = sqrt{a^2 + b^2} = sqrt{3^2 + (-4)^2} = sqrt{9+16} = 5 $$ Теперь вычисляем аргумент. Так как $a = 3 > 0$, то получаем аргумент: $$varphi = arctg frac{b}{a} = arctg frac{-4}{3} = -arctg frac{4}{3}.$$ |
| Ответ |
| $$ |z| = 5, varphi = -arctg frac{4}{3} $$ |
| Пример 2 |
| Найти модуль и аргумент комплексного числа $ z = 3i $ |
| Решение |
|
В данном случае отсутствует действительная часть, а вернее она равна нулю: $$ a = Re z = 0 $$ Мнимая часть комплексного числа равна: $$ b = Im z = 3 $$ Вычисляем модуль по уже известной формуле: $$ |z| = sqrt{a^2 + b^2} = sqrt{0^2 + 3^2} = sqrt{9} = 3 $$ А вот аргумент здесь попадает под правило при $a = 0, b>0$ и значит равен $$varphi = frac{pi}{2}.$$ |
| Ответ |
| $$ |z| = 3, varphi = frac{pi}{2} $$ |
| Пример 3 |
| Найти модуль и аргумент комплексного числа $$ z = 1+sqrt{3}i $$ |
| Решение |
|
Выписываем действительную и мнимую часть: $$ a = 1 $$ $$ b = sqrt{3} $$ Так как $ a > 0 $, то аргумент равен $$ varphi = arctg frac{sqrt{3}}{1} = arctg sqrt{3} = frac{pi}{3} $$ Находим модуль извлекая квадратный корень из суммы квадратов действительной и мнимой части: $$|z| = sqrt{1^2 + (sqrt{3})^2} = sqrt{1+3}=2.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ varphi = frac{pi}{3}, |z| = 2 $$ |
| Пример 4 |
| Найти аргумент комплексного числа $$ z = -1 + sqrt{3}i $$ |
| Решение |
|
Действительная часть $$ a = Re z = -1 $$ Мнимая часть $$ b = Im z = sqrt{3} $$ Так как $ a < 0 $ и $ b > 0 $, то пользуемся второй формулой: $$ varphi = arg z = pi + arctg frac{sqrt{3}}{-1} = pi + arctg (-sqrt{3}) = $$ $$ = pi – arctg(sqrt{3}) = pi – frac{pi}{3} = frac{2pi}{3}. $$ |
| Ответ |
| $$ varphi = frac{2pi}{3} $$ |
Модулем комплексного числа z=x+iyz = x+iy называется вещественное число, равное
∣z∣=x2+y2.|z| = sqrt{x^2+y^2}.
Модуль всегда определен (другими словами, модуль есть у любого комплексного числа): в самом деле, какими бы ни были xx и yy, сумма квадратов x2+y2x^2+y^2 есть число неотрицательное, а значит, из него можно извлечь квадратный корень, и он тоже будет неотрицательным числом. Модуль равен нулю в единственном случае: если z=0z=0, то есть x=y=0x=y=0. Если же хотя бы одна из координат x,yx, y отлична от нуля, ее квадрат будет строго положительным, и, следовательно, значение выражения x2+y2sqrt{x^2+y^2} также будет строго положительным. Итак, модуль любого ненулевого числа есть строго положительное число.
Мы знаем, что любое вещественное число можно представить как комплексное число с нулевой мнимой частью:
x=x+0⋅i.x = x + 0 cdot i.
Для такого числа формула модуля дает следующий результат:
∣z∣=x2+02=x2=∣x∣.|z| = sqrt{x^2+0^2} = sqrt{x^2} = |x|.
Таким образом, для вещественных чисел новое (комплексное) определение модуля совпадает со старым. Так и должно быть, если мы расширяем известное понятие.
Говорят, что понятие модуля комплексного числа обобщает понятие модуля вещественного числа.
Как найти модуль комплексного числа
Модуль числа выражает расстояние от этого числа до нуля. В самом деле, на плоскости расстояние между точками с координатами (x,y)(x,y) и (x1,y1)(x_1,y_1) вычисляется по формуле
d=(x−x1)2+(y−y1)2.d = sqrt{(x-x_1)^2+(y-y_1)^2}.
Если в этой формуле положить x1=y1=0x_1=y_1=0, то есть в качестве второй точки взять начало координат, то мы получим
d=x2+y2.d = sqrt{x^2+y^2}.
Эта формула выражает расстояние до начала координат от точки (x,y)(x,y), и это расстояние в точности равно модулю комплексного числа x+yi.x+yi.
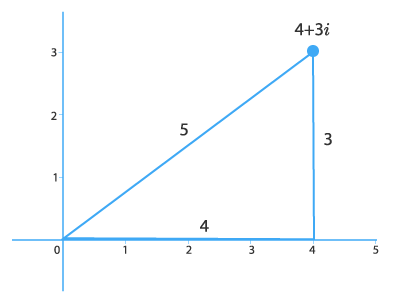
Для примера на следующем рисунке изображено комплексное число 4+3i,4+3i, модуль которого равен 42+32=25=5sqrt{4^2+3^2} = sqrt{25} = 5. Отрезок длины 55, соединяющий начало координат с точкой (4,3)(4,3), служит гипотенузой прямоугольного треугольника с катетами 44 и 33.
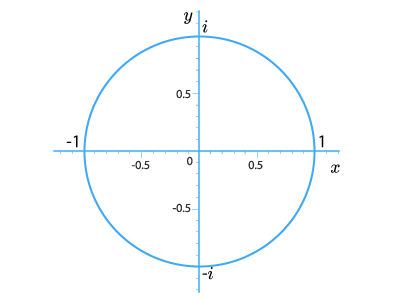
Все комплексные числа, модуль которых равен определенному положительному числу rr, образуют окружность радиуса rr с центром в нуле. На следующем рисунке изображена окружность радиуса 11, на которой лежат все комплексные числа единичного модуля (среди них числа 1,1, −1,-1, ii и −i-i).
Пример решения задачи
Найти модули комплексных чисел 6+8i, 8−6i, −15, 4i,32+12i.6+8i, 8-6i, -15, 4i, frac{sqrt{3}}{2}+frac{1}{2}i.
Решение
∣6+8i∣=62+82=100=10.|6+8i| = sqrt{6^2+8^2} = sqrt{100} = 10.
∣8−6i∣=82+(−6)2=100=10.|8-6i| = sqrt{8^2+(-6)^2} = sqrt{100} = 10.
∣−15∣=∣−15+0⋅i∣=(−15)2+02=152=15.|-15| = |-15+0 cdot i| = sqrt{(-15)^2+0^2} = sqrt{15^2} = 15.
∣4i∣=∣0+4i∣=02+42=42=4.|4i| = |0+4i| = sqrt{0^2+4^2} = sqrt{4^2} = 4.
∣32+12i∣=(32)2+(12)2=34+14=1=1.|frac{sqrt{3}}{2}+frac{1}{2}i| = sqrt{left(frac{sqrt{3}}{2}right)^2 + left(frac{1}{2}right)^2} = sqrt{frac{3}{4} + frac{1}{4}} = sqrt{1} = 1.
Тест на тему “Модуль комплексного числа”
Содержание:
- Аргумент комплексного числа
Определение: Модулем комплексного числа 
называется число 
, то есть 
.
Свойство 1. Если 
, где 
, то 
. Доказательство этого свойства очевидным образом получается из определения модуля комплексного числа. Таким образом, понятие модуля комплексного числа является развитием и обобщением понятия модуля действительного числа.
Свойство 2. Модуль комплексного числа равен модулям противоположного и сопряженного этому числу чисел. Доказательство. Рассмотрим комплексное число 
, а также противоположное 
и сопряженное 
ему числа. Найдем их модули:
Свойство доказано.
Замечание. Число 
равно модулю (длине) вектора 
, то есть 
.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Пример 1.
Найдите 
. Решение:
Так как 5 — действительное число, то по свойству 1 получаем: 
. Ответ: 5.
Пример 2.
Найдите 
. Решение:
Запишем число 
в алгебраической форме: 
. Тогда, по определению модуля комплексного числа, получим: 
. Ответ: 1.
Пример 3.
Найдите 
. Решение:
Число 
представлено в алгебраической форме. По определению модуля комплексного числа получим: 
. Ответ: 
.
Возможно вам будут полезны данные страницы:
Пример 4.
Изобразите на комплексной плоскости все комплексные числа с модулем, равным 
. Решение:
Все комплексные числа с модулем 
изображаются точками комплексной плоскости, которые являются концами радиус-векторов длины 
. Множество таких точек есть окружность с центром в начале координат и радиусом 
.
Не нарушая общности рассуждений, можно сделать следующий вывод. Свойство 3. Изображением множества комплексных чисел с модулем 
на комплексной плоскости является окружность с центром в начале координат и радиусом 
. Доказательство этого утверждения состоит в последовательном применении определения модуля комплексного числа и определения окружности с центром в начале координат и радиусом 
.
Пример 5.
Изобразите на комплексной плоскости все комплексные числа с модулем, меньшим или равным 2. Решение:
Все комплексные числа с модулем, меньшим или равным 2, изображаются точками комплексной плоскости, которые являются концами радиус-векторов длины, меньшей или равной 2. Множество таких точек есть круг с центром в начале координат и радиусом 2.
Пример 6.
Изобразите на комплексной плоскости все такие комплексные числа, что 
. Решение:
Все комплексные числа с модулем, меньшим 4, изображаются точками комплексной плоскости, которые являются концами радиус-векторов длины, меньшей 4. Множество таких точек есть внутренняя часть круга с центром в начале координат и радиусом 4.
Пример 7.
Изобразите на комплексной плоскости все комплексные числа с модулем, большим или равным 3. Решение:
В данной задаче рассматриваются все точки плоскости, кроме внутренних точек круга с центром в начале координат и радиусом 3.
Пример 8.
Изобразите на комплексной плоскости все комплексные числа 
, удовлетворяющие условию 
. Решение:
В данной задаче рассматриваются точки комплексной плоскости, которые являются концами радиус-векторов длины, большей или равной 2 и меньшей 4. Множество таких точек есть внутренняя часть круга с центром в начале координат и радиусом 4 без внутренней части круга с тем же центром и радиусом 2. Это кольцо, ограниченное двумя концентрическими окружностями с центром в начале координат и радиусами 2 и 4 (при этом внутренняя окружность включена в множество, а внешняя — не включена).
Пример 9.
Изобразите на комплексной плоскости все комплексные числа, удовлетворяющие условию
. Решение:
В данной задаче рассматриваются все точки плоскости, кроме точек, расположенных между концентрическими окружностями и на меньшей окружности. Центры окружностей — начало координат, радиусы равны 2 и 4.
Пример 10.
Изобразите на комплексной плоскости множество чисел 
таких, что 
. Решение:
Напомним, что геометрической интерпретацией модуля разности двух чисел, в том числе и комплексных, является расстояние между соответствующими точками. В данном случае речь идет о расстоянии от некоторой точки г комплексной плоскости до точки 
. Таким образом, получаем круг радиуса 4 с центром в точке 
.
Пример 11.
Изобразите на комплексной плоскости множество чисел г таких, что 
. Решение:
В данной задаче нужно изобразить множество точек комплексной плоскости, расстояние от каждой из которых до точки (5; 0) меньше или равно расстоянию до точки (-7; 0). Это прямая 
и правая полуплоскость, ограниченная этой прямой.
Аргумент комплексного числа
Радиус-вектор точки 
комплексной плоскости задается двумя числами: 
— длиной (модулем) вектора, 
— углом между вектором и положительным направлением оси 
.
Замечание 5. Если — аргумент комплексного числа 
, то любое число вида 
, где 
, также является аргументом данного числа . Верно и обратное утверждение: если число 
является аргументом данного комплексного числа , то оно представимо в виде 
, где 
— некоторое целое число. Оба утверждения очевидным образом следуют из свойства периодичности тригонометрических функций.
Свойство 4. Два ненулевых комплексных числа равны тогда и только тогда, когда их модули равны, а аргументы отличаются на
, где
, где 
. Предлагаем читателю доказать этот факт самостоятельно.Пример 12.
Изобразите на комплексной плоскости л все комплексные числа с аргументом
Решение:
Все комплексные числа с аргументом 
изображаются точками комплексной плоскости, которые являются концами ненулевых радиус-векторов, образующих с положительным направлением оси абсцисс угол . Множество таких точек есть луч 
, который образует с положительным направлением оси абсцисс угол . Заметим, что при этом имеется в виду луч без начальной точки.
Пример 13.
Изобразите на комплексной плоскости все комплексные числа с аргументом 
. Решение:
Все комплексные числа с аргументом 
изображаются точками комплексной плоскости, которые являются концами ненулевых радиус-векторов, образующих с положительным направлением оси абсцисс угол 
. Множество таких точек есть луч 
, который образует с положительным направлением оси абсцисс угол . Напомним, что при этом имеется в виду луч без начальной точки.
Пример 14.
Изобразите на комплексной плоскости все комплексные числа с аргументами 
. Решение:
Все комплексные числа с аргументами 
изображаются точками комплексной плоскости, которые являются концами ненулевых радиус-векторов, образующих с положительным направлением оси абсцисс углы 
или 
. Множество таких точек есть прямая 
с выколотой точкой (0; 0).
Пример 15.
Изобразите на комплексной плоскости все комплексные числа с аргументами 
такими, что 
. Решение:
Все комплексные числа с указанными аргументами изображаются точками комплексной плоскости, расположенными ниже лучей 
. Это угол без одной из сторон и вершины (см. рис.).
Пример 16.
Изобразите на комплексной плоскости все комплексные числа с аргументами 
такими, что 
. Решение:
Все комплексные числа с указанными аргументами изображаются точками комплексной плоскости, расположенными между лучами 
и 
. Это угол без одной из сторон и вершины (см. рис.).
Лекции:
- Пределы функций примеры решения
- Найти предел используя правило Лопиталя
- Решение неравенств
- Элементы дифференциальной геометрии
- Неопределенный интеграл
- Декартовы координаты на плоскости и в пространстве
- Наибольшее значение функции
- Степенные ряды. Теорема Абеля
- Построить ряд по степеням
- Интегрирование рациональных дробей
Что такое комплексное число
Комплексное число — это выражение типа (z;=;a;+;ib). Здесь a и b будут являться любыми действительными числами, а i — специальным числом, называемым мнимой единицей. Действительная часть комплексного числа обозначается как (a;=;RE;z ), а мнимая часть — (b;=;Im;z).
Во множестве комплексных чисел содержится множество вещественных чисел. Если множество комплексных чисел — это всевозможные пары (x, y), то содержащееся в нем множество вещественных чисел — это пары (x, 0). Те же комплексные числа, которые задают пары (0, y) являются мнимыми.
Что такое модуль комплексного числа
Модуль комплексного числа — это длина вектора, который изображает комплексное число.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Любое комплексное число кроме 0 может быть выражено в тригонометрической форме.
(z;=;left|zright|;cdot;(cosleft(varphiright);+;isinleft(varphiright)))
В этом виде (left|zright|) — модуль комплексного числа z. Может обозначаться как p и r.
Если (left|zright|;=;r,) то r будет обозначать длину радиус-вектора точки M (x, y).
Вычисление модуля комплексного числа, если в алгебраической форме оно выглядит как z = x + iy, возможно по следующей формуле:
(left|zright|;=;sqrt{x^2;+;y^2})
То есть модуль комплексного числа можно вычислить как квадратный корень из суммы квадратов действительной и мнимой его частей.
Модуль комплексного числа имеет следующие свойства:
- Модуль не отрицателен — (left|xright|;geq;0). (left|xright|;=;0) только в том случае, если z = 0.
- Модуль суммы двух комплексных чисел будет меньше или равен сумме модулей: (left|z_1;+;z_2right|;leq;left|z_1right|;+;left|z_2right|.)
- Модуль результата умножения двух комплексных числе будет равен произведению модулей: (left|z_1;cdot;z_2right|;=;left|z_1right|;cdot;left|z_2right|.)
- Модуль результата деления двух комплексных чисел будет равняться частному модулей: (left|z_1;div;z_2right|;=;left|z_1right|;div;left|z_2right|.)
- Модуль неравенства комплексных чисел будет равен расстоянию между этими числами на комплексной плоскости: (left|z_1;-;z_2right|;=;sqrt{left(x_1;-;x_2right)^2;+;left(y_1;-;y_2right)^2}).
Что такое аргумент комплексного числа
Аргумент комплексного числа — это угол (varphi) радиус-вектора точки, соответствующей комплексному числу (z;:;varphi;=;arg;z) на комплексной плоскости. Этот угол измеряется в радианах.
Каждое комплексное число, которое не равно нулю, имеет бесконечное множество аргументов. Эти аргументы отличаются друг от друга на целое число полный оборотов — (360^circ;cdot;k) при k — любое число.
Связь аргумента комплексного числа с его координатами отражена в следующих формулах:
(tanleft(varphiright);=;frac ba)
(cosleft(varphiright);=;frac a{sqrt{a^2;+;b^2}})
(sinleft(varphiright);=;frac b{sqrt{a^2;+;b^2}})
Важно помнить, что ни одна из этих формул отдельно недостаточна для того, чтобы найти аргументы. Формулы используются в совокупности, а также учитывается номер четвертый на координатной плоскости, в которой находится комплексное число.
Аргумент может быть записан в тригонометрической форме. Для комплексного числа (z = x + iy), это будет выглядеть следующим образом:
(z;=;r;(cosleft(varphiright);+;i;sinleft(varphiright)))
Здесь (r) будет модулем комплексного числа (z), а (varphi) — arg z.
Важно отметить, arg z имеет смысл лишь при (z neq 0), комплексное число ноль не имеет аргумента.
Как вывести формулу модуля
В соответствии с теоремой Пифагора длина вектора с координатами a и b равна (sqrt{a^2;+;b^2}).
Так как именно эта величина называется модулем комплексного числа (z = a + bi), тогда (left|xright|;=;sqrt{a^2;+;b^2}).
Примеры решения задач
Задача
Найти модуль числа (z;=;-5;+;15i)
Решение
(x;=;Re;z;=;-15) — действительная часть, а (y;=;Im;z;=;15) — мнимая часть комплексного числа (z;=;-5;+;15i.)
Таким образом, модуль числа равен следующему выражению:
(r;=;sqrt{x^2;+;y^2};=sqrt{{(-5)}^2;+;15^2};=;sqrt{25;+;225};=;sqrt{250} )
Ответ: (r;=;sqrt{250})
Задача
Найти расстояние между числами (z_1;=;1;-;3i,;z_2;=;-2;+;2i) на комплексной плоскости.
Решение
Расстояние между двумя комплексными числами находятся как модуль разности комплексных чисел. Используем необходимую формулу:
(left|z_1;-;z_2right|;=;sqrt{{(x_1;-;x_2)}^2;+;left(y_1;-;y_2right)^2};=;sqrt{(1;-;{(-2))}^2;+;{(-2;-;2)}^2};=;sqrt{34})
Ответ: (sqrt{34})
Задача
Найти значение аргумента комплексного числа (sqrt{34}) и выразить его в тригонометрической форме.
Решение
Если действительно частью комплексного числа (z;=;1;+;sqrt{3i}) является число (x = Re z = 1), а мнимой частью является (y = Im z;=sqrt3), то аргумент можно вычислить по формуле:
(varphi;=;arg;z;=;arctg;frac yx;=;arctg;frac{sqrt3}1;=;arctg;sqrt3;=;frac{mathrmpi}3)
Теперь для нахождения тригонометрической формы записи комплексного числа необходимо найти модуль.
(r;=;sqrt{x^2;+;y^2};=;sqrt{1^2;+;{(sqrt3)}^2};=;sqrt{1+3};=;sqrt4;=;2)
Исходя из этого, тригонометрическая форма комплексного числа выглядит следующим образом:
(z;=;2;(cosleft(frac{mathrmpi}3right);+;i;sinleft(frac{mathrmpi}3right)))
Ответ: аргумент равен (frac{mathrmpi}3). Тригонометрическая форма записана выше.
Задача
Найти модуль и аргумент числа (z = 2 – i)
Решение
Найдем (left|zright|;=;sqrt{2^2;+;{(-;1)}^2};=;sqrt5.)
Так как (Re z = 2 > 0), (Im z = -1 < 0), точка расположена в 4 четверти. Тогда из равенства (tanleft(varphiright);=;-frac12) следует:
(varphi;=;arctanleft(-frac12right))
Ответ: (varphi;=;arctanleft(-frac12right))
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Длина радиус-вектора, который изображает заданное комплексное число $z=a+bi$, называется модулем данного комплексного числа.
Модуль заданного комплексного числа вычисляется по следующей формуле:
[r=|z|=|a+bi|=sqrt{a^{2} +b^{2} } .]
Пример 1
Вычислить модуль заданных комплексных чисел $z_{1} =13,, , z_{2} =4i,, , , z_{3} =4+3i$.
Решение:
Модуль комплексного числа $z=a+bi$ вычислим по формуле: $r=sqrt{a^{2} +b^{2} } $.
Для исходного комплексного числа $z_{1} =13$ получим $r_{1} =|z_{1} |=|13+0i|=sqrt{13^{2} +0^{2} } =sqrt{169} =13$
Для исходного комплексного числа $, z_{2} =4i$ получим $r_{2} =|z_{2} |=|0+4i|=sqrt{0^{2} +4^{2} } =sqrt{16} =4$
Для исходного комплексного числа $, z_{3} =4+3i$ получим $r_{3} =|z_{3} |=|4+3i|=sqrt{4^{2} +3^{2} } =sqrt{16+9} =sqrt{25} =5$
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Угол $varphi $, образованный положительным направлением вещественной оси и радиус-вектором $overrightarrow{OM} $, который соответствует заданному комплексному числу $z=a+bi$, называется аргументом данного числа и обозначается $arg z$.
Примечание 1
Модуль и аргумент заданного комплексного числа в явном виде используются при представлении комплексного числа в тригонометрической или показательной форме:
- $z=rcdot (cos varphi +isin varphi )$ – тригонометрическая форма;
- $z=rcdot e^{ivarphi } $ – показательная форма.
Пример 2
Записать комплексное число в тригонометрической и показательной формах, заданное следующими данными: 1) $r=3;varphi =pi $; 2) $r=13;varphi =frac{3pi }{4} $.
«Модуль и аргумент комплексного числа» 👇
Решение:
1) Подставим данные $r=3;varphi =pi $ в соответствующие формулы и получим:
$z=3cdot (cos pi +isin pi )$ – тригонометрическая форма
$z=3cdot e^{ipi } $ – показательная форма.
2) Подставим данные $r=13;varphi =frac{3pi }{4} $ в соответствующие формулы и получим:
$z=13cdot (cos frac{3pi }{4} +isin frac{3pi }{4} )$ – тригонометрическая форма
$z=13cdot e^{ifrac{3pi }{4} } $ – показательная форма.
Пример 3
Определить модуль и аргумент заданных комплексных чисел:
1) $z=sqrt{2} cdot (cos 2pi +isin 2pi )$; 2) $z=frac{5}{3} cdot (cos frac{2pi }{3} +isin frac{2pi }{3} )$; 3) $z=sqrt{13} cdot e^{ifrac{3pi }{4} } $; 4) $z=13cdot e^{ipi } $.
Решение:
Модуль и аргумент найдем, используя формулы записи заданного комплексного числа в тригонометрической и показательной формах соответственно
[z=rcdot (cos varphi +isin varphi );] [z=rcdot e^{ivarphi } .]
1) Для исходного комплексного числа $z=sqrt{2} cdot (cos 2pi +isin 2pi )$ получим $r=sqrt{2} ;varphi =2pi $.
2) Для исходного комплексного числа $z=frac{5}{3} cdot (cos frac{2pi }{3} +isin frac{2pi }{3} )$ получим $r=frac{5}{3} ;varphi =frac{2pi }{3} $.
3) Для исходного комплексного числа $z=sqrt{13} cdot e^{ifrac{3pi }{4} } $ получим $r=sqrt{13} ;varphi =frac{3pi }{4} $.
4) Для исходного комплексного числа $z=13cdot e^{ipi } $ получим $r=13;varphi =pi $.
Аргумент $varphi $ заданного комплексного числа $z=a+bi$ можно вычислить, используя следующие формулы:
[varphi =tgfrac{b}{a} ;cos varphi =frac{a}{sqrt{a^{2} +b^{2} } } ;sin varphi =frac{b}{sqrt{a^{2} +b^{2} } } .]
На практике для вычисления значения аргумента заданного комплексного числа $z=a+bi$ обычно пользуются формулой:
$varphi =arg z=left{begin{array}{c} {arctgfrac{b}{a} ,age 0} \ {arctgfrac{b}{a} +pi ,a
или решают систему уравнений
$left{begin{array}{c} {cos varphi =frac{a}{sqrt{a^{2} +b^{2} } } } \ {sin varphi =frac{b}{sqrt{a^{2} +b^{2} } } } end{array}right. $. (**)
Пример 4
Вычислить аргумент заданных комплексных чисел: 1) $z=3$; 2) $z=4i$; 3) $z=1+i$; 4) $z=-5$; 5) $z=-2i$.
Решение:
1) $z=3$
Так как $z=3$, то $a=3,b=0$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{0}{3} =arctg0=0.]
2) $z=4i$
Так как $z=4i$, то $a=0,b=4$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{4}{0} =arctg(infty )=frac{pi }{2} .]
3) $z=1+i$.
Так как $z=1+i$, то $a=1,b=1$. Вычислим аргумент исходного комплексного числа, решая систему (**):
[left{begin{array}{c} {cos varphi =frac{1}{sqrt{1^{2} +1^{2} } } =frac{1}{sqrt{2} } =frac{sqrt{2} }{2} } \ {sin varphi =frac{1}{sqrt{1^{2} +1^{2} } } =frac{1}{sqrt{2} } =frac{sqrt{2} }{2} } end{array}right. .]
Из курса тригонометрии известно, что $cos varphi =sin varphi =frac{sqrt{2} }{2} $ для угла, соответствующего первой координатной четверти и равного $varphi =frac{pi }{4} $.
4) $z=-5$
Так как $z=-5$, то $a=-5,b=0$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{0}{-5} +pi =arctg0+pi =0+pi =pi .]
5) $z=-2i$
Так как $z=-2i$, то $a=0,b=-2$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{-2}{0} =arctg(-infty )=frac{3pi }{2} .]
Примечание 3
Аргумент чисто мнимых чисел равен соответственно:
- $frac{pi }{2} $ с положительной мнимой частью;
- $frac{3pi }{2} $ с отрицательной мнимой частью.
Решение:
Число $z_{1} $ изображено точкой $(3;0)$, следовательно, длина радиус-вектора равна 3, т.е. $r=3$, а аргумент $varphi =0$ по примечанию 2.
Число $z_{2} $ изображено точкой $(-2;0)$, следовательно, длина соответствующего радиус-вектора равна 2, т.е. $r=2$, а аргумент $varphi =pi $ по примечанию 2.
Число $z_{3} $ изображено точкой $(0;1)$, следовательно, длина соответствующего радиус-вектора равна 1, т.е. $r=1$, а аргумент $varphi =frac{pi }{2} $ по примечанию 3.
Число $z_{4} $ изображено точкой $(0;-1)$, следовательно, длина соответствующего радиус-вектора равна 1, т.е. $r=1$, а аргумент $varphi =frac{3pi }{2} $ по примечанию 3.
Число $z_{5} $ изображено точкой $(2;2)$, следовательно, длина соответствующего радиус-вектора равна $sqrt{2^{2} +2^{2} } =sqrt{4+4} =sqrt{8} =2sqrt{2} $, т.е. $r=2sqrt{2} $, а аргумент $varphi =frac{pi }{4} $ по свойству прямоугольного треугольника.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
