Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 мая 2021 года; проверки требуют 16 правок.
| Магнитная индукция | |
|---|---|
 |
|
| Размерность | MT−2I−1 |
| Единицы измерения | |
| СИ | Тл |
| СГС | Гс |
| Примечания | |
| Векторная величина |
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Магни́тная инду́кция — векторная физическая величина, являющаяся силовой характеристикой магнитного поля, а именно характеристикой его действия на движущиеся заряженные частицы и на обладающие магнитным моментом тела.
Стандартное обозначение: 
Величина магнитной индукции фигурирует в ряде важнейших формул электродинамики, включая уравнения Максвелла.
Для измерения магнитной индукции 
Вектор 

Физический смысл[править | править код]
Магнитная индукция 



- (по величине
).
Косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (вектор 
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещённую в предполагаемое однородным (на расстояниях порядка размера рамки) магнитное поле, к произведению силы тока 
Магнитная индукция выступает основной, фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля 
Способы расчёта[править | править код]
Общий случай[править | править код]
В общем случае расчёт магнитной индукции проводится совместно с расчётом электрической составляющей электромагнитного поля посредством решения системы уравнений Максвелла:
,
где 





Магнитостатика[править | править код]
В магнитостатическом пределе[3] расчёт магнитного поля может быть выполнен с использованием формулы Био—Савара—Лапласа. Вид этой формулы несколько различен для ситуаций, когда поле создаётся текущим по проводу 

.
В магнитостатике эта формула играет ту же роль, что закон Кулона в электростатике. Формула позволяет вычислить магнитную индукцию в вакууме. Для случая магнитной среды необходимо использовать уравнения Максвелла (без слагаемых с производными по времени).
Если заранее очевидна геометрия поля, помогает теорема Ампера о циркуляции магнитного поля[4] (эта запись является интегральной формой уравнения Максвелла для 
.
Здесь 

- Простые примеры
Вектор магнитной индукции прямого провода с током 

,
где 
Вектор магнитной индукции прямого внутри соленоида с током 

,
где 
Связь с напряжённостью[править | править код]
Магнитная индукция и напряжённость магнитного поля связаны через соотношение
,
где 
Основные уравнения[править | править код]
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в большое число уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, — это электростатика.
Некоторые из уравнений:
- из которого следуют выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле,
- Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
- (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).
- Выражение для плотности энергии магнитного поля
.
- Оно входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля, и в лагранжиан электромагнитного поля, и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).
Типичные значения[править | править код]
| объект |  , Тл , Тл |
объект |  , Тл , Тл
|
|---|---|---|---|
| магнитоэкранируемая комната | 10-14 | солнечное пятно | 0,15 |
| межзвёздное пространство | 10-10 | небольшой магнит (Nd-Fe-B) | 0,2 |
| магнитное поле Земли | 5*10-5 | большой электромагнит | 1,5 |
| 1 см от провода с током 100 А | 2*10-3 | сильный лабораторный магнит | 10 |
| небольшой магнит (феррит) | 0,01 | поверхность нейтронной звезды | 108 |
Примечания[править | править код]
См. также[править | править код]
- Векторный потенциал
- Уравнения Максвелла
- Электромагнитное поле
- Тензор электромагнитного поля
- Напряжённость магнитного поля
Магнитная индукция
Магнитная индукция — это силовая характеристика магнитного поля в выбранной точке пространства. Она определяет силу, с которой магнитное поле воздействует на заряженную частицу, что движется внутри него. Магнитная индукция считается фундаментальной характеристикой магнитного поля (как напряжённость для электрического поля).
Магнитная индукция описывает магнитную силу (вектор) на тестовом объекте (например, на куске железа) в каждой точке пространства. Простыми словами: если естественный магнит поднести к магнитным веществам (таким, как железо, никель, кобальт и т. д.), это вызовет в них магнитные свойства, которые называются “магнитной индукцией”. Магнитная индукция используется для создания искусственных магнитов.
Магнитная индукция также называется плотностью магнитного потока.
Магнитная индукция измеряется:
- в системе СИ единицей тесла (Тл),
- в системе СГС единицей гаусс (Гс).
Соотношение между Тл и Гс: 1 Тл = 10 000 Гс.
Магнитная индукция — это векторная величина и обозначается буквой B со стрелочкой:

Индукция (от лат. inducere — вводить, наведение) — производство токов в цепи под действием магнита или другого тока.
Формулы вычисления магнитной индукции
Формула магнитной индукции:

Где:
- B — индукция магнитного поля (в Тл)
- Mmax — максимальный крутящий момент магнитных сил, приложенных к рамке (в Нм)
- l — длина проводника (в м)
- S — площадь рамки (в м²)
Другие формулы, где встречается B
Эти формулы также можно использовать для её расчёта.
Сила Ампера:

Где:
- Fa — сила Ампера (в Н — ньютон)
- I — сила тока (в А — ампер)
- B — индукция магнитного поля (в Тл)
- L — длина проводника (в м)
- α — угол между вектором В и одним из направлений (силы тока, скорости или др.; измеряется в рад. или град.)
Сила Лоренца:

Где:
- Fл — сила Лоренца (в Н — ньютон)
- q — заряд частицы (в Кл — кулон)
- v — скорость (в м/с)
- B — индукция (в Тл)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Магнитный поток:

Где:
- Ф — магнитный поток (в Вб – вебер)
- B — индукция (в Тл)
- S — площадь рамки (в м²)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Электромагнитная индукция и магнитная индукция: какая между ними разница?
Электромагнитная индукция — это производство электродвижущей силы, создаваемой в результате относительного движения между магнитным полем и проводником.
Магнитная индукция может производить постоянный магнит, но может и не производить.
Электромагнитная индукция создаёт ток, но таким образом, что этот созданный ток противодействует изменению магнитного поля.
В электромагнитной индукции используются магниты и электрические цепи, а в магнитной индукции используются только магниты и магнитные материалы.
Узнайте также про:
- Магнитное поле,
- Магнитное поле Земли,
- Уравнения Максвелла
- Напряженность электрического поля.
Что такое магнитная индукция и магнитный поток
Магнитное поле, так же как и электрическое поле, является одной из сторон электромагнитного поля и представляет собой один из видов материи. Оно возникает, например, при движении электрических зарядов и, в частности, вокруг проводов с током.
Магнитное поле обладает энергией называемой энергией магнитного поля, которая проявляет себя различным образом, например в действии одного провода с током на другой провод с током, находящийся в магнитном поле первого, или в действии магнитного поля проводника с током на магнитную стрелку.
Физический смысл магнитной индукции
Прежде, чем перейти к рассмотрению формулы магнитной индукции, нужно выяснить, чем объясняется возникновение самого явления в системе. Соленоид не является плоским элементом и включает в себя спираль из проводника (металла). При отсутствии воздействующих на него магнитных явлений находящиеся в кристаллической решетке материала спирали электрозаряды ведут себя статично. Когда в соленоиде движется постоянный магнитный элемент, формирующий поле, под его влиянием движутся и заряженные частицы, тогда в индуктивном элементе появляется электрический ток, сила которого определяется характеристиками магнитного и спирального элемента и тем, как быстро происходит движение.
Важно! Имеющие одинаковую ориентацию поля суммируются, образуя общее поле. Когда передвижение заряженных частиц в соленоиде прекращается, сердечник перестает проявлять магнитные характеристики, если он выполнен из мягкого металла (к стальным изделиям это правило не относится).
Чем характеризуется магнитная индукция
Более мелкой единицей магнитного потока, не относящейся к системе СИ, является максвелл
1 мкс = 10-8вб = 1 гс•см2.
Так как магнитная индукция характеризуется числом магнитных линий, проходящих через единицу площади поверхности, перпендикулярной направлению поля, то магнитный поток будет характеризоваться числом линий, проходящих через площадь S.
Единицы измерения магнитной индукции
В международной системе единиц (СИ) сила измеряется в ньютонах, ток — в амперах, длина — в метрах, поэтому единица измерения магнитной индукции
[B] = [F : (Il)] = н : (a • м) = дж/м : (a • м) = (в • k) : (a • м2) = (в • а • сек) : (a • м2) = (в • сек) : м2
Единица вольт-секунда называется вебер (вб), а вебер, деленный на квадратный метр, — тесла (тл),
таким образом:
[B] = вб : м2 = тл
Кроме единицы тесла, иногда применяется гаусс (гс) — единица магнитной индукции, не принадлежащая к системе СИ, при этом
1 гс — 10-4 тл, или 1 тл = 104 гс.
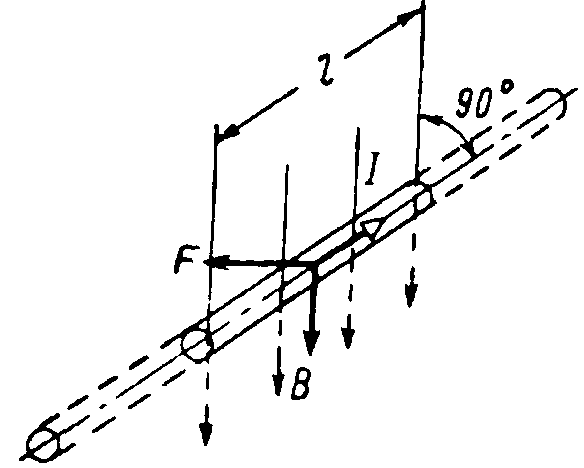
Рис. 3. Провод с током в магнитном поле.
Магнитная индукция — векторная величина. Направление вектора магнитной индукции совпадает с направлением поля в данной точке.
Магнитное поле, во всех точках которого векторы магнитной индукции одинаковы по величине и параллельны друг другу, называется однородным.
Линии магнитной индукции можно использовать не только для указания направления поля, но и для характеристики его интенсивности.
Для этого условно через единичную площадку, перпендикулярную к направлению поля, проводят число линий, равное или пропорциональное величине магнитной индукции в данном месте поля.
Произведение магнитной индукции В на площадь S, перпендикулярную к вектору магнитной индукции, называется магнитным потоком, т. е.
Ф = BS.
Формула магнитной индукции:
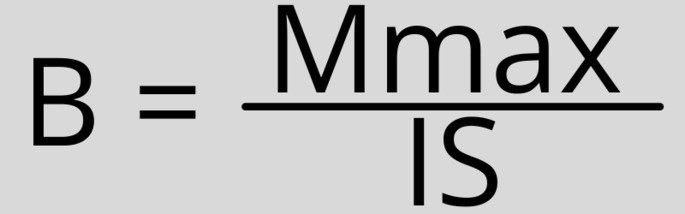
Формула магнитной индукции: B = Mmax/IS
Где:
- B — индукция магнитного поля (в Тл)
- Mmax — максимальный крутящий момент магнитных сил, приложенных к рамке (в Нм)
- l — длина проводника (в м)
- S — площадь рамки (в м²)
Формула для определения модуля магнитной индукции
Если проводник расположен перпендикулярно линиям магнитной индукции 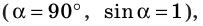
поле действует на проводник с максимальной силой:
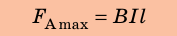
Отсюда получаем формулу для определения модуля магнитной индукции:
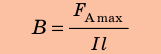
Обратите внимание! Значение магнитной индукции не зависит ни от силы тока в проводнике, ни от длины проводника, а зависит только от свойств магнитного поля.
Например, если уменьшить силу тока в проводнике, то уменьшится и сила Ампера, с которой магнитное поле действует на проводник, а вот значение магнитной индукции останется неизменным.
В СИ единица магнитной индукции — тесла (Тл), единица силы — ньютон (Н), силы тока — ампер (А), длины — метр (м), поэтому:
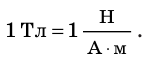
1 Тл — это индукция такого однородного магнитного поля, которое действует с максимальной силой 1 Н на проводник длиной 1 м, в котором течет ток силой 1 А.
- Заказать решение задач по физике
Пример №3
Докажите, что два параллельных проводника, в которых текут токи одного направления, притягиваются.
Анализ физической проблемы. Около любого проводника с током существует магнитное поле, следовательно, каждый из двух проводников находится в магнитном поле другого. На первый проводник действует сила Ампера со стороны магнитного поля, созданного током во втором проводнике, и наоборот. Определив по правилу левой руки направления этих сил, выясним, как будут вести себя проводники.
Решение
Решая задачу, выполним пояснительные рисунки: изобразим проводники А и В, покажем направления тока в них и т. д.
Выясним направление силы Ампера, которая действует на проводник А, находящийся в магнитном поле проводника В.
- С помощью правила буравчика найдем направление линий магнитной индукции магнитного поля, созданного проводником В(рис. 1, а). Выясняется, что вблизи проводника А магнитные линии направлены к нам (обозначено «•»).
- Воспользовавшись правилом левой руки, определим направление силы Ампера, действующей на проводник А со стороны магнитного поля проводника В (рис. 1, б).
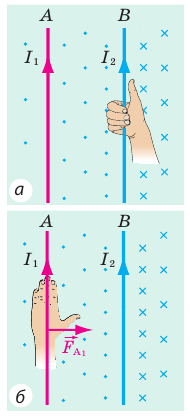
Рис. 1
3. Приходим к выводу: проводник А притягивается к проводнику В.
Теперь выясним направление силы Ампера, которая действует на проводник В, находящийся в магнитном поле проводника А.
1) Определим направление линий магнитной индукции магнитного поля, созданного проводником А (рис. 2, а). Выясняется, что вблизи проводника В магнитные линии направлены от нас (обозначено 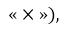
2) Определим направление силы Ампера, действующей на проводник В (рис. 2, б).
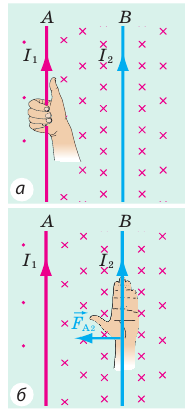
Рис. 2
3) Приходим к выводу: проводник В притягивается к проводнику А.
Ответ: два параллельных проводника, в которых текут токи одного направления, притягиваются.
Пример №4
Прямой проводник (стержень) длиной 0,1 м и массой 40 г находится в горизонтальном однородном магнитном поле индукцией 0,5 Тл. Стержень расположен перпендикулярно магнитным линиям поля (рис. 3).
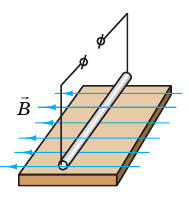
Рис. 3
Ток какой силы и в каком направлении следует пропустить по стержню, чтобы стержень не давил на опору (завис в магнитном поле)?
Анализ физической проблемы. Стержень не будет давить на опору, если сила Ампера уравновесит силу тяжести. Это произойдет при условиях: 1) сила Ампера будет направлена противоположно силе тяжести (то есть вертикально вверх); 2) значение силы Ампера будет равно значению силы тяжести: 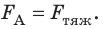
Дано:
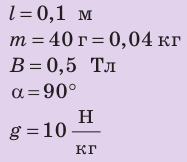
Найти:

Поиск математической модели, решение
1. Определим направление тока. Для этого расположим левую руку так, чтобы линии магнитного поля входили в ладонь, а отогнутый на 90° большой палец был направлен вертикально вверх. Четыре вытянутых пальца укажут направление от нас. Следовательно, ток в проводнике нужно направить от нас.
2. Учитываем, что 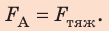
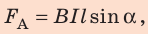
где 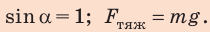
Следовательно, 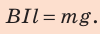
Из последнего выражения найдем силу тока: 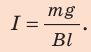
Проверим единицу, найдем значение искомой величины.
Вспомним: 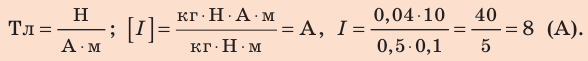
Ответ: 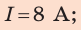
от нас.
Подводим итоги:
Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Значение силы Ампера находят по формуле: 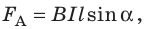
где В — индукция магнитного поля; I — сила тока в проводнике; 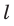
— длина активной части проводника; 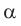
— угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Направление силы Ампера определяют по правилу левой руки: если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец укажет направление силы Ампера.
Другие формулы, где встречается B
Эти формулы также можно использовать для её расчёта.
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
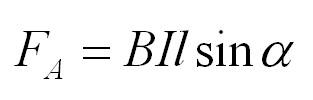
Это и есть сила Ампера. Угол альфа– угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
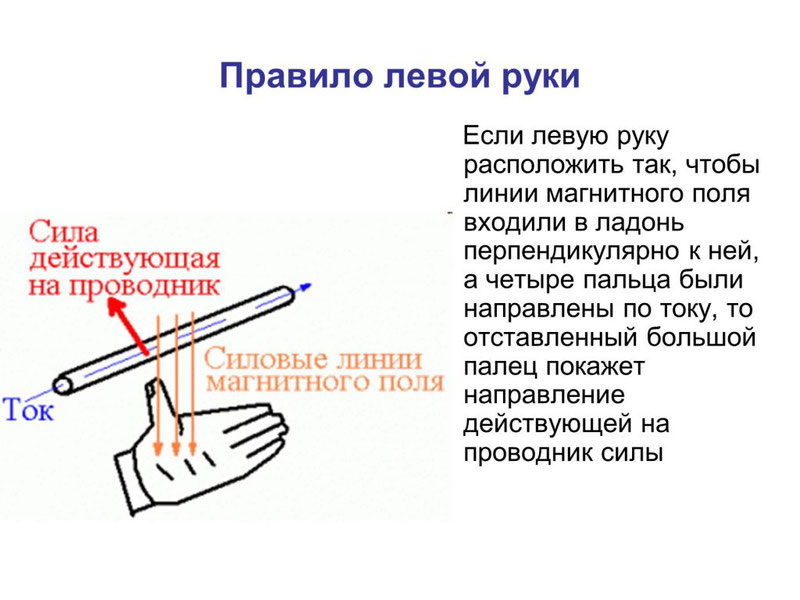
Характеристика силы действующей на проводник с током
Между полюсами подковообразного постоянного магнита подвесим на тонких и гибких проводах прямой алюминиевый проводник (рис. 4.1, а). Если через проводник пропустить ток, проводник отклонится от положения равновесия (рис. 4.1, б). Причина такого отклонения — сила, действующая на проводник с током со стороны магнитного поля. Доказал наличие этой силы и выяснил, от чего зависят ее значение и направление, А. Ампер. Именно потому эту силу называют силой Ампера.
Рис. 4.1. Опыт, демонстрирующий действие магнитного поля на алюминиевый проводник: при отсутствии тока магнитное поле на проводник не действует (а); если в проводнике течет ток, на проводник действует магнитное поле и проводник отклоняется (б)
Сила Ампера — это сила, с которой магнитное поле действует на проводник с током.
Сила Ампера прямо пропорциональна силе тока в проводнике и длине активной части проводника (то есть части, расположенной в магнитном поле). Сила Ампера увеличивается с увеличением индукции магнитного поля и зависит от того, под каким углом к линиям магнитной индукции расположен проводник.
Значение силы Ампера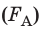
вычисляют по формуле:
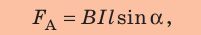
где 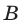
— магнитная индукция магнитного поля; 
— сила тока в проводнике; 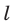
— длина активной части проводника; 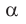
— угол между направлением вектора магнитной индукции и направлением тока в проводнике (рис. 4.2).
Обратите внимание! Магнитное поле не будет действовать на проводник с током 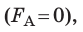
если проводник расположен параллельно магнитным линиям поля 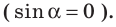
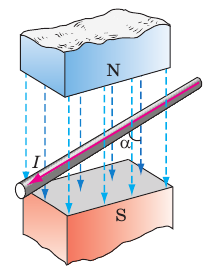
Рис. 4.2. Угол 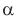
— это угол между направлением вектора магнитной индукции и направлением тока в проводнике
Чтобы определить направление силы Ампера, используютправило левой руки:
Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец укажет направление силы Ампера (рис. 4.3).
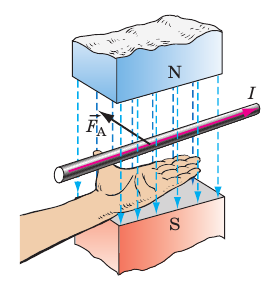
Рис. 4.3. Определение направления силы Ампера по правилу левой руки
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа– это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
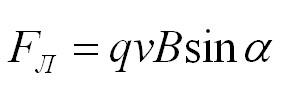
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
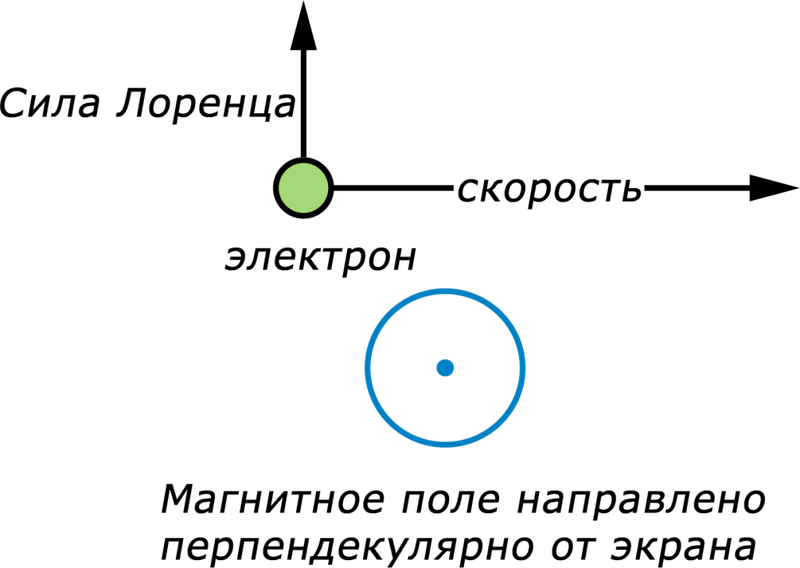
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
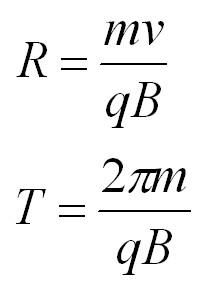
Магнитный поток

Магнитный поток: Ф = BS cosα
Где:
- Ф — магнитный поток (в Вб — вебер)
- B — индукция (в Тл)
- S — площадь рамки (в м²)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Вектор магнитной индукции
Определение
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как →B. Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B=FAmaxIl..
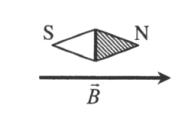
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
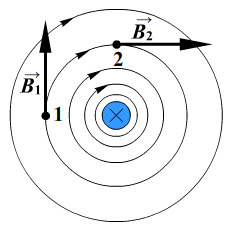
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Частные случаи формул для вычисления величины вектора магнитной индукции
Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):
![]()
где R – радиус витка.
Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:
![]()
где r – расстояние от оси проводника до точки, в которой рассматривается поле.
В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:
![]()
где n – количество витков соленоида на единицу длины; I – сила тока в витке.
Действие магнитного поля на рамку с током
Когда в наружное поле помещают рамку из проводникового материала (проволоки), и в ней создается электроток, со стороны поля на нее будет воздействовать сила Ампера. При однородности поля равнодействующая амперовых сил получится нулевой. При этом их момент таковым не будет. Вследствие этого рамка будет поворачиваться вокруг своей оси. Индукционный вектор будет образовывать прямой угол с рамочной плоскостью.
Зависимость магнитной индукции
На электромагнитную индукцию абсолютно не влияют, ни сила тока, ни длина проводника. Она находится в прямой зависимости и связи, только с магнитным полем. Таким образом, при уменьшении силы тока в проводнике, без изменения каких-либо других показателей, происходит уменьшение не индукции, прямо пропорционально связанной с силой тока, а той силы, с которой магнитное поле воздействует на проводник. При этом, значение самой магнитной индукции остается постоянным. Благодаря этим качествам, электромагнитная индукция выступает в роли количественной характеристики магнитного поля.
Измерение магнитной индукции производится в теслах, по формуле: 1 Тл=1 Н/(А*м). Физическую зависимость этой величины от различных факторов, можно определить в ходе проведения несложного эксперимента. Необходимо взять весы, где на одной стороне прикрепляется проводник, а на другой стороне расположены гири. Проводник находится в постоянном электромагнитном поле, при этом, его масса и вес гирь имеют одинаковое значение.
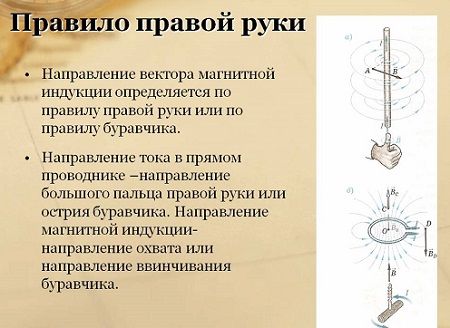
После уравновешивания весов, по проводнику пропускается электрический ток. Вокруг него происходит образование магнитного поля, определяемое в соответствии с правилом правой руки. В результате, наблюдается взаимодействие полей постоянного магнита и самого проводника. При этом, равновесие весов будет нарушено. Из-за протекания тока, сторона весов с проводником начинает опускаться. Для того, чтобы вычислить силу воздействия поля на этот проводник, нужно уравновесить его с помощью гирь. Сила их тяжести рассчитывается по специальной формуле, и будет равняться силе магнитного поля, воздействующей на проводник с током. Соотношение этой силы с длиной проводника и силой тока является постоянной величиной. Данная количественная характеристика находится в зависимости только от поля и представляет собой ни что иное, как модуль вектора магнитной индукции.
Изменения в магнитосфере Земли
Характеристики земного МП меняются, в основном, вследствие того, что оно смещается относительно земного шара. Люди привыкли, что северный конец стрелы должен устремляться к северу. При обратной намагниченности диполя планеты ситуация будет противоположной. В обсерваториях фиксируются данные о состоянии МП планеты, и на их основе создаются геомагнитные карты. Они демонстрируют наличие отклонений в напряженности МП и положении силовых линий в некоторых уголках Земли. Эти явления называют магнитными аномалиями. Иногда их используют как индикаторы местоположения определенных ископаемых ресурсов.
Связь между индукцией и степенью напряженности поля широко используется в расчетах. Она позволяет вывести выражения для нахождения значения индукции в проводниках разных форм, сделанных из материалов с различными показателями магнитной проницаемости.
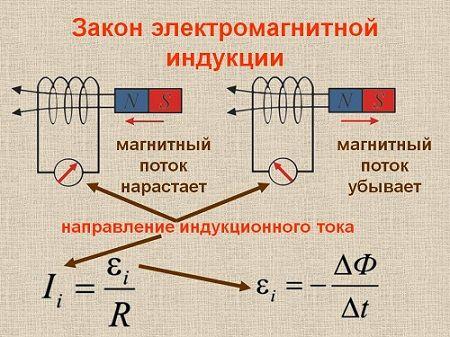
Явление электромагнитной индукции
Явление электромагнитной индукции было открыто английским ученым.
Электромагнитная индукция и магнитная индукция: какая между ними разница?
Электромагнитная индукция — это производство электродвижущей силы, создаваемой в результате относительного движения между магнитным полем и проводником.
Магнитная индукция может производить постоянный магнит, но может и не производить.
Электромагнитная индукция создаёт ток, но таким образом, что этот созданный ток противодействует изменению магнитного поля.
В электромагнитной индукции используются магниты и электрические цепи, а в магнитной индукции используются только магниты и магнитные материалы.
Пример определения магнитного поля
Поместим в магнитное поле перпендикулярно его направлению участок прямолинейного провода длиной l, по которому проходит ток I (рис. 3).
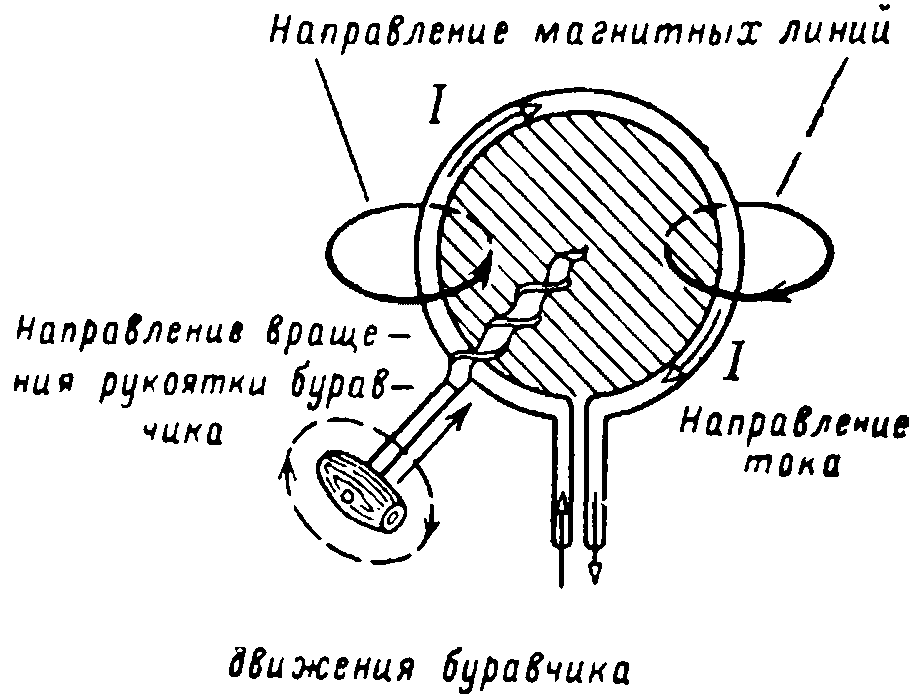
Из опыта можно убедиться, что на участок провода будет действовать сила F, по величине пропорциональная току, длине участка проводника и интенсивности магнитного поля, которая характеризуется величиной магнитной индукции В.
Таким образом, сила
F = IBl
Рис. 2. Правило буравчика для кольцевого тока.
Из написанного следует, что
B = F : (Il)
т. е. магнитная индукция измеряется отношением механической силы, действующей на участок провода, по которому проходит ток, к произведению тока и длины участка провода, причем провод должен быть расположен перпендикулярно направлению поля.
Предыдущая
ТеорияВатт – единица измерения мощности
Следующая
ТеорияЧто такое чередование фаз по цвету и как его проверить?
Свойством поля магнитного в любой его точке с позиции силы выступает вектор магнитной индукции [overrightarrow{mathrm{B}}].
Вектор индукции магнитного поля: главные понятия
Рассмотрим определение вектора индукции магнитного поля. Индукцию определяют как предел отношения F силы, воздействующий на магнитное поле, на ток [text { Idl }] к произведению элементарного тока [text { I }] со значением элемента проводника [text { dl }]. Другими словами, магнитная индукция действует по направлению перпендикулярно [perp] по направлению тока (или по-другому к элементу проводника [text { dl }Rightarrow] из (1), а также вектор магнитной индукции поля перпендикулярен [perp] к направлению силы, которая действует с магнитного поля.
Вектор магнитной индукции однородного поля и неоднородного
Если [overrightarrow{mathrm{B}}=mathrm{const}], то поле является однородным. Если оно не изменяется с течением времени, то про него говорят, что поле постоянное.
Вектор индукции магнитного поля: важные формулы
Важно!
Формула с векторами преобразуется в модульную форму, потому что векторы задают направление, а модульная форма — значения, которые необходимы для решения задачи.
Формула
Модуль вектора индукции однородного поля находят следующим образом:
[mathrm{B}=frac{mathrm{M}_{max }}{mathrm{P}_{mathrm{m}}}].
где [mathrm{M}_{max }] — вращающий момент в максимуме действует на контур с элементарным током, помещенный в магнитное поле, где в данном случае [mathrm{P}_{mathrm{m}}=mathrm{I} cdot mathrm{S}] — магнитный момент контура (S — площадь определенного контура).
Модуль вектора индукции магнитного поля: производные формулы
Есть еще формулы для определения модуля магнитной индукции. Она определяется как отношение силы в максимуме [mathrm{F}_{max }], которое реагирует на проводник длины (при этом L= 1 м) к силе элементарного тока [text { I }] в проводнике:
[B=frac{F_{max }}{I cdot L}]
В вакууме модуль индукции будет равен:
[mathrm{B}=mu 0 cdot mathrm{H}]
Чтобы найти вектор индукции через силу Лоренца, следует преобразовать формулу: [overrightarrow{mathrm{F}}=mathrm{q} cdot[overrightarrow{mathrm{V}} times overrightarrow{mathrm{B}}]] (Крестом обозначается произведение векторов)
[vec{F}=B cdot q cdot v cdot sin alpha]
[B=frac{F}{sin alpha cdot q v}]
В данном случае угол α — это угол между вектором индукции и скорости. Стоит отметить, что направление силы Лоренца [overrightarrow{mathrm{F}}] перпендикулярно [perp] каждому вектору, направлено по правилу Буравчика. Под символом q подразумевается заряд в магнитном поле.
Интересно
В СИ единицей модуля магнитной индукции принимается 1 Тесла (кратко — Тл), где [1 Tл=frac{H}{Aм}]
Как определяется направление вектора индукции магнитного поля?
За направление вектора индукции магнитного поля [overrightarrow{mathrm{B}}] используют направление, в котором устанавливается под воздействием поля утвердительного нормали к току с контору. Другими словами объясняют так: вектор идет в направление поступательного перемещения правого винта при вращении по направлению передвижения тока внутри контура.
Вектор индукции [overrightarrow{mathrm{B}}] обладает направлением, которое начинается со стрелки южного полюса [text { S }] (она свободна передвигается в поле) к полюсу северному [text { N }].
Магнитное поле возникает из-за электрических зарядов (элементарными токами), движущиеся в нем.
Для того чтобы определить направление вектора магнитной индукции в проводнике с элементарным током, используют правило правой руки (Буравчика). Они формулируются так:
- Для катушки с током: 4 согнутых пальца руки, которые обхватывают катушку, направляют по течению току. В это время оставленный большой палец на [90^{circ}] указывает на направление магнитной индукции [overrightarrow{mathrm{B}}] в середине катушки.
- Для прямого проводника с элементарным током: большой палец руки, который оставляется на [90^{circ}], направить по течению элементарного тока. В это время 4 согнутых пальца, которые держат проводник, показывают сторону, куда направлена индукция магнитного поля.
Задания по теме
Разберем примеры, в которых будет задействована данная формула и свойства.
Пример 1
Условие задачи:
Проводник представлен в квадратной форме. Каждая из сторон равна d. В данный момент по нему проходит элементарный ток силы I. Найдите индукцию магнитного поля в месте, где диагонали квадрата пересекаются.
Решение задачи следующее:
Сделаем рисунок, в котором плоскость совпадает с плоскостью проводника. Изобразим направление вектора индукции магнитного поля.
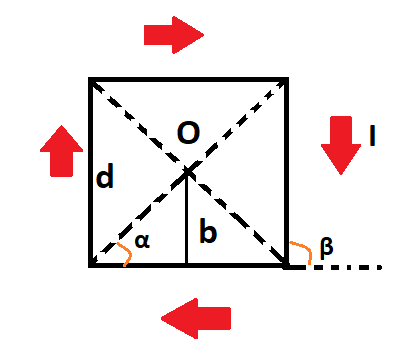
В данной точке О получаются проводники с элементарным током, которые расположены прямолинейно и вектор магнитной индукции поля перпендикулярен плоскости. Направления напряжености полей определяется в соответствием с правилом правого винта,то есть перпендикулярны плоскости изображения. Поэтому сумму векторов по принципу суперпозиции надо заменить на алгебраический вид. Получим следующее выражение: B=B1+B2+B3+B4
Из симметричности рисунка можно увидеть, что модули вектора индукции магнитного поля одинаковы. Получаем следующее: B=4B1
В разделе физике «Электромагнетизм» использовали одну из формул, чтобы рассчитать модуль индукции прямолинейного проводника с элементарным током.
Чтобы формула подошла к данной задачи, ее применяют в следующем виде:
[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{4 mathrm{pi b}}(cos alpha-cos beta)]
углы α и β, которые отмечены на рисунке:
[beta=pi-alpha rightarrow cos beta=cos (pi-alpha)=-cos alpha]
Используем формулу [B_{1}=frac{I cdot mu_{0}}{4 pi b}(cos alpha-cos beta)] и преобразуем с применением тригонометрического свойства:
[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{2 mathrm{pi b}} cdot cos alpha]
Поскольку у нас квадратная форма, то следует заметить следующее:
[mathrm{b}=mathrm{d} 2, alpha=frac{pi}{4} rightarrow cos alpha=frac{sqrt{2}}{2}]
Возьмем выведенные формулы и получим конечное выражение, то есть:
[mathrm{B}=4 cdot frac{mathrm{I} cdot mu_{0}}{pi mathrm{d}} cdot frac{sqrt{2}}{2}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]
Ответ: [mathrm{B}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]
Нет времени решать самому?
Наши эксперты помогут!
Пример 2
Условие задачи:
Бесконечно проводник с элементарным током (I) согнут под 90 градусов, который изображен на рисунке. Найдите вектор магнитной индукции однородного поля в точке А.
Решение задачи:
В точке А получается из двух частей проводника, то есть:
[overrightarrow{mathrm{B}}=mathrm{B}_{mathrm{II}}+mathrm{B}_{perp}]
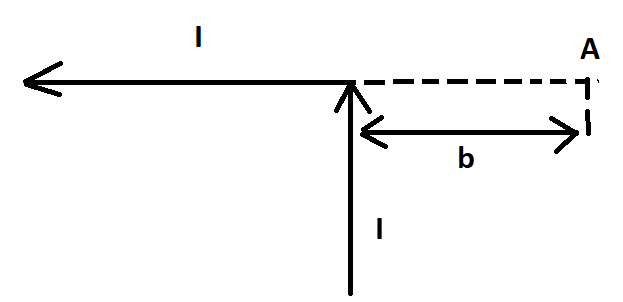
Теперь посмотрим горизонтальный участок, где расположена точка А. Данная область проводника с элементарным током формирует поле в этой точке. Вектор индукции магнитного поля [mathrm{B}_{mathrm{II}}] равен нулю, потому что в А все углы между с радиус-векторами и с элементарным током равны π.
Следовательно, произведение векторов [[mathrm{d} vec{ l } vec{r}]] и поток вектора индукции магнитного поля в законе Био-Савара-Лапласа будет равен нулю:
[overrightarrow{mathrm{B}}=frac{mu_{0}}{4 pi} oint frac{mathrm{I}[mathrm{d} vec{l} vec{r}]}{mathrm{r}^{3}}]
В этом случае [vec{r}] — радиус-вектор, который идет от элемента [mathrm{Idvec{l}}] к точке А, в которой находится индукция магнитного поля [overrightarrow{mathrm{B}}].
Индукция бесконечного проводника в точке А была бы равна:
[mathrm{B}^{prime}=frac{mu_{0}}{2 pi} frac{mathrm{I}}{mathrm{b}}]
Но так как полу бесконечный проводник, то следуя из принципа суперпозиции, получается следующее выражение для проводника магнитной индукций равна:
[mathrm{B}=mathrm{B}_{perp}=frac{1}{2} mathrm{~B}^{prime}=frac{mu_{0}}{Pi} frac{mathrm{I}}{mathrm{b}}]
Ответ: [mathrm{B}=frac{mu_{0}}{pi} frac{mathrm{I}}{mathrm{b}}]
Индукция магнитного поля


4.2
Средняя оценка: 4.2
Всего получено оценок: 127.
4.2
Средняя оценка: 4.2
Всего получено оценок: 127.
Проводник с электрическим током всегда порождает магнитное поле. Для его описания используются различные величины, одной из которых является индукция. Рассмотрим это понятие подробнее.
Индукция магнитного поля
Обнаружить магнитное поле можно по действию на движущиеся заряды или на проводник с током. При этом можно видеть, что направление возникающей силы зависит от направления электрического тока.
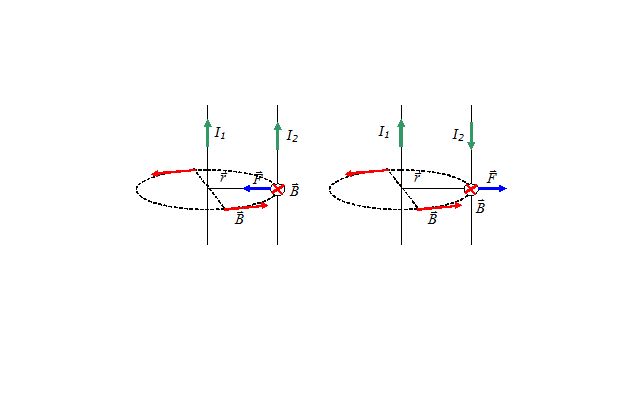
Таким образом, можно ввести силовую характеристику магнитного поля – векторную величину индукции магнитного поля $overrightarrow B$. Модуль этой величины будет характеризовать силу, с которой магнитное поле действует на ток (интенсивность), а векторный характер – направление.
Направление магнитной индукции
Магнитные силы, как и любые другие силы, имеют направление. Для его определения служат специальные правила.
Правило буравчика
Согласно этому правилу, если направление поступательного движения острия буравчика при ввинчивании совпадает с направлением тока в проводнике, то направление вращательного движения буравчика в каждой точке совпадает с направлением вектора индукции магнитного поля.
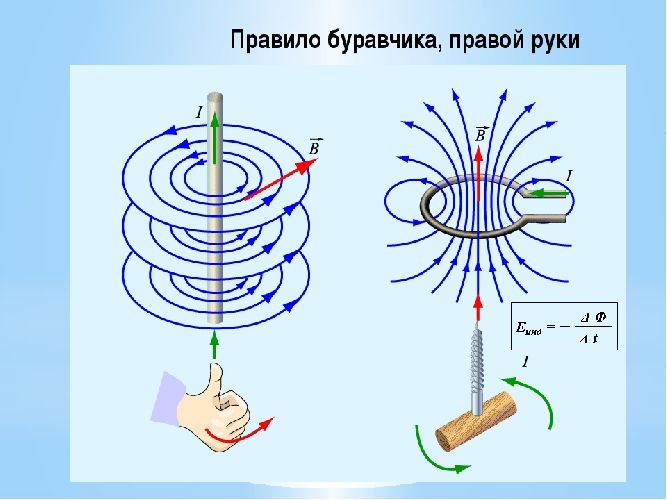
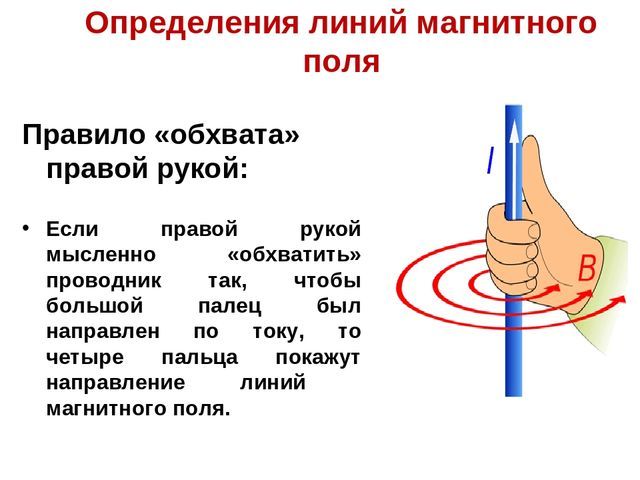
Правило обхвата правой рукой
Приведенное правило зачастую недостаточно понятно из-за того, что буравчик в современном мире используется нечасто. Поэтому гораздо удобнее применять правило охвата правой рукой: если большой палец правой руки указывает направление тока, то остальные пальцы будут показывать направление магнитных линий.
Данное правило удобнее еще и потому, что его можно применять и для определения направления магнитной индукции катушки с током, в этом случае четыре пальца направляются вдоль витков катушки, в направлении тока в них, а большой палец укажет направление вектора магнитной индукции. То есть, большой палец в обоих случаях указывает на прямую линию, а остальные пальцы – на охватывающую.
Модуль магнитной индукции
Закон, определяющий силу, с которой магнитное поле действует на проводник с током, был открыт А.Ампером. Согласно этому закону, сила, действующая на проводник, пропорциональна силе тока в проводнике, его длине и модулю магнитной индукции:
$$F=I{big|overrightarrow Bbig|}Δlthinspace sinthinspacealpha$$
Максимальная сила соответствует перпендикулярному расположению линий магнитной индукции и тока. Зная эту силу, можно получить формулу индукции магнитного поля:
$$B={F_{max}over IΔl}$$
Из этой же формулы можно получить единицу измерения магнитной индукции – Тесла:
$$Тл={Нover А×м}$$,
то есть, индукция силой 1 тесла – эта индукция, которая действует на проводник с силой тока 1 Ампер длинной 1 метр с силой 1 Ньютон.
1 Тл – это очень сильное магнитное поле. Обычное магнитное поле Земли имеет значение около 0,05 мТл. Индукция поля бытового магнита из защелок составляет около 5 мТл. Самое сильное магнитное поле, с которым может столкнуться обычный человек – это сила поля МРТ-томографа. Здесь значение индукции может доходить до 3 Тл !

Что мы узнали?
Индукция магнитного поля – это векторная величина, характеризующую интенсивность поля. Чем выше индукция, тем с большей силой поле действует на проводник с током. Направление магнитной индукции определяется правилом буравчика или правилом обхвата правой руки.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 127.
А какая ваша оценка?
![{displaystyle {vec {F}}=q^{*}left[{vec {v}}times {vec {B}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eaf19b61520d51d208329c484d386ffbf8e9977)



