Введем понятие абсолютное величины или модуля дроби. Эти понятия нужны для вычисления действий дробей.
Модуль положительной дроби.
Понятие модуля числа или что такое модуль числа можно посмотреть нажав на ссылку.
Определение:
Модулем положительной дроби – это сама дробь.
Например:
Модуль дроби (frac{1}{2}) будет равна дроби (frac{1}{2}), то есть той же самой дроби.
(Bigl|frac{1}{2} Bigl| =frac{1}{2})
Модуль отрицательной дроби.
Определение:
Модулем отрицательной дроби является противоположная ей дробь или положительная ей дробь.
Рассмотрим пример:
Модуль дроби (-frac{2}{3}) будет равна дроби с противоположным знаком, то есть с плюсом (frac{2}{3}).
(Bigl|-frac{2}{3} Bigl| =frac{2}{3})
Определение:
Модуль нуля равен нулю.
|0|=0
Определение:
У противоположных чисел модули равны.
Рассмотрим пример:
Модуль дроби (frac{4}{7}) равен (frac{4}{7}) и модуль противоположной дроби (-frac{4}{7}) равен (frac{4}{7}).
(Bigl|-frac{4}{7} Bigl| = Bigl|frac{4}{7} Bigl| =frac{4}{7})
Вопросы по теме:
Назовите модуль положительного числа?
Ответ: то же положительное число.
Назовите модуль отрицательного числа?
Ответ: противоположное число отрицательному числу.
Назовите модуль 0?
Ответ:0
Пример №1:
Решите модули дробей: а) (frac{4}{5}) б) (-frac{2}{7}) в) (frac{-0}{3}) г) (frac{3}{-8}) е) 0 ж) (frac{0}{-2})
Решение:
а) (Bigl|frac{4}{5} Bigl| =frac{4}{5})
б) (Bigl|- frac{2}{7} Bigl| =frac{2}{7})
в) (Bigl|frac{-0}{3} Bigl| =frac{0}{3}=0)
г) (Bigl|frac{3}{-8} Bigl| =frac{3}{8})
е) |0|=0
ж) (Bigl|frac{0}{-2} Bigl| =frac{0}{2}=0)
Пример №2:
Сравните модули дробей: а) (Bigl|-frac{1}{3} Bigl|) и (Bigl|frac{1}{3} Bigl|) б) (Bigl|-frac{9}{2} Bigl|) и (Bigl|-frac{6}{11} Bigl|)
Решение:
а) Чтобы сравнить модули дробей нужно их посчитать:
(Bigl|-frac{1}{3} Bigl| = frac{1}{3}) и (Bigl|frac{1}{3} Bigl| = frac{1}{3})
Видно, что дроби одинаковы, поэтому ставим знак равно.
(Bigl|-frac{1}{3} Bigl| = Bigl|frac{1}{3} Bigl|)
б)Раскроем модули дробей.
(Bigl|-frac{9}{2} Bigl| = frac{9}{2}) и (Bigl|-frac{6}{11} Bigl| = frac{6}{11})
Получили две дроби (frac{9}{2}) и (frac{6}{11}). Дробь (frac{9}{2}) неправильная, поэтому эта дробь больше 1. А дробь правильная, поэтому меньше 1. Получаем: (frac{9}{2}>frac{6}{11})
(Bigl|-frac{9}{2} Bigl| > Bigl|-frac{6}{11} Bigl|)
Математика
6 класс
Урок №35
Отрицательные дроби
Перечень рассматриваемых вопросов:
- Понятие отрицательной дроби и противоположных чисел.
- Символьное обозначение противоположного числа.
- Модуль дроби.
Тезаурус
Числа, которые отличаются только знаками, называют противоположными.
Из двух противоположных чисел одно всегда положительное, другое – отрицательное.
Число нуль противоположно самому себе.
Модулем отрицательной дроби называют противоположную ей дробь.
Модуль нуля равен нулю.
Модули противоположных чисел равны.
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Числа, вида:
Если перед ними поставить «+», получим то же самое число.
Если перед положительной дробью поставить знак «–», то получим новое число, которое называется отрицательным дробным числом или отрицательной дробью.
Определение
Числа, которые отличаются только знаками, называют противоположными.
Из двух противоположных чисел одно всегда положительное, другое отрицательное.
Число нуль противоположно самому себе.
Запишем символьное обозначение противоположных чисел.
a – число
– а – число, противоположное а
Чтобы получить противоположное число, нужно просто поменять его знак на противоположный.
Знак «минус» – символ противоположности.
(– a) – не значит, что a отрицательное, (– a) – значит, что необходимо взять число, противоположное a.
Если перед дробью (с любым знаком) поставить знак «+», получится то же самое число:
Определение:
Модулем отрицательной дроби называют противоположную ей дробь.
Определение:
Модуль нуля равен нулю.
|0| = 0
Свойства противоположных чисел:
Модули противоположных чисел равны.
Иногда знак «–» записывают не перед дробью, а в числителе или знаменателе дроби.
Задача
Иван-царевич проиграл Соловью-разбойнику 3/8 всего золота, что имел с собой в путешествии. Сколько золотых момент он оказался должен, если монет у него было 53? Сколько ему не хватило для полного расчёта?
Решение:
Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.
Какие числа представлены?
Варианты ответов:
смешанная дробь
обыкновенная дробь
целое положительное число
целое отрицательное
Правильный ответ
№ 2. Вставьте в текст нужные слова.
Модулем …дроби называют …ей дробь.
Варианты слов для вставки:
дробь
противоположную
отрицательной
положительной
отрицательную
Для выполнения задания, обратимся к теоретическому материалу урока.
Правильный ответ
Модулем отрицательной дроби называют противоположную ей дробь.
Отрицательные дроби
Отрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:
| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 | . |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус можно ставить перед дробью, перед числителем или перед знаменателем:
| – | 2 | = | -2 | = | 2 | . |
| 7 | 7 | -7 |
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.
| – | 2 | + (- | 1 | ) | . |
| 5 | 4 |
Приведём дроби к общему знаменателю:
| – | 2 | + (- | 1 | ) = | -8 | + | -5 | . |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | – | 13 | . |
| 20 | 20 | 20 | 20 | 20 |
| – | 2 | + (- | 1 | ) = | -8 | + | -5 | = |
| 5 | 4 | 20 | 20 |
| = | -8 + (-5) | = | -13 | = | – | 13 | . |
| 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
| – | 5 | – (- | 11 | ) = | – | 5 | + (+ | 11 | ) = |
| 12 | 12 | 12 | 12 |
| = | – | 5 | + | 11 | = | -5 + 11 | = | 6 | . |
| 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
| – | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:
| – | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
| – | 2 | · | 4 | = | – | 2 · 4 | = | – | 8 | . |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | – | 4 · 2 | = | – | 8 | . |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
| – | 2 | : (- | 4 | ) = | -2 | : | -4 | = |
| 3 | 5 | 3 | 5 |
| = | -2 · 5 | = | -10 | = | 10 | . |
| 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Математика. 6 класс
Конспект урока
Перечень рассматриваемых вопросов:
- Понятие отрицательной дроби и противоположных чисел.
- Символьное обозначение противоположного числа.
- Модуль дроби.
Числа, которые отличаются только знаками, называют противоположными.
Из двух противоположных чисел одно всегда положительное, другое – отрицательное.
Число нуль противоположно самому себе.
Модулем отрицательной дроби называют противоположную ей дробь.
Модуль нуля равен нулю.
Модули противоположных чисел равны.
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Числа, вида:
Если перед ними поставить «+», получим то же самое число.
Если перед положительной дробью поставить знак «–», то получим новое число, которое называется отрицательным дробным числом или отрицательной дробью.
Числа, которые отличаются только знаками, называют противоположными.
Из двух противоположных чисел одно всегда положительное, другое отрицательное.
Число нуль противоположно самому себе.
Запишем символьное обозначение противоположных чисел.
– а – число, противоположное а
Чтобы получить противоположное число, нужно просто поменять его знак на противоположный.
Знак «минус» – символ противоположности.
(– a) – не значит, что a отрицательное, (– a) – значит, что необходимо взять число, противоположное a.
Если перед дробью (с любым знаком) поставить знак «+», получится то же самое число:
Модулем отрицательной дроби называют противоположную ей дробь.
Модуль нуля равен нулю.
Свойства противоположных чисел:
Модули противоположных чисел равны.
Иногда знак «–» записывают не перед дробью, а в числителе или знаменателе дроби.
Иван-царевич проиграл Соловью-разбойнику 3/8 всего золота, что имел с собой в путешествии. Сколько золотых момент он оказался должен, если монет у него было 53? Сколько ему не хватило для полного расчёта?
Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.
Какие числа представлены?
целое положительное число
№ 2. Вставьте в текст нужные слова.
Модулем …дроби называют …ей дробь.
Варианты слов для вставки:
Для выполнения задания, обратимся к теоретическому материалу урока.
Модулем отрицательной дроби называют противоположную ей дробь.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/reshenie-uravnenij-s-drobyami
http://resh.edu.ru/subject/lesson/6888/conspect/
[/spoiler]
н6 класс
УРОК № 63. Глава 3. Рациональные числа (38 часов)
Тема. Отрицательные дроби.
Цель. Ознакомить
учащихся с понятием отрицательных дробей; научиться находить модуль
положительных и отрицательных дробей.
Задачи урока:
образовательные: формировать понятие отрицательных дробей, навыки
нахождения модуля дроби.
развивающие: формировать умения анализировать,
выделять главное;
воспитательные: воспитывать наблюдательность, дисциплинированность,
позитивное отношение к учебе
Планируемые результаты:
Предметные: Формулируют понятие отрицательных
дробей, противоположных дробей. Правило модуля положительных и отрицательных
дробей.
Находят неизвестное число, для которого
верно равенство, выполняют сравнение модулей дробей, оформляют решение анализируют
полученные результаты.
Личностные:
Формирование мотивации к индивидуальной и
совместной деятельности на уроке.
Формирование навыка осознанного выбора
решения.
Ход
урока.
I. Организационный момент.
II. Проверка
домашнего задания.
III. Актуализация
опорных знаний.
1. Как называются
числа, расположенные в ряду целых чисел:
1) Справа от нуля?
2) Слева от нуля?
2. Какие числа
называются противоположными?
3. Чему равен
модуль положительного числа?
4. Чему равен
модуль отрицательного числа?
5. Чему равен
модуль нуля?
IV. Объяснение нового
материала.
Отрицательные
дроби.
Запишите: 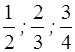
Как называются записанные числа?
Ранее изучались обыкновенные дроби – их
ещё называют положительными дробями.
Если перед положительной дробью
поставить знак «+», то получится то же самое число, т.е. 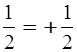
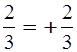
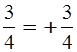
Если перед положительной дробью
поставить знак «–», то получится новое число, которое называют отрицательным
дробным числом, или отрицательной дробью. Например: ;
;
.
Определение.
Числа,
отличающиеся только знаком, называют противоположными.
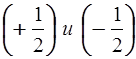
Если перед
дробью (любого знака) поставить знак «+», то получится то же самое число: 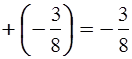
Если перед
дробью (любого знака) поставить знак «–», то получится число, противоположное
данной дроби: 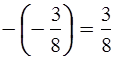
Определение.
Модулем
положительной дроби называют саму эту дробь.
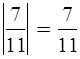
Определение.
Модулем
отрицательной дроби называют противоположную ей дробь.
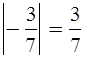
Определение.
Модуль
нуля равен нулю.
.
Определение.
Модули
противоположных чисел равны.
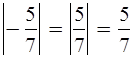
Иногда знак «–» записывают не перед
дробью, а в числителе или знаменателе дроби.
Пример
1.
Запишите дроби так, чтобы знак «–» стоял в числителе, а затем в знаменателе:
1) 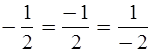
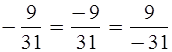
V. Решение
упражнений.
Уч.с.89 № 442(а-г). Упростите
запись по образцу (рассмотрены в учебн.):
Самостоятельно
записываем в тетрадь с комментариями.
а) ; б)
; в)
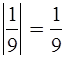
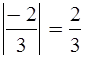
Уч.с.89
№ 443(а,е,ж,з).
Упростите запись по образцу:
а) 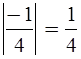
е) 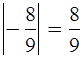
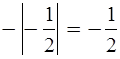
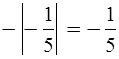
Уч.с.89 № 445(г-е). Запишите дроби
так, чтобы знак «–» стоял в числителе по образцу:
г) 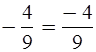
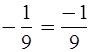
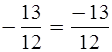
Уч.с.89 № 446(г-е). Запишите дроби
так, чтобы знак «–» стоял в знаменателе по образцу:
г) 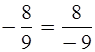
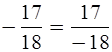
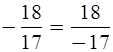
Уч.с.90 № 447(нечетные). Запишите дроби
так, чтобы знак «–» стоял перед чертой дроби:
1) 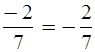
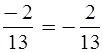
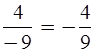
Уч.с.90 № 450(а,в,д). Вычислите:
а) 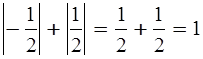
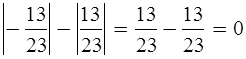
д) 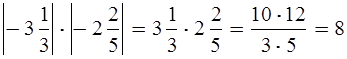
VI. Рефлексия (подведение итогов)
Когда два числа разных по знаку равны? (когда
они противоположны)
Существуют ли противоположные дроби? (да.
Например, 1/2 и – 1/2)
Отрицательной дробью называется та дробь, ….. (перед
которой стоит знак «минус»)
Что называют модулем положительной дроби?
(саму эту дробь)
Что называют модулем отрицательной дроби?
(противоположную ей положительную дробь)
Чему равен модуль нуля? (модуль нуля
равен нулю)
VII. Домашнее
задание. § 3.1 (выучить теорию). №445(а-в),
446(а-в).
VIII.
Конспект урока математики в 6-а классе
по теме «Отрицательные дроби»
Учитель: Щупановская Л.А.
Дата урока – 26.02.2018
Тип урока – открытие новых знаний
Цель урока: ознакомить учащихся с понятием отрицательных дробей; научить находить модуль положительных и отрицательных дробей
Задачи урока:
образовательные: формировать понятие отрицательных дробей, навыки нахождения модуля дроби.
развивающие: формировать умения анализировать, выделять главное;
воспитательные: воспитывать наблюдательность, дисциплинированность, позитивное отношение к учебе
Планируемые результаты:
Предметные: Формулируют понятие отрицательных дробей, противоположных дробей. Правило модуля положительных и отрицательных дробей.
Находят неизвестное число, для которого верно равенство, выполняют сравнение модулей дробей, оформляют решение анализируют полученные результаты.
Личностные:
Формирование мотивации к индивидуальной и совместной деятельности на уроке.
Формирование навыка осознанного выбора решения.
Формирование универсальных учебных действий учащихся
- Познавательные – воспитывать познавательный интерес к предмету; учить анализировать имеющуюся информацию; учить осуществлять выбор наиболее эффективных способов решения образовательных задач в зависимости от конкретных условий.
- Регулятивные – учить целеполаганию; планировать свои действия в соответствии с поставленной задачей; умению вносить коррективы в действие после его завершения на основе учёта сделанных ошибок; оценивать правильность выполнения действий.
- Коммуникативные – организовывать и планировать учебное сотрудничество с учителем и сверстниками; контролировать действие партнёра.
- Личностные – формирование учебно-познавательного интереса к деятельности; воспитание доброжелательного отношения к окружающим; формирование умения проводить объективный самоанализ деятельности.
Основные понятия, проводимые на уроке: положительная дробь, отрицательная дробь, противоположное число, знак числа, модуль числа
Основные ресурсы:
- Учебник «Математика. 6 класс», С.М. Никольский, М: «Просвещение», 2017
Дополнительные ресурсы
- Карточки для доски, задания на листах (работа в парах)
Организация пространства
- Фронтальная работа
- Индивидуальная работа
- Работа в парах
Ход урока
I. Организационный этап.
Цель: создать благоприятный психологический и эмоциональный настрой на работу
– Здравствуйте. Пожалуйста, садитесь. Я очень рада всех вас видеть здесь и сейчас бодрыми и здоровыми. К работе готовы?
Если сегодня на уроке мы будем
думать основательно и коллективно,
решать оперативно,
отвечать доказательно,
писать старательно, то
новые открытия ждут нас обязательно!
Итак, начинаем.
II. Мотивация к учебной деятельности. Определение темы. Постановка целей и задач урока
В сокровищнице занимательного математического фольклора есть такая задача: «Бутылка с пробкой стоит 11 монет, причем бутылка на 10 монет дороже пробки. Сколько стоит пробка?». Прелесть этой задачи в том, что, не долго думая, все дают ответ: «Пробка стоит одну монету». И, конечно, ошибаются! Некоторые, сделав проверку и убедившись в своей ошибке, тут же заявляют, что задача вовсе не имеет решения. Действительно, эта задача не решается в целых числах, но зато существуют дробные числа, подходящие для ее решения: десять с половиной монет стоит бутылка, и полмонеты – пробка.
– О чем сегодня на уроке пойдет речь? (о дробях)
– В нашей жизни есть что-то хорошее, и не очень; есть полезное и вредное; есть север, а есть юг, бывает очень жарко, а бывает очень холодно. С чем ассоциируются эти слова? Как вы думаете почему я сопоставляю данные слова? Что может это означать?
– Как мы обозначим тему урока? (отрицательные дроби) Записываю на доске
– А на какие вопросы вы бы хотели получить ответы?
III. Актуализация знаний
/ Учитель предлагает письменно ответить на вопросы «да» или «нет» /
- Если перед положительной дробью поставить знак «минус», то получится отрицательная дробь. (да)
- Дробные числа, отличающиеся только знаком, называются противоположными. (да)
- Из двух противоположных дробей больше та, перед которой стоит знак «минус» (нет)
- Отрицательные дроби располагаются на координатной оси слева от нуля (да)
- Нуль противоположен самому себе (да)
Проверьте себя. Откройте учебники на стр. 87 и проверьте свой предположения.
А что еще вы узнали, читая теорию? Показываю карточки
| ; | –
|
| | –
– =
– =
IV. Первичное усвоение новых знаний
Начертите координатную ось. Единичный отрезок 5 см.
Отметьте на чертеже точку А () и точку А1 с противоположной координатой.
Какая из двух дробей отрицательная? Почему?
Запишите, чему равен модуль отрицательной дроби, положительной дроби.
Какой вывод мы можем сделать?
Отметьте на координатной оси точку В ( )
Где располагается данная точка? Почему?
Запишите эту дробь ниже.
Почему мы говорим, что эта дробь отрицательная? (перед дробью стоит минус)
Может ли знак «минус» быть в другом месте? Где? Запишите.
Эти равенства верны? (да)
V. Первичная проверка понимания Задание на листе (работа в парах)
Фамилия, имя _______________________________________________________________
- Упростите по образцу:
|
а) |
||||||||||||||||||||||
|
б) |
||||||||||||||||||||||
|
в) |
||||||||||||||||||||||
|
г) |
||||||||||||||||||||||
- Подумайте и допишите:
|
а) |
||||||||||||||||||||||
|
б) |
||||||||||||||||||||||
|
в) |
||||||||||||||||||||||
|
г) |
||||||||||||||||||||||
- Сравните:
|
а) |
||||||||||||||||||||||
|
б) |
||||||||||||||||||||||
|
в) |
||||||||||||||||||||||
|
г) |
||||||||||||||||||||||
Сбор материалов. Запечатывание в конверт. Назначаю 1 эксперта для проверки заданий, а тот, в свою очередь, назначает еще двух себе в помощь.
Предлагаю заполнить первую часть листа самооценки
VI. Первичное закрепление
Учебник стр. 89 № 445,446
VII. Рефлексия (подведение итогов)
Когда два числа разных по знаку равны? (когда они противоположны)
Существуют ли противоположные дроби? (да. Например, 1/2 и – 1/2)
Отрицательной дробью называется та дробь, ….. (перед которой стоит знак «минус»)
Что называют модулем положительной дроби? (саму эту дробь)
Что называют модулем отрицательной дроби? (противоположную ей положительную дробь)
Чему равен модуль нуля? (модуль нуля равен нулю)
Предлагаю заполнить вторую часть листа самооценки
VIII. Информация о домашнем задании. Инструктаж.
ДЗ : 1) Прочитать и осмыслить п. 3,1.; 2) стр. 90 № 447-449
Приложение.
Лист самооценки работы на уроке
Фамилия, имя __________________________________________________
Оцени свою работу в паре:
|
Утверждение |
Полностью согласен |
Частично согласен |
Не согласен |
Затрудняюсь ответить |
|
Я активно участвовал при решении всех заданий |
|
|
|
|
|
Мое мнение совпадало с мнением партнера |
|
|
|
|
|
Я всегда принимаю решение партнера |
|
|
|
|
|
Большинство решений предложено мной |
|
|
|
|
|
Мне интереснее и полезнее работать в паре |
|
|
|
|
|
В паре работать тяжелее, чем самому |
|
|
|
|
Оцени свою работу на уроке:
|
Утверждение |
Полностью согласен |
Частично согласен |
Не согласен |
Затрудняюсь ответить |
|
Я активно работал(а) на уроке |
|
|
|
|
|
Тема урока была сложная и я ничего не понял(а) |
|
|
|
|
|
Материал урока я усвоил (а) |
|
|
|
|
|
На уроке мне было комфортно |
|
|
|
|
|
Мы выполняли очень сложные задания, мне было трудно |
|
|
|
|
|
На уроке я открыл(а) для себя новые знания |
|
|
|
|













