Плотность тока проводимости, смещения, насыщения: определение и формулы
В данной статье мы рассмотрим плотность тока и формулы для нахождения различных видов плотности тока: проводимости, смещения, насыщения.
Плотность тока – это векторная физическая величина, характеризующая насколько плотно друг к другу располагаются электрические заряды.
- Плотность тока проводимости
- Плотность тока смещения
- Плотность тока насыщения
Плотность тока проводимости
Ток проводимости – это упорядоченное движение электрических зарядов, то есть обыкновенный электрический ток, который возникает в проводнике. В большинстве случаев, когда речь заходит о токе, имеют ввиду именно ток проводимости.
В данном случае плотность тока – это векторная характеристика тока равная отношению силы тока I в проводнике к площади S поперечного сечения проводника (перпендикулярному по отношению к направлению тока). Эта величина показывает насколько плотно заряды располагаются на всей площади поперечного сечения проводника. Она обозначается латинской буквой j. Модуль плотности электрического тока пропорционален электрическому заряду, который протекает за определенное время через определенную площадь сечения, расположенную перпендикулярно по отношению к его направлению.
Если рассмотреть идеализированной проводник, в котором электрический ток равномерно распределен по всему сечению проводника, то модуль плотности тока проводимости можно вычислить по следующей формуле:
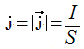
j – Плотность тока [A/м2]
I – Сила тока [A]
S – Площадь поперечного сечения проводника [м2]
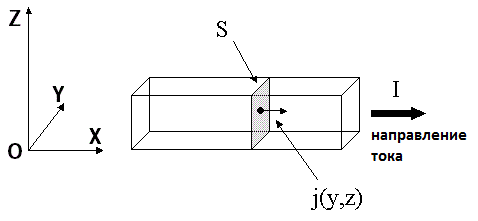
Исходя из этого мы можем представить силу тока I как поток вектора плотности тока j, проходящий через поперечное сечение проводникаS. То есть для вычисления силы тока, текущей через определенное поперечное сечение нужно проинтегрировать (сложить) произведения плотности тока в каждой точке проводника jn на площадь поверхности этой точки dS:
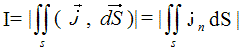
I – сила тока [А]
jn – составляющая вектора плотности тока в направлении течения тока (по оси OX) [A/м2]
dS – элемент поверхности площади [м2]
Исходя из предположения, что все заряженные частицы двигаются с одинаковым вектором скорости v, имеют одинаковые по величине заряды e и их концентрация n в каждой точке одинаковая, получаем, что плотность тока проводимости j равна:
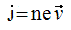
j – плотность тока [А/м2]
n – концентрация зарядов [м-3]
e – величина заряда [Кл]
v – скорость, с которой движутся частицы [м/с]
Плотность тока смещения
В классической электродинамике существует понятие тока смещения, который пропорционально равен быстроте изменения индукции электрического поля. Он не связан с перемещением каких-либо частиц поэтому, по сути, не является электрическим током. Несмотря на то, что природа этих токов разная, единица измерения плотности у них одинаковая – A/м2.
Ток смещения – это поток вектора быстроты изменения электрического поля ∂E/∂t через S – некоторую поверхность. Формула тока смещения выглядит так:
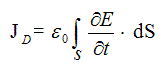
JD – ток смещения [А]
ε0 – электрическая постоянная, равная 8,85·10-12 Кл2/(H·м2)
∂E/∂t – скорость изменения электрического поля [Н/(Кл·с)]
ds – площадь поверхности [м2]
Плотность тока смещения определяется по следующей формуле:
для вакуума:
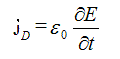
для диэлектрика:
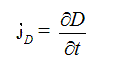
jD – ток смещения [А/м2]
ε0 – электрическая постоянная, равная 8,85·10-12 Кл2/(H·м2)
∂E/∂t – скорость изменения электрического поля [Н/(Кл·с)]
∂D/∂t – скорость изменения вектора эл. индукции [Кл/м2·с)]
Плотность тока насыщения
В физической электронике используют понятие плотности тока насыщения. Эта величина характеризует эмиссионную способность металла, из которого сделан катод, и зависит от его вида и температуры.
Плотность тока насыщения выражается формулой, которая была выведена на основе квантовой статистики Ричардсоном и Дешманом:
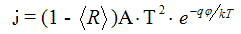
j – плотность тока насыщения[А/м2]
R – среднее значение коэффициента отражения электронов от потенциального барьера
A – термоэлектрическая постоянная со значением 120,4 А/(K2·см2)
T– температура [К]
qφ – значение работы выхода из катода электронов [эВ], q – электронный заряд [Кл]
k – постоянная Больцмана, которая равна 1,38·10-23 Дж/К
Что такое ток смещения и ток проводимости
Содержание
- 1 Природа токов смещения
- 2 Свойства тока смещения в конденсаторе
- 3 Закон полного тока
- 4 Ток смещения в современной радиоэлектронике
- 5 Видео по теме
Максвелл, выстраивая теорию электромагнитного поля, выдвинул гипотезу, что его возникновение связано не только с движением зарядов, но и с временными изменениями электрического поля. Чтобы объяснить количественные соотношения между изменяющимся электрическим полем и создаваемым им магнитным полем, ученый ввел такое понятие, как токи смещения. Они не выделяют джоулевой теплоты, но могут создавать магнитное поле.

Великий ученый и его теория
Природа токов смещения
В природе существуют токи двух видов: проводимости и связанных зарядов. В последнем случае ток возникает в результате перемещения электронов и ядер внутри молекулы. Током проводимости называют направленное перемещение свободных зарядов на большие расстояния. Иначе говоря, этот ток обусловлен движением зарядов под действием электрического поля. Чем сильнее поле, тем большей силы будет ток.
Ток абсорбции или смещения в отличие от электротока проводимости не подчиняется законам, составляющим основу электротехники, в частности закону Ома. Он не пропорционален электрическому полю и проводимости среды (ток смещения зависит от диэлектрической проницаемости). Ток смещения (ТС) — это определение физической величины, пропорциональной скорости изменения электрической индукции. Основная функция ТС — обеспечение непрерывности линий электротока.

Определение параметров ТС
Свойства тока смещения в конденсаторе
Судя по исследованиям электрической цепи, включающей конденсатор, переменный ток через этот элемент проходит, а постоянный — нет. При подключении постоянного напряжения ток вначале растёт, а после медленно понижается, асимптотически приравниваясь к какой-то определённой величине. Неожиданный рост амплитуды сначала и постепенное ее понижение происходит из-за электрического смещения. Это связано с тем, что внутри емкости имеется диэлектрик. Наличие в цепи переменного тока Максвелл также связал с тем, что в обкладках конденсатора появляется ток смещения или абсорбционный ток.

Наличие ТС в конденсаторе
Исходя из непрерывности линий электрического тока на границе проводник-конденсатор, можно сказать, что ток проводимости переходит в ток смещения. Для определения значения тока проводимости используется формула:

Значение тока проводимости
Для поиска производной dq/dt обкладка конденсатора окружается случайным замкнутым контуром S, также используется теорема Гаусса для вектора индукции:

Величина свободного электрозаряда
Если продифференцировать данную формулу по t, получим выражение, позволяющее вычислить ток смещения в диэлектрике конденсатора:

Определение ТС в диэлектрике
Если учесть, что , то получается, что величина плотности тока смещения равняется той скорости, с которой изменяется электромагнитное поле внутри конденсатора:

Плотность ТС в диэлектрике
Плотность тока смещения в вакууме находится по другой формуле:

Плотность ТС в вакууме
Закон полного тока
Наряду с ТС Максвелл ввел еще одно понятие — полный ток.

Формула полного электротока
Плотность полного тока в зоне пространства, где есть токи проводимости и переменное поле, находится так:

Плотность полного тока
У слагаемых данного уравнения могут быть одинаковые знаки или разные. Поэтому плотность может равняться нулю, быть больше или меньше тока проводимости.

Функции полного тока
По мысли Максвелла теорема о циркуляции векторов Н или В должна включать полный ток, который охватывается случайным контуром. Таким образом,

Закон полного тока
Такое уравнение считается законом полного тока в описании Максвелла. Отсюда напрашивается вывод, что изменяющееся поле создаст изменяющееся магнитное поле.
Согласно выводам Максвелла, взаимосвязь между изменяющимся электрическим и магнитным полем можно описать системой уравнений:

Уравнения Максвелла
В физическом сообществе не сразу были приняты представления Максвелла о ТС и электромагнитных волнах. Сам ученый не дожил до триумфа своих уравнений. Что ТС существует, пришлось признать после экспериментов Генриха Герца, наглядно показавших распространение электромагнитных волн через слой диэлектрика и пустое пространство.
Ток смещения в современной радиоэлектронике
Термин ТС в практической радиоэлектронике имеет абсолютно другой смысл и никак не связан с максвелловскими уравнениями. Для электронного прибора в качестве напряжения смещения выступает постоянное напряжение, которое прикладывается к управляемому электроду с целью достижения необходимого режима по постоянному току. Через прибор при этом проходит постоянный анодный ток, именно его и называют током смещения. Для операционного усилителя (ОУ), мощного генератора радиочастот, силовых ключей в состоянии покоя ТС равен нулю.
Видео по теме
Что такое ток смещения
Определение
Ток смещения или абсорбционный ток — величина, которая прямо пропорциональна скорости изменения электрической индукции.
Каждому переменному магнитному полю свойственно вихревое электрическое поле. Проводя исследования разных электромагнитных процессов, Дж. К. Максвелл определил существование обратного явления, когда электрическое поле, изменяясь, приводит к появлению вихревого магнитного поля.
Данное утверждение является одним из основных в теории Максвелла. Известно, что магнитное поле является признаком любого тока. Основываясь на данном факте, ученый определил переменное электрическое поле, как ток смещения. При измерении он будет отличаться от тока проводимости, который представляет собой следствие движения заряженных частиц в виде электронов и ионов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Токи смещения можно наблюдать только тогда, когда электрическое смещение (vec{D}) переменно, то есть наблюдают его колебания. Объемную плотность тока в этом случае можно измерить и рассчитать по формуле:
(vec{j}=frac{dvec{D}}{dt})
Вывод данного физического содержания теории Максвелла о токах смещения позволяет утверждать, что переменные электрические поля являются источниками переменных магнитных полей. Следует отметить, что для определения плотности тока смещения используют производную вектора (vec{D})
Ток смещения в диэлектрике
Вектор электрической индукции измеряется по формуле:
(vec{D}=varepsilon _{0}vec{E}+vec{P})
Где (varepsilon _{0}) — электрическая постоянная, (vec{E}) — вектор напряженности, (vec{P}) — вектор поляризации.
Уравнение для тока смещения будет иметь следующий вид:
(vec{j}=varepsilon _{0}frac{dvec{E}}{dt}+frac{dvec{P}}{dt})
Где (frac{dvec{P}}{dt}) — плотность тока поляризации.
Токи поляризации являются следствием движения связанных заряженных частиц, которые не обладают принципиальными отличиями по сравнению со свободными зарядами. Основываясь на данном факте, можно объяснить порождение магнитного поля токами поляризации. Принципиальной новизной отличается вторая часть уравнения тока смещения:
(varepsilon _{0}frac{dvec{E}}{dt})
Данная формула не обладает связью с перемещением заряженных частиц, но также формирует магнитное поле. Можно сделать вывод, что в вакуумной среде любое изменение электрического поля по времени является причиной образования магнитного поля.
Нужно обратить внимание на то, что определение тока смещения для диэлектриков имеет какое-то обоснование, так как в них действительно можно наблюдать смещение зарядов в атомах и молекулах. Но этот термин применяют и к вакууму, в котором отсутствуют заряды, а, следовательно, и их смещение.
Полный ток
При наличии в проводнике переменного тока, внутри него будет образовано переменное электрическое поле. Таким образом, проводник будет вмещать в себе ток проводимости (j) и ток смещения. Магнитное поле проводника рассчитывают, как сумму вышеуказанных токов, то есть полный ток:
(vec{j_{p}}=vec{j}+frac{dvec{D}}{dt})
Роль данных слагаемых определяется двумя факторами:
- электропроводность вещества;
- частота переменного тока.
В зависимости от перечисленных характеристик можно наблюдать следующие процессы:
- Вещества с хорошей проводимостью такие, как металлы, при низкой частоте переменного тока: плотность тока смещения обладает небольшой мощностью, в то время как ток проводимости достаточно велик. В данной ситуации током смещения целесообразно пренебречь по сравнению с током проводимости.
- В веществах, для которых характерно высокое сопротивление, то есть изоляторах, при токе с большой частотой ведущая роль отведена току смещения. В этом случае в уравнении для общего тока слагаемые могут обладать одинаковыми или противоположными знаками.
Поэтому величина полного тока может быть меньше, либо превышать ток проводимости, а также равняться нулю. Таким образом, в общем случае переменных токов полный ток определяет магнитное поле. При размыкании контура на концах проводника наблюдают обрыв только тока проводимости. В диэлектрике между концами проводника возникает ток смещения, замыкающий ток проводимости. В итоге, из понятия электрического тока, как полного тока, вытекает утверждение, что в природе все токи замкнуты.
Как найти плотность тока смещения, формула
С целью установить количественную связь между изменяющимся электрическим полем и магнитным полем, которое вызвано электрическим, Максвелл ввел в рассмотрение ток смещения. Определение справедливо в случае работы с диэлектриками. В данных веществах заряженные частицы меняют положение по причине воздействия на них электрического поля.
В случае вакуумной среды заряды отсутствуют, хотя магнитное поле существует. То есть термин «тока смещения» не совсем удачный, однако его смыл абсолютно верный. Вывод, который сделал ученый, состоит в том, что любое переменное электрическое поле образует переменное магнитное поле. Токи проводимости в условиях проводника будут замкнуты токами смещения в диэлектрике или в вакууме. Переменным электрическим полем в конденсаторе создается такое же магнитное поле, как если бы между пластинами был ток проводимости, по величине равный току в металлическом проводнике.
Исходя из данного пояснения, можно рассчитать ток смещения. Поверхностная плотность поляризационных зарядов и вектор электрического смещения равны:
(sigma =Evarepsilon varepsilon _{0})
(vec{D} =Evarepsilon varepsilon _{0})
(sigma =vec{D})
Величину полного заряда на поверхности диэлектрика, а также на пластинах конденсатора, можно рассчитать по формуле:
(q=sigma S)
Где S — площадь обкладки конденсатора.
(I_{sm}=frac{dq}{dt}=frac{dleft(qS right)}{dt})
Тогда можно записать следующую формулу:
(I_{sm}=Sfrac{dD}{dt})
Таким образом, ток смещения является величиной, пропорциональной скорости, с которой изменяется вектор электрического смещения (vec{D})
Отсюда вытекает определение тока смещения. Плотность тока смещения можно найти по формуле:
(vec{j}=frac{dvec{D}}{dt})
Вихревое магнитное поле (vec{B}) образуется в результате протекания тока смещения, связано с направлением вектора (frac{dvec{D}}{dt}) правилом правого винта. Относительная диэлектрическая проницаемость среды рассчитывается по формуле:
(varepsilon =1+x)
Где х — диэлектрическая восприимчивость среды.
В таком случае, можно получить уравнение:
(D=varepsilon varepsilon _{0}E=(1+x)varepsilon _{0}E)
(D=varepsilon _{0}E+varepsilon _{0}Ex)
Вектор поляризации равен:
(vec{P_{i}}=varepsilon _{0}xE)
Таким образом, получим равенство:
(I_{sm}=varepsilon _{0}frac{dvec{E}}{dt}+frac{dvec{P_{i}}}{dt})
Плотность тока смещения в вакууме:
(varepsilon _{0}frac{dvec{E}}{dt})
Плотность тока поляризации:
(frac{dvec{P_{i}}}{dt})
Плотность тока обусловлена перемещением зарядов в диэлектрике.
находится в одной плоскости с П-образным проводником, вектор скорости
|
I |
O |
рамки v перпендикулярен проводнику. |
|||
|
4. В магнитном поле, создаваемом длинным |
|||||
|
прямым проводником с током I , находится |
|||||
|
квадратная рамка со стороной а. Рамку поворачивают |
|||||
|
O |
вокруг оси ОО′ на 180o (рис. 50). Найти, какой заряд |
||||
|
протекает через поперечное сечение проводника |
|||||
|
b |
X |
рамки. Проводник находится в одной плоскости с |
|||
|
рамкой, расстояние между проводником и осью ОО′ |
|||||
|
Рис. 50 |
|||||
|
равно b. |
|||||
|
5. |
Квадратная |
рамка со стороной a перемещается в пространстве с |
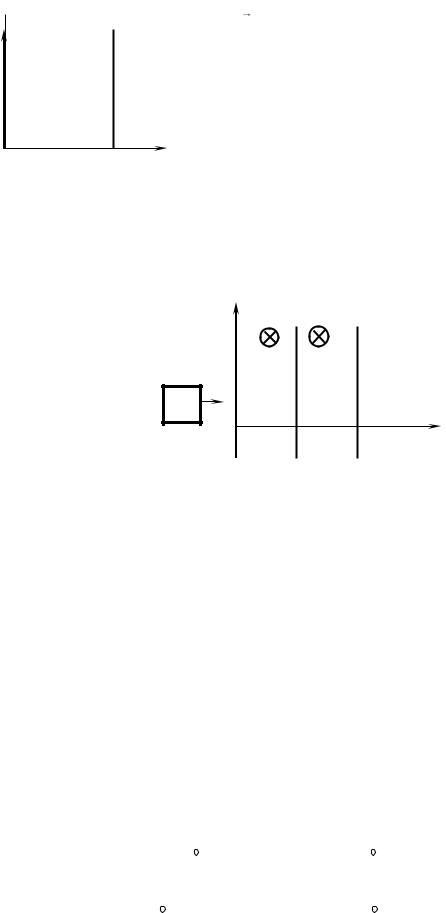
постоянной скоростью v в областях с различными значениями модуля вектора индукции магнитного поля (рис. 51). Построить график зависимости ЭДС индукции рамки от координаты ее левой стороны x.
B0 3B0
Рис. 51
ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ
Уравнения Максвелла в дифференциальной форме:
|
, B 0; |
||||
|
, E B ; |
||||
|
t |
; , D . |
|||
|
, H j D |
||||
t
Эквивалентные им уравнения Максвелла в интегральной форме:
|
B |
|||||||||
|
E, dl |
t |
, dS ; |
B, dS 0; |
||||||
|
L |
S |
S |
|||||||
|
D |
|||||||||
|
dV. |
|||||||||
|
H , dl j |
t |
, dS ; D, dS |
|||||||
|
L |
S |
S |
V |
62

Величину D называют плотностью тока смещения. Для изотропных
t
|
сред в случае достаточно слабых и медленно меняющихся полей уравнения |
|||
|
Максвелла дополняются следующими материальными уравнениями: |
|||
|
D 0 E, B 0 H, j |
E . |
||
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ |
|||
|
Задача 1. Точечный заряд |
q = 1,6 10 19 |
Кл движется равномерно и |
|
|
( v 106 м/с). Найти вектор |
|||
|
прямолинейно с нерелятивистской скоростью v |
плотности тока смещения в точке P , находящейся на расстоянии r = 10 мкм от заряда на прямой, перпендикулярной его траектории и проходящей через заряд
(рис. 52).
|
Решение: |
|||||||||||||||||||||||||||||||
|
Плотность |
тока |
смещения |
D |
dD |
|||||||||||||||||||||||||||
|
jсм |
|||||||||||||||||||||||||||||||
|
t |
|||||||||||||||||||||||||||||||
|
D |
|||||||||||||||||||||||||||||||
|
определяется |
приращением |
вектора |
D |
через |
|||||||||||||||||||||||||||
|
промежуток времени dt . Выражение для вектора D |
D |
||||||||||||||||||||||||||||||
|
в случае точечного заряда легко найти с помощью |
|||||||||||||||||||||||||||||||
|
r |
|||||||||||||||||||||||||||||||
|
теоремы Гаусса: |
|||||||||||||||||||||||||||||||
|
D |
, |
||||||||||||||||||||||||||||||
|
qer |
|||||||||||||||||||||||||||||||
|
4 r 2 |
er |
r |
|||||||||||||||||||||||||||||
|
где |
– единичный вектор, определяющий |
||||||||||||||||||||||||||||||
|
er |
|||||||||||||||||||||||||||||||
|
направление |
радиус-вектора |
точки |
наблюдения P |
q |
v dt |
||||||||||||||||||||||||||
|
относительно заряда. |
|||||||||||||||||||||||||||||||
|
За |
промежуток |
времени |
dt |
заряд |
совершит |
Рис. 52 |
|||||||||||||||||||||||||
|
перемещение |
dt . Приращение вектора смещения |
||||||||||||||||||||||||||||||
|
v |
|||||||||||||||||||||||||||||||
|
равно |
D. |
Модуль |
приращения |
определяется из подобия |
|||||||||||||||||||||||||||
|
dD D |
|||||||||||||||||||||||||||||||
|
треугольников (см. рис. 52): |
dD vD dt vq dt . |
||||||||||||||||||||||||||||||
|
r |
4 r 3 |
||||||||||||||||||||||||||||||
|
Учитывая векторный характер величин и их направления, можем записать |
|||||||||||||||||||||||||||||||
|
j |
j = 12,7 А/м 2 . |
||||||||||||||||||||||||||||||
|
qv , |
|||||||||||||||||||||||||||||||
|
см |
см |
||||||||||||||||||||||||||||||
|
4 r 3 |
|||||||||||||||||||||||||||||||
|
Ответ: |
j |
qv , j |
= 12,7 А/м 2 . |
||||||||||||||||||||||||||||
|
см |
см |
||||||||||||||||||||||||||||||
|
4 r 3 |
|||||||||||||||||||||||||||||||
Задача 2. Плоский воздушный конденсатор, площадь каждой пластины которого S = 100 см 2 , включен последовательно в цепь переменного тока.
63
Найти максимальную плотность тока смещения в конденсаторе, если амплитуда синусоидального тока в подводящих проводах I0 = 1 мА.
Решение:
Сила тока в цепи меняется по закону I I0 cos t . Из определения силы тока I dq / dt получаем зависимость заряда на пластине конденсатора от времени:
|
q |
I0 |
sin t . |
|||||||||||||||||
|
Связь между модулем вектора D и плотностью заряда пластины легко |
|||||||||||||||||||
|
найти с помощью теоремы Гаусса: |
|||||||||||||||||||
|
D |
q |
I0 sin t |
, |
||||||||||||||||
|
S |
|||||||||||||||||||
|
S |
|||||||||||||||||||
|
где – поверхностная плотность заряда пластины конденсатора. |
|||||||||||||||||||
|
Отсюда находим модуль плотности тока смещения и его максимальное |
|||||||||||||||||||
|
значение. |
|||||||||||||||||||
|
j |
см |
D |
I0 cos t |
, j |
см0 |
I0 |
= 0,1 А/м 2 . |
||||||||||||
|
t |
S |
S |
|||||||||||||||||
|
Ответ: j |
см0 |
I0 |
= 0,1 А/м 2 . |
||||||||||||||||
|
S |
|||||||||||||||||||
Задача 3. Пространство между обкладками плоского конденсатора, имеющими форму круглых дисков, заполнено однородной слабо проводящей средой с удельной проводимостью и диэлектрической проницаемостью . Расстояние между обкладками d . Пренебрегая краевыми эффектами, найти напряженность магнитного поля между обкладками на расстоянии r от их оси, если на конденсатор подано напряжение U U0 cos t .
Решение:
Проекции векторов напряженности электрического поля и смещения
|
между обкладками на ось конденсатора равны |
|||||||
|
E |
U |
U0 cos t |
, D 0 E 0 |
U0 cos t |
. |
||
|
d |
d |
d |
|||||
Между обкладками возникают как ток проводимости, так и ток смещения, плотности которых равны
|
j E |
U0 cos t |
, jсм |
D |
0 sin t |
. |
||
|
d |
t |
d |
|||||
Эти токи порождают магнитное поле, напряженность которого можно вычислить, воспользовавшись уравнением Максвелла:
64

|
(H , dl ) |
||||
|
j |
D , dS . |
|||
|
S |
t |
|||
|
В качестве вспомогательного замкнутого контура L , по которому выполняется |
||||
|
интегрирование, выберем окружность радиусом |
r , лежащую в плоскости, |
|||
|
перпендикулярной оси конденсатора с центром |
на оси. |
В силу симметрии |
||
|
задачи напряженность магнитного поля |
направлена |
по касательной к |
||
|
H |
выбранной окружности и постоянна по величине. Тогда последнее выражение можно переписать:
H 2 r ( j jсм ) r 2 .
Напряженность магнитного поля равна
H rU0 ( cos t 0 sin t) . 2d
Ответ: H rU0 ( cos t 0 sin t) . 2d
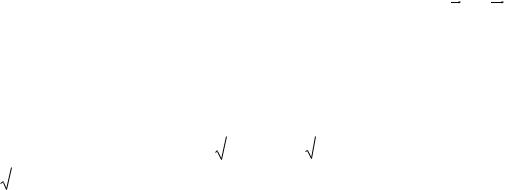
Задача 4. Ток, текущий по длинному прямому соленоиду, радиус сечения которого R = 5 см, меняют так, что магнитное поле внутри соленоида
возрастает со временем по закону B t 2 , где = 5 Тл/с 2 . Найти плотность
тока смещения как функцию расстояния r от оси соленоида. Вычислить плотность тока смещения при r = 2 см и t =4 с.
Решение:
Изменяющееся со временем магнитное поле порождает вихревое электрическое поле, напряженность которого вычислим воспользовавшись уравнением Максвелла:
|
E, dl |
B |
|||||
|
, dS |
. |
|||||
|
t |
||||||
|
S |
||||||
|
В качестве вспомогательного замкнутого контура |
L , |
по которому выполняется |
интегрирование, выберем окружность радиусом r , лежащую в плоскости,
перпендикулярной оси соленоида с центром на оси. В силу симметрии задачи
напряженность электрического поля E направлена по касательной к выбранной окружности и постоянна по величине. Тогда последнее выражение можно переписать:
2 rE r 2 dBdt r 2 2 t, r R;
2 rE R2 dBdt R2 2 t, r R.
65

Знак минус определяет направление вектора E . В дальнейшем его учитывать не будем. Из полученных выражений находим E , D и jсм внутри и вне соленоида
|
E rt, D |
0 |
E |
rt, j |
см |
D |
r, r R; |
|||||||||||||
|
0 |
t |
0 |
|||||||||||||||||
|
E |
R2t |
, D |
E |
R2t |
, j |
D |
R2 |
||||||||||||
|
0 |
0 |
см |
t |
0 |
, r R. |
||||||||||||||
|
r |
r |
r |
|||||||||||||||||
|
Ответ: j |
r, r R; |
j |
R2 |
= 0,177 нА/м 2 . |
|||||||||||||||
|
см |
см |
0 |
, r R , j |
см |
|||||||||||||||
|
0 |
r |
||||||||||||||||||
Задача 5. По жесткому непроводящему тонкому круговому кольцу массой m равномерно распределен заряд q . Кольцо может свободно вращаться
вокруг оси, совпадающей с осью симметрии кольца. Вначале кольцо покоится,
а магнитное поле равно нулю. Затем включается однородное магнитное поле
B(t) , перпендикулярное плоскости кольца и произвольно меняющееся по
величине во времени. Найти зависимость от времени угловой скорости кольца.
Решение:
Изменяющееся со временем магнитное поле порождает вихревое электрическое поле, которое действует на заряды, распределенные по кольцу, приводя во вращение кольцо в замкнутом контуре, совпадающем с кольцом, возникает ЭДС индукции:
|
B |
dB |
|||||||
|
i |
(E, dl ) |
t |
, dS |
= R2 |
, |
|||
|
dt |
||||||||
|
S |
где R – радиус кольца. Знак минус отражает правило Ленца.
За промежуток времени dt через произвольное поперечное сечение
|
контура пройдет заряд dq |
q |
dt . Работа ЭДС за этот промежуток времени |
|
|
2 |
|||
|
равна |
|
dA dq R2 |
dB q |
dt |
q R2 |
dB |
. |
|||||
|
i |
dt |
2 |
2 |
|||||||
|
Эта работа идет на приращение кинетической энергии кольца: |
||||||||||
|
mv 2 |
||||||||||
|
dA dT d |
. |
|||||||||
|
2 |
Линейная скорость v R . Таким образом, получаем
|
m 2 R2 |
q R2 |
||||
|
d |
dB , или 2m d q dB . |
||||
|
2 |
2 |
||||
66
Интегрирование с учетом начальных условий дает выражение для угловой скорости:
|
(t) |
q |
B(t) . |
||||||
|
2m |
||||||||
|
Выражение в векторном виде |
||||||||
|
q |
||||||||
|
(t) |
B(t) . |
|||||||
|
2m |
||||||||
|
q |
||||||||
|
Ответ: (t) |
B(t) . |
|||||||
|
2m |
||||||||
|
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ |
||||||||
|
1. Точечный |
заряд q = 1,6 10 19 |
Кл |
движется |
равномерно и |
||||
|
( v 106 м/с). |
Найти вектор |
|||||||
|
прямолинейно с нерелятивистской скоростью v |
плотности тока смещения в точке P , находящейся на расстоянии r = 10 мкм от заряда на прямой, совпадающей с его траекторией движения.
2. Определить величину напряженности магнитного поля в плоском
|
конденсаторе, |
одна |
из |
пластин |
которого удаляется |
от неподвижной другой |
|
пластины со скоростью |
|||||
|
v (v = 20 м/с), перпендикулярной пластинам. Разность |
|||||
|
потенциалов |
между |
пластинами |
U =20 кВ остается |
постоянной. Начальное |
расстояние между пластинами равно 0,5 м. Вычислить разность потенциалов в момент t = 0,1 с.
3. Длинный прямой соленоид имеет n витков на единицу длины. По нему течет переменный ток I I0 sin t , I0 = 8 А, = 300 рад/с. Найти плотность
тока смещения внутри соленоида как функцию расстояния r от оси соленоида. Радиус сечения соленоида равен 30 см. Вычислить амплитуду тока смещения при r = 10 см.
4. Плоский конденсатор образован двумя дисками, между которыми находится однородная слабопроводящая среда. Конденсатор зарядили и отключили от источника напряжения. Пренебрегая краевыми эффектами, определить магнитное поле внутри конденсатора в процессе разрядки
|
конденсатора. |
||||
|
5. В некоторой |
области инерциальной системы |
отсчета |
имеется |
|
|
вращающееся с угловой |
модуль |
индукции |
||
|
скоростью магнитное поле, |
||||
|
которого равен B . Найти , E в этой области как функцию векторов |
B и . |
67
11. ЭЛЕКТРОМАГНИТЫЕ ВОЛНЫ.
ЭНЕРГИЯ И ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ Уравнения Максвелла, записанные в однородной изотропной среде без
|
токов и зарядов: |
||||||||||||||||||||||
|
, |
||||||||||||||||||||||
|
, E B , |
, H D |
|||||||||||||||||||||
|
t |
t |
|||||||||||||||||||||
|
( , B) 0, ( , D) , |
||||||||||||||||||||||
|
приводят к волновым уравнениям |
||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||
|
2 E |
0 |
E и 2 H |
0 |
H |
||||||||||||||||||
|
0 |
t |
2 |
0 |
t 2 |
||||||||||||||||||
|
2 |
2 |
2 |
||||||||||||||||||||
|
(здесь 2 |
– оператор Лапласа). Функции, которые являются |
|||||||||||||||||||||
|
x2 |
y 2 |
z 2 |
||||||||||||||||||||
их решениями, представляют собой уравнения волн для векторов E и H . Таким образом, электрическое и магнитное поля, образуя единое
электромагнитное поле, могут существовать в отсутствие зарядов и токов в виде электромагнитных волн. Фазовая скорость их распространения, как
|
следует из волновых уравнений, равна |
||||||||||
|
v |
1 |
c |
, |
|||||||
|
0 0 |
||||||||||
|
3 108 м/с совпадает со скоростью распространения света в |
||||||||||
|
где c 1/ |
0 0 |
|||||||||
|
вакууме. |
Простейшим и одним из наиболее важных решений волнового уравнения
|
является решение в виде плоской волны: |
|||||||
|
0 ) , |
|||||||
|
E E0 cos( t kr |
0 ), H H0 cos( t kr |
||||||
где k – волновой вектор, задающий направление распространения плоской электромагнитной волны. Модуль волнового вектора называется волновым числом. Оно определяется выражением
|
k k |
2 , |
|||||||||
|
v |
||||||||||
|
где 2 v / – |
||||||||||
|
длина волны. Векторы E, H и k |
взаимно ортогональны и |
|||||||||
|
образуют правовинтовую систему. Поворот |
вектора |
E |
к вектору H дает |
|||||||
|
направление k . |
Связав с направлениями |
k , E, H |
орты прямоугольной |
|||||||
|
декартовой системы координат i , |
j, k |
соответственно, |
можно получить для |
ненулевых проекций векторов соотношение
68

P w .
|
0 Ey |
0 H z . |
||||
|
Оно выполняется в любой момент времени в любой точке пространства, а |
|||||
|
также для амплитуд векторов. Векторы E, H |
совершают колебания в одной фазе. |
Электромагнитная волна, как и другие волны, переносит энергию. Плотность энергии электромагнитной волны равна сумме плотностей энергий электрического и магнитного полей:
|
w |
E 2 |
H 2 |
EH |
|||||
|
2 |
2 |
v . |
||||||
|
0 |
0 |
|||||||
|
Плотность потока энергии |
||||||||
|
S |
E, H |
называют вектором Пойнтинга. На практике измеряется интенсивность волны, которая равна модулю среднего по времени значения плотности потока энергии
|
E 2 |
||||||
|
I S |
0 |
/ |
0 |
/ 2 . |
||
|
0 |
Наряду с энергией электромагнитная волна обладает импульсом.
|
Плотность импульса электромагнитной волны в вакууме дается выражением |
|||
|
E, H |
|||
|
p |
c2 |
. |
|
При поглощении телом падающая на его поверхность электромагнитная волна передает телу импульс. В соответствии со вторым законом Ньютона на тело со стороны волны действует сила, равная скорости изменения импульса тела. Если волна падает перпендикулярно поверхности тела и происходит полное поглощение волны, то давление на поверхность тела равно
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Плоская электромагнитная волна падает нормально на поверхность плоскопараллельного слоя толщиной l = 2 м из немагнитного вещества, диэлектрическая проницаемость которого экспоненциально падает от значения 1 = 4 на передней поверхности до 2 =2,25 – на задней. Найти время
распространения данной фазы волны через этот слой.
Решение:
Для немагнитной среды 1. Тогда скорость распространения волны
равна v c / 
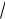 . Перпендикулярно поверхности слоя проводим ось OX , начало
. Перпендикулярно поверхности слоя проводим ось OX , начало
которой совмещаем с границей слоя, на которую падает волна. Тогда зависимость диэлектрической проницаемости от координаты x будет даваться выражением
1e kx ,
где коэффициент k определяется из условия 2 1e kl .
69

Разобьем слой на тонкие слои, границы которых определяются координатами x и x dx . Время прохождения такого слоя
|
1 |
e kx / 2 dx . |
||||||||||||||||||||||||||||||||||||||||||||||||
|
dt |
dx |
dx |
|||||||||||||||||||||||||||||||||||||||||||||||
|
v |
c |
c |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Время распространения фазы волны через весь слой равно |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
l |
1 |
kx / 2 |
1 |
2 |
kx / 2 |
l |
2l( 1 |
2 ) |
|||||||||||||||||||||||||||||||||||||||||
|
t |
e |
dx |
e |
= 11,6 нс. |
|||||||||||||||||||||||||||||||||||||||||||||
|
c ln( |
/ |
||||||||||||||||||||||||||||||||||||||||||||||||
|
c |
c |
k |
0 |
) |
|||||||||||||||||||||||||||||||||||||||||||||
|
0 |
1 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Ответ: |
t |
2l( 1 |
2 ) |
= 11,6 нс. |
|||||||||||||||||||||||||||||||||||||||||||||
|
c ln( |
/ |
2 |
) |
||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Задача 2. В вакууме распространяется плоская электромагнитная волна, |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
которая описывается уравнениями |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
E |
E0 cos( t kr ), H H0 cos( t kr ) . |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Исходя из уравнений Максвелла, выразить через заданные векторы |
и |
||||||||||||||||||||||||||||||||||||||||||||||||
|
E0 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
. Для E = 160 В/м и k = 0,5 м 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
k |
вектор H |
0 |
вычислить H |
0 |
. |
||||||||||||||||||||||||||||||||||||||||||||
|
0 |
Решение:
Поля зависят только от фазы t kx x ky y kz z . Поэтому частные
производные полевых величин по координатам можно представить следующим образом:
|
d |
k |
d |
, |
k |
d |
, |
k |
d |
. |
||||||||||||||
|
x |
x |
y |
z |
||||||||||||||||||||
|
x d |
d y |
d z |
d |
||||||||||||||||||||
|
Воспользуемся уравнением Максвелла: |
, |
||||||||||||||||||||||
|
, E B |
|||||||||||||||||||||||
|
t |
|||||||||||||||||||||||
|
где B 0 H . |
Подставим в уравнение заданные выражения для полей. Ротор напряженности электрического поля вычислим через определитель, воспользовавшись его свойствами. В результате получим
|
ex |
ey |
|||
|
kx |
k y |
|||
|
0 H0 ( )sin( t kr ) |
||||
|
E0x |
E0 y |
|||
|
В вакууме |
kc k / |
0 0 . |
||
|
окончательный результат: |
|
ez |
d cos |
|||||||
|
kz |
k , E0 sin( t kr ) . |
|||||||
|
d |
||||||||
|
E0z |
||||||||
|
Подстановка |
этого |
выражения дает |
70
|
k , E , H |
|||||||||||||||||||||||||||
|
H |
0 |
/ 0 |
0 E =0,42 А/м. |
||||||||||||||||||||||||
|
0 |
0 |
0 |
|||||||||||||||||||||||||
|
0 |
|||||||||||||||||||||||||||
|
k |
0 |
||||||||||||||||||||||||||
|
k , E . H |
|||||||||||||||||||||||||||
|
Ответ: |
H |
0 |
/ 0 |
0 E |
=0,42 А/м. |
||||||||||||||||||||||
|
0 |
0 |
0 |
0 |
||||||||||||||||||||||||
|
k |
0 |
||||||||||||||||||||||||||
|
Задача |
3. |
Плоская |
электромагнитная волна |
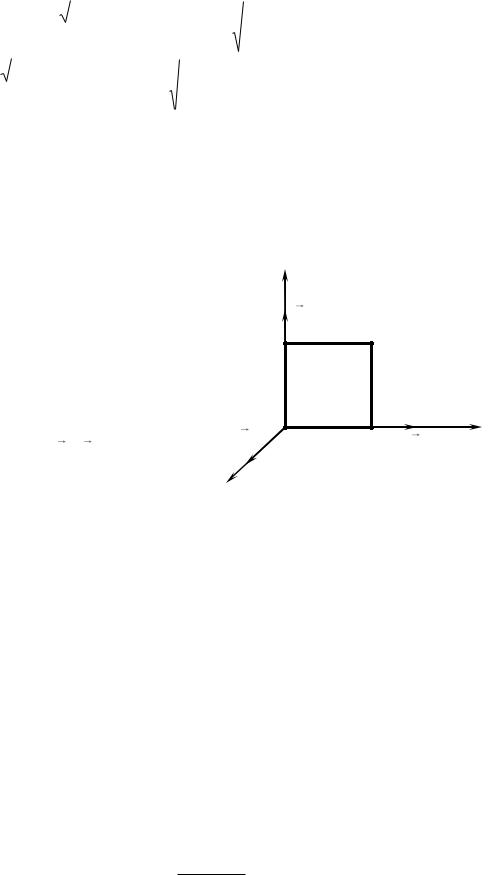
E E0 cos( t kx) , |
распространяющаяся в вакууме, наводит ЭДС индукции в квадратном контуре со стороной l (рис. 53). Найти зависимость от времени ЭДС индукции в
контуре по заданным E0 = 20 мВ/м, = 2 108
Решение:
Для вычисления ЭДС с учетом ее направления выберем обход контура по часовой стрелке. На участке контура 1–2 во
|
всех |
точках |
напряженность |
поля |
|||
|
cos t , |
||||||
|
E E |
а |
на |
участке |
3–4 |
||
|
0 |
||||||
|
E E0 cos( t kl). |
С учетом определения |
ЭДС на некотором участке:
b
i (E, dl ) ,
рад/с, l = 1,5 м.
Y
E0
2 3
1 4
|
a |
||||
|
получаем |
Z |
|||
|
i |
E0l cos t , i |
E0l cos( t l / c) . |
Рис. 53 |
|
|
На участках |
2–3 и 4–1 ЭДС равна нулю, так как вектор E |
перпендикулярен отрезкам, задающим эти участки. Сложив ЭДС на всех участках, получаем ЭДС в контуре:
i E0l(cos t cos( t l / c)) = 60 cos t мВ.
Ответ: i E0l(cos t cos( t l / c)) = 60 cos t мВ.
Задача 4. Плоский воздушный конденсатор, обкладки которого имеют форму дисков радиусом R = 8 см, подключен к переменному синусоидальному напряжению частоты = 2000 рад/с. Найти отношение амплитудных значений магнитной и электрической энергий внутри конденсатора.
Решение:
В соответствии с условием задачи напряжение на конденсаторе меняется по закону U U0 sin t . Проекция напряженности электрического поля на
направление OX , перпендикулярное обкладкам конденсатора, равна
Ex U0 sin t , b
где b – расстояние между обкладками конденсатора.
71

Изменяющееся со временем электрическое поле приводит к появлению тока смещения, плотность которого равна
|
j |
Dx |
Ex |
0U0 cos t . |
|
|
см |
t |
0 t |
b |
Ток смещения приводит к возникновению магнитного поля в пространстве
между обкладками конденсатора. Для определения напряженности магнитного
поля воспользуемся теоремой о циркуляции вектора H :
(H , dl ) dtd S ( jсм , dS ).
В качестве замкнутого контура выберем окружность радиусом r R ,
лежащую в плоскости, параллельной обкладкам конденсатора. Центр окружности лежит на оси симметрии конденсатора. Тогда по теореме о циркуляции получаем
|
H 2 r jсм r |
2 |
H |
0U0 r cos t |
. |
|
2b |
||||
Для вычисления энергии магнитного поля разбиваем объем между пластинами конденсатора на коаксиальные с осью симметрии конденсатора цилиндрические слои толщиной dr и внутренним радиусом r . Область изменения r : 0 r R . Энергия магнитного поля равна
|
Wм wм |
R |
H 2 |
R |
2U 2 2r 2 cos2 t |
||||||||||||||
|
dV |
0 |
b 2 r dr |
0 |
0 0 |
b 2 r dr |
|||||||||||||
|
V |
0 |
2 |
0 |
2 4b2 |
||||||||||||||
|
2 U 2 2 R4 cos2 |
t |
. |
||||||||||||||||
|
0 |
0 |
0 |
||||||||||||||||
|
16b |
||||||||||||||||||
|
Энергия электрического поля в силу однородности поля E в |
||||||||||||||||||
|
пространстве между обкладками равна |
||||||||||||||||||
|
W w V |
E |
2 |
U 2 R2 sin2 |
t |
. |
|||||||||||||
|
0 |
b R2 |
0 0 |
||||||||||||||||
|
э |
э |
2 |
2b |
|||||||||||||||
Подставив максимальные значения энергий, получим искомое отношение:
|
Wм max |
0 0R2 2 |
= 3,6 10 14 . |
||||||||||||
|
Wэ max |
8 |
|||||||||||||
|
Ответ: |
Wм max |
0 0R2 2 |
= |
3,6 10 14 . |
||||||||||
|
Wэ max |
8 |
E |
||||||||||||
|
Задача 5. Сила тока в очень длинном |
H |
|||||||||||||
|
соленоиде радиусом |
R =10 см медленно |
|||||||||||||
|
увеличивается от 0 до |
I0 = 20 А. Число |
L |
||||||||||||
|
витков |
соленоида |
на |
единицу |
длины |
||||||||||
|
равно n |
= 1000 м |
1 |
. Найти количество |
S |
r |
|||||||||
|
энергии, протекающей через замкнутый |
||||||||||||||
|
коаксиальный с соленоидом |
цилиндр |
Рис. 54 |
||||||||||||
|
72 |

длиной l = 0,5 м и радиусом основания r 5 см за полное время возрастания
тока (рис. 54). Сравнить полученное выражение с энергией магнитного поля внутри выделенного цилиндра.
Решение:
Напряженность магнитного поля в соленоиде параллельна его оси симметрии. Ее модуль равен
H nI .
Изменение со временем силы тока приводит к изменению со временем напряженности магнитного поля. В свою очередь это вызывает появление вихревого электрического поля, напряженность которого можно вычислить с помощью теоремы о циркуляции. В качестве замкнутого контура выберем окружность на поверхности указанного в условии задачи цилиндра. Тогда
|
d |
dI |
|||||||||
|
(E, dl ) |
(B, dS ) |
E 2 r 0n |
r2 . |
|||||||
|
dt |
dt |
|||||||||
|
S |
||||||||||
|
Напряженность электрического поля определятся выражением |
||||||||||
|
E |
0nr dI |
. |
||||||||
|
2 |
dt |
|||||||||
|
Знак минус указывает на то, что напряженность E направлена по касательной к |
||||||||||
|
окружности в соответствии с правилом левого винта. Векторы E и |
H взаимно |
|||||||||
|
ортогональны. Плотность потока энергии – вектор Пойнтинга: |
||||||||||
|
S E, H . |
Во всех точках замкнутого цилиндра вектор S перпендикулярен оси цилиндра и направлен к ней. Поэтому поток энергии через основания цилиндра будет равен нулю. Модуль вектора Пойнтинга равен
S EH 0n2rI dI . 2 dt
Поток энергии, поступающий в цилиндр, равен произведению модуля вектора Пойнтинга на площадь боковой поверхности цилиндра l2 r . За промежуток времени от 0 до t в цилиндр поступит количество энергии, равное
|
t |
n2rI dI |
I 0 |
n2r 2lI 2 |
||||||||||||
|
W |
0 |
2 rl dt 0n |
2r 2l I dI |
0 |
0 . |
||||||||||
|
2 |
dt |
||||||||||||||
|
0 |
0 |
2 |
|||||||||||||
|
Энергия магнитного поля внутри цилиндра равна |
|||||||||||||||
|
W w |
V |
H 2 |
r 2l |
n2r 2lI 2 |
|||||||||||
|
0 |
0 |
0 W = 0,49 Дж. |
|||||||||||||
|
м |
м |
2 |
2 |
||||||||||||
Энергия, поступившая в цилиндр через его поверхность, равна энергии созданного внутри цилиндра магнитного поля.
73
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для школьников (для лучшего понимания физики).
Накал лампочки, включенной в цепь переменного (синусоидального) тока, содержащую конденсатор, показывает, что конденсатор пропускает через себя переменный ток. Чем объясняется замкнутость такой цепи?
Прежде, чем ответить на этот вопрос, надо рассмотреть необходимые нам понятия – это понятие вектора электрического смещения D и понятие тока смещения Iсм.
Вектор электрического смещения
Вектор электрического смещения D (его ещё называют просто электрическим смещением или электрической индукцией), как и вектор напряженности Е, является характеристикой электрического поля.
Вектором электрического смещения D называется величина, определяемая соотношением
где Е– напряжённость электрического поля в диэлектрике; Р – вектор поляризации диэлектрика.
Вектор электрического смещения D введён для удобства расчёта электрических полей в разных диэлектриках, находящихся, например, в поле конденсатора..
Мы видели, что при помещении диэлектрика в электрическое поле Ео конденсатора, диэлектрик поляризуется – на его гранях появляются связанные отрицательные и положительные заряды.
Связанные заряды создают своё электрическое поле Есв, направленное навстречу внешнему полю Ео, то есть связанные заряды ослабляют внешнее электрическое поле.
Напряжённость поля, создаваемого связанными (или поляризационными) зарядами, равна отношению плотности связанных зарядов к электрической постоянной:
(Подобная формула была получена в Занятии 48 для напряжённости поля плоского конденсатора. Мы применяем её здесь, потому что связанные заряды тоже создают своего рода конденсатор. Внутри диэлектрика связанные заряды компенсируют друг друга, нескомпенсированными остаются только связанные заряды на границах диэлектрика).
Вектор поляризации диэлектрика (дипольный момент единицы объёма диэлектрика) равен плотности связанных зарядов:
(На рисунке индекс у значка плотности обозначен буквой р а в формуле стоит индекс св – плотность связанных зарядов и плотность поляризационных зарядов это одно и то же).
К этим уравнениям добавим ещё две формулы, связывающие результирующую напряжённость поля Е в диэлектрике с напряжённостью внешнего электрического поля Ео (поля конденсатора) и напряжённостью поля Есв, созданного связанными зарядами диэлектрика:
Е = Ео – Есв и
Последняя формула говорит о том, что диэлектрик ослабляет внешнее электрическое поле в “эпсилон” раз.
Совместная запись четырёх последних уравнений даёт зависимость вектора поляризации диэлектрика от напряжённости электрического поля Е в диэлектрике:
то есть вектор поляризации диэлектрика пропорционален напряжённости электрического поля в диэлектрике.
Приведённый в статье “Диэлектрик в электрическом поле. Поляризация диэлектрика. Ток поляризации” рисунок (повторим его) и показывает поляризацию диэлектрика, то есть возникновение на гранях диэлектрика связанных зарядов.
Результирующее поле в диэлектрике Е = Ео – Есв направлено в ту же сторону, что и Ео, так как Есв всегда меньше Ео.
Видим, что на границе с диэлектриком густота силовых линий (линий напряжённости Е) скачком изменяется, т. е. силовые линии на границе диэлектрика разрываются.
Причина этого явления заключается в том, что линии напряжённости Е начинаются как на свободных зарядах (зарядах на обкладках конденсатора), так и на связанных зарядах.
Вектор электрического смещения D связан с напряжённостью Е электрического поля формулой, в которую входит произведение диэлектрической проницаемости диэлектрика на напряжённость электрического поля в этом диэлектрике.
Представим, что между обкладками конденсатора параллельно им находятся два диэлектрика с разной диэлектрической проницаемостью. Напряжённость электрического поля в них тоже будет разной. Но произведение диэлектрической проницаемости на напряжённость поля (индукция поля D в каждом диэлектрике) будут иметь одинаковое значение
На рисунке ниже электрическое поле конденсатора изображено векторами D или линиями индукции, которые на границе диэлектрика не разрываются, то есть индукция D имеет одинаковое значение для любой среды в конденсаторе..
Полезно посмотрите, как производится расчёт полей Е в разных диэлектриках, помещённых между обкладками конденсатора – решение такой задачи дано в конце статьи “Связь между вектором напряжённости электрического поля и вектором электрического смещения”
Теперь посмотрим, что понимается под током смещения.
Ток смещения
Опыты показали, что вихревое магнитное поле образуется не только вокруг провода с током (см. статью “Какое одинаковое свойство имеют изменяющееся во времени электрическое поле и ток проводимости”. Такое же вихревое магнитное поле создаётся изменяющимся во времени электрическим полем.
Понятие “ток смещения” было введено Максвеллом при создании им теории электромагнитного поля. Током смещения он назвал величину, пропорциональную скорости изменения индукции электрического поля
(здесь в числителе записано изменение индукции D электрического поля, а в знаменателе время, за которое это изменение произошло).
Формулу для тока смещения можно получить с применением теоремы Гаусса, согласно которой поток вектора электрического смещения D сквозь замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности.
Под потоком вектора электрического смещения D через замкнутую поверхность понимается количество N силовых линий, пронизывающих эту поверхность (поток вектора D сквозь замкнутую поверхность можно обозначать буквой N, а можно буквой Ф).
Чтобы найти выражение для силы тока смещения Iсм, было рассмотрено прохождение переменного (синусоидального) тока по электрической цепи, в которую включен конденсатор ёмкостью С и лампочка.
Для применения теоремы Гаусса одну из обкладок конденсатора окружили воображаемой замкнутой поверхностью (на рисунке сечение этой поверхности плоскостью чертежа показано пунктирной линией).
По цепи течёт переменный ток, тогда можно представить, что за элементарный интервал времени dt, внутрь этой поверхности от источника переменного напряжения входит заряд dq (dq=Idt).
Тогда, согласно теореме Гаусса, происходит изменение потока вектора D электрического смещения через воображаемую замкнутую поверхность на
Здесь I -ток проводимости.
Последнее уравнение связывает ток проводимости со скоростью изменения электрического поля внутри провода.
Но, согласно понятию “ток смещения”, I см выражается такой же формулой, так как под током смещения понимается величина пропорциональная скорости изменения электрического поля.
Тогда правая часть последнего уравнения и является током смещения, то есть формулы для тока смещения и тока проводимости одинаковы.
Ток проводимости в проводе и в обкладках конденсатора (это тоже проводник) можно представить в виде линий тока проводимости.
Внутри обкладки конденсатора линии тока проводимости расходятся, а внутри конденсатора (между обкладками) линии тока проводимости замыкаются линиями тока смещения.
Таким образом, внутри конденсатора электрическая цепь замыкается током смещения (изменяющимся во времени электрическим полем).
Надо помнить что понятие “ток смещения” это условное понятие, что под током смещения понимается изменяющееся со временем электрическое поле. С обычным током его роднит только одно – это способность создавать вблизи магнитное поле.
Вернёмся к рисунку
Считая электрическое поле конденсатора однородным и не выходящим за пределы конденсатора, выражение для потока вектора электрического смещения можно записать в виде
где S – площадь обкладки конденсатора (площадь части замкнутой поверхности, проходящей внутри конденсатора параллельно его обкладкам).
Тогда используя формулу, связывающую D и Е
получим выражение для тока смещения:
а выражение для плотности тока смещения запишется в виде:
так как под плотностью тока понимается заряд, проходящий через единицу площади сечения в единицу времени.
Если использовать связь между D, Е и Р для однородного изотропного диэлектрика:
то выражение для плотности тока смещения примет вид:
то есть ток смещения в конденсаторе в присутствие диэлектрика можно условно представить в виде двух слагаемых: первое связано с изменением напряжённости Е электрического поля, второе – с изменением поляризованности диэлектрика (с током поляризации).
Таким образом, материал, рассмотренный в этой статье, позволяет сделать вывод, что замкнутость цепи переменного тока, содержащей конденсатор, обеспечивается током смещения, составной частью которого является ток поляризации.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Для школьников предлагаются подборки материала по темам:
!. Механика. Кинематика. Равномерное прямолинейное движение.
2. Равнопеременное прямолинейное движение.
Предыдущая запись: Какое одинаковое свойство имеют изменяющееся во времени электрическое поле и ток проводимости. Направление тока поляризации”.
Следующая запись: Ёмкость уединённого проводника. Ёмкость конденсатора. Почему диэлектрик повышает ёмкость конденсатора?
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
