Как найти модуль полета камня

Условие задачи:

Камень, брошенный с земли под углом 45° к горизонту, через 0,8 с после начала движения имел вертикальную составляющую скорости 12 м/с. Чему равно расстояние между точкой бросания и местом падения камня?

Задача №1.6.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(alpha=45^circ), (t_1=0,8) с, (v_y=12) м/с, (L-?)

Решение задачи:

Для решения задачи необходимо сделать рисунок. Мы его сделали за вас, можете взглянуть на него справа, для увеличения кликнув на нем мышью.

Поскольку нужно определить дальность полета, то запишем уравнения движения камня в проекциях на введенные нами оси, а далее уже определим, каких данных нам не хватает. Уравнения, как всегда, выглядят стандартно, поскольку в задаче нет ничего необычного.

[left{ begin{gathered}
ox:x = {v_0}cos alpha cdot t,,,,,,,,,,,,,,,,(1) hfill \
oy:y = {v_0}sin alpha cdot t – frac{{g{t^2}}}{2},,(2) hfill \
end{gathered} right.]

Когда камень ударится о землю, его ордината (y) будет равна нулю, поэтому приравняем уравнение (2) к нулю и найдем корни получившегося уравнения.

[y = 0 Rightarrow {v_0}sin alpha  cdot t – frac{{g{t^2}}}{2} = 0]

[tleft( {{v_0}sin alpha – frac{{gt}}{2}} right) = 0]

[left[ begin{gathered}
t = 0 hfill \
t = frac{{2{v_0}sin alpha }}{g} hfill \
end{gathered} right.]

Первый корень не удовлетворяет условию падения камня, поскольку он не мог взлететь и удариться о землю в ту же секунду.

Тогда второй корень подставим в уравнение (1) и получим формулу для определения дальности полета.

[L = frac{{2{v_0}cos alpha  cdot {v_0}sin alpha }}{g} = frac{{v_0^2sin 2alpha }}{g}]

Отлично, значит нам необходимо узнать начальную скорость камня (в момент броска), и после мы сможем сосчитать ответ. Для этого запишем уравнение скорости для вертикальной ее составляющей.

[{v_y} = {v_{0y}} – gt_1 = {v_0}sin alpha  – gt_1]

Из него выразим начальную скорость камня и подставим ее в формулу дальности полета.

[{v_0} = frac{{{v_y} + gt_1}}{{sin alpha }}]

В итоге получена формула в общем виде:

[L = {left( {frac{{{v_y} + gt_1}}{{sin alpha }}} right)^2}frac{{sin 2alpha }}{g}]

Как всегда, подставим все известные величины в СИ и подсчитаем ответ:

[L = {left( {frac{{12 + 10 cdot 0,8}}{{sin 45^circ }}} right)^2}frac{{sin 90^circ }}{{10}} = 80; м]

Ответ: 80 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.

Смотрите также задачи:

1.6.2 Баскетболист бросает мяч в кольцо. Скорость мяча после броска
1.6.4 Минимальная скорость при движении тела, брошенного под углом
1.6.5 На некоторой высоте одновременно из одной точки брошены

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

ЕГЭ 2020 по физике пройдет 9 июля. У выпускников есть больше месяца на подготовку, и это здорово. Давайте не тратить время на переживания, а решать задачи по механике вместе с преподавателем TutorOnline Андреем Алексеевичем.

Задача № 1

Камень бросают с поверхности земли вертикально вверх. Через некоторое время он падает обратно на землю. Как изменяются в течение полета камня следующие физические величины: модуль скорости камня, пройденный камнем путь, модуль перемещения камня?

Для каждой величины определите соответствующий характер изменения:

1) сначала увеличивается, затем уменьшается;

2) сначала уменьшается, затем увеличивается;

3) все время увеличивается.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Решение

Когда камень летит вверх, сила тяжести и сила сопротивления воздуха противодействуют его движению, модуль его скорости уменьшается. В точке максимального подъема скорость движения камня обращается в нуль. После этого камень начинает ускоренно двигаться к земле, соответственно, модуль его скорости увеличивается. (2)

Путь — это физическая величина, показывающая пройденное телом расстояние. Это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем. Камень сначала двигался вверх, а затем в обратном направлении – падал вниз. Пройденный путь будет равен удвоенной высоте подъема. (3)

Перемещение тела — это изменение радиус-вектора тела. Модуль этой величины можно найти по формуле:

|ᴧr| = |y(t) – y₀| = y(t)

При этом, начало оси Oy начинается в месте броска камня. То есть, по сути, это расстояние между точкой броска и камнем. Эта величина сначала увеличивается, а потом уменьшается. (1)

Ответ: 231.

Задача № 2

С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой “m” (Рис. 1).

Рис. 1

Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой “2m”?

Для каждой величины (время движения, ускорение, модуль работы силы трения) определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Решение

Обозначим силы, действующие на тело и угол наклона плоскости через “α”. На тело действуют три силы: сила тяжести, сила трения и сила реакции опоры. (Рис. 2)

Рис. 2

Второй закон Ньютона в проекции на оси параллельную и перпендикулярную плоскости приобретает вид:

N – mg cosα = 0

mg sinα – F_тр = ma

Принимая во внимание, что коробочка скользит, можем для силы трения скольжения написать:

F_тр = μN

Решим систему полученных уравнений и получим:

a = g (sinα – μ·cosα)

получаем, что ускорение коробочки с грузом не зависит от массы, а значит, оно не изменится при увеличении массы груза в 2 раза. (3)

Раз не изменяется ускорение, с которым коробочка соскальзывает вдоль плоскости, не изменится и время спуска. (3)

Модуль силы трения, оказывается равным:

F_тр = μ·mg·cosα

то есть он зависит от массы.

Модуль работы силы трения пропорционален произведению модуля силы трения на перемещение. Следовательно, при увеличении массы груза, модуль работы силы трения также увеличивается. (1)

Ответ: 331.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Практическое занятие № 5

Тема

Моделирование поведения динамических
объектов в Simulink

Цель

Получение навыков создания моделей в
системе моделирования Simulink

Построение и исследование моделей
физических, динамических объектов

Разработка и исследование модели полета
тела, брошенного с начальной скоростью
под углом к горизонту

Краткие теоретические сведения

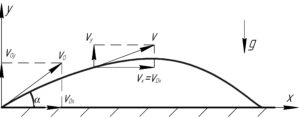
Предположим, что наблюдатель, находясь
над уровнем земли на высоте одного
метра, бросил камень под углом 30 градусов
к горизонту с начальной скоростью 20
м/сек. Необходимо реализовать траектории
полета камня под действием силы тяжести
и определить расстояние от наблюдателя
до точки падения камня. Влиянием атмосферы
на полет камня пренебречь.

У

равнения движения камня, как это
следует из школьного курса физики, имеют
вид:

где
1
м, v = 20 м/сек,
,
9,
81 м/сек.

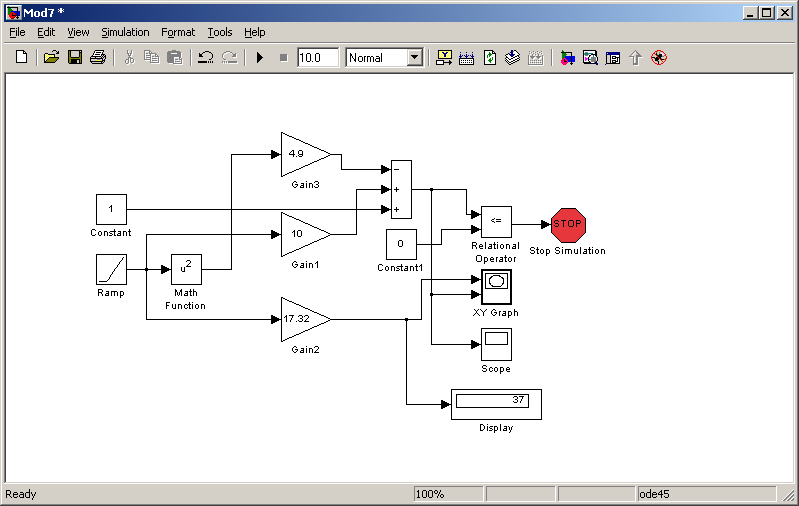
На рис.1. дана структурная модель
траектории полета камня.

Рис. 1 — Структурная схема модели
траектории камня

Значение текущей высоты полета камня
формируется на выходе сумматора. Длина
пути, пройденного камнем до встречи с
землей, формируется на выходе блока
Gain2. Входной сигнал ( t )
формируется блоком Ramp. Сигнал
окончания моделирования формируется
блоками Relational
Operator и Stop
Simulation, в момент
времени, когда высота y сравняется
с нулем, т.е. камень достигнет земли.

На рис. 2 и 3 показаны соответственно
траектория камня на экране виртуального
двухкоординатного регистратора (блок
XY Gaph) и график изменения во времени
высоты полета камня.

Рис. 2 — Траектория камня на экране
двухкоординатного регистратора

Рис. 3 — График изменения во времени
высоты полета камня

Цифровой регистратор Display отображает
решение задачи: “Расстояние от наблюдателя
до точки падения камня на землю» – 37 м.

Описание используемых блоков

Графопостроитель
ХУ Graph

Назначение: Строит график одного
сигнала в функции другого (график вида
Y(X)).

Параметры:

x-min – минимальное значение сигнала
по оси X.

x-max – максимальное значение сигнала
по оси X

y-min – минимальное значение сигнала
по оси Y.

y-max –максимальное значение сигнала
по оси Y

Sample time – шаг модельного времени.

Блок имеет два входа: верхний вход
предназначен для подачи сигнала, который
является аргументом (X), нижний –
для подачи значений функции (Y).

Графопостроитель можно использовать
и для построения временных зависимостей.
Для этого на первый вход следует подать
временной сигнал с выхода блока Clock.

Блок остановки моделирования Stop
Simulation

Назначение: Обеспечивает завершение
расчета, если входной сигнал блока
становится не равным нулю.

Параметры:

Нет.

При подаче на вход блока ненулевого
сигнала Simulink выполняет текущий шаг
расчета, а затем останавливает
моделирование. Если на вход блока подан
векторный сигнал, то для остановки
расчета достаточно, чтобы один элемент
вектора стал ненулевым.

Блок вычисления операции отношения
Relational Operator

Назначение: Блок сравнивает текущие
значения входных сигналов.

Параметры:

Relational Operator – тип операции отношения
(выбирается из списка):

• = = – тождественно равно.

• ~ = – не равно.

• < – меньше.

• < = – меньше или равно.

• > = – больше или равно.

• > – больше.

В операции отношения первым операндом
является сигнал, подаваемый на первый
(верхний) вход блока, а вторым операндом
сигнал, подаваемый на второй (нижний)
вход. Выходным сигналом блока является
1, если результат вычисления операции
отношения есть “ИСТИНА” и 0, если
результат – “ЛОЖЬ”. Входные сигналы
блока могут быть скалярными, векторными
или матричными. Если оба входных сигнала
– векторы или матрицы, то блок выполняет
поэлементную операцию сравнения, при
этом размерность входных сигналов
должна совпадать. Если один из входных
сигналов – вектор или матрица, а другой
входной сигнал – скаляр, то блок выполняет
сравнение скалярного входного сигнала
с каждым элементом массива. Размерность
выходного сигнала, в этом случае, будет
определяться размерностью векторного
или матричного сигнала, подаваемого на
один из входов. Для операций = =
(тождественно равно) и ~ = (не равно)
допускается использовать комплексные
входные сигналы. Входные сигналы также
могут быть логического типа (boolean).

Варианты заданий

Задание формулируется следующим образом:
«Выполнить моделирование поведения
тела, брошенного с начальной скоростью
под углом к горизонту. Определить для
каждого из десяти значений начальной
скорости из заданного в варианте
интервала, оптимальный угол бросания
камня по критерию максимального значения
расстояния от точки падения тела до
наблюдателя».

Вариант 1. Скоростьv
= 5 — 6 м/сек.

Вариант 2. Скоростьv
= 6 — 7 м/сек.

Вариант 3. Скоростьv
= 7 — 8 м/сек.

Вариант 4. Скоростьv
= 8 — 9 м/сек.

Вариант 5. Скоростьv
= 9 — 10 м/сек.

Вариант 6. Скоростьv
= 10 — 11 м/сек.

Вариант 7. Скоростьv
=11 — 12 м/сек.

Вариант 8. Скоростьv
= 12 — 13 м/сек.

Вариант 9. Скоростьv
= 13 — 14 м/сек.

Вариант 10. Скоростьv
= 14 — 15 м/сек.

Вариант 11. Скоростьv
= 15 — 16 м/сек.

Вариант 12. Скоростьv
= 16 — 17 м/сек.

Вариант 13. Скоростьv
= 17 — 18 м/сек.

Вариант 14. Скоростьv
= 18 — 19 м/сек.

Порядок выполнения практического
задания

1. Получите у преподавателя вариант
   задания.

2. Изучите теоретическую часть.

3. Изучите блоки
   XY Graph, Relational Operator, Stop
   Simulation.

4. Разработайте и отладьте в Simulink модель
   рис.1.

5. Модифицируйте модель на рис. 1 так, чтобы
   удобно было проводить исследования
   поведения тела, брошенного с начальной
   скоростью под углом к горизонту. Для
   этого введите в модель блоки, явно
   задающие значения скорости и угла
   бросания и внесите другие необходимые
   изменения.

6. Выполните расчеты на подготовленной
   модели и соберите данные, необходимые
   для подготовки отчета о проделанной
   работе. Для этого проведите десять
   серий экспериментов для каждого
   выбранного Вами значения скорости из
   заданного в варианте интервала. При
   зафиксированном значении скорости
   меняйте угол бросания с тем, чтобы
   удовлетворить критерий максимизации
   расстояния от точки падения тела до
   наблюдателя.

7. Оформите отчет о выполнении практического
   занятия.

8. Защитите отчет.

Содержание отчета о проделанной работе

1. Название и цель практического занятия.

2. Вариант задания.

3. Математическая модель задачи.

4. Окно с вычислительной моделью.

5. Окно с результатами моделирования.

6. Анализ результатов и выводы.

7. Использованная литература.

Литература

1. Васильев В.В., Симак Л.А.,
   Рыбникова А.М. Математическое и
   компьютерное моделирование систем и
   процессов в среде MATLAB/SIMULINK:
   Учебное пособие.- Киев: Изд-во НАН
   Украины.-2008.- 91 с.

2. Терехин В.В. Моделирование
   в системе MATLAB. Часть 2. SIMULINK: Учебное
   пособие.-Новокузнецк: Изд-во Кузбассвузиздат,
   2004.- 376 с.

Соседние файлы в папке ПрактикумКМ

• #
• #
• #
• #
• #
• #