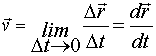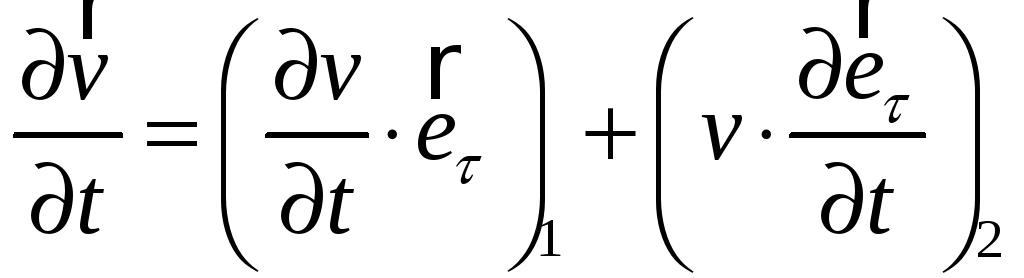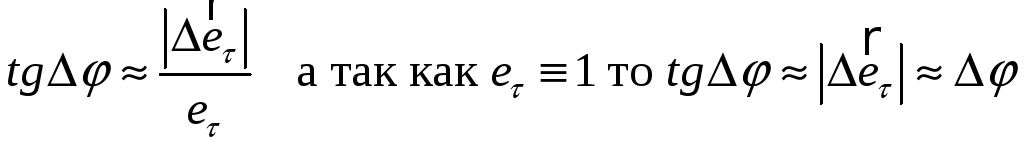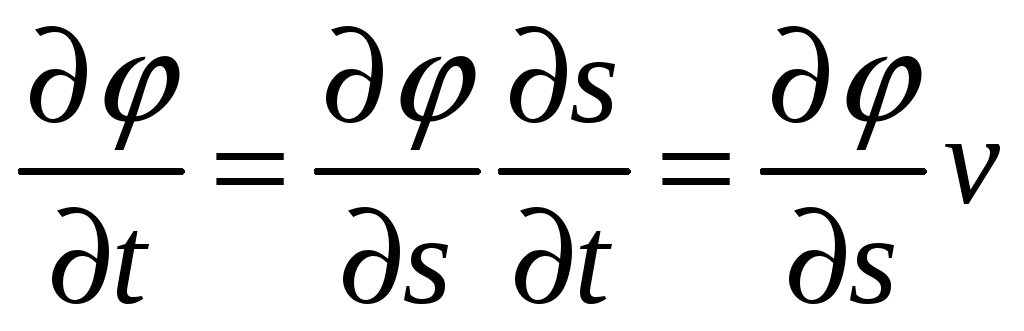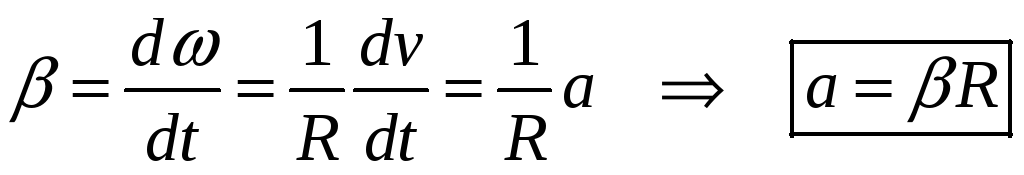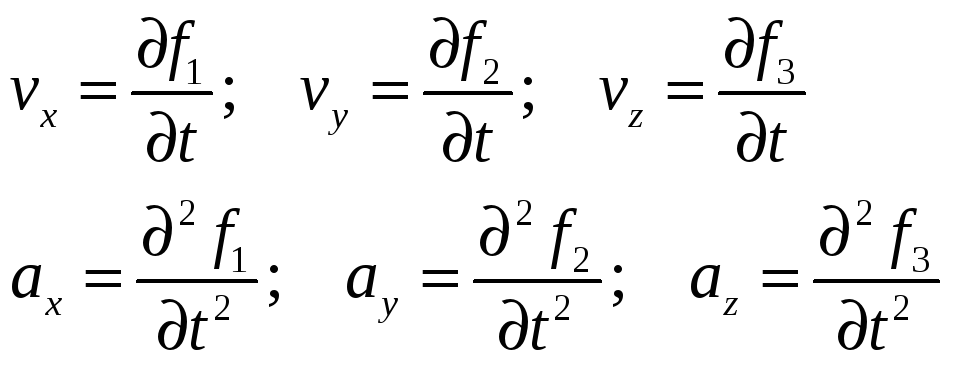Как найти модуль приращения радиус вектора

0 Пользователей и 1 Гость просматривают эту тему.

---

---

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Положение материальной точки в пространстве задается радиус-вектором

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

1. МЕХАНИКА

1.1. Кинематика

1.1.1. Краткие теоретические сведения

Положение материальной точки в пространстве задается

радиус-вектором ,

где – единичные векторы направлений (орты);

x, y, z – координаты точки (рис. 1.1.1).

Абсолютное значение радиус-вектора .

Кинематические уравнения движения :

(в векторной форме)

или (в координатной форме) , где t – время.

Уравнение траектории может быть получено из кинематических уравнений координат исключением времени.

Средняя скорость , где – перемещение материальной точки за время  t .

Средняя скалярная (путевая) скорость: , где – путь, пройденный точкой за время .

Мгновенная скорость , ,

где – проекции скорости на оси координат.

Абсолютное значение скорости .

Ускорение ,

где – проекции ускорения на оси координат.

Абсолютное значение ускорения .

При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющей

. Абсолютное значение этих ускорений: ,

где R – радиус кривизны в данной точке траектории.

Путь где – модуль скорости; и – начальный и конечный моменты времени, соответствующие пройденному пути.

Перемещение ,

где – векторы, соответствующие начальному и конечному положениям материальной точки.

Кинематические уравнения равнопеременного движения ()

,

где – начальная скорость.

Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением)  . Кинематическое уравнение вращательного движения  = f ( t ).

Средняя угловая скорость = / t ,

где  – изменение угла поворота за интервал времени  t . Мгновенная угловая скорость .

Угловое ускорение .

Кинематические уравнения равнопеременного вращения (  = const ) ,

где  0 – начальная угловая скорость.

Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами (рис. 1.1.3 и 1.1.4):

.

Рис. 1.1.3 Рис. 1.1.4

.1.2. Методические указания

В кинематике следует различать прямую и обратную задачи. В прямой задаче необходимо получить закон движения, если известны скорость, либо ускорение. В этих случаях используют формулы п. 1.1.1, предварительно проанализировав условие задачи. При анализе необходимо установить начальные условия и записать их в форме дополнительных уравнений. Начальные условия служат для определения констант интегрирования скорости или ускорения.

Систему координат необходимо выбирать в зависимости от условий задачи, чтобы математическое решение было упрощено. Во многих случаях этому требованию удовлетворяет декартова система координат.

Следует обратить внимание на то, что законы движения в координатной форме содержат не путь, проходимый движущимся телом, а только его координаты.

В обратных задачах задается закон движения, из которого скорость и ускорение находятся простым дифференцированием.

Как правило, закон движения удобно записывать либо в координатной форме, либо в векторной как изменение радиус-вектора материальной точки или центра масс системы в зависимости от координат и времени.

1.2. Динамика

1.2.1. Краткие теоретические сведения

Уравнение движения материальной точки (второй закон Ньютона)

в векторной форме , или при m = const , ,

где – векторная сумма внешних сил, действующих на материальную точку; m – масса; – ускорение;

– импульс; N – число внешних сил действующих на точку.

В координатной форме (скалярной): , , ,

где под знаком суммы стоят проекции сил на соответствующие оси координат.

C ила упругости ,

где – коэффициент упругости (жесткость в случае пружины); x – абсолютная деформация.

Сила гравитационного взаимодействия ,

где G – гравитационная постоянная;

и – массы взаимодействующих тел, рассматриваемых как материальные точки;

– расстояние между ними.

Сила трения скольжения ,

где  – коэффициент трения скольжения; N – сила нормальной реакции.

1.2.2. Методические указания

При решение задач данного раздела используются законы Ньютона. При этом особое внимание надо уделять анализу сил, действующих на рассматриваемое тело. Он должен включать: происхождение сил – в результате взаимодействия с каким телом возникла данная сила; природу сил – тяготение, упругость, трение; характер – от каких величин и как зависит данная сила.

Уравнение второго закона Ньютона следует записывать в векторной форме, а затем проецировать его на оси системы координат, выбранной в зависимости от условий задачи.

Законы Ньютона справедливы только для инерциальных систем отсчета. Почти во всех рассматриваемых задачах систему отсчета, связанную с Землей, можно считать инерциальной, если пренебрегать ее ускорением относительно системы неподвижных звезд. Отсюда вытекает ограничение в выборе системы отсчета: она не должна иметь ускорения относительно Земли.

При описании движения тел, связанных между собой, второй закон Ньютона целесообразно применять к каждому телу в отдельности, установив предварительно связь между координатами и кинематическими параметрами этих тел. При этом часто приходится накладывать дополнительные условия на характер связей.

1.3. Законы сохранения

1.3.1. Краткие теоретические сведения

1. Координаты центра масс системы материальных точек

; ; ,

где m – масса i – ой материальной точки; , , – ее координаты.

2. Закон сохранения импульса выполняется в замкнутой системе и записывается в виде: , где N – число материальных точек (или тел), входящих в систему.

3. Работа, совершаемая постоянной силой : ,

где  – угол между направлениями векторов силы и перемещения .

4. Мощность: , где – работа, совершаемая за промежуток времени .

5. Кинетическая энергия материальной точки (или тела, движущегося поступательно): .

6. Потенциальная энергия упруго деформированного тела (сжатой или растянутой пружины): , где – жесткость пружины, х – величина деформации.

7. Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массами m 1 и m 2 , находящихся на расстоянии r друг от друга: .

8. Потенциальная энергия тела, находящегося в однородном поле силы тяжести : , где h – высота тела над уровнем, принятым за начало отсчета потенциальной энергии.

9. Закон сохранения энергии в механик е выполняется в замкнутой системе, в которой действуют только консервативные силы, и записывается в виде: .

1.3.2. Методические указания

Используя законы сохранения (импульса, энергии), можно найти связь между параметрами движения тела (координатами, скоростями) или системы тел в различных состояниях. В некоторых случаях, когда характер сил взаимодействия (закон изменения силы со временем, время взаимодействия) неизвестен, только законы сохранения позволяют найти по известным параметрам (координаты, скорости) системы в одном состоянии ее параметры в другом состоянии. Подобная ситуация, в частности, имеет место при кратковременных взаимодействиях, таких как удар, взрыв и т. п.

Решение задачи необходимо начинать с анализа сил, действующих на каждое тело системы. Такой анализ должен показать, целесообразно ли рассматривать каждое тело в отдельности либо систему тел; возможно ли к выбранной системе применять тот или иной закон сохранения.

Закон сохранения импульса можно применять, строго говоря, только к замкнутым системам, т. е. к системам тел, на которые не действуют внешние силы (либо векторная сумма внешних сил равна нулю). Природа внутренних сил не является существенной, к числу этих сил могут, например, относиться и силы трения.

При составлении уравнений на основании закона сохранения импульса следует обращать внимание на то, что скорости всех рассматриваемых тел должны определяться относительно одной и той же системы отсчета, а также на векторный характер закона.

Использование закона сохранения полной механической энергии предполагает консервативность рассматриваемой системы. И это условие обязательно необходимо проверять.

Если энергия системы включает потенциальную энергию тел во внешнем консервативном поле, то можно говорить о законе сохранения энергии одного тела, находящегося во внешнем консервативном поле, в частности, в поле тяжести Земли. Подобное рассмотрение предполагает, что расчеты производятся в системе отсчета, связанной со вторым телом, в данном случае с Землей.

При определении изменения энергии следует обращать внимание на то, что изменение потенциальной энергии тела во внешнем консервативном поле равно работе сил поля, взятой с обратным знаком. Сама потенциальная энергия не может быть вычислена без предварительного выбора начала отсчета потенциальной энергии.

1.6. Элементы механики жидкостей

1.6.1. Краткие теоретические сведения и методические

указания к решению задач

Используется единый подход к изучению жидкостей и газов, т. к. в ряде механических явлений их поведение определяется одинаковыми параметрами и идентичными уравнениями. Поэтому пользуются единым термином «жидкость».

1. Давление жидкости – скалярная физическая величина, определяемая нормальной поверхностной силой, действующей со стороны жидкости на единицу площади:

, , , Па = Н/м 2 .

2. Закон Паскаля : жидкость (или газ) передает производимое на нее поверхностными силами внешнее давление по всем направлениям без изменения.

3 . Закон Архимеда : на тело, погруженное в жидкость (газ), действует со стороны жидкости направленная вверх сила, равная весу жидкости, объем которой совпадает с объемом погруженной в жидкость части тела:

, ,

где  – плотность жидкости, V – объем погруженной в жидкость части тела.

Жидкость, плотность которой с изменением давления не изменяется, называется несжимаемой.

4. Давление в жидкости .

– давление на свободной поверхности жидкости, часто оно равно атмосферному.

В точке А , погруженной в жидкость на высоту h , давление равно р (рис. 1.6.1) ,

где – гидростатическое давление.

6. Уравнение Бернулли для стационарного течения идеальной несжимаемой жидкости:

,

где – полное давление, р – статическое давление, – гидростатическое давление, – динамическое давление.

7. Идеальная жидкость – физическая абстракция – жидкость, в которой отсутствуют силы внутреннего трения.

Формула Торричелли , определяющая скорость истечения идеальной жидкости через малое отверстие в открытом широком сосуде:

,

где h – глубина, на которой находится отверстие относительно свободной поверхности жидкости в сосуде.

Контрольное задание состоит из двух частей:

1 часть – задания открытого типа, необходимо не только выбрать единственный правильный ответ, но и дать пояснение к его решению.

2 часть – задания закрытого типа, необходимо представить подробное решение.

1.1. Физическая теория объяснила все известные в данной области физики явления и предсказала существование новых, неизвестных ранее явлений. Каким образом эта теория может быть опровергнута?

1. Созданием новой теории, предсказывающей другие неизвестные явления.

2. Теория будет опровергнута, если при проведении эксперимента предсказанные ею новые явления не будут обнаружены.

А. Только 1. Б . Только 2. В . Или 1, или 2. Г . Ни 1,ни 2. Д . Такая теория не может быть опровергнута.

1.2. На горизонтально движущуюся ленту транспортера соскальзывают кирпичи. Скорость ленты транспортера относительно Земли , скорость кирпича векторы и направлены параллельно. Через какой промежуток времени кирпич станет непо­движным относительно ленты, если коэффициент трения кирпича о ленту равен ?

А . Б. В . Г . Д.

1.3. Цилиндрический сосуд высотой 40 см заполнен водой. В боковой стенке сосуда есть три отверстия. Первое отверстие находится на расстоянии 10 см, второе — на расстоянии 20 см и третье — на расстоянии 30 см от основания сосуда. Если сосуд заполнен водой до верха, то из какого отверстия струя достигнет поверхности, на которой стоит сосуд, в наибольшем удалении от стенки сосуда?

А . Из первого. Б. Из второго. В. Из третьего. Г . Из первого и третьего. Д. Из всех трех одинаково.

1.4. В какую фазу Луны приливы в земных океанах и морях достигают максимального значения?

А. Только в полнолуние. Б. Только в новолуние. В . В полнолуние и новолуние. Г . В первую и последнюю четверть. Д. Высота прилива не зависит от фаз Луны.

1.5. Какую примерно силу нужно приложить к малому поршню гидравлического подъемника для подъема автомобиля массой 1000 кг, если площадь малого поршня 10 см 2 , площадь большого поршня 0,1 м 2 ?

А. 100 кг. Б. 10 кг. В . 1000 Н. Г . 100 Н. Д. 10 6 Н.

Кинематика вращательного движения твердого тела

Вращательное движение очень распространенно в природе и технике. Недаром, вторая техническая революция цивилизованного общества началась с изобретения человеком колеса. Без знания основных законов вращательного движения совершенно невозможно понять ни закономерностей движения планет и космических аппаратов, ни законов микромира.

Законы вращательного движения – это не новые законы механики, а лишь результат приспособления законов ньютоновской механики к данной задаче, оформления их математически в удобной для рассмотрения и решения той или иной задачи, связанной с вращательным движением.

Для описания вращательного движения нельзя пользоваться такой моделью как материальная точка, здесь уместно говорить о системе материальных точек, из которых состоит твердое тело. Целесообразно использовать абстрактную модель абсолютно твердого тела.

Абсолютно твердым телом называют такое тело, расстояние между двумя соседними точками которого в процессе вращения остается неизменным.

Наиболее простой случай вращательного движения абсолютно твердого тела – это вращение его относительно закрепленной (неподвижной) оси.

При вращательном движении абсолютно твердого тела все точки двигаются по окружностям, центры которых лежат на прямой ОО’, называемой осью вращения.

Точки тела М1, М2, и. т.д. двигаются по окружностям разного радиуса, т. е. по пути, считая по длине дуги окружности, а, следовательно и скорости – различны. Поэтому, линейными характеристиками нельзя охарактеризовать вращательное движение, как это было сделано в поступательном движении.

Рассмотрим, как ведут себя материальные точки твердого тела лежащие в плоскости, перпендикулярной оси вращения. Пусть точка М двигается по окружности радиуса R, положение которой относительно оси ОО’ можно задать с помощью радиус-вектора ŕ . Нетрудно заметить, что радиусы-векторы, соединяющие все точки твердого тела с центрами описываемых ими окружностей, поворачиваются за один и тот же промежуток времени ∆t на одинаковый угол ∆φ.

Следовательно, для всех точек твердого тела можно ввести однозначные характеристики за данный промежуток времени: угловой путь, угловую скорость, угловое ускорение.

В качестве кинематических характеристик вращательного движения твердого тела выбраны: вектор углового перемещения φ, угловая скорость ω, угловое ускорение ε.

При малых углах поворота |dφ|=dφ и направлен вдоль оси вращения ОО’ против часовой стрелки (правило правого винта).

Векторы, направления которых связываются с направлением вращения, называются аксиальными векторами , которые не имеют определенных точек приложения: они могут откладываться от любой точки оси вращения.

При вращательном движении с течением времени угловой путь изменяется. Быстроту изменения углового пути со временем характеризуют векторная величина , называемая угловой скоростью, численно равная первой производной от угла поворота по времени

Если радиус-вектор точки М, вращающейся по окружности, за любые равные промежутки времени поворачивается на одинаковые углы, то такое вращательное движение принято называть равномерным.

Взяв отношение изменения длин дуг окружностей по радиусу, получим значение углового пути:

Таким образом, угловой путь можно вычислить за время как отношение изменения длины дуги к радиусу окружности, по которой движется точка твердого тела при вращении.

, выразим (16) точку величину (17). Поделим правую и левую часть данного уравнения на величину , отношение – характеризует среднюю линейную скорость, а – характеризует среднюю угловую скорость. Перейдя к пределу этих отношений при условии что, Δt→0, получим мгновенные значения линейной угловой скорости в данный момент времени

V=R*ω, или в векторной форме можно записать как (19) так как

Таким образом, быстроту изменения углового пути со временем характеризует векторная физическая величина , называемая угловой скоростью, численно равная первой производной от угла поворота по времени.

В системе СИ угловой путь (угол поворота) измеряют в радианах – это центральный угол, опирающийся на дугу, длина которой равна радиусу. , т. к длина окружности

При равномерном движении по окружности угловая скорость является постоянной величиной ω=const. Кроме этих кинематических величин равномерное движение тела по окружности можно выразить через период и частоту вращения.
Время, в течении которого тело (точка) совершает один оборот, называется периодом вращения. (21)

Число полных оборотов N связано с угловым путем соотношением (22)

Число оборотов тела (точки) вокруг центра вращения за единицу времени называют частотой вращения.

Исходя из определений периода и частоты можно записать следующее соотношения: , (24)

В системе СИ период выражают секундах [T]=[1c]=[c], то частота []=.

Кроме равномерного вращательного движения твердого тела рассматривают случай, когда ω≠const и изменяется со временем. Быстроту изменения угловой скорости со временем характеризует физическая величина – угловое ускорение.

Пусть за время ∆t линейная и угловая скорости точки твердого тела получили приращение на величину ∆V, . Используя соотношение между этими величинами, запишем

Поделим левую часть и правую часть уравнения на ∆t, за которое произошло изменение скоростей

Величина – характеризует среднее линейное ускорение – характеризует среднее угловое ускорение, тогда =R* (27)

Для получения мгновенных значений соответствующих величин необходимо использовать формулу (26) и взять предел этих отношений, устремив

Таким образом, угловое ускорение есть первая производная от угловой скорости по времени или в векторной форме (28)

При ускоренном движении вектор сонаправлен вектору , а при замедленном меняет свое направление на противоположное.

При вращательном движении абсолютно твердого тела относительно закрепленной оси вращения угловые характеристики для всех точек этого тела одинаковы. Линейные характеристика S, V, a – различны для разных точек.

Вектор – носит название полного ускорения, который описывает изменение величины и направление скорости. Эти изменения мы рассматривали в формуле (14) и ниже. Теперь нам необходимо выразить тангенциальное и нормальное ускорение произвольной точки твердого тела, вращающегося вокруг неподвижной оси, через угловую скорость и угловое ускорение этого тела.

тогда модуль полного ускорения

1.5 Основные формулы для решения задач.

1. Задание радиус – вектора в координатной форме:

2. Модуль радиус вектора:

3. Приращение радиус-вектора:

4. Средняя скорость:

5. Мгновенная скорость:

6. Задание вектора скорости в координатной форме:

7. Модуль скорости:

8. Вычисление скорости при прямолинейном движении

10. Мгновенное ускорение:

11. Задание вектора ускорения в координатной форме:

12. Модуль ускорения:

13. Средняя угловая скорость:

14. Мгновенная угловая скорость:

15. Среднее угловое ускорение:

16. Мгновенное угловое ускорение:

17. Связь линейной скорости с угловой:

18. Полное ускорение:

19. Модуль полного ускорения:

20. Связь между линейными кинематическими характеристиками с соответствующими угловыми:

1.6. Задачи для самостоятельного решения.

1. Вектор скорости изменил направление на обратное. Найти: 1) Приращение вектора скорости ; 2) Модуль приращения ; 3) Приращение модуля .

2. Начальное значение радиус-вектора , конечное значение – . Найти:

1) Приращение радиус вектора;

2) Модуль приращения;

3) Приращение модуля ;

3. Радиус-вектор точки изменяется со временем по закону: . Найти модуль скорости и ускорение точки, модуль скорости и ускорения в момент времени .

4. Радиус-вектор точки изменяется со временем по закону: . Найти приближенное значение пути S, пройденного точкой за десятую секунду своего движения.

5. Точка движется со скоростью , где с=1м/с2. Найти:

1) Модуль скорости точки в момент времени t=2c;

2) Ускорение точки и его модуль ;

3)Пройденный путь S точкой с момента времени t1=1c до момента t2=4c.

6. Зависимость координат частиц от времени имеет вид: , Найти:

1) Радиус-вектор частицы , скорость , ускорение ;

2) Модуль радиус-вектора , скорости , ускорения ;

7. Кинематическое уравнение движения материальной точки оси Ox имеет вид: , где A=4м, В=2м/с, С=-0,5 м/с3. Для момента времени t=2c определить:

1) Координату x точки; 2) Мгновенную скорость V; 3) Мгновенное значение ускорения .

8. Уравнение прямолинейного движения по оси Ох имеет вид: , где А=3м/с, В=-0,25 м/с2. Построить графики зависимости координаты и пути от времени для заданного вида движения.

9. Движение материальной точки задано уравнением: , где A=4м, В=-0,05 м/с2. Определить момент времени t, в который скорость точки V равна нулю. Найти координату, скорость и ускорение в этот момент времени. Построить графики зависимости координаты, пути, скорости и ускорения для данного вида движения.

10. Точка движется по прямой и зависимость пройденного пути от времени задается уравнением: , где С=0,1 м/с2, D=0,03 м/с3. Определить: 1) Время t, в момент которого ускорение точки a=2 м/с2. 2) Среднее значение ускорения точки за этот промежуток времени.

11. Тело участвует в двух вращениях, происходящих со скоростью и , где с=1с-2. На какой угол повернется тело за первые 3с? Вокруг какой оси произойдет этот поворот?

12. Материальная точка движется по плоскости согласно уравнению . Написать зависимость скорости от времени и ускорения от времени .

13. Движение материальной точки задано уравнением: , где А=10 м, В=-5м/с2, С=10 м/с. Найти: 1) траекторию движения; 2) найти зависимость скорости и ускорения от времени; Для момента времени t=1c вычислить: а) модуль скорости и ускорения ; б) модуль тангенциального ускорения ; в) модуль нормального ускорения .

14. Точка движется по окружности радиусом R=10м согласно уравнению , где А=2 м/с3. В какой момент времени t нормальное ускорение аn точки будет равно тангенциальному aτ? Определить полное ускорение точки а в этот момент.

15. Диск радиусом R=10см вращается вокруг неподвижной оси так, что зависимость угла поворота диска от времени задается уравнением: , где В=1с-1, С=1с-2, D=1с-3. Определить для точек на ободе диска к концу t=2c после начала движения: 1) величину тангенциального aτ ускорения; 2) нормальное ускорение аn; 3) полное ускорение а.

16. Движение точки по кривой задано уравнением: и , где А=1м/с3; В=2 м/с. Найти уравнение траектории точки, её скорость V и полоне ускорение a в момент времени t=0,8с.

17. Диск радиусом R=10см, находившийся в состоянии покоя начал вращаться с постоянным угловым ускорением . Найти тангенциальное aτ ускорения, нормальное ускорение аn, полное ускорение а точек на окружности диска в конус второй секунды после начала вращения.

18. Маховик начал вращаться равноускоренно и за промежуток времени достиг частоты вращения n=300 мин-1. Определить угловое ускорение маховика и число полных N оборотов, которое он сделал за это время.

19. Диск вращается с угловым ускорением . Сколько оборотов N сделает диск, при изменении частоты вращения от n1=240мин-1 до n2=90мин-1? Найти промежуток времени , в течении которого это изменение произойдет.

20. Найти угловое ускорение колеса, если известно, что через после начала равноускоренного движения вектор полного ускорения точки, лежащей на оводе, составляет угол α=600 с направлением вектора линейной скорости этой точки.

1. Радиус-вектор это:

б) направленный отрезок прямой, начало которого в начале координат, а конец упирается в движущуюся материальную точку;

в) направленный отрезок прямой заданный только числовым значением.

2. Каким способом можно разложить радиус-вектор ?

а)

б)

в)

3. Если , то модуль радиус-вектора :

а)

б)

в)

4. Радиус-вектор , то модуль радиус-вектора равен:

а) 5; б) 25; в) .

5. Перемещение это:

а) вектор, соединяющий начальное положение мат. Точки с её конечным положением;

б) расстояние, пройденное точкой вдоль траектории её движения;

в) отрезок прямой, соединяющий начало траектории движения мат. точки с концом этой траектории.

6. В каком случае

а) криволинейного движения;

б) прямолинейного движения;

в) движения по окружности, эллипсу, гиперболе.

7. В координатной форме вектор скорости задается:

а)

б)

в)

8. Модуль вектора скорости можно вычислить по формуле:

а)

б)

в)

г)

9. Какое из движущихся равномерно, тел имеет большую скорость:

а) 1; б) 2; в) 3; г) 4.

10. Равномерным называют движение скорость которого:

а) остается постоянной с изменением времени;

б) изменяется одинаково за любые равные промежутки времени;

в) монотонно возрастает за любые промежутки времени;

11. Среднее ускорение мат. точки это:

а) скалярная величина, равная отношению изменения скорости к тому промежутку времени, за которое это изменение произошло;

б) предел отношения изменения скорости к тому промежутку времени, за которое это изменение произошло;

в) векторная величина, равная отношению изменения скорости к тому промежутку времени, за которое это изменение произошло.

12. Мгновенное значение ускорения это:

а) первая производная от скорости по времени t;

б) отношение изменения скорости к изменению времени;

в) первая производная от пройденного пути по времени.

13. В координатной форме вектор ускорения можно задать только:

а) ;

б) ;

в) .

14. Модуль вектора ускорения можно вычислить:

а)

б)

в)

15. Выбрать правильную последовательность определений ускорений:

а) Тангенциальное, полное, нормальное;

б) Нормальное, полное, тангенциальное;

в) Полное, тангенциальное, нормальное.

16. Выбрать правильное направление вектора полного ускорения при равноускоренном движении мат. точки:

а) 1; б) 2; в) 3; г) 4;

17. Если то движение мат. точки является:

а) прямолинейным ускоренным;

б) равномерным по окружности;

в) ускоренным по окружности.

18. Если то движение мат. точки:

а) ускоренное по окружности;

б) равномерное прямолинейное;

в) криволинейное с переменным ускорением.

19. Направление вектора определяется правилом правого винта, то это:

а) радиальный вектор;

б) аксиальный вектор;

в) коллинеарный вектор.

20. При вращательном движении твердого тела, если соблюдается условие что то

а) вектор не совпадает по направлению с вектором вдоль оси вращения;

б) оба вектора коллинеарные;

в) оба вектора взаимно перпендикулярны.

21. При условии, что , то оба вектора…:

б) взаимно перпендикулярны;

в) имеют противоположное направление вдоль оси вращения;

22. Диск радиуса R катится равномерно и прямолинейно, без скольжения. Модуль перемещения произвольной точки на ободе диска за один полный оборот равен:

а) 2πR; б)2R; в) 0; г) R.

23. Изменение модуля скорости тела, двигающегося по окружности со скоростью V=5 м/с, при прохождении четверти окружности равно:

а) 4,8 м/с; б) 3,5 м/с; в) 6,2 м/с; г) 1,4 м/с; д) 0 м/с.

24. Траектория движения точки на конце лопасти винта вертолета, равномерно поднимающегося вертикально вверх в системе отсчета связанной с корпусом вертолета, представляет собой:

а) окружность; б) винтовую линию; в) параболу; г) прямую линию.

25. За время t=6 c точка прошла путь, равный половине длины окружности радиусом R=0,8 м. Определить среднюю путевую скорость за это время и модуль вектора средней скорости .

[spoiler title=”источники:”]

http://gigabaza.ru/doc/64673.html

http://pandia.ru/text/78/252/13655.php

[/spoiler]

В прошлой статье мы немножко разобрались с тем, что такое механика  и зачем она нужна. Мы уже знаем, что такое система отсчета,  относительность движения и материальная точка. Что ж, пора двигаться дальше!  Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики  и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад  в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат  (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной  от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь  – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Лучший ответ по мнению автора

dr=r2-r1=(-1-4)i+(-2+3)j+(3-12)k=-5i+j-9k |dr|=sqrt((-5)^2+1^2+(-9)^2)=sqrt(25+1+81)=sqrt(107)=10.34 |r1|=sqrt(16+9+144)=sqrt(169)=13 |r2|=sqrt(1+4+9)=sqrt14=3.74 d|r|=3.74-13=-9.26 21.09.15 Лучший ответ по мнению автора

Лекция
№2

Механика

Кинематика
поступательного и вращательного движения

(Материальная
точка, система отсчета, перемещение,
скорость, ускорение, основная задача
кинематики)

Кинематика
– это раздел механики, где изучаются
способы описания движений независимо
от причин, обусловливающих эти движения,
то есть, в основном, геометрические
свойства движения. Массы тел и действующие
на них силы в кинематике не рассматриваются.
В лекциях по кинематике рассмотрены
три вопроса, необходимых для понимания
физических основ механики: кинематика
частицы, кинематика твердого тела и
преобразование скорости и ускорения
при переходе от одной системы отсчета
к другой

     Если
размеры тела при описании его движения
несущественны, то его движение можно
рассматривать как движение материальной
точки в пространстве. Это самая простая
модель для описания реального тела. Так
как в дальнейшем будут рассматриваться
движения тела обладающего массой, но в
пренебрежении ее размерами, внутренней
структуры и формы, то введем в рассмотрение
единый термин частица,
понимая под ним материальную точку.
Существует несколько способов описания
движения частицы: векторный (геометрический)
и координатный. Рассмотрим их
последовательно.

     Векторный
способ.
В этом способе положение интересующей
нас частицы А задают радиусом-вектором

,
проведенным из некоторой неподвижной
точки О выбранной системы
отсчета
в
точку А. Под системой отсчета в механике
понимают совокупность: тело отсчета,
способ измерения расстояний (“линейка”)
и способ измерения времени (“часы”).
При движении частицы А ее радиус-вектор
меняется в общем случае как по модулю,
так и по направлению, т. е. радиус-вектор

зависит
от времени t.

Рис. 2.1. Векторный способ описания движения частицы

     Геометрическое
место точек, где тело побывало за время
своего движения, называется траекторией
частицы
А.
При векторном способе описания траекторией
будет положение концов радиус-вектора

во
все моменты времени.

     Введем
понятие скорости
частицы. Скорость характеризует быстроту
движения частицы. Пусть за промежуток
времени
точка
А переместилась из точки 1 в точку 2 (рис.
2.1). Из рисунка видно, что вектор
перемещения

частицы
А представляет собой приращение
радиус-вектора
за
время (t :
.
Отношение
называют
средним
вектором скорости
<>
за время (t. Вектор <>
совпадает по направлению с
.
Определим теперь вектор скорости

частицы
в данный момент времени как предел
отношения
при
t→ 0, т. е.

(2.1)

     Это
значит, что вектор скорости
частицы
в данный момент времени равен производной
от радиус-вектора
по
времени и направлен по касательной к
траектории в данной точке в сторону
движения частицы А (как и вектор
).
Модуль вектора
равен

     Заметим,
что в общем случае модуль приращения
радиус-вектора
не
равен изменению модуля радиус-вектора

.
Например, если
меняется
только по направлению при движении
частицы по окружности, то
но

.

     Движение
частицы характеризуется также ускорением.
Вектор ускорения
определяет
скорость изменения вектора скорости

со
временем:

,

(2.2)

     т.
е. равен производной от вектора скорости
по времени. Направление вектора
совпадает
с направлением вектора
–
приращением вектора
за
время dt. Модуль вектора
определяется
аналогично модулю вектора
.
Пусть, например, радиус-вектор частицы
зависит от времени t по закону

,

     где

и

–
постоянные векторы. Найдем скорость
и
ускорение
частицы:

Модуль
вектора скорости

.

     Таким
образом, зная зависимость
,
можно найти скорость
и
ускорение
частицы
в каждый момент времени.

     Возникает
и обратная задача: можно ли найти
и

,
зная зависимость от времени ускорения

?

     Оказывается,
для получения однозначного решения
этой задачи одной зависимости

недостаточно,
так как необходимо еще знать начальные
условия,
а именно – скорость
и
радиус-вектор
частицы
в некоторый начальный момент
.
Чтобы в этом убедиться, рассмотрим
простой случай, когда при движении
ускорение частицы
остается
постоянным.

     Определим
сначала скорость частицы
.
Согласно (2.2),
за интервал времени dt малое приращение
скорости
.
Интегрируя это выражение по времени от
t = 0 до t, определим конечное приращение
вектора скорости за это время:

.

     Но
величина
–
это еще не искомая скорость
.
Для нахождения
,
необходимо знать скорость
в
начальный момент времени
.
Тогда
,
или

     Аналогично
вычисляется и радиус-вектор
частицы.
Согласно (2.1),
за интервал времени dt малое приращение
радиус-вектора
.
После интегрирования этого выражения
с учетом определенной выше зависимости

,
определим приращение радиуса-вектора
за время от t = 0 до t:

.

     Для
нахождения самого радиус-вектора

необходимо
знать положение частицы в начальный
момент времени
.
Тогда
,

     или

.

     Координатный
способ.
В этом способе с телом отсчета жестко
связывают определенную систему координат
(декартову, косоугольную или криволинейную).
Выбор вида системы координат определяется
рядом соображений: характером или
симметрией задачи, постановкой вопроса,
а также стремлением упростить
математическое решение задачи. Для
простоты рассмотрим декартову систему
координат x,у,z. Изучение движений частицы
в других координатах оставим для задач.

     Запишем
проекции радиус-вектора
на
оси координат. Вектор
определяет
положение интересующей нас частицы
относительно начала координат О в момент
t:

     Закон
движения
частицы
– это зависимость координат от времени.
Он задает положение частицы в каждый
момент времени, ее скорость и ускорение.
Cпроектировав (2.1)
и (2.2),
например, на OX, получим формулы,
определяющие проекции векторов скорости
и ускорения на эту ось:

,

(2.3)

      где
dx- проекция вектора перемещения
на
ось х,

(2.4)

     здесь

–
проекция вектора приращения скорости

на
ось х. Такие же соотношения получаются
для у- и z-проекций соответствующих
векторов. Из этих формул видно, что
проекции векторов скорости и ускорения
равны соответственно первой и второй
производным координат по времени.

     Зависимости

полностью
определяют движение частицы. Зная их,
можно найти не только положение частицы,
но и проекции ее скорости и ускорения,
а следовательно, модуль и направление
векторов
и

в
любой момент времени. Например, модуль
вектора скорости определяется формулой

,

     а
направление вектора
задается
направляющими косинyсами по формулам:

(2.5)

     где
,
β ,γ – углы между вектором
и
осями х, у, z соответственно. Направляющие
косинусы всегда удовлетворяют соотношению

.
Аналогичными формулами определяются
модуль и направление вектора ускорения

.

     С
помощью закона движения можно найти
траекторию частицы, зависимость
пройденного ею пути от времени, зависимость
скорости от положения частицы и т.д.

     Нахождение
скорости и закона движения частицы по
заданному ускорению называется обратной
задачей. Ее решение проводится, как и в
векторном способе, путем интегрирования
(в данном случае проекций ускорения по
времени). Задача и здесь имеет однозначное
решение, если кроме ускорения заданы
еще и начальные условия: проекции
скорости и координаты частицы в начальный
момент времени.

Вернемся
к определению ускорения частицы

.
Выразим

Здесь
е_τ
является еденичным вектором (ортом)
вдоль направления вектора скорости.
Отсюда:

Первая
часть нашего равенства характеризует
изменение модуля скорости со временем
и направлена вдоль вектора скорости
эта часть носит название: линейное
или
тангенциальное
ускорение.

Перейдем
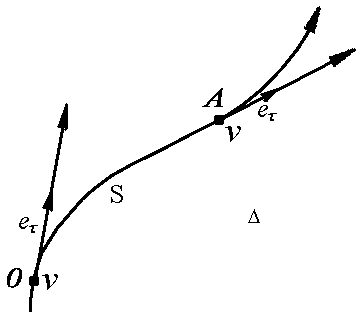
ко второй части равенства. Рассмотрим
изменение единичного вектора
е_τ
при
его повороте за малый промежуток времени
t
. Для этого совместим начало вектора е_τ
в первоначальный момент времени с
началом этого вектора в момент времени
через промежуток t
. При этом вектор соединяющий конец
первого вектора с концом второго вектора
будет приращением (разностью) этих
векторов е_τ
.

При
малом повороте вектора е_τ

При
малых 

Отсюда
вторая исходное уравнение приобретает
вид

Производная
по времени от угла поворота есть угловая
скорость. Представим угловую скорость
в виде:

Таким
образом, мы установили связь между
абсолютными значениями угловой и
линейной скоростью.

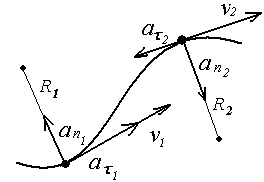
Исходное
выражение для ускорения точки может
быть записано в окончательном виде:

В
этом выражении первый член правой части
является тангенциальным ускорением,
которое направлено в сторону или
навстречу движению точки. Второй член
называется нормальным или центростремительным
ускорением. Центростремительное
ускорение всегда перпендикулярно
вектору скорости движения точки и
направлено к центру кривизны траектории.

Полное
ускорение направлено находится по
правилу векторного сложения и является
результирующим вектором векторов
тангенциального и нормального ускорения.
Его абсолютная величина определяется
как:

Вернемся
к рассмотрению вращательного движения,
характеристиками которого является
угол поворота тела и угловая скорость.

Угловая
скорость, как и угол поворота, являются
векторами (псевдо векторами) направление
которых перпендикулярно плоскости
вращения и совпадает с направлением
вкручивания правого винта, если тот
вращается в сторону рассматриваемого
вращения.

Есть
еще одна векторная характеристика
вращательного движения, это угловое
ускорение.

Направление
этого вектора (псевдо вектора) совпадает
или противоположно вектору угловой
скорости в зависимости от того
увеличивается или уменьшается угловая
скорость объекта.

Равномерное
вращение так же характеризуется периодом
T
(временем одного оборота тела) и частотой
вращения 
(количеством полных оборотов в единицу
времени).

Период
измеряется в секундах, частота – в
обратных секундах, угол поворота – в
радианах, угловая скорость – в радианах
в секунду, угловое ускорение – в радианах
в секунду за секунду.

Вернемся
к выражению для углового ускорения,
распишем его и получим связь между
линейным и угловым ускорением

Основной
задачей кинематики является
нахождение положения движущейся
матеоиальной точки, ее скорости, ускорения
в любой интересующий нас момент времени.

Пусть
известен вид функции, выражающей
зависимость координат точки от времени

x
= f₁(t),
y
=f₂(t),
z
= f₃(t).
Тогда подставляя значение времени в
эти выражения, получим координаты точкив
интересующий момент времени.
Продифференцировав по времени и
продифференцировав дважды по времени
функции определяющие координаты точки,
получим соответственно значение
компонент скорости и ускорения точки.

Возможно
так же и обратная задача: по функциям
выражающим временную зависимость
компонент ускорения от времени найти
компоненты скорости и координаты точки
в интересующий момент времени. Эта
задача решается совершением обратной
операции интегрированием. Однократное
интегрирование дает значение компонент
скорости, двукратное дает значение
координат точки.

Так
как интегрирование определяет функцию
с точностью до произвольной постоянной
величины. Для решения поставленной
задачи должны быть заданы начальные
условия определяемые из дополнительных
соображений.

Начальные
условия это параметры механического
состояния заданные в определенный
момент времени. Обычно удобен для этих
случаев начальный момент, когда
t
= 0
.

Соседние файлы в папке Лекции 1 симестр

• #
• #
• #
• #
• #
• #
• #
• #
• #