Как найти модуль приращения вектора скорости - Сайт, где вы сможете решить свои вопросы

Макеты страниц

Материальная точка при своем движении описывает некоторую линию. Эта линия называется траекторией. В зависимости от формы траектории различают прямолинейное движение, движение по окружности, криволинейное движение и т. п.

Пусть материальная точка (в дальнейшем для краткости мы будем называть ее частицей) переместилась вдоль некоторой траектории из точки 1 в точку 2 (рис. 3.1). Расстояние между точками 1 и 2, отсчитанное вдоль траектории, называется путем, пройденным частицей. Мы будем обозначать его буквой s.

Прямолинейный отрезок, проведенный из точки 1 в точку 2, называется перемещением частицы. Обозначим его символом . Предположим, что частица совершает последовательно два перемещения: (рис. 3.2). Суммой этих перемещений естественно назвать такое перемещение которое приводит к тому же результату, что и первые два перемещения вместе.

Рис. 3.1.

Рис. 3.2.

Таким образом, перемещения характеризуются численным значением и направлением и, кроме того, складываются по правилу параллелограмма. Отсюда следует, что перемещение есть вектор.

Рис. 3.4.

В обыденной жизни под скоростью понимают путь, проходимый частицей за единицу времени. Если за равные, сколь угодно малые промежутки времени частица проходит одинаковые пути, движение частицы называют равномерным. В этом случае скорость, которой обладает частица в каждый момент времени, можно вычислить, разделив путь s на время t.

В физике под скоростью понимают векторную величину, характеризующую не только быстроту перемещения частицы по траектории, но и направление, в котором движется частица в каждый момент времени.

Тогда приращение модуля вектора равно нулю . В то же время модуль приращения вектора , т. е. отличен от нуля (он равен длине отрезка 2—3). Сказанное справедливо для любого вектора а: в общем случае Из рис, 3.4 [видно, что путь вообще говоря, отличен по величине от модуля перемещения Однако, если брать отрезки пути и перемещения соответствующие все меньшим промежуткам времени , то различие между будет убывать и их отношение в пределе станет равным единице:

На этом основании можно заменить в формуле (3.3) через в результате чего получится выражение

Таким образом, модуль скорости равен производной пути по времени.

Очевидно, что величина, называемая в обыденной жизни скоростью, на самом деле представляет собой модуль скорости v. При равномерном движении модуль скорости остается неизменным в то время как направление вектора v изменяется произвольным образом (в частности, может быть постоянным).

В соответствии с формулой (3.1) элементарное перемещение частицы равно

(3.5)

Иногда для наглядности мы будем обозначать элементарное перемещение символом , т. е. писать (3.5) в виде

Вектор скорости, как и всякий другой вектор, можно представить в виде

где — проекции вектора v на координатные оси. Вместе с тем равный v вектор согласно формуле (2.43) выглядит следующим образом:

Из сравнения выражений (3.7) и (3.8) вытекает, что

Следовательно, проекция вектора скорости на координатную ось равна производной по времени соответствующей координаты движущейся частицы.

Приняв во внимание (2.10), получим формулу:

Вектор скорости можно представить в виде , где v — модуль скорости, а — орт вектора v. Введем орт касательной к траектории , условившись направлять его в ту же сторону, что и v. Тогда, очевидно, орты совпадут, так что можно написать следующее выражение:

Получим еще одно выражение для v. С этой целью подставим в формулу (3.1) радиус-вектор в виде . Согласно (2.49)

Для простоты ограничимся случаем, когда траектория является плоской кривой, т. е. такой кривой, все точки которой лежат в одной плоскости. Примем эту плоскость за плоскость х, у. В формуле (3.12) вектор v оказался представленным в виде суммы двух составляющих (рис. 3.6). Первая составляющая, которую мы обозначим равна

Она направлена вдоль радиуса-вектора и характеризует быстроту изменения модуля . Вторая составляющая, которую мы обозначим , равна

Она характеризует быстроту изменения радиуса-вектора по направлению.

Воспользовавшись формулой (2.56), можно написать, что

где — угол между радиусом-вектором и осью — перпендикулярный к радиусу-вектору орт, направленный в сторону возрастания угла (в формуле (2.56) этот орт был обозначен Подставив это значение в (3.14), получим

(3.15)

Мы ввели обозначения и чтобы подчеркнуть, что составляющая и соответствующий орт связаны с изменением угла

Рис. 3.6.

Очевидно, что векторы взаимно перпендикулярны: Следовательно,

Рассмотрим вопрос о том, как, зная величину скорости в каждый момент времени, вычислить путь, проходимый частицей с момента времени до момента Разобьем промежуток времени на N малых, не обязательно одинаковых промежутков: Весь путь s, пройденный частицей, можно представить как сумму путей пройденных за соответствующие промежутки времени :

В соответствии с формулой (3.4) каждое из слагаемых может быть приближенно представлено в виде

где — промежуток времени, за который был пройден путь — одно из значений скорости за время Следовательно,

Написанное равенство выполняется тем точнее, чем меньше промежутки времени . В пределе при стремлении всех нулю (количество промежутков будет при этом неограниченно возрастать) приближенное, равенство станет точным:

Полученное выражение представляет собой определенный интеграл от функции взятый в пределах от до . Таким образом, путь, проходимый частицей за промежуток времени от до равен

Подчеркнем, что здесь идет речь о модуле скорости. Если взять интеграл от самой скорости , то получится вектор перемещения чаетицы из точки, в которой она была в момент в точку, в которой она оказалась в момент

(см. (3.5)).

Если изобразить график зависимости а от t (рис. 3.7), то пройденный путь можно представить как площадь фигуры, ограниченной кривой и прямыми Действительно, произведение численно равно площади t-й полоски. Сумма (3.17) равна площади, ограниченной сверху ломаной линией, образованной верхними краями всех подобных полосок. При стремлении всех к нулю ширина полосок убывает (одновременно число их растет), и ломаная линия в пределе сольется с кривой v=v(t). Таким образом, путь, пройденный за время с момента до момента численно равен площади, ограниченной графиком функции осью времени t и прямыми

Рис. 3.7.

Заметим, что среднее значение модуля скорости за время от до по определению равно

Подставив сюда выражение (3.18) для s, получим:

Аналогично вычисляются средние значения любых скалярных или векторных функций. Например, среднее значение скорости равно

(см. (3.19)). Среднее значение функции у на промежутке от до определяется выражением

Оглавление

ПРЕДИСЛОВИЕ
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ВВЕДЕНИЕ
ЧАСТЬ 1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
§ 1. Механическое движение
§ 2. Некоторые сведения о векторах
§ 3. Скорость
§ 4. Ускорение
§ 5. Кинематика вращательного движения
ГЛАВА II. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
§ 6. Классическая механика. Границы ее применимости
§ 7. Первый закон Ньютона. Инерциальные системы отсчета
§ 8. Масса и импульс тела
§ 9. Второй закон Ньютона
§ 10. Единицы и размерности физических величин
§ 11. Третий закон Ньютона
§ 12. Принцип относительности Галилея
§ 13. Силы
§ 14. Упругие силы
§ 15. Силы трения.
§ 16, Сила тяжести и вес
§ 17. Практическое применение законов Ньютона
ГЛАВА III. ЗАКОНЫ СОХРАНЕНИЯ
§ 18. Сохраняющиеся величины
§ 19. Кинетическая энергия
§ 20. Работа
§ 21. Консервативные силы
§ 22. Потенциальная энергия во внешнем поле сил
§ 23. Потенциальная энергия взаимодействия
§ 24. Закон сохранения энергии
§ 25. Энергия упругой деформации
§ 26. Условия равновесия механической системы
§ 27. Закон сохранения импульса
§ 28. Соударение двух тел
§ 29. Закон сохранения момента импульса
§ 30. Движение в центральном поле сил
§ 31. Задача двух тел
ГЛАВА IV. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА
§ 32. Силы инерции
§ 33. Центробежная сила инерции
§ 34. Сила Кориолиса
§ 35. Законы сохранения в неинерциальных системах отсчета
ГЛАВА V. МЕХАНИКА ТВЕРДОГО ТЁЛА
§ 36. Движение твердого тела
§ 37. Движение центра масс твердого тела
§ 38. Вращение тела вокруг неподвижной оси
§ 39. Момент инерции
§ 40. Понятие о тензоре инерции
§ 41. Кинетическая энергия вращающегося твердого тела
§ 42. Кинетическая энергия тела при плоском движении
§ 43. Применение закона динамики твердого тела
§ 44. Гироскопы
ГЛАВА VI. ВСЕМИРНОЕ ТЯГОТЕНИЕ
§ 45. Закон всемирного тяготения
§ 46. Гравитационное поле
§ 47. Принцип эквивалентности
§ 48. Космические скорости
ГЛАВА VII. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
§ 49. Общие сведения о колебаниях
§ 50. Малые колебания
§ 51. Комплексные числа
§ 52. Линейные дифференциальные уравнения
§ 53. Гармонические колебания
§ 54. Маятник
§ 55. Векторная диаграмма
§ 56. Биения
§ 57. Сложение взаимно перпендикулярных колебаний
§ 58. Затухающие колебания
§ 59. Автоколебания
§ 60. Вынужденные колебания
§ 61. Параметрический резонанс
ГЛАВА VIII. РЕЛЯТИВИСТСКАЯ МЕХАНИКА
§ 62. Специальная теория относительности
§ 63. Преобразования Лоренца
§ 64. Следствия из преобразований Лоренца
§ 65. Интервал
§ 66. Преобразование и сложение скоростей
§ 67. Релятивистское выражение для импульса
§ 68. Релятивистское выражение для энергии
§ 69. Преобразования импульса и энергии
§ 70. Взаимосвязь массы и энергии
§ 71. Частицы с нулевой массой покоя
ГЛАВА IX. ГИДРОДИНАМИКА
§ 72. Линии и трубки тока. Неразрывность струи
§ 73. Уравнение Бернулли
§ 74. Истечение жидкости из отверстия
§ 75. Силы внутреннего трения
§ 76. Ламинарное и турбулентное течения
§ 77. Течение жидкости в круглой трубе
§ 78. Движение тел в жидкостях и газах
ЧАСТЬ 2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
§ 79. Статистическая физика и термодинамика
§ 80. Масса и размеры молекул
§ 81. Состояние системы. Процесс
§ 82. Внутренняя энергия системы
§ 83. Первое начало термодинамики
§ 84. Работа, совершаемая телом при изменениях объема
§ 85. Температура
§ 86. Уравнение состояния идеального газа
§ 87. Внутренняя энергия и теплоемкость идеального газа
§ 88. Уравнение адиабаты идеального газа
§ 89. Политропические процессы
§ 90. Работа, совершаемая идеальным газом при различных процессах
§ 91. Ван-дер-ваальсовский газ
§ 92. Барометрическая формула
ГЛАВА XI. СТАТИСТИЧЕСКАЯ ФИЗИКА
§ 93. Некоторые сведения из теории вероятностей
§ 94. Характер теплового движения молекул
§ 95. Число ударов молекул о стенку
§ 96. Давление газа на стенку
§ 97. Средняя энергия молекул
§ 98. Распределение Максвелла
§ 99. Экспериментальная проверка закона распределения Максвелла
§ 100. Распределение Больцмана
§ 101. Определение Перреном числа Авогадро
§ 102. Макро- и микросостояния. Статистический вес
§ 103. Энтропия
ГЛАВА XII. ТЕРМОДИНАМИКА
§ 104. Основные законы термодинамики
§ 105. Цикл Карно
§ 106. Термодинамическая шкала температур
§ 107. Примеры на вычисление энтропии
§ 108. Некоторые применения энтропии
§ 109. Термодинамические потенциалы
ГЛАВА XIII. КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ
§ 110. Отличительные черты кристаллического состояния
§ 111. Классификация кристаллов
§ 112. Физические типы кристаллических решеток
§ 113. Дефекты в кристаллах
§ 114. Теплоемкость кристаллов
ГЛАВА XIV. ЖИДКОЕ СОСТОЯНИЕ
§ 115. Строение жидкостей
§ 116. Поверхностное натяжение
§ 117. Давление под изогнутой поверхностью жидкости
§ 118. Явления на границе жидкости и твердого тела
§ 119. Капиллярные явления
ГЛАВА XV. ФАЗОВЫЕ РАВНОВЕСИЯ И ПРЕВРАЩЕНИЯ
§ 121. Испарение и конденсация
§ 122. Равновесие жидкости и насыщенного пара
§ 123. Критическое состояние
§ 124. Пересыщенный пар и перегретая жидкость
§ 125. Плавление и кристаллизация
§ 126. Уравнение Клапейрона—Клаузиуса
§ 127. Тройная точка. Диаграмма состояния
ГЛАВА XVI. ФИЗИЧЕСКАЯ КИНЕТИКА
§ 128. Явления переноса
§ 129. Средняя длина свободного пробега
§ 130. Диффузия в газах
§ 131. Теплопроводность газов
§ 132. Вязкость газов
§ 133. Ультраразреженные газы
§ 134. Эффузия
ПРИЛОЖЕНИЯ
I. Вычисление некоторых интегралов
II. Формула Стирлинга
III. Симметричные тензоры второго ранга

Источник

В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Источник

Что такое скорость?

Скорость – важнейшее понятие кинематики.

Скорость точки определение

Определение скорости точки:

Скорость равна отношению перемещения к промежутку времени, за которое совершилось данное перемещение.

Скорость точки формула

Формула скорости точки:

v = r/t

Жирным шрифтом здесь обозначены векторные величины, т.о. скорость является вектором.

Обратите внимание, что речь идёт об очень маленьком участке траектории, на этом участке мы и рассматриваем перемещение. На таком маленьком отрезке траектории движение должно быть практически равномерным. Только при таких условиях мы можем применять формулу v = r/t. На большем, т.е. более протяженном, участке траектории эта формула не годится в общем случае.

Направление вектора скорости

Вектор скорости всегда направлен по касательной к траектории в том месте, где мы его рассматриваем.

Модуль вектора скорости

Модуль вектора скорости равен отношению приращения длины пути к соответствующему промежутку времени:

|v| = S/t

Обратите внимание, что это приращение длины пути соответствует нашему приращению вектора перемещения в формуле в начале данной статьи. Из раздела «Путь и перемещение» мы знаем как соотносятся приращение длины пути и приращение вектора перемещения, вот так:

S = ±|r|

Источник

Определение скорости при координатном способе

задания
движения

Воспользуемся
уравнением (4)
и возьмем от него производную по времени

.
(8)

В
(8)
при единичных векторах стоят проекции
вектора скорости на координатные оси

.
(9)

Проекции
скорости на координатные оси определяются
как первые производные по времени от
соответствующих координат.

Зная
проекции, можно найти модуль вектора и
его направление

,
(10)

.
(11)

Определение
скорости при естественном способе

задания
движения

Пусть
дана траектория материальной точки и
закон изменения криволинейной координаты.
Предположим, при t₁
точка имел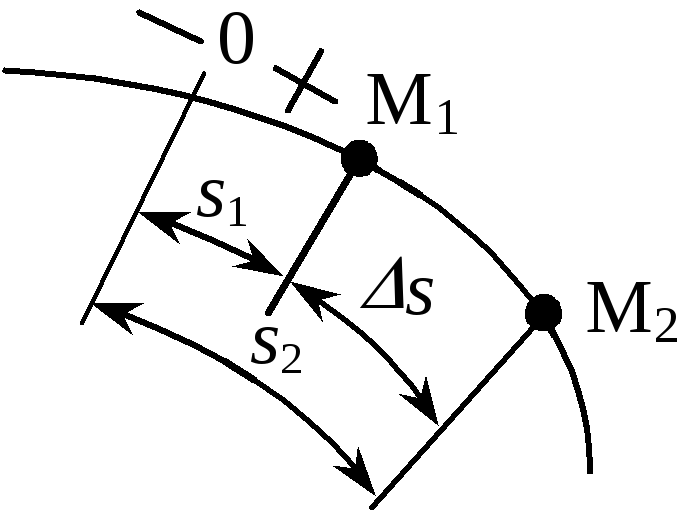а
координатуs₁,
а при t₂
– координату s₂.
За время
координата
получила приращение
,
тогда средняя скорость точки

Для
нахождения скорости в заданный момент
времени перейдем к пределу

.
(12)

Вектор
скорости точки при естественном способе
задания движения определяется как
первая производная по времени от
криволинейной координаты.

Ускорение точки

Под
ускорением материальной точки понимают
векторную величину, характеризующую
быстроту изменения вектора скорости
точки по величине и направлению с
течением времени.

Ускорение точки при векторном способе
задания движения

Рассмотрим
точку в два момента времени t₁
()
иt₂
(),
тогда– приращение времени,– приращение скорости.

Вектор
всегда
лежит в плоскости движения и направлен
в сторону вогнутости траектории.

Подсредним
ускорением точки
за время t
понимают
величину

.
(13)

Для
нахождения ускорения в заданный момент
времени перейдем к пределу

.
(14)

Ускорение
точки в данный момент времени определяется
как вторая производная по времени от
радиус-вектора точки или первая
производная от вектора скорости по
времени.

Вектор
ускорения расположен в соприкасающейся
плоскости и направлен в сторону вогнутости
траектории.

Ускорение точки при координатном способе задания движения

Воспользуемся
уравнением связи векторного и координатного
способов задания движения

И возьмем от него
вторую производную

.
(15)

В
уравнении (15)
при единичных векторах стоят проекции
вектора ускорения на координатные оси

.
(16)

Проекции
ускорения на координатные оси определяются
как первые производные по времени от
проекций скорости или как вторые
производные от соответствующих координат
по времени.

Модуль и направление
вектора ускорения можно найти по
следующим выражениям

,
(17)

,
,.
(18)

Ускорение точки при естественном способе задания движения

Пусть
точка движется по криволинейной
траектории. Рассмотрим два ее положения
в моменты времениt
(s,
M,
v)
и t₁
(s₁,
M₁,
v₁).

Ускорение
при этом определяется через его проекции
на оси естественной системы координат,
движущейся вместе с точкой M.
Оси при этом направлены следующим
образом:

M
– касательная, направлена вдоль касательной
к траектории, в сторону положительного
отсчета расстояния,

Mn
– главная нормаль, направлена по нормали,
лежащей в соприкасающейся плоскости,
и направлена в сторону вогнутости
траектории,

Mb
– бинормаль, перпендикулярна плоскости
Mn
и образует с первыми осями правую тройку.

Так
как вектор ускорения лежит в соприкасающейся
плоскости, то a_b=0.
Найдем проекции ускорения на другие
оси.

.
(19)