Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.
Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.
Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.
Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.
Путь
Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Вектор перемещения
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Рис. 1.1. Вектор перемещения и пройденный путь.
На рис. 1.1:
![]()
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
Правило сложения векторов
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).
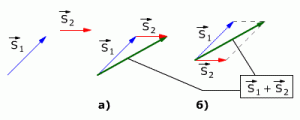
Рис. 1.2. Сложение векторов перемещений.
На рис 1.2 показаны правила сложения векторов S1 и S2:
а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма
Проекции вектора перемещения
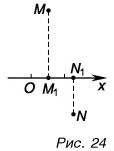
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения ![]() (см.рис. 1.3).
(см.рис. 1.3).
Выберем ось ОХ так, чтобы вектор ![]() лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно Аx и Вx. Длина отрезка АxВx на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть
лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно Аx и Вx. Длина отрезка АxВx на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть
Sx = AxBx
ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор ![]() с проекцией вектора на какую-либо ось (например, Sx). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.
с проекцией вектора на какую-либо ось (например, Sx). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.
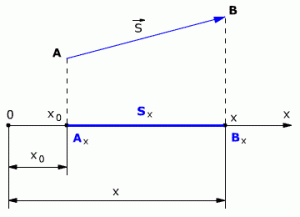
Рис. 1.3. Проекция вектора перемещения.
Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть
Sx = x – x0
Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:
Sy = y – y0 Sz = z – z0
Здесь x0, y0, z0 — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).
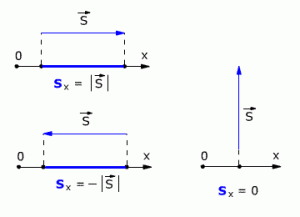
Рис. 1.4. Модули проекции вектора перемещения.
Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.
Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).
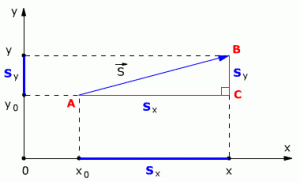
Рис. 1.5. Движение тела на плоскости.
Определим проекции вектора перемещения на осях ОХ и OY:
Sx = x – x0 Sy = y – y0
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как
АС = sx CB = sy
По теореме Пифагора
S2 = Sx2 + Sy2
Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:
![]()
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.
Преподаватель который помогает студентам и школьникам в учёбе.
Проекция вектора на ось в физике – формулы и определения с примерами
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка 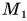
Как определяют проекцию вектора на ось
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора  на ось Ох обозначена через
на ось Ох обозначена через  а проекция вектора
а проекция вектора 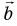 — через
— через 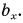
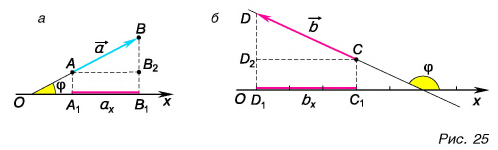
Проекция 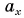 — число положительное, т. к. угол
— число положительное, т. к. угол 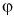 на рисунке 25, а — острый. Проекция
на рисунке 25, а — острый. Проекция 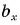 — число отрицательное
— число отрицательное 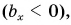 т. к. угол
т. к. угол 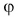 на рисунке 25, б — тупой.
на рисунке 25, б — тупой.
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
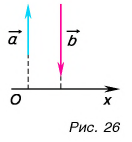
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 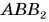 на рисунке 25, а. Его гипотенуза
на рисунке 25, а. Его гипотенуза 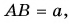 катет
катет 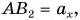 а угол между ними равен
а угол между ними равен 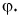 Следовательно,
Следовательно,

Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
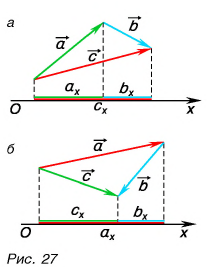
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 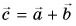 следует равенство для проекций:
следует равенство для проекций: 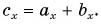 Не забывайте о знаках проекций.
Не забывайте о знаках проекций.
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
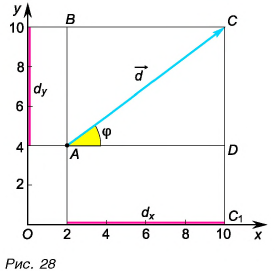
Рассмотрим вектор 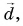 лежащий в плоскости
лежащий в плоскости 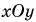 (рис. 28). Его проекции на оси
(рис. 28). Его проекции на оси 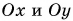 определим из рисунка:
определим из рисунка: 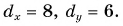
Модуль вектора 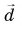 находим по теореме Пифагора из треугольника ACD:
находим по теореме Пифагора из треугольника ACD: 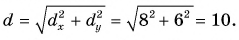 Разделив
Разделив 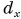 на
на 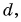 получим:
получим: 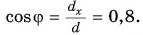 По значению косинуса находим угол
По значению косинуса находим угол 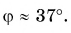
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
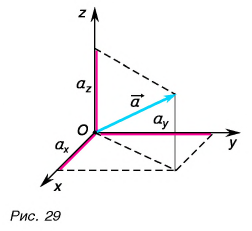
Вектор в пространстве определяется тремя проекциями: 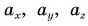 (рис. 29).
(рис. 29).
Главные выводы:
- Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
- Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
- Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
- Проекция суммы векторов на ось равна сумме их проекций на эту ось.
Пример №1
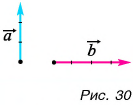
1. Определите сумму и разность взаимно перпендикулярных векторов  (рис. 30). Найдите модули векторов суммы
(рис. 30). Найдите модули векторов суммы  и разности
и разности 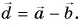
Решение
Сумму векторов 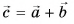 находим по правилу треугольника (рис. 31, а) или параллелограмма (рис. 31, б). Так как векторы
находим по правилу треугольника (рис. 31, а) или параллелограмма (рис. 31, б). Так как векторы 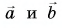 взаимно перпендикулярны, модуль вектора
взаимно перпендикулярны, модуль вектора 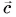 находим по теореме Пифагора:
находим по теореме Пифагора: 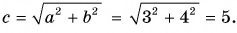 Разность векторов
Разность векторов 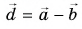 определим по правилам вычитания векторов (рис. 32, а, б).
определим по правилам вычитания векторов (рис. 32, а, б).

Модуль вектора 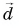 находим аналогично:
находим аналогично:
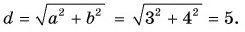
Ответ: 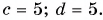
- Заказать решение задач по физике
Пример №2
Выразите вектор 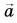 через векторы
через векторы 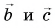 (рис. 33). Как связаны между собой проекции этих векторов на оси Ох и Оу?
(рис. 33). Как связаны между собой проекции этих векторов на оси Ох и Оу?
Решение
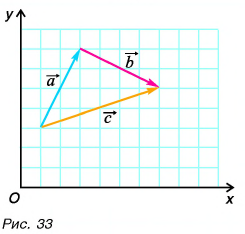
По правилу треугольника находим: 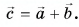 Отсюда
Отсюда 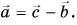 Определив координаты
Определив координаты  начальных и конечных точек векторов
начальных и конечных точек векторов 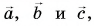 находим проекции этих векторов:
находим проекции этих векторов: 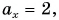

Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы: 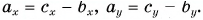
Ответ: 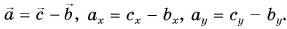
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
Проекцией вектора
на ось называется вектор, который
получается в результате перемножения
скалярной проекции вектора на эту ось
и единичного вектора этой оси. Например,
если аx – скалярная
проекция вектора а на
ось X, то аx·i –
его векторная проекция на эту
ось.
Обозначим векторную
проекцию также,
как и сам вектор, но с индексом той оси
на которую вектор проектируется. Так,
векторную проекцию вектора а на
ось Х обозначим аx (жирная буква,
обозначающая вектор и нижний индекс
названия оси) или ![]() (нежирная
(нежирная
буква, обозначающая вектор, но со стрелкой
наверху (!) и нижний индекс названия
оси).
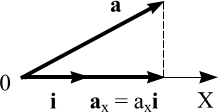
Скалярной
проекцией вектора
на ось называется число,
абсолютная величина которого равна
длине отрезка оси (в выбранном масштабе),
заключённого между проекциями точки
начала и точки конца вектора. Обычно
вместо выражения скалярная
проекция говорят
просто – проекция.
Проекция обозначается той же буквой,
что и проектируемый вектор (в обычном,
нежирном написании), с нижним (как
правило) индексом названия оси, на
которую этот вектор проектируется.
Например, если на ось Х проектируется
вектора, то
его проекция обозначается аx.
При проектировании этого же вектора на
другую ось, если ось
Y , его проекция будет обозначаться
аy .
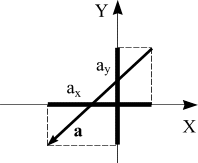 Чтобы
Чтобы
вычислить проекцию вектора на
ось (например, ось X) надо из координаты
точки его конца вычесть координату
точки начала, то есть
аx =
хк −
xн.
Проекция
вектора на ось – это число. Причем,
проекция может быть положительной, если
величина хк больше
величины хн,
отрицательной, если
величина хк меньше
величины хн
и
равной нулю, если хк равно
хн .
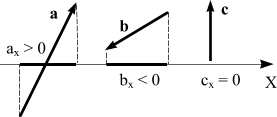 Проекцию
Проекцию
вектора на ось можно также найти, зная
модуль вектора и угол, который он
составляет с этой осью.
Из
рисунка видно,
что аx =
а Cos α
то есть, проекция вектора на
ось равна произведению модуля вектора
на косинус угла между направлением оси
и направлением
вектора.
Если угол острый, то
Cos α > 0 и аx >
0, а, если тупой, то косинус тупого угла
отрицателен, и проекция вектора на ось
тоже будет отрицательна.
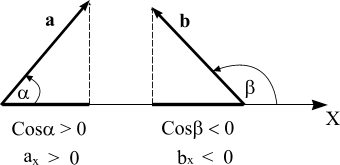 Углы,
Углы,
отсчитываемые от оси против хода часовой
стрелки, принято считать положительными,
а по ходу – отрицательными. Однако,
поскольку косинус – функция четная, то
есть, Cos α = Cos (− α), то при вычислении
проекций углы можно отсчитывать как по
ходу часовой стрелки, так и против.
Чтобы
найти проекцию вектора на ось надо
модуль этого вектора умножить на косинус
угла между направлением оси и направлением
вектора.
10. Линейные операции над векторами и их основные свойства. Линейные операции над векторами Сложение векторов
Пусть
даны два вектора ![]() и
и ![]() .
.
Приложим вектор ![]() к
к
точке ![]() (концу
(концу
вектора ![]() )
)
и получим вектор ![]() (рис.1.7,а;
(рис.1.7,а;
здесь и далее равные векторы отмечены
одинаковыми засечками).
Вектор ![]() называется суммой
называется суммой
векторов ![]() и
и ![]() и
и
обозначается ![]() .
.
Это нахождение суммы называется правилом
треугольника.
Сумму
двух неколлинеарных векторов ![]() и
и ![]() можно
можно
найти по правилу
параллелограмма.
Для этого откладываем от любой
точки ![]() векторы
векторы ![]() и
и ![]() ,
,
а затем строим параллелограмм ![]() (рис.
(рис.
1.7,6). Диагональ ![]() параллелограмма
параллелограмма
определяет сумму:
![]()
Для
нахождения суммы нескольких векторов
можно построить ломаную из равных им
векторов. Тогда замыкающий вектор,
соединяющий начало первого вектора
ломаной с концом последнего ее вектора,
равен сумме всех векторов ломаной. На
рис.1.7,в изображена сумма ![]() четырех
четырех
векторов ![]() .
.
Таким способом (правило
ломаной)
можно сложить любое конечное число
векторов. Заметим, что сумма векторов
не зависит от точек приложения слагаемых
и от порядка суммирования. Например,
“выстраивая цепочку” векторов для
суммы в виде ![]() ,
,
получим вектор, равный вектору ![]() .
.
Если ломаная получилась замкнутой, то
сумма равна нулевому вектору.
Соседние файлы в предмете Алгебра и геометрия
- #
- #
- #
- #
Ось – это направление. Значит, проекция на ось или на направленную прямую считается одним и тем же. Проекция бывает алгебраическая и геометрическая. В геометрическом понимают проекцию вектора на ось как вектор, а алгебраическом – число. То есть применяются понятия проекция вектора на ось и числовая проекция вектора на ось.
Если имеем ось L и ненулевой вектор AB→, то можем построить вектор A1B1⇀, обозначив проекции его точек A1 и B1.
A1B→1 будет являться проекцией вектора AB→ на L.
Проекцией вектора на ось называют вектор, начало и конец которого являются проекции начала и конца заданного вектора. npLAB→→ принято обозначать проекцию AB→ на L. Для построения проекции на L опускают перпендикуляры на L.
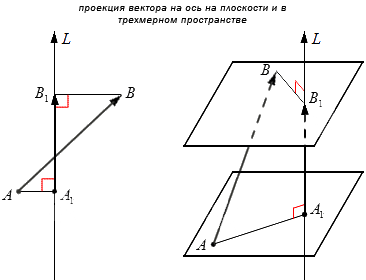
Пример проекции вектора на ось.
На координатной плоскости Оху задается точка M1 (x1, y1). Необходимо построить проекции на Ох и Оу для изображения радиус-вектора точки M1. Получим координаты векторов (x1, 0) и (0, y1).
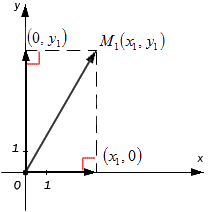
Если идет речь о проекции a→ на ненулевой b→ или проекции a→ на направление b→, то имеется в виду проекция a→на ось, с которой совпадает направление b→. Проекция a→ на прямую, определяемая b→, имеет обозначение npb→a→→. Известно, что когда угол междуa→ и b→, можно считать npb→a→→ и b→ сонаправленными. В случае, когда угол тупой, npb→a→→ и b→противоположно направлены. В ситуации перпендикулярностиa→ и b→, причем a→ – нулевой, проекция a→ по направлению b→ является нулевым вектором.
Числовая проекция вектора на ось
Числовая характеристика проекции вектора на ось – числовая проекция вектора на заданную ось.
Числовой проекцией вектора на ось называют число, которое равно произведению длины данного вектора на косинус угла между данным вектором и вектором, который определяет направление оси.
Числовая проекция AB→ на L имеет обозначениеnp LAB→, а a→ на b→ – npb→a→.
Исходя из формулы, получим npb→a→=a→·cosa→, b→^, откуда a→ является длиной вектора a→, a⇀, b→^ – угол между векторами a→ и b→.
Получим формулу вычисления числовой проекции: npb→a→=a→·cosa→, b→^. Она применима при известных длинах a→ и b→ и угле между ними. Формула применима при известных координатах a→ и b→, но имеется ее упрощенный вид.
Узнать числовую проекцию a→ на прямую по направлению b→ при длине a→ равной 8 и углом между ними в 60 градусов. По условию имеем a⇀=8, a⇀, b→^=60°. Значит, подставляем числовые значения в формулу npb⇀a→=a→·cosa→,b→^=8·cos 60°=8·12=4.
Ответ: 4.
При известном cos(a→, b→^)=a⇀, b→a→·b→, имеем a→, b→ как скалярное произведение a→ и b→. Следуя из формулы npb→a→=a→·cosa⇀, b→^, мы можем найти числовую проекцию a→ направленную по вектору b→ и получим npb→a→=a→, b→b→. Формула эквивалента определению, указанному в начале пункта.
Числовой проекцией вектора a→ на ось , совпадающей по направлению с b→, называют отношение скалярного произведения векторовa→ иb→ к длине b→. Формула npb→a→=a→,b→b→ применима для нахождения числовой проекции a→ на прямую, совпадающую по направлению с b→, при известных a→ и b→ координатах.
Задан b→=(-3, 4). Найти числовую проекцию a→=(1, 7) на L.
Решение
На координатной плоскости npb→a→=a→, b→b→ имеет вид npb→a→=a→, b→b→=ax·bx+ay·bybx2+by2, при a→=(ax, ay) и b→=bx, by. Чтобы найти числовую проекцию вектора a→ на ось L, нужно: npLa→=npb→a→=a→,b→b→=ax·bx+ay·bybx2+by2=1·(-3)+7·4(-3)2+42=5.
Ответ: 5.
Найти проекцию a→ на L, совпадающей с направлением b→, где имеются a→=-2, 3, 1 и b→=(3, -2, 6). Задано трехмерное пространство.
Решение
По заданнымa→=ax, ay, az и b→=bx, by, bz вычислим скалярное произведение: a⇀, b→=ax·bx+ay·by+az·bz. Длину b→ найдем по формуле b→=bx2+by2+bz2. Отсюда следует, что формула определения числовой проекции a→ будет: npb→a⇀=a→, b→b→=ax·bx+ay·by+az·bzbx2+by2+bz2.
Подставляем числовые значения: npLa→=npb→a→=(-2)·3+3·(-2)+1·632+(-2)2+62=-649=-67.
Ответ: -67.
Просмотрим связь междуa→ на L и длиной проекции a→ на L. Начертим ось L, добавив a→ и b→ из точки на L, после чего проведем перпендикулярную прямую с конца a→ на L и проведем проекцию на L. Существуют 5 вариаций изображения:
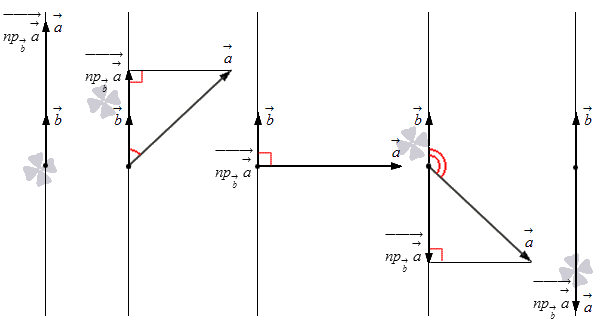
Первый случай при a→=npb→a→→ означает a→=npb→a→→, отсюда следует npb→a→=a→·cos(a,→b→^)=a→·cos0°=a→=npb→a→→.
Второй случай подразумевает применение npb→a→⇀=a→·cosa→,b→, значит, npb→a→=a→·cos(a→,b→)^=npb→a→→.
Третий случай объясняет, что при npb→a→→=0→ получаем npb⇀a→=a→·cos(a→,b→^)=a→·cos90°=0, тогда npb→a→→=0 и npb→a→=0=npb→a→→.
Четвертый случай показывает npb→a→→=a→·cos(180°-a→,b→^) = -a→·cos(a →, b→^), следует npb→a→=a→·cos(a→,b→^)=-npb→a→→.
Пятый случай показывает a→=npb→a→→, что означаетa→=npb→a→→, отсюда имеем npb→a→=a→·cosa→,b→^=a→·cos180°=-a→=-npb→a→.
Числовой проекцией вектора a→ на ось L, которая направлена как и b→, имеет значение:
- длины проекции вектора a→ на L при условии, если угол между a→ и b→ меньше 90 градусов или равен 0: npb→a→=npb→a→→ с условием 0≤(a→,b→)^<90°;
- ноля при условии перпендикулярности a→ и b→: npb→a→=0, когда (a→, b→^)=90°;
- длины проекции a→ на L, умноженной на -1, когда имеется тупой или развернутый угол векторов a→ и b→: npb→a→=-npb→a→→ с условием 90°<a→,b→^≤180°.
Дана длина проекцииa→ на L, равная 2. Найти числовую проекциюa→ при условии, что угол равен 5π6 радиан.
Решение
Из условия видно, что данный угол является тупым: π2<5π6<π. Тогда можем найти числовую проекцию a→ на L: npLa→=-npLa→→=-2.
Ответ: -2.
Дана плоскость Охyzс длиной вектора a→ равной 63,b→(-2, 1, 2) с углом в 30 градусов. Найти координаты проекции a→ на ось L.
Решение
Для начала вычисляем числовую проекцию вектораa→: npLa→=npb→a→=a→·cos(a→,b→)^=63·cos30°=63·32=9.
По условию угол острый, тогда числовая проекция a→= длине проекции вектора a→: npLa→=npLa→→=9. Данный случай показывает, что векторы npLa→→ и b→ сонаправлены, значит имеется число t, при котором верно равенство: npLa→→=t·b→. Отсюда видим, что npLa→→=t·b→, значит можем найти значение параметра t: t=npLa→→b→=9(-2)2+12+22=99=3.
Тогда npLa→→=3·b→ с координатами проекции вектора a→ на ось L равны b→=(-2,1, 2), где необходимо умножить значения на 3. Имеем npLa→→=(-6, 3, 6). Ответ: (-6, 3, 6).
Необходимо повторить ранее изученную информацию об условии коллинеарности векторов.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
2.1. Теорема Пифагора
Прямоугольный треугольник — треугольник, в котором один из углов прямой (то есть равен 90°). Сторона, противолежащая прямому углу, называется гипотенузой. Стороны, образующие прямой угол, называются катетами (см. рис.).
Для любого прямоугольного треугольника справедлива теорема Пифагора:
Гипотенузу можно найти по формуле:
Катет можно найти по формуле:
2.2 Как найти и
из прямоугольного треугольника?
Рассмотрим прямоугольный треугольник с катетами a и b и гипотенузой c. Обозначим через α угол, лежащий напротив катета a (см. рис.).
Тогда, катет a — противолежащий катет для угла α (лежит напротив угла); катет b — прилежащий катет (непосредственно образует угол).
Синус угла α — отношение противолежащего катета к гипотенузе:
Косинус угла α — отношение прилежащего катета к гипотенузе:
Тангенсом угла α — отношение противолежащего катета к прилежащему:
2.3 Как найти проекции вектора, если известен его модуль и направление?
1) Опускаем перпендикуляры на ось Ox и ось Oy;
2) Проекции равны:
3) Правило знаков.
Пусть даны вектор и ось Ox. Из начала и конца вектора
опустим перпендикуляры на ось Ox. Пусть A и B — основания этих перпендикуляров (см. рис.).
Проекция вектора
на ось Ox (Oy) равна длине отрезка AB, взятой со знаком плюс, если угол φ между вектором
и осью Ox (Oy) является острым, и взятой соответственно со знаком минус, если φ тупой (или развернутый). Если угол φ прямой, то
То есть:
Получаем:
2.4 Как найти проекции вектора, если известны координаты начала и конца вектора?
Пусть и
) — координаты начала и конца вектора соответственно. Тогда проекции
2.5 Как найти модуль вектора, если известны его проекции на оси?
Если известны проекции вектора и
на оси координат, то модуль вектора легко найти по формуле:
2.6 Как найти модуль вектора, если известны координаты конца и начала вектора?
Пусть и
— координаты начала и конца вектора
соответственно. Тогда модуль вектора находится по формуле:
2.7 Теорема косинусов.
Для треугольника со сторонами a, b и c, углом α справедлива теорема:
2.8 Как сложить вектора, направленные вдоль одной прямой?
Пусть даны вектора и
имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.).
Из рисунка видно, что модуль вектора равен:
2.9 Как вычитать вектора, направленные вдоль одной прямой?
Пусть даны вектора и
имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.). Вектор
— это вектор, длина которого равна длине вектора
, но имеет противоположное направление.
Из рисунка видно, что модуль вектора равен:
2.10 Как сложить вектора, направленные под прямым углом друг к другу?
Пусть даны вектора и
имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.).
Из рисунка видно, что модуль вектора равен:
2.11 Как вычитать вектора, направленные под прямым углом друг к другу?
Пусть даны вектора и
имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.). Вектор
— это вектор, длина которого равна длине вектора
но имеет противоположное направление.
Из рисунка видно, что модуль вектора равен:
2.12 Как сложить вектора, направленные под углом α друг к другу?
Пусть даны вектора и
, имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.).
По теореме косинусов, получаем:
2.13 Как вычитать вектора, направленные под прямым углом друг к другу?
Пусть даны вектора и
имеющие одинаковое направление. Для нахождения вектора
помещаем начало вектора
в конец вектора
и соединяем начало вектора
с концом вектора
(см. рис.). Вектор
— это вектор, длина которого равна длине вектора
, но имеет противоположное направление.
По теореме косинусов, получаем:
2.14 Площадь треугольника.
Площадь любого треугольника можно найти по формуле
2.15 Площадь прямоугольника.
Площадь любого прямоугольника можно найти по формуле
2.16 Площадь трапеции.
Площадь любой трапеции можно найти по формуле
2.17 Длина окружности.
Длина окружности равна:
2.18 Длина дуги.
Длина дуги:

