6.1. Классификация трубопроводов
В
зависимости от соотношения линейных и
местных потерь трубопроводы делятся
на короткие
и длинные,
в зависимости от конструкции гидравлической
системы – на простые
и сложные.
короткие
трубопроводы – это трубопроводы
сравнительно небольшой длины, на которых
смонтировано значительное количество
местных сопротивлений и поэтому местные
потери сопоставимы с линейными. Это,
например, системы объемных гидравлических
приводов всех назначений, системы смазки
различных устройств.
Кроме
того, это трубопроводы, некорректный
расчет которых может вызвать отказ
работы устройства (сифоны, всасывающие
линии насосов и т.п.).
при
расчете коротких трубопроводов
учитываются как линейные, так и местные
потери:
hсум
= Σhл.п+Σhм.п.
задачи
решаются с применением уравнений
неразрывности и Д.Бернулли для потока
реальной жидкости.
Длинные
трубопроводы – это трубопроводы
значительной длины, в которых линейные
потери являются основными. Это
водопроводные системы всех назначений,
нефтепроводы и т.п. системы.
При
расчете таких трубопроводов определяются
только линейные потери, а на местные
добавляют 5…10% от линейных, т.е.
hсум
= (1,05…1,1)hл.п.
Простые
трубопроводы – это трубопроводы, как
правило, одного диаметра, не имеющие
ответвлений.
Сложные
трубопроводы имеют различного рода
ответвления или состоят из нескольких
линий (параллельного соединения,
тупиковые, замкнутые, или кольцевые).
6.2. Расходная характеристика трубопровода (модуль расхода)
Вспомним
формулу линейных потерь – формулу Дарси
– Вейсбаха:
.
Выразим
в этой формуле скорость V
через расход Q
из соотношения
:

(6.1)
Для
трубопровода определенного диаметра
комплекс величин

постоянной (1/К2),
кроме коэффициента гидравлического
трения λ. На основании понятия
среднеэкономической скорости Vс.э
покажем, что и указанный коэффициент λ
можно отнести к этому комплексу, т.к. в
этом случае, число Рейнольдса будет
иметь определенное значение:
,
и на графике Никурадзе коэффициент λ в
этом случае будет иметь конкретное
значение.
Обоснуем
правомерность введения понятия
среднеэкономической скорости следующими
рассуждениями.
Гидравлическую
систему, например водопроводную, для
пропуска определенного расхода можно
выполнить из труб разного диаметра. При
этом с увеличением диаметра d,
следовательно, уменьшением скорости V
капитальные затраты будут расти, а
эксплуатационные затраты будут
уменьшаться из-за снижения гидравлических
потерь. Скорость, при которой суммарные
затраты будут иметь минимальное значение,
будем называть среднеэкономической
скоростью Vс.э
= 0,8…1,3 м/с (рис.6.1).
рис.6.1
Тогда
формула линейных потерь (6.1) примет вид
,
(6.2)
где
К – расходная характеристика трубопровода
(модуль расхода), зависит от материала
трубопровода, диаметра и расхода. берется
из таблиц.
6.3. Гидравлические характеристики трубопроводов
Гидравлической
характеристикой трубопровода называется
зависимость напора, который необходимо
создать в трубопроводе для пропуска по
нему определенного расхода, т.е. Н=f(Q).
Рассмотрим
некоторые особенности этой характеристики.
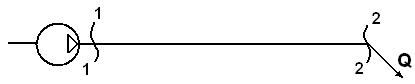
1.
Представим себе горизонтальный
трубопровод длиной l
и диаметром d, питаемый, например, от
насоса с постоянным расходом Q
(рис.6.2).
рис.
6.2
Составив
уравнение Бернулли для сечений 1-1 и 2-2,
получим, что напор в сечении 1-1 тратится
на преодоление линейных потерь hл.п,
т.е. Н = hл.п..
тогда
формулу (6.2) представим в виде
.
(6.3)
Обозначим
.
Для конкретного трубопровода это будет
постоянная величина, тогда выражение
(6.3) примет вид
.
(6.4)
Такая
явно квадратичная зависимость свойственна
только турбулентному режиму движения
(рис.6.3).
рис.
6.3
Из
рис. 6.3 видно, что, например, для пропуска
расхода Qi
в трубопроводе необходимо создать
напор Нi.
2.
Допустим, что насос подает жидкость в
трубопровод с преодолением статического
напора Нст
(рис.6.4).
рис.
6.4
Сначала
характеристика совпадает с линией ОН
(ординатой). Дальнейшее увеличение
напора расходуется на преодоление
гидравлических сопротивлений hп,
которые увеличиваются с увеличением
расхода Q.
Таким образом, аналитическое выражение
такой характеристики будет иметь вид
.
(6.5)
3.
мы
имеем, например, семейство характеристик
1,2,3 (рис.6.5). Простой анализ позволяет
сделать вывод, что они принадлежат
трубопроводам различного диаметра,
т.е. d1>d2>d3.
Таким образом, например, трубопровод 1
может пропустить больший расход при
меньшем напоре, чем трубопроводы 2 и 3.
Рис.
6.5 Рис. 6.6
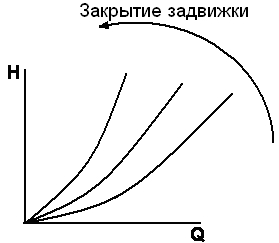
4.
Гидравлическую характеристику
трубопровода определенного диаметра
можно изменить, например, с помощью
задвижки. В выражении Н=ВQ2
изменяется коэффициент В. Задвижкой в
этом случае вводится дополнительное
сопротивление, эквивалентное определенной
длине трубопровода (рис.6.6).
5.
Примем, что насос подает жидкость в
трубопровод с верхнего бака в нижний
(рис.6.7), т.е. имеет место «отрицательного»
статического напора. В этом случае напор
Н` без насоса обеспечит расход в
трубопроводе Q`.
Для увеличения расхода подключается
насос.
Рис.
6.7
6.
гидравлическая
сеть состоит из нескольких трубопроводов
различного диаметра и длины, соединенных
последовательно (рис.6.8).
Рис.
6.8
Очевидно,
что
;
;

(6.6)
Суммарную
характеристику можно получить по
выражению (6.6) или построением характеристик
отдельных ее участков 1,2 и 3 с последующим
графическим их сложением (рис.6.9).
Рис.
6.9
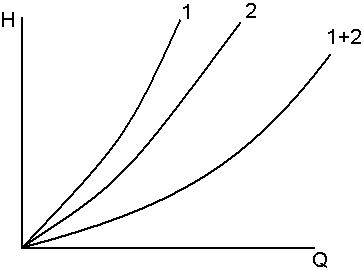
7.
гидравлическая
сеть состоит из нескольких трубопроводов
различного диаметра и длины, соединенных
параллельно (рис. 6.10).
Рис.
6.10
Очевидно,
что
.
В точках А и В напор одинаков для
трубопровода с расходомQ1
и Q2.
следовательно,
падение напора в каждой ветке одинаково,
т.е. Н=Н1=Н2
или
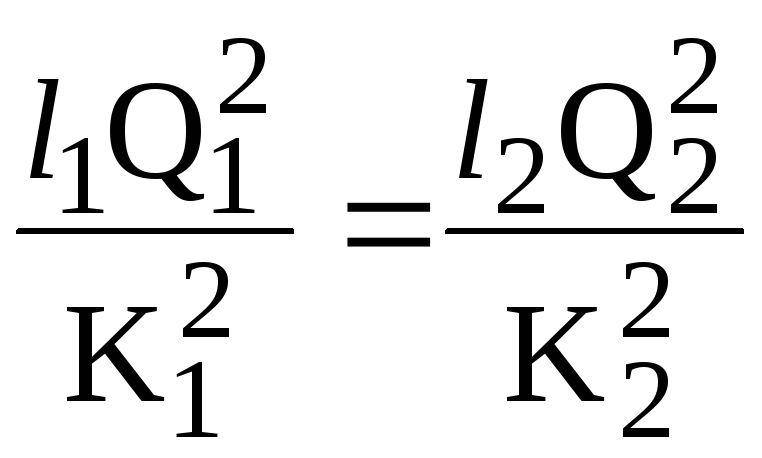
(6.7)
Суммарную
характеристику получают построением
характеристик отдельных ее участков с
последующим графическим их сложением
(рис.6.11).
Рис.
6.11
Соседние файлы в папке гидравлика
- #
- #
Гидравлический расчет длинных трубопроводов
2.3.1. Определение длинных трубопроводов
Длинными трубопроводами принято считать трубопроводы, в которых потери напора по длине значительно превышают потери напора на преодоление местных сопротивлений.
В этом случае потерями напора от местных сопротивлений можно пренебречь или при необходимости учесть их суммарно увеличением потерь напора на трение по длине потока на 5 – 10 %, принимая
hw = (1,05 – l,10).hf . (2 – 1)
Примерами длинных трубопроводов могут служить трубопроводы водопроводных сетей, сетей для транспортирования нефтепродуктов на значительные расстояния и т.д.
В зависимости от гидравлической схемы работы трубопроводы подразделяются на простые и сложные (рис. 2.1).
Рис. 2.1
Рекомендуемые материалы
Простым называется трубопровод, состоящий из одной линии труб (без ответвлений) с постоянным расходом по всей длине трубопровода. Простой трубопровод может иметь постоянный диаметр по всей своей длине (рис.2.1,а) или отдельных участков труб разного диаметра (последовательное соединение труб) (рис. 2.1,6).
Сложным называется трубопровод, состоящий из нескольких линий или имеющий переменный расход по длине вследствие отвода жидкости в узлах (местах разветвлений трубопровода) или непрерывной раздачи ее в пути.
Сложные трубопроводы подразделяются на:
– параллельно-разветвленные (рис.2 – 1,в );
– тупиковые (рис.2.1,г);
– кольцевые (рис.2.1,д);
– с непрерывным путевым расходом жидкости (рис.2.1,е).
2.3.2. Водопроводная формула
На участках трубопровода постоянного диаметра и расхода имеет место напорное равномерное движение жидкости, уравнение которого (1 – 5) имеет вид:

Пьезометрический уклон Ip в этом уравнении представляет собой потерю напора, обусловленную трением, на единицу длины потока, т. е. 
Подставив последнее выражение в уравнение равномерного напорного движения и решая его относительно hf , получим:
Обозначив
С2.w2.R = K2 ,
последнюю зависимость приведем к виду:

Это выражение и называется водопроводной формулой, в которой:
– hf – потери напора на трение в трубе диаметром d и длиной L;
– Q – расход воды;
– K – модуль расхода (или расходная характеристика), 
Из уравнения (1 – 5) следует, что

При расчетах водопроводных труб величину, обратную квадрату модуля расхода часто обозначают через A
Тогда водопроводная формула (2 – 2) переписывается в виде:
Hf = A.Q2.L, (2 – 4)
где

2.3.3. Расчет простого водопровода
Рассмотрим простой трубопровод постоянного диаметра d, подающего воду из точки A, где установлена водонапорная башня или насос, в точку B , где находится потребитель воды (жилое или служебное здание, отдельный объект, водоразборная колонка и т.п.) (рис. 2 – 2).
Введем следующие обозначения:
– zA и zB – высота положения (нивелировочные отметки) точек A и B;
– HA и HB – начальный и конечный напоры;
– L – длина трубопровода;
– Q – расход трубопровода.
Составим уравнение Бернулли для сечений 1 – 1 и 2 – 2:
Учитывая, что
H = hf ,
Рис. 2.2
В последних формулах Н – действующий напор.
Таким образом действующий в трубопроводе постоянный напор Н затрачивается на преодоление гидравлических сопротивлений в пути между сечениями 1 – 1 и 2 – 2, главным образом, на преодоление сопротивлений трения по длине потока.
При расчете простого трубопровода могут встретиться задачи трех типов:
Задача 1.Определение расхода трубопровода Q;
Задача 2.Определение начального или конечного напора (H1 или Н2);
Задача 3. Определение диаметра трубопровода.
2.3.4. Расчет элементов сложного трубопровода
А. Последовательное соединение труб.
При последовательном соединении труб может иметь место два расчетных случая:
I случай, когда начальный расход Q проходит транзитом по всей системе без отвода воды в каких-либо точках (узлах) системы (пример простого трубопровода);
II случай, когда в отдельных узлах трубопровода отводится некоторый расход воды (пример сложного трубопровода).
Рассмотрим трубопровод, состоящий из труб разных диаметров d1, d2,и d3 при длине участков, соответственно L1, L2 и L3 (рис. 2 – 3). Пусть начальный и конечный напоры Н1 и Н2 известны, а требуется определить величину расхода Q, проходящего транзитом по всей системе.
Если вода из системы никуда не отводится (т.е. qС = 0 и qД = 0), то
Q1 = Q2 = Q3 = Q.
Общая потеря напора в трубопроводе будет складываться из потерь на отдельных участках
hf1 + hf2 + hf3 = hf..
Последнее выражение с учетом водопроводной формулы можно переписать в виде

Рис. 2.3
При последовательном соединение труб с отводом воды в сторону
Q1 = Q; Q2 = Q – qС; Q3 = Q – (qС + qД). (2 – 10)
Подставив вьражения расходов Q2 и Q3 из уравнений расходов (2 – 10) в уравнение общей потери напора получим

Б. Параллельное соединение труб.
При решении задач по определению расхода параллельно-разветвленного трубопровода число неизвестных расходов будет равно числу участков труб (по схеме на рис. 2.4 – четыре участка).
Рис. 2.4
Поэтому число уравнений, составляемых для такого трубопровода, должно быть равно числу участков. Все виды расчетных уравнений для параллельно-разветвленного трубопровода можно разделить на три группы:
Уравнение общей потери напора в системе:

Уравнение равенства потери напора в параллельных ветвях:
Сегментация мирового рынка – лекция, которая пользуется популярностью у тех, кто читал эту лекцию.


Уравнения распределения расходов в системе:


По найденным значениям расходов, аналогично описанному выше, определяются потери напора в отдельных участках системы и строится пьезометрическая линия.
Расчет водопроводной сети. Расчет водопровода с краном, служащим для выпуска воды из водопровода в атмосферу
Страницы работы
Содержание работы
Санкт-Петербургский государственный
политехнический университет
Инженерно-строительный факультет
Кафедра гидравлики
Расчетно-графическое задание №3
Дисциплина: Гидравлика
Тема: Расчет длинных трубопроводов
Выполнил студент группы 3013/2 Кулакова
М.Н.
Преподаватель Локтионова Е.А.
«_____»______________2011г.
Санкт-Петербург
2011
Оглавление
1. Расчет водопроводной сети ………………………………………………………4
1.1.
Выбор магистрали………………………………………………………………4
1.2. Расчет магистрали………………………………………………………………4
1.3. Расчет ответвлений………………………………………………………..……6
2. Расчет водопровода с краном, служащим для выпуска воды из
водопровода в атмосферу……………………………………………………….11
2.1. Определение расходов QI
max, QII
max, QC
max
…………………………………11
2.2. Построение кривых зависимостей QI = f1(QC), QII = f2(QC) и пьезометрических
линий P-P………………………………………………………15
2.3. Построение пьезометрической линии при QC = 0,75QI max …………………16
Литература…………………………………………………………………………..17
1.
Расчет водопроводной сети
1.1. Выбор магистрали
Для выбора магистрали
необходимо учесть следующие условия:
1) Линия магистрали должна быть наиболее
длинной. Для этого необходимо сравнить длины труб на участке 3-4 ( l3-4) и 3-6 (l3-6):
l3-4=1320 м;
l3-6=1300 м.
Выбирается
наибольшая длина трубы, следовательно l3-4=1320 м.
2) Магистраль должна быть наиболее
нагружена расходами. Для этого сравниваем расходы воды, забираемые в конечных
точках
сети 4 (q4) и 6 (q6):
q4=4,4 л/с;
q6=10,3л/с.
Выбирается
наибольший расход воды, следовательно q6=10,3 л/с.
3) Магистраль должна проходить по
наиболее высоким отметкам поверхности земли.
Учитывая все
выше перечисленные условия, в данном варианте выбирается магистраль 1-2-3-6.
1.2. Расчет магистрали
Для каждого участка
трубопровода назначается экономическая скорость. Принято считать Vэк=1 м/с. Данная скорость необходима
для расчета площади сечения трубы на каждом участка магистрали:
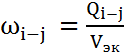
Также площадь сечения трубы можно
найти по формуле:
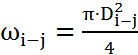
Можно получить формулу для нахождения
диаметра трубы:
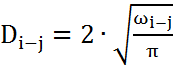
Теперь ведется расчет для
магистрали 1-2-3-6, для которой сначала собираются расчетные расходы:
Q3-6 = q6 = 10,3 л/с;
Q2-5= q5 + q’*l2-5= 9,7 + 0,017*1260=31,12 л/с;
Q2-3 = q4 + q6 = 4,4 + 10,3 = 14,7 л/с;
Q1-2 = q2 + q6
+ q4 + q5 + q’l2-5 = 10,3+ 8,2 + 4,4 +9,7 + 0,017 *
1260 = 54,02 л/с .
Воспользовавшись формулой
(1) необходимо рассчитать площадь сечения трубы на каждом участке магистрали:
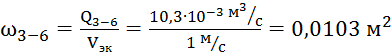
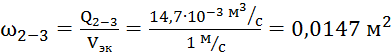
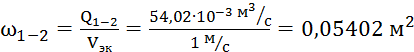
По известным значениям
площадей сечений труб определяется диаметр труб на каждой магистрали.
Полученные результаты округляются до ближайшего стандартного значения по табл. 4.6, стр. 40 [1].
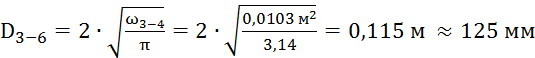
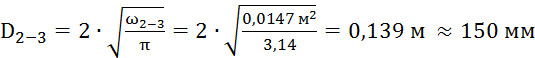
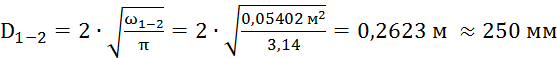
Из табл. 4.6, стр. 40 [1] в
соответствии с выбранными диаметрами берутся значения модулей расхода (kср) для каждого участка магистрали:
K3-6 = 98,22 л/с, K3-62 = 9,6472*103 (л/с)2
;
K2-3 = 160,62 л/с, K2-32 = 25,799*103 (л/с)2;
K1-2 = 627,74 л/с, K1-22 = 3,941*105 (л/с)2.
Затем необходимо вычислить
потери напора на каждом участке магистрали:
;
;
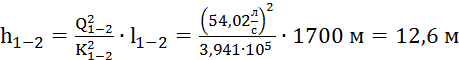
Суммарная потеря напора для данной
магистрали:
.
Высоту водонапорной башни
можно определить через отметки уровней воды и потерь напора:
;
;
;
;
.
Имея потери напора на
каждом участке магистрали, а также высоту башни, можно построить
пьезометрическую линия P-P (рис. 1).
1.3. Расчет ответвлений
Необходимо рассчитать
ответвления 2-5 и 3-4 (рис. 2а и 2б).
,
=18,3 м (из расчета магистрали),
;
.
Рассчитаем модуль
расхода:
, Q3-4 = q4 = 4,4 л/с ,
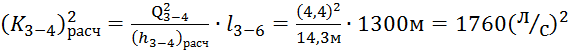
(K3-6)расч ≈ 41,95 л/с .
По табл. 4.6, стр.40 [1]
ближайшее большее значение модуля расхода
(Kср)станд = 53,9 л/с ((Kср)2станд = 2,9052*103
(л/с)2), что соответствует диаметру трубы Dстанд=100 мм. Тогда:
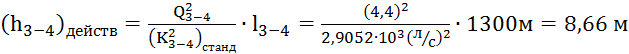
Аналогично для
ответвления 2-5:
,
=34,6 м (из расчета магистрали),
;
.
Тогда модуль расхода:
,
Q2-5 = q5 + 0,55*q’*l2-5 = 9,7 л/с + 0,55*0,017 л/с *1260 м =
21,48 л/с ,
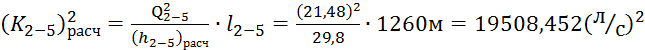
(K2-5)расч ≈ 139,67 л/с .
По табл. 4.6, стр.40 [1]
ближайшее большее значение модуля расхода
(Kср)станд = 160,62 л/с ((Kср)2станд = 25,799*103
(л/с)2), что соответствует диаметру трубы Dстанд=150 мм. Тогда:
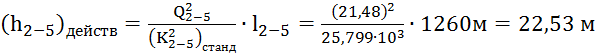
Вычислив значения потерь
напора на каждом ответвлении, изобразим продольные профили для ответвлений (рис
2а,2б).
2. Расчет водопровода с краном, служащим для выпуска воды
из водопровода в атмосферу
2.1. Определение расходов QI max,
QII max, QC max
Принимаем, что расход QII направлен вниз и составим система
уравнений следующий вид:
1) Первый участок: ,
2) Четвертый участок: ,
3) Второй участок: ,
4) Третий участок: ,
5)
QII
max = Q2 max + Q3 max ,
6)
QC
max = QI max + QII max ;
где
По
заданным диаметрам необходимо найти модули расхода для каждого участка,
использовав табл.4.6. стр.40,[1]:
K1 = 160,62 л/с (для D1 =150 мм) → K1,32 = 25,799*103 (л/с)2
;
K2,4 = 98,22 л/с (для D2 =D4
= 125 мм) → K2,42 = 9,6472*103 (л/с)2 ;
K3= 53,90 л/с (для D3 = 100 мм) → K32
= 2,9052*103 (л/с)2.
Из 1)
следует, что ,
.
Приравняем 3) и 4) уравнения, и
тогда:
,
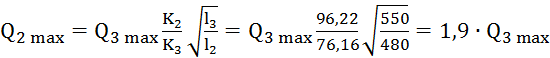
Полученное соотношение подставим в 5)
уравнение:
.
Теперь сложим уравнения 2) и 4), а
вместо QII max подставим 2,9Q3 max:
,
,
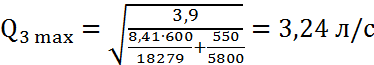
Q2 max = 1,9*Q3 max = 1,9*3,24 л/с = 6,16 л/с.
Подставим полученные значения Q2 max и Q3 max в уравнение 5) и получим:
QII max = Q2 max + Q3
max = (6,16+3,24) л/с = 9,4 л/с .
Зная QI max и QII max можно вычислить QС max по уравнению 6):
QC max = QI
max + QII max = (10,35 + 9,4) л/с = 19,75 л/с .
Отметку можно вычислить из уравнения 2):
.
Необходимо выполнить проверку
полученных результатов. Для этого подставим их в уравнения исходной системы:
1) ;
2) ;
3) ;
4) ;
5) ;
6) .
Итак, получились следующие
значения:
,
QC max = 19,75 л/с,
QI max = 10,35 л/с,
QII max = 9,4 л/с,
Q2 max = 6,16 л/с,
Q3 max = 3,24 л/с.
2.2. Построение кривых зависимостей QI
= f1(QC), QII = f2(QC) и
пьезометрической линии P-P
Графики зависимости
строятся по трем точкам (рис. 4):
– первая точка: кран полностью
открыт, то есть откладываются точки
QC max, QI max, QII max;
– вторая точка: кран закрыт, то
есть QС = 0, QI = QII = Q.
Примерно нарисуем
пьезометрическую линию P-P (рис. 3).
, (*)
Q = Q2
+ Q3 ,
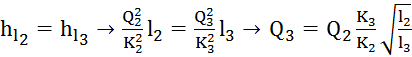
пусть 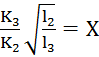
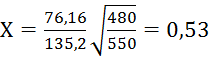
Q = Q2 + X*Q2 = Q2(1+X) = 1,53Q2 → Q2 = 0,65Q.
Подставим Q2 = 0,65Q в уравнение (*):
,
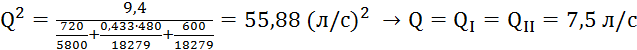
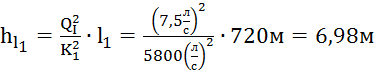
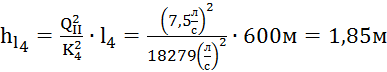
– третья точка: второй
бак (II) не работает (нейтрален), то есть QII = 0, QI = QC.
Примерно нарисуем еще одну
пьезометрическую линию P-P (рис. 3).
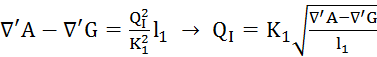
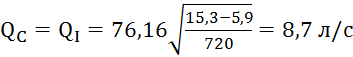
2.3. Построение пьезометрической
линии при QC = 0,75QI max
Теперь
рассмотрим случай, когда Q’C = 0,75QI max=0,75*10,35л/с = 7,76 л/с.
Необходимо нанести Q’С = 7,76 л/с на график зависимости (рис. 4) и в результате
получаем значения Q’I и Q’II.
Q’I = 8,5 л/с;
Q’II = 0,7 л/с.
Для
построения окончательной пьезометрической линии необходимы значения потерь
напоров hl1 и hl4:
,
.
Строим пьезометрическую
линию для случая, когда Q’C = 0,75QI max (рис. 3).
Литература
1. Кожевникова Е.Н.,
Лаксберг А.И., Локтионова Е.А. Механика жидкости и газа (гидравлика). Справочник:
Учеб. пособие. СПб.: Изд-во Политехн. ун-та, 2007. 90с.
2. Кожевникова Е.Н.,
Локтионова Е.А., Орлов В.Т. Механика жидкости и газа (гидравлика). Метод.
рекомендации для выполнения и оформления курсовых и расчетно-графических работ.
СПб.: Изд-во Политехн. ун-та, 2006. 39 с.
Похожие материалы
- Расчет канала на равномерное и неравномерное движение. Расчет гидравлического прыжка
- Определение средний скорости движения, глубину равномерного движения воды в канале. Определение критической глубины и критического уклона в канале
- Гидравлический расчет элементов водохозяйственного комплекса
Информация о работе
Тип:
Расчетно-графические работы