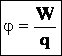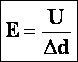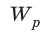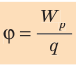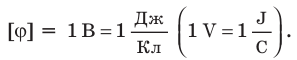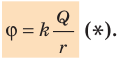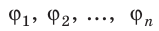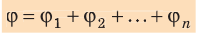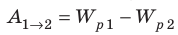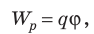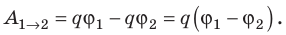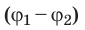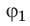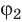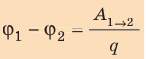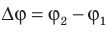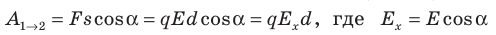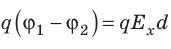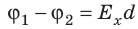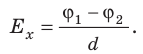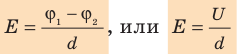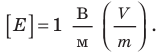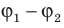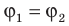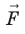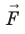|
Потенциал. Разность потенциалов. Напряжение. |
|
|
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: – энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
|
|
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
|
|
– следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
|
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах: |
|
|
Разность потенциалов |
|
|
|
|
|
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
|
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
|
|
Связь между напряженностью и напряжением. |
|
|
Из доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
|
|
Из этого соотношения видно:
|
|
|
Эквипотенциальные поверхности. ЭПП – поверхности равного потенциала. Свойства ЭПП: – работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; – вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
|
|
|
|
|
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
|
|
Потенциальная энергия взаимодействия зарядов. |
|
|
|
|
|
Потенциал поля точечного заряда |
|
|
|
|
|
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
|
|
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |
Условие задачи:
Определить разность потенциалов (по модулю) между точками, отстоящими от заряда 4 нКл на расстоянии 16 и 20 см.
Задача №6.3.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(q=4) нКл, (r_1=16) см, (r_2=20) см, (Delta varphi-?)
Решение задачи:
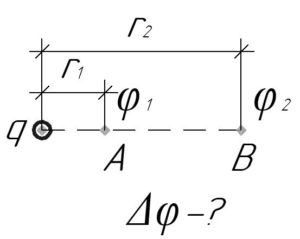
[varphi = frac{{kq}}{r};;;;(1)]
Коэффициент пропорциональности (k) равен 9·109 Н·м2/Кл2.
Тогда потенциал в точках A и B можно найти соответственно по таким формулам:
[left{ begin{gathered}
{varphi _1} = frac{{kq}}{{{r_1}}} hfill \
{varphi _2} = frac{{kq}}{{{r_2}}} hfill \
end{gathered} right.]
Из формулы (1) видно, что чем дальше находится точка, в которой определяют потенциал, тем потенциал меньше (так как ({r_1} < {r_2}), то ({varphi_1} > {varphi_2})). Поэтому модуль разности потенциалов (Delta varphi) следует искать, используя такую формулу:
[Delta varphi = {varphi _1} – {varphi _2}]
Учитывая формулы из вышеприведённой системы, имеем:
[Delta varphi = frac{{kq}}{{{r_1}}} – frac{{kq}}{{{r_2}}}]
Напоследок приведём формулу под общий знаменатель:
[Delta varphi = frac{{kqleft( {{r_2} – {r_1}} right)}}{{{r_1}{r_2}}}]
Произведём вычисления:
[Delta varphi = frac{{9 cdot {{10}^9} cdot 4 cdot {{10}^{ – 9}} cdot left( {0,2 – 0,16} right)}}{{0,16 cdot 0,2}} = 45;В]
Ответ: 45 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.10 Сколько электронов следует передать металлическому шарику радиусом 7,2 см
6.3.12 Расстояние между точечными зарядами 10 и -1 нКл равно 1,1 м. Найти
6.3.13 В двух вершинах равностороннего треугольника со стороной 0,5 м находятся
Понятие электрического потенциала является одним из важных основ теории электростатики и электродинамики. Понимание его сущности является необходимым условием для дальнейшего изучения этих разделов физики.
Содержание
- 1 Что такое электрический потенциал
- 2 Свойства потенциала
- 3 Разность потенциалов
- 4 Эквипотенциальные поверхности
Что такое электрический потенциал
Пусть в поле, создаваемым неподвижным зарядом Q, помещён единичный заряд q, на который действует сила Кулона F=k*Qq/r.
Здесь и далее k=((1/4)*π* ε0* ε), где ε0 — электрическая постоянная (8,85*10-12 Ф/м), а ε – диэлектрическая постоянная среды.
Внесённый заряд под действием этой силы может перемещаться, а сила при этом совершит определенную работу. Это означает, что система из двух зарядов обладает потенциальной энергией, зависящей от величины обоих зарядов и расстояния между ними, причём величина этой потенциальной энергии не зависит от величины заряда q. Здесь и вводится определение электрического потенциала – он равен отношению потенциальной энергии поля к величине заряда:
φ=W/q,
где W – потенциальная энергия поля, создаваемого системой зарядов, а потенциал является энергетической характеристикой поля. Чтобы переместить заряд q в электрическом поле на какое-то расстояние, надо затратить определённую работу на преодоление кулоновских сил. Потенциал точки равен работе, которую надо затратить для перемещения единичного заряда из этой точки в бесконечность. При этом надо отметить, что:
- эта работа будет равна убыли потенциальной энергии заряда (A=W2-W1);
- работа не зависит от траектории перемещения заряда.
В системе СИ единицей измерения потенциала является один Вольт (в русскоязычной литературе обозначается буквой В, в зарубежной – V). 1 В=1Дж/1 Кл, то есть, можно говорить о потенциале точки в 1 вольт, если для перемещения заряда в 1 Кл в бесконечность потребуется совершить работу в 1 Джоуль. Название выбрано в честь итальянского физика Алессандро Вольта, внесшего значительный вклад в развитие электротехники.
Чтобы наглядно представить, что такое потенциал, его можно сравнить с температурой двух тел или температурой, замеренной в разных точках пространства. Температура служит мерой нагрева объектов, а потенциал – мерой электрической заряженности. Говорят, что одно тело нагрето более другого, также можно сказать, что одно тело заряжено более, а другое – менее. Эти тела обладают разным потенциалом.
Значение потенциала зависит от выбора системы координат, поэтому требуется какой-то уровень, который надо принять за ноль. При измерении температуры за базовую границу можно принять, например, температуру тающего льда. Для потенциала за нулевой уровень обычно принимают потенциал бесконечно удаленной точки, но для решения некоторых задач за нулем можно считать, например, потенциал земли или потенциал одной из обкладок конденсатора.
Свойства потенциала
Среди важных свойств потенциала надо отметить следующие:
- если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ1+φ2+φ3+φ4+φ5+…+φn;
- если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q1/r1+q2/r2+q3/r3+…+qn/rn), где r – расстояние от соответствующего заряда то рассматриваемой точки.
Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r2, где:
- p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
- r – расстояние до диполя;
- ά – угол между плечом диполя и радиус-вектором r.
Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r2.
Разность потенциалов
Если две точки обладают определённым потенциалом, и если они не равны, то говорят о том, что между двумя точками существует разность потенциалов. Разность потенциалов возникает между точками:
- потенциал которых определяется зарядами разных знаков;
- точкой с потенциалом от заряда любого знака и точкой с нулевым потенциалом;
- точками, имеющими потенциал равного знака, но отличающимися по модулю.
То есть, разность потенциалов не зависит от выбора системы координат. Можно провести аналогию с бассейнами с водой, расположенными на разной высоте относительно нулевой отметки (например, уровня моря).
Вода каждого бассейна имеет определенную потенциальную энергию, но если соединить два любых бассейна трубкой, то в каждой из них возникнет поток воды, расход которой определяется не только размерами трубки, но и разностью потенциальных энергий в гравитационном поле Земли (то есть, разностью высот). Абсолютное значение потенциальных энергий значения в данном случае не имеет.
Точно так же, если соединить проводником две точки с разным потенциалом, по нему потечёт электрический ток, определяемый не только сопротивлением проводника, но и разностью потенциалов (но не их абсолютным значением). Продолжая аналогию с водой, можно сказать, что вода в верхнем бассейне скоро закончится, и если не найдется той силы, которая переместит воду обратно наверх (например, насоса), то и поток очень быстро прекратится.
Так и в электрической цепи – чтобы поддерживать разность потенциалов на определенном уровне, потребуется сила, переносящая заряды (точнее, носители зарядов) к точке с наибольшим потенциалом. Такая сила называется электродвижущей силой и сокращенно обозначается ЭДС. ЭДС может носить различную природу – электрохимическую, электромагнитную и т.п.
На практике имеет значение в основном разность потенциалов между начальной и конечной точками траектории движения носителей зарядов. В этом случае эту разность называют напряжением, и оно в СИ также измеряется в вольтах. О напряжении в 1 Вольт можно говорить, если поле совершает работу в 1 Джоуль при перемещении заряда в 1 Кулон из одной точки в другую, то есть 1В=1Дж/1Кл, и Дж/Кл также может являться единицей измерения разности потенциалов.
Эквипотенциальные поверхности
Если потенциал нескольких точек одинаков, и эти точки образуют поверхность, то такая поверхность называется эквипотенциальной. Таким свойством обладает, например, сфера, описанная вокруг электрического заряда, ведь электрическое поле убывает с расстоянием одинаково во все стороны.
Все точки этой поверхности имеют одинаковую потенциальную энергию, поэтому при перемещении заряда по такой сфере работа затрачиваться не будет. Эквипотенциальные поверхности систем из нескольких зарядов имеют более сложную форму, но у них есть одно интересное свойство – они никогда не пересекаются. Силовые линии электрического поля всегда перпендикулярны поверхностям с одинаковым потенциалом в каждой их точке. Если эквипотенциальную поверхность рассечь плоскостью, получится линия равных потенциалов. Она имеет те же свойства, что и эквипотенциальная поверхность. На практике равный потенциал имеют, например, точки на поверхности проводника, помещенного в электростатическое поле.
Разобравшись с понятием потенциала и разности потенциалов, можно приступать к дальнейшему изучению электрических явлений. Но не ранее, потому что без понимания базовых принципов и понятий углубить знания не получится.
Понятие потенциала в физике
Из курса физики известно, что работа некоторых сил, например силы тяжести, не зависит от траектории движения тела, а зависит лишь от величины перемещения.
Такие силы и силовые поля, в которых они действуют, называют потенциальными или консервативными.
Сила, действующая на заряд, помещенный в однородное электростатическое поле, также относится к потенциальным и определяется формулой:
Формула 1
F→=q·E→,
где q — электрический заряд, Кл;
E→ — напряженность электрического поля, В.
В механике работа определяется как произведение силы на расстояние между точками – началом и концом движения и косинусом угла α между векторами силы и скорости. Аналогично выведем формулу для определения работы электростатического поля при перемещении заряда из одного положения в другое.
Формула 2
A=F→·Δr·cosα=q·E→·Δr·cosα=q·E→·(r2-r1)·cosα=(q·E→·r2-q·E→·r1)·cosα.
Величину q·E→·r1 называют потенциальной энергией поля.
Определение 1
Потенциальная энергия является мерой работы, которую совершат силы при перемещении объекта в потенциальном поле.
Работа зависит от разницы потенциальных энергий в начальной и конечной точке. Тогда работу можно представить как:
Формула 3
A=-(W2-W1).
Примечание
Знак «минус» в выражении для работы означает, что если уменьшить потенциальную энергию с помощью силового воздействия, работа поля будет положительной. Если потенциальную энергию увеличить — работа будет отрицательной.
Поместим в некоторую точку неподвижный заряд q, чтобы создать электростатическое поле. Когда заряд q1 попадает в это поле, заряды q и q1 не взаимодействуют друг с другом, на заряд q1 действует само поле. Чтобы ввести новую характеристику поля, не зависящую от помещенных в него зарядов, необходимо поделить потенциальную энергию на заряд q. Полученную величину называют потенциалом.
Определение 2
Потенциал (от слова potentia — сила, возможность) — скалярная величина в физике, равная отношению потенциальной энергии к величине заряда.
В электрике принято следующее обозначение потенциала: φ.
Формула 4
φ=Wq.
Нулевым принято считать потенциал бесконечно удаленной точки (r→∞).
Ток в цепи всегда течет от большего потенциала к меньшему.
Формула для потенциала одного заряда приведена выше. На практике любое заряженное тело можно разделить на несколько элементов, каждый из которых будет иметь свой потенциал. Тогда потенциал системы, состоящей из двух и более зарядов:
Формула 5
φ=φ1+φ2+φ3+…
Понятие разности потенциалов, формула нахождения
Подставим выражение для потенциала в точке в формулу для работы:
Формула 6
A=-(W2-W1)=-(qφ2-qφ1)=-q(φ2-φ1).
Физическую величину, смысл которой заключается в разнице между потенциалами в начальной и конечной точках траектории, называют разностью потенциалов или напряжением (U).
Формула 7
U=φ1-φ2.
В самом простом случае, когда на рассматриваемую цепь или участок цепи действует только электростатическое поле, напряжение можно считать равным разности потенциалов. В иных случаях напряжение в проводнике определяют как сумму разности потенциалов и работу внешних сил (ЭДС), возникающих, например, в результате закона электромагнитной индукции. Тогда напряжение:
Формула 8
U=(φ1-φ2)+ЭДС.
Чтобы понять связь между напряжением и напряженностью, рассмотрим простой конденсатор в виде двух пластин с постоянной емкостью.
Между положительно и отрицательно заряженными пластинами образуется электростатическое поле напряженностью overrightarrow Е. Линии напряженности между обкладками параллельны, а модуль напряженности одинаков.
Если положительный заряд поместить рядом с положительной пластиной, он начнет двигаться в сторону отрицательной пластины, значит, поле совершит некоторую работу. Так как векторы скорости перемещения заряда и напряженности лежат на параллельных прямых, работа:A=F→·S.
Длина перемещения равна расстоянию между обкладками, а сила воздействия поля: F→=q·E→.
Тогда:A=q·E→·SиA=qU.
Приравняем выражения для работы, получим:q·E→·S=q·U.
Напряжение и напряженность связаны формулой:
Формула 9
U=E→·S
Разместим протяженный проводник в электростатическом поле. Будем считать, что линии напряженности расположены горизонтально.
Пусть проводник будет двигаться перпендикулярно линиям напряженности. В этом случае работа по перемещению заряда не совершается, так как косинус угла между векторами силы и скорости движения равен нулю. То есть все точки на поверхности проводника имеют один и тот же потенциал.
Определение 3
Эквипотенциальные поверхности — поверхности, у которых потенциалы в каждой точке одинаковы. Эквипотенциальные поверхности представляют собой плоскость для однородного поля и сферы для поля одиночного заряда.
Единица разности потенциалов
Коробка уравнивания потенциалов
В честь ученого (Алессандро Вольта), впервые доказавшего существование разницы потенциалов, единица измерения названа Вольт. В международной системе единиц напряжение обозначается символами:
- В – в русскоязычной литературе;
- V – в англоязычной литературе.
Кроме этого, существуют кратные обозначения:
- мВ – милливольт (0.001 В);
- кВ – киловольт (1000 В);
- МВ – мегавольт (1000 кВ).
Измерение контактной разности потенциалов
Основная проблема заключатся в том, что контактная разность потенциалов не может быть измерена напрямую, вольтметром, хотя значение ЭДС в цепи с соединением двух различных проводников может составлять от долей до единиц вольт.
Контактная потенциальная разница существенно влияет на вольтамперную характеристику измеряемой цепи. Наглядным примером может служить полупроводниковый диод, где подобное явление возникает на границе соприкосновения полупроводников с разным типом проводимости.
Разность потенциалов на практике
С общепринятой точки зрения, разность потенциалов – это напряжение между двумя выбранными точками цепи. В то же время напряжение между каждой из этих точек и третьей точкой будет отличаться в полном соответствии с определением.
Наглядный пример:
- Точка А в электрической схеме – напряжение 10 В относительно провода заземления;
- В точке В напряжение составляет 25 В относительно того же провода.
Необходимо найти напряжение между точками А и В.
В данном случае искомая разность составляет:
UAB= ϕА-ϕВ=10-25=15 В.
Рассматриваемые понятия важны для минимального объема знаний в области электротехники и электроники, поскольку на них основываются все расчеты и практические решения. Без этих азов невозможно более углубленное изучение электрических дисциплин.
Потенциал. Эквипотенциальные поверхности.
В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W1 — W2 на заряд q, получим
Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.
Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:
Единица потенциала — вольт:
Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.
С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде
Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ1 — φ2 )> 0, то потенциал φ1 больше чем потенциал φ2 . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.
Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ∞ ). Поскольку φ∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,
Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле
По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.
Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.
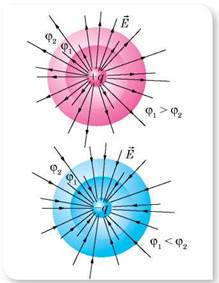
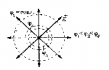
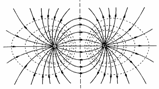
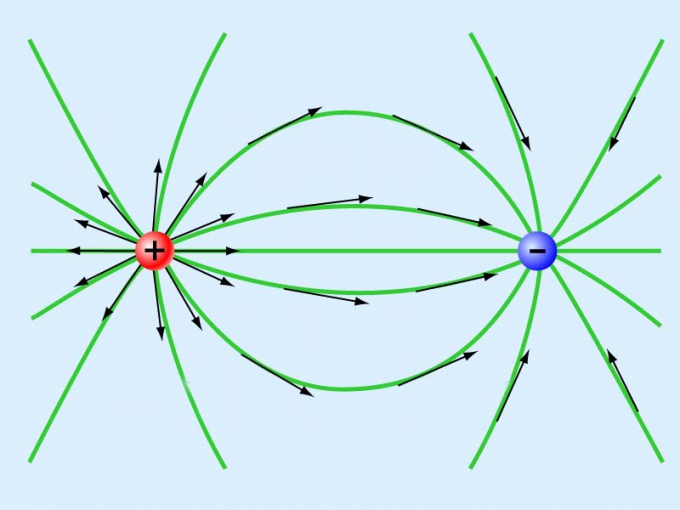
Эквипотенциальные поверхности электрических полей, созданных точечными зарядами разных знаков
Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.
В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ1 + φ2 + φ3 . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.
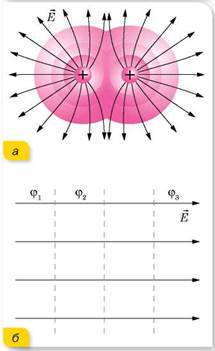
Эквипотенциальные поверхности: а — поля двух одинаковых зарядов б — однородного поля
Что называют потенциалом электростатического поля
Потенциал
электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии
электрического заряда, помещенного в данную точку поля, к значению q этого заряда:
Единица потенциала в Си — вольт:
Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле:
Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.
Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов
полей, созданных каждым зарядом:
Как определяют разность потенциалов
Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком:
. Поскольку
то
Выражение
называют разностью потенциалов, где
— значение потенциала в начальной точке траектории движения заряда,
— значение потенциала в ее конечной точке.
Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:
Единица разности потенциалов в Си — вольт:
= 1 В (V).
Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов
− также называют напряжением (U). Важно не путать изменение потенциала
и разность потенциалов (напряжение)
.
Как связаны напряженность однородного электростатического поля и разность потенциалов
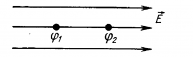
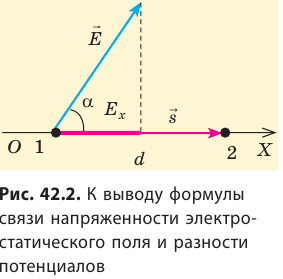
Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2: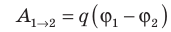
— проекция вектора
на ось Ох, проведенную через точки 1 и 2.
Приравняв оба выражения для работы, получим:
, откуда:
, или
Если заряд перемещается в направлении напряженности электрического поля (
) , последняя формула примет вид:
Из последней формулы следует единица напряженности в Си — вольт на метр:
Какие поверхности называют эквипотенциальными
Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.
Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.
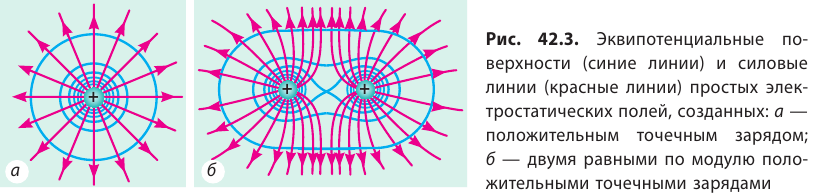
Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).
Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q (
), а на эквипотенциальной поверхности
Работу электростатического поля также можно представить через силу
действующую на заряд со стороны поля: A F= scosα , где α — угол между векторами
и
Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы
а следовательно, и вектор напряженности
поля в любой точке перпендикулярны вектору перемещения
Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).
Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.
Для чего нужен потенциометр электрику
Что такое коэффициент мощности
Данный прибор широко применяется в практике для модуляции напряжения. Дело в том, что у многих источников (особенно заточенных под автономное функционирование: аккумуляторные элементы, солнечные батареи и т.д.) константное напряжение, не поддающееся управлению без специальных устройств, что может вызвать проблемы. Чтобы уменьшить исходное напряжение такого элемента, используют устройства-делители, снабженные потенциометрами.
Потенциометр-реостат
Как работает потенциометр? Он представляет собой резистор, имеющий пару выводов и подвижный ползунок с еще одним выводом. Подключаться такое переменное устройство сопротивления может двумя способами:
- По типу реостата, с использованием ползункового вывода и одного из пары других. Сопротивление замеряется движением ползунка по корпусу резистора. Регуляция цепного электротока в таком случае возможна при последовательном подключении такого реостата и источника напряжения.
- Потенциометрическим методом, задействующим каждый вывод из имеющейся у прибора тройки. Два главных вывода включаются параллельно источнику, снятие сниженного напряжения реализуется с ползункового механизма и одного вывода. В этом случае через резисторное устройство течет электроток, создающий спад напряжения между ползунком и боковыми выводами. В такой модели на источник питания ложится большая нагрузка, так как для точности регуляции и отсутствия сбоев необходимо, чтобы резисторное сопротивление в несколько раз уступало нагрузочному.
Потенциометрическое подключение прибора
Таким образом, понятие потенциала используется в разных областях физики: как в механике, так и в изучении электричества. В последнем случае оно выступает в качестве характеристики поля. Непосредственно рассматриваемая величина измерению не поддается, зато можно измерить разность, тогда один заряд берется за точку отсчета.
Понятие потенциала, разности потенциалов
С понятием напряжения электрического тока тесно связано понятие «потенциал» , или «разность потенциалов». Хорошо, обратимся снова к нашей водопроводной аналогии.
Наш резервуар находится на возвышенности что позволяет воде беспрепятственно стекать по трубе вниз. Так как бак с водой на высоте, то и потенциал этой точки будет более высоким или более положительным чем тот что находится на уровне земли. Видите что получается?
У нас появилось две точки имеющие разные потенциалы, точнее разную величину потенциала.
Получается, для того чтобы электрический ток мог бежать по проводу, потенциалы не должны быть равны. Ток бежит от точки с большим потенциалом к точки с меньшим потенциалом.
Помните такое выражение, что ток бежит от плюса к минусу. Так вот это все тоже самое. Плюс это более положительный потенциал а минус более отрицательный.
Кстати а хотите вопрос на засыпку? Что произойдет с током, если величины потенциалов будет периодически меняться местами?
Тогда мы будем наблюдать то как электрический ток меняет свое направление на противоположное каждый раз как потенциалы поменяются. Это получится уже переменный ток. Но его мы пока рассматривать не будем, дабы в голове сформировалось ясное понимание процессов.
Общие сведения
Электрические явления начали интересовать философов ещё со времёнДревней Греции. Существует легенда, согласно которой люди, жившие более двух тысяч лет назад, находили на острове Магнезия камни, притягивающие к себе металлические предметы. Их назвали магнитами. В то же время философ Фалес обнаружил любопытное свойство янтаря. Если его потереть об шерсть, то к нему прилипали лёгкие предметы. Благодаря этим двум явлениям природы и было открыто электричество, ранее называемое янтарностью.
Но на протяжении многих столетий учёные не могли объяснить силы, заставляющие взаимодействовать тела между собой. Существенный вклад в развитие учения внёс Отто Герик, создавший первую электромашину.
Затем Питера ван Мушенбрук смог изготовить источник электричества, названный лейденской банкой. С этого момента начался бум изучения явлений. В своё время их исследовали такие физики, как Гильберт, Кулон, Ампер, Эдисон, Франклин, Вольт, Фарадей.
Благодаря их стараниями стало известно, что электричество и магнетизм — это явления, не существующие друг без друга. Описывать их начали, ведя характеристику, названную электромагнитным полем. Возникновение же последней связано с существованием заряда и возможностью его переноса элементарными частицами. Их условно разделили на два вида:
- отрицательные;
- положительные.
В природе если тело находится в равновесии, то есть на него не оказывается стороннее воздействие, движение частиц происходит хаотично и обусловлено тепловыми процессами.
Но если носители заставить двигаться в одном направлении, возникнет ток. Характеризуется он силой и работой которую необходимо затратить для переноса заряда из одной точки поля в другую.
Затраченную при движении энергию называютэлектродвижущей силой, описывающейся напряжением. Величиной зависящей от изменения потенциала поля в той или иной его точке. В 1827 году Георг Ом опытным путём доказал пропорциональную зависимость силы тока и напряжения. Этот фундаментальный закон был назван его именем, записывается так: I = U / R. Правило установило, что сила электротока зависит от работы, совершаемой полем для переноса заряда из точки A в B.
Предыдущая
РазноеДелаем токопроводящий клей из подручных материалов
Следующая
РазноеЧто такое фаза в электричестве?
Как найти разность потенциалов
Электростатика – один из наиболее сложных разделов физики. При изучении силовых полей важно знать о такой величине, как потенциал, которая характеризует поле в конкретно взятой точке, и уметь находить разность потенциалов, т.е. электрическое напряжение.
Вам понадобится
- лист бумаги, ручка
Инструкция
Перед тем, как разобраться, что же такое электрическое напряжение и как его вычислять, необходимо ознакомиться еще с рядом понятий.
Согласно определению, электрическое напряжение между двумя точками появляется тогда, когда в одной из них есть избыток электронов по отношению к другой. По своему заряду частицы могут быть отрицательными «?» и положительными «+». Разноименные частицы будут притягиваться друг к другу. Когда в одной точке не хватает электронов, вокруг нее образует положительное поле. Чем больше эта нехватка, тем сильнее поле. Соответственно, когда в другой точке электроны в избытки, частица стремится их отдать, образуя вокруг себя отрицательное поле. Таким образом получаются два потенциала, которые стремятся обменяться электронами. Пока этого не произошло, между ними существует напряжение, т.е. разность потенциалов.
Исходя из вышесказанного, получается, что разность потенциалов равняется работе электрического поля, осуществленной для того, чтобы переместить единичный положительный заряд из точки 1 в точку 2. Разность потенциалов измеряется в вольтах (В).
Чтобы рассчитать разность потенциалов, воспользуйтесь формулой U=Aq , где U – это искомое электрическое напряжение, A – работа электростатического поля, а q – электрический заряд.
Для нахождения работы необходима своя формула. Согласно ей A=-(W2-W1)=-(ф2-ф1)q=q?ф. q – величина постоянная, а ф – это потенциал, который вы можете вычислить по формуле ф=kqr. k – это коэффициент жесткости, равный 9*10^9 H*м^2/Кл^2. r – это расстояние от источника поля до данной точки.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.