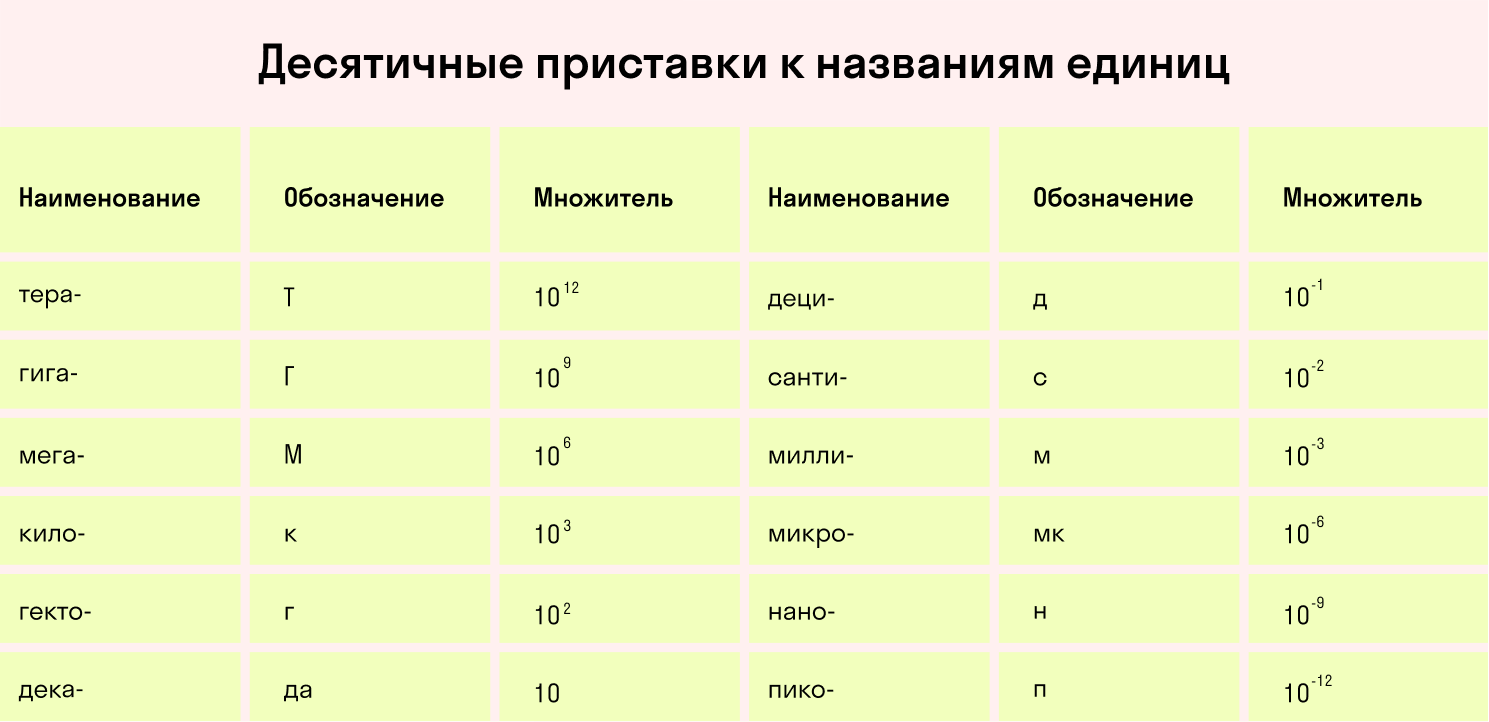
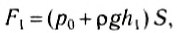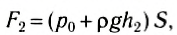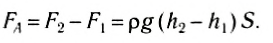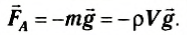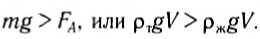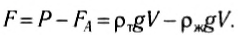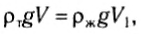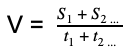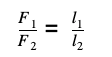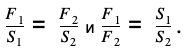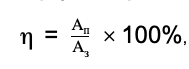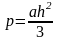Закон Архимеда:
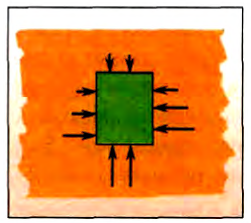
На поверхность тела, погруженного в жидкость, действуют силы давления. Так как давление увеличивается с глубиной погружения, то силы давления, действующие на нижнюю часть тела, всегда больше, что отражено на рисунке 169 длиной стрелок. Поэтому можно ожидать, что равнодействующая сил давления будет направлена вверх. Опыт подтверждает это предположение.
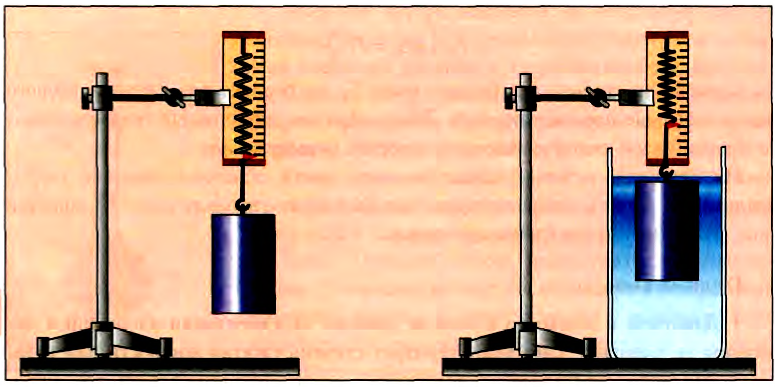
Если подвешенное к крючку динамометра тело опустить в воду, то показания динамометра уменьшатся (рис. 170).
Равнодействующая сил давления на тело, погруженное в жидкость, называется выталкивающей силой или силой Архимеда.
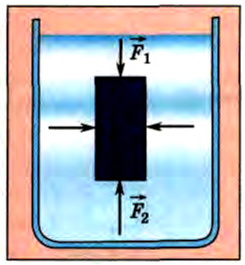
Рассмотрим тело, имеющее форму прямоугольного параллелепипеда, погруженное в жидкость так, что его основания расположены горизонтально (рис. 171). Силы давления, действующие на боковые грани тела, уравновешены. Они сжимают тело. Силы же, действующие на основания параллелепипеда, не одинаковы. Модуль силы давления, действующей на верхнее основание:
где p0 — внешнее давление, h1 — высота столба жидкости над верхним основанием, р — плотность жидкости, S — площадь основания.
Рис. 171
Модуль силы давления жидкости, действующей на нижнее основание:
где h2 — глубина, на которой находится нижнее основание. Поскольку h2 > h1 , то F2> F1, и, следовательно, равнодействующая будет направлена вверх и по модулю равна:
Так как ( h2 – h1 ) — высота параллелепипеда, то
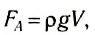
где V=S( h2 – h1 ) — объем тела.
В векторном виде выражение для силы Архимеда примет вид:
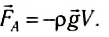
Мы получили выражение выталкивающей силы для прямоугольного параллелепипеда, погруженного в жидкость. Однако эта формула справедлива для тела любой формы. Действительно, выталкивающая сила, действующая на тело (рис. 172), есть равнодействующая сил давления жидкости на его поверхность. Представим себе, что тело удалено, и его место занято той же жидкостью (рис. 173). Давление на поверхность такого мысленно выделенного объема будет таким же, каким было давление на поверхность самого тела. Значит, и равнодействующая сила давления па тело (выталкивающая сила) равна равнодействующей силе давления на выделенный объем жидкости. Но этот объем жидкости находится в равновесии. Силы, действующие на него, — это сила тяжести 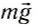
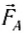
Таким образом,
Итак, на тело, погруженное в жидкость, действует выталкивающая сила, равная по модулю весу жидкости в объеме, занимаемом телом (вытесненный объем), и приложенная в центре масс этого объема (центре давления).
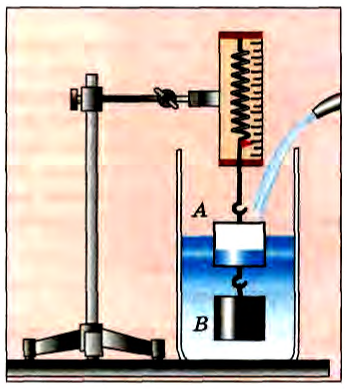
Это и есть закон Архимеда, экспериментально установленный Архимедом более 2200 лет тому назад. Примерная схема опыта Архимеда изображена на рисунках 174, 175, 176. Пустой стакан А («ведерко Архимеда») и сплошной цилиндр В, имеющий объем, в точности равный вместимости стакана, подвесим к динамометру (см. рис. 174). Затем, подставив сосуд с водой, погрузим цилиндр в воду. Равновесие нарушится, и растяжение динамометра уменьшится (см. рис. 175). Разность показаний динамометра как раз равна выталкивающей силе, действующей на цилиндр. Если наполнить стакан водой, то пружина динамометра снова растянется до первоначальной длины (см. рис. 176). Таким образом, доказано, что выталкивающая сила, действующая на погруженное тело, равна силе тяжести жидкости в объеме тела.
По третьему закону Ньютона если жидкость действует на погруженное тело, то и тело действует на жидкость. Эта сила направлена вертикально вниз и равна по модулю силе Архимеда. Это утверждение доказывается следующим опытом. Неполный стакан с водой уравновешивают на весах. Затем в стакан погружают тело, подвешенное на штативе. При этом чашка со стаканом опускается, и для восстановления равновесия приходится добавить на другую чашку гири, вес которых равен весу воды, вытесненной телом.
Сила Архимеда действует также на тела в воздухе. Однако плотность воздyxa мала, и действием выталкивающей силы в большинстве случаев можно пренебречь.
Выталкивающая сила действует на тела в жидкостях и газах, потому что они сжаты силой притяжения к Земле. В состоянии невесомости сила Архимеда не действует.
Рис. 176
Главные выводы:
- Из-за того что давление увеличивается с глубиной погружения, на тело, погруженное в жидкость (газ), действует выталкивающая сила.
- На тело, погруженное в жидкость или газ, действует выталкивающая :ила, равная по модулю весу жидкости в объеме, занимаемом телом. Эта :ила приложена в центре давления.
- Тело, погруженное в жидкость, действует на жидкость с силой, равной по модулю выталкивающей силе и противоположно направленной.
- В невесомости сила Архимеда отсутствует.
Плавание тел и воздухоплавание:
Закон Архимеда дает возможность объяснить все вопросы, связанные с плаванием тел. Погрузим полностью тело в жидкость и предоставим самому себе. Если сила тяжести больше силы Архимеда, то оно будет тонуть, пока не упадет на дно сосуда (рис. 177). Если сила тяжести меньше силы Архимеда, то оно будет всплывать, поднимаясь к поверхности жидкости (см. рис. 177). В том случае, когда сила тяжести в точности равна выталкивающей силе, оно будет находиться в равновесии и плавать внутри жидкости.
Рис. 177
Рассмотрим тела, которые тонут в жидкости. Если тело однородное, т. е. во всех точках имеет одну и ту же плотность, то нетрудно показать, что в этом случае плотность тела больше плотности жидкости. Действительно:
Отсюда следует, что рт > рж.
Если тело неоднородное, т. е. плотность тела неодинакова в различных точках, например тело с пустотами внутри, то под плотностью тела необходимо понимать среднюю плотность: (рт)>рж.
Для тонущих тел неправильной формы, объем которых трудно найти при помощи измерения размеров тела, закон Архимеда позволяет экспериментально определить плотность тела. Для этого тело необходимо дважды взвесить: один раз в воздухе, а другой раз — погружая его в жидкость, плотность которой известна. Первое взвешивание дает значение силы тяжести: P = pTgV. Результат второго взвешивания F дает разность между силой тяжести mg и выталкивающей силой FA:
Заменив в этой формуле объем тела V на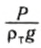
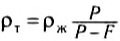
В случае неоднородного тела определяемая по этой формуле величина рT даст среднюю плотность.
Если тело, погруженное в жидкость, находится в равновесии, то плотность тела (или его средняя плотность) равна плотности жидкости. Можно проделать следующий опыт. Куриное яйцо тонет в пресной воде, но плавает в соленой. При растворении соли плотность раствора увеличивается. При этом концентрация раствора постепенно уменьшается кверху, т. е. раствор является неоднородной жидкостью. Его плотность вверху меньше, чем внизу. Поэтому в таком растворе куриное яйцо вначале будет тонуть, а затем остановится, не достигнув дна, и будет плавать на такой глубине, где его плотность равна средней плотности раствора на данной глубине.
Другим примером плавания тел под водой является плавание подводных лодок (рис. 178). Они должны иметь возможность всплывать и погружаться в воду, а также плыть под поверхностью воды. Так как объем лодки остается во всех случаях неизменным, то для выполнения этих маневров на лодке должна быть предусмотрена возможность изменения ее массы. В лодке сделан ряд балластных отсеков, которые при помощи специальных устройств можно заполнить забортной водой (при этом масса лодки увеличивается, и она погружается) и освободить от воды (при этом масса лодки уменьшается, и она всплывает). Конечно, трудно подобрать такую массу воды, чтобы выталкивающая сила в точности была равна силе тяжести. Поэтому для сохранения заданной глубины нужно все время изменять количество балласта либо все время двигаться, маневрируя рулями глубины.
Рис. 178
Если сила тяжести тела, погруженного в жидкость, меньше силы Архимеда, то оно всплывает. Поднявшись на поверхность, оно плавает так, что часть его выступает из жидкости. В этом случае плотность тела меньше плотности жидкости. В самом деле, на тело, плавающее таким образом, действуют сила тяжести mg = pTgV и выталкивающая сила FA= pTgV1, где V1 — объем погруженной в жидкость части тела:
и так как V1 < V, то из (2) следует, что рT < рж. Из (2) также следует, что объем тела, погруженного в жидкость, зависит от отношения плотностей жидкости и тела. Так, для льдины, плавающей на воде, под водой находится примерно 92 % ее объема (плотность льда 920 
На основании закона плавания тел сконструирован прибор — ареометр, с помощью которого измеряют плотности жидкостей. Ареометр представляет собой стеклянный сосуд с грузиком и длинным отростком, на котором нанесена шкала (рис. 179, а). При плавании в жидкости ареометр погружается на большую или меньшую глубину в зависимости от плотности жидкости (рис. 179, б). Чем больше плотность жидкости, тем меньше он погружается. На шкале непосредственно отмечаются значения плотности жидкости. Ареометр применяется обычно для точных измерений в жидкостях с близкими плотностями.
Рис. 179
Сплошные тела плавают в жидкости так, чтобы равновесие было устойчивым. Для доказательства этого утверждения рассмотрим плавание бревна в воде. Если бревно однородное, то оно плавает, так как показано на рисунке 180. Очевидно, что сила тяжести приложена в центре масс бревна С, а выталкивающая сила в центре масс вытесненной жидкости D (центре давления). Причем линии действия этих сил совпадают. В отклоненном положении (рис. 181) центр масс вытесненной жидкости смещается относительно бревна, и возникает момент сил, который возвращает бревно в исходное состояние.
Тело, имеющее полости, куда жидкость не проникает при плавании, вытеснит такой же объем, что и сплошное тело. Поэтому и сила Архимеда для такого тела такая же, как и для сплошного. Но масса тела с полостями меньше массы сплошного тела. Поэтому при достаточно больших полостях такое тело может плавать, хотя плотность вещества тела больше плотности жидкости (например, корабли, лодки и т. п.). Объем вытесненной кораблем воды значительно больше объема стали, из которой сделан корпус судна, поэтому он может плавать, несмотря на то что плотность стали в 8 раз больше плотности воды.
Если пространство внутри судна заполнить водой, например, в случае течи, то вытесненный объем воды уменьшится и судно начнет тонуть.
Полет воздушного шара или дирижабля (рис. 182) в воздухе напоминает плавание подводной лодки под водой. Если масса всего летательного аппарата, в том числе и масса газа, заполняющего оболочку, меньше массы воздуха в объеме, вытесняемом аппаратом, то он поднимается вверх. Если эти массы равны- шар неподвижно висит в воздухе. Если масса аппарата с газом больше массы вытесняемого воздуха, то аппарат опускается.
Рис. 182
Главные выводы:
- Тело, погруженное в жидкость, тонет, плавает внутри жидкости или всплывает, если плотность тела (средняя плотность) больше, равна или меньше плотности жидкости соответственно.
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике
- Гармонические колебания в физике
- Условия равновесия тел в физике
- Равновесие тел в физике
- Давление в жидкостях и газах в физике
- Закон Паскаля
Давление, сила давления — Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
- Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности.
- Сила давления направлена перпендикулярно поверхности.
- Формула давления: p = F / S, где F — модуль силы, S — площадь поверхности.
- Единица измерения давления в СИ: паскаль (Па).1 Па = 1 Н/м 2 Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.
Формулу для расчета силы давления вывести несложно: F = p × S В задачах по физике за 7 класс сила давления, как правило, равна весу тела.
Как найти давление в физике?
Давление. Единицы давления. — Человек на лыжах, и без них. По рыхлому снегу человек идёт с большим трудом, глубоко проваливаясь при каждом шаге. Но, надев лыжи, он может идти, почти не проваливаясь в него. Почему? На лыжах или без лыж человек действует на снег с одной и той же силой, равной своему весу.
- Однако действие этой силы в обоих случаях различно, потому что различна площадь поверхности, на которую давит человек, с лыжами и без лыж.
- Площадь поверхности лыж почти в 20 раз больше площади подошвы.
- Поэтому, стоя на лыжах, человек действует на каждый квадратный сантиметр площади поверхности снега с силой, в 20 раз меньшей, чем стоя на снегу без лыж.
Ученик, прикалывая кнопками газету к доске, действует на каждую кнопку с одинаковой силой. Однако кнопка, имеющая более острый конец, легче входит в дерево. Значит, результат действия силы зависит не только от её модуля, направления и точки приложения, но и от площади той поверхности, к которой она приложена (перпендикулярно которой она действует). Опыт.Результат действия данной силы зависит от того, какая сила действует на единицу площади поверхности. По углам небольшой доски надо вбить гвозди. Сначала гвозди, вбитые в доску, установим на песке остриями вверх и положим на доску гирю. В этом случае шляпки гвоздей лишь незначительно вдавливаются в песок. Опыт. Вторая иллюстрация. От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия этой силы. В рассмотренных примерах силы действовали перпендикулярно поверхности тела. Вес человека был перпендикулярен поверхности снега; сила, действовавшая на кнопку, перпендикулярна поверхности доски.
- Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением,
- Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности: давление = сила / площадь,
- Обозначим величины, входящие в это выражение: давление — p, сила, действующая на поверхность, — F и площадь поверхности — S,
Тогда получим формулу: p = F/S Понятно, что бóльшая по значению сила, действующую на ту же площадь, будет производить большее давление. За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 м 2 перпендикулярно этой поверхности,
- Единица давления — ньютон на квадратный метр ( 1 Н / м 2 ).
- В честь французского ученого Блеза Паскаля она называется паскалем ( Па ).
- Таким образом, 1 Па = 1 Н / м 2,
- Используется также другие единицы давления: гектопаскаль ( гПа ) и килопаскаль ( кПа ).1 кПа = 1000 Па; 1 гПа = 100 Па; 1 Па = 0,001 кПа; 1 Па = 0,01 гПа.
Пример, Рассчитать давление, производимое на пол мальчиком, масса которого 45 кг, а площадь подошв его ботинок, соприкасающихся с полом, равна 300 см 2, Запишем условие задачи и решим её. Дано : m = 45 кг, S = 300 см 2 ; p = ? В единицах СИ: S = 0,03 м 2 Решение: p = F / S, F = P, P = g·m, P = 9,8 Н · 45 кг ≈ 450 Н, p = 450/0,03 Н / м 2 = 15000 Па = 15 кПа ‘Ответ’: p = 15000 Па = 15 кПа
Что называется давлением формула?
Давление твёрдого тела. Формула для вычисления давления твёрдого тела. Давление газа. Атмосферное давление. Гидростатическое давление внутри жидкости. Формула для вычисления давления внутри жидкости. Силу, действующую перпендикулярно поверхности какого-либо тела, принято называть силой давления,
Чему равна сила давления?
Давление — физическая величина, численно равная силе, действующей на единицу площади поверхности, перпендикулярно этой поверхности. В международной системе единиц давление измеряют в ньютонах на квадратный метр, или в паскалях: 1 Па = 1 Н м 2 ; давление = сила площадь p = F S.
Как найти давление с помощью массы и площади?
Зная свою массу и площадь ботинка,вычислите,какое давление вы производите при ходьбе и стоя на месте.Указание.Площадь опоры ботинка определите следующим образом.Поставте на лист клетчатой бумаги и обведите контур той части подошвы,на которую опираеться нога.Сосчитайте число полных квадратиков,попавших внутрь контура,и прибавте к нему половину числа неполных квадратиков,через которые прошла линия контура.Полученное число умножте на площадь одного кводратика(площадь квадратика 1/4см(в квадрате))и найдитеплощадь подошвы! НАДО НАПИСАТЬ ВЫВОД ПОСЛЕ ТОГО КАК ВСЕ ЭТО СДЕЛАЕШЬ УМОЛЯЮ РЕБЯТ ПОМОГИТЕ Пусть масса равна 50 кг.число полных квадратиков — 698.Число половинок — 56.Найдем площадь подошвы:(698+(56/2))*(1/4)=103,7 см²Переведем в систему СИ:S1=103,7 см² = 0,01037 м².Выражение, для определения давления тела на плоскость имеет вид:P=F/S, где F — сила давления на плоскость, S — площадь плоскости.В нашем случае сила давления, это вес:F=m*gПлощадь одной ноги:S1=0,01037 м²Площадь опоры, когда стоишь:S=2*S1После поставления этих выражений в формулу давления, получаем:Когда идешь, площадь опоры одна нога:P=m*g/(S1)=50*9,8/0,01037= 47251 Па.Когда стоишь, площадь опоры две ноги:P=m*g/(S)=50*9,8/(2*0,01037)= 23625,5 Па.
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Зная свою массу и площадь ботинка,вычислите,какое давление вы производите при ходьбе и стоя на месте.Указание.Площадь
Как найти давление все формулы?
Давление, сила давления — Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
- Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности.
- Сила давления направлена перпендикулярно поверхности.
- Формула давления: p = F / S, где F — модуль силы, S — площадь поверхности.
- Единица измерения давления в СИ: паскаль (Па).1 Па = 1 Н/м 2 Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.
Формулу для расчета силы давления вывести несложно: F = p × S В задачах по физике за 7 класс сила давления, как правило, равна весу тела.
Что показывает давление Физика 7 класс?
Урок физики по теме «Давление».7-й класс Класс: 7 Цели урока:
- Образовательные:
- продолжить формирование знаний о природе, явлениях и законах в единой системе;
- ввести новое понятие – давление;
- рассмотреть характеристики давления (определение, формула, единицы измерения, способы измерения, способы изменения).
- Воспитательные: продолжить:
- воспитывать у учащихся умение слушать ответ товарища;
- формировать у учащихся аккуратность, при работе с записями в тетради.
- Развивающие: продолжить:
- формирование умения высказывать умозаключения;
- формирование умения выделять главное в прочитанном тексте;
- формирование умения излагать прочитанное своими словами, логично, последовательно;
- вырабатывать умение работать с демонстрационным оборудованием.
Оснащение урока:
- мультимедийный проектор;
- компьютер;
- экран;
- презентация;
- дощечка с вбитыми в неё гвоздями;
- гиря массой 1 кг;
- кювета с песком;
- манометр.
План урока:
- Организационный момент.
- Актуализация знаний.
- Постановка учебной проблемы.
- Изучение нового материала.
- Закрепление нового материала.
- Подведение итогов урока.
- Домашнее задание.
- Рефлексия.
- ХОД УРОКА
- 1. Организационный момент
- Учитель: Сегодня вам представиться возможность вместе со мной исследовать новую физическую величину, а какую вы поможете мне определить чуть позже.
- 2. Актуализация знаний (Слайды 1; 2)
- Что является причиной изменения скорости тела и (или) его деформации?
- От чего зависит результат действия силы на тело?
- Какой буквой латинского алфавита обозначается сила?
- Какова единица измерения силы в СИ?
- С помощью какого прибора можно измерить силу?
- Какова единица измерения длины в СИ?
- Какова единица измерения площади в СИ?
- Что такое вес тела?
3. Постановка учебной проблемы (Слайд 3) Учитель: Почему нам нравится кататься на лыжах и не нравится ходить в ботинках по глубокому снегу? Ученики: На лыжах мы не проваливаемся в снег так глубоко как в ботинках. Учитель: Почему же результат действия одной и той же силы – веса нашего тела оказывается различным? Ученики: Площадь опоры различная.
Учитель: Верно. Ведь площадь поверхности лыжи почти в 20 раз больше площади подошвы. Поэтому, стоя на лыжах, человек действует на каждый квадратный сантиметр площади поверхности снега с силой, в 20 раз меньшей, чем стоя на снегу без лыж. Как вы думаете, возможно ли забить гвоздь в деревянный брус, ударяя молотком по его острию с такой же силой, как и по шляпке? Ученики: Нет.
Учитель: Почему? Ученики: Т.к. одна и та же сила удара распределяется по большей площади. Учитель: И на единицу площади поверхности дерева в первом случае действует сила во много раз меньшая, чем во втором. Учитель: Сравните модули сил в приведённых примерах? Ученики: Модули сил одинаковы.
Учитель: Сравните направления сил? Ученики: Направления сил одинаковы, перпендикулярны поверхности. Учитель: К чему приложены силы? Ученики: Во всех случаях силы приложены к опоре. Учитель: Сравните результаты действия сил? Ученики: Разные. Учитель: От чего же ещё зависит результат действия силы? Ученики: От площади поверхности, перпендикулярно которой она действует.
Учитель: Необходимо ввести физическую величину, которая характеризовала бы результат действия силы на площадь поверхности, перпендикулярно которой она действует. Как вы назвали бы такую величину? Стоя на лыжах, сидя на стуле, прикалывая кнопку к доске, какое действие мы на них оказываем? Ученики: Мы давим на эти тела.
- Что характеризует?
- Физический смысл (что показывает величина?).
- Определение.
- Обозначение.
- Определительная формула.
- Единица измерения в СИ.
- Способы измерения.
- Приборы для измерения.
- Применение.
Учитель: Составим конспект. Что характеризует давление? Ученики: Давление характеризует зависимость результата действия силы от площади поверхности, перпендикулярно которой она действует. (Слайд 6) Учитель: Верно. Запишем это в конспект. Что показывает давление? Ученики: Давление показывает силу, приходящуюся на единицу площади поверхности, перпендикулярно которой она действует.
- Слайд 7) Учитель: Верно.
- Запишем это в конспект.
- Рассмотрим следующую задачу: Трактор весом 60000 Н имеет площадь обеих гусениц 2 м2,
- Определите давление, которое оказывает трактор на почву? (Слайд 8) Ученики: Чтобы определить давление надо силу поделить на площадь опоры.
- Учитель: Верно, запишите этот ответ в конспект в виде схемы определения давления.
(Слайд 9) Давайте сформулируем это определение. (Слайд 10) Давление вещества обозначается латинской буквой «пэ». Как обозначается сила и площадь вы знаете. Составьте формулу для расчёта давления. (Слайд 11) Прочтите по буквам полученную формулу. Получите единицу измерения давления в СИ.
- Слайд 12) Откройте учебник на стр.101 и начиная с предпоследнего абзаца прочтите о том как иначе называется единица измерения давления и почему она так называется? 1Па – это давление, которое оказывает фольга размером 10 см на 10 см на горизонтальную поверхность (на ладонь).
- На следующей странице учебника найдите какие ещё применяются единицы измерения давления? (Слайд 13) Что означает р = 2Па ? Ученики: Это означает, что на поверхность площадью 1м 2 перпендикулярно ей действует сила 2Н.
(Слайд 14) Учитель: Что означает р = 50Па? Ученики: Это означает, что на поверхность площадью 1м 2 перпендикулярно ей действует сила 50Н. Учитель: Предложите способ измерения давления, которое оказывает учебник физики на стол. Ученики: Надо измерить вес учебника динамометром, измерить линейкой длину сторон и вычислить площадь опоры.
Затем нужно по формуле рассчитать давление. Учитель: Верно, но сила давления – это не обязательно вес тела, так при прокалывании ткани иглой силой давления является мышечная сила кисти руки человека. Как же в общем случае описать способ измерения давления? Ученики: измерить: F динамометром; S с помощью линейки; вычислить: р по формуле.
(Слайд 15) Учитель: Верно. Так же давление в жидкости или газе можно измерить специальным прибором – манометром. Подробнее с устройством и принципом действия манометра вы познакомитесь на одном из ближайших уроков. (Слайд 16) Откройте стр.104 вашего учебника и в тексте §36 найдите: как можно увеличить или уменьшить давление и где это используется? (Слайды 17; 18; 19) (Проводится обсуждение по прочитанному материалу.) ОК-13: «Давление». Давление – это скалярная физическая величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности. Обозначения:
- p – давление, F – приложенная сила,
- S – площадь поверхности (площадь опоры тела )
p = 2Па – это означает, что на поверхность площадью 1м 2 перпендикулярно ей действует сила 2Н. Способ измерения.
| измерить: | F динамометром S с помощью линейки |
| вычислить: | р по формуле |
ul>
Чтобы надо (иглы, зубы, клыки, когти, жала, ножи) Чтобы надо (лыжи, гусеницы, мокроступы) 5,Закрепление нового материала Учитель: Кто из вас сможет провести опыты, подтверждающие наши выводы? Набор необходимого оборудования перед вами: контейнер с песком, дощечка с вбитыми в неё 4-мя гвоздями, гиря, Ученики: Если поставить дощечку на песок шляпками вниз, то гвозди погрузятся в песок не так глубоко, как если бы мы поставили её на острые концы гвоздей.
Это доказывает, чтос уменьшением площади опоры давление увеличивается. Если поставить дощечку на песок шляпками вниз, и сверху поставить гирю, то гвозди глубже погрузятся в песок, чем в случае без гири. Это доказывает, что сувеличением силы давления (веса тела) давление тоже увеличивается. Учитель: Знаете ли вы, что: (Слайды 20; 21),
втыкая пальцем иглу или булавку в ткань, мы создаем давление около 100 000 000 Па, когда жалит оса, то она оказывает на кожу человека давление 30 000 000 000 Па, очень высокие давления существуют в глубинах небесных тел! Кто быстрее?! Решаем устно! (Слайды 22; 23) 1.
Что произойдет, если шарики в шариковых ручках будут делать меньшего размера? Почему? 2. Может ли быть человеку на каменном ложе так же комфортно, как и на пуховой перине? На твердых камнях возлегает И твердость оных презирает Для крепости великих сил, Считая их за мягкий ил.М.В.Ломоносов 3. Почему буря, которая летом валит живые деревья, часто не может свалить стоящее рядом сухое дерево без листьев, если оно не подгнило? Решаем письменно в тетрадях для решения задач: (Слайд 24) №1 Выразите в паскалях давление: 5гПа; 0,4кПа №2 Рысь весом 300 Н сидит на ветке дерева.
Какое давление она оказывает на ветку, если она занимает место площадью 0,05 м 2 ? 6. Подведение итогов урока (Слайд 25) 1. Что нового вы узнали сегодня на уроке? 2. Что показывает давление? 3. Назовите единицу измерения давления в СИ.4. Как можно увеличить или уменьшить давление? 7.
- §§35; 36 (читать и учить опыты) ОК – 13 (к проговору),
- №441; №442; №450
8. Рефлексия (Слайд 27) Учитель: Если вы поднимаете руки вверх – ответ «да», если опускаете вниз – «нет», если вы складываете руки на парте – «не знаю».1) Вы поняли новый материал? 2) Вы всё успели записать? 3) Вам было интересно? 4) Вы устали? Литература:
- Сборник задач по физике.7–9 кл.: пособие для общеобразоват. учреждений / В.И. Лукашик, Е.В. Иванова. – 25-е изд. – М.: Просвещение, 2011. – 230 с.: ил.
- Контрольные и самостоятельные работы по физике.7 класс: к учебнику А.В. Пёрышкина «Физика 7 класс» / О.И. Громцева. – 5-е изд., перераб. и доп. – М.: Издательство «Экзамен», 2013. – 109, с.
- Сборник задач по физике: 7–9 кл.: к учебникам А.В. Пёрышкина и др. «Физика.7 класс», «Физика.8 класс», «Физика.9 класс» / А.В. Пёрышкин; Сост.Г.А. Лонцова. – 9-е изд., перераб. и доп.– М.: Издательство «Экзамен», 2013. – 269, с.
- Тематическое и поурочное планирование по физике: 7 класс: К учебнику
- А.В. Перышкина «Физика.7 класс» / Р.Д. Минькова, Е.Н. Панаиоти. – 2-е изд.- М.: Издательство «Экзамен», 2004. – 127, с.: ил.
- Физика.7 кл.: учеб. для общеобразоват. учреждений / А.В. Пёрышкин, – 2-е изд., стереотип. – М. Дрофа, 2013. – 221, с.: ил.
- Энциклопедия для детей. Биология. – 6-е изд., испр. / ред. коллегия: М. Аксёнова, Г. Вильчек и др. – М.: Мир энциклопедий Аванта+, Астрель, 2007. – 672 с.: ил.
Интернет-ресурсы: 1.2.5.04.2014 Читать подробнее: Урок физики по теме «Давление».7-й класс
Как перевести давление?
Таблица соотношений единиц измерения давления —
| Единицы | бар | мбар | КПа | psi (фунт/дюйм 2 ) | фут вод.ст. | дюйм вод.ст. | мм рт.ст. | дюйм рт.ст. | кг/см 2 | атм |
| 1 бар | — | 1000 | 100 | 14,5038 | 33,4553 | 401,463 | 750,064 | 29,53 | 1,01972 | 0,98692 |
| 1 мбар | 0,001 | — | 0,1 | 0,0145 | 0,03346 | 0,40146 | 0,75006 | 0,02953 | 0,00102 | 0,00099 |
| 1 КПа | 0,01 | 10 | — | 0,14504 | 0,33455 | 4,01463 | 7,50064 | 0,2953 | 0,0102 | 0,00987 |
| 1 psi | 0,06895 | 68,9476 | 6,89476 | — | 2,30666 | 27,6799 | 51,7151 | 2,03602 | 0,07031 | 0,06805 |
| 1 фут вод.ст. | 0,02989 | 29,8907 | 2,98907 | 0,43353 | — | 12 | 22,4199 | 0,88267 | 0,03048 | 0,0295 |
| 1 дюйм вод.ст | 0,00249 | 2,49089 | 0,24909 | 0,03613 | 0,08333 | — | 1,86833 | 0,07356 | 0,00254 | 0,00246 |
| 1 мм рт.ст. | 0,00133 | 1,33322 | 0,13332 | 0,01934 | 0,0466 | 0,53524 | — | 0,03937 | 0,00136 | 0,00132 |
| 1 дюйм рт.ст. | 0,03386 | 33,8639 | 3,38639 | 0,49115 | 1,13293 | 13,5951 | 25,4 | — | 0,03453 | 0,03342 |
| 1 кг/см 2 | 0,98067 | 980,665 | 98,0665 | 14,2233 | 32,8084 | 393,701 | 735,561 | 28,959 | — | 0,96784 |
| 1 атм | 1,01325 | 1013,25 | 101,325 | 14,696 | 33,8985 | 406,782 | 760 | 29,9213 | 1,03323 | — |
Как пишется давление?
| давление | |
|---|---|
| СИ | Па |
| СГС | дин·см — 2 |
| Примечания | |
| скалярная величина |
Как найти S в физике?
Чтобы сравнить большие и малые, широкие и узкие тела, используют единицы площади, Запомни, как выполняется переход от одних единиц к другим! 1 км 2 = 1000 м ⋅ 1000 м = 1000000 м 2 ; 1 см 2 = 0,01 м ⋅ 0,01 м = 0,0001 м 2 ; 1 дм 2 = 0,1 м ⋅ 0,1 м = 0,01 м 2 ; 1 мм 2 = 0,001 м ⋅ 0,001 м = 0,000001 м 2,1 м 2 = 1000 мм ⋅ 1000 мм = 1000000 мм 2 ; 1 м 2 = 100 см ⋅ 100 см = 10000 см 2 ; 1 м 2 = 10 дм ⋅ 10 дм = 100 дм 2 ; 1 м 2 = 0,001 км ⋅ 0,001 км = 0,000001 км 2, Вычисление площади поверхности тела Чтобы определить площадь тела, используют формулы: площадь прямоугольника (S) можно рассчитать, умножив длину прямоугольника на ширину прямоугольника. S = l 1 ⋅ l 2, Площадь треугольника S = ah 2, где (a) — сторона, (h) — высота, проведённая к данной стороне. Площадь круга S = π R 2 π ≈ 3,14, где (R) — радиус круга.
Что такое давление для чайников?
Давление – скалярная физическая величина, равная силе, действующей на единицу площади поверхности. В международной системе СИ измеряется в Паскалях и обозначается буквой p. Единица измерения давления – 1 Паскаль. Русское обозначение – Па, международное – Pa.
В чем измеряется давление?
Единицы измерения давления
| Паскаль (Pa, Па) | Фунт-сила на квадратный дюйм (psi) | |
|---|---|---|
| 1 ат | 98066,5 | 14,223 |
| 1 атм | 101325 | 14,696 |
| 1 мм рт. ст. | 133,322 | 0,019337 |
| 1 мм вод. ст. | 9,80665 | 1,4223⋅10 — 3 |
Как найти массу с помощью давления?
Тело давит на поверхность с силой в 30Н. Найти массу тела.
Чтобы найти массу тела через его давление на поверхность, будем использовать формулу: F = P = m * g, откуда выразим: m = F / g.Постоянные и переменные: F — сила давления на поверхность со стороны рассматриваемого тела (F = 30 Н); g — ускорение свободного падения (g ≈ 10 м/с 2 ).Вычисление: m = F / g = 30 / 10 = 3 кг.Ответ: На поверхность давит тело массой 3 кг.
Знаешь ответ? Как написать хороший ответ? Будьте внимательны!
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Тело давит на поверхность с силой в 30Н. Найти массу тела.
Как найти давление если известна площадь?
Как найти площадь, если известны сила и давление? Определение давления Р говорит, что давление это сила F приложенная к единицы площади S, на которую она действует. Для того чтобы найти давление Р, надо силу F разделить на площадь S. Запишем это формулой Р = F / S. Выразим площадь S из формулы S = F / Р.Ответ: S = F / Р Знаешь ответ? Как написать хороший ответ? Будьте внимательны!
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Как найти площадь, если известны сила и давление?
Как найти высоту в физике давление?
Как найти высоту, зная давление, плотность. Если в данном случае речь идёт о высоте столба какой-либо жидкости, то из формулы давления p=ρ*g*h можно выразить искомую высоту: h=p/(ρ*g). Ответ: р/(ρ*g) Знаешь ответ? Как написать хороший ответ? Будьте внимательны!
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Как найти высоту, зная давление, плотность.
Как найти V в физике?
Формула скорости пути времени и их единицы измерения Скорость при равномерном движении показывает какой путь прошло тело за единицу времени.Скорость обозначается — v.Единица измерения — м/с (метров в секунду)Формула v=S/t, где S — путь пройденный телом, t — время, за которое тело прошло путь.Путь — это расстояние, которое преодолело тело.Путь обозначается — S.Единица измерения — метры.Формула S=v*t, где v- скорость тела, t — время, за которое тело прошло путь.Время.Время обозначается — t.Единица измерения — секунды.
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Формула скорости пути времени и их единицы измерения
Как высчитывать давление?
Давление — это отношение силы, действующей перпендикулярно поверхности, к площади этой поверхности. Давление — величина скалярная.
Как найти давление в физике 10 класс?
Урок 15. основы гидромеханики — Физика — 10 класс — Российская электронная школа
- ВАЖНО!
- Силой давления называется сила, действующая перпендикулярно некоторой поверхности.
- Результатом действия силы давления является давление.
- Отношение модуля силы давления F к площади поверхности S, на которую эта сила действует, называется давлением:
- $p = frac $.
- Закон Паскаля: силы давления в данной точке покоящейся в ИСО жидкости (газа) действуют во всех направлениях одинаково.
- Гидростатическое давление
- Давление жидкости на некоторой глубине определяется по формуле
- $p = p_ + rho gh$;
- где $p_ $ – атмосферное давление; $rho$ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – глубина.
- Атмосферное давление – это давление атмосферы, действующее на все находящиеся в ней предметы и на земную поверхность.
Нормальное или среднее значение атмосферного давления равно 760 мм ртутного столба, что соответствует 101325 Па.Т.е.1 мм рт. ст. = 133,322 Па.
- Зависимость атмосферного давления от высоты имеет сложный вид из-за сжимаемости воздуха (в отличие от жидкостей).
- Закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости.
- $F_ = rho_ж cdot g cdot V_m$,
- где $rho_ж$ – плотность жидкости; $g$ – ускорение свободного падения; $V_m$ – объём погружённой в жидкость части тела.
Как найти V в физике?
Формула скорости пути времени и их единицы измерения Скорость при равномерном движении показывает какой путь прошло тело за единицу времени.Скорость обозначается — v.Единица измерения — м/с (метров в секунду)Формула v=S/t, где S — путь пройденный телом, t — время, за которое тело прошло путь.Путь — это расстояние, которое преодолело тело.Путь обозначается — S.Единица измерения — метры.Формула S=v*t, где v- скорость тела, t — время, за которое тело прошло путь.Время.Время обозначается — t.Единица измерения — секунды.
Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. :)Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
Читать подробнее: Формула скорости пути времени и их единицы измерения
Как в физике обозначается давление?
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 сентября 2021 года; проверки требуют 5 правок,
| давление | |
|---|---|
| Размерность | L −1 MT −2 |
| Единицы измерения | |
| СИ | Па |
| СГС | дин · см -2 |
| Примечания | |
| скалярная величина |
Давле́ние на поверхность — интенсивная физическая величина, численно равная силе, действующей на единицу площади поверхности перпендикулярно этой поверхности. В данной точке давление определяется как отношение нормальной составляющей силы, действующей на малый элемент поверхности, к его площади : Среднее давление по всей поверхности есть отношение нормальной составляющей силы, действующей на данную поверхность, к её площади : Давле́ние сплошной среды — скалярная интенсивная физическая величина ; характеризует состояние среды и является диагональной компонентой тензора напряжений, В простейшем случае изотропной равновесной неподвижной среды не зависит от ориентации. Для обозначения давления обычно используется символ — от лат. pressūra «давление». В соответствии с рекомендациями ИЮПАК давление в классической механике рекомендуется обозначать как, менее рекомендуемо обозначение, Осмотическое давление часто обозначается буквой π, Давление идеального газа (вообще говоря, системы пренебрежимо мало взаимодействующих частиц) на стенку ищется как 0}2p_ ,dj_ }»> где — проекция импульса на ось сближения со стенкой, а — аналогичная проекция вектора плотности потока, для которого (размерность пространства, вообще говоря, зависит от задачи) где — концентрация, — функция распределения вероятности. В частности, при распределении Максвелла, интеграл легко берётся и получается:,
Давление
Известно, что человеку удобнее ходить по глубокому снегу на лыжах, так как при этом он меньше проваливается под снег. А разрезать предметы удобнее остро отточенным ножом. Причина этого – давление. В первом случае мы стремимся уменьшить давление на снег, а во втором случае, мы стараемся максимально увеличить давление.
Формула давления твердого тела
Рассмотрим твердое тело, например, кирпич. Пусть он лежит на горизонтальной поверхности и давит на нее своим весом (рис. 1).
Рис. 1. Твердое тело опирается на поверхность площадью S и давит на нее своим весом mg
На рисунке символом S обозначена нижнее основание тела – это площадь, на которую тело опирается (давит). Сила, с которой тело давит на поверхность – это сила тяжести mg.
Давление, которое твердое тело оказывает на поверхность, можно рассчитать так:
[ large boxed{ P = frac{F_{perp}}{S} }]
Примечание: Эта формула подходит для расчета давления твердых тел. Существует еще одна формула, с помощью которой рассчитывают давление жидкостей.
( P left( text{Па}right) ) – давление;
( F_{perp} left(H right) ) – сила, которая давит (сила давления). Эта сила располагается под прямым углом к поверхности;
( S left( text{м}^{2}right) ) – площадь, на которую давит сила.
Иногда в условии задачи указывают площадь в квадратных сантиметрах, или других единицах, отличающихся от основных единиц, принятых в СИ. Чтобы правильно рассчитать давление, нужно уметь переводить площадь в квадратные метры.
В системе СИ давление измеряется в Паскалях.
[ large 1 text{Па} = frac{1 H}{1 text{м}^{2}} ]
Поэтому, перед решением задач, нужно давление переводить в Паскали, если в условии встретятся другие единицы измерения давления.
В некоторых школьных задачах просят найти не давление, а силу давления. Нужно уметь их различать.
Сила давления, как и любая сила, измеряется в Ньютонах. Именно она давит на поверхность.
А давление — это дробь, в числителе расположена сила, которая давит, а в знаменателе — площадь поверхности, на которую давят. Давление измеряют в Паскалях.
Примечание: Давление – это сила, деленная на площадь. Сила должна располагаться перпендикулярно поверхности (рис. 2а).
Когда сила не перпендикулярна поверхности
Силу раскладываем на проекции, если она направлена к поверхности не под прямым углом (рис. 2б). Выберем часть силы, расположенную перпендикулярно поверхности. Именно эту часть силы и нужно подставлять в формулу для расчета давления.
Рис. 2. Если сила, которая давит на поверхность, направлена не под прямым углом к поверхности, раскладываем силу на проекции и выбираем часть, которая располагается к поверхности перпендикулярно
Оценка статьи:
Загрузка…
Шпаргалки по физике за 7 класс
В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачать шпаргалку со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).
Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Измерение физических величин
Измерением называют определение с помощью инструментов и технических средств числового значения физической величины.
Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения.
В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:
ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.
Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.
Выделяют прямое и косвенное измерение:
-
при прямом измерении результат можно увидеть непосредственно на шкале инструмента;
-
при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).
Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.
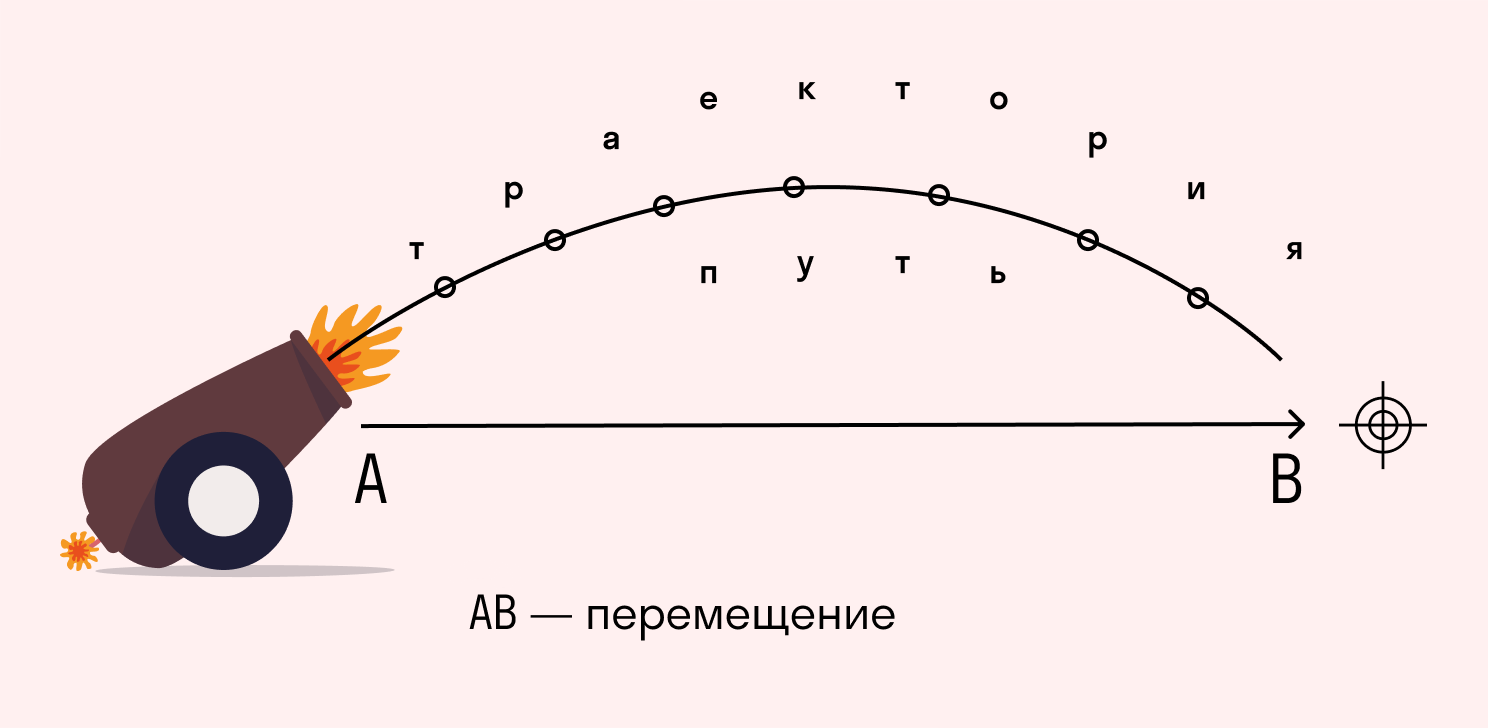
Механическое движение: формулы за 7 класс
Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики.
Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.
Изучение механического движения в курсе по физике за 7 класс включает следующие термины:
-
Перемещение тела — минимальное расстояние, которое соединяет две выбранные точки траектории движения.
-
Траектория движения — мысленная линия, вдоль которой перемещается тело.
-
Путь — длина траектории тела от начальной до конечной точки.
-
Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.
-
Ускорение — быстрота изменения скорости, с которой движется тело.
Равномерное движение — механическое движение, при котором тело за любые равные промежутки времени проходит одно и то же расстояние.
Формула скорости равномерного прямолинейного движения:
V = S / t, где S — путь тела, t — время, за которое этот путь пройден.
Формула скорости равномерного криволинейного движения:
где S1 и S2 — отрезки пути, а t1 и t2 — время, за которое был пройден каждый из них.
Единица измерения скорости в СИ: метр в секунду (м/с).
Формула скорости равноускоренного движения:
V = V0 + at, где V0— начальная скорость, а — ускорение.
Единица измерения ускорения в СИ: м/с2.
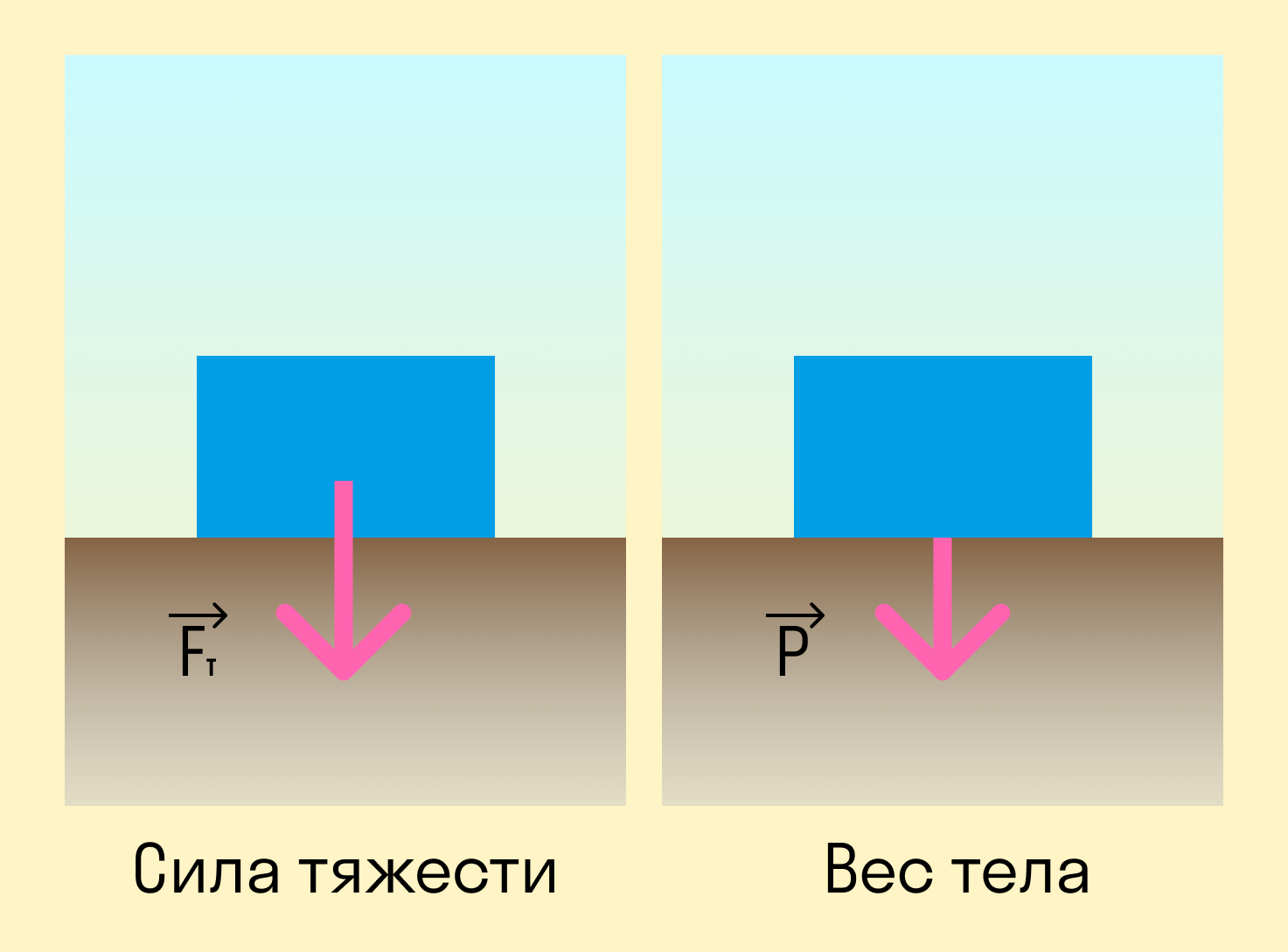
Сила тяжести, вес, масса, плотность
Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.
Вес тела или вещества — это физическая величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес.
Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.
Формула веса:
P = mg, где m — масса тела, g — ускорение свободного падения.
Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.
g = 9,806 65 м/с2 или 9,8 Н/кг
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.
Fтяж = mg
Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.
Плотность тела или вещества – величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему.
Формула плотности:
ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.
Единица измерения плотности в СИ: кг/м3.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Механический рычаг, момент силы
О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз.
Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы.
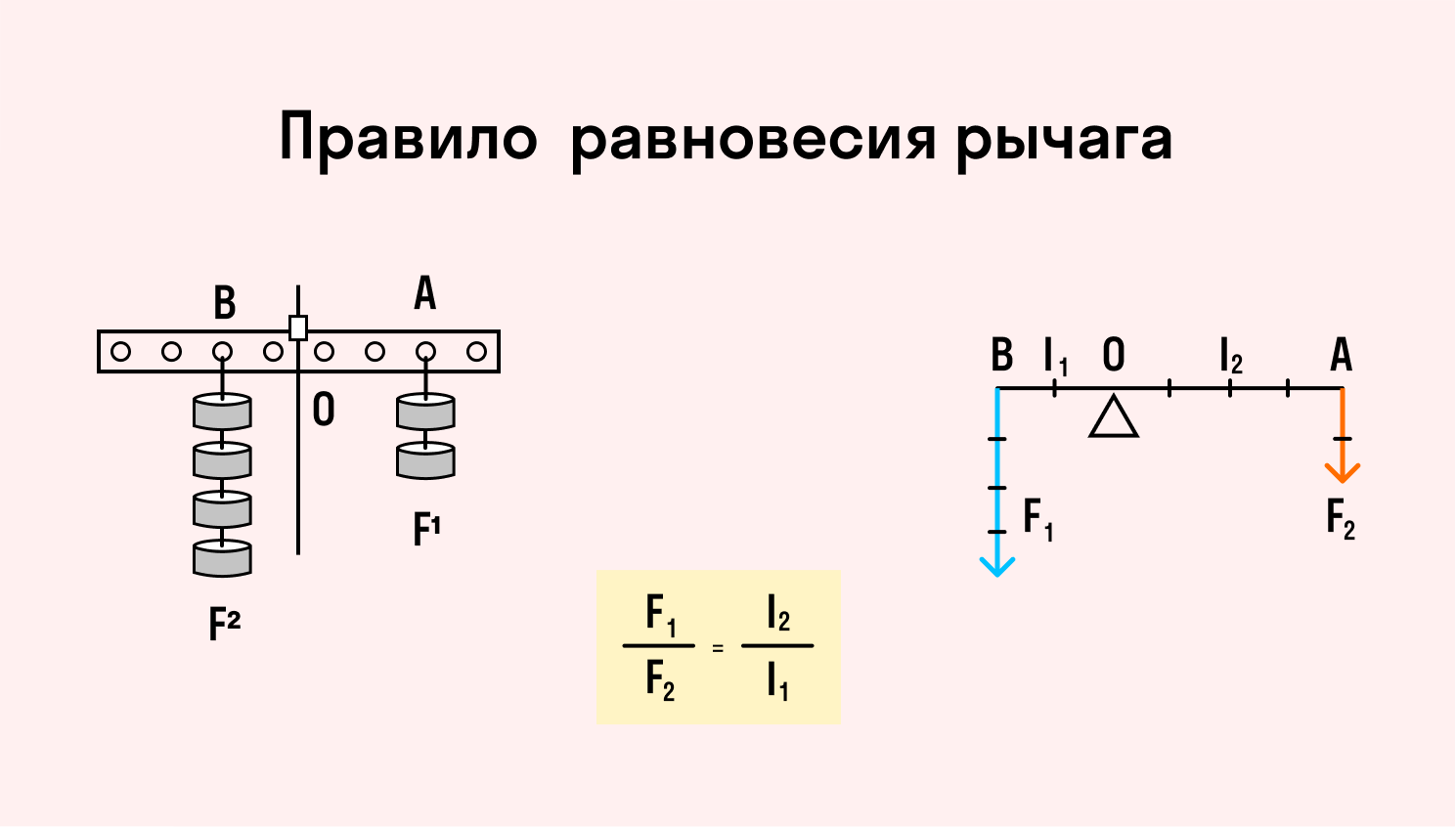
Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.
Уравнение равновесия рычага:
F1 × l1 = F2 × l2
Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.
Момент силы — это физическая величина, равная произведению модуля силы F на ее плечо l.
Формула момента силы:
M = F × l, где F — модуль силы, l — длина плеча.
Единица измерения момента силы в СИ: ньютон-метр (Н·м).
Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.
Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении.
Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.
М1 + М2 + Мn + … = 0
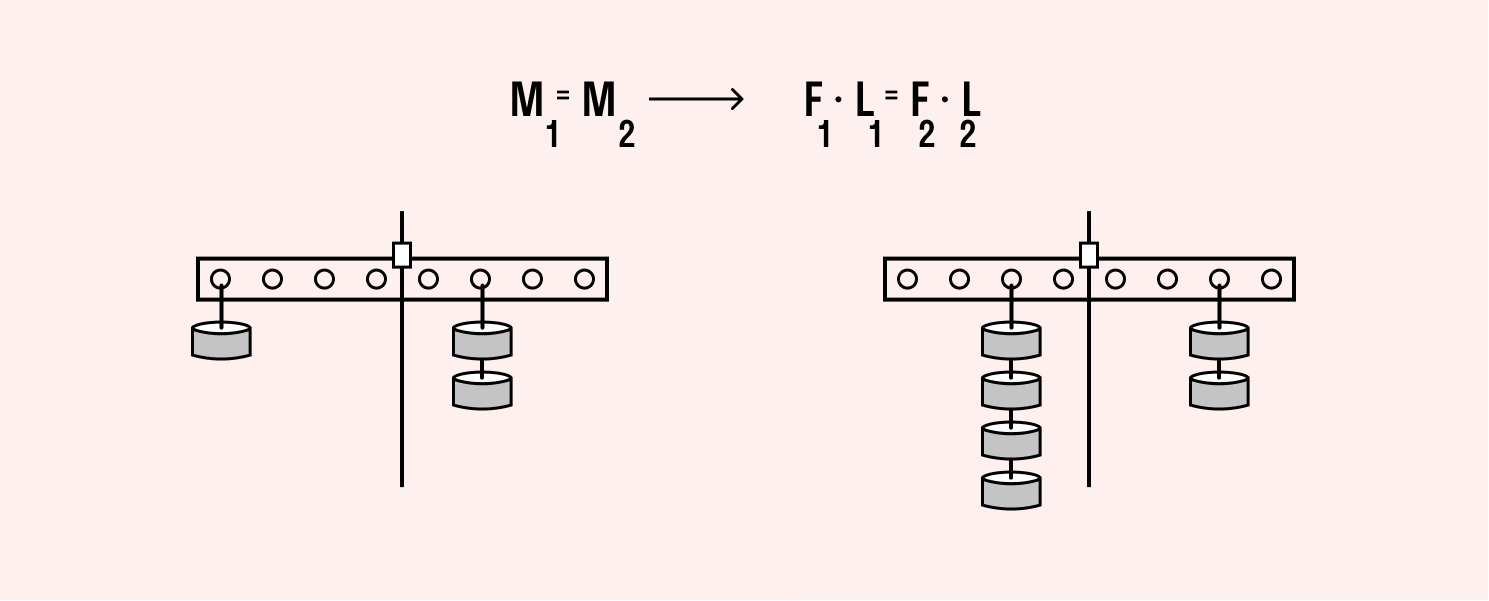
Давление, сила давления
Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности.
Сила давления направлена перпендикулярно поверхности.
Формула давления:
p = F / S, где F — модуль силы, S — площадь поверхности.
Единица измерения давления в СИ: паскаль (Па).
1 Па = 1 Н/м2
Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.
Формулу для расчета силы давления вывести несложно:
F = p × S
В задачах по физике за 7 класс сила давления, как правило, равна весу тела.
Давление газов и жидкостей
Жидкости и газы, заполняющие сосуд, давят во всех направлениях: на стенки и дно сосуда. Это давление зависит от высоты столба данного вещества и от его плотности.
Формула гидростатического давления:
р = ρ × g × h, где ρ — плотность вещества, g — ускорение свободного падения, h — высота столба.
g = 9,8 м/с2
Единица измерения давления жидкости или газа в СИ: паскаль (Па).
Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.
Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления.
Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:
p = F / S, где F — модуль силы, S — площадь поверхности.
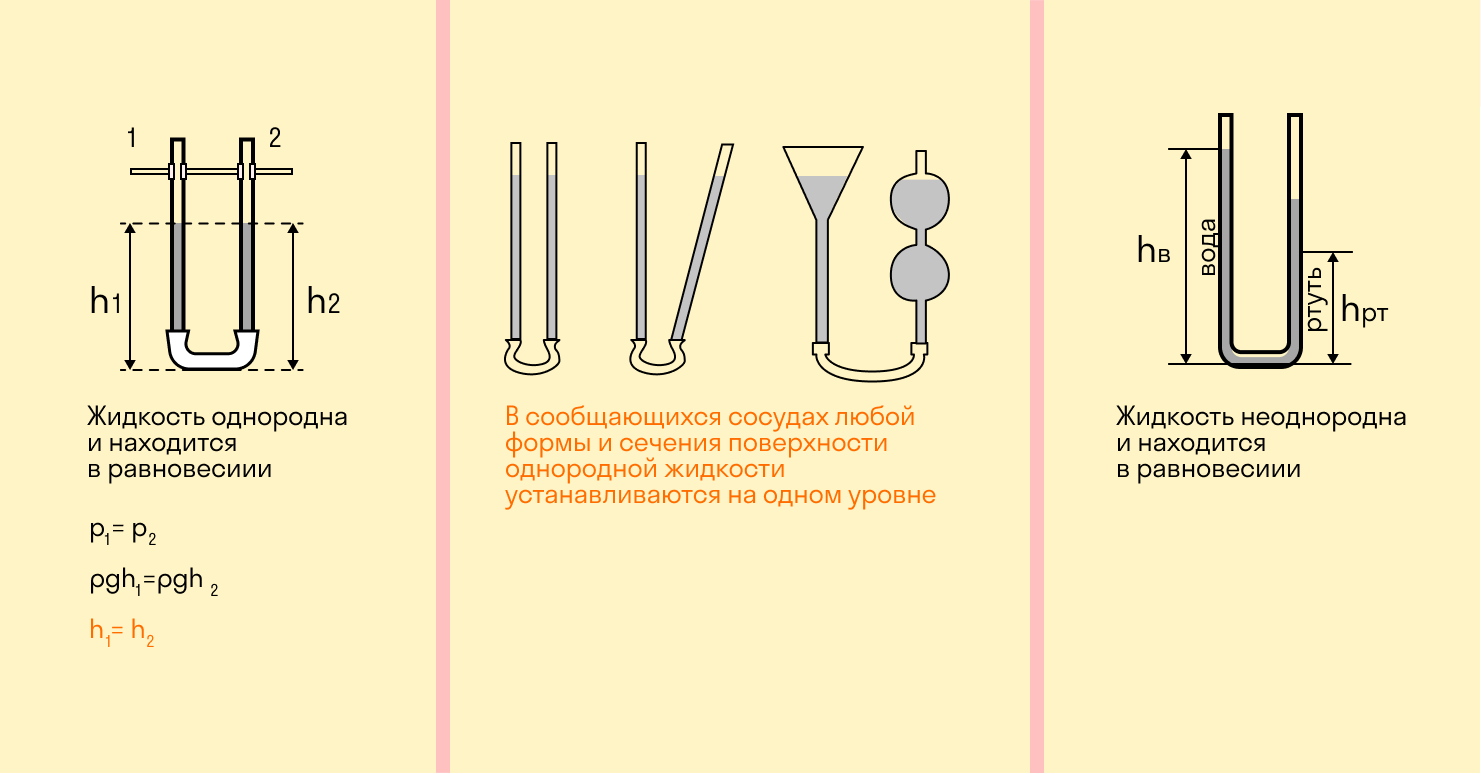
Сообщающиеся сосуды
Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.
Если ρ1 = ρ2, то h1 = h2 и ρ1gh1 = ρ2gh2, где:
p — плотность жидкости,
h — высота столба жидкости,
g = 9,8 м/с2.
Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.
Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.
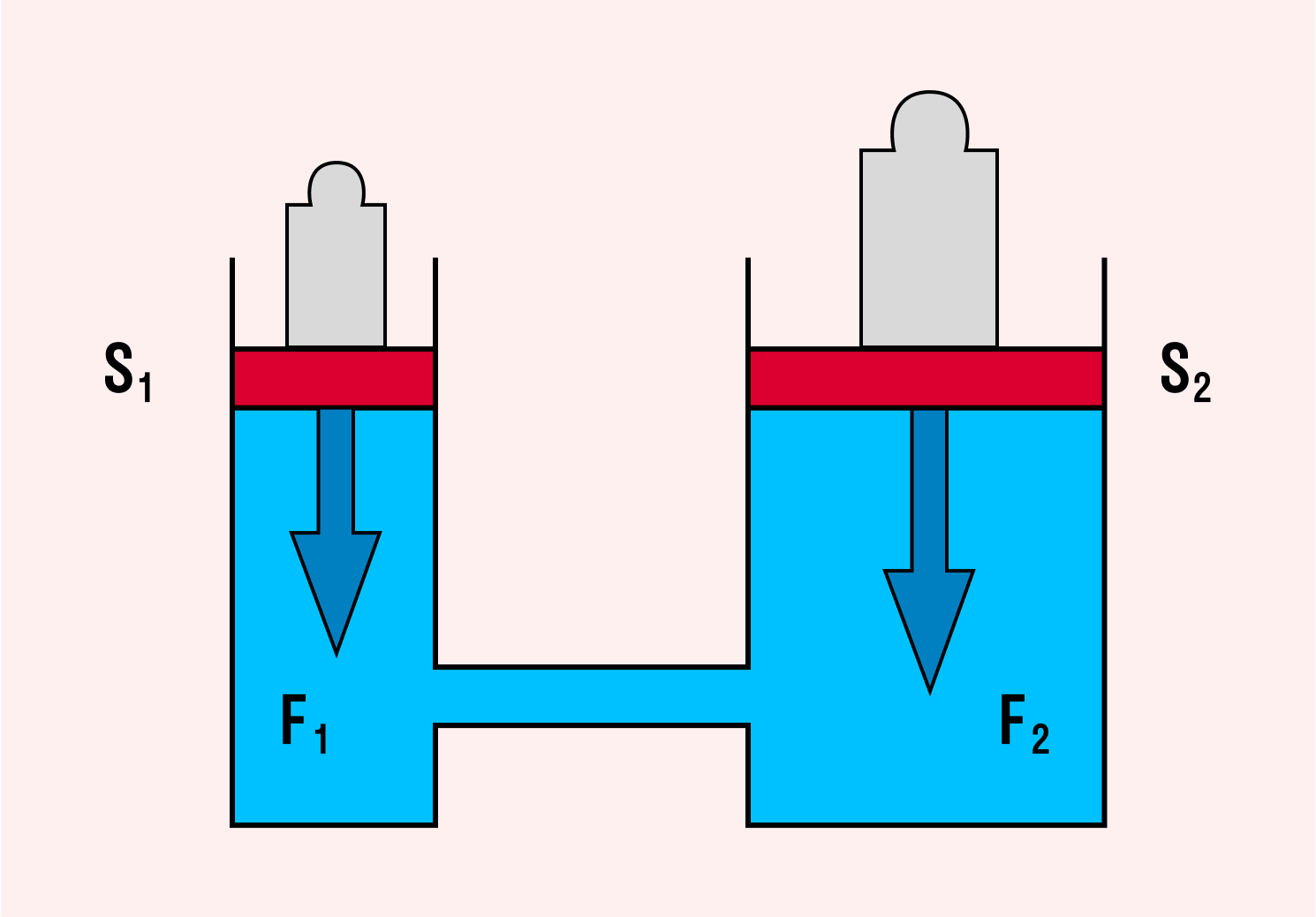
Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.).
Если под поршнем 1 образуется давление p1 = f1/s1, а под поршнем 2 будет давление p2 = f2/s2, то, согласно закону Паскаля, p1 = p2
Следовательно,
Силы, действующие на поршни гидравлического пресса F1 и F2, прямо пропорциональны площадям этих поршней S1 и S2.
Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.
Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.
Формула архимедовой силы:
Fa = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с2.
Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:
-
если плотность тела выше плотности среды, оно уйдет на дно;
-
если плотность тела ниже, оно всплывет на поверхность.
Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.
Работа, энергия, мощность
Механическая работа — это физическая величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение.
Формула работы в курсе физики за 7 класс:
A = F × S, где F — действующая сила, S — пройденный телом путь.
Единица измерения работы в СИ: джоуль (Дж).
Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.
Мощность — это физическая величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения.
Формула мощности:
N = A / t, где A — работа, t — время ее совершения.
Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.
N = F × v, где F — сила, v — средняя скорость тела.
Единица измерения мощности в СИ: ватт (Вт).
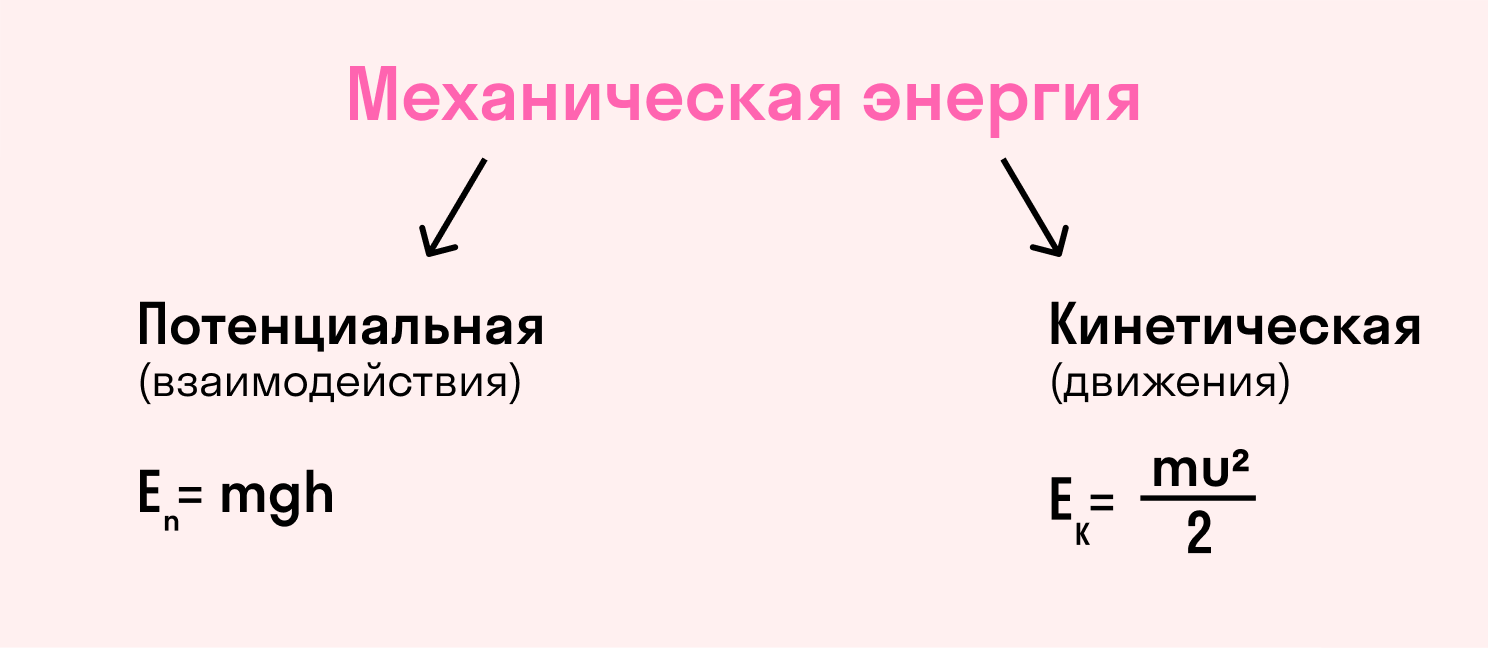
Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.
-
Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.
-
Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.
Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:
|
Кинетическая энергия |
Пропорциональна массе тела и квадрату его скорости. |
Ek = mv2/2 |
|
Потенциальная энергия |
Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания. |
Ep= mgh |
|
Полная механическая энергия |
Складывается из кинетической и потенциальной энергии. |
E = Ek+Ep |
|
Сохранение и превращение энергии |
Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу. |
Ek+ Ep= const |
Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.
Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии.
Формула для расчета КПД:
где Ап— полезная работа, Аз— затраченная работа.
КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.
Удачи на экзаменах!
Для
вычисления силы давления жидкости
используют закон Паскаля, согласно
которому3 давление жидкости на площадку
равно площади S
,умноженной на глубину её погружения h
,на плотность
и на ускорение силы тяжести
т.е.

7.4.1. (о
давлении жидкости на погруженную в нее
вертикальную стенку).
В
жидкость, удельный вес которой равен
f,
погружена вертикальная стенка.
Определить численное значение (модуль)
силы гидростатического давления жидкости
на эту стенку.

Решение.
Из гидростатики известно, что давление
жидкости на погруженную в нее горизонтальную
пластинку численно равно весу столба
жидкости, опирающегося на эту пластинку,
т. е. произведению площади этой пластинки
на ее расстояние от свободной
поверхности жидкости и на удельный вес
жидкости.
Если
площадь пластинки S,
ее
расстояние от свободной поверхности
жидкости h,
а
удельный вес жидкости γ, то модуль силы
давления
P
= Shγ. (11,7)
Но
эта формула верна только для пластинки,
занимающей в жидкости горизонтальное
положение. Если же пластинка, погруженная
в жидкость, занимает не горизонтальное
положение, а, например, вертикальное,
то ее различные точки находятся на
различной глубине, а поэтому о расстоянии
всей пластинки от свободной поверхности
жидкости не имеет смысла говорить, и
формула (11,7)
для
вычисления модуля силы давления на эту
пластинку непригодна.
Отнесем
пластинку ABCD
к
прямоугольной системе координат (см.
чертеж), причем ось Оу
расположим
на поверхности жидкости. Абсциссы точек
А
и В
соответственно
равны а
и
b,
а
линия CD
определяется
уравнением y=f(x),
где
f(x)
—
непрерывная функция на отрезке [а,
b]
Разделим
отрезок [а,
b]
на
n
произвольных частей и построим
прямоугольники, как показано на чертеже.
Площадь пластинки EFKH
примем
приближенно равной площади прямоугольника
EFGH,
т.
е. произведению f(xi)∆xi.
Чтобы
вычислить приближенно величину давления
на этот прямоугольник, повернем его
вокруг стороны EH
так,
чтобы он принял горизонтальное положение.
Теперь уже к этой площадке применима
формула (11,7), и приближенно
величина
давления жидкости на прямоугольник
EFGH
будет
равна
(f(xi)
∆xi)
xiγ
Эта
величина тем меньше будет отличаться
от истинной величины давления на
пластинку EFKH,
чем
на большее число n
разделен
отрезок [а,
b].
Поступая
так же со всеми прямоугольниками, мы
найдем, что приближенно модуль силы
давления определяется интегральной
суммой
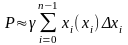
(постоянная
величина γ
входит в каждое слагаемое, а потому
вынесена за знак суммы). При составлении
интегральной суммы мы точку на каждом
частичном отрезке взяли в его левом
конце. Как известно, на предел интегральной
суммы это не повлияет.
За
точное значение модуля силы давления
примем предел, к которому стремится
эта сумма, когда наибольший из отрезков
∆xi
стремится
к нулю, а число n
этих
отрезков неограниченно увеличивается

Так
как ∆xi
→0,
то каждое произведение xi
f(xi)
∆xi
—
величина бесконечно малая, и здесь
опять-таки мы имеем дело с определением
предела суммы неограниченно возрастающего
количества бесконечно малых величин.
Можем
записать, что модуль силы давления
жидкости на вертикально погруженную в
нее стенку равен
(11.8)
7.4.2.
Определить силу давления воды на
вертикальную стену, имеющую форму
полукруга радиуса
диаметр которого находится на поверхности
воды
Решение.

Полукруг
разделим на элементарные полоски
прямыми, параллельными поверхности
воды. Заштрихованную полоску примем за
прямоугольник.
Тогда


Поэтому
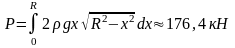
7.4.3.
Найти давление воды на поверхность
шара диаметром 4м, если его центр находится
на глубине 3м от поверхности воды.
Решение.
Проведём через центр шара вертикальную
плоскость и выберем на ней прямоугольную
систему координат


Рассечем
шар на глубине h
горизонтальной плоскостью. При изменении
h
на dh
площадь
,где
-дифференциал
дуги окружности. Давление

Выразив
dp
через одну переменную х и интегрируя в
пределах оси х=-2 до х=2,найдём давление
воды на всю поверхность шара.
Из
уравнения окружности
найдём
и затем


Следовательно

7.4.4. Прямоугольная
пластинка со сторонами а
дм и
h
дм вертикально
погружена в жидкость удельного веса
γ. Сторона длиной а
дм
лежит
на поверхности жидкости. Определить
численное значение силы давления,
испытываемого каждой стороной пластинки.
Решение.
Применим формулу (11,8). В ней нижний предел
интегрирования нужно взять равным нулю,
верхний равен h,
f
(х)=а,
а
потому модуль силы давления
(давление
получилось в килограммах, так как стороны
прямоугольника выражены в дециметрах).
При
решении задачи значительно большую
пользу принесло бы повторение рассуждений,
проведенных в предыдущей задаче, чем
использование готовой формулы (11,8).
7.4.5.Плотина
имеет форму половины эллипса, малая
ось которого 2b
лежит на поверхности жидкости. Большая
ось эллипса — 2а.
Вычислить
численное значение давления воды на
плотину.
Указание.
Если расположить оси, как это сделано
на чертежe
то эллипс определится уравнением
Вырежем
полоску на глубине х
шириною
∆x.
Площадь этой полоски равна 2y∆x.
Величину
у
определить
из уравнения эллипса. Принять удельный
вес воды γ=1.
Численное
значение давления равно
Можно
было сразу воспользоваться готовой
формулой (11,8), в которой взять

Ответ.
Если полуоси эллипса выражены в
дециметрах, то численно давление
получится в килограммах

Если
заменить эллипс половиной круга (а
=b)
то

7.4.6. Найти
численное значение давления воды (γ=
1)
на треугольные щиты, показанные на
чертеже.
Указание.
а) Уравнение АВ
б)
уравнение ОС:
.
Ответ,
а)
;
б)
;
7.4.7. Поперечное
сечение стенки резервуара, наполненного
водой, представляет дугу АВ
круга
радиуса а
дм, центр
О
которого
лежит на поверхности воды, а центральный
угол АОВ
равен
α. Определить давление воды на эту дугу
(см. чертеж).
Указание.
1. Дугу АВ
разделить
на n
частей.
-
Учесть,
что давление направлено по перпендикуляру
к поверхности и численно равно
произведению длины элемента ∆s
на его глубину DC
и
на удельный вес γ жидкости. -
Длина
дуги окружности равна произведению ее
радиуса на число радианов, содержащихся
в центральном угле, опирающемся на эту
дугу, т. е.
∆s=a∆φ
DC=asinφ;
γ=1,
а потому на элемент ∆s
дуги АВ
численное
значение силы давления ∆p
приближенно равно
∆p=(a sinφ)a∆φ=
a2sinφ∆φ.
-
Найти
проекции ∆X
u
∆Y
силы
∆р
на
оси Ох
и Оу:
∆X=(
a2sinφ∆φ)cos(90-φ)=
a2sin2φ∆φ;
∆Y=
a2sinφ
cosφ∆φ.

Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #