Формула силы Лоренца
Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле.
Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы.
![[ F = q cdot v cdot B cdot sin alpha ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-56b936f6bd44c97e0c5e02e6cf9d1b64_l3.png)
Здесь 
– сила Лоренца, 
– заряд частицы, 
– модуль вектора индукции магнитного поля, 
– скорость частицы, 
– угол между вектором индукции магнитного поля и направления движения.
Единица измерения силы – Н (ньютон).
Сила Лоренца — векторная величина. Сила Лоренца принимает своё наибольшее значение когда векторы индукции и направления скорости частицы перпендикулярны (
).
Направление силы Лоренца определяют по правилу левой руки:
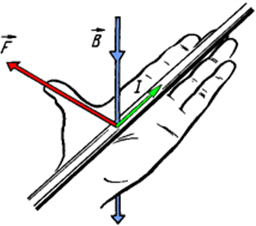
Если вектор магнитной индукции входит в ладонь левой руки и четыре пальца вытянуты в сторону направления вектора движения тока, тогда отогнутый в сторону большой палец показывает направление силы Лоренца.
В однородном магнитном поле частица будет двигаться по окружности, при этом сила Лоренца будет центростремительной силой. Работа при этом не будет совершаться.
Примеры решения задач по теме «Сила Лоренца»
| Задание | Найти силу Лоренца, действующую на частицу с зарядом 10 Кл, движущаяся со скоростью 9 м/с под углом  к вектору магнитной индукции.Индукция магнитного поля равна 3 Тл. |
| Решение | Подставим значения в формулу: |
![[ F = q cdot v cdot B cdot sin alpha = 10 cdot 9 cdot 3 cdot sin 60 ^circ approx 270 cdot 0,866 approx 233,83 (H) ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2d26198b8178e2242037c81fe59e1bd2_l3.png)
![[ F = q cdot v cdot B cdot sin alpha ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c660c12c55c4b9a4008b0e84ec1ec01a_l3.png)
Кроме того, по 2 закону Ньютона:
![[ F = m a ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f61b3470bcc840fc847af1ab6e4180db_l3.png)
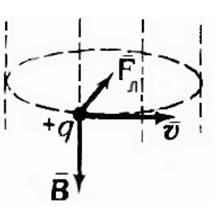
В данном случае сила Лоренца направлена к центру окружности и ускорение, ею создаваемое, направлено туда же, то есть это и есть центростремительное ускорение. Значит:
![[ F = q cdot v cdot B cdot sin alpha = ma text{ } rightarrow text{ } a = frac{q cdot v cdot B cdot sin alpha}{m} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b7565b8ec1ffcb91d3386feffb981aa5_l3.png)
Осталось узнать α. Обратим внимание на рисунок. – это угол между вектором скорости и направлением вектора магнитной индукции. Нетрудно увидеть, что эти векторы перпендикулярны, т.е. .
Сила Лоренца — основные понятия, формулы и определение с примерами
Центростремительное (нормальное) ускорение появляется при криволинейном движении тела и характеризует скорость изменения направления скорости с течением времени. Оно вычисляется по формуле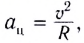 
Согласно закону Ампера на проводник с током в магнитном поле действует сила, которую можно рассматривать как результат действия магнитного поля на все движущиеся в проводнике заряды. Отсюда можно сделать вывод, что магнитное поле оказывает силовое действие на каждый движущийся заряд.
По закону Ампера на проводник длиной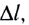 
Поскольку электрический ток — направленное движение заряженных частиц, то силу тока можно представить в виде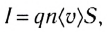 
где q — величина заряда одной частицы, n — концентрация заряженных частиц (число частиц в единице объема проводника),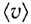 
— средняя скорость упорядоченного движения заряженных частиц, S — площадь поперечного сечения проводника.
Тогда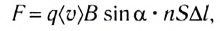 
где 
— число заряженных частиц, упорядоченно движущихся во всем объеме проводника длиной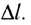 
Разделив модуль силы F на число частиц N, получим модуль силы, действующей на один движущийся заряд со стороны магнитного поля: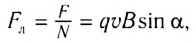 
где v — модуль скорости движущегося заряда.
Выражение для силы, с которой магнитное поле действует на движущийся заряд, в 1895 г. впервые получил голландский физик Хендрик Антон Лоренц. В его честь эта сила называется силой Лоренца: 
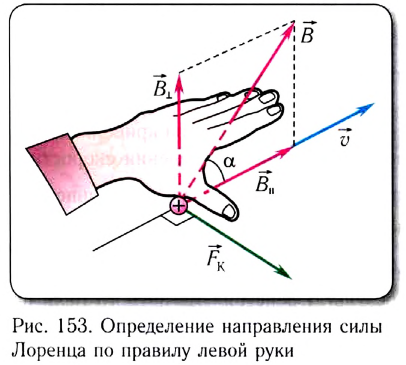
Как определить направление силы Лоренца
Направление силы Лоренца определяется по правилу левой руки (рис. 153):
если левую руку расположить так, чтобы перпендикулярная к скорости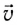 
составляющая вектора индукции 
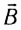магнитного поля входила в ладонь, а четыре вытянутых пальца указывали направление движения положительно заряженной частицы, то отогнутый на 90° большой палец укажет направление силы Лоренца 
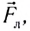действующей на частицу со стороны магнитного поля. Для отрицательно заряженной частицы (например, для электрона) направление силы будет противоположным.
Поскольку сила Лоренца перпендикулярна вектору скорости, то она не может изменить модуль скорости, а изменяет только ее направление и, следовательно, работы не совершает.
Таким образом, если поле однородно, то при движении частицы перпендикулярно к магнитной индукции поля ее траекторией будет окружность (рис. 154, а), плоскость которой перпендикулярна к магнитному полю.
Ускорение частицы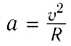 
(R — радиус окружности) направлено к центру окружности. Используя второй закон Ньютона, можем найти период обращения частицы по окружности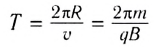 
и радиус окружности
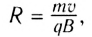
описываемой частицей в магнитном поле.
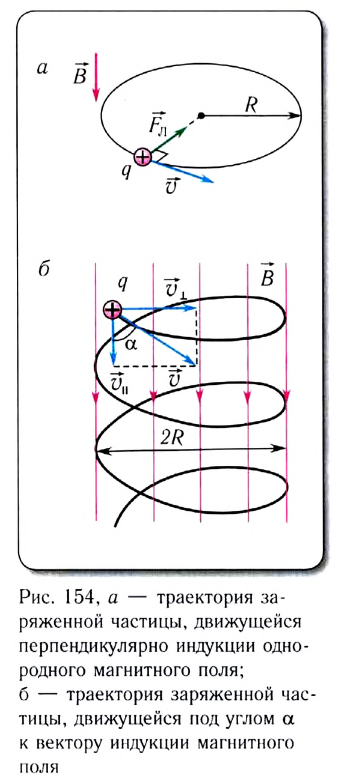
Если скорость направлена под углом к индукции магнитного поля, движение заряда можно представить в виде двух независимых движений (рис. 154, б):
В результате сложения обоих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю (см. рис. 154, б). Период этого движения определяется по формуле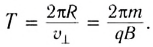 
Действие силы Лоренца широко применяется в различных электротехнических устройствах:
- электронно-лучевых трубках телевизоров и дисплеев;
- ускорителях заряженных частиц (циклотронах);
- масс-спектрометрах — приборах, определяющих отношение зарядов частиц к их массе по радиусу окружности, описываемой ими в магнитном поле;
- магнитогидродинамических генераторах ЭДС (МГД-генератор — устройство для генерации электрических токов, использующее проводящие жидкости, движущиеся в магнитном поле).
Что такое сила Лоренца
Силой Лоренца FЛ называют силу, действующую на электрически заряженную частицу, двигающуюся в электромагнитном поле, определяя действия на нес электрической» и магнитного полей одновременно. Это выражается формулой:
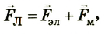
где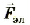 
— электрическая составляющая силы Лоренца, описывающая взаимодействие движущейся частицы и равная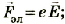 
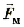— магнитная составляющая силы Лоренца, определяющая взаимодействие заряженной частицы с магнитным полем.
Сила Лоренца действует на движущуюся электрически заряженную частицу в электромагнитном поле.
Для упрощения рассмотрим случай, когда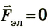 
, а сила Лоренца равна магнитной составляющей.
Выясним, как можно рассчитать силу, действующую на движущуюся заряженную частицу в магнитном поле. Как известно, электрический ток в проводнике — это упорядоченное движение заряженных частиц. Согласно электронной теории сила тока рассчитывается по формуле:
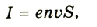
где I — сила тока; е — заряд частицы;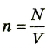 
— концентрация частиц в проводнике; V — объем; 
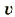— скорость движения частиц; S площадь поперечного сечения проводники.
Действие магнитного поля на проводник с током является действием магнитного поля на все движущиеся заряженные частицы. Поэтому формулу силы Ампера можно записать с учетом выражения силы тока в электронной теории:
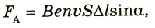
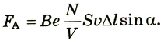
Если учесть, то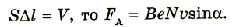 
Если сила Ампера является равнодействующей всех сил, действующих на N частиц, то на одну частицу будет действовать сила в N раз меньше:
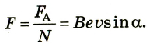
Это и есть формула для расчета магнитной составляющей силы Лоренца: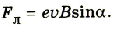 
Магнитная составляющая силы Лоренца 
Анализ этой формулы позволяет сделать выводы, что:
- магнитная составляющая силы Лоренца действует только на движущуюся частицу (
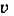≠ 0); - магнитная составляющая не действует на движущуюся частицу, которая движется вдоль линии магнитной индукции (а = 0).
≠ 0);Направление магнитной составляющей силы Лоренца, как и силы Ампера, определяется по правилу левой руки. При этом необходимо учитывать, что это справедливо для положительно заряженных частиц. Если определять направление силы Лоренца, действующей на электрон или другую отрицательно заряженную частицу, то, применяя правило левой руки, нужно мысленно изменять направление движения на противоположное.
Сила Лоренца направлена всегда под некоторым углом к скорости частицы, поэтому она придает ей центростремительное ускорение (рис. 2.15).
Для случая, если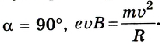 
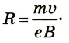
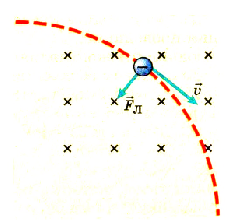
Рис. 2.15. Сила Лоренца придает частице центростремительное ускорение
Таким образом, заряженная частица, попадая в магнитной поле, начинает двигаться по дуге окружности. При иных значениях α ≠ О траектория движения частицы в магнитном поле приобретает форму спирали.
Наблюдать действие силы Лоренца можно с помощью электронно-лучевой трубки, которая есть во многих осциллографах (рис. 2.16), Если включить питание осциллографа, то на его экране можно увидеть светлое пятно, появившееся в месте падения электронов на экран. Если теперь сбоку поднести к трубке постоянный магнит, то пятно сместится, что подтверждает действие магнитного поля на движущиеся электроны.
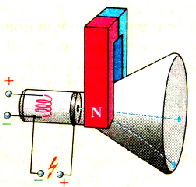
Рис. 2.16. Магнитное поле смещает электронный пучок в трубке осциллографа
Действие силы Лоренца применяется во многих приборах и технических установках. Так, смещение электронного луча, который «рисует» изображение на экране вакуумного кинескопа телевизора или дисплея компьютера, совершается магнитным полем специальных катушек, в которых проходит электрический ток, изменяющийся во времени по определенному закону,
В научных исследованиях применяют так называемые циклические ускорители заряженных частиц, в них магнитное поле мощных электромагнитов удерживает заряженные частицы на круговых орбитах.
Весьма перспективными для развития электроэнергетики являются магнито-гидродипамические генераторы (МГД-генераторы) (рис. 2.17). Поток высокотемпературного газа (плазмы), который образуется при сгорании органического топлива и имеет высокую концентрацию ионов обоих знаков, пропускается через магнитное ноле.
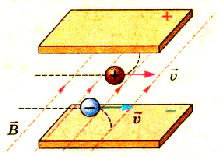
Puc. 2.17. Схема, объясняющая действие МГД-генератора
Вследствие действия силы Лоренца ионы отклоняются от прежнего направления движения и оседают на специальных электродах, сообщая им определенный заряд. Полученную при этом разность потенциалов можно использовать для получения электрического тока. Такие установки в будущем могут существенно повысить КПД тепловых «электростанций за счет выработки дополнительной электроэнергии при прохождении газов, которые после выхода из топки имеют довольно высокую температуру и высокую ионизацию, через MГД-генераторы.
Пример решения задачи
Электрон влетает в однородное магнитное поле с индукцией 10 -4 Тл перпендикулярно к линиям магнитной индукции. Его скорость 1.6 . 10 6 м/с. Найти радиус окружности, по которой движется электрон.
Отсюда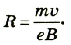 
Подставим значения физических величин:
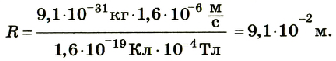
Ответ: электрон будет двигаться по круговой орбите, радиус которой 9,1 ∙ 10 -2 м.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как найти силу действующую на частицу
Сила Ампера, действующая на отрезок проводника длиной Δ с силой тока , находящийся в магнитном поле ,
может быть выражена через силы, действующие на отдельные носители заряда.
Пусть концентрация носителей свободного заряда в проводнике есть , а – заряд носителя. Тогда произведение υ , где модуль скорости упорядоченного движения носителей по проводнику, а – площадь поперечного сечения проводника, равно току, текущему по проводнику:
Выражение для силы Ампера можно записать в виде:
Эту силу называют силой Лоренца . Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов и для положительно заряженной частицы показано на рис. 1.18.1.
Сила Лоренца направлена перпендикулярно векторам и
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору то частица будет двигаться по окружности радиуса
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 1.18.2).
Период обращения частицы в однородном магнитном поле равен
Это выражение показывает, что для заряженных частиц заданной массы период обращения не зависит от скорости υ и радиуса траектории .
Угловая скорость движения заряженной частицы по круговой траектории
называется циклотронной частотой . Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 1.18.3.
Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров ( дуантов ). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте . Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка .
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20 Ne и 22 Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника , проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей , в котором частицы движутся в скрещенных однородных электрическом и магнитном полях . Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость заряженных частиц направлена перпендикулярно векторам и
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила и магнитная сила Лоренца. При условии эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью .
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов . Измеряя радиусы траекторий при известных значениях υ и можно определить отношение . В случае изотопов () масс-спектрометр позволяет разделить частицы с разными массами.
Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10 –4 .
Если скорость частицы имеет составляющую вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора а шаг спирали – от модуля продольной составляющей υ|| (рис. 1.18.5).
Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы , то есть полностью ионизированного газа при температуре порядка 10 6 K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации. В качестве примера на рис. 1.18.6 изображена траектория движения заряженной частицы в магнитной «бутылке» (или ловушке ).
Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 1.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена.
Сила Лоренца — сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.
Модуль силы Лоренца обозначается как FЛ. Единица измерения — Ньютон (Н).
Модуль силы Лоренца численно равен отношению модуля силы F, действующий на участок проводника длиной l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника:
FЛ=FN
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка ∆l и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля →B можно считать неизменным в пределах этого отрезка проводника.
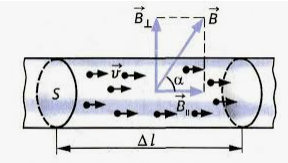
Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (число зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
I=qnvS
Модуль силы, действующей со стороны магнитного поля на выбранные элемент тока, равен:
F=|I|ΔlBsinα
Подставляя сюда выражение, полученное для силы тока, получим:
F=|qnvS|ΔlBsinα=|q|nvSΔlBsinα
Учтем, что число заряженных частиц в рассматриваемом объеме равно произведению величины этого объема на концентрацию самих частиц:
N=nSΔlB
Тогда:
F=|q|vNBsinα
Следовательно, на каждый движущийся заряд действует сила Лоренца, равная:
FЛ=FN=|q|vNBsinαN=|q|vBsinα
α — угол между вектором скорости движущегося заряда и вектором магнитной индукции.
Пример №1. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45o к вектору магнитной индукции.
FЛ=|q|vBsinα=0,005·200·0,3·√22≈0,2 (Н)
Направление силы Лоренца
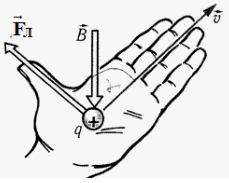
Сила Лоренца перпендикулярна вектору магнитной индукции и вектору скорости движущегося заряда. Ее направление определяется с помощью правила левой руки:
Если левую руку расположить так, чтобы составляющая магнитной индукции →B, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.
Пример №2. Протон p имеет скорость →v, направленную горизонтально вдоль прямого длинного проводника с током I (см. рисунок). Куда направлена действующая на протон сила Лоренца?
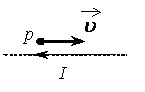
В точке, в которой находится протон, вектор магнитной индукции направлен в сторону от наблюдателя. Это следует из правила буравчика. Теперь применим правило левой руки. Для этого четыре пальца левой руки направим в сторону движения протона — вправо. Ладонь развернем в сторону наблюдателя, чтобы линии магнитной индукции входили в нее перпендикулярно. Теперь отставим на 90 градусов большой палец. Он показывает вверх. Следовательно, сила Лоренца, действующая на протон, направлена вверх.
Работа силы Лоренца
Поскольку вектор силы Лоренца направлен перпендикулярно скорости движения заряда, угол между перемещением этого заряда и этой силы равен 90о. Работа любой силы определяется формулой:
A=Fscosα
Но так как косинус 90о равен 0, сила Лоренца не совершает работу. Это значит, что сила Лоренца не влияет на модуль скорости перемещения заряда. Но она может менять вектора его скорости.
Полная сила, действующая на заряд
При решении задач, в которых заряженная частица находится одновременно в электрическом и магнитном полях, нужно учитывать, что не нее действует сразу две силы. Со стороны магнитного поля — сила Лоренца. Со стороны электрического поля — сила →Fэл, действующая на неподвижный заряд, помещенный в данную точку поля. Она равна произведению этого заряда на напряженность электрического поля:
→Fэл=q→E
Следовательно, полная сила, действующая на заряд, равна:
→F=→Fэл+→Fл=q→E+|q|→v→Bsinα
Пример №3. В пространстве, где существует одновременно однородное и постоянное электрическое и магнитное поля, по прямолинейной траектории движется протон. Известно, что напряженность электрического поля равна →E. Какова индукция →B магнитного поля?
Прямолинейное движение протона возможно в двух случаях:
- Вектор →E направлен вдоль траектории движения протона. Тогда вектор →B также должен быть направлен вдоль этой траектории, и его модуль может быть любым, так как магнитное поле на частицу действовать не будет.
- Векторы →E, →B и →v взаимно перпендикулярны, и сила, действующая на протон со стороны электрического поля, равна по модулю и противоположна по направлению силе Лоренца, действующей на протон со стороны магнитного поля (см. рисунок).
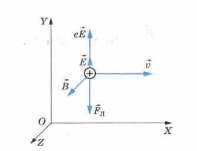
Заряд протона равен модулю заряда электрона — e. Сложим силы, действующие на протон по оси ОУ:
e→E+→FЛ=0
В скалярной форме:
eE−evB=0
Следовательно:
B=Ev
Задание EF17621
Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения силы Лоренца.
3.Выразить модуль вектора магнитной индукции.
4.Определить недостающие величины.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Напряжение на обкладках конденсатора: U = 2160 В.
• Радиус окружности, по которой движется протон в однородном магнитном поле: R = 20 см.
• Масса протона: m = 1,673·10–27 кг.
• Заряд протона: q = 1,6·10–19 Кл.
20 см = 0,2 м
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
По условию задачи протон движется перпендикулярно вектору магнитной индукции. Поэтому синус угла между вектором скорости и вектором магнитной индукции будет равен 1. А протон имеет положительный заряд. Тогда:
FЛ=qvB
Сила Лоренца сообщает протону центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
qvB=mv2R
Отсюда модуль вектора магнитной индукции равен:
B=mv2qvR=mvqR
Энергия заряда, движущегося в электрическом поле, определяется формулой:
W=qU
Но энергию заряда также можно выразить как кинетическую энергию движения:
W=Eк=mv22
Приравняем правые части выражений и получим:
qU=mv22
Отсюда ускорение протона равно:
v=√2qUm
Конечная формула для определения модуля вектора магнитной индукции:
B=mvqR=mqR√2qUm=√2UmqR2
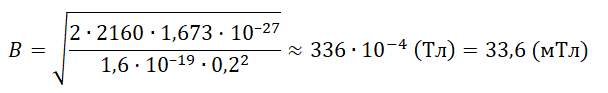
Ответ: 33,6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17600
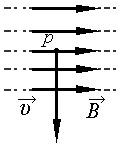Протон движется в однородном магнитном поле со скоростью υ, направленной перпендикулярно вектору магнитной индукции B (см. рисунок). Как направлена сила Лоренца, действующая на протон?
а) влево
б) вправо
в) к нам
г) от нас
Алгоритм решения
- Определить, каким способом можно найти направлений силы Лоренца, действующей на протон.
- Применить правила и найти направление силы Лоренца.
Решение
Силу Лоренца, действующую на заряженную частицу, можно найти с помощью правила левой руки. Для этого мысленно расположим четыре пальца левой руки в сторону, совпадающей с направлением движения положительной частицы (протона). Относительно рисунка пальца будут направлены вниз. Теперь развернем ладонь так, чтобы в нее входили линии магнитной индукции. Теперь отклоним на 90 градусов большой палец. Он будет направлен от плоскости рисунка к нам. Это и есть направление силы Лоренца, действующей на протон.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17749
Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью α-частица, радиус окружности, частота обращения и энергия α-частицы по сравнению с протоном должны:
- увеличиться
- уменьшиться
- не измениться
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Записать формулу для определения силы Лоренца.
2.Установить, от чего зависят перечисленные в таблице физические величины.
3.Определить характер их изменения при изменении заряда.
Решение
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
Если вместо протона взять альфа-частицу, то заряд увеличится вдвое, так как альфа-частица содержит 2 протона. Сила Лоренца прямо пропорционально зависит от величины заряда. Следовательно, она тоже увеличится вдвое. Скорость движения заряда по условию задачи остается постоянной, как и модуль вектора магнитной индукции.
Сила Лоренца будет сообщать альфа-частице центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
|q|vBsinα=mv2R
Отсюда:
|q|Bsinα=mvR
R=mv|q|Bsinα
Заряд альфа-частицы больше заряда протона вдвое. Она также содержит 2 нейтрона, поэтому ее масса примерно в 4 раза больше массы протона. Следовательно, радиус движения альфа-частицы увеличится примерно вдвое.
Частота обращения альфа-частицы связана с ее линейной скоростью формулой:
v=2πRν
Так как скорость остается постоянной, то при увеличении радиуса частота обращения должна уменьшиться.
Энергия альфа-частицы будет больше, чем у протона, вращающегося с той же скоростью. Это связано с тем, что ее кинетическая энергия будет примерно в 4 раза больше (так как во столько раз больше ее масса).
Ответ: 121
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.9k
На прошлых уроках мы с вами начали знакомство с магнитными
полями. Давайте с вами вспомним, что магнитное поле — это особая форма материи,
созданная движущимися (относительно определённой инерциальной системы отсчёта)
электрическими зарядами или переменными электрическими полями.
Силовой характеристикой магнитного поля является вектор
магнитной индукции, направление которого в данной точке совпадает с
направлением силовой магнитной линии, проходящей через эту точку:
Так же мы с вами установили, что на проводник с током,
помещённый в магнитное поле, со стороны магнитного поля действует сила,
называемая силой Ампера. Её модуль равен произведению силы тока, модуля вектора
магнитной индукции, длины отрезка проводника и синуса угла между направлениями вектора магнитной индукции и элемента тока:
Поскольку электрический ток представляет собой упорядоченное
движение заряженных частиц, то это означает, что магнитное поле, действуя на
проводник с током, действует тем самым на каждую из этих движущихся заряженных
частиц. Следовательно, силу Ампера можно рассматривать как результат сложения
сил, действующих на каждую движущуюся заряженную частицу.
Силу, с которой магнитное поле действует на заряженную
частицу, движущуюся в этом поле, называют силой Лоренца.
Своё название сила получила в честь выдающегося голландского
физика Хендрика Антона Лоренца — основателя электронной теории строения
вещества.
Модуль силы Лоренца определяется отношением силы Ампера,
действующей на участок проводника, находящийся в магнитном поле, к числу
заряженных частиц, упорядоченно движущихся в этом участке проводника:
Давайте с вами рассмотрим прямолинейный участок проводника с
током длиной Δl и
площадью поперечного сечения S. При этом будем считать, что длина
участка проводника и его площадь поперечного сечения настолько малы, что вектор
магнитной индукции поля можно считать одинаковым в пределах этого участка
проводника.
Итак, на участок проводника с током, находящимся в магнитном
поле, действует сила Ампера, модуль которой равен произведению силы тока,
модуля вектора магнитной индукции, длины отрезка проводника и синуса угла между
направлениями вектора магнитной индукции и элемента тока:
Теперь давайте с вами вспомним, что сила тока в проводнике
определяется зарядом, прошедшим через поперечное сечение проводника за единицу
времени:
Здесь ∆t — это промежуток времени, за который
заряженная частица проходит участок проводника длиной ∆l.
Пусть модуль заряда одной частицы равен q.
Тогда суммарный заряд всех частиц равен произведению модуля заряда одной
частицы на общее число частиц в выбранном участке проводника: Q = qN.
Перепишем уравнение для силы тока с учётом последнего
равенства.
Полученное равенство подставим в закон Ампера:
Обратите внимание на отношение ∆l/∆t — это есть не что иное, как модуль средней скорости
заряженной частицы, упорядоченно движущейся в магнитном поле внутри проводника:
Теперь подставим полученное выражение для силы Ампера в формулу
для силы Лоренца:
После упрощения получим, что модуль силы Лоренца равен
произведению заряда частицы, модуля её средней скорости, модуля вектора
индукции магнитного поля и синуса угла между вектором магнитного поля и вектором
скоростью движения частицы:
Направление силы Лоренца определяют по правилу левой руки:
если левую руку расположить так, чтобы составляющая магнитной индукции,
перпендикулярная скорости упорядоченного движения заряда, входила в ладонь, а
четыре пальца были направлены по движению положительного заряда (или против
движения отрицательного заряда), то отогнутый на 90о большой палец укажет
направление действующей на заряд силы Лоренца.
Анализ данного правила позволяет нам утверждать, что сила
Лоренца, действующая на движущуюся в магнитном поле частицу, перпендикулярна
вектору скорости этой частицы. Следовательно, сила Лоренца не совершает
работы. Тогда, согласно теореме о кинетической энергии, это означает, что сила
Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль
скорости частицы. А значит заряженная частица в магнитном поле движется с
постоянной по модулю скоростью, но при этом направление скорости непрерывно
изменяется.
Вид траектории заряженной частицы в магнитном поле зависит от
угла между скоростью влетающей в поле частицы и магнитной индукцией. Рассмотрим
такую ситуацию. Пусть протон, ускоренный разностью потенциалов U влетает в однородное магнитное поле сначала параллельно
линиям индукции, затем — перпендикулярно, и, наконец, под некоторым углом к
ним. Индукция магнитного поля равна B. Для
каждого случая определите радиус кривизны траектории протона и период его
обращения.
Итак, рассмотрим первый случай, когда протон, двигаясь по
силовой линии в электрическом поле ускоренно, приобретает скорость, с которой
влетает в однородное магнитное поле так, что его вектор скорости направлен
вдоль поля (или противоположно направлению индукции магнитного поля).
Очевидно, что в этом случае угол между направлением вектора
скорости и индукции магнитного поля либо равен нулю, либо 180о.
Тогда, согласно формуле, сила Лоренца, действующая на протон,
равна нулю и частица будет продолжать двигаться равномерно прямолинейно.
Теперь рассмотрим второй случай, когда протон влетает в
однородное магнитное поле перпендикулярно линиям его индукции.
В этом случае на протон в магнитном поле действует сила
Лоренца, направленная перпендикулярно вектору скорости (направление силы
Лоренца определяем по правилу левой руки). Как мы уже выяснили, сила Лоренца не
может изменить модуль скорости заряженной частицы — она лишь меняет её направление.
А так как магнитное поле однородно и вектор скорости частицы перпендикулярен
линиям магнитной индукции, то протон под действием силы Лоренца начнёт
двигаться по окружности.
С другой стороны, такое движение заряженной частицы в
магнитном поле будет подчиняться второму закону Ньютона:
И нам осталось рассмотреть последний случай, когда частица
влетает в магнитное поле под заданным углом к силовым линиям.
Подобное явление происходит в магнитном поле Земли.
Движущиеся с огромными скоростями заряженные частицы из космоса «захватываются»
магнитным полем Земли и образуют вокруг неё радиационные пояса. В них заряженные
частицы перемещаются по винтообразным траекториям между северным и южным
магнитными полюсами. И только в полярных областях небольшая часть частиц
вторгается в верхние слои атмосферы, вызывая восхитительные полярные сияния.
В заключении урока отметим, что действие магнитного поля на
движущийся заряд широко используется в технике. Вспомните хотя бы
электронно-лучевые трубки, применяемые в кинескопах телевизоров, где пучок
летящих к экрану электронов отклоняется с помощью магнитных катушек.
Сила Лоренца используется и в циклотронах — особых
ускорителях заряженных частиц. Обычный циклотрон состоит из двух полых
полуцилиндров разного диаметра (дуантов), находящихся в однородном магнитном
поле. Его принцип действия достаточно прост.
В зазоре между цилиндрами находится заряженная частица. В
этом зазоре создаётся переменное электрическое поле с постоянным периодом,
равным периоду обращения частицы. Это поле каждые пол периода разгоняет
частицу, увеличивая при этом радиус её обращения (период обращения частицы не
увеличивается). На последнем витке частица вылетает из циклотрона.
Действие силы Лоренца используют и в масс-спектрографах —
устройствах, предназначенных для разделения частиц по их удельным зарядам, то
есть по отношению заряда частицы к её массе, и по полученным результатам точно
определять массы частиц. На экране вы видите схему простейшего
масс-спектрографа. Цифрами один и два обозначены две диафрагмы, между которыми
создаются взаимно перпендикулярные электрическое и магнитное поля. Заряженная
частица, пройдя через первую диафрагму попадает в эти поля и, если сила
Лоренца, действующая на неё, равна электростатической силе, то она сможет
пройти через вторую диафрагму. Ионы же с другими скоростями отклонятся в полях
и через вторую диафрагму не пройдут.
За диафрагмой создаётся постоянное магнитное поле,
заставляющее заряженные частицы двигаться по окружности, радиус кривизны
которой можно измерить, поставив на пути частиц фотопластинку. Так как скорость
частиц одинакова и определяется постоянной прибора, то, зная заряд ионов, можно
легко определить их массу.
Ещё одно устройство, в котором применяется действие силы
Лоренца — это ТОКАМАК (тороидальная камера с магнитными катушками).
В нём плазма (напомним, что это частично или полностью
ионизированный газ) удерживается в специально создаваемом сильном магнитном
поле. ТОКАМАК считается наиболее перспективным устройством для осуществления
управляемого термоядерного синтеза.
»
Статьи
» Физика » Задачи
Найти модуль и направление силы, действующей на частицу массы m
|
Найти модуль и направление силы, действующей на частицу массы m при ее движении в плоскости xy по закону x = A sin wt, y = B cos wt. Решение
|
Категория: Задачи | Добавил: Creator (01.01.2018) |
| Просмотров: 3590 | Теги: направление, плоскость, частица, модуль, сила, масса, закон, движение | Рейтинг: 3.6/5 |
| Всего комментариев: 0 | |
Войдите:
Из опыта известно, что магнитное поле оказывает действие не только на проводники с током, но и на отдельные заряды, которые движутся в магнитном поле. Сила, которая действует на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и задается выражением
(1)
где В — индукция магнитного поля, в котором заряд движется.
Чтобы определить направление силы Лоренца используем правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, для Q<0 — противоположны), то отогнутый большой палец покажет направление силы, которая действует на положительный заряд. На рис. 1 продемонстрирована взаимная ориентация векторов v, В (поле имеет направление на нас, на рисунке показано точками) и F для положительного заряда. Если заряд отрицательный, то сила действует в противоположном направлении. Модуль силы Лоренца, как уже известно, равен
где α — угол между v и В.
Подчеркнем еще раз, что магнитное поле не оказывает действия на покоящийся электрический заряд. Этим магнитное поле существенно отличается от электрического. Магнитное поле действует только на движущиеся в нем заряды.
Зная действие силы Лоренца на заряд можно найти модуль и направление вектора В, и формула для силы Лоренца может быть применена для нахождения вектора магнитной индукции В.
Поскольку сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, то данная сила может менять только направление этой скорости, не изменяя при этом ее модуля. Значит, сила Лоренца работы не совершает. Другими словами, постоянное магнитное поле не совершает работы над движущейся в этом поле заряженной частицей и, следовательно, кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
В случае, если на движущийся электрический заряд вместе с магнитным полем с индукцией В действует еще и электрическое поле с напряженностью Е, то суммарная результирующая сила F, которая приложена приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца:
Это выражение носит название формулы Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.
Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамикедействует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического и магнитного полей. В Международной системе единиц (СИ)выражается как:F=q(E+(v умножыть В))
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом.
Макроскопическим проявлением силы Лоренца является сила Ампера.
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца
