Как найти модуль силы если известны масса, время, конечная скорость?
(напишите в формулах).
На этой странице сайта размещен вопрос Как найти модуль силы если известны масса, время, конечная скорость? из категории
Физика с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 5 – 9 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.
Сила, масса и ускорение
Расчеты
Сила — это физическая векторная величина, устанавливающая с какой силой другие тела или поле воздействуют на данное тело.
Обобщая опытные факты, Ньютон открыл основной закон динамики, сформулировав его таким образом:
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение.
Чтобы рассчитать силу (F), нужно массу (m) умножить на ускорение (a):
F = m * a
Единица измерения ускорения м/с2;
массы кг;
единица силы Н.
В системе СИ за единицу измерения силы принята сила, сообщающая телу массой 1 кг ускорение 1 м/с2, она была названа ньютоном (Н).
Исходя из определения ньютона, 1 Н равен 1 кг.м/с2.
Если известна масса тела m и действующая на него сила F, можно вычислить ускорение тела:
a = F / m
Согласно второго закона Ньютона, приобретенное телом ускорение будет прямо пропорционально силе F и обратно пропорционально массе m.
Быстро и правильно вычислить ускорение, силу, массу тела, установить их зависимость между собой вам поможет онлайн калькулятор.
Расчет силы, массы и ускорения онлайн
Мы знаем, что тело может двигаться равномерно и прямолинейно. В таком случае его скорость постоянна и не меняется по величине и направлению. Если же скорость тела меняет величину или величину и направление, то тело движется с определенным ускорением a→.
С точки зрения кинематики нас не интересует, почему тело движется тем или иным образом. Динамика в физике, наоборот, рассматривает взаимодействие тел как причину, которая определяет характер движения.
Взаимодействие тел определяет характер движения.
Динамика – раздел механики, в котором изучаются законы взаимодействия тел.
1 закон Ньютона
Законы динамики были сформулированы Исааком Ньютоном и опубликованы в 1687 году. Три закона Ньютона составляют основу классической механики, которая на протяжении нескольких столетий (вплоть до 20 века) главенствовала, как основная научная парадигма.
Классическая механика справедлива для тел, движущихся с малыми скоростями (скоростями, которые значительно меньше скорости света). Вообще законы Ньютона были выведены путем эмпирических наблюдений и обобщения опытных фактов.
Представим изолированное тело, на которое не действуют никакие другие тела. Это самая простая механическая система. Для описания движения тела необходима система отсчета.
Напомним, что система отсчета – это тело отсчета и связанные с ним системы координат и часов (отсчета времени). Причем в разных системах отсчета движение тела будет разным.
Сформулируем первый закон Ньютона. Он говорит о существовании так называемых инерциальных систем отсчета (ИСО) и называете также законом инерции. Существуют разные определения первого закона Ньютона.
Существуют системы отсчета, называемые инерциальными. В таких системах отсчета тела движутся равномерно и прямолинейно или покоятся, если на них не действуют другие тела или если их действие скомпенсировано.
Инерция – это свойство тел сохранять свою скорость при отсутствии на него воздействий со стороны других тел. Именно поэтому второе название первого закона Ньютона – закон инерции.
Первая формулировка закона инерции была выведена еще Галилео Галилеем в 1632 году. Ньютон лишь обобщил его выводы.
В классической механике законы движения формулируются для инерциальных систем отсчета.
При описании движения тел у поверхности Земли системы отсчета, связанные с Землей, можно приблизительно считать и инерциальными. Отклонения от закона инерции обнаруживаются при повышении точности экспериментов и обусловлены вращением Земли вокруг своей оси.
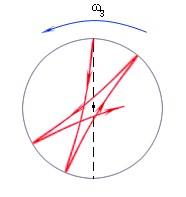
Приведем пример, иллюстрирующий неинерциальность системы отсчета, связанной с Землей. Рассмотрим колебания маятника Фуко. Это массивный шар, подвешенный на длинной нити и совершающий малые колебания относительно положения равновесия.
Плоскость колебаний маятника Фуко относительно Земли не остается неизменной вследствие вращения Земли. Проекция траектории маятника на поверхность Земли имеет вид розетки. Будь система инерциальной, плоскость качения маятника относительно Земли оставалась бы неизменной.
Еще одна система, которую можно приближенно принять за инерциальную – гелиоцентрическая система отсчета. Начало координат в ней помещено в центр Солнца, а оси направлены на отдаленные звезды. Эта система отсчета еще называется системой Коперника. Именно ее использовал Ньютон при выводе закона Всемирного тяготения (1682 г.).
Система отсчета, связанная с поездом, который с постоянной скоростью движется по прямым рельсам, также может считаться инерциальной. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно.
Что является причиной изменения скорости тела в инерциальной системе отсчета? Согласно первому закону Ньютона, это взаимодействие с другими телами. Чтобы количественно описать движение тела и взаимодействие его с другими телами, необходимо ввести понятия массы и силы.
Масса
Масса – физическая величина, мера инертности тела. Чем больше масса, тем больше инертность.
Единица измерения массы в международной системе СИ – килограмм (кг).
Масса в физике – скалярная и аддитивная величина.
Это значит, что если тело состоит из нескольких частей массами m1, т2, т3, .. , тn, то его общая масса будет равна сумме масс составных частей: m=m1+т2+т3+..+тn.
Вы наверняка замечали, что разные тела по-разному меняют свою скорость. Тяжелый грузовик остановить гораздо сложнее, чем игрушечную машинку, так как он обладает большей массой и, соответственно, инертностью.
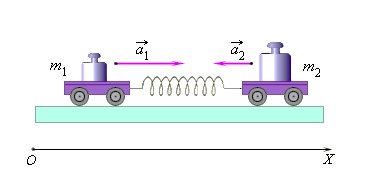
В результате взаимодействия двух тел меняются их скорости. Это значит, что в процессе взаимодействия тела приобретают ускорения. При любых воздействиях отношение ускорений двух тел остается постоянным. При этом, массы тел обратно пропорциональны ускорениям, которые они приобретают.
m1m2=-a2a1
Здесь a1 и a2 – проекции векторов ускорений a1 →и a2 →на ось OX. Знак минус означает, что ускорения тел направлены в противоположные стороны.
Какие есть способы измерения массы тела? Самый простой и очевидный – сравнить массу тела с массой эталона. В системе СИ, как уже говорилось, mэт=1 кг.
Сила
Сила – векторная физическая величина, количественная мера взаимодействия тел.
В системе СИ сила измеряется в Ньютонах (Н).
Именно сила – причина изменения движения тела. На тело может действовать несколько сил, которые имеют различную физическую природу. Например, сила тяжести, сила трения скольжения и сила трения качения, сила упругости и т.д.
Равнодействующая сила – векторная сумма всех сил, действующих на тело.
Как измерить силу? Необходимо установить эталон силы и найти способ сравнить другие силы с этим эталоном.
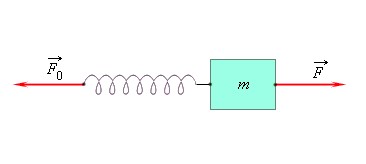
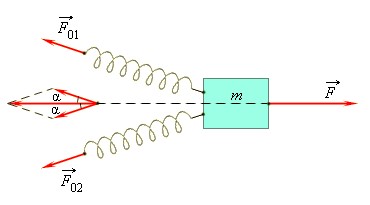
В качестве эталона можно использовать, например, силу, с которой растянутая до определенной величины пружина действует на прикрепленное к ней тело. Способ сравнения сил очень прост: если под действием двух сил (измеряемой F→ и эталонной F→0) тело движется равномерно или покоится, то эти силы равны по модулю.
F=F0.
Если измеряемая сила больше эталонной, то можно добавить еще одну эталонную пружину. При соблюдении условий, указанных выше, можно сказать, что в таком случае
F=2F0.
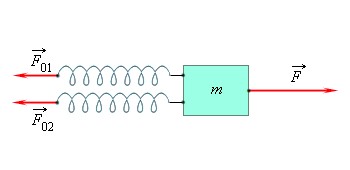
Для сравнения сил, меньших чем 2F0, можно использовать схему, приведенную ниже.
За эталон силы в международной системе СИ принята сила в 1 Ньютон. Это такая сила, которая сообщает телу массой 1 килограмм ускорение, равное 1 мс2.
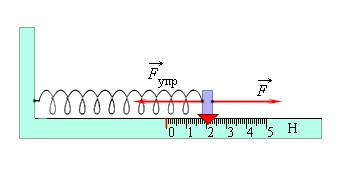
Прибор для измерения силы – динамометр. По сути, это пружина, откалиброванная специальным образом. При растяжении пружины приложенная сила указывается на шкале динамометра.
Формула модуля равнодействующей силы в физике
Формула модуля равнодействующей силы
На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.
Формула равнодействующей всех сил
Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(1right).]
Формула (1) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.
Складывают векторы, используя правило треугольника (рис.1)
правило параллелограмма (рис.2).
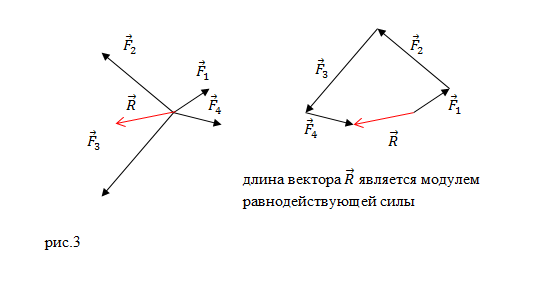
или многоугольника (рис.3):
Второй закон Ньютона и формула модуля равнодействующей
Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:
[overline{F}=sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(2right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач с решением
Пример 1
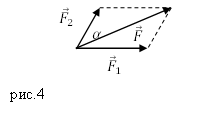
Задание. К материальной точке приложены силы, направленные под углом $alpha =60{}^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?
Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline{F}$ найдем, применяя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{40}^2+{20}^2+2cdot 40cdot 20{cos (60{}^circ ) }}approx 52,92 left(Нright).]
Ответ. $F=52,92$ Н
Пример 2
Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A{cos (omega t)(м) }$, где $s$ – путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?
Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:
[overline{F}=moverline{a}left(2.1right).]
Следовательно, модуль силы можно найти как:
[F=ma left(2.2right).]
Ускорение точки будем искать, используя связь между ним и перемещением точки:
[a=frac{d^2s}{dt^2}left(2.3right).]
Первая производная от $s$ по времени равна:
[frac{ds}{dt}=frac{d}{dt}(A{cos (omega t))=-Aomega {rm sin}?(omega t) (м) }left(frac{м}{с}right)(2.4);;]
вторая производная:
[frac{d^2s}{dt^2}=-A{omega }^2{cos left(omega tright) } left(frac{м}{с^2}right)(2.5).]
Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:
[F=mA{omega }^2{cos left(omega tright) }left(Нright).]
Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:
[F_{max}=mA{omega }^2 left(Нright).]
Ответ. $F=mA{omega }^2{cos left(omega tright) }left(Нright); F_{max}=mA{omega }^2 left(Нright)$
Читать дальше: формула периода колебаний математического маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Загрузить PDF
Загрузить PDF
Сила – это физический термин, который определяется как воздействие, заставляющее объект изменять свою скорость, направление движения или вращаться. Сила может ускорять объект под действием толчка или тяги. Отношение между силой, массой и ускорением было определено Исааком Ньютоном во втором законе движения, который гласит: сила, действующая на объект, равна произведению его массы на ускорение. Если вы хотите узнать, как измерить силу, следуйте данной пошаговой инструкции.
-
1
Разберитесь в соотношении между силой, массой и ускорением. Сила, действующая на объект – это произведение его массы на ускорение. Это соотношение можно представить в виде следующей формулы: Сила = Масса x Ускорение. Далее приведены другие положения, которые нужно иметь в виду при расчете силы:[1]
- Стандартная единица измерения массы – килограммы (кг).
- Стандартная единица измерения ускорения – м/с2.
- Стандартная единица измерения силы – ньютон (Н). Ньютон – это производная стандартная единица измерения. 1N = 1 кг x 1м/с2.
-
2
Измерьте массу заданного объекта. Масса объекта – это количество содержащейся в нем материи. Масса объекта всегда неизменна, неважно на какой планете он находится, тогда как вес меняется в зависимости от силы притяжения; ваша масса одинакова и на Земле, и на Луне.[2]
В метрической системе массу можно выражать в граммах в граммах или килограммах. Скажем, объект, с которым мы имеем дело – это грузовик, масса которого – 1000 кг.- Чтобы найти массу заданного объекта, поместите его на тройные рычажные или двойные чашечные весы. При этом будет получена масса в килограммах или граммах.
- В английской системе единиц измерения масса может быть выражена в фунтах. Поскольку сила также может быть выражена в фунтах, с целью уточнения использования данной величины был придуман термин “фунт-масса”. Однако если вы нашли массу объекта с использованием фунтов в английской системе, то будет лучше перевести ее в метрическую систему. Зная массу объекта в фунтах, вы можете перевести ее в килограммы просто умножив значение на 0,45.
-
3
Измерьте ускорение объекта. В физике ускорение определяется как изменение скорости, т.е. скорость в определенном направлении в единицу времени. Кроме общепринятого определения ускорения как повышения скорости, оно также может подразумевать замедление объекта или изменение направления его движения. Подобно измерению скорости с помощью спидометра, ускорение можно измерить акселерометром. Пусть ускорение грузовика массой 1000 кг, с которым мы имеем дело, составляет 3м/с2.
- В метрической системе скорость выражается в сантиметрах в секунду или в метрах в секунду, а ускорение – в сантиметрах в секунду за секунду (сантиметрах в секунду в квадрате) или в метрах в секунду за секунду (метрах в секунду в квадрате).
- В английской системе единиц измерения одним из способов выражения скорости являются футы в секунду, т.е. ускорение будет выражаться в футах в секунду в квадрате.
-
4
Умножьте массу объекта на ускорение. В результате вы получите значение силы. Просто подставьте известные числа в уравнение и вы узнаете силу объекта. Не забудьте указать ответ в ньютонах (Н).[3]
- Сила = Масса x Ускорение
- Сила = 1000 кг x 3м/с2
- Сила = 3000Н
Реклама
-
1
Найдите массу, зная силу и ускорение. Если вы знаете силу и ускорение объекта, то просто подставьте их в ту же формулу и найдете массу объекта. Вот как это сделать:
- Сила= Масса x Ускорение
- 3Н = Масса x 3м/с2
- Масса = 3Н/3м/с2
- Масса = 1 кг
-
2
Найдите ускорение, зная силу и массу. Если вы знаете силу и массу объекта, просто подставьте их в ту же формулу, чтобы найти ускорение объекта. Вот как это сделать:
- Сила= Масса x Ускорение
- 10Н = 2 кг x Ускорение
- Ускорение = 10Н/2кг
- Ускорение = 5м/с2
-
3
Найдите ускорение объекта. Если вы хотите найти силу объекта, вы можете вычислить его ускорение, зная массу. Все, что вам нужно сделать – это воспользоваться формулой для нахождения ускорения объекта.[4]
Формула имеет вид (Ускорение = Конечная скорость – Начальная скорость)/Время.- Пример: Бегун развивает скорость 6 м/с за десять секунд. Каково его ускорение?
- Конечная скорость составляет 6 м/с. Начальная скорость равна 0 м/с. Время равно 10 с.
- Ускорение = (6 м/с – 0 м/с)/10с = 6м/с/10с = 0,6м/с2
Реклама
Советы
- Если вы работаете с английскими единицами, то разделите ответ на коэффициент пересчета. Как было отмечено выше, в английской системе “фунт” может быть единицей измерения как силы, так и массы. Когда фунт используется в качестве единицы силы, его называют “фунт-сила”. Коэффициент пересчета равен 32,174 фунт-футов делить на фунт-силу за секунду в квадрате; 32,174 – это ускорение свободного падения на Земле в футах в секунду в квадрате. (Для упрощения вычислений, мы округлим это значение до 32)
- Обратите внимание, что взаимосвязь силы, массы и ускорения означает, что объект с малой массой и высоким ускорением может обладать такой же силой, что и объект с большой массой и низким ускорением.
- Массу можно выражать в слагах. Один слаг равен 32,174 фунтов массы. Слаг – это количество массы, которую сила в 1 фунт ускоряет на 1 фут в секунду в квадрате. При умножении массы в слагах на ускорение в футах в секунду в квадрате коэффициент перевода не используется.
- Масса 20 г, движущаяся с ускорением 5 сантиметров в секунду в квадрате, несет силу 20 умножить на 5, или 100 грамм-сантиметров в секунду в квадрате. (Грамм-сантиметр на секунду в квадрате называется диной).
- Так, масса 640 фунтов массы, движущаяся с ускорением 5 футов в секунду в квадрате несет силу приблизительно 640 умножить на 5 поделить на 32 или 100 фунтов силы.
- Вес – это выражение массы, на которую действует ускорение свободного падения. У поверхности Земли это ускорение примерно равно 9,8 метров в секунду в квадрате (9,80665), или 32 футов в секунду в квадрате (32,174). Так, в метрической системе 100 килограмм массы весят около 980 ньютонов, а 100 грамм массы – около 980 дин. В английской системе масса и вес могут быть выражены одной и той же единицей, поэтому 100 фунтов массы весят 100 фунтов силы. Поскольку пружинные весы измеряют силу притяжения объекта, они фактически измеряют вес, а не массу. (В повседневном обиходе разницы между этими понятиями нет, пока единственной силой притяжения в рассматриваемом вопросе является таковая на поверхности Земли).
- Масса 150 килограмм, движущаяся с ускорением 10 метров в секунду в квадрате несет силу 150 умножить на 10, или 1500 килограмм-сантиметров в секунду в квадрате. (Килограмм-метр в секунду в квадрате называется ньютон).
- Силы могут иметь специальные названия в зависимости от того, как они действуют на объект. Сила, которая ускоряет объект, называется тягой, тогда как сила, замедляющая объект, носит название торможения. Сила, изменяющая то, как объект вращается вокруг своей оси, называется моментом.
Реклама
Что вам понадобится
- Рычажные или пружинные весы
- Акселерометр
- Карандаш и бумага или калькулятор
Об этой статье
Эту страницу просматривали 35 205 раз.