В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться!

Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.
Сила и модуль силы
В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.
Что такое модуль силы?
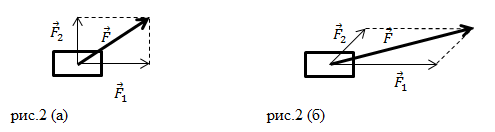
Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.
Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.
Модуль равнодействующих двух сил определяется по формулам:
- F=F1 + F2 (в случае сил с одинаковым направлением)
- F=F1 – F2 (силы с разным направлением)
Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.
Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).
Что это модуль скорости?

Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.
Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.
Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:
v = S/t = (x – x0)/t.
Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.
Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:
- Вычисляется скорость v21 на базе закона сложения скоростей v2 = v21 + v1, а значит v21 = v2 – v1.
- Определяется модуль скорости тела согласно теореме Пифагора.
Модуль импульса и модуль оси
Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается? Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.
Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее. Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
На чтение 11 мин Просмотров 2.5к. Опубликовано 07.05.2019
Содержание
- Сила и модуль силы
- Что такое модуль силы?
- Что это модуль скорости?
- Модуль импульса и модуль оси
В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться! 
Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.
Сила и модуль силы
В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.
Что такое модуль силы?
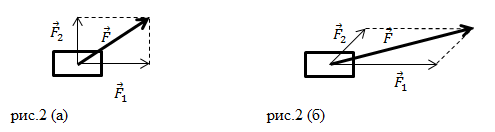
Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.
Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.
Модуль равнодействующих двух сил определяется по формулам:
- F=F1 + F2 (в случае сил с одинаковым направлением)
- F=F1 — F2 (силы с разным направлением)
Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.
Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).
Что это модуль скорости?

Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.
Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.
Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:
v = S/t = (x — x0)/t.
Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.
Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:
- Вычисляется скорость v21 на базе закона сложения скоростей v2 = v21 + v1, а значит v21 = v2 – v1.
- Определяется модуль скорости тела согласно теореме Пифагора.
Модуль импульса и модуль оси

Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается? Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.
Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее. Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
В 7 классе вы узнали, что равномерным движением называют такое движение, при котором за равные интервалы времени тело проходит равные части пути (см. § 1-ж). Например, если поезд ежечасно проезжает 60 км, ежеминутно проезжает 1 км и так далее, то движение равномерное. Итак, скорость равномерного движения:
υ – скорость равномерного движения, м/с
l – пройденный телом путь, м
Δ t – интервал времени движения, с
Поскольку пройденный путь и интервал времени – скалярные величины, то скорость равномерного движения является скаляром тоже. То есть, имея только числовое значение, она ничего не говорит нам о пространственном направлении изучаемого движения.
Обратим внимание: если движение является не только равномерным, но и прямолинейным, то путь тела равен модулю перемещения. Поэтому, пользуясь аналогией с предыдущей формулой, в физике определяют скорость равномерного прямолинейного движения:
 – скорость равнопрямолинейного движения, м/с
– скорость равнопрямолинейного движения, м/с
 – перемещение тела, м
– перемещение тела, м
Δ t – интервал времени движения, с
Поскольку перемещение – векторная величина, то скорость равномерного прямолинейного движения является вектором тоже, то есть величиной, имеющей не только числовое значение, но и пространственное направление.
Из геометрии мы знаем, что в результате произведения вектора на положительный скаляр получается новый вектор, направление которого совпадает с направлением исходного, а модуль равен произведению модуля исходного вектора на скаляр. Последняя формула – пример произведения вектора s на положительный скаляр ¹/ Δ t. Поэтому направление скорости равномерного прямолинейного движения всегда совпадает с направлением перемещения.
- При равномерном движении тело проходит равные части пути .
- Скорость равномерного движения находят делением пройденного пути на .
- Скорость равномерного движения является скалярной величиной, так как .
- Являться скалярной величиной – значит не давать информации .
- Модуль перемещения тела совпадает с пройденным путём, .
- Формулу для скорости равнопрямолинейного движения вводят, .
- Делением перемещения тела на интервал времени движения находят .
- Подобно перемещению, вектором является и .
- Являться вектором – значит быть .
- Поскольку скаляр ¹/ Δ t положителен, то .
Задача 1. Минутная стрелка часов-курантов на Спасской башне Кремля имеет длину 327 см. Найдите скорость движения её конца-указателя.
Решение. Поскольку конец стрелки движется по окружности циферблата, траектория движения является криволинейной. Наряду с этим движение является равномерным, так как за любые равные интервалы времени, например, за каждую минуту, конец стрелки проходит равные части пути (деления на циферблате, равные друг другу по всей длине окружности).
Поэтому мы применяем формулу из первой рамки в начале параграфа:
| υ = | . l . | = | 2 π R | ≈ | 2 · 3,14 · 327 см | ≈ | 2054 см | ≈ 34 см/мин |
| Δ t | Δ t | 60 мин | 60 мин |
Задача 2. Турист прошёл на север 3 км, затратив на это 45 минут, а затем повернул на восток и прошёл ещё 4 км, затратив на это 1 час. За какое время он прошёл бы из начальной в конечную точку маршрута, двигаясь прямолинейно с таким же модулем скорости, как и прежде?
Решение. Часть этой задачи мы уже решили в § 12-в, поэтому знаем, что расстояние между начальной и конечной точками равно 5 км. Но какова скорость туриста? Сначала найдём модули скоростей на обоих этапах:
| υ 1 = | . s 1 . | = | 3 км | = 4 км/ч | ; | υ 2 = | . s 2 . | = | 4 км | = 4 км/ч |
| Δ t 1 | 0,75 ч | Δ t 2 | 1 ч |
Мы видим, что модули обеих скоростей равны и соответствуют скорости человека, идущего пешком. Значит, это значение можно принять за модуль скорости равнопрямолинейного движения и «по гипотенузе»:
| υ = | . s . | ⇒ | Δ t | = | . s . | = | 5 км | = 1,25 ч | = 1 час 15 мин |
| Δ t | υ | 4 км/ч |
Примечание. Если бы в условии задачи не было слова «прямолинейно», мы не смогли бы её решить вообще. Поскольку турист может идти по извилистой тропинке, мы не смогли бы определить его путь, а по нему – время. Именно поэтому мы использовали формулу из второй рамки, поскольку в ней присутствует перемещение, а не путь.
- Траектория конца стрелки криволинейна, .
- Наряду с непрямолинейностью траектории конца стрелки, его .
- Равномерность этого движения мы обосновываем тем, что .
- Поскольку движение равномерно, но непрямолинейно, .
- Конец стрелки ежеминутно передвигается на .
- Как должен идти турист по условию задачи?
- После первой пары вычислений мы обнаруживаем: .
- Поскольку модули скоростей равны, то их .
- При отсутствии какого термина задача будет не решаема?
- Если движение туриста непрямолинейно, то будет невозможно .
Физика.ru • Клуб для учителей физики, учащихся 7-9 классов и их родителей
Основываясь на определении скорости, мы можем утверждать, что скорость является вектором. Она непосредственно выражается через вектор-перемещения, отнесенный к промежутку времени, и должна обладать всеми свойствами вектора перемещения.
Направление вектора скорости, так же как направление физически малого вектора перемещения, определяется по чертежу траектории. В этом можно наглядно убедиться на простых примерах.
Если к вращающемуся точильному камню прикоснуться железной пластинкой, то снимаемые им опилки приобретут скорость тех точек камня, к которым прикасалась пластинка, и затем улетят в направлении вектора этой скорости. Все точки камня движутся по окружностям. Во время опыта хорошо видно, что отрывающиеся раскаленные частички-опилки уходят по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек вращающегося точильного камня.
Обратите внимание на то, как расположены выходные трубы у кожуха центробежного водяного насоса или у сепаратора для молока. В этих машинах частицы жидкости заставляют двигаться по окружностям и затем дают им возможность выйти в отверстие, расположенное в направлении вектора той скорости, которую они имеют в момент выхода. Направление вектора скорости в этот момент совпадает с направлением касательной к траектории движения частиц жидкости. И выходная труба тоже направлена по этой касательной.
Точно так же обеспечивают выход частиц в современных ускорителях электронов и протонов при ядерных исследованиях.
Итак, мы убедились, что направление вектора скорости определяется по траектории движения тела. Вектор скорости всегда направлен вдоль касательной к траектории в той точке, через которую проходит движущееся тело.
Для того чтобы определить, в какую сторону вдоль касательной направлен вектор скорости и каков его модуль, нужно обратиться к закону движения. Допустим, что закон движения задан графиком, показанным на рис. 1.54. Возьмем приращение длины пути  соответствующее малому вектору
соответствующее малому вектору  по которому определяется вектор скорости. Вспомним, что
по которому определяется вектор скорости. Вспомним, что  Знак
Знак  указывает
указывает

направление движения по траектории, а следовательно, определяет ориентировку вектора скорости вдоль касательной. Очевидно, что через модуль этого приращения длины пути будет определяться модуль скорости.
Таким образом, модуль вектора скорости и ориентировку вектора скорости вдоль касательной к траектории можно определить из соотношения

Здесь  является алгебраической величиной, знак которой указывает, в какую сторону по касательной к траектории направлен вектор скорости.
является алгебраической величиной, знак которой указывает, в какую сторону по касательной к траектории направлен вектор скорости.
Итак, мы убедились, что модуль вектора скорости может быть найден по графику закона движения. Отношение  определяет угол наклона а касательной на этом графике. Наклон касательной на графике закона движения будет тем больше, чем больше
определяет угол наклона а касательной на этом графике. Наклон касательной на графике закона движения будет тем больше, чем больше  т. е. чем больше в выбранный момент скорость движения.
т. е. чем больше в выбранный момент скорость движения.
Еще раз обратим внимание на то, что для полного определения скорости требуется одновременное знание траектории и закона движения. Чертеж траектории позволяет определить направление скорости, а график закона движения — ее модуль и знак.
Если теперь мы обратимся снова к определению механического движения, то убедимся в том, что после введения понятия скорости для полного описания любого движения больше ничего не требуется. Используя понятия радиус-вектора, вектора перемещения, вектора скорости, длины пути, траектории и закона движения, можно получить ответы на все вопросы, связанные с определением особенностей любого движения. Все эти понятия взаимосвязаны друг с другом, причем знание траектории и закона движения позволяет найти любую из этих величин.

§4. Примеры из физики
Простейшие примеры векторов в физике – скорость и сила.
1. Всякое движение можно представить как результат сложения нескольких движений, его составляющих. Скорость результирующего движения изображается по величине и направлению диагональю параллелограмма, построенного на отрезках, изображающих составляющие скорости, как на сторонах. Рассмотрим конкретный пример.
Рыбак переправляется на лодке `A` через реку, которая течёт в сторону, указанную стрелкой (рис. 18). Пусть скорость течения воды `vec(v_1)` изображается по величине и направлению отрезком `AB`, а скорость `vec(v_2)` движения лодки относительно воды под влиянием усилий гребца изображается отрезком `AC` (в стоячей воде лодка двигалась бы по направлению `AC` со скоростью `vec(v_2)`). Лодка будет двигаться относительно берега по направлению `AM` со скоростью `vec v`, изображаемой диагональю `AD` параллелограмма, построенного на векторах `vec(v_1)` и `vec(v_2)` (в данном случае параллелограмм `ABCD` является прямоугольником).
2. Сила – как векторная величина – всегда имеет определённое направление, модуль, а также точку приложения.
Часто встречаются случаи, когда на тело действуют несколько сил. Тогда бывает удобно заменить их одной силой, которая производит на тело такое же действие, как и несколько одновременно действующих сил. Такую силу (если она существует) называют равнодействующей. Нахождение равнодействующей нескольких сил осуществляется с помощью правил векторного сложения, при этом слагаемые силы называют составляющими.
Так, несколько сил, действующих на одну и ту же точку тела, всегда можно заменить одной равнодействующей, как бы ни были направлены силы и каковы бы ни были их величины. Пусть, например, на тело действуют четыре силы `vec(F_1)`, `vec(F_2)`, `vec(F_3)` и `vec(F_4)`, приложенные к одной точке `O` и лежащие в одной плоскости (рис. 19). Тогда их равнодействующая `vec F` будет равна векторной сумме этих сил, найденной по правилу многоугольника (рис. 20).
Найти равнодействующую `vec R` трёх равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми силами равны между собой.
`F_1 = F_2 = F_3 = F`.
См. рис. 21. Углы между парами векторов `vec(F_1)` и `vec(F_2)`, `vec(F_2)` и `vec(F_3)`, а также между векторами `vec(F_1)` и `vec(F_3)`, равны друг другу и равны `120^@`. Сложим силы `vec(F_2)` и `vec(F_3)` по правилу параллелограмма. Вследствие равенства модулей сил `vec(F_2)` и `vec(F_3)` этот параллелограмм есть ромб. Сумма сил `vec(F_2) + vec(F_3)` есть диагональ ромба, поэтому углы между парами векторов `vec(F_2)` и `vec(F_2) + vec(F_3)`, а также `vec(F_3)` и `vec(F_2) + vec(F_3)` равны по `60^@`, т. е. векторы `vec(F_1)` и `vec(F_2) + vec(F_3)` направлены вдоль одной прямой, но в противоположные стороны. Силовой параллелограмм, построенный на векторах `vec(F_2)` и `vec(F_3)`, состоит из двух равносторонних треугольников, поэтому модуль силы
`|vec(F_2) + vec(F_3)| = F_2 = F_3 = F = F_1`, т. е `vec F_1 = – (vec(F_2) + vec(F_3))`,
откуда следует `vec(F_1) + vec(F_2) + vec(F_3) = 0`.
К телу приложено `6` сил, лежащих в одной плоскости и составляющих друг с другом углы в `60^@`. Силы последовательно равны `1`, `2`, `3`, `4`, `5` и `6 Н`. Найти равнодействующую `vec R` этих шести сил.
Сложение сил по правилу многоугольника здесь нецелесообразно. Поступим иначе. Сложим сначала попарно силы, направленные вдоль одной прямой (см. рис. 22 а, б, в).
Получим
`|vec(F_2) + vec(F_4)| = 4 – 1 = 3`,
аналогично `|vec(F_2) + vec(F_5)| = 5 – 2 = 3` и `|vec(F_3) + vec(F_6)| = 6 – 3 = 3`.
Сумма сил `vec(F_2) + vec(F_5)` направлена вдоль вектора `vec(F_5)`. Туда же направлена и сумма сил `vec(F_1) + vec(F_4) + vec(F_3) + vec(F_6)`, причём модуль этой силы равен `3`. В итоге получаем, что сумма всех шести сил `vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)` направлена вдоль направления силы `vec(F_5)`, а модуль этой силы `|vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)| = 3 + 3 = 6 Н`.
Найти равнодействующую `vec R` пяти равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми соседними силами равны между собой (см. рис. 23). (Эти углы, разумеется, равны `360^@ //5 = 72^@`.)
В отличие от предыдущего примера здесь мы имеем нечётное число сил, поэтому невозможно образовать из них целое число пар. Поступим иначе. Возьмём какую-нибудь силу, например, `vec(F_1)`, а остальные сгруппируем в пары и попарно сложим их (см. рис. 24):
`vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`.
Почему удобна именно такая группировка сил в пары? Дело в том, что обе суммы сил (и `vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`) направлены вдоль линии действия силы `vec(F_1)`. Ясно, что равнодействующая всех сил будет направлена вдоль линии действия силы `vec(F_1)`. Модули сумм сил легко найти из геометрии. Например, в силовом параллелограмме, построенном на векторах `vec(F_2)` и `vec(F_5)`, который является ромбом, длина диагонали ромба (модуль силы `vec(F_2) + vec(F_5)`) равна удвоенной половинке диагонали, а та легко ищется из любого из четырёх прямоугольных треугольников, на которые ромб разбивается диагоналями. В результате
`|vec(F_2) + vec(F_5) | = 2F cos 72^@`,
где `F` – модуль любой из пяти исходных сил. Аналогично
`|vec(F_3) + vec(F_4)| = 2F cos 36^@`.
В итоге для модуля искомой силы получаем формулу
`R = F(1 + 2 cos 72^@ – 2 cos 36^@)` (*).
Для углов `72^@` и `36^@` нет таких простых формул, как для углов `30^@`, `45^@` или `60^@`. Пользуясь калькулятором, можно, однако, показать, что согласно формуле (*) `R = 0`.
Имеется и более красивое доказательство того, что результирующий вектор есть нулевой вектор. В самом деле, мы довольно произвольно взяли в качестве силы, которой не хватило пары, силу `vec(F_1)`. Если бы в качестве такой взять силу `vec(F_2)`, а в пары объединить `vec(F_1)` и `vec(F_3)` (одна пара) и `vec(F_4)` и `vec(F_5)`, то, повторив рассуждения, получим, что равнодействующая всех пяти сил `vec R` должна быть направлена вдоль линии действия силы `vec(F_2)`. Возможно ли, чтобы вектор был одновременно направлен вдоль двух несовпадающих друг с другом направлений (и `vec(F_1)`, и `vec(F_2)`; а на самом деле, как догадался читатель, ещё и вдоль направления действия сил `vec(F_3)`, `vec(F_4)` и `vec(F_5)`!)? Ненулевым вектор не может быть! Остаётся одна возможность: суммарный вектор – нулевой!
В примерах 10 и 11 мы искали по правилу параллелограмма суммы сил.
В примере 12 нас интересовала лишь проекция равнодействующей силы на направление (например, силы `vec(F_1)`).
В следующих примерах наш интерес будет также скорее не к равнодействующей силе, а только к каким-то её проекциям.
Электрический фонарь весом `Q = 16 Н` укреплён, как показано на рис. 25.
Определите отношение натяжений `T_1` и `T_2` в проволоках `BA` и `BC`, углы наклона которых даны на рисунке.
В условиях равновесия сумма всех сил, приложенных к точке `B`, равна нулю. Поэтому проекция равнодействующей всех сил на горизонтальное направление тоже равна нулю. Проекция силы со стороны проволоки, идущей к фонарю, на это направление равна нулю (эта сила вертикальна). Остаются вклады от двух натяжений со стороны проволок `BA` и `BC`. Горизонтальную ось направим слева направо. Тогда имеем: T1, гор+T2, гор=0T_{1,;mathrm{гор}}+T_{2,;mathrm{гор}}=0 (см. рис. 26), т. е.
`T_1 * cos 60^@ – T_2 cos 45^@ = 0`
(или `T_1 * sin 30^@ – T_2 sin 45^@ = 0`), откуда получаем `T_1//T_2 = sqrt2`.
Однородная массивная верёвка подвешена за два конца на разных высотах (см. рис. 27). Масса верёвки `m`. Углы, которые составляет верёвка с вертикалью в точках закрепления, равны `30^@` и `60^@`.
Определите силы натяжения верёвки вблизи её точек крепления.
Задача кажется очень трудной, т. к. не ясно, какую роль играет неизвестная нам форма верёвки, которую она примет под действием сил тяжести всех частей верёвки. (В предыдущем примере мы не интересовались провисанием проволок под действием силы тяжести, молчаливо считая провисание малым.) И всё же задача в той постановке, в какой дана, имеет простое решение. Мысленно проведём горизонтальную ось слева направо. Поскольку верёвка находится в равновесии, то сумма проекций всех сил на горизонтальное направление равна нулю. Сила тяжести верёвки имеет нулевую проекцию на это направление (эта сила направлена вертикально). Снова остаются вклады от двух натяжений (см. рис. 28):
T1, гор+T2, гор=0T_{1,;mathrm{гор}}+T_{2,;mathrm{гор}}=0, или `- T_1 * sin 30^@ + T_2 sin 60^@ = 0`.
Полагая `sin 30^@ = 1//2` и `sin 60^@ = sqrt3 //2`, находим `T_1 // T_2 = sqrt3`. Мысленно проведём ещё и вертикальную ось, направив её вниз. Сумма проекций всех сил на эту ось также равна нулю:
`mg – T_1 cos 30^@ – T_2 cos 60^@ = 0`.
Учитывая найденное ранее соотношение между `T_1` и `T_2` и значения `cos 60^@ = 1//2` и `cos 30^@ = sqrt3 //2`, получаем:
`mg – sqrt3 * T_2 * sqrt3 //2 – T_2 //2 = 0`,
откуда
`T_2 = mg//2` и `T_1 = sqrt3 mg//2`.
На гладкой наклонной плоскости с углом наклона `alpha` лежит брусок массой `m`. Какую горизонтальную силу нужно приложить к бруску, чтобы он находился в покое (рис. 29)?
Определите также модуль нормальной силы реакции на брусок со стороны наклонной плоскости.
Брусок по условию задачи покоится. Значит, сумма всех сил, приложенных к бруску, равна нулю. Равны нулю и суммы проекций сил на любые направления, в частности, на направление вдоль наклонной плоскости и перпендикулярное ему. Нормальная сила реакции `vec N` со стороны наклонной плоскости имеет равную нулю составляющую вдоль наклонной плоскости.
Проекция сила тяжести `m vec g` на ось `Ox` вдоль наклонной плоскости (рис. 30) равна `- mg sin alpha`, а проекция горизонтальной силы `F` на эту ось равна `F cos alpha`. Других сил вдоль наклонной плоскости не действует (плоскость, по условию задачи, гладкая, т. е. сила трения пренебрежимо мала). Приравнивая нулю сумму проекций на ось `Ox` всех сил, действующих на тело, получаем: `- mg sin alpha + F cos alpha = 0`, откуда находим
`F = mg (sin alpha)/(cos alpha) = mg * bbb”tg” alpha`.
Для отыскания `N` обратимся к проекциям сил на направление `Oy`. Приравняем нулю и сумму проекций на ось `Oy`:
`N – mg cos alpha – F sin alpha = 0`,
откуда `N = mg cos alpha + F sin alpha`, или с учётом найденного значения `F`:
`N = mg cos alpha + mg (sin^2 alpha)/(cos alpha) = mg (cos^2 alpha + sin^2 alpha)/(cos alpha)`,
тогда с учётом основного тригонометрического тождества, `sin^2 alpha + cos^2 alpha = 1`, получаем окончательно
`N = (mg)/(cos alpha)`.
На шероховатой поверхности доски лежит брусок массой `m`. К нему приложена сила, направленная под углом `alpha` к горизонту (см. рис. 31).
Определите модуль нормальной силы реакции со стороны поверхности.
Поскольку брусок не проваливается и не подскакивает вверх, то сумма проекций сил на вертикальную ось равна нулю:
`N + F * sin alpha – mg = 0`,
(см. рис. 32), откуда находим
`N = mg – F * sin alpha`.
Часто совершенно безосновательно приравнивают силу реакции `N` силе тяжести `mg`. Мы видим, что даже в случае горизонтальной поверхности это в общем случае не так. Для наклонной плоскости это тоже не так. В предыдущем примере нормальная сила реакции равнялась `mg//cos alpha`. Кстати, если бы удерживающая сила `F` действовала там не вдоль горизонтали, а вдоль наклонной плоскости, то для удержания бруска на наклонной плоскости потребовалась бы сила величиной `F = mg sin alpha`, а нормальная сила реакции была бы равна `N = mg cos alpha` (и снова не равнялась бы `mg`!)
Докажите это самостоятельно.
Самолёт взлетает с аэродрома со скоростью v=220 км/чv=220;mathrm{км}/mathrm ч под углом `alpha = 20^@` к горизонту. Найдите модули горизонтальной и вертикальной составляющих скорости самолёта.
(См. рис. 33). В данном примере мы имеем дело с весьма простым случаем разложения скорости на два взаимно перпендикулярных направления:
`vec v = vec(v _sf”гор”) + vec(v_sf”верт”)`,
vгор=v cos α≈207 км/чv_mathrm{гор}=v;cos;alphaapprox207;mathrm{км}/mathrm ч, vверт=v sin α≈75 км/чv_mathrm{верт}=v;sin;alphaapprox75;mathrm{км}/mathrm ч.
В безветренную погоду самолёт летит на север со скоростью 180 км/ч180;mathrm{км}/mathrm ч (50 м/с50;mathrm м/mathrm с) относительно земли. С какой скоростью относительно земли будет лететь самолёт, если дует западный ветер со скоростью 10 м/с10;mathrm м/mathrm с?
(См. рис. 34). В данном случае мы имеем дело со сложением движений: `vec(v_sf”с”) = vec(v_sf”св”) + vec(v_sf”в”)`, где `vec(v_sf”св”)` – скорость самолёта относительно воздуха (модуль которой равен скорости самолёта относительно земли в безветренную погоду), а `vec(v_sf”в”)` – скорость воздуха. Далее по теореме Пифагора получаем:
vс=502+102=2600≈51 м/сv_mathrm с=sqrt{50^2+10^2}=sqrt{2600}approx51;mathrm м/mathrm с.
Лодка пытается пересечь реку, текущую со скоростью u=3 км/чu=3;mathrm{км}/mathrm ч. Скорость лодки в стоячей воде v=5 км/чv=5;mathrm{км}/mathrm ч. Под каким углом `alpha` к нормали к берегу надо направить лодку, чтобы она двигалась поперек реки (без сноса)? Какой будет при этом модуль скорости лодки `v` относительно берега?
Как и в примере 9, мы также имеем дело со случаем сложения движений. Но там было проще: не требовалось выбирать никакой стратегии, рыбак лишь наблюдал, как снесёт его лодку течением воды в реке. Если бы вода в реке покоилась, то, направив корпус лодки под углом `alpha` к нормали, мы заставили бы её двигаться в направлении вектора `vec V` (см. рис. 35). В действительности, вода в реке не стоячая, а имеет скорость `vec u` Поэтому сносимая течением лодка будет двигаться в направлении вектора `vec v` таком, что `vec v = vec V + vec u`. Учитывая, что оба треугольника в параллелограмме на рис. 35 прямоугольные (по условию, лодка должна двигаться перпендикулярно берегам), находим
`sin alpha = u//V = 3//5`, `alpha ~~ 37^@`,
а по теореме Пифагора v=V2-u2=4 м/сv=sqrt{V^2-u^2}=4;mathrm м/mathrm с.
Лодка пытается пересечь реку, текущую со скоростью u=5 км/чu=5;mathrm{км}/mathrm ч. Скорость лодки в стоячей воде V=3 км/чV=3;mathrm{км}/mathrm ч. Под каким углом `alpha` к нормали к берегу надо направить корпус лодки, чтобы её снесло как можно меньше? Под каким углом `beta` к нормали к берегу будет при этом плыть лодка?
В данном примере скорость лодки относительно воды меньше, чем скорость воды в реке, `V < u`, поэтому реализовать план из предыдущего примера (рис. 35) невозможно. Наша цель состоит в том, чтобы направить корпус лодки под таким углом `alpha` к нормали к берегу, чтобы сносимая течением лодка двигалась под углом `beta`, по возможности наименьшим (см. рис. 36 ф, б, в).
В данном примере складывать скорости (лодки относительно воды `vec V` и воды в реке `vec u`) удобно по правилу треугольника, а не параллелограмма: приставим начало вектора `vec V` к концу вектора `vec u`. Выбирая оптимальный план (с наименьшим углом сноса), будем мысленно поворачивать вектор `vec V`. При этом конец вектора будет описывать окружность с центром в конце вектора `vec u`. Из рисунков видно, что минимальному углу сноса лодки `beta` соответствует случай, когда вектор `vec v = vec V + vec u` направлен по касательной к этой окружности. При этом вектор `vec V _|_ vec v` т. е. треугольник скоростей на рис. 36 в прямоугольный. Отсюда получаем:
`sin alpha = V//u = 3//5`; `alpha ~~37^@`; `beta = 90^@ – alpha ~~53^@`.
Лодку вытягивают из воды, стоя на крутом берегу и выбирая верёвку, которая привязана к носу лодки, со скоростью `v` (см. рис. 37).
Какой будет скорость лодки `u` в момент, когда верёвка будет составлять угол `alpha` с горизонтом? Верёвка нерастяжима.
Традиционная ошибка решающих эту задачу состоит в том, что пытаются разложить движение лодки на два направления – горизонтальное и вертикальное, делая (неправильное!) построение, как показано на рис. 38а и получая неверный ответ `u = v * cos alpha`. Что здесь неправильно? В отличие от самолёта из примера 17, который двигался под отличным от нуля углом к горизонту (см. рис. 33), здесь лодка движется горизонтально! Сделаем другое разложение скорости лодки `vec u` по двум направлениям – вдоль верёвки (в данный момент времени!) и перпендикулярно ей (см. рис. 38б).
Проекция вектора `vec u` на направление верёвки будет равна скорости `v`, с которой выбирают верёвку: `v = u cos alpha`, поэтому `u = v/(cos alpha)`.
Поясним ещё, почему проекция вектора `vec u` на направление верёвки будет равна скорости `v` с которой выбирают верёвку. Если мы имеем абсолютно твердое тело (АТТ), деформациями в котором можно пренебречь, или нерастяжимую нить (но уже максимально натянутую), то как бы ни двигались АТТ или нерастяжимая нить, они будут обладать следующим свойством. Возьмём две произвольные точки `A` и `B` нити или АТТ и мысленно соединим их прямой. Тогда составляющие скоростей выбранных точек вдоль этой прямой в любой момент времени будут равны друг другу: vA∥→=vB∥→overrightarrow{v_{Aparallel}}=overrightarrow{v_{Bparallel}} (см. рис. 39). В противном случае изменялось бы расстояние между точками `A` и `B`. Составляющие скорости, перпендикулярные отрезку прямой `AB`, могут быть при этом любыми.
Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов (см. рис. 40). В некоторый момент времени силы натяжения тросов, идущих от лодок 1 и 2, равны друг другу по модулю и равны `F`. Угол между тросами равен `2 alpha`. Какая равнодействующая сила приложена к буксируемой лодке со стороны тянущих её лодок? Чему будет равна эта сила в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?
Две силы нужно сложить по правилу параллелограмма, который в данном случае будет ещё и ромбом с перпендикулярными друг другу диагоналями, разбивающими его на четыре равных прямоугольных треугольника. Из геометрии рис. 41 видно, что модуль равнодействующей силы `R` равен удвоенной длине прилежащего катета: `R = 2F cos alpha`. При стремлении угла между направлениями тросов к нулю `R -> 2F` (`cos alpha -> 1` при `alpha -> 0`).
Хитрее оказывается похожая задача, когда заданы не силы, а скорости.
Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов (см. рис. 42). В некоторый момент времени модули скоростей лодок 1 и 2 равны друг другу и равны `v_1 = v_2 = v`. Найти модуль и направление скорости буксируемой лодки `u`. Тросы нерастяжимы. Чему будет равна эта скорость в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?
Ясно, что «решение» `u = 2v cos alpha` (как в предыдущем примере) не подходит, т. к. при `alpha -> 0` мы получили бы, что `u -> 2v`, чего не может быть. Если, например, две собаки в упряжке бегут с одинаковыми скоростями `v` в одном направлении, то и скорость упряжки будет равна этой же скорости `v` (если, конечно, упряжка не отцепилась или к ней не подключили дополнительно мотор).
Решение задачи такое же, как в примере 21. В данном примере важнейшими словами являются «Тросы нерастяжимы». Ясно, что правильное построение, учитывающее это условие, должно быть таким, как на рис. 43, откуда немедленно получаем `v = u cos alpha`, поэтому `u = v/(cos alpha)`. Тогда в предельном случае, когда `alpha -> 0`, имеем `u -> v`, как и должно быть.
Заметим, что четырёхугольник на рис. 43 весьма мало похож на параллелограмм из предыдущего примера. Еще меньше будет похож на параллелограмм этот четырёхугольник, когда модули скоростей `v_1 != v_2` (см. рис. 44).
Две лодки буксируют третью с помощью двух тросов (рис. 45). В некоторый момент времени скорость 2-ой лодки в 2 раза больше, чем скорость 1-ой, `v_2 = 2v_1 = 2v`, а угол между тросами равен `90^@`. В каком направлении и с какой скоростью движется в этот момент буксируемая лодка? Тросы нерастяжимы.
В данном случае четырёхугольник на рис. 44 будет прямоугольником – см. рис. 46 (т. е. всё же параллелограммом).
По определению тангенса угла `”tg”varphi _1 = v_2 //v_1 = 2`, откуда, пользуясь калькулятором, находим `varphi _1 ~~63^@`; `varphi _2 = 90^@ – varphi _1 ~~ 27^@`.
Модуль скорости буксируемой лодки найдём по теореме Пифагора (раз уж у нас «случайно» появились прямоугольные треугольники):
`u = sqrt(v_1^2 + v_2^2) = sqrt(v^2 + (2v)^2) = sqrt5 * v ~~ 2,2 v`.
Содержание:
Движение и силы:
Вы уже знаете, каким сложным является хаотическое движение молекул. В повседневной жизни мы встречаемся с более простыми видами движения. Движутся люди, автомобили (рис. 76), самолеты, Солнце, Луна и другие тела. Окружающий нас мир немыслим без движения. Характеристики многих движений можно легко определить и описать с помощью несложных математических формул.

Как установить, движется или нет данное физическое тело? Рассмотрим пример. Вы стоите на остановке и вдали видите автобус (рис. 77). Движется он или нет? Несмотря на то что вращения колес не видно, вы уверенно определяете, что автобус движется. Изменяется с течением времени его положение относительно киоска, деревьев, домов, неподвижных относительно поверхности Земли. Точно так же мы судим о движении облаков и птиц в небе, рыб в аквариуме, футболистов на поле, поездов и любых других тел.

Изменение положения тела в пространстве относительно других тел с течением времени называется механическим движением. Следовательно, движение происходит в пространстве и во времени.
Рассмотрим еще один пример. Вы едете в электричке (рис. 78). Можно ли сказать, что, сидя в ней, вы находитесь в состоянии покоя? И да, и нет. Да — потому, что вы не движетесь по электричке, т. е. с течением времени ваше положение относительно электрички не меняется. Нет — потому, что вместе с электричкой вы движетесь относительно поверхности Земли. А если электричка остановилась? Теперь вы находитесь в состоянии покоя относительно электрички и поверхности Земли, но движетесь вместе с Землей вокруг Солнца (рис. 79), перемещаясь за каждую секунду примерно на 30 км относительно звезд.

Таким образом, покой и движение относительны. Относительны и характеристики движения. Это легко увидеть на опыте. Укрепите светоотражатель (фликер) на ободе колеса вашего велосипеда. Какова будет кривая, которую опишет фликер (ее называют траекторией) при движении колеса? Относительно вас или вашего друга, едущего рядом с вами, фликер будет двигаться по окружности. А стоящий человек, мимо которого вы проезжаете, увидит, что фликер описывает не окружность, а сложную кривую (рис. 80). Следовательно, траектория тоже относительна.

Главные выводы:
- Механическое движение — это изменение положения тела в пространстве относительно другого тела или тел с течением времени.
- Механическое движение и покой относительны.
Траектория, путь и время
Для решения научных и практических задач необходимо уметь описывать механическое движение тела или его частей, определять характеристики движения и устанавливать связи между ними.
Какими физическими величинами описывается механическое движение?
Проведите мелом по доске. Мел при движении описывает линию, которая хорошо видна на доске.
В голубом небе часто отчетливо видны белые следы позади летящих самолетов (рис. 81). Быстро мчащийся катер оставляет на поверхности воды пенистую дорожку (рис. 82).


Линия, которую описывает тело при своем движении, называется траекторией.
Мы привели примеры движений, когда траектория — видимая линия. Но чаще всего она невидима. Однако траекторию всегда можно изобразить, если отметить точками положения движущегося тела в различные моменты времени, а затем соединить эти точки. Несложно, например, представить траекторию летящего ядра (рис. 83).
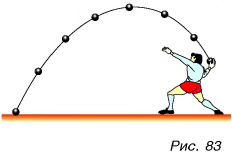
Если траектория движения — прямая линия, движение называется прямолинейным. Например, такова траектория падающего с дерева яблока (рис. 84). Если же траектория — кривая линия, то движение называется криволинейным (см. рис. 83).

Длина той части траектории, которую описывает тело за данный промежуток времени, называется путем, пройденным телом за этот промежуток времени.
Обозначается путь обычно буквой s. Путь это физическая величина. Его можно измерить или вычислить по формуле. Единицей пути в СИ является 1 метр (1 м). На практике путь часто измеряют в кратных единицах — километрах — или в дольных — сантиметрах, миллиметрах, микрометрах.
А что такое промежуток времени? Допустим, вы отправляетесь в путешествие на поезде «Минск — Москва». Поставим вопрос: за какой промежуток времени поезд пройдет путь s = 212 км от Минска до Орши? Ответить на этот вопрос очень легко. Во-первых, нужно знать момент времени, когда поезд отправляется из Минска. Обозначим его буквой t с индексом 1, т. е. 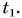 Во-вторых, нужно знать момент времени, когда поезд прибывает в Оршу. Обозначим его
Во-вторых, нужно знать момент времени, когда поезд прибывает в Оршу. Обозначим его 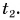 Промежуток времени, за который поезд проходит путь от Минска до Орши, равен:
Промежуток времени, за который поезд проходит путь от Минска до Орши, равен:
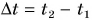
(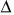 — греч. «дельта» — знак, обозначающий в математике и физике изменение величины, т. е. разность ее конечного и начального значений). Так, если в нашем примере
— греч. «дельта» — знак, обозначающий в математике и физике изменение величины, т. е. разность ее конечного и начального значений). Так, если в нашем примере 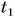 = 20 ч 10 мин,
= 20 ч 10 мин, 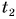 = 23 ч 15 мин, то
= 23 ч 15 мин, то 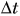 = 3 ч 5 мин.
= 3 ч 5 мин.
Для краткости вместо «промежуток времени» будем говорить «время».
Единицей времени в СИ является 1 секунда (1 с). Иногда удобнее использовать кратные единицы времени: минуту (мин) и час (ч). Существуют и такие единицы времени, как сутки (сут), год. Вы, конечно, знаете, что одни сутки равны 24 ч, 1 год равен 365 (366) сут.
Для измерения времени служат различные Рис. 87 приборы, например метроном (рис. 85), часы (рис. 86), секундомер (рис. 87).



Для практических целей полезно научиться отсчитывать про себя секунды, произнося числа через равные интервалы времени.
При прохождении лечебных процедур иногда необходимо фиксировать определенный промежуток времени, например 1 мин или 5 мин. В таких случаях удобно использовать песочные часы (рис. 88).

Для любознательных:
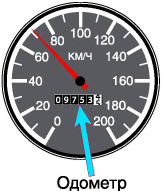
Для измерения пройденного пути в автомобилях имеется специальный прибор — одометр (от греч. «дорога» и «мера») (см. рис.). Одометр включает:
- датчик, фиксирующий обороты колеса;
- счетчик, подсчитывающий обороты;
- индикатор, фиксирующий путь, который проехал автомобиль.
Главные выводы:
- Траектория — линия, которую описывает тело при своем движении.
- Если траектория — прямая линия, то движение называется прямолинейным, если траектория — кривая линия, то движение криволинейное.
- Путь — длина той части траектории, которую описывает тело за данный промежуток времени.
Равномерное движение и скорость
Среди всего разнообразия движений тел наиболее просто описывается равномерное прямолинейное движение. Что представляет собой это движение? Как его охарактеризовать?
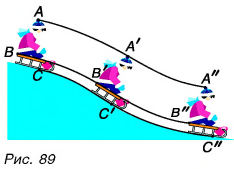
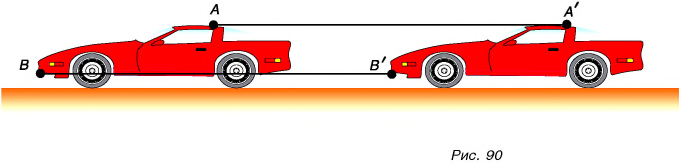
Рассмотрим пример. Девочка на санках спускается с горки. Понаблюдаем за движением нескольких точек, например А, B, С (рис. 89). Эти точки движутся совершенно одинаково, описывая равные траектории. Движение, при котором все точки тела описывают одинаковые по форме и равные по длине траектории, называется поступательным. А если тело движется поступательно, нужно ли изучать движение всего тела или достаточно изучить движение только одной его точки? Рис. 90 Ведь все точки (рис. 89, 90) движутся совершенно одинаково. В данном учебном пособии мы будем изучать движение тела, не рассматривая его форму, размеры, т. е. будем моделировать тело точкой.
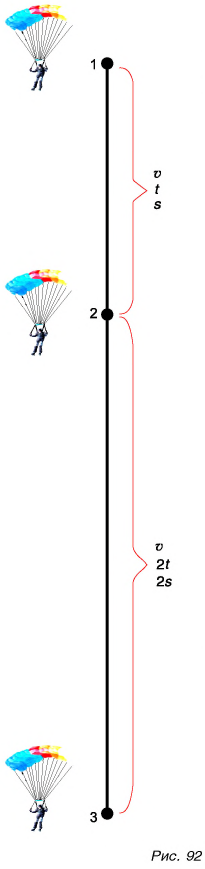
Как определить, какой путь пройдет тело при движении за данный промежуток времени? Пусть тележка (рис. 91) движется прямолинейно. Будем отмечать ее положения, точнее положения точки A, через равные промежутки времени. Это можно сделать, установив на тележке капельницу с вытекающими через равные промежутки времени, например через 2 с, каплями. Определим пути, проходимые тележкой за  = 2 с на первом, втором, третьем и последующих участках движения.
= 2 с на первом, втором, третьем и последующих участках движения.
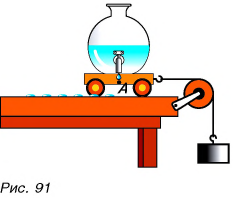
Подобрав груз, можно достичь того, что пути, пройденные тележкой за равные промежутки времени 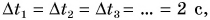 окажутся равными
окажутся равными 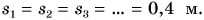 Если уменьшить промежутки времени, то во столько же раз уменьшатся и проходимые пути.
Если уменьшить промежутки времени, то во столько же раз уменьшатся и проходимые пути.
Движение, при котором тело за любые равные промежутки времени проходит равные пути, называется равномерным.
Найдем отношения путей к соответствующим промежуткам времени:
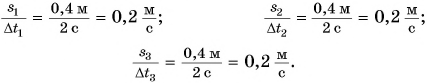
Величина 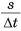 новая физическая величина, называемая скоростью. Обозначается скорость буквой
новая физическая величина, называемая скоростью. Обозначается скорость буквой 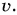
Тогда для равномерного прямолинейного движения можно записать формулу:

Из формулы (1) следует, что скорость равномерного прямолинейного движения есть физическая величина, равная отношению пути, пройденного телом, к промежутку времени.
Из формулы (1) легко найти путь, пройденный за любой промежуток времени, и промежуток времени:

На примере с капельницей вы убедились, что при равномерном прямолинейном движении скорость является постоянной величиной.
При равномерном прямолинейном движении с увеличением промежутка времени увеличивается путь (рис. 92), но скорость остается постоянной.
Значит, скорость является характеристикой движения. Теперь можно дать еще одно определение равномерного прямолинейного движения, используя его характеристику — скорость: равномерное прямолинейное движение — это движение но прямой с постоянной скоростью.
Единицей скорости в СИ является 1 метр в секунду 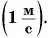 На практике часто используют другие единицы. Например, скорость обычных транспортных средств (автобуса, поезда, самолета и др.) удобно выражать в километрах в час
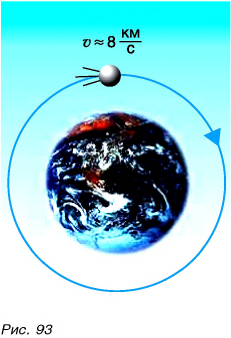
На практике часто используют другие единицы. Например, скорость обычных транспортных средств (автобуса, поезда, самолета и др.) удобно выражать в километрах в час 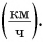 Скорость космических ракет, спутников (рис. 93) выражают в километрах в секунду
Скорость космических ракет, спутников (рис. 93) выражают в километрах в секунду 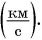 При решении задач, как правило, все физические величины выражают в основных единицах СИ.
При решении задач, как правило, все физические величины выражают в основных единицах СИ.
Пусть автомобиль движется но шоссе со скоростью 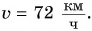 Выразим эту скорость в метрах в секунду
Выразим эту скорость в метрах в секунду 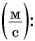
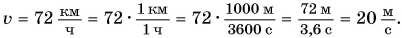
Скорость движения пешехода  Выразите ее самостоятельно в метрах в секунду
Выразите ее самостоятельно в метрах в секунду 
Максимальная скорость движения в природе — скорость распространения света в пустоте (рис. 94).

Она равна 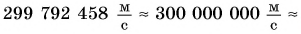
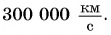 Вас не удивило огромное значение этой скорости? Сравните ее со скоростью звука в воздухе –
Вас не удивило огромное значение этой скорости? Сравните ее со скоростью звука в воздухе – 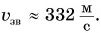 Теперь легко объяснить, почему гром вы слышите позже, чем видите молнию, хотя молния и гром возникают практически одновременно.
Теперь легко объяснить, почему гром вы слышите позже, чем видите молнию, хотя молния и гром возникают практически одновременно.
Из формулы 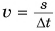 следует, что для нахождения скорости нужно знать путь и промежуток времени, за который этот путь пройден. Но люди изобрели и широко применяют приборы, которые непосредственно показывают скорость, например, стрелкой на циферблате. Такие приборы называются спидометрами (рис. 95). Если скорость движения автомобиля равна
следует, что для нахождения скорости нужно знать путь и промежуток времени, за который этот путь пройден. Но люди изобрели и широко применяют приборы, которые непосредственно показывают скорость, например, стрелкой на циферблате. Такие приборы называются спидометрами (рис. 95). Если скорость движения автомобиля равна 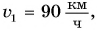 а самолета —
а самолета — 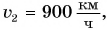 то за одно и то же время самолет преодолеет в 10 раз больший путь, а это значит, что самолет движется в 10 раз быстрее автомобиля.
то за одно и то же время самолет преодолеет в 10 раз больший путь, а это значит, что самолет движется в 10 раз быстрее автомобиля.
Таким образом, скорость характеризует быстроту движения, т. е. показывает, как быстро тело меняет свое положение в пространстве относительно других тел.
Главные выводы:
- Скорость — количественная характеристика быстроты движения.
- Определить скорость движения можно, разделив пройденный путь на затраченный промежуток времени.
- Если скорость постоянна, то движение равномерное.
Графики пути и скорости при равномерном прямолинейном движении
Можно ли выразить связь пути s и времени t не через формулы, а каким-либо другим способом? Для этого используются графики.
Поясним суть графического метода на конкретном примере. Пусть самолет движется равномерно и прямолинейно со скоростью 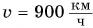 (рис. 96). Опишем движение самолета графически, т. е. построим графики зависимости пути и скорости движения самолета от времени движения.
(рис. 96). Опишем движение самолета графически, т. е. построим графики зависимости пути и скорости движения самолета от времени движения.

Путь s от начального момента времени 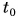 до момента времени t равен
до момента времени t равен 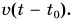 Начальный момент времени
Начальный момент времени 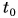 примем за нуль
примем за нуль 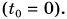 Тогда формула пути упростится:
Тогда формула пути упростится: 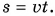
Найдем значения пути для различных значений промежутка времени и занесем их в таблицу 1.

Например, если t = 3ч, то
Теперь построим график зависимости пути от времени. По оси абсцисс в определенном масштабе (например, 1 см — 1 ч) будем откладывать промежутки времени движения, а по оси ординат (в масштабе 1 см — 900 км) — путь (рис. 97).
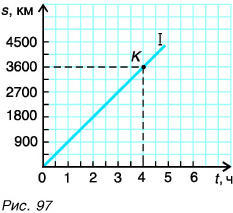
Прямая I выражает графическую зависимость пути от времени равномерного движения самолета. Эту прямую называют графиком пути. График пути напоминает известный вам из математики график функции 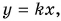 выражающей прямую пропорциональную зависимость у от х.
выражающей прямую пропорциональную зависимость у от х.
Ценность графика пути в том, что он, как и соотношение 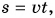 позволяет решить главную задачу — найти путь s, пройденный телом за произвольный промежуток времени
позволяет решить главную задачу — найти путь s, пройденный телом за произвольный промежуток времени
Например, нас интересует путь самолета за промежуток времени t = 4 ч. Для этого из точки на горизонтальной оси, соответствующей времени t = 4 ч (см. рис. 97), проводим перпендикуляр до пересечения с графиком (точка К). Из найденной точки К опускаем перпендикуляр на ось ординат и получаем ответ без вычислений. Путь s = 3600 км.
А что представляет собой график скорости? Он выражает зависимость скорости от времени. Так как скорость с течением времени не изменяется, то различным моментам времени соответствует одно и то же значение скорости. Составим таблицу 2 и построим прямую, выражающую зависимость скорости от времени, откладывая по оси абсцисс время, а по оси ординат — скорость (рис. 98).

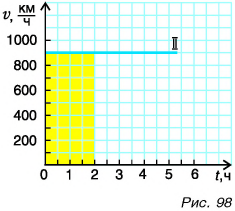
График скорости равномерного прямолинейного движения — прямая, параллельная оси времени.
Прямая II изображает график скорости движения самолета. Что дает график скорости? Он не только показывает значение скорости, но и позволяет найти пройденный путь. Рассчитаем путь самолета за промежуток времени t = 2 ч. Согласно формуле 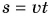 этот путь
этот путь 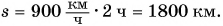 Посмотрим на это произведение с точки зрения геометрии. Первый множитель
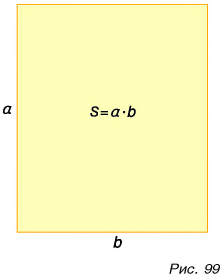
Посмотрим на это произведение с точки зрения геометрии. Первый множитель 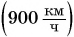 выражает одну сторону закрашенного прямоугольника (см. рис. 98), второй (2 ч) другую. Из математики вы уже знаете, что перемножением сторон a и b находят площадь S прямоугольника (рис. 99). Конечно, площадь не есть путь, речь идет только о численном равенстве. Пройденный путь численно равен площади фигуры под графиком скорости.
выражает одну сторону закрашенного прямоугольника (см. рис. 98), второй (2 ч) другую. Из математики вы уже знаете, что перемножением сторон a и b находят площадь S прямоугольника (рис. 99). Конечно, площадь не есть путь, речь идет только о численном равенстве. Пройденный путь численно равен площади фигуры под графиком скорости.
Для любознательных:
Площадью фигуры под графиком скорости определяется путь не только при равномерном прямолинейном, но и при любом другом движении. Например, путь за промежуток времени  (см. рис.) численно равен площади закрашенной фигуры:
(см. рис.) численно равен площади закрашенной фигуры: 
Главные выводы:
- График пути выражает зависимость пройденного пути от времени движения тела.
- Путь при равномерном прямолинейном движении можно определить по формуле
 по графику пути или с помощью графика скорости.
по графику пути или с помощью графика скорости.
Пример №1
Легковой и грузовой автомобили равномерно движутся в одном направлении но параллельным полосам прямолинейного участка
шоссе. Скорость движения легкового автомобиля 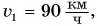 грузового —
грузового — 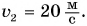 Каким будет расстояние между автомобилями через промежуток времени t = 3,0 мин, если в начальный момент автомобили находились рядом?
Каким будет расстояние между автомобилями через промежуток времени t = 3,0 мин, если в начальный момент автомобили находились рядом?
Запишем условие и выразим величины через основные единицы СИ.
Дано:
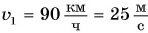
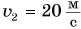
t = 3, 0 мин = 180 с
Решение:
Найдем путь, который проехал каждый из автомобилей за промежуток времени t:

Расстояние между автомобилями:
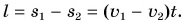
Подставим значения и вычислим:
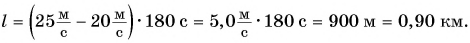
Ответ: 
Пример №2
Графики зависимости пути от времени равномерных прямолинейных движений пешехода Димы (1) и велосипедиста Пети (2) представлены на рисунке 102. Во сколько раз отличаются скорости движения мальчиков?
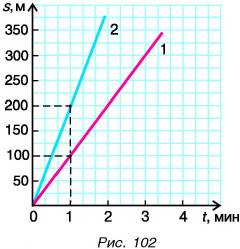
Решение
Из графиков следует, что за промежуток времени t = 1 мин Дима прошел путь 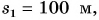 а Петя проехал
а Петя проехал 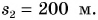
Скорость движения Димы:
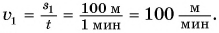
Скорость движения Пети:
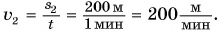
Отношение:
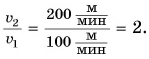
Ответ: скорость движения Пети на велосипеде в 2 раза больше скорости движения Димы пешком.
Этот же ответ можно было получить проще:
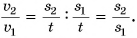
Из графика для одного и того же момента времени, например t = 1 мин (либо 2 мин и т. д.), определяем пути 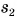 и
и 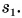 Тогда
Тогда
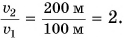
Неравномерное (переменное) движение. Средняя скорость
Проанализируйте движение автобуса. Он уменьшает скорость перед остановкой. Затем в течение какого-то промежутка времени стоит на остановке, т. е. его скорость равна нулю, после чего скорость увеличивается. Значит, скорость автобуса в процессе движения изменяется, т. е. является переменной величиной.
Движение, при котором скорость изменяется, называется неравномерным (переменным).
Практически все движения, наблюдаемые в природе и технике, — неравномерные. С изменяющейся скоростью движутся, например, люди, птицы (рис. 103), дельфины (рис. 104), поезда, падают предметы (рис. 105). Но как же тогда характеризовать это движение?



Неравномерное движение характеризуется средней скоростью. Как определить среднюю скорость? Рассмотрим пример. Вы едете на экскурсию в Брест поездом. Поезд проходит от Минска до Бреста путь s = 330 км. На прохождение этого пути затрачивается время t = 4,5 ч. В течение данного времени поезд стоит на станциях, движется то с увеличивающейся, то с уменьшающейся скоростью.
Среднюю скорость находят путем деления всего пути на весь промежуток времени, за который этот путь пройден. Обозначим среднюю скорость 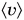 и запишем формулу:
и запишем формулу:
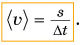
Тогда поезд «Минск — Брест» движется со средней скоростью

Вас не удивило, что мы использовали формулу равномерного движения? Да, действительно формально мы нашли среднюю скорость так, как будто поезд весь путь s = 330 км двигался равномерно с постоянной скоростью 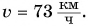 Это, конечно же, не означает, что он на самом деле двигался равномерно. На отдельных участках пути скорость движения поезда была как значительно большей
Это, конечно же, не означает, что он на самом деле двигался равномерно. На отдельных участках пути скорость движения поезда была как значительно большей 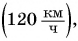 так и меньшей, чем
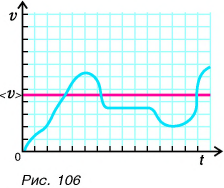
так и меньшей, чем 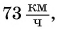 и даже равной нулю (рис. 106).
и даже равной нулю (рис. 106).
Для любознательных:
Средняя скорость дает лишь приблизительное представление о быстроте движения тела. Описание переменного движения более сложно по сравнению с описанием равномерного.
Например, если скорость поезда на участке разгона возрастает от О до 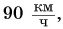 то в различных точках траектории она принимает различные значения из этого промежутка. Таким образом, можно говорить не только о средней скорости на данном участке траектории, но и о скорости в данной точке траектории. Такую скорость называют в физике мгновенной скоростью.
то в различных точках траектории она принимает различные значения из этого промежутка. Таким образом, можно говорить не только о средней скорости на данном участке траектории, но и о скорости в данной точке траектории. Такую скорость называют в физике мгновенной скоростью.
Главные выводы:
- Характеристикой неравномерного движения является средняя скорость.
- Для вычисления средней скорости нужно путь разделить на весь промежуток времени, затраченный на прохождение этого пути.
Пример №3
Катя прошла путь 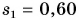 км за промежуток времени
км за промежуток времени 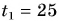 мин. Затем остановилась и в течение промежутка времени
мин. Затем остановилась и в течение промежутка времени 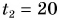 мин разговаривала с подругой, после чего прошла путь
мин разговаривала с подругой, после чего прошла путь 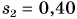 км за промежуток времени
км за промежуток времени 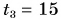 мин. Определите среднюю скорость движения Кати.
мин. Определите среднюю скорость движения Кати.
Дано:
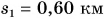
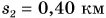
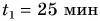
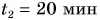
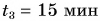
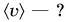
Решение
Весь путь, который прошла Катя:
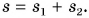
Весь затраченный промежуток времени:
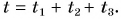
Средняя скорость движения Кати:
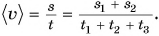
Вычислим 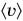 :
:
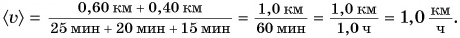
Ответ: 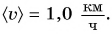
Пример №4
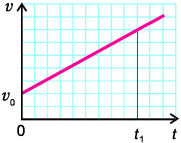
По графику скорости (рис. 107) определите путь и среднюю скорость движения велосипедиста за промежуток времени t = 0,60 ч.
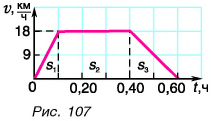
Решение
Искомый путь численно равен площади фигуры под графиком скорости. Путь 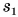 велосипедист проехал за промежуток времени
велосипедист проехал за промежуток времени 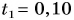 ч. Он численно равен площади прямоугольного треугольника, закрашенного в голубой цвет:
ч. Он численно равен площади прямоугольного треугольника, закрашенного в голубой цвет:
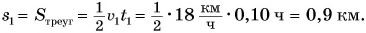
Аналогично можно найти пути 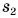 и
и 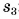 :
:
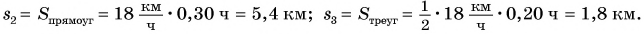
Весь путь: 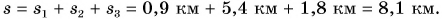
Средняя скорость движения велосипедиста:
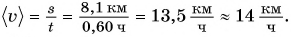
Ответ: 
Почему изменяется скорость движения тела
Равномерное прямолинейное движение, т. е. движение с постоянной скоростью, — лишь модель реального движения. В жизни всякое движение (от движения огромных планет до движения невидимых частиц) чаще всего происходит с изменяющейся скоростью. Что является причиной изменения скорости?
Рассмотрим опыты. На столе лежит стальной шарик Он находится в состоянии покоя относительно стола. Чтобы заставить шарик двигаться, можно толкнуть его рукой или приблизить к нему магнит (рис. 111). В обоих случаях на шарик действуют другие тела (рука, магнит), что и является причиной изменения скорости движения шарика. А как долго шарик будет двигаться после толчка? Опыт показывает, что скорость движения шарика уменьшается, а через некоторое время его движение прекращается. Почему?
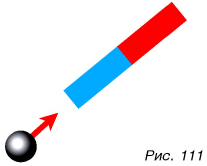
Проведем другой опыт. Три одинаковых шарика одновременно скатываются с одинаковой высоты (рис. 112). Дорожки, по которым затем о движутся шарики, отличаются: первая посыпана песком, вторая покрыта тканью, а третья — стеклом. Движение но третьей дорожке продолжается дольше, поскольку трение здесь наименьшее. Значит, причина прекращения движения шарика — трение между поверхностями шарика и стола и, конечно, сопротивление воздуха. А если бы мы смогли убрать эти причины, шарик двигался бы с постоянной скоростью сколько угодно долго.
Движение тела без действия на него других тел, как и покой, — его естественное состояние.
То, что тело остается в покое, если нет действия других тел, вполне понятно. Но как же тело может само но себе двигаться, если в повседневной жизни мы видим, что тело движется только тогда, когда Рис. 113 на него действует другое тело? Санки (рис. 113) надо тянуть за веревку, лодка плывет под действием весел (рис. 114). А были бы нужны веревка и весла, если бы не было сопротивления движению? Если бы вода не оказывала сопротивления движению, лодка после толчка двигалась бы бесконечно долго с постоянной скоростью.


Итак, если тело находится в состоянии покоя или в состоянии движения, то оно стремится сохранять это состояние (не изменять скорость), пока на него не подействуют другие тела.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения (сохранять свою скорость неизменной) при отсутствии действия на него других тел называется инерцией.
С инерцией нам приходится встречаться постоянно. При резком торможении автобуса пассажиры наклоняются вперед, так как продолжают двигаться по инерции. При резком разгоне автобуса они отклоняются назад. Почему? Л может ли автомобиль остановиться мгновенно? Нет. Как бы ни были сильны тормоза, инерция препятствует мгновенному торможению. Именно из-за инерции тормозной путь автомобиля тем больше, чем больше скорость его движения. Мы уверены, что, помня об инерции, вы не будете перебегать улицу перед движущимся транспортом и научите не делать этого своих младших братьев и сестер. А сколько неприятностей из-за инерции случается, пока мы учимся кататься на коньках!
Инерция может приносить человеку не только неприятности, но и огромную пользу. В водяных и паровых турбинах, а также в ветряных двигателях (рис. 115) используется инерция движения воды, пара, ветра. Инерция играет полезную роль при применении удара, от выколачивания пыли до насадки на рукоятку молотка. Космонавт благодаря инерции может выйти в открытый космос (рис. 116) и не отстать от корабля.


Для любознательных:
Древнегреческий философ Аристотель (IV в. до н. э.) считал, что только покой — естественное состояние тела, а движение — насильственное. Тело стремится к своему естественному состоянию, поэтому, если не поддерживать движение, оно прекращается.
Ошибка Аристотеля состояла в том, что он верил в инерцию покоя, но не понимал, что телам столь же свойственна инерция движения.
Спустя приблизительно 2000 лет после Аристотеля итальянский ученый Галилео Галилей смог вообразить идеализированный мир мир без трения. В результате он пришел к выводу о том, что движение тела без действия на него других тел, как и покой, является его естественным состоянием.
Главные выводы:
- Если на тело не действуют другие тела, то оно либо находится в состоянии покоя, либо движется равномерно и прямолинейно (по инерции).
- Изменить состояние покоя или движения тела можно только воздействием на него другого тела или тел.
Масса тела и плотность вещества
Одинаково ли легко изменить скорость различных тел? Мимо нас пролетает комар. Трудно ли изменить его скорость? Достаточно просто дунуть (рис. 117, а). А если проезжает груженый автомобиль МАЗ (рис. 117, б)? Инерция есть у всех тел, но это свойство проявляется у них в разной степени. Оно почти незаметно у комара, но очень заметно у автомобиля, для изменения скорости которого требуются большие и длительные воздействия.

Для характеристики инерции тела в физике используется физическая величина, называемая массой. Чем массивнее тело, тем труднее изменить его скорость, тем больше оно противится таким изменениям. Масса тела — мера его инерции. Иногда говорят: мера его инертности.
Обозначим массу тела буквой m. Основной единицей массы в СИ является 1 килограмм (1 кг). Полезно знать, что 1 л воды при комнатной температуре имеет массу, практически равную 1 кг. Соответственно, масса 1 мл равна 1 г. Обратите внимание! В килограммах измеряется единственная физическая величина — масса.
От чего зависит масса тела? Сравните разгон и торможение груженого и порожнего автомобилей. Понятно, что масса тела зависит от количества вещества в теле (от числа молекул). Дело в том, что массой (т. е. инерцией) обладает каждая молекула, поэтому массу всего тела можно рассматривать как сумму масс всех его молекул. Будут ли одинаковыми массы тел, если они содержат одинаковое число молекул? Да, если тела состоят из одного и того же вещества. Нет, если тела состоят из различных веществ (например, алюминиевая и золотая ложки). А теперь сравним массы разных веществ, имеющих одинаковый объем.
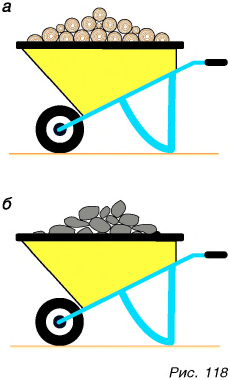
Задумайтесь над вопросом: какую тележку легче сдвинуть с места — нагруженную сухими дровами (рис. 118, а) или нагруженную камнями (рис. 118, б), имеющими равный с дровами объем? Конечно, тележку с дровами. Ее масса меньше. Значит, масса единицы объема дров и единицы объема камней разная.
Масса вещества, содержащегося в единице объема, называется плотностью вещества.
Чтобы найти плотность, необходимо массу вещества разделить на его объем. Плотность обозначается греческой буквой 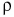 (ро). Тогда
(ро). Тогда
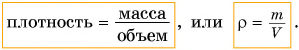
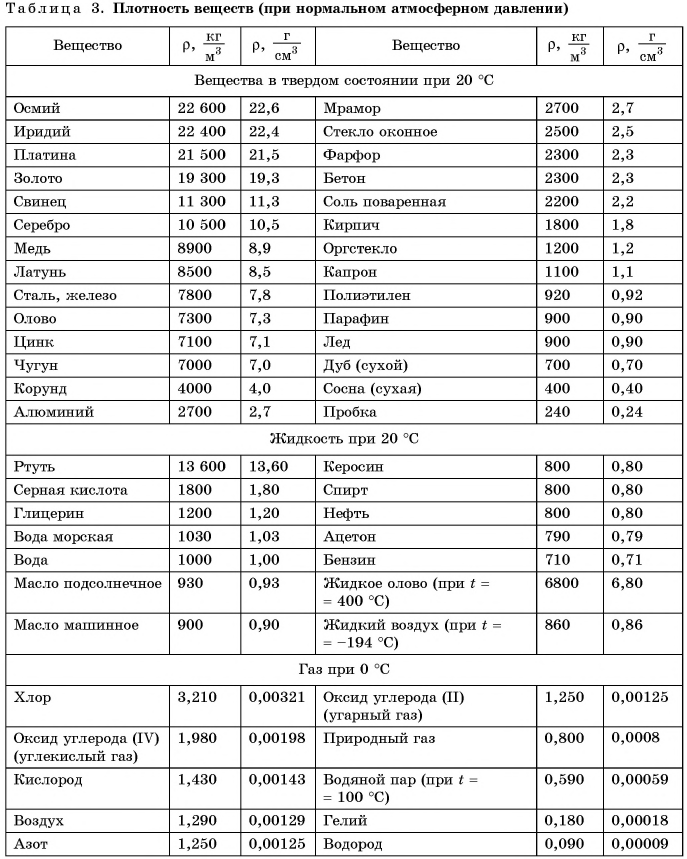
Единицей измерения плотности в СИ является 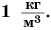 Плотности различных веществ определены на опыте и представлены в таблице 3.
Плотности различных веществ определены на опыте и представлены в таблице 3.
На рисунке 119 изображены массы известных вам веществ в объеме 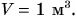
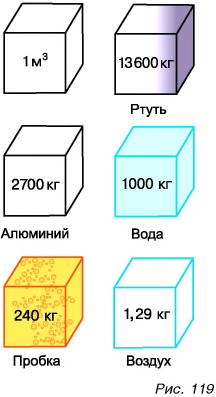
У большинства веществ плотность в твердом состоянии больше, чем в жидком. Например, плотность олова в твердом состоянии 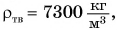 а в жидком (при температуре 400 °С)
а в жидком (при температуре 400 °С) 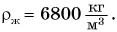
Плотность вещества в жидком состоянии больше, чем в газообразном. Чем это можно объяснить? Вспомните о различии в расстояниях между молекулами. Самые большие расстояния — между молекулами газа. Поэтому плотность сжиженного воздуха (при -194 °С) равна 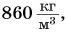 а в газообразном состоянии —
а в газообразном состоянии — 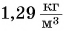 (при 0 °С).
(при 0 °С).
Зная плотность и объем тела, легко найти массу:
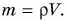
Формулу 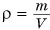 можно использовать не только для однородных тел, но и для тел, имеющих полости или состоящих из разных веществ. Только в этом случае формула выражает среднюю плотность тела (сравните со средней скоростью):
можно использовать не только для однородных тел, но и для тел, имеющих полости или состоящих из разных веществ. Только в этом случае формула выражает среднюю плотность тела (сравните со средней скоростью):
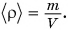
Для любознательных:
Твердое вещество, состоящее из молекул 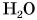 (лед), имеет плотность
(лед), имеет плотность 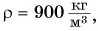 жидкое (вода) —
жидкое (вода) — 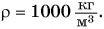
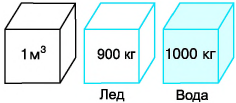
Вы заметили особенность? Плотность льда меньше плотности воды, что указывает на более плотную упаковку (т. е. меньшие промежутки) молекул в жидком состоянии вещества (вода), чем в твердом (лед).
Из всех видов деревьев наименьшей плотностью обладает древесина бальзового дерева 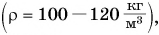 растущего в тропиках Центральной и Южной Америки.
растущего в тропиках Центральной и Южной Америки.
Средняя плотность Вселенной ничтожно мала 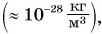 а вещество нейтронных звезд имеет очень большую плотность
а вещество нейтронных звезд имеет очень большую плотность 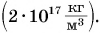
Главные выводы:
- Чем больше масса тела, тем труднее изменить скорость его движения.
- Плотность вещества показывает, какая масса вещества содержится в единице его объема.
- Плотность вещества в различных агрегатных состояниях разная.
- Тела, состоящие из разных веществ, характеризуются средней плотностью.
Пример №5
Средняя плотность тела человека примерно равна плотности воды. Зная свою массу, вычислите объем тела.
Дано:
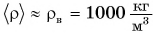

Решение
Определим с помощью весов свою массу m. Например, m = 50 кг. Тогда объем тела
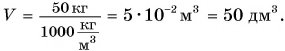
Ответ: 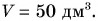
Сила
Изменить скорость движения тела можно воздействием на него другого тела. Чем больше это воздействие, тем сильнее изменяется скорость. Напрягая мышцы рук, вы увеличиваете скорость тележки. Ваш старший брат или отец может сильнее подействовать на тележку и увеличить скорость ее движения больше.
С помощью какой физической величины можно количественно определить, насколько сильно воздействует одно тело на другое, например человек на тележку? Такой величиной является сила.
Сила — количественная мера воздействия одного тела на другое.
В приведенном примере результатом воздействия является изменение скорости, значит, сила — причина изменения скорости движения тела.
Однако действие одного тела на другое приводит не только к изменению скорости. Подействуем на пружину гирей (подвесим ее к пружине) (рис. 120, а). Действие гири на пружину вызывает ее удлинение (рис. 120, б). Гиря, стоящая на тонкой доске (рис. 121), прогибает ее. Сжимая пальцами ластик, вы изменяете его форму. В этих случаях действие одного тела на другое, т. е. сила, вызывает изменение размеров или формы тела.
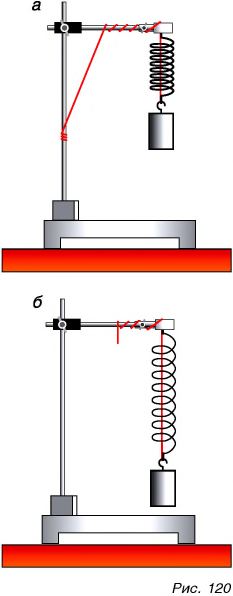
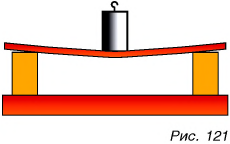
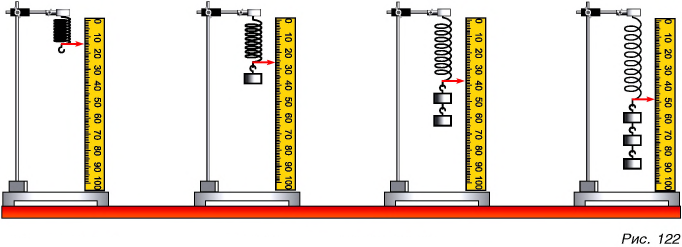
Изменение размеров или формы тела называется деформацией. Значит, сила является не только причиной изменения скорости, но и причиной деформации тела. Чем больше сила, тем больше деформация. Действительно, подействуйте на пружину более тяжелой гирей, т. е. большей силой, и растяжение пружины будет больше (рис. 122).
Сила не может существовать сама по себе. Если мы говорим, что на тело действует сила, это означает только то, что на тело действует другое тело.
Обычно силу обозначают буквой F и изображают в виде стрелки. Направление стрелки указывает направление действия силы. Начало стрелки совпадает с точкой приложения силы. Абсолютное число, выражающее длину стрелки, называют модулем силы.
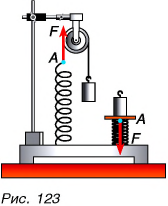
Итак, сила характеризуется модулем, направлением и точкой приложения. Пусть на одинаковые пружины действуют две одинаковые гири (рис. 123). Одна пружина растягивается под действием гири, другая — сжимается. Модули действующих на пружины сил одинаковы, но направления у сил разные.
На рисунке 124 изображены два тела (арбуз и яблоко), действующие на стол с одинаково направленными, но имеющими разные модули силами. Эти силы приложены к крышке стола в точках  и
и 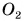 и направлены вертикально вниз. Модуль силы
и направлены вертикально вниз. Модуль силы 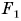 больше модуля силы
больше модуля силы 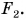
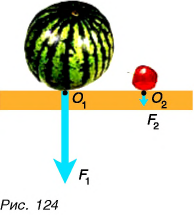
Чаще всего тело испытывает не одно, а сразу два или более действий, причем иногда противоположного направления. Как изменится скорость движения тела в этом случае? Если модули противоположно направленных сил равны, то, как и в математике при сложении равных но модулю, но противоположных но знаку чисел, мы получим в результате нуль. Такие силы мы будем называть компенсирующими друг друга. В этом случае, как и при отсутствии сил, скорость тела изменяться не будет. На рисунке 125 силы, приложенные к одному и тому же телу (ветке), компенсируют друг друга, и тело находится в состоянии покоя.
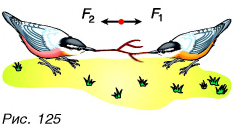
Для любознательных:
В повседневной жизни слово «сила» часто используется в сочетаниях «сила огня», «сила духа», «сила воли» и т. д. В физике слово «сила» употребляется только в смысле количественной меры такого воздействия, которое либо меняет скорость движения тела, либо деформирует его, либо вызывает то и другое одновременно. Действие даже самой малой силы обязательно приводит к тому или иному результату. От нажатия на стол пальцем крышка стола неизбежно прогнется, хотя это не всегда заметно.
Главные выводы:
- Сила является количественной мерой воздействия одного тела на другое.
- Сила является причиной изменения скорости движения тела и его деформации.
- Сила характеризуется модулем, направлением и точкой приложения.
Явление тяготения и сила тяжести
Посмотрите на глобус. Это модель Земли. Земля имеет форму, близкую к форме шара. Нам это кажется естественным. Но каково было недоумение людей, впервые услышавших об этом! Они никак не могли поверить, что люди, живущие на противоположной стороне Земли (рис. 126), не падают в бездну.

Почему люди одинаково устойчивы в любом месте Земли? Земля притягивает к себе все тела.
Если бы Земля не обладала притяжением, брошенные горизонтально или вверх тела, двигаясь но инерции, никогда не вернулись бы на Землю. Тем не менее мяч, брошенный вертикально вверх, возвращается обратно (рис. 127, а). Траектория мяча, брошенного горизонтально, но мере движения искривляется (рис. 127, б). Спутник движется вокруг Земли по круговой орбите (рис. 127, в). Искривление траектории мяча, спутника есть также результат притяжения этих тел к Земле.
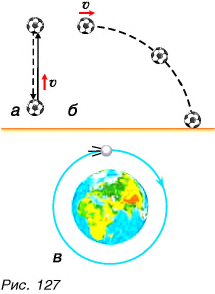
Сила, с которой Земля притягивает к себе тело, называется силой тяжести.
Зависит ли сила тяжести от массы тела? Конечно, да. Из жизненного опыта мы хорошо знаем, что, чем больше масса налитой в ведро воды, тем труднее его удерживать. Слона Земля притягивает гораздо сильнее, чем зайца (рис. 128).
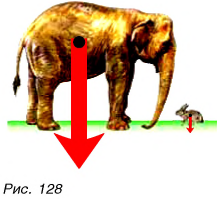
Во сколько раз увеличивается масса тела, во столько раз возрастает сила тяжести 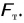 Иначе говоря, действующая на тело сила тяжести прямо пропорциональна массе тела:
Иначе говоря, действующая на тело сила тяжести прямо пропорциональна массе тела:
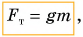
где 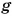 — коэффициент пропорциональности (о его числовом значении вы узнаете из § 25).
— коэффициент пропорциональности (о его числовом значении вы узнаете из § 25).
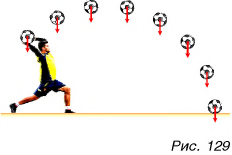
Сила тяжести направлена вертикально вниз (рис. 129) и приложена к центру однородного тела.
А обладают ли другие планеты притяжением, как Земля? Английский физик и математик Исаак Ньютон пришел к выводу, что притяжение свойственно всем планетам и вообще любому телу, обладающему массой, т. е. всем телам Вселенной. Поэтому явление взаимного притяжения тел названо всемирным тяготением.
Для любознательных:
Сила тяжести зависит не только от массы тела, которое притягивается, но и от массы того тела, которое притягивает (Земля, Луна и др.).
Все небесные тела притягивают к себе любые другие тела. Но так как массы и размеры небесных тел различны, то разной будет и действующая сила притяжения. Так, на Луне сила тяжести, действующая на тело, будет почти в 6 раз меньше, чем на Земле.
Масса Земли очень большая: 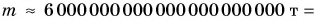
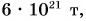 поэтому ее притяжение так велико. Земля притягивает не только тела, находящиеся на ее поверхности, но и удаленные от нее (искусственные спутники, Луну). Но мере удаления сила притяжения уменьшается (уменьшается
поэтому ее притяжение так велико. Земля притягивает не только тела, находящиеся на ее поверхности, но и удаленные от нее (искусственные спутники, Луну). Но мере удаления сила притяжения уменьшается (уменьшается 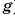 ), но сохраняется прямо пропорциональная зависимость силы тяжести от массы тела.
), но сохраняется прямо пропорциональная зависимость силы тяжести от массы тела.
Еще сильнее притяжение Солнца, так как его масса примерно в 300 000 раз больше массы Земли. Именно поэтому Земля и другие планеты движутся вокруг Солнца.
Главные выводы:
- Все тела во Вселенной обладают свойством притягивать к себе другие тела.
- Сила, с которой Земля притягивает к себе тело, называется силой тяжести.
- Сила тяжести, действующая на тело, прямо пропорциональна его массе.
Пример №6
Плотность железного бруска в 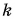 раз больше плотности деревянного. Объем железного бруска в
раз больше плотности деревянного. Объем железного бруска в 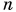 раз меньше объема деревянного. Во сколько раз отличаются силы тяжести, действующие на бруски?
раз меньше объема деревянного. Во сколько раз отличаются силы тяжести, действующие на бруски?
Дано:
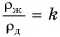
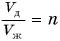
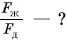
Решение
Силы тяжести, действующие на бруски, равны:
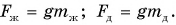
Массы брусков равны: 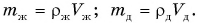
Отношение сил:
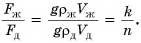
Ответ: 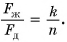
Сила упругости
На горизонтальном столе лежит шар. Как и на всякое тело, на него действует сила тяжести  (рис. 132, а). Но почему он не падает вниз? Этому препятствует опора (крышка стола). В чем выражается действие опоры на лежащее на ней тело?
(рис. 132, а). Но почему он не падает вниз? Этому препятствует опора (крышка стола). В чем выражается действие опоры на лежащее на ней тело?
Из § 21 вы знаете, что приложенная к телу сила (даже очень большая) не вызывает изменения скорости движения тела, если она скомпенсирована (уравновешена) приложенной к нему противоположно направленной другой силой. Как возникает эта другая сила? В приведенном примере шар, притягиваясь Землей, давит на крышку стола. Сила давления 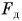 приложена к крышке стола и направлена вниз (рис. 132, б). Действуя на крышку, эта сила прогибает ее, т. е. деформирует крышку, хотя данная деформация и не заметна для глаз.
приложена к крышке стола и направлена вниз (рис. 132, б). Действуя на крышку, эта сила прогибает ее, т. е. деформирует крышку, хотя данная деформация и не заметна для глаз.
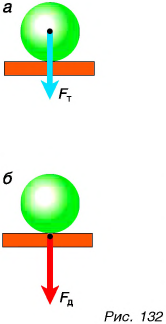
Вас. не должно удивлять утверждение, что любая, даже незначительная, сила давления (например, сила давления мухи, севшей на стол) вызывает деформацию. Деформации поверхности стола, на которую давит гиря, не видно. Но попробуйте положить под гирю поролон (рис. 133), и вы заметите его прогиб, т. е. деформация станет очевидной.
Вернемся к примеру с шаром. Деформированная опора, стремясь распрямиться, действует на шар с силой, направленной вверх (рис. 134), — силой упругости. Именно сила упругости 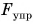 и компенсирует действие силы тяжести
и компенсирует действие силы тяжести 
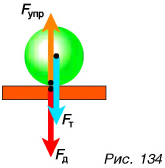
Проделаем еще один опыт. Подвесим шар к пружине, укрепленной на штативе. Шар, притягиваясь к Земле (рис. 135, а), движется и растягивает (деформирует) пружину. Деформирующая сила  приложена к пружине и направлена вниз. Но движение шара не продолжается неограниченно. Что же препятствует движению?
приложена к пружине и направлена вниз. Но движение шара не продолжается неограниченно. Что же препятствует движению?
Как и в случае с лежащим шаром, сила упругости 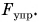 Она приложена к висящему шару, направлена противоположно деформирующей силе и равна ей по числовому значению. А теперь поместим шар на пружину сверху (рис. 135, б). Пружина сожмется под действием силы давления
Она приложена к висящему шару, направлена противоположно деформирующей силе и равна ей по числовому значению. А теперь поместим шар на пружину сверху (рис. 135, б). Пружина сожмется под действием силы давления  приложенной к ней. Препятствовать движению шара будет сила упругости
приложенной к ней. Препятствовать движению шара будет сила упругости  с которой пружина действует на шар.
с которой пружина действует на шар.
Итак, сила, действующая на тело со стороны деформированной опоры или подвеса, называется силой упругости.
Вы заметили закономерность? Сила упругости  приложена к телу, вызвавшему деформацию опоры или подвеса. Она противоположна но направлению и численно равна деформирующей силе
приложена к телу, вызвавшему деформацию опоры или подвеса. Она противоположна но направлению и численно равна деформирующей силе  Но стоит убрать деформирующую силу — и растяжение, сжатие или прогиб исчезают, т. е. деформированное тело (пружина, стол) восстанавливает свои первоначальные размеры и форму.
Но стоит убрать деформирующую силу — и растяжение, сжатие или прогиб исчезают, т. е. деформированное тело (пружина, стол) восстанавливает свои первоначальные размеры и форму.
Для любознательных:
Иногда после действия большой деформирующей силы тело не возвращается к первоначальной форме. Например, покупая в магазине батон, вы определяете его свежесть, деформируя специальной ложкой. При действии на батон небольшой силы он после снятия воздействия восстанавливает форму, но если вы переусердствуете, нажимая ложкой, батон так и не сможет избавиться от своего непривлекательного деформированного вида.
Поскольку сила упругости возникает в ответ на воздействие (опора, подвес реагируют на воздействие), то силу упругости часто называют еще силой реакции.

Главные выводы:
- Сила упругости (сила реакции) возникает в ответ на действие деформирующей силы.
- Сила упругости приложена к телу, вызвавшему деформацию опоры или подвеса.
- Сила упругости противоположна деформирующей силе, но их модули равны.
Вес тела
При взаимодействии тел на каждое из них со стороны другого действует сила. Рассмотрим действие друг на друга тела и его горизонтальной опоры или тела и его вертикального подвеса.
На рисунке 140 представлены различные тела. Каждое из этих тел, притягиваясь к Земле, действует на опору или подвес с силой, которая вам хорошо знакома из предыдущего параграфа. Это сила давления на опору или сила натяжения подвеса. Иначе эту силу называют весом тела.

Почему тело действует на опору или подвес? Потому что его притягивает Земля. Неподвижные опора или подвес не позволяют телу падать и сами испытывают действие силы.
Вес — это сила, с которой тело вследствие притяжения Земли действует на опору или подвес.
Обозначим вес буквой Р и укажем вес каждого тела на рисунке 140. Вес мяча приложен к опоре (крышке стола), направлен вниз и является уже известной вам силой давления. Вес собаки приложен к земле в местах соприкосновения ее лап с землей и равен сумме четырех сил:
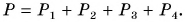
Определите сами и изобразите вес всех ос шальных тел, представленных на рисунке 140.
А теперь еще раз сравним силу тяжести и вес тела. У этих сил есть общее: они вызваны притяжением Земли. Эти силы очень часто (подчеркиваем — часто, но не всегда) численно равны друг другу. Но у силы тяжести и веса есть различия.
Во-первых, они приложены к разным телам: сила тяжести — к телу (шару), а вес. — к опоре или подвесу (крышке стола, нити) (рис. 141, а, б).
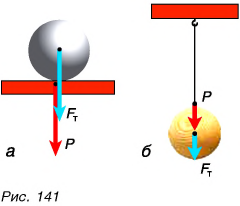
Во-вторых, сила тяжести в данном месте Земли имеет строго определенное значение 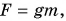 а вес тела может быть не только равен, но и больше или меньше этого значения.
а вес тела может быть не только равен, но и больше или меньше этого значения.
Докажем это с помощью опыта. Подвесим груз на пружине (рис. 142, а). Если мы будем равномерно поднимать и опускать этот груз, то удлинение пружины, а значит, и сила упругости и вес груза будут оставаться такими же, как в случае неподвижного груза. Но если мы неравномерно (с разгоном) опустим (рис. 142, б) или поднимем (рис. 142, в) груз в вертикальном направлении, то будут наблюдаться изменения в растяжении пружины, что указывает на изменения веса тела.
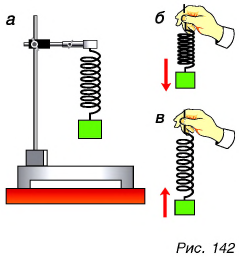
Для любознательных:
Вам известно, что действующая на тело сила тяжести на других планетах может быть как больше, так и меньше, чем на Земле. Значит, и вес тела на этих планетах будет другим.
А может ли тело вообще потерять вес? Космонавты и все тела в космическом корабле свободно парят, не оказывая действия на опору или подвес, т. е. их вес Р = 0. Это состояние тела называется невесомостью.
Невесомость можно создать и на Земле. Пустим свободно падать груз вместе с пружиной. Пружина не растягивается, а, значит, вес груза равен нулю. Это и есть невесомость.
Главные выводы:
- Вес тела — сила, приложенная к опоре или подвесу.
- Вес неподвижного или равномерно движущегося тела численно равен силе тяжести.
- Вес тела, движущегося неравномерно, может изменяться и быть больше силы тяжести, меньше и даже равным нулю.
Единица силы и измерение силы
Сила характеризуется числовым значением (модулем), направлением и точкой приложения. Чтобы определить числовое значение силы, нужно измерить силу, т. е. сравнить ее с другой силой, принятой в качестве единицы силы. Что принято за единицу силы?
Главный результат действия силы — изменение скорости движения тела, которая сама по себе никогда не изменяется. Исходя из этого, была выбрана в СИ единица силы — 1 ньютон (1 Н), названная в честь английского ученого Исаака Ньютона. Существуют кратные и дольные единицы силы: 1 кН = 1000 Н, 1 мН = 0,001 Н.
Сила, как вы знаете, может не только изменить скорость, но и вызвать деформацию тела. Пружина растягивается (рис. 143), потому что на нее действует вес груза, который притягивает Земля.
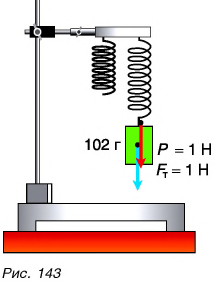
Какой массой должно обладать тело, чтобы действующая на него сила тяжести равнялась 1,0 И? Исследования показали, что с силой F = 1,0 Н Земля притягивает тело массой m = 0,102 кг.
Определим значение коэффициента  , входящего в формулу силы тяжести
, входящего в формулу силы тяжести 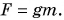 Из формулы видно, что
Из формулы видно, что 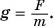 Так как на тело массой 0,102 кг Земля действует с силой
Так как на тело массой 0,102 кг Земля действует с силой 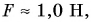 то:
то:
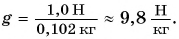
Значит, если масса тела равна 1,0 кг, то действующая на него сила тяжести 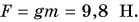 Следовательно, и вес этого тела (если оно находится в состоянии покоя или движется равномерно) Р = 9,8 Н. Ни в коем случае нельзя приравнивать вес и массу, что, к сожалению, часто встречается в быту. Это разные физические величины, и единицы у них разные. Масса измеряется в килограммах, вес — в ньютонах (рис. 144). Если ваша масса m = 50 кг, то ваш вес
Следовательно, и вес этого тела (если оно находится в состоянии покоя или движется равномерно) Р = 9,8 Н. Ни в коем случае нельзя приравнивать вес и массу, что, к сожалению, часто встречается в быту. Это разные физические величины, и единицы у них разные. Масса измеряется в килограммах, вес — в ньютонах (рис. 144). Если ваша масса m = 50 кг, то ваш вес 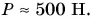

Как измерить силу? Для этого нужно создать измерительный прибор. Будем подвешивать к пружине сначала одну гирю массой m = 102 г = = 0,102 кг, затем две, три и т. д. Отметим метками положения указателя (рис. 145), напротив которых ставим значения 1 Н, 2 Н, 3 Н и т. д.
Пружина с указателем и шкалой представляет собой прибор для измерения сил — динамометр (от греч. dynamis — сила и metreo — измеряю) (рис. 146). Динамометром можно измерять не только вес тела, но и любые силы.

Динамометры бывают различных типов и размеров в зависимости от того, для измерения больших или малых сил они предназначены. Для измерения мускульной силы руки используют динамометр силомер (рис. 147, а). Определить силу тяги трактора позволяет тяговый динамо метр (рис. 147, б).

Для проведения различных исследований удобен динамометр с реечной передачей (рис. 148). Он позволяет измерять не только силу, направленную вниз, например создаваемую лежащим на опоре А телом (рис. 148, а), или вес подвешенного 1 к подвесу Б тела. Таким динамометром можно измерить и силу, направленную вверх (рис. 148, б).
Для любознательных:
Значение коэффициента  , равное
, равное 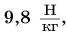 характерно только для Земли (оно несколько изменяется в зависимости от географической широты места и от высоты подъема тела над поверхностью Земли; с увеличением высоты значение
характерно только для Земли (оно несколько изменяется в зависимости от географической широты места и от высоты подъема тела над поверхностью Земли; с увеличением высоты значение  уменьшается).
уменьшается).
Для Луны этот коэффициент в б раз меньше, т. е. 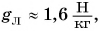 для Юпитера
для Юпитера 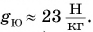 Для Солнца
Для Солнца 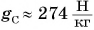 (почти в 30 раз больше, чем для Земли).
(почти в 30 раз больше, чем для Земли).
Главные выводы:
- В СИ единицей силы является 1 ньютон.
- Силу измеряют с помощью динамометра.
- С силой F = 1 Н Земля притягивает тело массой m = 0,102 кг.
- В формуле
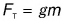 силы тяжести, с которой Земля действует на тело, постоянный коэффициент
силы тяжести, с которой Земля действует на тело, постоянный коэффициент 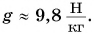
Пример №7
Зависимость силы тяжести, действующей на песок в песочных часах, от его объема представлена на рисунке 149. Определите плотность песка. Коэффициент 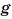 примите равным
примите равным 
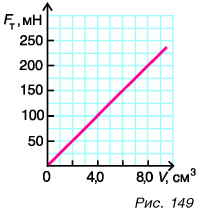
Решение
Плотность песка 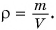 Масса песка
Масса песка 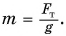 Силу тяжести для данного объема песка, например
Силу тяжести для данного объема песка, например 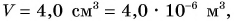 определим по данным графика
определим по данным графика 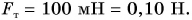 Тогда
Тогда 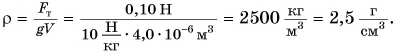
Ответ: 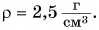
- Заказать решение задач по физике
Сложение сил и равнодействующая сила
На любое тело действует хотя бы одна сила — сила тяжести. Но чаще всего на тело действует несколько сил. Например, на шарик (рис. 151) действуют Земля и нить (две силы). Каков результат их действия?
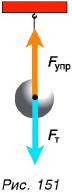
Решим такую задачу. Вы с другом перевозите на тележке груз, причем один из вас тянет тележку, прикладывая силу 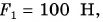 другой толкает ее, действуя с силой
другой толкает ее, действуя с силой 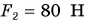 (рис. 152). Какова сила, которая двигает тележку?
(рис. 152). Какова сила, которая двигает тележку?
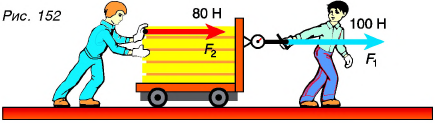
Эта сила 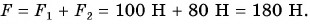 А изменилось бы движение тележки, если бы ее тянул один человек, прикладывая силу F = 180 Н? Нет, эффект был бы таким же. Значит, одна сила F оказывает на тележку такое же действие, как две одновременно действующие силы
А изменилось бы движение тележки, если бы ее тянул один человек, прикладывая силу F = 180 Н? Нет, эффект был бы таким же. Значит, одна сила F оказывает на тележку такое же действие, как две одновременно действующие силы 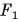 и
и 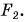
Сила, которая оказывает на тело такое же действие, как несколько одновременно действующих на него сил, называется равнодействующей этих сил.
Как направлена равнодействующая? Проведем опыт. К нижнему крючку динамометра подвесим груз весом 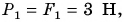 а на столик поместим груз весом
а на столик поместим груз весом 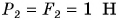 (рис. 153, а). Динамометр показывает действие на него силы F = 4 Н. Сила F — сумма весов нижнего и верхнего грузов. Эти силы направлены вертикально вниз. Заменим два груза одним весом 4 Н и подвесим его к динамометру (рис. 153, б). Динамометр показывает, что действие одного груза такое же, как и двух грузов весом
(рис. 153, а). Динамометр показывает действие на него силы F = 4 Н. Сила F — сумма весов нижнего и верхнего грузов. Эти силы направлены вертикально вниз. Заменим два груза одним весом 4 Н и подвесим его к динамометру (рис. 153, б). Динамометр показывает, что действие одного груза такое же, как и двух грузов весом 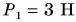 и
и 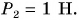 Значит, сила
Значит, сила 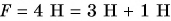 — равнодействующая двух сил, приложенных к динамометру. Изобразим эти силы схематически (см. рис. 153, в).
— равнодействующая двух сил, приложенных к динамометру. Изобразим эти силы схематически (см. рис. 153, в).
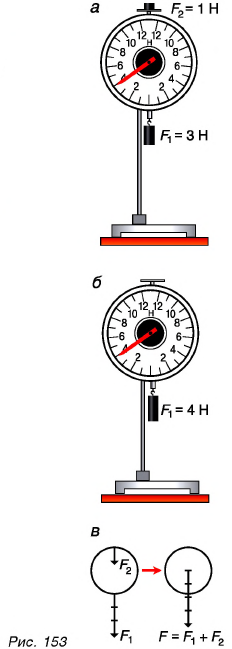
Модуль равнодействующей сил, действующих на тело в одном направлении но одной прямой, равен сумме модулей этих сил. Направление равнодействующей такое же, как и отдельных сил.
Изменим опыт: с помощью другого динамометра подействуем на данный динамометр вверх силой  (рис. 154, а). Приложенные к динамометру силы направлены в противоположные стороны. Динамометр показывает силу
(рис. 154, а). Приложенные к динамометру силы направлены в противоположные стороны. Динамометр показывает силу  Это и есть равнодействующая двух противоположно направленных сил. Она направлена вверх, что подтверждается изменением направления поворота стрелки реечного динамометра.
Это и есть равнодействующая двух противоположно направленных сил. Она направлена вверх, что подтверждается изменением направления поворота стрелки реечного динамометра.
Значит, действие двух противоположно направленных сил можно заменить одной силой, модуль которой равен разности модулей двух приложенных сил и которая направлена в сторону большей силы (рис. 154, б).
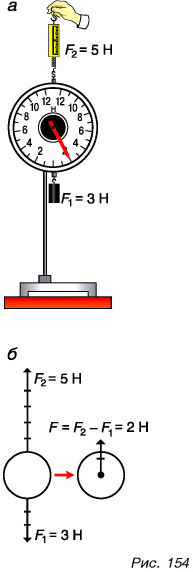
А если силы 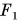 и
и 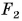 имеют равные модули? Тогда равнодействующая сила равна нулю. Происходит компенсация сил (см. § 21).
имеют равные модули? Тогда равнодействующая сила равна нулю. Происходит компенсация сил (см. § 21).
Ответим еще на один важный вопрос: как ведет себя тело при скомпенсированных силах, т. е. при нулевом значении равнодействующей?
Проведем опыт. Возьмем пенопластовую пластинку А очень малой массы. Подействуем на пластинку одинаковыми по модулю силами упругости нитей 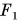 и
и 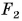 (рис. 155). Других сил нет. Силой тяжести, действующей на пластинку, можно пренебречь. Равнодействующая сил
(рис. 155). Других сил нет. Силой тяжести, действующей на пластинку, можно пренебречь. Равнодействующая сил 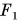 и
и 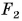 равна нулю. Пластинка находится в состоянии покоя. Толкнем пластинку. Она придет в движение и, если трение мало, будет двигаться равномерно, т. е. с постоянной скоростью. Но после прекращения толчка на пластинку по-прежнему действуют только силы
равна нулю. Пластинка находится в состоянии покоя. Толкнем пластинку. Она придет в движение и, если трение мало, будет двигаться равномерно, т. е. с постоянной скоростью. Но после прекращения толчка на пластинку по-прежнему действуют только силы 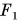 и
и 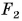 , их равнодействующая равна нулю. Опыт позволяет сделать очень важный вывод: если равнодействующая сил, приложенных к телу, равна нулю, тело находится в состоянии покоя или движется равномерно и прямолинейно. Приведите примеры, подтверждающие этот вывод.
, их равнодействующая равна нулю. Опыт позволяет сделать очень важный вывод: если равнодействующая сил, приложенных к телу, равна нулю, тело находится в состоянии покоя или движется равномерно и прямолинейно. Приведите примеры, подтверждающие этот вывод.
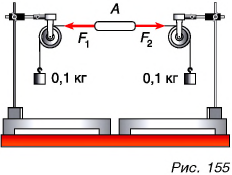
А если продолжить опыт и подвесить к одной нити два груза, а к другой — три? Пластинка придет в движение с увеличивающейся скоростью (рис. 156), ведь равнодействующая сил упругости нитей  и
и  , приложенных к пластинке, уже не будет равна нулю.
, приложенных к пластинке, уже не будет равна нулю.
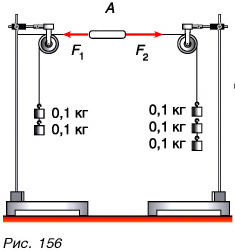
Внимание! Находить равнодействующую можно только для сил, приложенных к одному телу.
Для любознательных:
Если приложенные к телу силы действуют не вдоль одной прямой, то модуль равнодействующей силы не равен арифметической сумме этих сил. В показанном на рисунке опыте приложенные силы — 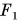 = 3 Н,
= 3 Н,  = 4 Н — перпендикулярны друг другу, а модуль равнодействующей F равен не 7 Н, а 5 Н, т. е. меньше суммы
= 4 Н — перпендикулярны друг другу, а модуль равнодействующей F равен не 7 Н, а 5 Н, т. е. меньше суммы 
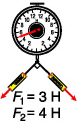
Главные выводы:
- Действие нескольких сил, приложенных к телу, можно заменить одной силой — их равнодействующей.
- Направление равнодействующей двух сил, действующих вдоль одной прямой, совпадает с направлением большей из них.
- Если равнодействующая сил, приложенных к телу, равна нулю, то оно либо покоится, либо движется равномерно и прямолинейно.
- Если равнодействующая всех сил, приложенных к телу, не равна нулю, скорость тела изменяется.
Пример №8
На автомобиль массой m = 2,0 т, движущийся равномерно по прямолинейному горизонтальному участку шоссе, действует сила сопротивления движению 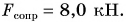 Определите силу тяги, развиваемую двигателем автомобиля. Изобразите все силы, действующие на автомобиль (масштаб: 0,5 см — 4000 Н). Найдите их равнодействующую.
Определите силу тяги, развиваемую двигателем автомобиля. Изобразите все силы, действующие на автомобиль (масштаб: 0,5 см — 4000 Н). Найдите их равнодействующую.
Дано:
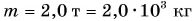
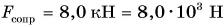
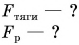
Решение
Если автомобиль движется равномерно, то равнодействующая всех сил, приложенных к нему, равна нулю. На автомобиль действуют: сила тяжести 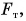 сила упругости
сила упругости 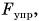 сила тяги
сила тяги 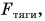 сила сопротивления
сила сопротивления 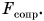
Изобразим 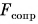 в рекомендуемом масштабе (рис. 157). Так как движение автомобиля равномерное, то равнодействующая сил:
в рекомендуемом масштабе (рис. 157). Так как движение автомобиля равномерное, то равнодействующая сил:
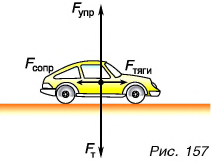
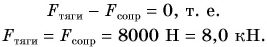
Аналогично 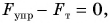 значит,
значит, 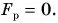
Ответ: 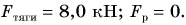
Трение и сила трения
Кто из вас не катался с горы на санках? Приобретя большую скорость, санки (рис. 158), выехав на горизонтальный участок, останавливаются. Почему? Вспомните, что действующая на тело сила может изменить скорость его движения. Этой силой является сила трения скольжения. А что нужно сделать, чтобы санки продолжали движение с той же скоростью? Необходимо скомпенсировать силу трения. Для этого следует тянуть санки горизонтально с силой, равной по модулю силе трения. От чего зависит сила трения?

Проведем опыт. Будем с помощью динамометра равномерно перемещать брусок по горизонтальной поверхности стола (рис. 159). Динамометр показывает, что на брусок действует сила тяги, но скорость движения бруска не изменяется. Значит, на брусок действует еще одна сила компенсирующая сила. Этой силой является сила трения 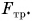 Равнодействующая сил
Равнодействующая сил 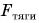 и
и  равна нулю. Обратите внимание, что модуль силы трения равен модулю силы тяги только в случае равномерного прямолинейного движения. Если же модуль силы тяги больше модуля силы трения, скорость движения тела будет возрастать. А если
равна нулю. Обратите внимание, что модуль силы трения равен модулю силы тяги только в случае равномерного прямолинейного движения. Если же модуль силы тяги больше модуля силы трения, скорость движения тела будет возрастать. А если  меньше
меньше  — убывать.
— убывать.
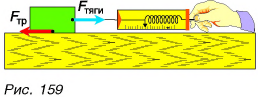
Итак, сила трения скольжения возникает при движении одного тела но поверхности другого и направлена в сторону, противоположную движению.
Почему возникает сила трения? Продолжим опыт. Будем равномерно перемещать брусок сначала по шероховатой, затем по обработанной поверхности доски. Сила тяги будет больше при движении по шероховатой поверхности (рис. 160, а). Значит, и модуль равной ей силы трения будет тем больше, чем более шероховатой, неровной окажется поверхность. При движении неровности цепляются друг за друга, деформируются, разрушаются. Это создает препятствия движению. А если бы поверхности были идеально гладкие, то возникла ли бы сила трения при движении одного тела по поверхности другого? Не спешите ответить «нет». При хорошо отполированных поверхностях расстояние между поверхностями тел или их участками при движении тел так мало, что станут существенными силы притяжения молекул поверхности одного тела к молекулам поверхности другого. Эти силы будут тормозить движение тел.
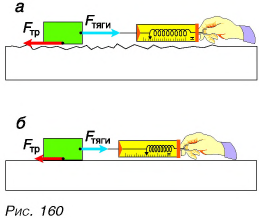
Значит, шероховатость поверхностей и силы притяжения между молекулами соприкасающихся поверхностей — причины возникновения сил трения.
Если при движении соприкасаются твердые поверхности тел, трение называют сухим.
От чего еще зависит сила сухого трения? Дадим ответ, исходя из опыта. Будем равномерно двигать брусок по различным поверхностям: по металлической, деревянной, резиновой — с примерно одинаковым качеством обработки (рис. 161). Динамометр показывает различную силу тяги. Следовательно, силы трения дерева но металлу, дерева по дереву, дерева по резине будут различны. Наибольшая сила трения возникнет при движении по поверхности резины. Не случайно подошвы в спортивной обуви (рис. 162) делают резиновыми и рельефными.
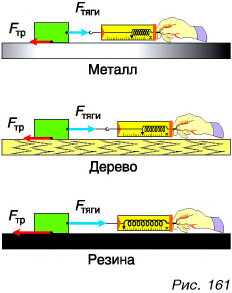

Поставим теперь на брусок гирю и сравним силы трения при равномерном движении ненагруженного бруска (рис. 163, а) и бруска с гирей (рис. 163, б). Видно, что во втором случае сила тяги, а значит, и сила трения увеличились. Но брусок с гирей с большей силой давит на поверхность, с которой соприкасается. Следовательно, сила трения тем больше, чем больше сила, прижимающая тело (брусок) к поверхности.
Как уменьшить трение? Здесь есть два пути. Первый — заменить трение скольжения трением качения. Проделаем такой опыт. Будем равномерно передвигать металлическую тележку по столу скольжением (рис. 164, а) и качением (рис. 164, б). Сила трения во втором случае значительно меньше, хотя материал поверхностей и прижимающая сила не изменяются. Значит, трение качения меньше трения скольжения. С тяжелым чемоданом справиться легко, если прикрепить к нему колеса.
Второй путь уменьшения трения скольжения — это смазывание трущихся поверхностей. Смазка (например, масло) заполняет все неровности трущихся поверхностей и располагается тонким слоем между ними так, что поверхности перестают касаться друг друга. При этом сухое трение заменяется трением слоев жидкости (масла), а оно в 8—10 раз меньше.
Опытный водитель никогда не отправится в далекий путь, не проверив, достаточно ли масла в двигателе машины. Объясните, зачем он это делает.
Для любознательных:
А знаете ли вы, что с помощью катков перемещают дома? Например, в городе Москве во время реконструкции улицы Тверской некоторые дома были передвинуты на другое место именно таким способом.
В машинах для замены трения скольжения трением качения используют шариковые и роликовые подшипники (см. рис.). Подшипники диаметром 1,5—2 мм применяют в точных измерительных приборах. Вращающийся вал машины или другого механизма не скользит но неподвижному вкладышу подшипника, а катится по нему на стальных шариках или роликах. Это снижает трение в 20—30 раз.

Главные выводы:
- Сила трения скольжения возникает при движении одного тела по поверхности другого.
- Сила трения скольжения направлена против движения.
- Сила трения зависит от свойств соприкасающихся поверхностей и силы, прижимающей тело к поверхности.
- Давление в физике
- Строение вещества в физике
- Физическое тело и вещество в физике
- Плотность и единицы плотности в физике
- Потенциальная энергия
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
- Работа, мощность и энергия
Роман Алексеевич Лалетин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Сила скорости представляет физическую величину, характеризуемую отношением перемещения к промежутку времени, за которое и произошло оное перемещение.
Понятие силы скорости
Замечание 1
Сила скорости представляет одну из главных характеристик механического движения.
Она является выражением самой сути движения, определяя то отличие, которое присутствует между телом в неподвижном и подвижном состояниях.
В системе измерений общепринятого формата скорость измеряется в метрах за секунду. Иными словами, в физике в качестве единицы скорости обозначена скорость определенного равномерного прямолинейного движения, за одну секунду при котором телом будет совершен путь в один метр. В качестве единицы измерения скорости зачастую выступает вышеуказанный формат, однако частые случаи измерения скорости и в других единицах. Чтобы измерить скорость транспортных средств, например, обычно применяют единицу измерения, которая характеризуется пройденными за час километрами.
Важно знать, что скорость представляет векторную величину. Направление вектора скорости определяют, согласно определенной траектории движения. Вектор скорости при этом будет всегда направленным по касательной к траектории в точке прохождения движущегося объекта передвижения.
Пример 1
В качестве примера можно рассмотреть колесо едущего автомобиля. Колесо в момент движения будет вращаться, а все его точки при этом движутся по окружности. Брызги, которые от него разлетаются, также будут лететь по касательным к данным окружностям, указывая таким образом направления векторов скоростей отдельно взятых точек колеса.
Сила скорости, таким образом, может считаться характеристикой направления движения тела (направления вектора скорости) и быстроты его перемещений (модуль вектора скорости). При этом скорость тела может оказаться и отрицательной. Это будет означать движение тела в том направлении, которое считается противоположным направлению оси координат в избранной системе отсчета.
«Сила скорости, формулы» 👇
Виды скорости
Сила скорости будет зависеть от времени. Согласно характеру зависимости ее от времени, движение существует в таком виде:
- равномерное (движение с постоянной по модулю скоростью);
- неравномерное (в этом случае имеет место так называемая «средняя скорость»).
Средняя скорость определяется на основании такой формулы:
$vec{U_ср} = frac{vec{delta s}}{delta t}$
Мгновенная скорость представляет показатель скорости в конкретный момент времени, являясь физической величиной, равной пределу, к которому будет стремиться средняя скорость в условиях бесконечного сокращения промежутка времени $delta t$:
$vec{U} = Lim_{delta tto 0}frac{vec{delta s}}{delta t}$
Мгновенная скорость, таким образом, в конкретный момент времени будет считаться соотношением очень незначительного перемещения $vec{delta s}$ к очень малому временному промежутку, за который и осуществлялось данное перемещение. Вектор мгновенной скорости направляется по касательной к траектории передвижения тела
Закон сложения скоростей на примерах
В разных системах отсчета силы скоростей движения тела будет связывать между собой классический закон сложения скоростей, который звучит таким образом: скорость тел относительно неподвижной системы отсчета равнозначна сумме скоростей в подвижной системе и наиболее подвижной системы отсчета в отношении к неподвижной.
На примерах можно рассмотреть движение пассажирского поезда по железной дороге при скорости 65 км/ч. По вагону такого поезда человек может перемещаться со скоростью, например, в 5 км/ч. Если воспринимать что железная дорога неподвижная и принимать ее за систему отсчета, тогда скорость человека относительно системы отсчёта (то есть относительно железной дороги), будет равна сложению скорости поезда и человека.
В первом случае скорость определяется сложением, поскольку человек перемещается в одном направлении с поездом, то есть скорость будет 70 км/ч (65 + 5).
Что касается второго случая, то он имеет место в ситуации, когда поезд и человек движутся в разных направлениях, то есть скорость получится 60 км/ч (65 – 5).
Однако это будет справедливым только в случае передвижения человека и поезда по одной линии. Если же имеет место перемещение человека под некоторым углом, тогда нужно будет учитывать и этот угол, понимая, что скорость является все-таки векторной величиной.
Вышеприведенный пример стоит рассмотреть более подробно для лучшего понимания действия силы скорости. Железная дорога в данном случае представляет неподвижную систему отсчета. В то же время, поезд, который по ней движется, будет подвижной системой. Вагон, по которому движется человек, представляет часть поезда.
Замечание 2
Относительно вагона скорость человека будет равной пяти километрам в час и характеризоваться такой величиной, как $vec{delta U_ч}$. Скорость поезда (и, соответственно, вагона) относительно неподвижной системы будет равной 65 км/ч, обозначим ее как $vec{delta U_в}$.
За незначительный промежуток времени $delta t$ успеют произойти такие события:
Человек будет перемещаться относительно вагона на расстояние $vec{delta S_ч}$;
Относительно железной дороги вагон будет перемещаться на такое расстояние: $vec{delta S_в}$.
В таком случае, за данный временной промежуток относительно железной дороги перемещение человека определяется таким образом:
$vec{delta S} = vec{delta S_ч}+vec{delta S_в}$
Это называется законом сложения перемещений. В приведенном примере перемещение человека относительно железной дороги будет равнозначно сумме его перемещений относительно вагона и также вагона относительно самой железной дороги:
$vec{delta S = vec{delta U_ч}delta t+vec{delta U_в}delta t}$
Скорость человека относительно железной дороги тогда будет равной:
$vec{U} = frac{vec{delta S}}{delta t}$
Поскольку $vec{delta S} = vec{delta S_ч}+vec{delta S_в}$, то
$U=frac{vec{delta S}}{delta t}=frac{{vec{delta S_ч}+vec{delta S_в}}{delta t}=frac{vec{delta S_ч}}{delta t}+{delta S_в}}{delta t}$
Скорость человека относительно вагона тогда будет определяться так:
$vec{delta U_ч} = frac{vec{delta S_ч}}{delta t}$
Скорость вагона относительно железной дороги составит:
$vec{delta U_в} = frac{vec{delta S_в}}{delta t}$
Таким образом, сила скорости человека относительно железной дороги определяется следующим образом:
$vec{U} = vec{delta U_ч}+vec{delta U_в}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
