Еще в древности было известно, что наэлектризованные тела взаимодействуют. Силу взаимодействия двух небольших заряженных шариков с помощью крутильных весов впервые измерил Шарль Кулон. Он сформулировал закон, который позже назвали его именем.
Так же, было выяснено, что сила, с которой два заряда притягиваются, или отталкиваются, зависит не только от самих зарядов, но и от вещества, в котором эти заряды находятся.
Опыт Кулона
Кулон нашел способ измерить взаимное действие двух зарядов. Для этого он использовал крутильные весы.
Ему не пришлось применять дополнительную особо чувствительную аппаратуру. Потому, что взаимное действие зарядов имело достаточную для наблюдения интенсивность.
Примечание: Опыт Кулона похож на опыт Кавендиша, который экспериментально определил гравитационную постоянную G.
Устройство крутильных весов
Такие весы (рис. 1) содержат перекладину — тонкий стеклянный стержень, расположенный горизонтально. Он подвешен на тонкой вертикально натянутой упругой проволоке.
На одном конце стержня находится небольшой металлический шарик. К другому концу прикреплен груз, который используется, как противовес.
Еще один металлический шарик, прикрепленный ко второй палочке из стекла, можно располагать неподалеку от первого шарика. Для этого в верхней крышке корпуса весов проделано отверстие.

Рис. 1. Устройство крутильных весов, использованных Кулоном для обнаружения силы взаимодействия зарядов
Если наэлектризовать шарики, они начнут взаимодействовать. А прикрепленная к проволоке перекладина, на которой находится один из шариков, будет поворачиваться на некоторый угол.
На корпусе весов на уровне палочки располагается шкала с делениями. Угол поворота связан с силой взаимного действия шариков. Чем больше угол поворота, тем больше сила, с которой шарики действуют друг на друга.
Чтобы сдвинувшийся шарик вернуть в первоначальное положение, нужно закрутить проволоку на некоторый угол. Так, чтобы сила упругости скомпенсировала силу взаимодействия шариков.
Для закручивания проволоки в верхней части весов есть рычажок. Рядом с ним расположен диск, а на нем – еще одна угловая шкала с делениями.
По нижней шкале определяют точку, в которую необходимо вернуть шарик. Верхней шкалой пользуются, чтобы установить угол, на который нужно рычажком закрутить проволоку.
С помощью крутильных весов Шарль Кулон выяснил, как именно сила взаимного действия зависит от величины зарядов и расстояния между зарядами.
В те годы единиц для измерения заряда не было. Поэтому ему пришлось изменять заряд одного шарика с помощью метода половинного деления.
Когда он касался заряженным шариком второго такого же шарика, заряды между ними распределялись поровну. Таким способом, можно было уменьшать заряд одного из шариков, участвующих в опыте, в 2, 4, 8, 16 и т. д. раз.
Так опытным путем Кулон получил закон, формула которого очень похожа на закон всемирного тяготения.
В память о его заслугах, силу взаимодействия зарядов называют Кулоновской силой.
Закон Кулона для зарядов в вакууме
Рассмотрим два точечных заряда, которые находятся в вакууме (рис. 2).

Рис. 2. Два положительных заряда q и Q, расположенных в вакууме на расстоянии r, отталкиваются. Силы отталкивания направлены вдоль прямой, соединяющей заряды
На рисунке 2 сила (large F_{Q} ) – это сила, с которой положительный заряд Q отталкивает второй положительный заряд q. А сила (large F_{q} ) принадлежит заряду q, с такой силой он отталкивает заряд Q.
Примечание: Точечный заряд – это заряженное тело, размером и формой которого можно пренебречь.
Силы взаимодействия зарядов, по третьему закону Ньютона, равны по величине и направлены противоположно. Поэтому, для удобства можно ввести обозначение:
[large F_{q} = F_{Q} = F]
Для силы взаимодействия зарядов в вакууме Шарль Кулон сформулировал закон так:
Два точечных заряда в вакууме,
взаимодействуют с силой
прямо пропорциональной
произведению величин зарядов
и обратно пропорциональной
квадрату расстояния между ними.
Формула для этого закона на языке математики запишется так:
[large boxed { F = k cdot frac {|q| cdot |Q| }{r^{2}} } ]
(F left( H right) ) – сила, с которой два точечных заряда притягиваются, или отталкиваются;
(|q| left( text{Кл}right) ) – величина первого заряда;
(|Q| left( text{Кл}right) ) – величина второго заряда;
(r left( text{м}right) ) – расстояние между двумя точечными зарядами;
(k ) – постоянная величина, коэффициент в системе СИ;
Сила – это вектор. Две главные характеристики вектора – его длина и направление.
Формула позволяет найти одну из характеристик вектора F — модуль (длину) вектора.
Чтобы определить вторую характеристику вектора F – его направление, нужно воспользоваться правилом: Мысленно соединить два неподвижных точечных заряда прямой линией. Сила, с которой они взаимодействуют, будет направлена вдоль этой прямой линии.
Сила Кулона – это центральная сила, так как она направлена вдоль прямой, соединяющей центры тел.
Примечание: Еще один пример центральной силы — сила тяжести.
Что такое коэффициент k с точки зрения физики
Постоянная величина (k ), входящая в формулу силы взаимодействия зарядов, имеет такой физический смысл:
(k ) — это сила, с которой отталкиваются два положительных точечных заряда по 1 Кл каждый, когда расстояние между ними равно 1 метру.
Значение постоянной k равно девяти миллиардам!
[large boxed { k = 9cdot 10^{9} left( H cdot frac{text{м}^{2}}{text{Кл}^{2}}right) } ]
Это значит, что заряды взаимодействуют с большими силами.

Рис. 3. Коэффициент k в формуле взаимодействия зарядов
Константу k можно вычислить опытным путем, расположив два известных заряда (не обязательно по 1 Кулону каждый) на удобном для измерений расстоянии (не обязательно 1 метр) и измерив силу из взаимного действия.
Нужно подставить известные величины зарядов, расстояние между ними и измеренную силу в такую формулу:
[large boxed { k = frac {F cdot r^{2}}{|q| cdot |Q|} } ]
Величина k связана с электрической постоянной (varepsilon) такой формулой:
[large boxed { k = frac{1}{4pi cdot varepsilon_{0}} } ]
Поэтому дробь из правой части этой формулы можно встретить в различных справочниках физики, где она заменяет коэффициент k.
Закон Кулона для зарядов в веществе
Если два точечных заряда находятся в веществе, то сила их взаимного действия будет меньше, чем в вакууме. Для зарядов в веществе закон Кулона выглядит так:
[large boxed { F = frac{1}{varepsilon} cdot k cdot frac {|q| cdot |Q| }{r^{2}} } ]
(F left( H right) ) – сила взаимодействия зарядов в веществе;
(|q| ; |Q| left( text{Кл}right) ) – величины зарядов;
(r left( text{м}right) ) – расстояние между зарядами;
( k = 9cdot 10^{9} ) – постоянная величина;
( varepsilon ) – диэлектрическая проницаемость вещества, для разных веществ различается, ее можно найти в справочнике физики;

Рис. 4. Два заряда -q и +Q, расположенные в вакууме на расстоянии r, притягиваются сильнее, нежели те же заряды, расположенные на таком же расстоянии в диэлектрике
Силы, с которыми заряды действуют друг на друга в веществе, отличаются от сил взаимодействия в вакууме в ( varepsilon ) раз:
[large boxed { F_{text{(в диэлектрике)}} = frac{1}{varepsilon} cdot F_{text{(в вакууме)}} } ]
Примечание: Читайте отдельную статью, рассказывающую, что такое диэлектрическая проницаемость и электрическая постоянная.
Физика,
вопрос задал simonovagalina9878,
4 года назад
Ответы на вопрос
Ответ:
Модуль силы кулоновского взаимодействия двух маленьких шариков равен 9 · 10⁹ H
Объяснение:
Дано:
r = 1 м
q₁ = q₂ = 1 Кл
k = 9 · 10⁹ (H · м²) / Кл²
Найти:
F – ?
——————————————–
Решение:
По закону Кулона:
- F = (k * |q₁| * |q₂|) / (r²)
Расчеты:
F = (9 · 10⁹ (H · м²) / Кл² * 1 Кл * 1 Кл) / (1 м²) = 9 · 10⁹ H
#SPJ1
solka0000:
будь ласка, допоможіть мене із задачою ,з фізики ,даю максимальну кількість балів
Новые вопросы
Задания Д16 B27 № 1303 

Как изменится модуль силы взаимодействия двух небольших металлических шариков одинакового диаметра, имеющих заряды и
если шары привести в соприкосновение и раздвинуть на прежнее расстояние?
1) увеличится в 9 раз
2) увеличится в 8 раз
3) увеличится в 3 раза
4) уменьшится в 3 раза
Спрятать решение
Решение.
Так как шарики имеют одинаковые размеры, после соприкосновения полный заряд перераспределится и поделится поровну между ними: Отсюда находим, что на каждом из шариков после соприкосновения будет заряд
Согласно закону Кулона, сила взаимодействия шариков прямо пропорциональна произведению модулей их зарядов. Отсюда находим, что модуль силы взаимодействия изменится в
Таким образом, модуль силы взаимодействия уменьшится в 3 раза.
Ответ: 4.

Закон Кулона
Закон сохранения электрического заряда
Напряженность
Принцип суперпозиции
Электрическое поле
Потенциал электростатического поля
Разность потенциалов
Теория
Совсем чуть−чуть.
Закон Кулона — сила, с которой два точечных заряда действуют друг на друга. Она обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их зарядов.
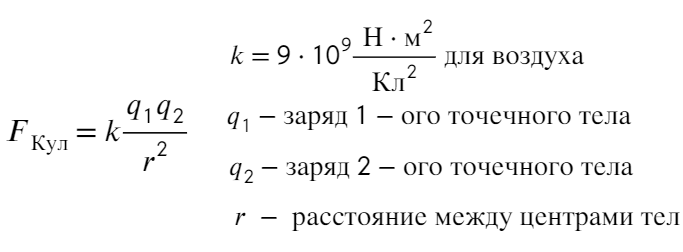
Заряды с одинаковым знаком отталкиваются, с разными — притягиваются. По III з. Ньютона сила действия одного заряда равна силе действия другого:
Наглядно рассказывается об этом в видео.
А напряженность — силовая характеристика электрического поля. По-простому: электрическое поле действует на заряд, и вот сила, с которой поле действует на заряд, и есть напряженность.
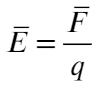
Напряженность НЕ зависит от величины заряда, помещенного в поле!
Задачи
Задача 1 Два одинаковых маленьких положительно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.
Скажем, что заряд одного шарика q, другого 5q. Тогда сила Кулона между ними:
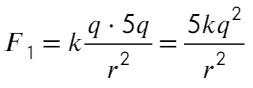
А если теперь соединить два шарика, то общий заряд разделится пополам (на каждый шарик). Общий заряд 5q + q = 6q, тогда на каждом шарике окажется по 3q. Тогда сила Кулона:
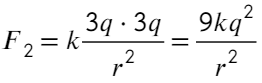
Отношение получится таким:
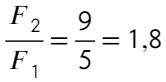
Ответ: 1,8
Задача 2 Два одинаковых маленьких разноименно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 4 раза. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₁ к F₂.
Та же самая задача? А вот и нет, одно слово другое: разноименно вместо положительных. Это значит, что один шарик будет заряжен положительно, другой отрицательно. По сравнению с первым случаем сила Кулона никак не изменится по модулю (только по нарпавлению).
А вот после соприкосновения изменится. Общий заряд: 5q − q = 4q или q − 5q = − 4q, тогда на каждый шар пойдет по 2q:
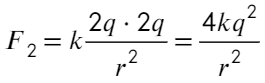
Отношение:
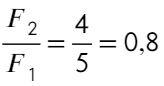
Ответ: 0,8
Задача 3 На нерастяжимой нити висит шарик массой 100 г, имеющий заряд 20 мкКл. Как необходимо зарядить второй шарик, который подносят снизу к первому шарику на расстояние 30 см, чтобы сила натяжения: а) увеличилась в 4 раза; б) рассмотреть случай невесомости?
В начальный момент времени на шарик действуют две силы:
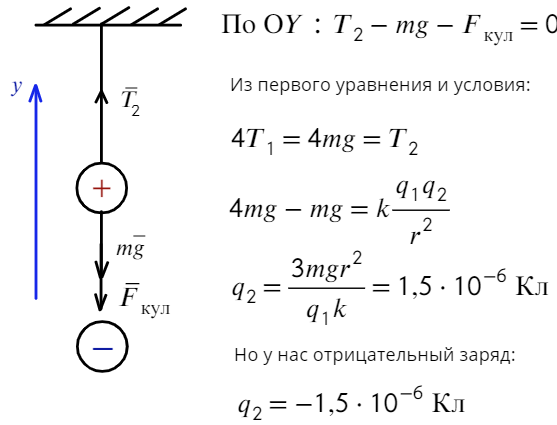
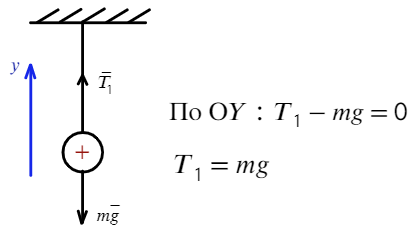 а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:
а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:
 б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:
б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:
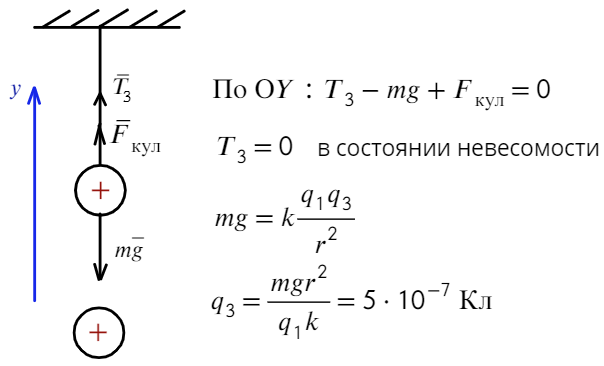 Ответ: −1,5 мкКл, 500 нКл.
Ответ: −1,5 мкКл, 500 нКл.
Задача 3 Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает с поверхности пластинки электрон, который попадает в электрическое поле с напряженностью 125 В/м. Найти расстояние, которое он пролетит прежде, чем разгонится до скорости, равной 1% от скорости света.
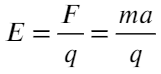
В задаче говорится про электрон, значит, его массу m = 9,1×10⁻³¹ кг и заряд q = 1,6 × 10⁻¹⁹ Кл можно посмотреть в справочных данных.
Найдем ускорение электрона в электрическом поле:
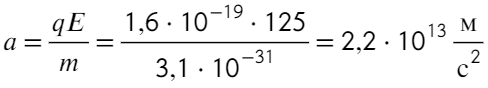
Остается найти пройденный путь в равноускоренном движении при нулевой начальной скорости:
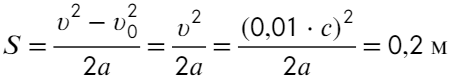
Ответ: 0,2 м
Задача 4 Полый заряженный шарик массой m = 0,4 г. движется в однородном горизонтальном электрическом поле из состояния покоя. Модуль напряженности электрического поля E = 500 кВ/м. Траектория шарика образует с вертикалью угол α = 45°. Чему равен заряд шарика?
Для начала разберемся, какие силы действуют на заряд:
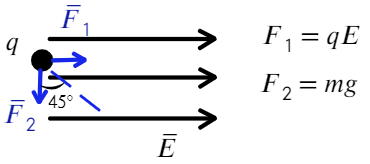
Заряд движется под углом 45 градусов, значит, отношением сил будет тангенс 45°:
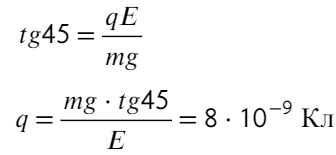
Ответ: 8×10⁻⁹ Кл
Задача 5 При нормальных условиях электрический «пробой» сухого воздуха наступает при напряжённости электрического поля 30 кВ/см. В результате «пробоя» молекулы газа, входящие в состав воздуха, ионизируются и появляются свободные электроны. Какую кинетическую энергию приобретёт такой электрон, пройдя в электрическом поле расстояние 10⁻⁵ см? Ответ выразите в электронвольтах. (ЕГЭ)
Задача кажется весьма тяжелой, но это обманчиво. Воспользуемся знакомой формулой напряженности:
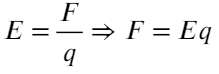
Домножим на длину обе части, тогда слева получится работа, а работа — это изменение энергии:
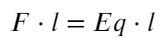
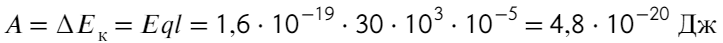
Переводить сантиметры не обязательно, они сократятся. Чтобы перевести джоули в электронвольты, нужно разделить на 1,6 × 10⁻¹⁹
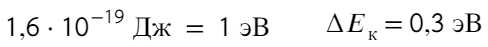
Ответ: 0,3 эВ
Задача 6 В вершинах равностороннего треугольника со стороной «а» находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника.
Покажем, как направлена напряженность: для двух положительных зарядов — от них (красные стрелочки), для отрицательного заряда — к нему (синяя стрелочка).
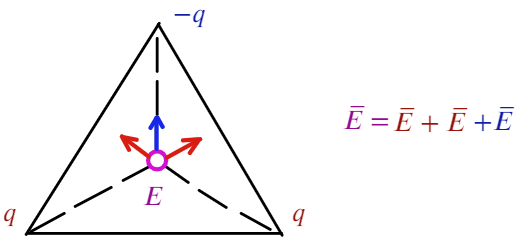
Угол между синим вектором и красным составляет 60°. Если продлить красный вектор до стороны, получится прямоугольный треугольник. Тогда, чтобы посчитать результирующую напряженность, спроецируем красные векторы на синий:
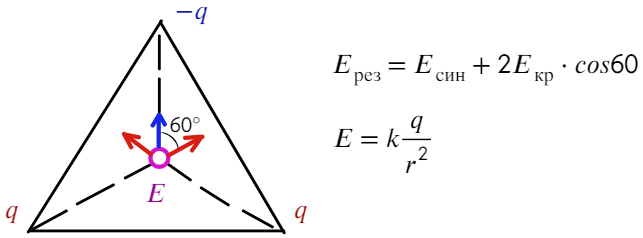
Остается разобрать на каком расстоянии находятся заряды от центра треугольника. Высоту треугольника можно найти по т. Пифагора, равна она а√3/2. А расстояние тогда составит 2/3 от высоты:
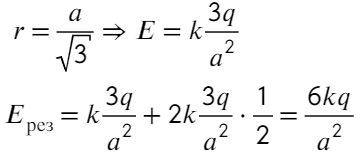
Ответ: 6kq/a²
Задача 6 Два шарика с зарядами Q = –1 нКл и q = 5 нКл соответственно, находятся в однородном электрическом поле с напряженностью Е = 18 В/м, на расстоянии r = 1 м друг от друга. Масса первого шарика равна M = 5 г. Определите, какую массу должен иметь второй шарик, чтобы они двигались с прежним между ними расстоянием и с постоянным по модулю ускорением. (ЕГЭ – 2016)
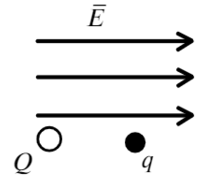
Направим ось X вправо и покажем, какие силы действуют на каждый заряд.
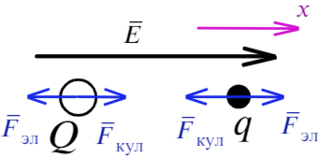
На положительный заряд электрическая сила действует по линиям напряженности, для отрицательного заряда все наоборот. Силы кулона направлены к зарядам, они разноименные. Составим уравнение для каждого заряда:
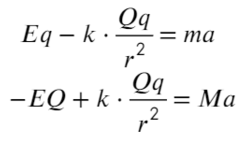
Сумма всех сила равна ma, потому что в условии сказано, что шарики двигаются с постоянным ускорением, а чтобы расстояние не менялось, двигаться они должны в одном направлении.
Разделим одно уравнение на другое и выразим массу:
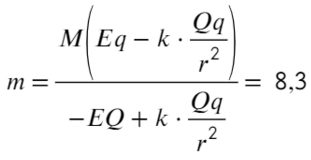
Ответ: 8,3 гр.
Задача 7 Четыре маленьких одинаковых шарика, связанных нерастяжимыми нитями одинаковой длины, заряженызарядами q, q, q и 2q. Сила натяжения нити, связывающей первый и второй шарики, равна T. Найти силу натяжения нити, связывающейвторой и третий шарики. (Росатом)
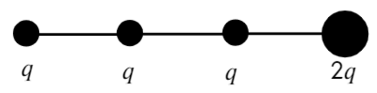
Покажем, каким силам противодействует сила натяжения Т. Воспользуемся принципом суперпозиции и законом Кулона:
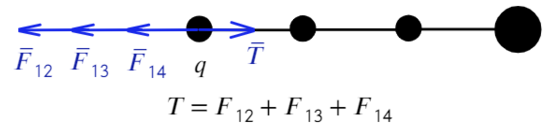
Сила натяжения Т удерживает первый шарик, других сил для него нет, значит, больше ничего для первого случая не требуется.
Как проще это запомнить: проводим линию перпендикулярно той нити, о которой говорим (красная черточка), после записываем только те силы между шариками, которые появляются по разные стороны от проведенной линии:
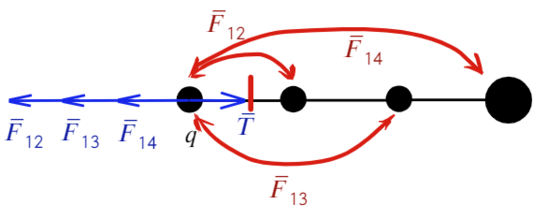
Теперь также составим уравнения для силы натяжения между вторым и третьим шариком:
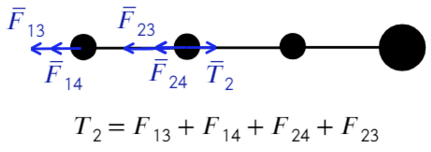
Распишим каждое уравнение по закону кулона, скажем, что расстояние между соседними шариками равно «а»:
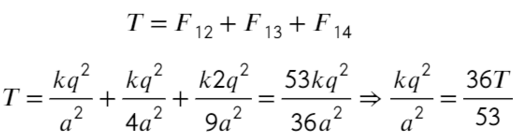
Второе уравнение с подстановкой выражения из первого:
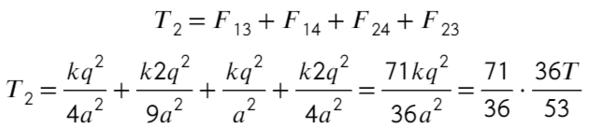
Ответ: 71T/53
Задача 8 Точечный заряд, расположенный в точке C, создаёт в точках A и B поле с напряжённостью Ea и Eb соответственно (см. рисунок; угол ACB — прямой). Найти напряжённость электрическогополя, создаваемого этим зарядом в точке M, являющейся основанием перпендикуляра, опущенного из точки C на прямую AB. (Росатом)
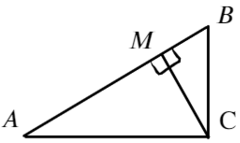
Запишем, чему равна напряженность в каждой из этих точек, взяв длины отрезков за a; b; h:
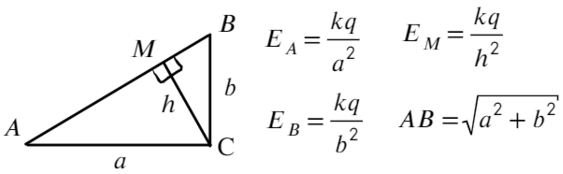
Площадь прямоугольного треугольника можно найти как полупроизведение катетов или как полупроизведение высоты и основания:
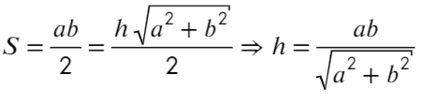
Возведем в квадрат получившиеся уравнение, а дальше смертельный номер: возводим в −1 степень и домножаем обе части на kq:
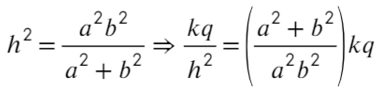
Выразим a² и b² через напряженность:
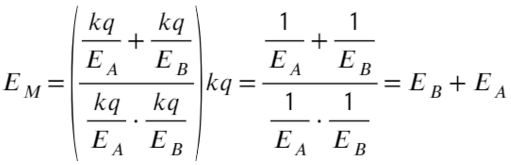
Ответ: Ea+Eb
Задача 9 Частицы с массами M и m, и зарядами q и −q соответственно вращаются с угловой скоростью ω по окружностям вокруг оси, направленной по внешнемуоднородному электрическому полю с напряжённостью E (рис.). Найдите расстояние L между частицами и расстояние H между плоскостями их орбит. (Всеросс. 2008)
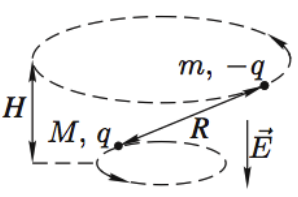 Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:
Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:
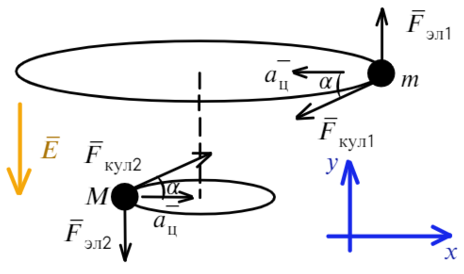
Запишем уравнения по осям на верхнюю частицу:
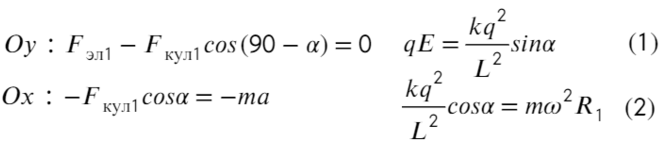
На нижнюю частицу:
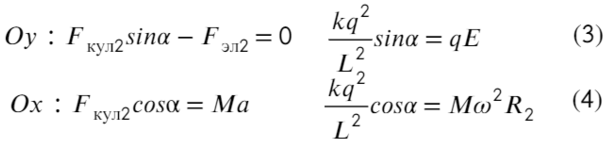
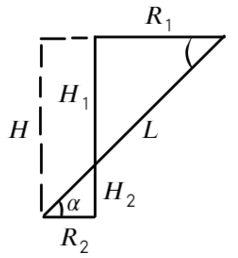
Построим два треугольника, которые показывают расстояние между частицами и высоту между ними.
Разделим уравнения друг на друга, а также выразим тангенс угла из этих треугольников:
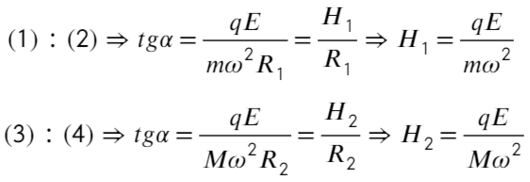
Сложим два уравнения, чтобы найти расстояние между плоскостями:
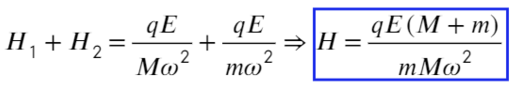
Пункт «а» решили, теперь с расстоянием разберемся: выразим из ур-ия (1) длину, а дальше из треугольника выразим синус угла альфа:
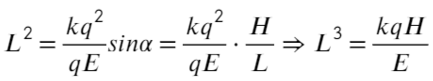
Вместо Н подставим то, что мы нашли:
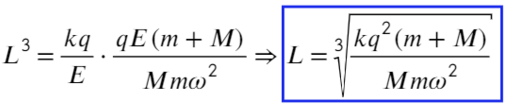
Задача 10 В точке O к стержню привязана непроводящая нить длиной R c зарядом q на конце. Известный эталонный заряд Q₂ и измеряемый заряд Q₁ установлены на расстояниях L₂ и L₁ от точки O. Все заряды одногознака и могут считаться точечными. Найдите величину заряда Q₁, если в состоянии равновесия нить отклонена на угол β от отрезка, соединяющегозаряды Q₂ и Q₁. (Всеросс. 2018)
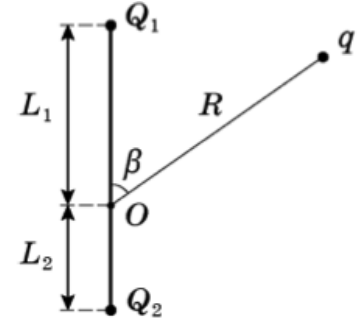
Проведем оси, подпишем расстояние от Q₁ до q и от Q₂ до q. Запишем ур-ия сил на каждую ось:
 Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:
Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:
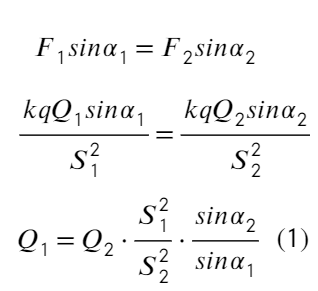
Из прямоугольных треугольников можно получить такие соотношения, а также из теоремы косинусов выразить S₁ и S₂:
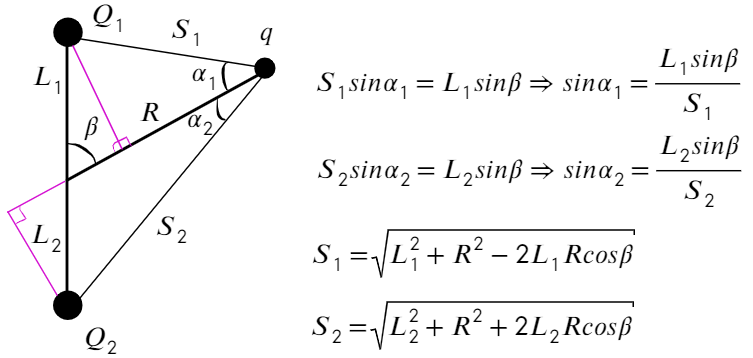
Подставим в ур-ие (1):
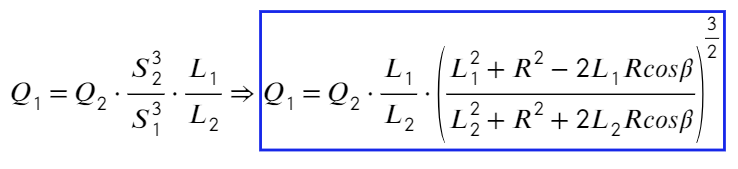
В качестве закрепления материала решите несколько похожих задач с ответами.
Будь в курсе новых статеек, видео и легкого технического юмора.
Введение
Тема урока: «Закон Кулона». Закон Кулона количественно описывает взаимодействие точечных неподвижных зарядов – то есть зарядов, которые находятся в статичном положении друг относительно друга. Такое взаимодействие называется электростатическим или электрическим и является частью электромагнитного взаимодействия.
Электромагнитное взаимодействие
Конечно, если заряды находятся в движении – они тоже взаимодействуют. Такое взаимодействие называется магнитным и описывается в разделе физики, который носит название «Магнетизм».
Стоит понимать, что «электростатика» и «магнетизм» – это физические модели, и вместе они описывают взаимодействие как подвижных, так и неподвижных друг относительно друга зарядов. И всё вместе это называется электромагнитным взаимодействием.
Электромагнитное взаимодействие – это одно из четырех фундаментальных взаимодействий, существующих в природе.
Электрический заряд
Что же такое электрический заряд? Определения в учебниках и Интернете говорят нам, что заряд – это скалярная величина, характеризующая интенсивность электромагнитного взаимодействия тел. То есть электромагнитное взаимодействие – это взаимодействие зарядов, а заряд – это величина, характеризующая электромагнитное взаимодействие. Звучит запутанно – два понятия определяются друг через друга. Разберемся!
Существование электромагнитного взаимодействия – это природный факт, что-то вроде аксиомы в математике. Люди его заметили и научились описывать. Для этого они ввели удобные величины, которые это явление характеризуют (в том числе электрический заряд) и построили математические модели (формулы, законы и т. д.), которые это взаимодействие описывают.
Закон Кулона
Выглядит закон Кулона следующим образом:
Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними. Она направлена вдоль прямой, соединяющей заряды, и является силой притяжения, если заряды разноименные, и силой отталкивания, если заряды одноименные.
Коэффициент k в законе Кулона численно равен:
![]()
Аналогия с гравитационным взаимодействием
Закон всемирного тяготения гласит: все тела, обладающие массой, притягиваются друг к другу. Такое взаимодействие называется гравитационным. Например, сила тяжести, с которой мы притягиваемся к Земле, – это частный случай именно гравитационного взаимодействия. Ведь и мы, и Земля обладаем массой. Сила гравитационного взаимодействия прямо пропорциональна произведению масс взаимодействующих тел и обратно пропорциональна квадрату расстояния между ними.
![]()
Коэффициент γ называется гравитационной постоянной.
Численно он равен: ![]() .
.
Как видите, вид выражений, количественно описывающих гравитационное и электростатическое взаимодействия, очень похож.
![]()
В числителях обоих выражений – произведение единиц, характеризующих данный тип взаимодействия. Для гравитационного – это массы, для электромагнитного – заряды. В знаменателях обоих выражений – квадрат расстояния между объектами взаимодействия.
Обратная зависимость от квадрата расстояния часто встречается во многих физических законах. Это позволяет говорить об общей закономерности, связывающей величину эффекта с квадратом расстояния между объектами взаимодействия.
![]()
Эта пропорциональность справедлива для гравитационного, электрического, магнитного взаимодействий, силы звука, света, радиации и т. д.
Объясняется это тем, что площадь поверхности сферы распространения эффекта увеличивается пропорционально квадрату радиуса (см. рис. 1).

Рис. 1. Увеличение площади поверхности сфер
Это будет выглядеть естественным, если вспомнить, что площадь сферы пропорциональна квадрату радиуса:
![]()
Физически это означает, что сила взаимодействия двух точечных неподвижных зарядов в 1 Кл, находящихся на расстоянии 1 м друг от друга в вакууме, будет равна 9·109 Н (см. рис. 2).

Рис. 2. Сила взаимодействия двух точечных зарядов в 1 Кл
Казалось бы, эта сила огромна. Но стоит понимать, что ее порядок связан с еще одной характеристикой – величиной заряда 1 Кл. На практике заряженные тела, с которыми мы взаимодействуем в повседневной жизни, имеют заряд порядка микро- или даже нанокулонов.
Коэффициент  и электрическая постоянная
и электрическая постоянная 
Иногда вместо коэффициента ![]() используется другая постоянная, характеризующая электростатическое взаимодействие, которая так и называется – «электрическая постоянная». Обозначается она
используется другая постоянная, характеризующая электростатическое взаимодействие, которая так и называется – «электрическая постоянная». Обозначается она ![]() . С коэффициентом
. С коэффициентом ![]() она связана следующим образом:
она связана следующим образом:
![]()
Выполнив несложные математические преобразования можно ее выразить и вычислить:
![]()
Обе константы, конечно, присутствуют в таблицах задачников. Закон Кулона тогда примет такой вид:
![]()
Обратим внимание на несколько тонких моментов.
Важно понимать, что речь идет именно о взаимодействии. То есть если мы возьмем два заряда, то каждый из них будет действовать на другой с силой, по модулю равной![]() . Эти силы будут направлены в противоположные стороны вдоль прямой, соединяющей точечные заряды.
. Эти силы будут направлены в противоположные стороны вдоль прямой, соединяющей точечные заряды.
Заряды будут отталкиваться, если они имеют один знак (оба положительные или оба отрицательные (см. рис. 3)), и притягиваться, если имеют разные знаки (один отрицательный, другой положительный (см. рис. 4)).
![]()
Рис. 3. Взаимодействие одноименных зарядов

Рис. 4. Взаимодействие разноименных зарядов
Точечный заряд
В формулировке закона Кулона присутствует термин «точечный заряд». Что это означает? Вспомним механику. Исследуя, например, движение поезда между городами, мы пренебрегали его размерами. Ведь размеры поезда в сотни или тысячи раз меньше расстояния между городами (см. рис. 5). В такой задаче мы считали поезд «материальной точкой» – телом, размерами которого в рамках решения некоторой задачи мы можем пренебречь.

Рис. 5. Размерами поезда в данном случае пренебрегаем
Так вот, точечные заряды – это материальные точки, обладающие зарядом. На практике, используя закон Кулона, мы пренебрегаем размерами заряженных тел в сравнении с расстояниями между ними. Если же размеры заряженных тел сопоставимы с расстоянием между ними, то из-за перераспределения заряда внутри тел электростатическое взаимодействие будет носить более сложный характер.
Задача 1
В вершинах правильного шестиугольника со стороной ![]() помещены друг за другом заряды
помещены друг за другом заряды ![]() . Найдите силу, действующую на заряд
. Найдите силу, действующую на заряд ![]() , расположенный в центре шестиугольника (см. рис. 6).
, расположенный в центре шестиугольника (см. рис. 6).

Рис. 6. Рисунок к условию задачи 1
Порассуждаем: заряд, находящийся в центре шестиугольника, будет взаимодействовать с каждым из зарядов, находящихся в вершинах шестиугольника. В зависимости от знаков это будет сила притяжения или сила отталкивания. С зарядами 1, 2 и 3, которые являются положительными, заряд, находящийся в центре, будет испытывать электростатическое отталкивание (см. рис. 7).

Рис. 7. Электростатическое отталкивание
А с зарядами 4, 5 и 6 (отрицательными) заряд в центре будет иметь электростатическое притяжение (см. рис. 8).

Рис. 8. Электростатическое притяжение
Суммарная сила, действующая на заряд, находящийся в центре шестиугольника, будет равнодействующей сил ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() и
и![]() , модуль каждой из которых можно найти с помощью закона Кулона. Приступим к решению задачи.
, модуль каждой из которых можно найти с помощью закона Кулона. Приступим к решению задачи.
Решение
Силы взаимодействия заряда, который находится в центре, с каждым из зарядов в вершинах зависит от модулей самих зарядов и расстояния между ними. Расстояние от вершин к центру правильного шестиугольника одинаковое, модули у взаимодействующих зарядов в нашем случае тоже равны (см. рис. 9).

Рис. 9. Расстояния от вершин до центра в правильном шестиугольнике равны
А значит, все силы взаимодействия заряда в центре шестиугольника с зарядами в вершинах будут равны по модулю. Воспользовавшись законом Кулона, мы можем найти этот модуль:
![]()
Расстояние от центра до вершины в правильном шестиугольнике равно длине стороны правильного шестиугольника, которая нам известна из условия, поэтому:
![]()
Теперь нам необходимо найти векторную сумму – для этого выберем систему координат: ось ![]() вдоль силы
вдоль силы ![]() , а ось
, а ось ![]() перпендикулярно
перпендикулярно ![]() (см. рис. 10).
(см. рис. 10).

Рис. 10. Выбор осей
Найдем суммарные проекции на оси – модуль каждой из них обозначим просто ![]() .
.
![]()
![]()
Так как силы ![]() и
и ![]() сонаправлены с осью
сонаправлены с осью ![]() , а
, а ![]() находятся под углом
находятся под углом ![]() к оси
к оси![]() (см. рис. 11).
(см. рис. 11).

Рис. 11. Направление сил относительно оси ![]()
Проделаем такие же действия для оси ![]() :
:
![]()
Знак «-» – потому что силы ![]() и
и ![]() направлены в противоположную сторону оси
направлены в противоположную сторону оси ![]() . То есть проекция суммарной силы на ось
. То есть проекция суммарной силы на ось ![]() , которую мы выбрали, будет равна 0. Получается, что суммарная сила будет действовать только вдоль оси
, которую мы выбрали, будет равна 0. Получается, что суммарная сила будет действовать только вдоль оси ![]() , остается подставить сюда только выражения для модуля сил взаимодействия и
, остается подставить сюда только выражения для модуля сил взаимодействия и ![]() и получить ответ. Суммарная сила будет равна:
и получить ответ. Суммарная сила будет равна:
![]()
Задача решена.
Диэлектрическая проницаемость
Еще один тонкий момент заключается вот в чем: в законе Кулона сказано, что заряды находятся в вакууме (см. рис. 12).

Рис. 12. Взаимодействие зарядов в вакууме
Это действительно важное замечание. Потому что в среде, отличной от вакуума, сила электростатического взаимодействия будет ослабляться (см. рис. 13).

Рис. 13. Взаимодействие зарядов в среде, отличной от вакуума
Чтобы учесть этот фактор, в модель электростатики была введена специальная величина, которая позволяет сделать «поправку на среду». Называется она диэлектрической проницаемостью среды. Обозначается, как и электрическая постоянная, греческой буквой «эпсилон», но уже без индекса.
Физический смысл этой величины заключается в следующем.
Сила электростатического взаимодействия двух точечных неподвижных зарядов в среде, отличной от вакуума, будет в ε раз меньше, чем сила взаимодействия таких же зарядов на таком же расстоянии в вакууме.
![]()
Таким образом, в среде, отличной от вакуума, сила электростатического взаимодействия двух точечных неподвижных зарядов будет равна:

Значения диэлектрической проницаемости различных веществ давно найдены и собраны в специальных таблицах (см. рис. 14).

Рис. 14. Диэлектрическая проницаемость некоторых веществ
Мы можем свободно использовать табличные значения диэлектрической проницаемости необходимых нам веществ при решении задач.
Важно понимать, что при решении задач сила электростатического взаимодействия рассматривается и описывается в уравнениях динамики как обычная сила. Решим задачу.
Задача 2
Два одинаковых заряженных шарика подвешены в среде с диэлектрической проницаемостью ![]() на нитях одинаковой длины
на нитях одинаковой длины ![]() , закрепленных в одной точке. Определите модуль заряда шариков, если нити находятся под прямым углом друг к другу (см. рис. 15). Размеры шариков пренебрежимо малы по сравнению с расстоянием между ними. Массы шариков равны
, закрепленных в одной точке. Определите модуль заряда шариков, если нити находятся под прямым углом друг к другу (см. рис. 15). Размеры шариков пренебрежимо малы по сравнению с расстоянием между ними. Массы шариков равны ![]() .
.

Рис. 15. Рисунок к условию задачи 2
Порассуждаем: на каждый из шариков будут действовать три силы – сила тяжести ![]() ; сила электростатического взаимодействия
; сила электростатического взаимодействия ![]() и сила натяжения нити
и сила натяжения нити  (см. рис. 16).
(см. рис. 16).

Рис. 16. Силы, действующие на шарики
По условию шарики одинаковые, то есть их заряды равны как по модулю, так и по знаку, а значит, сила электростатического взаимодействия в данном случае будет силой отталкивания (на рис. 16 силы электростатического взаимодействия направлены в разные стороны). Так как система находится в равновесии, будем использовать первый закон Ньютона:
![]()
Так как в условии сказано, что шарики подвешены в среде с диэлектрической проницаемостью ![]() , а размеры шариков пренебрежимо малы по сравнению с расстоянием между ними, то в соответствии с законом Кулона сила, с которой будут отталкиваться шарики, будет равна:
, а размеры шариков пренебрежимо малы по сравнению с расстоянием между ними, то в соответствии с законом Кулона сила, с которой будут отталкиваться шарики, будет равна:
![]()
Решение
Распишем первый закон Ньютона в проекциях на оси координат. Ось ![]() направим горизонтально, а ось
направим горизонтально, а ось ![]() вертикально (см. рис. 17).
вертикально (см. рис. 17).

Рис. 17. Выбор направления осей координат
![]()

Рис. 18. Силы в проекциях на оси координат
Так как на шарики действуют одинаковые силы тяжести и силы электростатического взаимодействия, нити тоже одинаковые – они отклонятся на одинаковые углы ![]() (см. рис. 19).
(см. рис. 19).

Рис. 19. Углы, на которые отклоняются шарики, одинаковые
В сумме эти углы дают нам ![]() , это означает, что:
, это означает, что:
![]()
![]()
Тогда из прямоугольного треугольника можно найти углом ![]() :
:
![]()
Добавим к двум уравнениям, которые мы записали, выражение для модуля силы электростатического взаимодействия:
![]()
Расстояние ![]() найдем геометрически – найдем прилежащий к углу
найдем геометрически – найдем прилежащий к углу ![]() катет и умножим его на 2:
катет и умножим его на 2:
![]()
Мы получили систему из 4-х уравнений:

Математическое решение можно пронаблюдать в свертке.
Ответ: 
Решение системы уравнений

Выразим из второго уравнения силу натяжения нити ![]() и подставим в первое:
и подставим в первое:
![]()
![]()
Отсюда выразим силу электростатического взаимодействия:
![]()
Приравняем выражение для силы электростатического взаимодействия, которое мы сейчас выразили с третьим уравнением:
![]()
Подставим сюда выражение для ![]()
![]()
Выразим искомый заряд ![]()
![]()

Так как угол ![]() , то
, то ![]() , тогда:
, тогда: 
На этом наш урок закончен. Спасибо за внимание.
Список литературы
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: Учеб. для общеобразоват. учреждений. Базовый и профильный уровни. 19-е издание – М.: Просвещение, 2010.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «physics.ru» (Источник)
- Интернет-портал «Класс!ная физика» (Источник)
Домашнее задание
- Запишите формулу закона Кулона.
- Как взаимодействуют разноименно заряженные тела?
- Решите задачу: два заряда, 10 нКл и -2 нКл, закреплены на расстоянии 10 см друг от друга. Определите силу, с которой они взаимодействуют.
