Электромагнитная
сила, действующая на заряженную частицу,
складывается из сил, действующих со
стороны электрического и магнитного
полей:
![]() . (3.2)
. (3.2)
Силу,
определяемую формулой (3.2), называют
обобщенной силой Лоренца. Учитывая
действие двух полей, электрического и
магнитного, говорят, что на заряженную
частицу действует электромагнитное
поле.
Рассмотрим
движение заряженной частицы в одном
только электрическом поле. При этом
здесь и далее предполагается, что частица
нерелятивистская, т.е. ее
скорость существенно меньше
скорости света. На частицу действует
только электрическая составляющая
обобщенной силы Лоренца
![]() .
.
Согласно второму закону Ньютона частица
движется с ускорением:
![]() ,
,
(3.3)
которое
направленно вдоль вектора
![]() в случае положительного заряда и против
в случае положительного заряда и против
вектора![]() в случае отрицательного заряда.
в случае отрицательного заряда.
Разберем
важный случай движения заряженной
частицы в однородном электрическом
поле. В этом случае частица движется
равноускоренно (![]() ).
).
Траектория движения частицы зависит
от направления ее начальной скорости.
Если начальная скорость равна нулю или
направлена вдоль вектора![]() ,
,
движение частицы прямолинейное и
равноускоренное. Если же начальная
скорость частицы направлена под углом
к вектору![]() ,
,
то траекторией движения частицы будет
парабола. Траектории движения заряженной
частицы в однородном электрическом
поле такие же, как и траектории свободно
(без сопротивления воздуха) падающих
тел в гравитационном поле Земли, которое
вблизи поверхности Земли можно считать
однородным.
Пример
3.1. Определить
конечную скорость частицы массой
![]() и зарядом
и зарядом![]() ,
,
пролетевшей в однородном электрическом
поле![]() расстояние
расстояние
![]() .
.
Начальная скорость частицы равна нулю.
Решение.
Так как поле однородно, а начальная
скорость частицы равна нулю, движение
частицы будет прямолинейным равноускоренным.
Запишем уравнения прямолинейного
равноускоренного движения с нулевой
начальной скоростью:

![]()
![]() .
.
Подставим
величину ускорения из уравнения (3.3) и
получим:
![]() .
.
В
однородном поле
![]() (см. 1.21). Величину
(см. 1.21). Величину![]() называют ускоряющей разностью потенциалов.
называют ускоряющей разностью потенциалов.
Таким образом, скорость, которую набирает
частица, проходя ускоряющую разность
потенциалов![]() :
:
![]() .
.
(3.4)
При
движении в неоднородных электрических
полях ускорение заряженных частиц
переменное, и траектории будут более
сложными. Однако, задачу о нахождении
скорости частицы, прошедшей ускоряющую
разность потенциалов
![]() ,
,
можно решить исходя из закона сохранения
энергии. Энергия движения заряженной
частицы (кинетическая энергия) изменяется
за счет работы электрического поля:
![]()
![]()
![]() .
.
Здесь
использована формула (1.5) для работы
электрического поля по перемещению
заряда
![]() .
.
Если начальная скорость частицы равна
нулю (![]() )
)
или мала по сравнению с конечной
скоростью, получим:![]() ,
,
откуда следует формула (3.4). Таким образом,
эта формула остается справедливой и в
случае движения заряженной частицы в
неоднородном поле. В этом примере
показаны два способа решения физических
задач. Первый способ основан на
непосредственном применении законов
Ньютона. Если же действующие на тело
силы переменны, бывает более целесообразным
использование второго способа, основанного
на законе сохранения энергии.
Теперь
рассмотрим движение заряженных частиц
в магнитных полях. Изменение кинетической
энергии частицы в магнитном поле могло
бы произойти только за счет работы силы
Лоренца:
![]() .
.
Но работа силы Лоренца всегда равна
нулю, значит кинетическая энергия
частицы, а вместе с тем и модуль ее
скорости не изменяются. Заряженные
частицы движутся в магнитных полях с
постоянными по модулю скоростями. Если
электрическое поле может быть ускоряющим
по отношению к заряженной частице, то
магнитное поля может быть только
отклоняющим, т. е. изменять лишь направление
ее движения.
Рассмотрим
варианты траекторий движения заряда в
однородном поле.
1.
Вектор магнитной индукции параллелен
или антипараллелен начальной скорости
заряженной частицы. Тогда из формулы
(3.1) следует
![]() .
.
Следовательно, частица будет двигаться
прямолинейно и равномерно вдоль линий
магнитного поля.

2.
Вектор магнитной индукции
перпендикулярен начальной скорости
частицы (на рис. 3.2 вектор магнитной
индукции направлен за плоскость чертежа).
Второй закон Ньютона для частицы имеет
вид:
![]() или
или![]() .
.
Сила
Лоренца постоянна по величине и направлена
перпендикулярно скорости и вектору
магнитной индукции. Значит, частица
будет двигаться все время в одной
плоскости. Кроме того, из второго закона
Ньютона следует, что и ускорение частицы
будет постоянно по величине и
перпендикулярно скорости. Это возможно
только тогда, когда траектория частицы
– окружность, а ускорение частицы
центростремительное. Подставляя во
второй закон Ньютона величину
центростремительного ускорения
![]() и величину силы Лоренца
и величину силы Лоренца![]() ,
,
находим радиус окружности:
![]()
![]()
![]() .
.
(3.5)
Отметим,
что период вращения частицы не зависит
от ее скорости:
 .
.

3. В общем случае
вектор магнитной индукции может быть
направлен под некоторым углом
![]() к начальной скорости частицы (рис. 3.3).
к начальной скорости частицы (рис. 3.3).
Прежде всего, отметим еще раз, что
скорость частицы по модулю остается
постоянной и равной величине начальной
скорости![]() .
.
Скорость![]() можно разложить на две составляющие:
можно разложить на две составляющие:
параллельную вектору магнитной индукции![]() и перпендикулярную вектору магнитной
и перпендикулярную вектору магнитной
индукции![]() .
.
Ясно,
что если бы частица влетела в магнитное
поле, имея только составляющую
![]() ,
,
то она в точности как в случае 1 двигалась
бы равномерно по направлению вектора
индукции.
Если
бы частица влетела в магнитное поле,
имея одну только составляющую скорости
![]() ,
,
то она оказалась бы в тех же условиях,
что и в случае 2. И, следовательно,
двигалась бы по окружности, радиус
которой определяется опять-таки из
второго закона Ньютона:
![]()
![]()
![]() .
.
Таким
образом, результирующее движение частицы
представляет собой одновременно
равномерное движение вдоль вектора
магнитной индукции со скоростью
![]() и равномерное вращение в плоскости,
и равномерное вращение в плоскости,
перпендикулярной вектору магнитной
индукции со скоростью![]() .
.
Траектория такого движения представляет
собой винтовую линию или спираль (см.
рис. 3.3). Шаг спирали![]() – расстояние, пролетаемое частицей
– расстояние, пролетаемое частицей
вдоль вектора индукции за время одного
оборота:
![]() .
.
Откуда
известны массы мельчайших заряженных
частиц (электрона, протона, ионов)? Каким
образом удается их «взвесить» (ведь, на
весы их не положишь!)? Уравнение (3.5)
показывает, что для определения массы
заряженной частицы нужно знать радиус
ее трека при движении в магнитном поле.
Радиусы треков мельчайших заряженных
частиц определяют с помощью камеры
Вильсона, помещенной в магнитное поле,
или с помощью более совершенной
пузырьковой камеры. Принцип их работы
прост. В камере Вильсона частица движется
в пересыщенном водяном паре и является
ядром конденсации пара. Микрокапельки,
конденсирующиеся при пролете заряженной
частицы, отмечают ее траекторию. В
пузырьковой камере (изобретенной лишь
полвека назад американским физиком Д.
Глейзером) частица движется в перегретой
жидкости, т.е. нагретой выше точки ее
кипения. Это состояние неустойчиво и
при пролете частицы происходит вскипание,
вдоль ее следа образуется цепочка
пузырьков.
Подобную
картину можно наблюдать, бросив в стакан
с пивом крупинку поваренной соли: падая,
она оставляет след из пузырьков газа.
Пузырьковые камеры являются важнейшим
инструментом для регистрации мельчайших
заряженных частиц, являясь по сути,
основными информативными приборами
экспериментальной ядерной физики.
Соседние файлы в папке Методички_Общая физика
- #
- #
- #
- #
- #
- #
- #
- #
Как найти скорость частицы
Часто при изучении школьного курса электромагнетизма или при научных исследованиях возникает необходимость установить скорость, с которой двигалась какая-нибудь элементарная частица, например, электрон или протон.

Инструкция
Допустим, дана следующая задача: электрическое поле с напряженностью Е и магнитное поле с индукцией В, возбуждены перпендикулярно друг другу. Перпендикулярно им, равномерно и прямолинейно движется заряженная частица с зарядом q и скоростью v. Требуется определить ее скорость.
Решение очень простое. Если частица по условиям задачи движется равномерно и прямолинейно, значит, ее скорость v постоянная. Таким образом, в соответствии с первым законом Ньютона, величины действующих на нее сил взаимно уравновешены, то есть в сумме они равны нулю.
Какие силы действуют на частицу? Во-первых, электрическая составляющая силы Лоренца, которая вычисляется по формуле: Fэл = qE. Во-вторых, магнитная составляющая силы Лоренца, которую вычисляют по формуле: Fм = qvBSinα. Поскольку по условиям задачи частица движется перпендикулярно магнитному полю, угол α = 90 градусам, и соответственно, Sinα = 1. Тогда магнитная составляющая силы Лоренца Fм = qvB.
Электрическая и магнитная составляющие уравновешивают друг друга. Следовательно, величины qE и qvB численно равны. То есть Е = vB. Следовательно, скорость частицы вычисляется по такой формуле: v = E/B. Подставив в формулу значения Е и В, вы вычислите искомую скорость.
Или, например, у вас такая задача: частица с массой m и зарядом q, двигаясь со скоростью v, влетела в электромагнитное поле. Его силовые линии (как электрические, так и магнитные) параллельны. Частица влетала под углом α к направлению силовых линий и после этого началась двигаться с ускорением а. Требуется вычислить, с какой скоростью она двигалась первоначально. Согласно второму закону Ньютона, ускорение тела с массой m вычисляется по формуле: a = F/m.
Массу частицы вы знаете по условиям задачи, а F – результирующая (суммарная) величина сил, действующих на нее. В данном случае на частицу действуют электрическая и магнитная оставляющие силы Лоренца: F = qE + qBvSinα.
Но поскольку силовые линии полей (по условию задачи) параллельны, то вектор электрической силы перпендикулярен вектору магнитной индукции. Следовательно, суммарная сила F вычисляется по теореме Пифагора: F = [(qE)^2 + (qvBSinα)^2]^1/2
Преобразуя, получите: am = q[E^2 +B^2v^2Sin^2α]^1/2. Откуда: v^2 = (a^2m^2 – q^2E^2)/(q^2B^2Sin^2α). После вычисления и извлечения квадратного корня, получите искомую величину v.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Пусть в однородном магнитном поле, индукция которого , движется частица со скоростью
, направленной перпендикулярно линиям индукции. Масса частицы m и заряд q. Так как сила Лоренца
перпендикулярна скорости
движения частицы (см. рис. 170), то эта сила изменяет только направление скорости, сообщая частице центростремительное ускорение, модуль которого согласно второму закону Ньютона:
В результате частица движется по окружности, радиус которой можно определить из формулы :
Период Т обращения частицы, движущейся по окружности в однородном магнитном поле:
(30.2)
Как следует из выражения (30.2), период обращения частицы не зависит от модуля скорости её движения и радиуса траектории, а определяется только модулем заряда частицы, её массой и значением индукции магнитного поля.
От теории к практике
В однородном магнитном поле, модуль индукции которого В = 4,0 мТл, перпендикулярно линиям индукции поля движется электрон. Чему равен модуль ускорения электрона, если модуль скорости его движения ? Масса и модуль заряда электрона mе = 9,1 · 10–31 кг и е = 1,6 · 10–19 Кл соответственно.
![]()
Подобное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Движущиеся с огромными скоростями заряженные частицы из космоса захватываются магнитным полем Земли и образуют так называемые радиационные пояса (рис. 170.2), в которых частицы перемещаются по винтообразным траекториям между северным и южным магнитными полюсами туда и обратно за промежуток времени порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния (рис. 170.3).
Если заряженная частица в момент возникновения внешнего электрического поля покоилась, то , где U — напряжение между точками, в которых находилась частица в моменты возникновения внешнего электрического поля и выхода из него, q — модуль заряда частицы. Поэтому модуль скорости частицы при выходе из электрического поля:
Если после этого частица попадает в однородное магнитное поле, индукция которого перпендикулярна направлению её скорости, то радиус окружности, по дуге которой будет двигаться частица,
, откуда
Величину называют удельным зарядом частицы. Поэтому если опытным путём определить радиус траектории движения частицы в магнитном поле, то, зная индукцию магнитного поля и ускоряющее напряжение электрического поля, можно рассчитать удельный заряд частицы. Этот метод используют при конструировании приборов, которые называют масс–спектрометрами.
Интересно знать
Поскольку сила Лоренца направлена под углом 90° к скорости движения заряженной частицы в каждой точке траектории (рис. 171), то работа этой силы при движении заряженной частицы в магнитном поле равна нулю. Поэтому кинетическая энергия частицы, движущейся в стационарном (не изменяющемся во времени) магнитном поле, не изменяется, т. е. стационарное магнитное поле нельзя использовать для ускорения заряженных частиц.
Увеличение кинетической энергии частицы, т. е. её разгон, возможно под действием электрического поля (в этом случае изменение кинетической энергии частицы равно работе силы поля). Поэтому в современных ускорителях (рис. 172) заряженных частиц электрическое поле используют для ускорения, а магнитное — для «формирования» траектории движения заряженных частиц.

![]()
1. Как определить модуль силы, действующей со стороны магнитного поля на движущуюся в нём заряженную частицу?
2. Как определяют направление силы Лоренца?
3. Заряженная частица движется в однородном магнитном поле со скоростью, направленной перпендикулярно линиям индукции. По какой траектории движется частица?
4. От чего зависит период обращения заряженной частицы в однородном магнитном поле?
![]()
5. Почему сила Лоренца изменяет направление скорости движения частицы, но не влияет на её модуль?
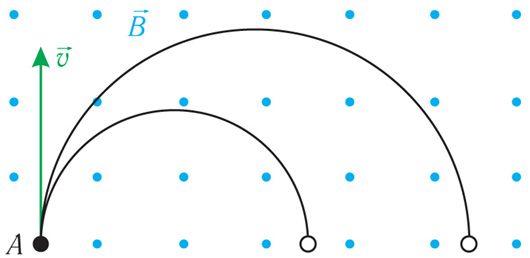
6. На рисунке 172.1 представлены траектории движения двух частиц, имеющих одинаковые заряды. Частицы влетают в однородное магнитное поле из одной точки А с одинаковыми скоростями. Определите знак заряда частиц. Объясните причину несовпадения траекторий их движения.
Содержание:
- Определение и формула скорости
- Скорость в разных системах координат
- Частные случаи формул для вычисления скорости
- Единицы измерения скорости
- Примеры решения задач
Определение и формула скорости
Определение
Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора
$bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v.
Это векторная величина. Математически определение вектора мгновенной скорости записывается как:
$$bar{v}=frac{d bar{r}}{d t}=dot{bar{r}}(1)$$
Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения.
Модуль скорости можно определить как первую производную от длины пути (s) по времени:
$$v=frac{d s}{d t}=dot{s}(2)$$
Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.
Скорость в разных системах координат
Проекции скорости на оси декартовой системы координат запишутся как:
$$v_{x}=dot{x} ; v_{y}=dot{y} ; v_{z}=dot{z}(3)$$
Следовательно, вектор скоростив декартовых координатах можно представить:
$$bar{v}=dot{x} bar{i}+dot{y} bar{j}+dot{z} bar{k}(4)$$
где $bar{i}, bar{j}, bar{k}$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:
$$v=sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}}(5)$$
В цилиндрических координатах модуль скорости вычисляют при помощи формулы:
$$v=sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}}(6)$$
в сферической системе координат:
$$v=sqrt{(r)^{2}+(r dot{theta})^{2}+(r dot{varphi} sin theta)^{2}}(7)$$
Частные случаи формул для вычисления скорости
Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const).
При равномерном движении скорость можно вычислить, применяя формулу:
$$v=frac{s}{t}(8)$$
где s– длина пути, t – время, за которое материальная точка преодолела путь s.
При ускоренном движении скорость можно найти как:
$$bar{v}=int_{t_{1}}^{t_{2}} bar{a} d t(9)$$
где $bar{a}$ – ускорение точки,
$t_{1} leq t leq t_{2}$ – отрезок времени, в течение которого рассматривается скорость.
Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:
$$bar{v}=bar{v}_{0}+bar{a} t$$
где $bar{v}_0$ – начальная скорость движения,
$bar{a} = const$ .
Единицы измерения скорости
Основной единицей измерения скорости в системе СИ является: [v]=м/с2
В СГС: [v]=см/с2
Примеры решения задач
Пример
Задание. Движение материальной точки А задано уравнением:
$x=2 t^{2}-4 t^{3}$ . Точка начала свое движение при
t0=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для
этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:
$$v=frac{d x}{d t}=4 t-12 t^{2}(1.1)$$
Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент
времении сравним результат с нулем:
$$v(t=0,5)=4 cdot 0,5-12(0,5)^{2}=-1 lt 0$$
Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.
Ответ. Против оси X.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Скорость материальной точки является функцией от времени вида:
$$v=10left(1-frac{t}{5}right)$$
где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии
10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.
Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:
$$x=int_{0}^{t} v d t=int_{0}^{t} 10left(1-frac{t}{5}right) d t=10 t-frac{10 t^{2}}{2 cdot 5}=10 t-t^{2}(2.1)$$
Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:
$$x=10 cdot 10-(10)^{2}=0(m)$$
Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат
приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:
$$
begin{array}{c}
10 t-t^{2}=10(2.2) \
t_{1}=5+sqrt{15} approx 8,8(c) ; t_{2}=5-sqrt{15} approx 1,13(c)
end{array}
$$
Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:
$$10 t-t^{2}=-10(2.3)$$
При решении уравнения (2.3) нам подойдет корень равный:
$$t_{3}=5+6=11 (c)$$
Ответ. 1) $x=0 mathrm{~m}$ 2) $t_{1}=8,8 mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$
Читать дальше: Формула средней скорости.
подскажите формулу. как найти скорость элементарной частицы?по какой формуле?и как она вообще обозначается??
Алина Ч.
Ученик
(228),
закрыт
12 лет назад
Дополнен 12 лет назад
задача:
Найти скорость элементарной частицы, если её полная энергия в 10 раз больше энергии покоя?
больше ничего не дано. если не сложно, то можно подробное решение)
вот собственно в этом заключается вся задача
Sorry 4377[MAN]
Мыслитель
(5249)
12 лет назад
Во первых у нас есть формула инштейна:
энергия = скорость света в квадрате
вычисляем оттуда релятивистскую массу
Дальше имеем преобразования лоренца :
релятивистская масса = масса покоя делить на единица минус (c^2/v^2)
с^2-скорость света в квадрате
v^2 – скорость частицы. тоже в квадрате
Дальше все выражаем и ищем.
