Формула скорости волны в физике
Формула скорости волны
Определение
Фронт волны (волновая поверхность) – это геометрическое место точек среды, для которых в некоторый момент времени фаза волны
имеет одно и то же значение.
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),]
где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).]
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right),]
где $T$ – период колебаний точек в волне.
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны – это не то же самое, что скорость колебания частиц среды в волне.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
[v=sqrt{frac{K}{rho }}left(4right),]
где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение:
[v=sqrt{frac{gamma p}{rho }}left(5right),]
где $gamma $ – показатель адиабаты; $p$ – давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
[v=sqrt{frac{E}{rho }}left(6right),]
где $E$ – модуль Юнга вещества стержня.
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
[v=sqrt{frac{G}{rho }left(7right),}]
где $G$ – модуль сдвига среды; $rho $ – плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
[u=v-frac{dv}{dlambda }left(8right).]
Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
Примеры задач с решением
Пример 1
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?
Решение. Сделаем рисунок.
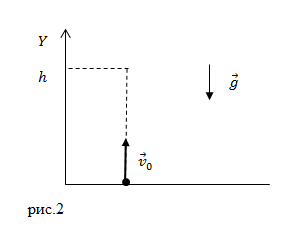
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
[v=frac{lambda }{T} left(1.1right).]
Найдем период колебаний как время одного полного колебания:
[T=frac{t}{N} left(1.2right).]
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
[v=frac{lambda N}{t}.]
Вычислим искомую скорость:
[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).]
Ответ. $v=5frac{м}{с}$
Пример 2
Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды?
Решение. Фазовую скорость движения волны найдем как:
[v=frac{lambda }{T}=lambda nu left(2.1right),]
где период – величина обратная частоте колебаний:
[T=frac{1}{nu }left(2.2right).]
Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac{м}{с}right).]
Скорость колебания частиц равна:
[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }]
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
[{left(frac{dxi }{dt}right)}_{max}=left|2omega right|left(2.4right).]
Циклическую частоту найдем как:
[omega =2pi nu ,]
тогда:
[{left(frac{dxi }{dt}right)}_{max}=left|2cdot 2pi nu right|=4pi nu .]
Вычислим максимальную скорость колебаний частиц:
[{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).]
Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$
Читать дальше: формула скорости свободного падения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Дано:
λ=15 м;λ=15, м;
T=0.20 с.T=0.20 ,с.
Найти:
v−?v-?
Решение:
Если волна движется со скоростью vv и за период она преодолевает расстояние в одну длину волны, то мы можем записать:
λ=vT;λ=vT;
v=λT.v=dfrac{λ}{T}.
Подставим числа и найдем скорость распространения волны:
v=150.2=75 м/с.v=dfrac{15}{0.2}=75,м/с.
Ответ: 75 м/с.75,м/с.
Содержание
- Как определить модуль скорости относительно земли
- Методы измерения модуля скорости
- Измерение модуля скорости с помощью приборов
- Ключевые моменты для определения модуля скорости
- Итог
- Как определить модуль скорости относительно земли
- Определение скорости относительно земли
- Методы измерения скорости относительно земли
- Итог
- Как определить модуль скорости относительно земли
- 1. Определите скорость путем измерения расстояния и времени
- 2. Используйте специальное оборудование
- 3. Определите скорость, используя наблюдения на звездах или спутниках
- 4. Используйте формулу для определения скорости относительно земли
- Общий итог
Как определить модуль скорости относительно земли
Модуль скорости — важная физическая величина, характеризующая скорость тела без учета направления движения. Для определения модуля скорости относительно земли существуют несколько методов, которые можно использовать в различных условиях.
Методы измерения модуля скорости
- Метод радара — этот метод используется в авиации и является одним из самых точных способов измерения скорости. Радар измеряет время, за которое эхо от самолета возвращается обратно к радару. Исходя из времени задержки, радар может вычислить скорость самолета.
- Метод Доплера — этот метод используется для измерения скорости звука или света. Объект, движущийся со скоростью приближения, вызывает сжатие волн, проходящих через него, а движущийся объект, отдаляющийся, — их растяжение. Измерив изменения длины волны, можно вычислить скорость объекта относительно источника волн.
- Метод GPS — этот метод используется для измерения скорости движения автомобиля или другого транспортного средства. GPS принимает сигналы со спутника, отслеживая положение автомобиля на поверхности Земли. Изменение координат со временем позволяет вычислить скорость движения.
Измерение модуля скорости с помощью приборов

В современной технике широко используются приборы для измерения скорости относительно земли. Они работают на основе принципа измерения воздействия тела на воздушную среду во время движения. Приведем несколько примеров таких приборов:
- Спидометр — прибор, который измеряет скорость автомобиля. Спидометр работает на основе измерения вращения колеса автомобиля, которое передается на датчик спидометра. Эта информация затем отображается на приборной панели автомобиля.
- Аттестат — прибор, который измеряет скорость самолета. Аттестат измеряет скорость с использованием давления на передней кромке самолета, которое затем преобразуется в число, представляющее скорость в милях в час.
- Гирокомпас — прибор, который измеряет направление и скорость движения корабля. Гирокомпас измеряет направление с помощью вращения жидкости внутри, а скорость движения вычисляется на основе измерения положения корабля и времени движения.
Ключевые моменты для определения модуля скорости
Определение модуля скорости относительно земли — не только измерение скорости тела, но и учет специфических условий, в которых это тело движется. Приведем несколько важных моментов, которые следует учитывать при определении модуль скорости относительно земли:
- Координаты — при движении тела важно учитывать его координаты на поверхности Земли. Наличие гор и других препятствий может существенно влиять на скорость тела.
- Температура воздуха — при определении модуля скорости следует учитывать температуру воздуха. Изменение температуры воздуха может изменить скорость звука или света, что повлияет на точность измерений.
- Направление движения — направление движения тела также может повлиять на его скорость относительно земли. Направление движения ветра, например, может увеличить или уменьшить скорость тела.
Итог

Определение модуля скорости относительно земли — важная задача, которая выполняется в различных отраслях техники. Для измерения скорости существуют несколько методов, каждый из которых подходит для определенных условий. Кроме того, при определении модуля скорости необходимо учитывать ряд факторов, которые могут оказать влияние на результаты измерений.
Измерение скорости — важный момент при проектировании и эксплуатации различных технических устройств. Правильное измерение скорости помогает обеспечить безопасность и эффективность технических систем.
Как определить модуль скорости относительно земли
Скорость — это величина, которую мы используем для измерения того, сколько расстояния пройдено за определенный промежуток времени. Она является одной из основных физических величин и имеет множество приложений в нашей жизни. Но как определить модуль скорости относительно земли? В этой статье мы рассмотрим методы, которые позволяют решить эту задачу.
Определение скорости относительно земли
Для определения скорости относительно земли необходимо знать две скорости: скорость объекта и скорость поверхности Земли в данной точке. Скорость поверхности Земли в разных точках может отличаться, поэтому для точного измерения необходимо знать ее конкретное значение в данном месте.
Методы измерения скорости относительно земли
- Измерение GPS
- Измерение с помощью инерциальных ускорителей
- Радары

GPS (Global Positioning System) — это система спутниковой навигации, которая позволяет определять положение объекта на земле с высокой точностью при помощи спутников. Большинство современных автомобильных навигаторов оснащены GPS-приемником и могут показывать скорость относительно земли.
Инерциальные ускорители — это приборы, которые измеряют изменение скорости объекта во все трех направлениях. Они широко используются в авиации и космической отрасли для измерения скорости объектов в космическом пространстве.

Радары — это устройства, которые используют электромагнитные волны для измерения скорости объектов. Они широко используются полицией для измерения скорости автомобилей. Радары могут измерять скорость объекта как относительно земли, так и относительно других объектов в небе.
Итог
Определение скорости относительно земли — это задача, которую можно решить при помощи различных инструментов. Независимо от используемого метода, необходимо знать скорость поверхности Земли в данной точке, чтобы получить точный результат. Однако, благодаря современным технологиям, измерение скорости относительно земли становится все более доступным и точным.
Как определить модуль скорости относительно земли
Скорость является важным параметром во многих науках, включая физику и астрономию. Модуль скорости относительно земли может быть определен с использованием нескольких различных методов.
1. Определите скорость путем измерения расстояния и времени
Самый простой способ определения скорости – это измерить расстояние и время, затраченное на его преодоление. Измерение расстояния можно выполнить с помощью линейки или мерной ленты, а время – с помощью секундомера. Если движение происходит в одной плоскости, то скорость можно вычислить по формуле:
скорость = расстояние / время.
Если движение не является линейным, то его можно представить в виде маршрута из нескольких отрезков, каждый из которых лежит в одной плоскости. Скорость для каждого отрезка можно вычислить по формуле выше, а затем определить общую скорость как среднюю арифметическую величину.
2. Используйте специальное оборудование
Существует много различных приборов, которые могут измерять скорость, такие как спидометры для автомобилей или лазерные измерители скорости для замера скорости движения объектов. Эти инструменты используют различные методы для измерения скорости, но все они дают точный результат.
3. Определите скорость, используя наблюдения на звездах или спутниках
Определение скорости по звездам является одним из старейших методов определения скорости. В течение длительного времени навигаторы использовали звезды для определения местоположения на земле и на море. Можно также использовать навигационные системы, такие как GPS, для определения скорости и местоположения объектов.
4. Используйте формулу для определения скорости относительно земли

Существует формула, которую можно использовать для вычисления модуля скорости относительно земли. Формула основывается на принципе доплеровского сдвига, который описывает изменение частоты электромагнитных волн, исходящих от движущегося объекта, в зависимости от относительной скорости между ним и наблюдателем.
скорость = λ / Δ t
где λ – длина волны излучения, Δ t – изменение времени на принимающем устройстве.

При использовании этой формулы необходимо иметь два источника излучения, один в фиксированной точке, который является эталоном, и один в движущейся точке. Затем можно измерить разницу в частотах между двумя сигналами и использовать формулу, чтобы определить скорость движения движущейся точки относительно эталона.
Общий итог
Определение модуля скорости относительно земли является важным измерением во многих научных областях, и существует несколько методов его выполнения, включая измерение расстояния и времени, использование специального оборудования, наблюдение на звездах или спутниках и применение формулы, основанной на принципе доплеровского сдвига.
- Для самостоятельного измерения скорости можно использовать линейку и секундомер.
- Для сбора более точных данных можно использовать специализированные приборы.
- Для изучения более дальних объектов можно использовать наблюдение на звездах и спутниках.
- Формула, основанная на принципе доплеровского сдвига, может быть использована для точного вычисления модуля скорости относительно земли.
Процесс распространения
колебаний в среде называется волновым
процессом (или волной).
Все разнообразие
волн в природе и технике подразделяют
на два типа: волны механические (упругие)
и электромагнитные.
Механическими
(или
упругими)
волнами называются механические
возмущения, распространяющимися в
упругой среде.
Различают волны
продольные и поперечные. В продольных
волнах частицы среды колеблются в
направлении распространения волны, в
поперечных
– в плоскости, перпендикулярной
направлению распространения. В жидкой
и газообразной среде возникают только
продольные волны. Поперечные волны
могут возникать только в твердых телах.
Волны распространяются
в среде с определенной скоростью.
Например.
Скорость
распространения продольных волн в
тонком стержне
![]() ,
,
где Е – модуль Юнга,
– плотность среды.

Скорость распространения
поперечных волн в изотропном твердом
теле
![]() ,
,
где
![]()
– модуль сдвига.
Скорость
распространения продольных (звуковых)
волн в жидкости и в газе
![]() ,
,
где К – модуль объемной упругости среды,
– плотность среды. Например, в воздухе:
![]() ,
,
где Т – термодинамическая температура,
измеренная по шкале Кельвина, t–
температура, измеренная по шкале Цельсия.
При распространении
колебаний в среде частицы не перемешаются
вместе с волной, а лишь колеблются около
своих положений равновесия. Поступательно
перемещаются лишь фаза и энергия
колебаний.
Графически волну
изображают так же, как и колебания
(рис.26.1).
Геометрическое
место точек, колеблющихся в одинаковых
фазах, называется волновой
поверхностью.
В зависимости от формы волновой
поверхности различают сферические,
плоские, цилиндрические волны.
Геометрическое место точек, до которых
доходят колебания с одинаковой фазой
к некоторому моменту времени t,
называется фронтом
волны. Фронт
волны является частным случаем волновой
поверхности.
Пусть плоская
волна распространяется вдоль оси х
(рис.26.1). Эта волна характеризуется:
длиной волны, периодом, амплитудой,
частотой, фазовой скоростью.
Расстояние, на
которое определенная фаза распространяется
за один период колебания, называется
длиной волны
.
λ=vT.
Из рисунка видно,
что
– это наименьшее расстояние между
точками, колеблющимися в одинаковых
фазах. Скорость распространения волны
(фазовая скорость) – равна скорости
перемещения в пространстве точек
поверхности, соответствующей любому
фиксированному значению фазы.
![]() .
.
Волна, распространяющаяся
в пространстве от какого-либо источника
называется бегущей
волной.

Уравнением волны называется
алгебраическое выражение, которое дает
зависимость смещения s
колеблющейся точки как функция ее
координат (х) и времени t:
![]() .
.
Допустим, что в
точке А упругой среды находится источник,
который колеблется по закону:
![]() .
.
Возьмем на оси 0Х
произвольную точку В, лежащую на
расстоянии х
от начала координат (рис.26.2.). Колебания
дойдут до точки В через промежуток
времени: =х/v.
То есть точка В начнет колебаться на
время
позже точки 0. Если считать, что колебания
не затухают, то можно определить смещение
точки B в некоторый момент времени t:
![]()
или
![]() .
.
(1)
Это уравнение
бегущей
волны.
В общем случае
уравнение плоской волны, распространяющейся
вдоль положительного направления оси
0Х имеет вид:
![]() ,
,
(2)
где
![]()
– начальная фаза колебаний;
![]() –
–
фаза плоской бегущей волны.
Для характеристики
волн используется волновой вектор
![]() ,
,
напрвление которого совпадает с
направлением распространения волны.
Длина этого вектора
![]()
называется волновым числом. Оно
характеризует скорость изменения фазы
в пространстве
![]() .
.
(3)
Учитывая (3),
уравнение (2) примет вид:
![]()
(4)
Уравнение волны,
распространяющейся вдоль отрицательного
направления оси 0Х отличается от (4)
знаком слагаемого kx.
Из условия
![]()
получаем выражение для фазовой скорости:
![]() .
.
Любую несинусоидальную
волну можно заменить эквивалентной ей
системой синусоидальных волн – группой
волн, или волновым пакетом.
Спектр частот такой волны – это
совокупность значений частот синусоидальных
волн.
Скорость
распространения волны может зависеть
от частоты (длины волны). В этом случае
говорят, что имеет место явление
дисперсии.
А такую среду называют диспергирующей.
В недиспергирующей среде все синусоидальные
волны, образующие волновой пакет, имеют
одинаковые фазовые скорости v. В
диспергирующей среде – разные. В этом
случае волновой пакет перемещается со
скоростью, называемой групповой.
Групповая скорость волны (пакета)
– это скорость переноса энергии этой
волной:
![]() .
.
Связь между групповой и фазовой
скоростями определяется выражением:
![]() .
.
В недиспергирующей среде:
![]()
и групповая скорость совпадает с фазовой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Когда в каком-нибудь месте твердой, жидкой или газообразной среды происходит возбуждение колебаний частиц, результатом взаимодействия атомов и молекул среды становится передача колебаний от одной точки к другой с конечной скоростью.
Волна – это процесс распространения колебаний в среде.
Виды механических волн
Различают следующие виды механических волн:
Поперечная волна: частицы среды смещаются в направлении, перпендикулярном направлению распространения механической волны.
Пример: волны, распространяющиеся по струне или резиновому жгуту в натяжении (рисунок 2.6.1);
Продольная волна: частицы среды смещаются в направлении распространения механической волны.
Пример: волны, распространяющиеся в газе или упругом стержне (рисунок 2.6.2).
Интересно, что волны на поверхности жидкости включают в себя и поперечную, и продольную компоненты.
Укажем важное уточнение: когда механические волны распространяются, они переносят энергию, форму, но не переносят массу, т.е. в обоих видах волн переноса вещества в направлении распространения волны не происходит. Распространяясь, частицы среды совершают колебания около положений равновесия. При этом, как мы уже сказали, волны переносят энергию, а именно энергию колебаний от одной точки среды к другой.
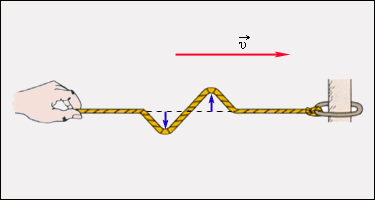
Рисунок 2.6.1. Распространение поперечной волны по резиновому жгуту в натяжении.
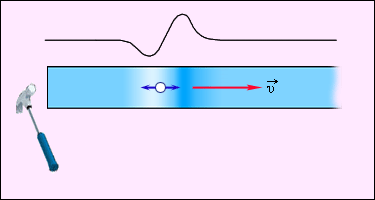
Рисунок 2.6.2. Распространение продольной волны по упругому стержню.
Модель твердого тела
Характерная черта механических волн – их распространение в материальных средах в отличие, например, от световых волн, способных распространяться и в пустоте. Для возникновения механического волнового импульса необходима среда, имеющая возможность запасать кинетическую и потенциальную энергии: т.е. среда должна иметь инертные и упругие свойства. В реальных средах эти свойства получают распределение по всему объему. К примеру, каждому небольшому элементу твердого тела присуща масса и упругость. Самая простая одномерная модель такого тела представляет из себя совокупность шариков и пружинок (рисунок 2.6.3).
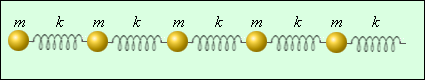
Рисунок 2.6.3. Простейшая одномерная модель твердого тела.
В этой модели инертные и упругие свойства разделены. Шарики имеют массу m, а пружинки – жесткость k. Такая простая модель дает возможность описать распространение продольных и поперечных механических волн в твердом теле. При распространении продольной волны шарики смещаются вдоль цепочки, а пружинки растягиваются или сжимаются, что есть деформация растяжения или сжатия. Если подобная деформация происходит в жидкой или газообразной среде, ее сопровождает уплотнение или разрежение.
Отличительная особенность продольных волн заключается в том, что они способны распространяться в любых средах: твердых, жидких и газообразных.
Если в указанной модели твердого тела один или несколько шариков получают смещение перпендикулярно всей цепочке, можно говорить о возникновении деформации сдвига. Пружины, получившие деформацию в результате смещения, будут стремиться вернуть смещенные частицы в положение равновесия, а на ближайшие несмещенные частицы начнет оказываться влияние упругих сил, стремящихся отклонить эти частицы от положения равновесия. Итогом станет возникновение поперечной волны в направлении вдоль цепочки.
В жидкой или газообразной среде упругая деформация сдвига не возникает. Смещение одного слоя жидкости или газа на некоторое расстояние относительно соседнего слоя не приведет к появлению касательных сил на границе между слоями. Силы, которые оказывают воздействие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. Аналогично можно сказать и о газообразной среде.
Таким образом, появление поперечных волн невозможно в жидкой или газообразной средах.
В плане практического применения особый интерес представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой f и длиной волны λ. Синусоидальные волны получают распространение в однородных средах с некоторой постоянной скоростью υ.
Запишем выражение, показывающее зависимость смещения y(x, t) частиц среды из положения равновесия в синусоидальной волне от координаты x на оси OX, вдоль которой распространяется волна, и от времени t:
y(x, t)=Acos ωt-xυ=Acos ωt-kx.
В приведенном выражении k=ωυ – так называемое волновое число, а ω=2πf является круговой частотой.
Бегущая волна
Рисунок 2.6.4 демонстрирует «моментальные фотографии» поперечной волны в момент времени t и t+Δt. За промежуток времени Δt волна перемещается вдоль оси OX на расстояние υΔt. Подобные волны носят название бегущих волн.
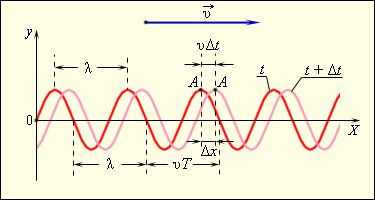
Рисунок 2.6.4. «Моментальные фотографии» бегущей синусоидальной волны в момент времени t и t+Δt.
Длина волны λ – это расстояние между двумя соседними точками на оси OX, испытывающими колебание в одинаковых фазах.
Расстояние, величина которого есть длина волны λ, волна проходит за период Т. Таким образом, формула длины волны имеет вид: λ=υT, где υ является скоростью распространения волны.
С течением времени t происходит изменение координаты x любой точки на графике, отображающем волновой процесс (к примеру, точка А на рисунке 2.6.4), при этом значение выражения ωt–kx остается неизменным. Спустя время Δt точка А переместится по оси OX на некоторое расстояние Δx=υΔt. Таким образом:
ωt-kx=ω(t+∆t)-k(x+∆x)=const или ω∆t=k∆x.
Из указанного выражения следует:
υ=∆x∆t=ωk или k=2πλ=ωυ.
Становится очевидно, что бегущая синусоидальная волна имеет двойную периодичность – во времени и пространстве. Временной период является равным периоду колебаний T частиц среды, а пространственный период равен длине волны λ.
Волновое число k=2πλ – это пространственный аналог круговой частоты ω=-2πT.
Сделаем акцент на том, что уравнение y(x,t)=Acos ωt+kx является описанием синусоидальной волны, получающей распространение в направлении, противоположном направлению оси OX, со скоростью υ=-ωk.
Когда бегущая волна получает распространение, все частицы среды гармонически колеблются с некоторой частотой ω. Это означает, что как и при простом колебательном процессе, средняя потенциальная энергия, являющаяся запасом некоторого объема среды, есть средняя кинетическая энергия в том же объеме, пропорциональная квадрату амплитуды колебаний.
Из вышесказанного можно сделать вывод, что, когда бегущая волна получает распространение, появляется поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.
Скорость распространения волны
Бегущие волны движутся в среде с определенными скоростями, находящимися в зависимости от типа волны, инертных и упругих свойств среды.
Скорость, с которой поперечные волны распространяются в натянутой струне или резиновом жгуте, имеет зависимость от погонной массы μ (или массы единицы длины) и силы натяжения T:
υ=Tμ.
Скорость, с которой продольные волны распространяются в безграничной среде, рассчитывается при участии таких величин как плотность среды ρ (или масса единицы объема) и модуль всестороннего сжатия B (равен коэффициенту пропорциональности между изменением давления Δp и относительным изменением объема ΔVV, взятому с обратным знаком):
∆p=-B∆VV.
Таким образом, скорость распространения продольных волн в безграничной среде, определяется по формуле:
υ=Bρ.
При температуре 20 °С скорость распространения продольных волн в воде υ≈1480 м/с, в различных сортах стали υ≈5–6 км/с.
Если речь идет о продольных волнах, получающих распространение в упругих стержнях, запись формулы для скорости волны содержит не модуль всестороннего сжатия, а модуль Юнга:
υ=Eρ.
Для стали отличие E от B незначительно, а вот для прочих материалов оно может составлять 20–30 % и больше.
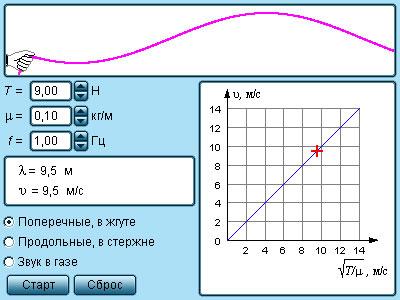
Рисунок 2.6.5. Модель продольных и поперечных волн.
Стоячая волна
Предположим, что механическая волна, получившая распространение в некоторой среде, встретила на пути некое препятствие: в этом случае характер ее поведения резко изменится. К примеру, на границе раздела двух сред с различающимися механическими свойствами волна частично отразится, а частично проникнет во вторую среду. Волна, пробегающая по резиновому жгуту или струне, отразится от зафиксированного конца, и возникнет встречная волна. Если у струны зафиксированы оба конца, появятся сложные колебания, являющиеся итогом наложения (суперпозиции) двух волн, получающих распространение в противоположных направлениях и испытывающих отражения и переотражения на концах. Так «работают» струны всех струнных музыкальных инструментов, зафиксированные с обоих концов. Схожий процесс возникает при звучании духовых инструментов, в частности, органных труб.
Если волны, распространяющиеся по струне во встречных направлениях, обладают синусоидальной формой, то при определенных условиях они образуют стоячую волну.
Допустим, струна длины l зафиксирована таким образом, что один из ее концов расположен в точке x=0, а другой – в точке x1=L (рисунок 2.6.6). В струне имеется натяжение T.
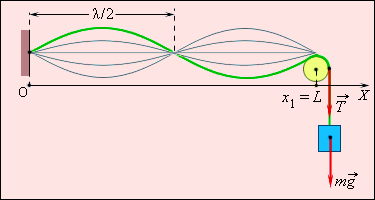
Рисунок 2.6.6. Возникновение стоячей волны в струне, зафиксированной на обоих концах.
По струне одновременно пробегают в противоположных направлениях две волны с одинаковой частотой:
- y1(x, t)=A cos (ωt+kx) – волна, распространяющаяся справа налево;
- y2(x, t)=A cos (ωt-kx) – волна, распространяющаяся слева направо.
Точка x=0 – один из зафиксированных концов струны: в этой точке падающая волна y1 в результате отражения создает волну y2. Отражаясь от зафиксированного конца, отраженная волна входит в противофазу с падающей. В соответствии с принципом суперпозиции (что есть экспериментальный факт) колебания, созданные встречными волнами во всех точках струны, суммируются. Из сказанного следует, что итоговое колебание в каждой точке определяется как сумма колебаний, вызванных волнами y1 и y2 в отдельности. Таким образом:
y=y1(x, t)+y2(x, t)=(-2A sin ωt) sin kx.
Приведенное выражение является описанием стоячей волны. Введем некоторые понятия, применимые к такому явлению как стоячая волна.
Узлы – точки неподвижности в стоячей волне.
Пучности – точки, расположенные между узлами и колеблющиеся с максимальной амплитудой.
Если следовать данным определениям, для возникновения стоячей волны оба зафиксированных конца струны должны являться узлами. Указанная ранее формула отвечает этому условию на левом конце (x=0). Чтобы условие было выполнено и на правом конце (x=L), необходимо чтобы kL=nπ, где n является любым целым числом. Из сказанного можно сделать вывод, что стоячая волна в струне появляется не всегда, а только тогда, когда длина L струны равна целому числу длин полуволн:
l=nλn2 или λn=2ln(n=1, 2, 3,…).
Набору значений λn длин волн соответствует набор возможных частот f
fn=υλn=nυ2l=nf1.
В этой записи υ=Tμ есть скорость, с которой распространяются поперечные волны по струне.
Каждая из частот fn и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота f1 носит название основной частоты, все прочие (f2, f3, …) называются гармониками.
Рисунок 2.6.6 иллюстрирует нормальную моду для n=2.
Стоячая волна не обладает потоком энергии. Энергия колебаний, «запертая» в отрезке струны между двумя соседними узлами, не переносится в остальные части струны. В каждом таком отрезке происходит периодическое (дважды за период T) преобразование кинетической энергии в потенциальную и обратно, подобно обычной колебательной системе. Однако, здесь имеется различие: если груз на пружине или маятник имеют единственную собственную частоту f0=ω02π, то струна характеризуется наличием бесконечного числа собственных (резонансных) частот fn. На рисунке 2.6.7 показано несколько вариантов стоячих волн в струне, зафиксированной на обоих концах.
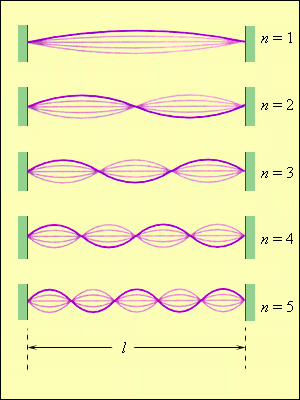
Рисунок 2.6.7. Первые пять нормальных мод колебаний струны, зафиксированной на обоих концах.
Согласно принципу суперпозиции стоячие волны различных видов (с разными значениями n) способны одновременно присутствовать в колебаниях струны.
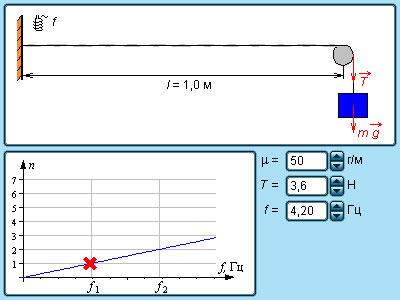
Рисунок 2.6.8. Модель нормальных мод струны.
