Как найти модуль смешанного произведения векторов

Как найти модуль смешанного произведения векторов

В данной публикации мы рассмотрим, как можно найти смешанное произведение трех векторов через вычисление определителя соответствующей матрицы, перечислим свойства этой операции, а также разберем пример решения задачи.

  • Нахождение смешанного произведения векторов

  • Свойства смешанного произведения векторов

  • Пример задачи

Нахождение смешанного произведения векторов

Смешанное произведение векторов равняется определителю матрицы, которая составлена из координат этих векторов.

Алгоритм действий следующей:

Допустим, у нас есть три вектора: a = {ax; ay; az}, b = {bx; by; bz} и с = {сx; сy; сz}. Чтобы найти их смешанное произведение (в декартовой системе) мы составляем матрицу с элементами, как показано ниже, и затем просто вычисляем ее определитель.

Формула смешанного произведения трех векторов

Свойства смешанного произведения векторов

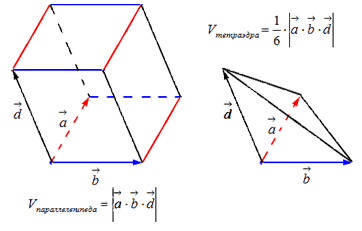
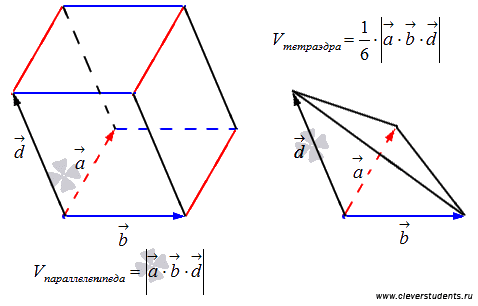
1. Модуль смешанного произведения трех векторов равняется объему параллелепипеда, который образован этими векторами.

Vпаралл. = |a · [b × c]|

2. Объем пирамиды, которая образована тремя векторами, равняется 1/6 от модуля смешанного произведения данных векторов.

Vпаралл. = 1/6 · |a · [b × c]|

3. Смешанное произведение трех ненулевых компланарных векторов равняется нулю.

4. a · [b × c] = b · (a · c) – c · (a · b)

5. a · [b × c] = b · [c × a] = c · [a × b] = –a · [c ×b] = –b · [a ×c] = –c · [b ×a]

6. a · [b × c] + b · [c × a] + c · [a × b] = 0 (тождество Якоби)

Пример задачи

Найдем смешанное произведение векторов a = {3; 8; 4}, b = {1; -10; 12} и с = {11; 5; 9}.

Решение:

Пример смешанного произведения трех векторов

a · [b × c] = 3 · (-10) · 9 + 11 · 8 · 12 + 1 · 5 · 4 – 11 · (-10) · 4 – 3 · 5 · 12 – 1 · 8 · 9 = -270 + 1056 + 20 + 440 – 180 – 72 = 994

Источник

Сме́шанное произведе́ние ({mathbf {a}},{mathbf {b}},{mathbf {c}}) векторов {mathbf {a}},{mathbf {b}},{mathbf {c}} — скалярное произведение вектора {mathbf {a}} на векторное произведение векторов {mathbf {b}} и {mathbf {c}}:

({mathbf {a}},{mathbf {b}},{mathbf c})={mathbf {a}}cdot left({mathbf {b}}times {mathbf c}right).

Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами {mathbf a},{mathbf b},{mathbf c}.

Свойства[править | править код]

  • Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
({mathbf a},{mathbf b},{mathbf c})=({mathbf b},{mathbf c},{mathbf a})=({mathbf c},{mathbf a},{mathbf b})=-({mathbf b},{mathbf a},{mathbf c})=-({mathbf c},{mathbf b},{mathbf a})=-({mathbf a},{mathbf c},{mathbf b});
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
langle {mathbf a},[{mathbf b},{mathbf c}]rangle =langle [{mathbf a},{mathbf b}],{mathbf c}rangle
({mathbf {a}},{mathbf {b}},{mathbf {c}})={begin{vmatrix}a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}\c_{x}&c_{y}&c_{z}end{vmatrix}}.
({mathbf {a}},{mathbf {b}},{mathbf {c}})=-{begin{vmatrix}a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}\c_{x}&c_{y}&c_{z}end{vmatrix}}.
В частности,

Три вектора, определяющие параллелепипед.

  • Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:
({mathbf a},{mathbf b},{mathbf c})=sum _{{i,j,k}}varepsilon _{{ijk}}a^{i}b^{j}c^{k}

(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).

Обобщение[править | править код]

В n-мерном пространстве естественным обобщением смешанного произведения, имеющего смысл ориентированного объема, является определитель матрицы ntimes n, составленной из строк или столбцов, заполненных координатами векторов. Смысл этой величины — ориентированный n-мерный объем (подразумевается стандартный базис и тривиальная метрика).

В произвольном базисе произвольной размерности смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивиты соответствующей размерности:

({mathbf a},{mathbf b},{mathbf c},ldots )=sum _{{i,j,k,ldots }}varepsilon _{{ijkldots }}a^{i}b^{j}c^{k}ldots

В двумерном пространстве таковым служит псевдоскалярное произведение.

См. также[править | править код]

  • Двойное векторное произведение
  • Векторное произведение
  • Скалярное произведение
  • Псевдоскалярное произведение

Примечания[править | править код]

  1. ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.

Ссылки[править | править код]

  • Смешанное произведение векторов и его свойства. Примеры решения задач
Источник

Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.

Термин

Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.

Определение 1

Смешанным произведением a→, b→ и d→ является та величина, которая равняется скалярному произведению a→×b→ и d→ , где a→×b→ – умножение a→ и b→ . Операцию умножения a→, b→ и d→ зачастую обозначают a→·b→·d→ . Можно преобразовать формулу так:a→·b→·d→=(a→×b→,d→) .

Умножение в системе координат

Мы можем умножить вектора, если они указаны на координатной плоскости.

Возьмем i→, j→, k→

Произведение векторов в данном конкретном случае будет иметь следующий вид:a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→

Определение 2

Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.

Из этого следует:

a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→

Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.

a→×b→=( ayazbybz·i→-axazbxbz·j→+axaybxby·k→, dx·i→+dy·j→+dz·k→)==ayazbybz·dx-axazbxbz·dy+axaybxby·dz=axayazbxbybzdxdydz

Таким образом, можно сделать вывод, что:

a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz

Определение 3

Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz .

Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.

  1. (λ·a→)·b→·d→=a→·(λ·b→)·d→=a→·b→·(λ·d→)=λ·a→·b→·d→    λ∈R ;
  2. a→·b→·d→=d→·a→·b→=b→·d→·a→;   a→·d→·b→=b→·a→·d→=d→·b→·a→ ;
  3. (a(1)→+a(2)→)·b→·d→=a(1)→·b→·d→+a(2)→·b→·d→a→·(b(1)→+b(2)→)·d→=a→·b(1)→·d→+a→·b(2)→·d→a→·b→·(d(1)→+d(2)→)=a→·b→·d(2)→+a→·b→·d(2)→

Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль.

Результатом умножения также будет нуль в том случае, если два или больше множителей равны.

Действительно, если a→=b→ , то, следуя определению векторного произведения [a→×b→]=a→·b→·sin 0 =0 , следовательно, смешанное произведение равно нулю, так как ([a→×b→], d→)=(0→, d→)=0 .

Если же a→=b→ или b→=d→ , то угол между векторами [a→×b→] и d→ равен π2 . По определению скалярного произведения векторов ([a→×b→], d→)=[a→×b→]·d→·cosπ2=0 .

Свойства операции умножения чаще всего требуются во время решения задач.
Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.

Пример 1

Докажите равенство ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→) , где λ – некоторое действительное число.

Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:

([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→)
Мы разобрали, что (([a→×b→], b→)=0. Из этого следует, что
([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→)==([a→×b→], d→)+([a→×b→], λ·a→)+0=([a→×b→], d→)+([a→×b→], λ·a→)

Согласно первому свойству ([a⇀×b⇀], λ·a→)=λ·([a⇀×b⇀],a→) , а ([a⇀×b⇀], a→)=0 . Таким образом, ([a⇀×b⇀], λ·a→) . Поэтому,
([a⇀×b⇀], d→+λ·a→+b→)=([a⇀×b⇀], d→)+([a⇀×b⇀], λ·a→)==([a⇀×b⇀], d→)+0=([a⇀×b⇀], d→)

Равенство доказано.

Пример 2

Необходимо доказать, что модуль смешанного произведения трех векторов не больше, чем произведения их длин.

Решение

Исходя из условия, можно представить пример в виде неравенства a→×b→, d→≤a→·b→·d→ .

По определению, преобразуем неравенство a→×b→, d→=a→×b→·d→·cos(a→×b→^, d→)==a→·b→·sin(a→, b→^)·d→·cos([a→×b→^], d)

Используя элементарные функции, можно сделать вывод, что 0≤sin(a→, b→^)≤1,  0≤cos([a→×b→^], d→)≤1 .

Из этого можно сделать вывод, что
(a→×b→, d→)=a→·b→·sin(a→, b→)^·d→·cos(a→×b→^, d→)≤≤a→·b→·1·d→·1=a→·b→·d→

Неравенство доказано.

Разбор типовых задач

Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz . 

Пример 3

В прямоугольной системе координат представлены 3 вектора с такими координатами: a→=(1, -2, 3),  b→(-2, 2, 1),  d→=(3,-2, 5) . Необходимо определить, чему равно произведение указанных векторов a→·b→·d→ .

Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz=1-23-2213-25==1·2·5+(-1)·1·3+3·(-2)·(-2)-3·2·3-(-1)·(-2)·5-1·1·(-2)=-7

Пример 4

Необходимо найти произведение векторовi→+j→, i→+j→-k→, i→+j→+2·k→ , где i→,j→, k→ – орты прямоугольной декартовой системы координат.

Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i→+j→=(1, 1, 0)i→+j→-k→=(1, 1, -1)i→+j→+2·k→=(1, 1, 2)

Используем формулу, которая использовалась выше
i→+j→×(i→+j→-k→, (i→+j→+2·k→)=11011-1112=0i→+j→×(i→+j→-k→, (i→+j→+2·k→)=0

Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.

Пример 5

В прямоугольной системе координат расположены три вектора a→,b→ и d→ , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4, 2 и 3. Необходимо умножить вектора.

Обозначим c→=a→×b→ .

Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что a→·b→·d→=([a→×b→], d→)=c→,d→=c→·d→·cos(c→, d→^) .

Используем длину вектора d→ , указанную в условии примера: a→·b→·d→=c→·d→·cos(c→, d→^)=3·c→·cos(c→, d→^) . Необходимо определить с→и с→, d→^ . По условию a→,b→^=π2, a→=4, b→=2 . Вектор c→ найдем с помощью формулы: c→=[a→×b→]=a→·b→·sina→, b→^=4·2·sinπ2=8
Можно сделать вывод, что c→ перпендикулярен a→ и b→ . Вектора a→, b→, c→ будут являться правой тройкой, так использована декартовая система координат. Векторы c→ и d→ будут однонаправленными, то есть, c→,d→^=0 . Используя выведенные результаты, решаем пример a→·b→·d→=3·c→·cos(c→, d→^)=3·8·cos 0=24 .

a→·b→·d→=24 .

Геометрический смысл

Используем множители a→, b→ и d→ .

Вектора a→, b→ и d→ исходят от одной точки. Используем их как стороны для построения фигуры.

Обозначим, что c→=[a→×b→]. Для данного случая можно определить произведение векторов как a→·b→·d→=c→·d→·cos(c→, d→^)=c→·npc→d→ , где npc→d→ – числовая проекция вектора d→ на направление вектора c→=[a→×b→] .

Абсолютная величина npc→d→ равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a→, b→ и d→ в качестве сторон. Исходя из этого, следует уточнить, что c→=[a→×b→] перпендикулярен a→ и вектору и вектору согласно определению умножения векторов. Величина c→=a→xb→ равняется площади параллелепипеда, построенного на векторах a→ и b→ .

Делаем вывод, что модуль произведения a→·b→·d→=c→·npc→d→ равен результату умножения площади основания на высоту фигуры, которая построена на векторах a→, b→ и d→ .

Определение 4

Абсолютная величина векторного произведения является объемом параллелепипеда: Vпараллелепипида=a→·b→·d→ .

Данная формула и является геометрическим смыслом.

Определение 5

Объем тетраэдра, который построен на a→,b→ и d→ , равняется 1/6 объема параллелепипеда Получаем, Vтэтраэда=16·Vпараллелепипида=16·a→·b→·d→ .

Геометрический смысл

Для того, чтобы закрепить знания, разберем несколько типичных примеров

Пример 6

Необходимо найти объем параллелепипеда, в качестве сторон которого используются AB→=(3, 6, 3), AC→=(1, 3, -2), AA1→=(2, 2, 2) , заданные в прямоугольной системе координат. Объем параллелепипеда можно найти, используя формулу об абсолютной величине. Из этого следует:AB→·AC→·AA1→=36313-2222=3·3·2+6·(-2)·2+3·1·2-3·3·2-6·1·2-3·(-2)·2=-18

Тогда, Vпараллелепипеда=-18=18 .

Vпараллелепипида=18

Пример 7

В системе координат заданы точки A(0, 1,  0), B(3, -1, 5),  C(1, 0, 3), D(-2, 3, 1) . Следует определить объем тетраэдра, который расположен на этих точках.

Воспользуемся формулой Vтэтраэдра=16·AB→·AC→·AD→ . Мы можем определить координаты векторов по координатам точек: AB→=(3-0, -1-1, 5-0)=(3, -2, 5)AC→=(1-0, 0-1, 3-0) =(1,-1, 3)AD→=(-2-0, 3-1, 1-0)=(-2, 2, 1)

Дальше определяем смешанное произведение AB→·AC→·AD→ по координатам векторов: AB→·AC→·AD→=3-251-13-221=3·(-1)·1+(-2)·3·(-2)+5·1·2-5·(-1)·(-2)-(-2)·1·1-3·3·2=-7 Объем Vтэтраэдра=16·-7=76 .

Vтэтраэдра=76 .

Источник

Смешанное произведение векторов и его свойства

Смешанным
произведением векторов называется
число,
равное скалярному произведению
векторана
векторное произведение векторови.
Смешанное произведение обозначается.

Геометрические
свойства смешанного произведения

1. Модуль
смешанного произведения некомпланарных
векторов равен
объемупараллелепипеда,
построенного на этих векторах.
Произведениеположительно,
если тройка векторов—
правая, и отрицательно, если тройка—
левая, и наоборот.

2. Смешанное
произведение равно
нулю тогда и только тогда, когда
векторыкомпланарны:

 векторы компланарны.

Докажем
первое свойство. Найдем по определению
смешанное произведение: ,
где—
угол между векторамии.
Модуль векторного произведения (по
геометрическому свойству 1) равен
площадипараллелограмма,
построенного на векторахи: .
Поэтому.
Алгебраическое значениедлины
проекции векторана
ось, задаваемую вектором,
равно по модулю высотепараллелепипеда,
построенного на векторах(рис.
1.47). Поэтому модуль смешанного произведения
равен объемуэтого
параллелепипеда:

Знак
смешанного произведения определяется
знаком косинуса угла .
Если тройкаправая,
тои
смешанное произведениеположительно.
Если же тройкалевая,
тои
смешанное произведениеотрицательно.

Докажем
второе свойство. Равенство возможно
в трех случаях:или(т.е.),или(т.е.
векторпринадлежит
плоскости векторови).
В каждом случае векторыкомпланарны
(см.
разд. 1.1).


Смешанным
произведением трех векторов называется
число, равное векторному произведению
первых двух векторов,,
умноженному скалярно на вектор.
Векторами это можно представить так

Так
как векторы на
практике задают в координатной форме,
то их смешанный произведение равен
определитель, построенном на их
координатамВ
силу того, что векторное произведение
антикомутативно, а скалярное произведение
коммутативно, то циклическая перестановка
векторов в смешанном произведении не
изменяет его значение. Перестановка
двух соседних векторов меняет знак на
противоположный


Смешанный
произведение векторов положительный,
если они образуют правую тройку и
отрицательный – если левую.

Геометрические
свойства смешанного произведения1.
Объем параллелепипеда, построенного
на векторах равен
модулю смешанного произведения этих
векторов.2.
Объем четырехугольной пирамиды равен
трети модуля смешанного произведения3.
Объем треугольной пирамиды равен одной
шестой модуля смешанного произведения4.
Векторы планарных
тогда и только тогда, когдаВ
координатах условие компланарности
означает равенство нулю определителяДля
практического усвоения рассмотрим
примеры.
Пример
1.

Определить,
какой тройкой (правой или левой) являются
векторы

Решение.

Найдем
смешанное произведение векторов и
по знаку выясним, какую тройку векторов
они образуют

Векторы
образуют правую тройку Векторы
образуют правую тройкуВекторы
образуют левую тройкуВекторы
образуют правую тройкуВекторы
образуют левую тройкуДанные
векторы линейно зависимы..
Смешанным
произведением трех векторов.
 Смешанным
произведением трех векторов называется
число

Геометрическое
свойство смешанного произведения:

Теорема
10.1.Объём
параллелепипеда, построенного на
векторах равен
модулю смешанного произведения этих
векторов

,

или
объём тетраэдра (пирамиды), построенного
на векторах равен
одной шестой модуля смешанного
произведения

.

Доказательство. Из
элементарной геометрии известно, что
объём параллелепипеда равен произведению
высоты на площадь основания

Площадь
основания параллелепипеда S равна
площади параллелограмма, построенного
на векторах (см.
рис. 1). Используя

Рис.
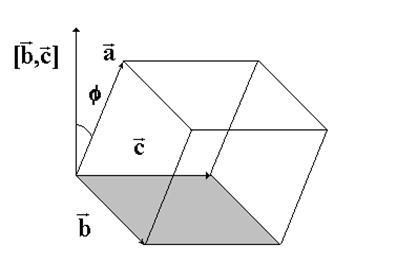
1. К доказательству теоремы 1.
геометрический
смысл векторного произведения векторов ,
получаем, что

.

Далее,
если тройка векторов является
правой (как на рис. 1), то высота
параллелепипеда равна проекции
векторана
вектор,
т.е.

Отсюда
получаемЕсли
тройка векторов левая,
то вектор и
вектор направлены
противоположно, тогдаилиТаким
образом, попутно доказано, что знак
смешанного произведения определяет
ориентацию тройки векторовтройка
правая и ‑
тройка левая). Докажем теперь вторую
часть теоремы. Из рис. 2 очевидно, что
объем треугольной призмы, построенной
на трех векторахравен
половине объема параллелепипеда,
построенного на этих векторах, то
есть Рис.
2. К доказательству теоремы 1.

Но
призма состоит из трех одинакового
объема пирамид OABC, ABCD и ACDE.
Действительно, объемы пирамид ABCD и ACDE равны,
так как они имеют равные по площади
основания BCD и CDE и
одинаковую высоту, опущенную из вершины A.
То же справедливо для высот и оснований
пирамид OABC и ACDE. Отсюда

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Содержание:

  • Формула
  • Примеры вычисления смешанного произведения векторов

Формула

Для того чтобы найти смешанное произведение
$(bar{a}$, $bar{b}$, $bar{c})$ трех векторов, заданных своими координатами
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right), b=left(b_{x} ; b_{y} ; b_{z}right)$ и $bar{c}=left(c_{x}, c_{y}, c_{z}right)$ необходимо
вычислить следующий определитель, где по
строкам записаны координаты заданных векторов, то есть

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{lll}a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z} \ c_{x} & c_{y} & c_{z}end{array}right|$$

Примеры вычисления смешанного произведения векторов

Пример

Задание. Вычислить смешанное произведение векторов
$bar{a}=(1 ; 3 ; 1)$, $bar{b}=(2 ; 1 ; 3)$, и $bar{c}=(3 ; 1 ; 2)$

Решение. Для нахождения смешанного произведения заданных векторов воспользуемся формулой

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{lll}a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z} \ c_{x} & c_{y} & c_{z}end{array}right|$$

Подставляя координаты заданных векторов, получим:

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{ccc}1 & 3 & 1 \ 2 & 1 & 3 \ 3 & 1 & 2end{array}right|$$

Определитель вычисляем по правилу треугольника:

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{ccc}1 & 3 & 1 \ 2 & 1 & 3 \ 3 & 1 & 2end{array}right|=1 cdot 1 cdot 2+3 cdot 3 cdot 3+2 cdot 1 cdot 1-$$
$$-1 cdot 1 cdot 3-3 cdot 2 cdot 2-3 cdot 1 cdot 1=2+27+2-3-12-3=13$$

Ответ. $(bar{a}, bar{b}, bar{c})=13$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Даны три вектора $bar{a}=(1 ;-2 ; 3), bar{b}=(3 ;-5 ; 6)$ и $bar{c}=(5 ;-4 ; 1)$. Проверить, являются ли они компланарными, если нет,
определить левую или правую тройку они образуют.

Решение. Найдем смешанное произведение этих векторов. Для этого воспользуемся формулой

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{lll}a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z} \ c_{x} & c_{y} & c_{z}end{array}right|$$

Подставляя координаты заданных векторов, получим

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{ccc}1 & -2 & 3 \ 3 & -5 & 6 \ 5 & -4 & 1end{array}right|$$

Определитель вычисляем по правилу треугольника:

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{ccc}1 & -2 & 3 \ 3 & -5 & 6 \ 5 & -4 & 1end{array}right|=1 cdot(-5) cdot 1+(-2) cdot 5 cdot 6+$$
$$+3 cdot 3 cdot(-4)-3 cdot(-5) cdot 5-3 cdot(-2) cdot 1-1 cdot 6 cdot(-4)=$$
$$-5-60-36+75+6+24=4 neq 0$$

Смешанное произведение заданных векторов не равно нулю, следовательно, векторы некомпланарные. Так как смешанное
произведение положительно, то делаем вывод, что заданные векторы образуют правую тройку.

Ответ. Векторы некомпланарны и образуют правую тройку.

Читать дальше: как найти вектор коллинеарный вектору.

Источник

Добавить комментарий