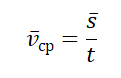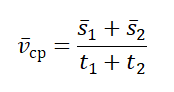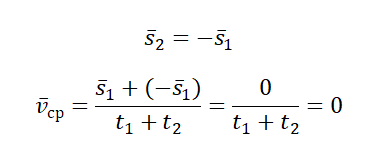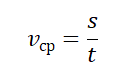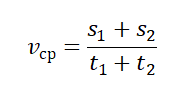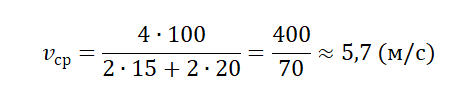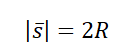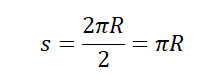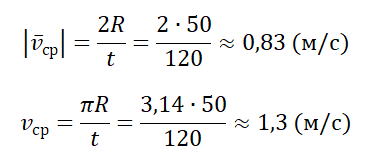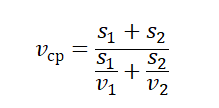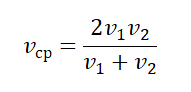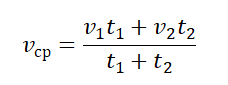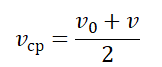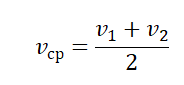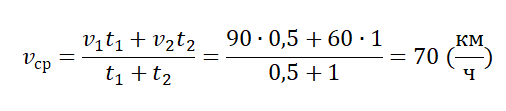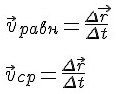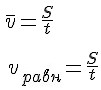Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
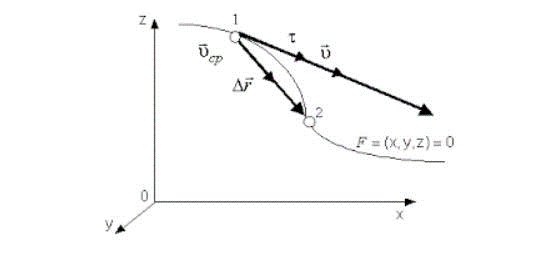
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Неравномерное движение и средняя скорость
теория по физике 🧲 кинематика
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
- vср= v ср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
- vср>v ср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
- Если известны скорости на первой и второй половине пути (s1=s2), средняя скорость равна:
- Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:
- Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:
- Если известны скорости тела за равные промежутки времени, его средняя скорость равна:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Модуль вектора средней скорости по окружности
§ 17. Переменное движение. Средняя скорость. Средний модуль скорости
1. Переменное движение.
Определение 1. Движение называется переменным , если за любые равные промежутки времени точка совершает различные перемещения.
Перемещение – вектор. Он может изменяться по модулю и направлению. При переменном движении за любые равные промежутки времени перемещения могут отличаться либо модулями, либо направлениями, либо и модулями и направлениями.
2. Средняя скорость.
Определение 2а. Средней скоростью переменного движения называется отношение перемещения ко времени, за которое это перемещение произошло.
Запишем формулу скорости равномерного движения и средней скорости переменного движения.
Если посмотреть на правые части этих равенств, заметим, что они одинаковы. В этом заключается смысл средней скорости.
Определение 2б. Под средней скоростью переменного движения понимают скорость некоторого воображаемого равномерного прямолинейного движения, у которого перемещение и время одинаковы с переменным движением.
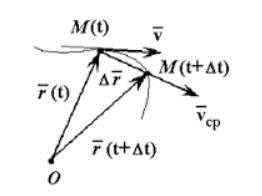
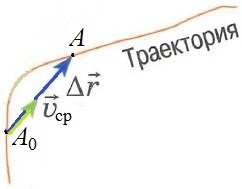
Согласно рисунку, представленному выше, это понимать надо так. Если бы точка двигалась не переменно по криволинейной траектории, а равномерно и прямолинейно прямо по вектору перемещения , то она за время попала бы в точку A из точки , если бы скорость этого воображаемого равномерного движения была бы одинаковой со средней скоростью переменного движения.
Модуль вектора средней скорости, или модуль средней скорости :
.
3. Средний модуль скорости.
На практике при составлении расписания движения поездов, автобусов используют ещё одно понятие средней скорости, которое называют средним модулем скорости, то есть средним по времени модулем всех скоростей, которые имела точка на различных участках траектории.
Определение 3а. Средним модулем скорости переменного движения называется отношение пути S ко времени t, за которое этот путь пройден.
– средний модуль скорости
Не надо путать средний модуль скорости с модулем вектора средней скорости.
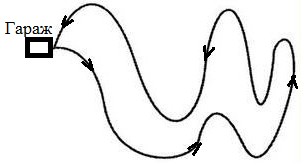
Например, если автобус вышел на маршрут в начале дня и к концу дня возвратился в гараж, то перемещение за всё время движения равно нулю . Поэтому равны нулю средняя скорость и её модуль:
, .
Но средний модуль скорости отличен от нуля, так как не равен нулю путь, пройденный автобусом:
.
Аналогично для бумеранга.
За время полёта бумеранга средняя скорость его движения и модуль средней скорости равны нулю, так как равно нулю перемещение бумеранга относительно точки А (см. рис.). Но так как путь, который проделал бумеранг, не равен нулю, то и средний модуль скорости движения бумеранга отличен от нуля.
Если посмотреть на правые части формул модуля скорости равномерного движения и среднего модуля скорости переменного движения, то увидим, что правые части равенств одинаковы.
В этом заключается смысл среднего модуля скорости.
Определение 3б. Средний модуль скорости переменного движения равен модулю скорости такого воображаемого равномерного прямолинейного движения, у которого путь и время одинаковы с переменным движением.
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
[spoiler title=”источники:”]
http://education-for.narod.ru/bas/kinematika/p17.html
[/spoiler]
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Определение и формулы
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
vср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Определение и формулы
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
- vср=vср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
- vср>vср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Полезные советы и формулы
- Если известны значения отдельных участков пути и скорости на этих участках, средняя скорость равна:
- Если известны скорости на первой и второй половине пути (s1=s2), средняя скорость равна:
- Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:
- Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:
- Если известны скорости тела за равные промежутки времени, его средняя скорость равна:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Алиса Никитина | Просмотров: 5.6k
Неравномерное прямолинейное движение. Средняя скорость
- График скорости при неравномерном прямолинейном движении
- Как найти путь и перемещение по графику скорости?
- Средняя скорость и средняя путевая скорость
- Задачи
- Лабораторная работа №3. Определение средней скорости движения тела
п.1. График скорости при неравномерном прямолинейном движении
Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.
Движение с переменной скоростью называют неравномерным.
Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.
Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=3 text{км/ч} $$ Построим график скорости для этого случая:
Графиком скорости (v_x=v_x(t)) при неравномерном прямолинейном движении, которое можно разбить на участки с постоянной скоростью, является ломаная линия.
п.2. Как найти путь и перемещение по графику скорости?
Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком (triangle t) на оси (t) (см. §8 данного справочника).
В таком случае, путь велосипедиста в нашем примере:
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км.
Если принять город A за начало отсчета с (x_0=0), то координата велосипедиста в конце пути: $$ x_{к}=x_0+s=0+6=6 text{(км)} $$ Перемещение по оси ОХ: (triangle x=x_{к}-x_0=6 text{(км)}).
Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=-3 text{км/ч} $$ Построим график скорости для этого случая:
Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная (v_x(t)) с осью (t): begin{gather*} x=v_{x1}cdot triangle t_1+|v_{x2}|cdottriangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*}
Если мы учтем знак (v_{x2}) и уберем модуль, то получим величину перемещения по оси ОХ: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ triangle x=9cdot 0,5-3cdot 0,5=4,5-1,5=3 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_{к}=x_0+triangle x=0+3=3 text{(км)} $$
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.
Пусть неравномерное прямолинейное движение разбито на (n) участков с постоянными скоростями. Каждому такому участку соответствует промежуток времени (triangle t_i) и постоянная скорость (v_{xi}, i=overline{1,n}).
Тогда:
Весь пройденный путь равен сумме площадей прямоугольников на графике скорости: $$ s=|v_{x1}|cdottriangle t_1+|v_{x2}|cdottriangle t_2+…+|v_{xn}|cdottriangle t_n $$ Величина перемещения по оси ОХ равна сумме площадей прямоугольников с учетом знака: $$ triangle x=v_{x1}cdottriangle t_1+v_{x2}cdottriangle t_2+…+v_{xn}cdottriangle t_n $$ Конечная координата равна: (x_{к}=x_0+triangle x).
п.3. Средняя скорость и средняя путевая скорость
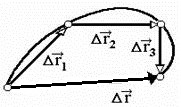
Средняя скорость на нескольких участках движения равна отношению общего перемещения к общему времени, затраченному на это перемещение: $$ overrightarrow{v_{cp}}=frac{overrightarrow{r_1}+overrightarrow{r_2}+…+overrightarrow{r_n}}{t_1+t_2+…+t_n}=frac{overrightarrow{r}}{t} $$
Средняя путевая скорость на нескольких участках движения равна отношению общего пути к общему времени, затраченному на этот путь: $$ v_{cp.п}=frac{s_1+s_2+…+s_n}{t_1+t_2+…+t_n}=frac{s}{t} $$
Если тело все время движется в одном направлении, величина средней скорости равна средней путевой скорости, т.к. на каждом участке путь совпадает с модулем перемещения.
Если тело меняет направление движения, величина средней скорости меньше средней путевой скорости.
В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 61=6 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости равна средней путевой скорости.
А вот для случая, когда велосипедист развернулся и пошел обратно: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 31=3 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости меньше средней путевой скорости.
п.4. Задачи
Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.
a)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=1 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=2 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+1cdot 2+2cdot 2=21 text{(м)} end{gather*} Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: (triangle x=s=21) (м)
Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (с)
Величина средней скорости равна средней путевой скорости: $$ |overrightarrow{v_{cp}}|=v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|=v_{cp.п}=3 text{(м/с)})
б)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=-2 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=1 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+2cdot 2+1cdot 2=21 text{(м)} end{gather*} Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2+v_{x3}cdot triangle t_3\ triangle x=5cdot 3-2cdot 2+1cdot 2=13 text{(м)} end{gather*} Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (c)
Величина средней скорости: $$ |overrightarrow{v_{cp}}|=frac{triangle x}{t}=frac{13}{7}approx 1,86 text{(м/с)} $$ Средняя путевая скорость: $$ v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|approx 1,86 text{(м/с)}; v_{cp.п}=3 text{(м/с)})
Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.
Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: (v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 40 | (frac{2d}{40}=frac{d}{20}) | (2d) |
| 2й участок | 80 | (frac{d}{80}) | (d) |
| Сумма | – | (t=frac{d}{20}+frac{d}{80}) | (s=2d+d=3d) |
Упростим сумму дробей: $$ t=frac{d}{20}+frac{d}{80}=frac{4d+d}{80}=frac{5d}{80}=frac{d}{16} $$ Получаем: $$ v_{cp}=frac st=frac{3d}{d/16}=3cdot 16=48 text{(км/ч)} $$
Ответ: 48 км/ч
Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 90 | (frac{s}{2cdot 90}=frac{s}{180}) | (frac s2) |
| 2й участок | 30 | (frac{s}{2cdot 30}=frac{s}{60}) | (frac s2) |
| Сумма | – | (t=frac{s}{180}+frac{s}{60}) | (s) |
Упростим сумму дробей: $$ t=frac{s}{180}+frac{s}{60}=frac{s+3s}{180}=frac{4s}{180}=frac{s}{45} $$ Получаем: $$ v_{cp}=frac st=frac{s}{s/45}=45 text{(км/ч)} $$
Ответ: 45 км/ч
Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (frac{d}{4t}) | (4t) | (d) |
| 2й участок | (frac{4d}{t}) | (t) | (4d) |
| 3й участок | (frac{45d}{20t}) | (20t) | (45d) |
| Сумма | – | (25t) | (50d) |
По условию средняя скорость: $$ v_{cp}=frac st=frac{50d}{25t}=2cdot frac dt=32Rightarrow frac dt=16 $$ Получаем: begin{gather*} v_1=frac{d}{4t}=frac{16}{4}=4 text{(км/ч)}\ v_2=frac{4d}{t}=4cdot 16=64 text{(км/ч)}\ v_3=frac{9d}{4t}=frac{9}{4}cdot 16=36 text{(км/ч)} end{gather*}
Ответ: 4 км/ч, 64 км/ч и 36 км/ч
Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?
Пусть (v) – скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость (v_{cp}) и сравним ее со скоростью (v).
Если (v_{cp}gt v), то турист выиграл время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (10v) | (frac{s}{2cdot 10v}=frac{s}{20v}) | (frac s2) |
| 2й участок | (frac{v}{2}) | (frac{s}{2cdot v/2}=frac sv) | (frac s2) |
| Сумма | – | (t=frac{s}{20v}+frac sv) | (s) |
Упростим сумму дробей: $$ t=frac{s}{20v}+frac sv=frac svleft(frac{1}{20}+1right)=frac{21}{20}cdot frac sv $$ Средняя скорость: $$ v_{cp}=frac{s}{frac{21}{20}cdotfrac sv}=frac{20}{21}vgt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет
п.5. Лабораторная работа №3. Определение средней скорости движения тела
Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.
Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.
Величина средней скорости при движении на двух участках определяется как средняя путевая скорость: $$ v_{cp}=frac{s_1+s_2}{t_1+t_2} $$ где (s_1) и (s_2) – длина первого и второго участка; (t_1) и (t_2) – время движения по каждому из участков.
Длина участков измеряется с помощью мерной ленты с ценой деления (triangle=1) см,
инструментальная погрешность равна: (d=frac{triangle}{2}=0,5) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: (triangle s_1=triangle s_2=d=0,5) см
Погрешность суммы двух длин: (triangle(s_1+s_2)= triangle s_1+triangle s_2=2d=1) см
Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: (triangle(t_1+t_2)=triangle t_1+triangle t_2)
Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2} $$ Абсолютная погрешность определения средней скорости: $$ triangle v_{cp}=v_{cp}cdot delta_{v_{cp}} $$
Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с. 
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин (delta_{s_1+s_2}=frac{triangle(s_1+s_2)}{s_1+s_2})
5. Проведите серии по 5 экспериментов для определения (t_1) и (t_2) с помощью секундомера.
6. Найдите (triangle t_1, triangle t_2, triangle(t_1+t_2), delta_{t_1+t_2})
7. По результатам измерений и вычислений найдите (v_{cp}, delta_{v_{cp}}) и (triangle v_{cp}).
8. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
1) Измерение длин
Цена деления мерной ленты (triangle =1) см
Инструментальная погрешность мерной ленты (d=frac{triangle}{2}=0,5) см
Результаты измерений:
(s_1=112) cм
(s_2=208) cм
Сумма длин участков: (s_1+s_2=112+208=320) (см)
Абсолютная погрешность суммы: (triangle (s_1+s_2)=triangle s_1+triangle s_2=2d=1) см
Относительная погрешность суммы: $$ delta_{s_1+s_2}=frac{triangle (s_1+s_2)}{s_1+s_2}=frac{1}{320}=0,3125% $$
2) Измерение времени
Цена деления секундомера (triangle =0,2) с
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1) с
Время движения по наклонному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_1) c | 1,5 | 1,6 | 1,5 | 1,4 | 1,4 | 7,4 |
| (triangle) c | 0,02 | 0,12 | 0,02 | 0,08 | 0,08 | 0,32 |
Найдем среднее время спуска с наклонного желоба: $$ t_1=frac{1,5+1,6+1,5+1,4+1,4}{5}=frac{7,4}{5}=1,48 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_1): $$ triangle_1=|1,5-1,48|=0,02; triangle_2=|1,6-1,48|=1,02 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,02+0,12+0,02+0,08+0,08}{5}=frac{0,32}{5}=0,064 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_1=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,064right}=0,1 text{c} $$ Округляем полученное значение времени до десятых. begin{gather*} t_1=(1,5pm 0,1) text{c}\ delta_{t_1}=frac{0,1}{1,5}=frac{1}{15}approx 6,7text{%} end{gather*} Время движения по горизонтальному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_2) c | 2,3 | 2,4 | 2,2 | 2,2 | 2,4 | 11,5 |
| (triangle) c | 0 | 0,1 | 0,1 | 0,1 | 0,1 | 0,4 |
Найдем среднее время движения по горизонтали: $$ t_2=frac{2,3+2,4+2,2+2,2+2,4}{5}=frac{11,5}{5}=2,3 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_2): $$ triangle_1=|2,3-2,3|=0; triangle_2=|2,4-2,3|=0,1 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0+0,1+0,1+0,1+0,1}{5}=frac{0,4}{5}=0,08 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_2=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,08right}=0,1 text{c} $$ Получаем: begin{gather*} t_2=(2,3pm 0,1) text{c}\ delta_{t_2}=frac{0,1}{2,3}=frac{1}{23}approx 4,4text{%} end{gather*}
3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8 text{(c)} $$ Абсолютная погрешность суммы: $$ triangle(t_1+t_2)=triangle t_1+triangle t_2=0,1+0,1=0,2 text{(c)} $$ Относительная погрешность суммы: $$ delta_{t_1+t_2}=frac{triangle (t_1+t_2)}{t_1+t_2}=frac{0,2}{3,8}=frac{1}{19}approx 5,3text{%} $$
4) Расчет средней скорости $$ v_{cp}=frac{s_1+s_2}{t_1+t_2}=frac{320}{3,8}approx 84,2 left(frac{text{см}}{text{c}}right) $$ Относительная ошибка частного: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2}=frac{1}{320}+frac{1}{19}approx 0,003125+0,0526approx 0,0557approx 0,056=5,6text{%} $$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_{cp}=v_{cp}cdotdelta_{v_{cp}}=84,2cdot 0,056approx 4,7 left(frac{text{см}}{text{c}}right) $$ Получаем: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Определение
Скорость — это термин, который характеризует изменение заданной координаты в движении.
В ситуации, когда координаты изменяют свое положение относительно оси, следовательно, их материальная точка будет находится в процессе движения.
Средняя скорость — это величина векторного типа, которая имеет определенное числовое равенство относительно перемещения совершаемого в конкретную единицу времени, и направлена совместно я с векторным перемещением.
Средняя скорость – довольно простое понятие в разделе кинематика.
Определение
Следовательно, средняя скорость – это конкретная величина, которая равна отношению пройденного пути, к величине времени, за которое данный путь пройден телом.
[v_{mathrm{cp}}=frac{S}{t}]
Основные моменты, на которые следует уделить внимание при определении средней скорости:
- Необходимое время, которое учитывается, когда тело в процессе движения может делать кратковременные остановки;
- Определение правильной величины средней скорость тела, которое начинает движение в пункте А и оканчивает его в пункте В. Но в процессе движения, может повернуть несколько раз обратно, а затем снова продолжает движение в заданном направлении, двигаясь в пункт В.
Модуль для определения средней скорости движения вычисляется по следующей формуле: V=s/t.
Определение
Мгновенная скорость — это некий числовой предел, к которому стремится показатель средней скорости.
Мгновенная скорость, как правило, характеризует заданное движение точки в конкретный и определенный момент времени.
Для любой категории характерно бесконечное количество точек. Потому что каждый временной интервал включает в себя бесконечное количество мгновений.
Когда сам временной интервал стремится к нулевому значению, то он автоматически преобразуется в мгновение.
Формула
Мгновение скорости можно определить по следующей формуле: v=s/Δt
где:
v – скорость мгновения, м/с
s – движение, перемещение тела, м ( если Δt→0 )
Δt – временной интервал, который стремится к нулевому значению, с.
Стоит отметить, что мгновенная скорость – это величина, которая изображена как вектор. Она равняется отношению движения к временному интервалу. А именно: промежуток времени, за который данное перемещение происходит, при условии, что временной интервал стремится к нулевому значению.
Временной интервал движения тела – это всегда скляр с положительным значением. Поэтому мгновенная скорость и ее векторное значение, всегда сонаправлено с перемещением, которое имеет значение стремящееся к нулю.
Нет времени решать самому?
Наши эксперты помогут!
Направление и перемещение действия средней и мгновенной скорости относительно координатной оси
Средняя скорость всегда направлена вместе с перемещением:
Для мгновенной скорости характерно движение в конкретный момент времени.
Направление векторной скорости, которая обозначается как: υ расположено по касательной, относительно криволинейной траектории.
Так как непрерывное малое перемещение однозначно совпадает с бесконечно малым элементом траектории.
Примеры решения задач по определению мгновенной и средней скорости
Пример №1:
Имеет ли способность мгновенная скорость, изменять свое значение только относительно направления, при этом не меняя модульную величину.
Используя основные термины и формулы, решим данную задачу. При решении необходимо рассмотреть пример:
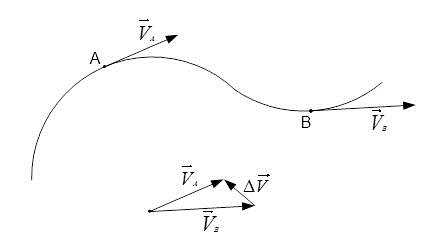
- Движение тела происходит по криволинейной траектории. На ней необходимо обозначить начальный и конечный пункты, а именно: точки А и В.
- Далее нужно обозначить основное направление мгновенной скорости в заданных ранее точках.
- Следует помнить, что мгновенная скорость имеет направление относительно касательной по траектории.
- Расстояние и скорость имеют одинаковые значения по модулю и, следовательно, равны 5 м/с.
[left|vec{V}_{A}right|=left|vec{V}_{B}right|=5 frac{м}{c}]
Следующее равенство вида: [vec{V}_{A}=vec{V}_{B}] будет неверным. Так как скорость – является векторной величиной. Поэтому очень важно задать не только числовое значение, но направление по которому будет осуществляться движение.
В случае, когда [vec{V}_{A}=vec{V}_{B}] можно составить равенство следующего вида:[vec{V}_{A}-vec{V}_{B}=0] однако определив вектор разности значений [Delta vec{V}], можно сделать вывод, что его значение не равно нулевому.
Следовательно, [vec{V}_{A} neq vec{V}_{B}], другими словами мгновенная скорость может быть равна нулевому значению и быть равной по модулю. Однако, при этом различаться по основному направлению движения.
Пример №2:
Возможно ли изменение по модульному значению мгновенной скорости, но при этом направление остается неизменным.
Алгоритм решения:
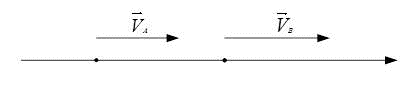
Рассмотрев рисунок, который приведен выше, можно сделать вывод, что:
- в точке А и в точке В направление движения мгновенной скорости одинаково;
- рассматриваемое тело, которое осуществляет движение, делает это с равным ускорением, следовательно:
[vec{V}_{A}=vec{V}_{B}]
§ 17. Переменное
движение. Средняя скорость. Средний
модуль скорости
1. Переменное
движение.
Определение
1. Движение
называется переменным,
если за любые равные промежутки
времени точка совершает различные
перемещения.
Перемещение
– вектор. Он может изменяться по модулю
и направлению. При переменном движении
за любые равные промежутки времени
перемещения могут отличаться либо
модулями, либо направлениями, либо и
модулями и направлениями.
2. Средняя
скорость.
Определение
2а. Средней
скоростью переменного движения
называется отношение перемещения
ко времени, за которое это
перемещение произошло.
Запишем
формулу скорости равномерного
движения и средней скорости
переменного движения.
Если
посмотреть на правые части этих
равенств, заметим, что они одинаковы. В
этом заключается смысл средней
скорости.
Определение
2б. Под средней
скоростью переменного движения
понимают скорость некоторого
воображаемого равномерного
прямолинейного движения, у которого
перемещение и время одинаковы с
переменным движением.
Согласно рисунку, представленному выше,
это понимать надо так. Если бы точка
двигалась не переменно по
криволинейной траектории, а равномерно
и прямолинейно прямо по вектору
перемещения ,
то она за время
попала бы в точку A из точки ,
если бы скорость этого воображаемого
равномерного движения была бы
одинаковой со средней скоростью
переменного движения.
Модуль
вектора средней скорости, или
модуль средней скорости:
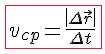
3. Средний
модуль скорости.
На
практике при составлении расписания
движения поездов, автобусов используют
ещё одно понятие средней скорости,
которое называют средним модулем
скорости, то есть средним по времени
модулем всех скоростей, которые имела
точка на различных участках траектории.
Определение
3а. Средним
модулем скорости переменного
движения называется отношение пути S
ко времени t, за которое этот
путь пройден.
–
средний модуль скорости
Не надо
путать средний модуль скорости с
модулем вектора средней скорости.
Например, если автобус вышел на маршрут
в начале дня и к концу дня возвратился в
гараж, то перемещение за всё время
движения равно нулю .
Поэтому равны нулю средняя скорость и
её модуль:
,
.
Но
средний модуль скорости отличен от
нуля, так как не равен нулю путь,
пройденный автобусом:
.
Аналогично для бумеранга.
За время
полёта бумеранга средняя скорость его
движения и модуль средней скорости
равны нулю, так как равно нулю
перемещение бумеранга относительно
точки А (см. рис.). Но так как путь,
который проделал бумеранг, не равен
нулю, то и средний модуль скорости
движения бумеранга отличен от нуля.
Если
посмотреть на правые части формул
модуля скорости равномерного движения
и среднего модуля скорости переменного
движения, то увидим, что правые части
равенств одинаковы.
В этом
заключается смысл среднего модуля
скорости.
Определение
3б. Средний
модуль скорости переменного
движения равен модулю скорости
такого воображаемого равномерного
прямолинейного движения, у которого
путь и время одинаковы с переменным
движением.