Как найти модуль ускорения движение по окружности

Как найти модуль ускорения движение по окружности

Понятия и определения

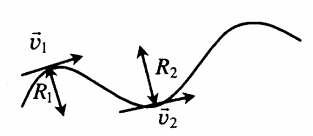
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

  1. Траектория движения тела есть окружность.
  2. Вектор скорости всегда направлен по касательной к окружности.
  3. Направление скорости постоянно меняется под действием центростремительного ускорения.
  4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Определение и формулы

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Определение и формулы

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Полезные факты

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

  • У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
  • У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
  • Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Определение и формула

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Задание EF18273

Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…

Алгоритм решения

  1. Записать исходные данные.
  2. Записать формулу для определения искомой величины.
  3. Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

  • Радиус окружности, по которой движется автомобиль: R = 100 м.
  • Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Ответ: 4

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17763

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза

Алгоритм решения

  1. Записать исходные данные.
  2. Определить, что нужно найти.
  3. Записать формулу зависимости центростремительного ускорения от частоты.
  4. Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
  5. Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

  • Радиус окружности R1 = R.
  • Радиус окружности R2 = 4R.
  • Центростремительное ускорение: aц.с. = a1 = a2.

Найти нужно ν2.

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Или:

Отсюда:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 21.9k

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 апреля 2021 года; проверки требуют 3 правки.

Разложение ускорения {displaystyle mathbf {a} (t)} на тангенциальное {displaystyle mathbf {a} _{tau }} и нормальное {mathbf a}_{n} (mathbf n — единичный вектор нормали)

Центростреми́тельное (норма́льное) ускоре́ние — составляющая ускорения тела, характеризующая быстроту изменения направления вектора скорости (вторая составляющая, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, с чем и связан термин.
Обозначается символом, выбранным для ускорения, с добавлением значка «нормальное»: {displaystyle {vec {a}}_{n}} (реже {displaystyle {vec {w}}_{n}}); в системе СИ измеряется в м/с2.

Пример движения с ненулевым центростремительным ускорением — движение по окружности (в таком случае {displaystyle {vec {a}}_{n}} направлено к центру окружности).

В классической механике нормальное ускорение вызывается компонентами сил, направленными ортогонально вектору скорости. Например, движение космического объекта на орбите характеризуется центростремительным ускорением, вызванным гравитацией. Составляющая суммы сил, обусловливающая наличие нормального ускорения, называется центростремительной силой. Связанное понятие для неинерциальных систем отсчёта — центробежная сила.

Осестремительное ускорение, рассматриваемое в случаях вращения тела вокруг оси, в проекции на плоскость, перпендикулярную оси, предстаёт как центростремительное.

Общая формула[править | править код]

Нормальное ускорение a_n вычисляется по формуле

a_{n}={frac {v^{2}}{R}}

или (с использованием соотношения {displaystyle v=omega R})

a_n = omega^2 R,

где v — (мгновенная) линейная скорость движения по траектории, omega  — (мгновенная) угловая скорость движения относительно центра кривизны траектории, R — радиус кривизны траектории в данной точке.

Выражения могут быть переписаны в векторном виде:

{displaystyle mathbf {a} _{n}={frac {v^{2}}{R}}mathbf {n} =omega ^{2}Rmathbf {n} }.

Здесь mathbf n — единичный вектор, направленный от данной точки траектории к центру кривизны траектории.

Эти формулы применимы как к частной ситуации равномерного движения ({displaystyle |{vec {v}}|=,}const), так и к произвольному случаю. В равномерном случае нормальное ускорение совпадает с полным. В общем же случае нормальное ускорение — это лишь компонента вектора {vec {a}}, перпендикулярная траектории движения (вектору vec{v}), а в полный вектор ускорения входит ещё и тангенциальная составляющая {displaystyle a_{tau }=dv/dt}, сонаправленная касательной к траектории движения[1].

Вывод формулы[править | править код]

Для разложения ускорения на тангенциальное и нормальное можно продифференцировать по времени вектор скорости, представленный в виде {displaystyle mathbf {v} =v,mathbf {tau } } через единичный вектор касательной {mathbf tau }:

{displaystyle mathbf {a} ={frac {dmathbf {v} }{dt}}={frac {d(vmathbf {tau } )}{dt}}={frac {mathrm {d} v}{mathrm {d} t}},mathbf {tau } +v{frac {dmathbf {tau } }{dt}}=mathbf {a} _{tau }+v{frac {dmathbf {tau } }{dl}}{frac {dl}{dt}}=mathbf {a} _{tau }+v^{2}{frac {dmathbf {tau } }{dl}}=mathbf {a} _{tau }+{frac {v^{2}}{R}}{frac {dmathbf {tau } }{dvarphi }}=mathbf {a} _{tau }+{frac {v^{2}}{R}},mathbf {n} }.

Здесь первое слагаемое — тангенциальное ускорение, а второе — нормальное ускорение. Через mathbf n обозначен единичный вектор нормали, R — радиус кривизны траектории в рассматриваемой точке, dl — элемент длины траектории. Малый участок любой кривой может считаться дугой окружности, причём её радиус и есть радиус кривизны R. В цепочке преобразований использованы очевидные соотношения {displaystyle dl/dt=v} и {displaystyle dl=R,dvarphi } (где dvarphi — малый угол поворота вокруг центра кривизны).

Равенство {displaystyle dmathbf {tau } /dvarphi =mathbf {n} } вытекает из геометрических соображений. Разность {displaystyle Delta mathbf {tau } =mathbf {tau } '-mathbf {tau } } единичных касательных векторов в рассматриваемой ({mathbf tau }) и близкой к ней ({displaystyle mathbf {tau } '}) точках траектории составляет по величине {displaystyle 2sin(Delta varphi /2)}, где Delta varphi — угол между {displaystyle mathbf {tau } '} и {mathbf tau }. Эта разность направлена под углом {displaystyle Delta varphi /2} к нормали mathbf n в рассматриваемой точке. При малости Delta varphi будет совпадение с вектором нормали mathbf n. Также при малости Delta varphi возможно разложении синуса в ряд Тейлора. В результате придём к {displaystyle Delta mathbf {tau } =Delta varphi ,mathbf {n} } или, для бесконечно малых, {displaystyle dmathbf {tau } /dvarphi =dvarphi /dvarphi ,mathbf {n} }.

О радиусе кривизны[править | править код]

Вычисление радиуса кривизны и координат центра кривизны траектории является математической задачей (см. Кривизна). Если кривая задана уравнением y = f(x), то радиус её кривизны в точке (x, y) находится как[2]

{displaystyle R={frac {(1+f'^{2})^{3/2}}{|f''|}}},

а положение центра кривизны — по формулам[2]

{displaystyle xi =x-{frac {f'(1+f'^{2})}{f''}},qquad eta =y+{frac {1+f'^{2}}{f''}}}.

Единичный вектор нормали в таком случае составит (vec{i}, vec{j} — орты)

{displaystyle {vec {n}}={frac {xi -x}{R}},{vec {i}}+{frac {eta -y}{R}},{vec {j}}}.

Если известна зависимость радиус-вектора материальной точки от времени {displaystyle {vec {r}}(t)} (с математической точки зрения это означает задание траектории в параметрическом виде), то радиус кривизны можно найти через ускорение:

{displaystyle R={frac {v^{2}}{sqrt {a^{2}-a_{tau }^{2}}}}},

где {displaystyle {vec {a}}=d{vec {v}}/dt} и {displaystyle a_{tau }=dv/dt}; предварительно находится скорость как {displaystyle {vec {v}}=d{vec {r}}/dt}. Центр кривизны в общем случае не будет совпадать с началом отсчёта радиус-вектора.

Мотивация, замечания[править | править код]

То, что разложение вектора ускорения на компоненты — одну вдоль касательной к траектории (тангенциальное ускорение) и другую ортогональную ей (нормальное ускорение) — может быть удобным и полезным, довольно очевидно само по себе. При движении с постоянной по модулю скоростью тангенциальная составляющая становится равной нулю, то есть в этом важном частном случае остается только нормальная составляющая. Кроме того, каждая из этих составляющих имеет ярко выраженные собственные свойства и структуру, и нормальное ускорение содержит в структуре своей формулы достаточно важное и нетривиальное геометрическое наполнение. Крайне важен также частный случай движения по окружности.

Абсолютная величина тангенциального ускорения зависит только от путевого ускорения, совпадая с его абсолютной величиной, в отличие от абсолютной величины нормального ускорения, которая от путевого ускорения не зависит, зато зависит от путевой скорости.

История понятия[править | править код]

Первым правильные формулы для центростремительного ускорения (или центробежной силы) получил, по-видимому, Гюйгенс. Практически с этого времени рассмотрение центростремительного ускорения входит в обычную технику решения механических задач.

Несколько позже эти формулы сыграли существенную роль в открытии закона всемирного тяготения (формула центростремительного ускорения использовалась для получения закона зависимости гравитационной силы от расстояния до источника гравитации, исходя из выведенного из наблюдений третьего закона Кеплера).

К XIX веку рассмотрение центростремительного ускорения становится уже совершенно рутинным как для чистой науки, так и для инженерных приложений.

См. также[править | править код]

  • Тангенциальное ускорение
  • Кривизна кривой
  • Центробежная сила

Примечания[править | править код]

  1. ↑ Как видно из формулы, при движении с постоянной путевой скоростью — тангенциальное ускорение попросту равно нулю.
  2. ↑ 1 2 Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», c. 368-370.
Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Ускорение точки при ее движении по окружности в физике – формулы и определения с примерами

Ускорение точки при ее движении по окружности:

При равномерном прямолинейном движении ускорение равно нулю. А почему ускорение возникает при движении по окружности? Как оно направлено? Чему равен его модуль?

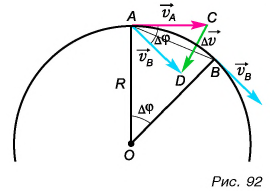
Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Пусть тело (рассматриваемое как материальная точка) движется по окружности радиусом R со скоростью, модуль которой не изменяется Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

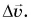Найдем ускорение тела в точке А. Перенесем вектор Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами в эту точку и построим вектор Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами Получились подобные равнобедренные треугольники ACD и ОАВ. Из их подобия следует:

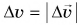Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

где Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами — модуль изменения скорости, 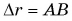Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами — модуль перемещения. Разделим обе части равенства (2) на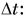 Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

При малых 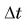Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами отношение 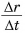Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами практически равно модулю скорости тела 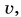Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами а отношение 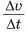Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами — модулю его ускорения а в той же точке. В результате равенство (3) примет вид 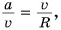Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами откуда

Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами
Формула (4) определяет модуль ускорения 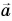Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами в случае движения тела по окружности при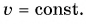 Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

А каково направление ускорения 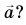Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами Оно совпадает с направлением вектора 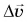Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами при малых 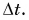Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами Из рисунка 92 видно, что чем меньше 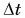Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами и вместе с ним угол 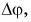Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами тем направление вектора 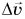Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами ближе к направлению на центр окружности.

Значит, ускорение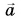Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами направлено по радиусу к центру окружности. Поэтому его называют центростремительным. В то же время вектор 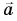Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами перпендикулярен скорости 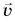Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами (т. е. направлен по нормали к ней). Поэтому ускорение 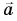Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами называют также и нормальным ускорением.

А как связано центростремительное ускорение с угловой скоростью? Подставляя в формулу (4) выражение 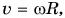Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами находим:

Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Отсюда, учитывая, что 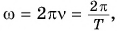Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами получим еще две полезные формулы:

Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Выведите самостоятельно выражение для центростремительного ускорения через угловую и линейную скорости:

Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Для любознательных:

А как направлено ускорение 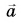Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами тела, движущегося по окружности, если модуль его скорости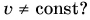 Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

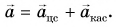На рисунке 93, а (вид сверху) мчащийся по кольцевой трассе автомобиль набирает скорость. Ускорение автомобиля Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами равно сумме двух составляющих: Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами Центростремительное ускорение 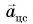Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами обусловлено изменением направления скорости. А касательное к траектории ускорение 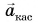Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами возникает из-за изменения модуля скорости. При наборе скорости вектор 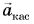Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами направлен так же, как 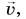Ускорение точки при ее движении по окружности в физике - формулы и определения с примерамиа вектор 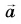Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами составляет с 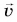Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами острый угол.

На рисунке 93, б автомобиль тормозит. Модуль скорости уменьшается, составляющая 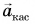Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами направлена противоположно вектору 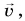Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами а угол между ускорением 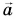Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами и скоростью 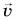Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами — тупой. В обоих случаях модуль ускорения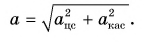Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами
 

Главные выводы:

  1. Тело, движущееся по окружности со скоростью, модуль которой 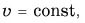Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами обладает центростремительным ускорением.
  2. Центростремительное ускорение перпендикулярно скорости и направлено к центру окружности.
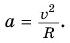
  3. Модуль центростремительного ускорения Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами
  • Заказать решение задач по физике

Пример решения задачи:

Период вращения 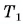Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами первого колеса в 4 раза больше периода вращения 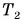Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами второго колеса, а его радиус 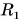Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами в 2 раза меньше радиуса 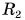Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами второго колеса. У какого колеса больше центростремительное ускорение точек на его ободе? Во сколько раз?

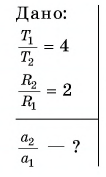
Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Решение

Согласно формуле (6) отношение модулей центростремительных ускорений точек на ободе второго и первого колеса:

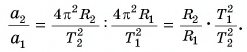
Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

По условию задачи:

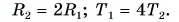
Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами
Тогда
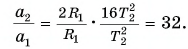
Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами
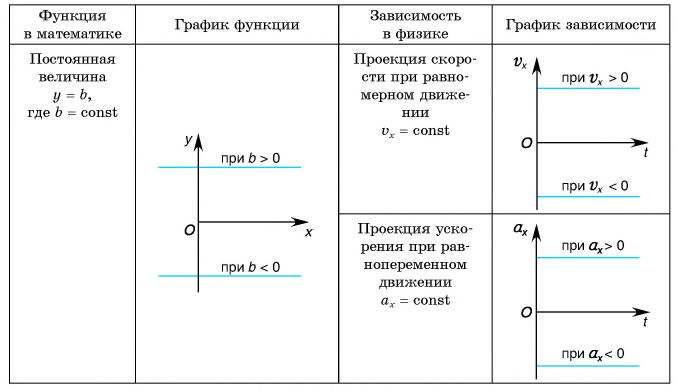
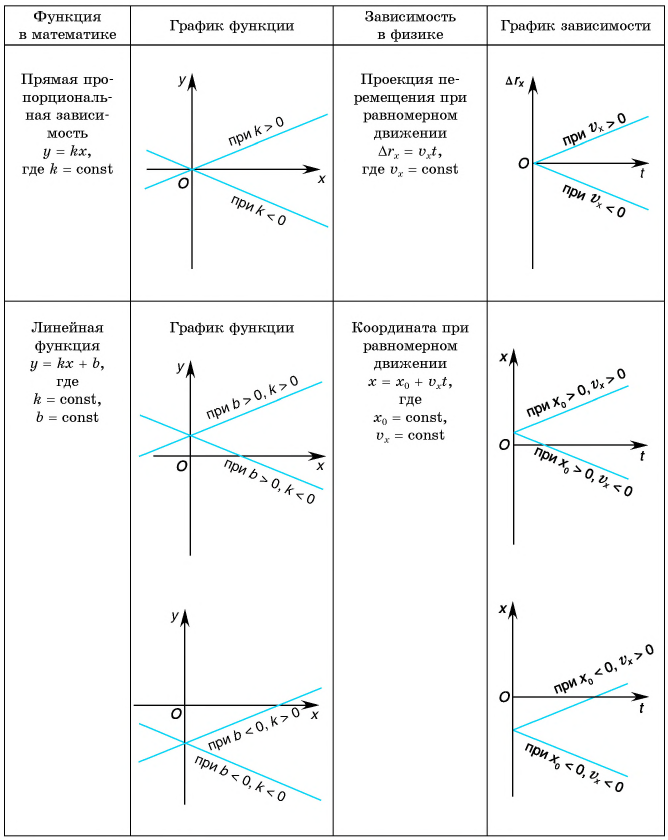
Ответ: Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Основные кинематические величины и их графики:

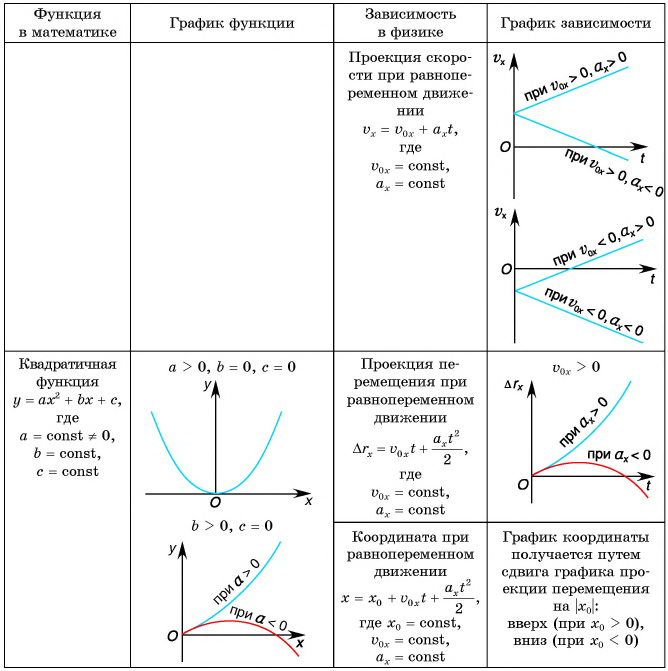
Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

  • Инерциальные системы отсчета
  • Энергия в физике
  • Мощность в физике
  • Взаимодействие тел
  • Ускорение в физике
  • Скорость при равнопеременном движении
  • Перемещение, координата и путь при равнопеременном движении
  • Криволинейное движение
Источник

Вы уже знаете, что прямолинейное движение, тем более
равномерное, встречается гораздо реже, нежели движение по криволинейной
траектории. Кто из вас не наблюдал, как вращается волчок? А кто не катался на
каруселях? Наконец, всем вам известно, что спутники обращаются вокруг планет
почти по круговым траекториям, а планеты — вокруг центрального тела нашей
Солнечной системы.

Криволинейных траекторий существует бесчисленное множество.
Но оказывается, что любую кривую мы можем представить в виде совокупностей дуг
окружностей разных радиусов и прямолинейных участков. Поэтому чаще всего
изучение криволинейного движения сводится к изучению движения точки по
окружности.

Мы будем изучать самый простой вид такого движения —
равномерное движение точки по окружности. При таком движении направления
векторов скорости и ускорения непрерывно изменяются, но вот их модули остаются
постоянным.

Итак, пусть материальная точка, равномерно движущаяся по
окружности радиуса R,
в некоторый момент времени t
занимает положение М и имеет скорость υ, а спустя некоторый
промежуток времени — положением М1 и скорость υ1.
Найдём модуль и направление вектора ускорения точки в положении М.

Давайте найдём вектор изменения скорости за исследуемый
промежуток времени:

Теперь давайте посмотрим на два треугольника ОММ1
и М1АВ. Что можно о них сказать? Во-первых, очевидно,
что это два равнобедренных треугольника, так как ОМ и ОМ1
— это радиусы окружности, а длины векторов скорости (их модули) одинаковы, так
как движение точки у нас равномерное. Наконец, угол  как
углы между двумя взаимно перпендикулярными сторонами. Следовательно, эти два
треугольника подобны. Поэтому мы можем записать, что модуль изменения скорости
точки так относится к модулю её скорости, как модуль перемещения к радиусу
окружности, по которой эта точка движется:

Как мы уже с вами знаем, отношение модуля изменения скорости
к промежутку времени, в течении которого это изменение
произошло, — это модуль среднего ускорения точки. А отношение модуля
перемещения к этому промежутку времени — это модуль средней скорости
перемещения:

Теперь давайте с вами вспомним, что при стремлении промежутка
времени к нулю отношение изменения скорости к промежутку времени, в течение
которого это изменение произошло, называется ускорением. А отношение
перемещения к промежутку времени называется мгновенной скоростью. Эти
определения справедливы и для модулей скорости и ускорения:

После простых преобразований получим, что модуль ускорения
точки при её движении по окружности прямо пропорционален квадрату модуля её
скорости и обратно пропорционален радиусу окружности:

Учитывая, что при равномерном движении точки по окружности
модуль её скорости и радиус окружности не меняются с течением времени, то и
модуль вектора ускорения всё время остаётся неизменным. Но вот его направление,
как и направление вектора скорости, меняется от точки к точке.

Найдём направление вектора ускорения.  Мы уже знаем, что
в общем случае вектор ускорения направлен так же, как и вектор изменения
скорости точки при стремлении промежутка времени к нулю. Но тогда точка М1
будет бесконечно близко подходить к точке М, а угол φ будет
стремиться к нулю. А вот угол  будет
стремиться к 90о. Значит, угол между вектором изменения скорости
точки и радиусом окружности стремится к нулю при стремлении к нулю промежутка
времени. Учитывая, что направление вектора ускорения совпадает с направлением
вектора изменения скорости, получим, что в пределе вектор мгновенного ускорения
направлен по радиусу к центру окружности. Поэтому ускорение точки при её
движении по окружности и называют центростремительным или нормальным, так
как оно направлено по нормали к вектору мгновенной скорости.

Задача 1. В ремённой передаче диаметр ведущего шкива
равен 6 см, а ведомого — 9 см. Сравните центростремительные ускорения
периферийных точек каждого шкива.

Задача 2. Два тела движутся по окружности радиусом 36
м в одном направлении с постоянными по модулю скоростями. Нормальное ускорение
первого тела равно 10 м/с2, а второго — 4 м/с2. Через
какой минимальный промежуток времени тела окажутся в одной точке траектории?

В заключение отметим, что равномерное движение точки по
окружности является движением с переменной скоростью и переменным ускорением,
так как направление их векторов непрерывно изменяется. Но их модули при этом
остаются неизменными.

Источник

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.


Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Движение по циклоиде*

Источник

Добавить комментарий