В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.
Что такое ускорение?
Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение – это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:
 Вам будет интересно:Смоленский государственный институт искусств: факультеты, специальности, сроки обучения, документы для поступления
Вам будет интересно:Смоленский государственный институт искусств: факультеты, специальности, сроки обучения, документы для поступления
a = dv/dt.
Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:
a = (v2 – v1)/(t2 – t1).
Где v2 и v1 – скорости в моменты времени t2 и t1 соответственно.
Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.
Движение по прямой и ускорение
Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.
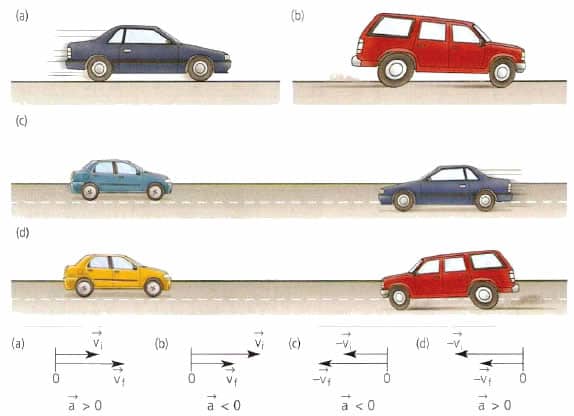
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:
v = v0±a*t;
l = v0*t±a*t2/2.
Здесь v0 – некоторая начальная скорость тела, которая может быть также равна нулю, l – пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак – – о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:
±a = (v – v0)/t;
±a = 2*(l – v0*t)/t2.
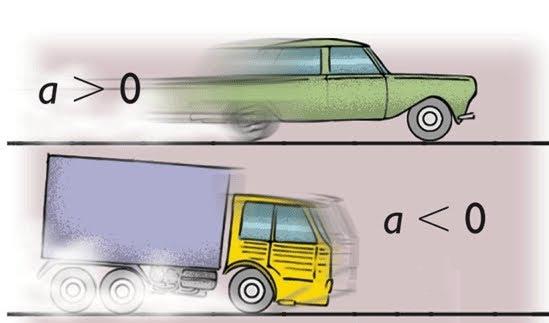
Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с2).
Полное ускорение и его компоненты при движении тела по кривой
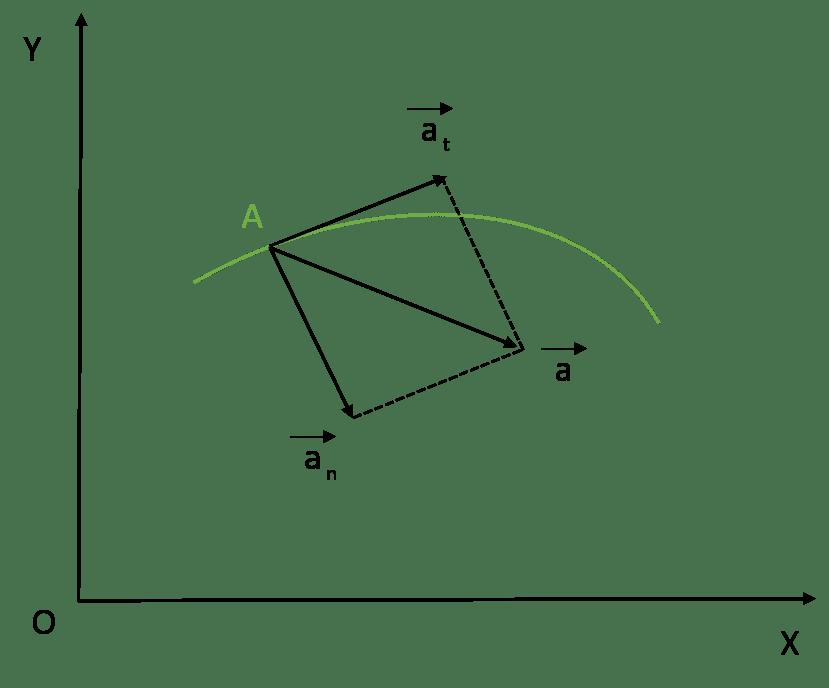
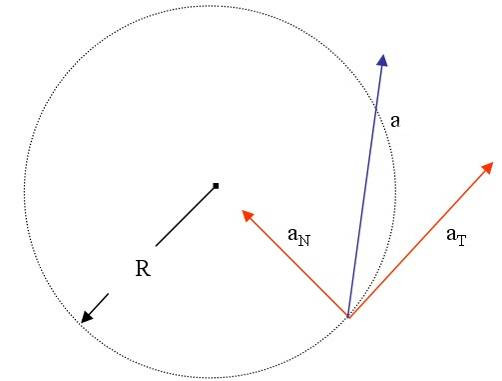
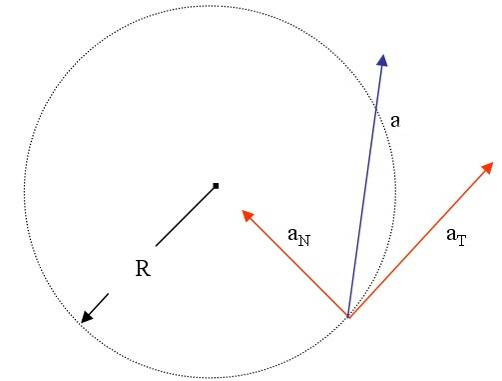
В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:
a = √(at2 + an2).
Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:
an = v2/r.
Здесь r – радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.
Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.
Угловое ускорение
Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:
α = dω/dt.
Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.
Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:
α = at/r.
Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.
Пример решения задачи
Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:
v = 2 + 3*t2 + 2*t3.
Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.
Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:
at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.
Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).
Нормальная компонента вычисляется так:
an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.
Теперь можно рассчитать полное ускорение. Оно будет равно:
a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.
То есть, полное ускорение практически полностью образовано нормальной компонентой.
Наконец, ускорение угловое определяется по формуле:
α = at/r = 76/0,2 = 380 рад/с2.
Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.
- Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
- Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
- Единица измерения ускорения — метр в секунду в квадрате (м/с2).
- Акселерометр — прибор для измерения ускорения.
Формула ускорения
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения
Проекция ускорения на ось ОХ

vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
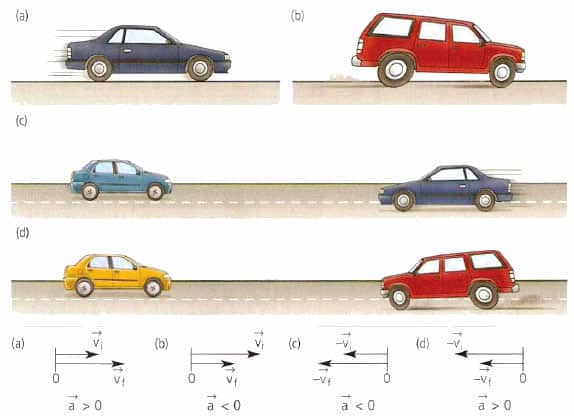
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
- Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
- Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
В момент времени t1 = 1с ускорение a = 2 м/с2. В момент времени t2 = 3 ускорение a = 0 м/с2.
Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17992
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18202
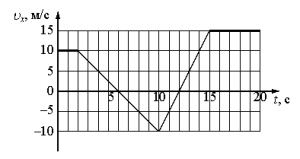
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?

Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.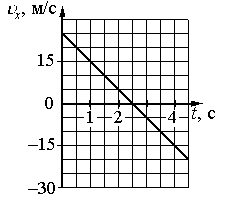
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.7k
В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.
Что такое ускорение?
Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение – это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:
a = dv/dt.
Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:
a = (v2 – v1)/(t2 – t1).
Где v2 и v1 – скорости в моменты времени t2 и t1 соответственно.
Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.
Движение по прямой и ускорение
Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:
v = v0±a*t;
l = v0*t±a*t2/2.
Здесь v0 – некоторая начальная скорость тела, которая может быть также равна нулю, l – пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак – – о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:
±a = (v – v0)/t;
±a = 2*(l – v0*t)/t2.
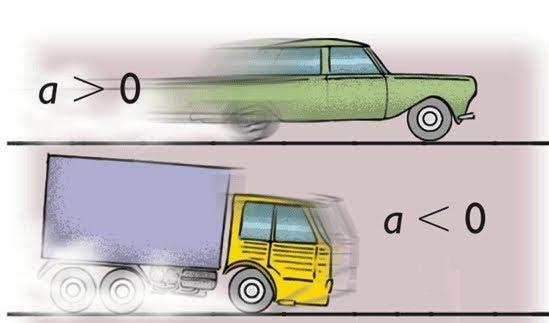
Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с2).
Полное ускорение и его компоненты при движении тела по кривой

В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:
a = √(at2 + an2).
Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:
an = v2/r.
Здесь r – радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.
Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.
Угловое ускорение
Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:
α = dω/dt.
Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.
Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:
α = at/r.
Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.
Пример решения задачи
Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:
v = 2 + 3*t2 + 2*t3.
Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.
Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:
at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.
Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).
Нормальная компонента вычисляется так:
an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.
Теперь можно рассчитать полное ускорение. Оно будет равно:
a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.
То есть, полное ускорение практически полностью образовано нормальной компонентой.
Наконец, ускорение угловое определяется по формуле:
α = at/r = 76/0,2 = 380 рад/с2.
Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.
| Ускорение | |
|---|---|
 |
|
| Размерность | LT−2 |
| Единицы измерения | |
| СИ | м/с² |
| СГС | см/с² |
| Примечания | |
| векторная величина |

Падающий мяч при отсутствии сопротивления воздуха ускоряется, то есть движется все быстрее и быстрее.
Ускоре́ние (обычно обозначается латинскими буквами a (от лат. acceleratio) или w) — физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени. Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости 
Например, тела, свободно падающие вблизи поверхности Земли вдоль вертикали, в случаях, когда испытываемое ими сопротивление воздуха мало, увеличивают свою скорость примерно на 9,8 м/с за секунду, то есть их ускорение примерно равно 9,8 м/с². При непрямолинейном движении учитывается изменение не только величины скорости, но и её направления: скажем, ускорение тела, движущегося по окружности с постоянной по модулю скоростью, не равно нулю: имеется постоянное по модулю (и переменное по направлению) ускорение, направленное к центру окружности.
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (русское обозначение: м/с2; международное: m/s2).
Ускорение в кинематике точки[править | править код]
Наиболее общий случай[править | править код]
Ускорение и связанные величины[править | править код]
Вектор ускорения материальной точки в любой момент времени находится путём однократного дифференцирования по времени вектора скорости материальной точки (или двукратного дифференцирования радиус-вектора):
Если на траектории точки известны координаты 


Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:
где
— вектор рывка.
Анализ движения по кривой[править | править код]

Траекторию движения материальной точки на малом участке можно считать плоской. Вектор ускорения 

где
— величина скорости,
— единичный касательный к траектории вектор, направленный вдоль скорости (касательный орт),
— орт главной нормали к траектории, который можно определить как единичный вектор в направлении
— орт бинормали к траектории, перпендикулярный одновременно ортам
и
(то есть ортогональный к мгновенной плоскости траектории),
— радиус кривизны траектории.
Слагаемое 

Векторы 

Итак, учитывая сказанное выше, вектор ускорения при движении по любой траектории можно записать как:
Важные частные случаи[править | править код]
Равноускоренное движение[править | править код]
Если вектор 
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). Обратное, вообще говоря, неверно.
Равноускоренное движение при переходе в другую инерциальную систему отсчёта остаётся равноускоренным.
Случай равноускоренного движения, когда ускорение (постоянное) и скорость направлены по одной прямой, но в разных направлениях, называется равнозамедленным движением. Равнозамедленное движение всегда одномерно. Движение можно рассматривать как равнозамедленное лишь до того момента, пока скорость не станет равной нулю. Кроме того, всегда существуют инерциальные системы отсчёта, в которых движение не является равнозамедленным.
Прямолинейное движение[править | править код]
Важным частным случаем движения с ускорением является прямолинейное движение, когда ускорение в любой момент времени коллинеарно скорости (например, случай падения тела с вертикальной начальной скоростью). В случае прямолинейного движения можно выбрать одну из координатных осей вдоль направления движения и заменить радиус-вектор и векторы ускорения и скорости на скаляры. При этом, при постоянном ускорении из приведённых выше формул вытекает, что
Здесь v0 и v — начальная и конечная скорость тела, a — его ускорение, s — пройденный телом путь.
Ряд практически важных формул связывают затраченное время, пройденный путь, достигнутую скорость и ускорение при равноускоренном прямолинейном движении с нулевой (
так что любые две из этих величин определяют две другие (здесь предполагается, что время отсчитывается от начала движения: t0 = 0).
Движение по окружности[править | править код]

Равномерное движение по окружности. Ускорение всегда перпендикулярно скорости и направлено к центру.

Пример неравномерного движения по окружности (математический маятник). Ускорение, складывающееся из тангенциальной и центростремительной компонент, в разные моменты изменяется от полностью касательного до полностью нормального к траектории.
Вектор ускорения
при движении точки по окружности можно разложить на два слагаемых (компоненты):
Тангенциальное или касательное ускорение 


Центростремительное или нормальное ускорение 


а модуль равен
где ω — угловая скорость относительно центра вращения, а r — радиус окружности.
Кроме этих двух компонент, используется также понятие угловое ускорение, показывающее, на сколько изменилась угловая скорость за единицу времени, и, аналогично линейному ускорению, вычисляемое следующим образом:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и угловой скорости сонаправлены (или хотя бы их скалярное произведение положительно), значение скорости растёт, и наоборот.
В частном случае равномерного движения по окружности векторы углового ускорения и тангенциального ускорения равны нулю, а центростремительное ускорение постоянно по модулю.
Ускорение при сложном движении[править | править код]
Говорят, что материальная точка (тело) совершает сложное движение, если она движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой, «лабораторной», системы отсчёта. Тогда абсолютное ускорение тела в лабораторной системе равно сумме относительного, переносного и кориолисова ускорений:
Последний член содержит векторное произведение угловой скорости вращения движущейся системы отсчёта и скорости материальной точки в этой движущейся системе.
Ускорения в кинематике твёрдого тела[править | править код]
Связь ускорений двух точек абсолютно твёрдого тела A и B можно получить из формулы Эйлера для скоростей этих точек:
где 
где 
Второе слагаемое называется осестремительным ускорением, а третье — вращательным ускорением[1].
Создание ускорения. Динамика точки[править | править код]
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие[4].
Классическая механика[править | править код]
Второй закон Ньютона применительно к нерелятивистскому движению (то есть к движению со скоростями, много меньшими скорости света) утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется инертной массой материальной точки):
Если известны масса материальной точки и (как функция времени) сила, действующая на неё, то из второго закона Ньютона известно и её ускорение: 
Релятивистская механика[править | править код]
В релятивистской физике второй закон Ньютона записывается в форме
что делает нахождение ускорения более сложной задачей, чем в классическом случае. В частности, длительное движение с постоянным ускорением принципиально невозможно (иначе скорость точки в конце концов превысит скорость света), а неизменность силы не означает неизменности ускорения: оно будет стремиться к нулю при нарастании скорости. Тем не менее, если зависимость 


Ускорение в теории относительности[править | править код]
В теории относительности движение тела с переменной скоростью вдоль мировой линии в 4-мерном пространстве-времени характеризуется определённой величиной, аналогичной ускорению. В отличие от обычного (трёхмерного) вектора ускорения, 4-вектор ускорения (называемый 4-ускорением) ai является второй производной от 4-вектора координат xi не по времени, а по пространственно-временному интервалу τ (или, что то же самое, по собственному времени) вдоль мировой линии тела:
В любой точке мировой линии 4-вектор ускорения всегда ортогонален к 4-скорости:
Это означает, в частности, что 4-скорости меняются не по модулю, а лишь по направлению: независимо от направления в пространстве-времени 4-скорость любого тела равна по модулю скорости света. Геометрически, 4-ускорение совпадает с кривизной мировой линии и является аналогом нормального ускорения в классической кинематике.
В классической механике значение ускорения не изменяется при переходе от одной инерциальной системы отсчета к другой, то есть ускорение инвариантно относительно преобразований Галилея. В релятивистской механике 4-ускорение является 4-вектором, то есть при преобразованиях Лоренца изменяется аналогично пространственно-временным координатам.
“Обычный” трёхмерный вектор ускорения 





Измерения ускорений[править | править код]
Используемые единицы[править | править код]
- метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ;
- сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС, имеет также собственное наименование гал, или галилео (применяется преимущественно в гравиметрии);
- g (произносится «же»), стандартное ускорение свободного падения на поверхности Земли, равное по определению 9,80665 м/с². В технических расчётах, не требующих точности выше 2 %, часто используется приближение g ≈ 10 м/с².
| м/с2 | фут/с2 | g | см/с2 | |
|---|---|---|---|---|
| 1 м/с² = | 1 | 3,28084 | 0,101972 | 100 |
| 1 фут/с² = | 0,304800 | 1 | 0,0310810 | 30,4800 |
| 1 g = | 9,80665 | 32,1740 | 1 | 980,665 |
| 1 см/с² = | 0,01 | 0,0328084 | 0,00101972 | 1 |
Технические средства[править | править код]
Приборы для измерения ускорения называются акселерометрами. Они не «детектируют» ускорение непосредственно, а измеряют силу реакции (укр.) (рус. опоры, возникающую при ускоренном движении. Поскольку аналогичные силы сопротивления возникают в поле тяготения, с помощью акселерометров можно измерять также гравитацию.
Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.
Значения ускорения в некоторых случаях[править | править код]
Значения ускорений различных движений:[5]
| Вид движения | Ускорение, м/с2 |
|---|---|
| Центростремительное ускорение Солнечной системы при орбитальном движении в Галактике | 2,2⋅10−10 |
| Центростремительное ускорение Земли при орбитальном движении вокруг Солнца | 0,0060 |
| Центростремительное ускорение Луны при орбитальном движении вокруг Земли | 0,0027 |
| Пассажирский лифт | 0,9—1,6 |
| Поезд метро | 1 |
| Автомобиль «Жигули» | 1,5 |
| Бегун на коротких дистанциях | 1,5 |
| Велосипедист | 1,7 |
| Конькобежец | 1,9 |
| Мотоцикл | 3—6 |
| Аварийное торможение автомобиля | 4—6 |
| Усэйн Болт, максимальное ускорение | 8[6] |
| Гоночный автомобиль | 8—9 |
| Торможение при открытии парашюта | 30 (3 g) |
| Запуск и торможение космического корабля | 40—60 (4—6 g) |
| Манёвр реактивного самолёта | до 100 (до 10 g) |
| Свая после удара копром | 300 (30 g) |
| Поршень двигателя внутреннего сгорания | 3×103 |
| Пуля в стволе винтовки | 2,5×105 |
| Микрочастицы в ускорителе | (2—50)×1014 |
| Электроны между катодом и анодом трубки цветного телевизора (20 кВ, 0,5 м) | ≈7×1015 |
| Электроны при соударении с люминофором трубки цветного телевизора (20 кВ) | ≈1022 |
| Альфа-частицы в атомном ядре | ≈1027 |
Примечание: здесь g ≈ 10 м/с2.
Понятие “обобщённое ускорение”[править | править код]
Если динамика механической системы описывается не в декартовых, а в обобщённых координатах 


См. также[править | править код]
- Ускорение свободного падения
- Собственное ускорение
- Релятивистски равноускоренное движение
- Приливное ускорение
- Кориолисово ускорение
- Рывок (кинематика)
Примечания[править | править код]
- ↑ 1 2 Маркеев А. П. Теоретическая механика. — М.: ЧеРо, 1999. — С. 59. — 572 с.
- ↑ Обзор результатов Ривальса: Appendice au Mémoire de M. Bresse // Journal de l’École polytechnique. — 1853. — Т. 20. — С. 109—115. Архивировано 9 марта 2016 года.
- ↑ Joulin L. Notice biographique sur M. le commandant Rivals // Mémoires de l’Académie royale des sciences, inscriptions et belles-lettres de Toulouse. — 1891. — Т. 3, вып. 9. — С. 535—539. Архивировано 8 марта 2016 года.
- ↑ Для того, чтобы использовать уравнение движения в форме, совпадающей с формой уравнения второго закона Ньютона, применительно к ускорениям, возникающим в неинерциальных системах отсчёта даже в отсутствие каких-либо воздействий на тело, вводят фиктивные силы инерции. Например, пусть тело массой m покоится в инерциальной системе отсчёта на некотором расстоянии R от оси. Если привести систему отсчёта во вращение с угловой скоростью ω вокруг этой оси, то система становится неинерциальной, а тело будет совершать видимое вращательное движение с линейной скоростью v=ωR по окружности вокруг оси. Для его описания во вращающейся системе отсчёта необходимо ввести центростремительное ускорение, которое можно формально считать результатом действия одной из сил инерции — силы Кориолиса, равной по модулю 2mvω и направленной к оси, перпендикулярно оси и скорости тела; при этом она наполовину компенсируется действием другой силы инерции — центробежной силы, равной по модулю mvω и направленной от оси вращения.
- ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп.. — М.: Наука, 1988. — С. 61. — 256 с. — ISBN 5-02-013833-9.
- ↑ График зависимости ускорения У. Болта от времени Архивная копия от 10 мая 2013 на Wayback Machine — забег на 100 м на летних Олимпийских играх 2008 года в Пекине
Ссылки[править | править код]
- Ландау Л. Д., Лифшиц Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6.
- David C. Cassidy, Gerald James Holton, and F. James Rutherford. Understanding physics. — Birkhäuser (англ.) (рус., 2002. — ISBN 978-0-387-98756-9.
- Pauli W. Theory of Relativity. — Dover, 1981. — ISBN 978-0-486-64152-2.
Как найти ускорение — определение и формулы расчета в физике
Содержание:
-
Что такое ускорение
- Единица измерения
-
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
Что такое ускорение
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})
Максимальное ускорение
(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х):
(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Насколько полезной была для вас статья?
Рейтинг: 1.94 (Голосов: 35)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так


















![{displaystyle {vec {a}}={vec {a}}_{r'}+{vec {a}}_{e}+2left[{vec {omega }}times {vec {v}}_{r'}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14c94b28221af9efd57db669ebd5baabb5db5e85)
![vec{v}_B = vec{v}_A + left[vec{omega}timesvec{AB}right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/674393e427cf0812f2a78e9593820b0f5f0dd0a7)
![vec{a}_B = vec{a}_A + left[vec{omega}times left[ vec{omega}times vec{AB}right] right] + left[ vec{varepsilon}times vec{AB} right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/73ba130aeb13035b7b570db42daa1c2bf8bd55f0)




