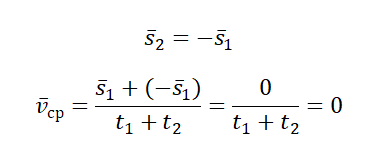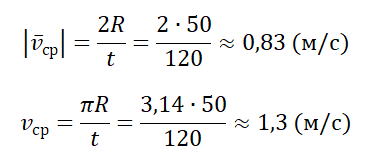Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Неравномерное движение и средняя скорость
теория по физике 🧲 кинематика
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
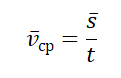
v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
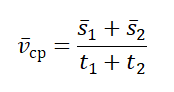
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
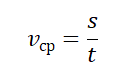
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
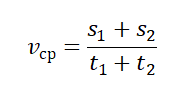
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
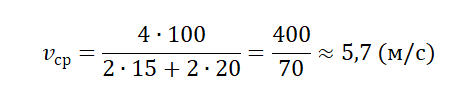
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
- vср= v ср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
- vср>v ср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
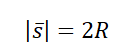
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
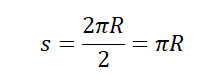
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
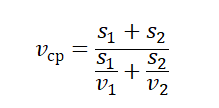
- Если известны скорости на первой и второй половине пути (s1=s2), средняя скорость равна:
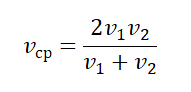
- Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:
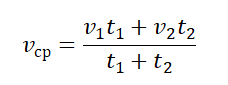
- Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:
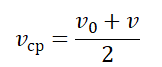
- Если известны скорости тела за равные промежутки времени, его средняя скорость равна:
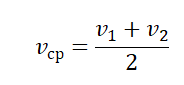
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Модуль вектора средней скорости по окружности
§ 17. Переменное движение. Средняя скорость. Средний модуль скорости
1. Переменное движение.
Определение 1. Движение называется переменным , если за любые равные промежутки времени точка совершает различные перемещения.
Перемещение – вектор. Он может изменяться по модулю и направлению. При переменном движении за любые равные промежутки времени перемещения могут отличаться либо модулями, либо направлениями, либо и модулями и направлениями.
2. Средняя скорость.
Определение 2а. Средней скоростью переменного движения называется отношение перемещения ко времени, за которое это перемещение произошло.
Запишем формулу скорости равномерного движения и средней скорости переменного движения.
Если посмотреть на правые части этих равенств, заметим, что они одинаковы. В этом заключается смысл средней скорости.
Определение 2б. Под средней скоростью переменного движения понимают скорость некоторого воображаемого равномерного прямолинейного движения, у которого перемещение и время одинаковы с переменным движением.
Согласно рисунку, представленному выше, это понимать надо так. Если бы точка двигалась не переменно по криволинейной траектории, а равномерно и прямолинейно прямо по вектору перемещения , то она за время попала бы в точку A из точки , если бы скорость этого воображаемого равномерного движения была бы одинаковой со средней скоростью переменного движения.
Модуль вектора средней скорости, или модуль средней скорости :
.
3. Средний модуль скорости.
На практике при составлении расписания движения поездов, автобусов используют ещё одно понятие средней скорости, которое называют средним модулем скорости, то есть средним по времени модулем всех скоростей, которые имела точка на различных участках траектории.
Определение 3а. Средним модулем скорости переменного движения называется отношение пути S ко времени t, за которое этот путь пройден.
– средний модуль скорости
Не надо путать средний модуль скорости с модулем вектора средней скорости.
Например, если автобус вышел на маршрут в начале дня и к концу дня возвратился в гараж, то перемещение за всё время движения равно нулю . Поэтому равны нулю средняя скорость и её модуль:
, .
Но средний модуль скорости отличен от нуля, так как не равен нулю путь, пройденный автобусом:
.
Аналогично для бумеранга.
За время полёта бумеранга средняя скорость его движения и модуль средней скорости равны нулю, так как равно нулю перемещение бумеранга относительно точки А (см. рис.). Но так как путь, который проделал бумеранг, не равен нулю, то и средний модуль скорости движения бумеранга отличен от нуля.
Если посмотреть на правые части формул модуля скорости равномерного движения и среднего модуля скорости переменного движения, то увидим, что правые части равенств одинаковы.
В этом заключается смысл среднего модуля скорости.
Определение 3б. Средний модуль скорости переменного движения равен модулю скорости такого воображаемого равномерного прямолинейного движения, у которого путь и время одинаковы с переменным движением.
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
[spoiler title=”источники:”]
http://education-for.narod.ru/bas/kinematika/p17.html
[/spoiler]
Содержание:
- Определение и формула средней скорости
- Вектор средней скорости
- Единицы измерения
- Примеры решения задач
Определение и формула средней скорости
Определение
Средней путевой скоростью материальной точки на отрезке времени
$Delta t$называется скалярная физическая величина, равная отношению
длины пути, пройденного точкой к промежутку времени, в течение которого данный путь пройден. Среднюю скорость обозначают:
$$langle vrangle, bar{v}, v_{s r}$$
Математически определение средней скорости можно записать в следующем виде:
$$langle vrangle(t+Delta t)=frac{Delta s}{Delta t}=frac{s(t+Delta t)-s(t)}{Delta t}(1)$$
где $Delta s=s(t+Delta t)-s(t)$ – длина пути, которую прошла точка за время
$Delta t$.
Если перейти к пределу при $Delta t rightarrow 0$ , получим:
$$lim _{Delta t rightarrow 0}langle vrangle=lim _{Delta t rightarrow 0} frac{Delta s}{Delta t}=frac{d s}{d t}=v(t)(2)$$
средняя путевая скорость в пределе совпадает с величиной (модулем) мгновенной скорости точки в момент времени t.
При равномерном движении:
$$langle vrangle=v(3)$$
Вектор средней скорости
Определение
Вектором средней скорости $langlevec{v}rangle$ материальной точки на
отрезке времени $Delta t$называют величину, равную приращению радиус-вектора,
который определяет положение данной точки к промежутку времени $Delta t$:
$$langlebar{v}rangle(t+Delta t)=frac{Delta bar{r}}{Delta t}=frac{bar{r}(t+Delta t)-bar{r}(t)}{Delta t}(4)$$
где $Delta bar{r}$ – приращение радиус-вектора материальной точки.
Вектор средней скорости в пределе при $Delta t rightarrow 0$ совпадает с вектором скорости в момент времени t:
$$lim _{Delta t rightarrow 0}langlebar{v}rangle=lim _{Delta t rightarrow 0} frac{Delta bar{r}}{Delta t}=frac{d bar{r}}{d t}=bar{v}(t)(5)$$
где $bar{v}(t)$ – вектор мгновенной скорости токи.
Если точка совершает равномерное и прямолинейное движение, то выполняется равенство:
$$langlebar{v}rangle=bar{v}(6)$$
Средняя путевая скорость и модуль вектора средней скорости равны
$(langle vrangle=|langlebar{v}rangle|)$ только при прямолинейном движении.
При всех остальных видах движения выполняется неравенство:
$$langle vrangle>|langlebar{v}rangle|(7)$$
Единицы измерения
Основной единицей измерения средней скорости в системе СИ является: м/с
В СГС: см/с
Примеры решения задач
Пример
Задание. Какова средняя скорость материальной точки за время ее движения, если точка прошла первую половину
пути имея скорость v1, остальную часть пути данная точка 1/2 времени двигалась со скоростью v2, последний
участок пути точка двигалась со скоростью v3.
Решение. В качестве основы для решения задачи формулу:
$$langle vrangle=frac{s}{Delta t}(1.1)$$
где время потраченное на путь ($Delta t$) делится на три части:
$$Delta t=t_{1}+t_{2}+t_{3}(1.2)$$
При этом имеют место следующие соотношения между отрезками пути, скоростью их преодоления и временем:
$$left{begin{array}{c}frac{1}{2} s=v_{1} t_{1} rightarrow t_{1}=frac{s}{2 v_{1}} \ frac{1}{2} s=v_{2} t_{2}+v_{3} t_{3} rightarrow t_{3}=frac{s}{2left(v_{2}+v_{3}right)}(1.3) \ t_{2}=t_{3}=frac{1}{2} tend{array}right.$$
$$langle vrangle=frac{2 v_{1}left(v_{2}+v_{3}right)}{v_{2}+v_{3}+2 v_{1}}$$
Ответ. $langle vrangle=frac{2 v_{1}left(v_{2}+v_{3}right)}{v_{2}+v_{3}+2 v_{1}}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова средняя скорость частицы, движущейся по оси Xза время в течение которого, она пройдет первые
s метров пути, если функция скорости задана уравнением: $v=A sqrt{x}$,
где A=const>0. Считать, что x=0 при t=0.
Решение. Сделаем рисунок.
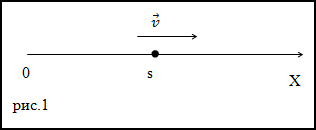
В качестве основы для решения задачи используем формулу для средней путевой скорости, так как движение прямолинейное,
то средняя путевая скорость равна модулю вектора средней скорости. По условию задачи точка движется по оси X, тогда:
$$langle vrangle(t+Delta t)=frac{Delta x}{Delta t}(2.1)$$
По условиям x(t=0)=0, среднюю скорость ищем, когда тело находится в точкеx=sследовательно, выражение (2.1) преобразуем к виду:
$$langle vrangle=frac{s}{t}(2.2)$$
Найдем зависимость скорости от времени, исходя из определения мгновенной скоростидля движения точки по оси X:
$$v=frac{d x}{d t}=A sqrt{x}(2.3)$$
Выразим из (2.2) x:
$$frac{d x}{sqrt{x}}=A d t rightarrow x=frac{A^{2} t^{2}}{4}(2.4)$$
Так как движение происходит по оси X, то $x=s=frac{A^{2} t^{2}}{4}$ . Выразим время, которое точка затратила на путьs :
$$t=frac{2 sqrt{s}}{A}(2.5)$$
Подставим время из (2.4) в формулу (2.2):
$$langle vrangle=frac{A}{2} sqrt{s}$$
Ответ. $langle vrangle=frac{A}{2} sqrt{s}$
Читать дальше: Формула угловой скорости.
§ 17. Переменное
движение. Средняя скорость. Средний
модуль скорости
1. Переменное
движение.
Определение
1. Движение
называется переменным,
если за любые равные промежутки
времени точка совершает различные
перемещения.
Перемещение
– вектор. Он может изменяться по модулю
и направлению. При переменном движении
за любые равные промежутки времени
перемещения могут отличаться либо
модулями, либо направлениями, либо и
модулями и направлениями.
2. Средняя
скорость.
![]()
Определение
2а. Средней
скоростью переменного движения
называется отношение перемещения
ко времени, за которое это
перемещение произошло.
Запишем
формулу скорости равномерного
движения и средней скорости
переменного движения.
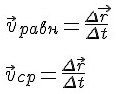
Если
посмотреть на правые части этих
равенств, заметим, что они одинаковы. В
этом заключается смысл средней
скорости.
Определение
2б. Под средней
скоростью переменного движения
понимают скорость некоторого
воображаемого равномерного
прямолинейного движения, у которого
перемещение и время одинаковы с
переменным движением.
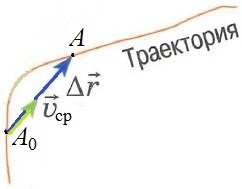
Согласно рисунку, представленному выше,
это понимать надо так. Если бы точка
двигалась не переменно по
криволинейной траектории, а равномерно
и прямолинейно прямо по вектору
перемещения ![]() ,
,
то она за время ![]()
попала бы в точку A из точки ![]() ,
,
если бы скорость этого воображаемого
равномерного движения была бы
одинаковой со средней скоростью
переменного движения.
Модуль
вектора средней скорости, или
модуль средней скорости:
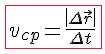 .
.
3. Средний
модуль скорости.
На
практике при составлении расписания
движения поездов, автобусов используют
ещё одно понятие средней скорости,
которое называют средним модулем
скорости, то есть средним по времени
модулем всех скоростей, которые имела
точка на различных участках траектории.
Определение
3а. Средним
модулем скорости переменного
движения называется отношение пути S
ко времени t, за которое этот
путь пройден.
![]() –
–
средний модуль скорости
![]()
Не надо
путать средний модуль скорости с
модулем вектора средней скорости.
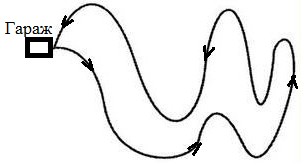
Например, если автобус вышел на маршрут
в начале дня и к концу дня возвратился в
гараж, то перемещение за всё время
движения равно нулю ![]() .
.
Поэтому равны нулю средняя скорость и
её модуль:
![]() ,
,
![]() .
.
Но
средний модуль скорости отличен от
нуля, так как не равен нулю путь,
пройденный автобусом:
![]() .
.
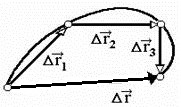
Аналогично для бумеранга.

За время
полёта бумеранга средняя скорость его
движения и модуль средней скорости
равны нулю, так как равно нулю
перемещение бумеранга относительно
точки А (см. рис.). Но так как путь,
который проделал бумеранг, не равен
нулю, то и средний модуль скорости
движения бумеранга отличен от нуля.
Если
посмотреть на правые части формул
модуля скорости равномерного движения
и среднего модуля скорости переменного
движения, то увидим, что правые части
равенств одинаковы.
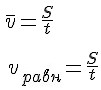
В этом
заключается смысл среднего модуля
скорости.
Определение
3б. Средний
модуль скорости переменного
движения равен модулю скорости
такого воображаемого равномерного
прямолинейного движения, у которого
путь и время одинаковы с переменным
движением.
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения υ=∆r∆t; υ↑↑∆r.
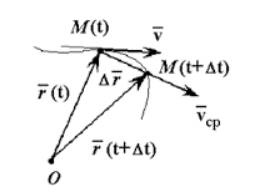
Рисунок 1. Средняя скорость сонаправлена перемещению
Модуль средней скорости по пути равняется υ=S∆t.
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆t к 0:
υ=lim∆t∆r∆t=drdt=r˙.
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение dr совпадает с бесконечно малым элементом траектории ds.
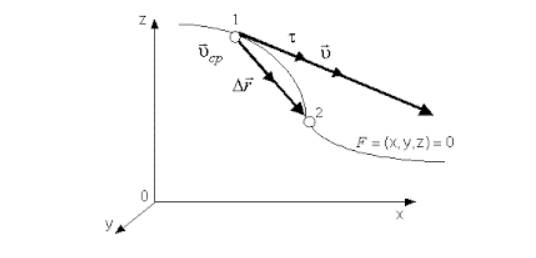
Рисунок 2. Вектор мгновенной скорости υ
Имеющееся выражение υ=lim∆t∆r∆t=drdt=r˙ в декартовых координатах идентично ниже предложенным уравнениям:
υx=dxdt=x˙υy=dydt=y˙υz=dzdt=z˙.
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
υ=υ=υx2+υy2+υz2=x2+y2+z2.
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r=rq1, q2, q3, тогда значение скорости запишется как:
υ=drdt=∑i=13∂r∂qi∂qi∂r=∑i=13∂r∂qiq˙i.
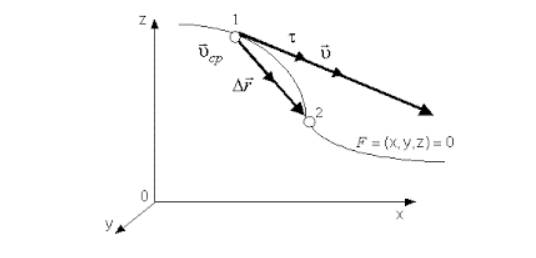
Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат
При сферических координатах предположим, что q1=r; q2=φ; q3=θ, то получим υ, представленную в такой форме:
υ=υrer+υφeφ+υθφθ, где υr=r˙; υφ=rφ˙sin θ; υθ=rθ˙; r˙=drdt; φ˙=dφdt; θ˙=dθdt; υ=r1+φ2sin2θ+θ2.
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением dr=υ(t)dt
Дан закон прямолинейного движения точки x(t)=0,15t2-2t+8. Определить ее мгновенную скорость через 10 секунд после начала движения.
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
υ(t)=x˙(t)=0.3t-2; υ(10)=0.3×10-2=1 м/с.
Ответ: 1 м/с.
Движение материальной точки задается уравнением x=4t-0,05t2. Вычислить момент времени tост, когда точка прекратит движение, и ее среднюю путевую скорость υ.
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
υ(t)=x˙(t)=4-0,1t.
4-0,1t=0;tост=40 с;υ0=υ(0)=4;υ=∆υ∆t=0-440-0=0,1 м/с.
Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0,1 м/с.
Одной из кинематических характеристик
движения точки является векторная
величина, называемая скоростью точки.
Скорость точки – это векторная величина,
характеризующая быстроту и направление
движения точки в данной системе отсчета.
Введем сначала понятие о средней скорости
точки за какой-нибудь промежуток времени.
Пусть движущаяся точка находится в
момент времени![]() в положении
в положении![]() (рис.
(рис.
1.3), определяемом радиус-вектором![]() ,
,
а в момент![]() приходит в положение
приходит в положение![]() ,
,
определяемое вектором![]() .
.
Тогда перемещение точки за промежуток
времени![]() определяется вектором
определяется вектором![]() ,
,
который будем называтьвектором
перемещения точки.Этот вектор
направлен по хорде, если точка движется
криволинейно (рис. 1.3,а), и вдоль самой
траектории![]() ,
,
когда движение является прямолинейным
(рис. 1.3,б).
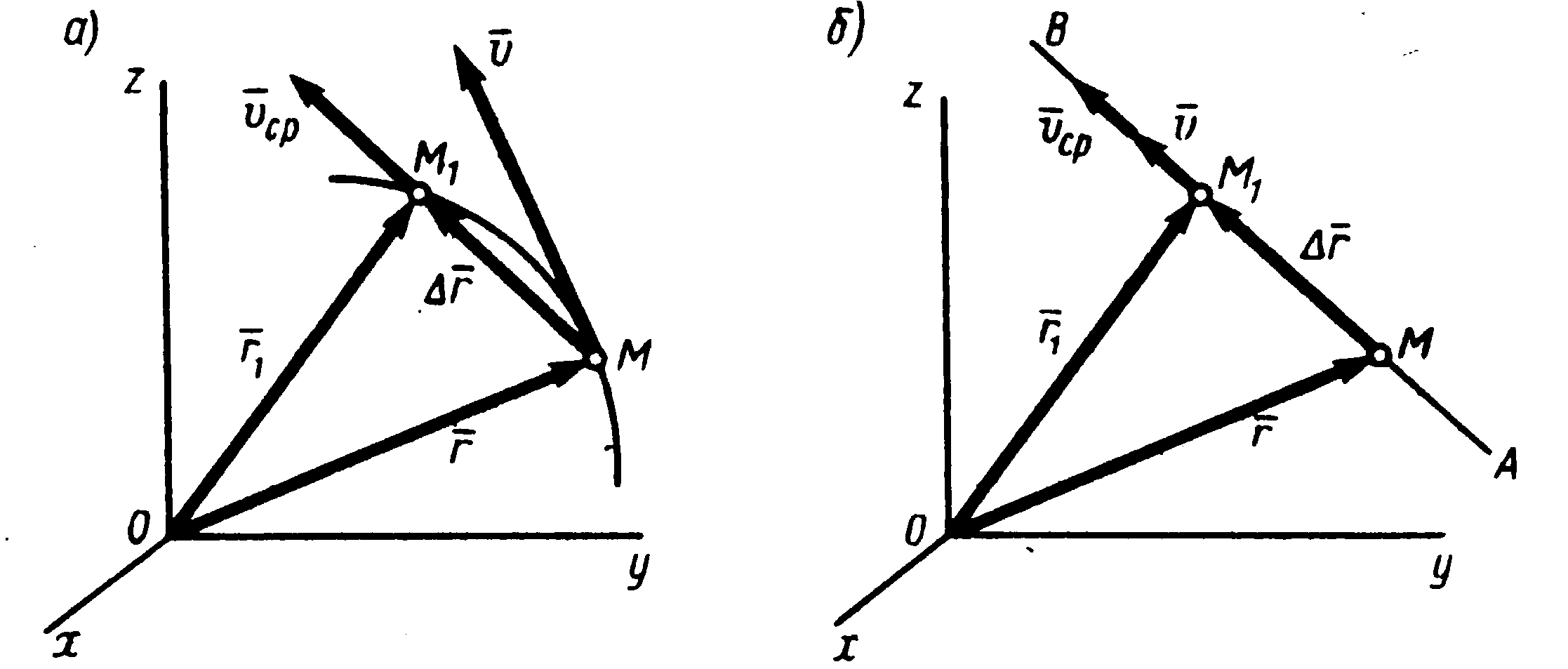
Рисунок
1.3
Из треугольника
![]() ,
,
видно, что![]() ,
,
следовательно,
![]() .
.
Отношение вектора перемещения точки к
соответствующему промежутку времени
дает векторную величину, называемую
средней по модулю и направлению скоростью
точки за промежуток времени
![]() :
:
|
|
(7) |
Направлен вектор
![]() так
так
же, как и вектор![]() ,
,
т.е. при криволинейном движении вдоль
хорды![]() ,
,
в сторону движения точки, а при
прямолинейном движении – вдоль самой
траектории.
Очевидно, что чем меньше промежуток
времени
![]() ,
,
тем величина![]() будет точнее характеризовать движение
будет точнее характеризовать движение
точки.
Поэтому скоростью точки
![]() в данный момент времени
в данный момент времени![]() называется векторная величина
называется векторная величина![]() ,
,
к которой стремится скорость![]() при
при
стремлении промежутка времени![]() к нулю.
к нулю.
![]() .
.
Предел отношения
![]() при
при![]() представляет собой первую производную
представляет собой первую производную
от вектора![]() по аргументу
по аргументу
![]() и обозначается
и обозначается![]() ,
,
тогда
|
|
(8) |
Итак, вектор скорости точки в данный
момент времени равен первой производной
от радиус-вектора точки по времени. Так
как предельным направлением секущей![]() является
является
касательная, то вектор скорости в данный
момент времени направлен по касательной
к траектории точки в сторону движения.
Размерность
скорости
![]() ,
,
т.е.![]() .
.
Единицы измерения![]() .
.
8.4. Вектор ускорения точки
Ускорением точки называется векторная
величина, характеризующая изменение с
течением времени модуля и направления
скорости.
Пусть в некоторый момент времени
![]() движущаяся
движущаяся
точка находится в положении![]() и имеет скорость
и имеет скорость![]() (рис.1.4),
(рис.1.4),
а в момент времени![]() приходит
приходит
в точку![]() и
и
имеет
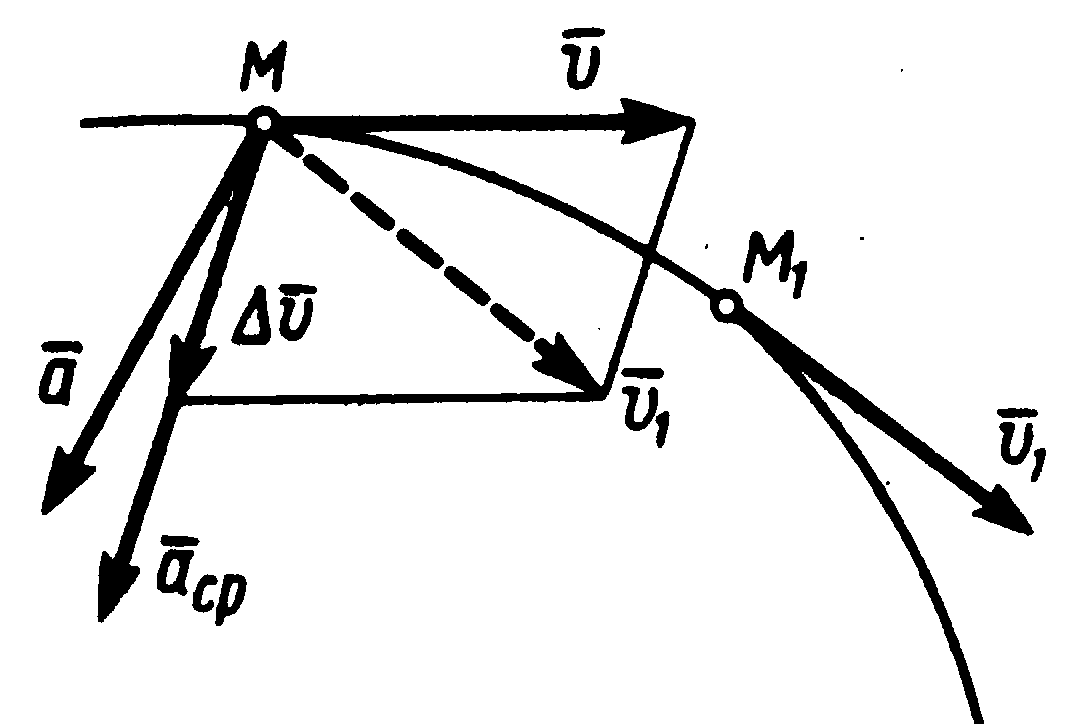
Рисунок
1.4
скорость
![]() .
.
Тогда за промежуток времени![]() скорость изменится на
скорость изменится на![]() .
.
Для построения вектора![]() отложим
отложим
от точки![]() вектор,
вектор,
равный![]() ,
,
и построим параллелограмм, в котором
диагональю будет![]() , а одной из сторон
, а одной из сторон![]() .
.
Тогда, очевидно,
вторая сторона и будет изображением
вектора
![]() .
.
Заметим, что вектор![]() всегда
всегда
направлен в сторону вогнутости траектории.
Отношение
![]() к
к![]() определяет вектор среднего ускорения
определяет вектор среднего ускорения
точки за промежуток времени![]() .
.
|
|
(9) |
Вектор среднего ускорения имеет то же
направление, что и вектор
![]() ,
,
т.е. направлен в сторону вогнутости
траектории. Тогда
![]()
или с учетом равенства (8),
|
|
(10) |
Следовательно, вектор ускорения точки
в данный момент времени равен первой
производной от вектора скорости или
второй производной от радиус-вектора
точки по времени.
Размерность
![]() ,
,
т.е.![]() .
.
Единица измерения![]() .
.
Вектор
![]() направлен, также как и вектор
направлен, также как и вектор![]() ,
,
лежит в плоскости этой кривой и направлен
в сторону её вогнутости.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #