Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.
Вес тела имеет электромагнитную природу (не путать с силой тяжести – она возникает между двумя телами и имеет гравитационную природу!). Обозначается P. Измеряется динамометром. Единица измерения — Н (Ньютон).
Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P↑↓N или P↑↓T.
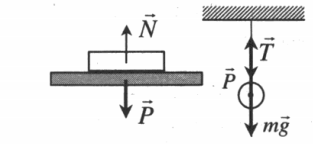
Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:
P = T; P = N; P = Fупр.
Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:
P0 = Fтяж = mg
Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.
Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.
Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:
P = mg = 16,38∙10 = 163,8 (Н)
Перегрузка
Перегрузка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности.
Перегрузка определяется отношением:
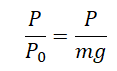
Перегрузка возникает, когда система, в которой находится тело, движется с ускорением.
Вес тела в движущейся равноускоренно системе
Вес тела в движущейся системе может быть больше или меньше веса того же тела в системе, которая находится в состоянии покоя:
- Если система движется равноускоренно в направлении ускорения свободного падения, вес тела меньше веса тела в неподвижной системе: при a↑↑g — P < P0.
- Если система движется равноускоренно в направлении, противоположном ускорению свободного падения, вес тела больше веса тела в неподвижной системе: при a↑↓g — P > P0.
- Если система движется с равномерной скоростью (ускорение равно нулю) в любом направлении по отношению к ускорению свободного падения, вес тела равен весу тела в неподвижной системе: при a = 0 — P = P0.
Применение законов Ньютона для определения веса тела
Опора или подвес неподвижны |
|
 |
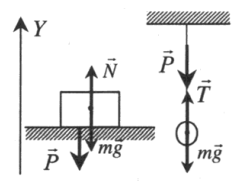Второй закон Ньютона в векторной форме:
N + mg = ma или T + mg = ma Проекция на ось ОУ: N – mg = 0 или T — mg = 0 |
Ускорение опоры направлено вверх |
|
 |
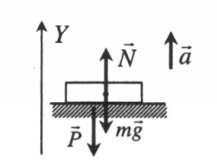Второй закон Ньютона в векторной форме:
N + mg = ma Проекция на ось ОУ: N – mg = ma Вес тела: P = N = ma + mg = m(a + g) |
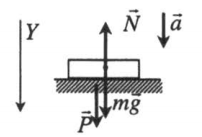
Ускорение опоры направлено вниз |
|
 |
Второй закон Ньютона в векторной форме:
N + mg = ma Проекция на ось ОУ: mg – N = ma Вес тела: P = N = mg – ma = m(g – a) |
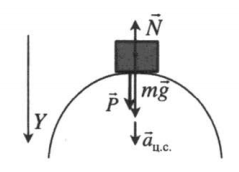
Вершина выпуклого моста |
|
 |
Второй закон Ньютона в векторной форме:
N + mg = maц.с. Проекция на ось ОУ: mg – N = m aц.с. Вес тела: P = N = mg – m aц.с. = m(g – aц.с.) |
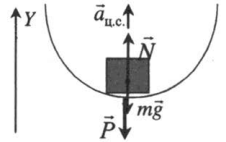
Нижняя точка вогнутого моста |
|
 |
Второй закон Ньютона в векторной форме:
N + mg = maц.с. Проекция на ось ОУ: N – mg = maц.с. Вес тела: P = N = maц.с. + mg = m(aц.с. + g) |
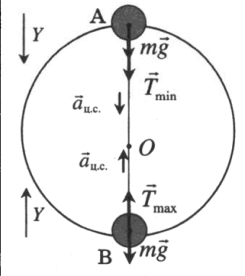
Полный оборот на подвесе |
|
 |
Второй закон Ньютона в векторной форме:
T + mg = ma Проекция на ось ОУ в точке А: T + mg = maц.с. Вес тела в точке А: P = T = maц.с. – mg = m (aц.с. – g) Проекция на ось ОУ в точке В: T – mg = maц.с. Вес тела в точке В: P = T = maц.с. + mg = m (aц.с. + g) Важно! Центростремительное ускорение всегда направлено к центру окружности. |
Пример №2. Автомобиль массой 1000 кг едет по выпуклому мосту с радиусом кривизны 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали невесомость?
Вес тела в верхней точке выпуклого моста равен:
P = m(g – aц.с.)
Чтобы пассажиры почувствовали состояние невесомости, вес тела должен быть равен 0:
m(g – aц.с.) = 0
Масса не может быть нулевой, поэтому:
g – aц.с. = 0
g = aц.с
Значит, пассажиры в верхней точке моста почувствуют невесомость, если центростремительное ускорение будет равно ускорению свободного падения. Центростремительное ускорение определяется формулой:
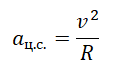
Отсюда скорость автомобиля в верхней точке моста должна быть равна:
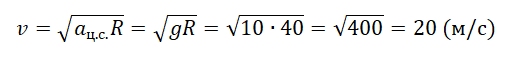
Задание EF18133
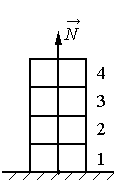Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…
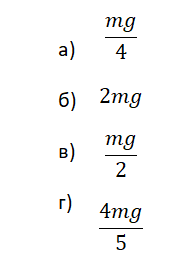
Алгоритм решения
1.Вычислить силу, с которой оставшиеся кирпичи давят на опору.
2.Применить третий закон Ньютона.
3.Определить силу, с которой действует горизонтальная опора на первый кирпич.
Решение
Так как кирпичи покоятся, вес каждого равен:
P = mg
Вес двух кирпичей равен:
2P = 2mg
Опора действует на первый кирпич с такой же силой, с какой на него действует два кирпича, оставшихся после того, как два верхних кирпича убрали.
Следовательно:
N = 2P = 2mg
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17624
Подъёмный кран поднимает груз с постоянным ускорением. На груз со стороны каната действует сила, равная по величине 8⋅103 H. На канат со стороны груза действует сила, которая:
а) 8∙103 Н
б) меньше 8∙103 Н
в) больше 8∙103 Н
г) равна силе тяжести, действующей на груз
Алгоритм решения
1.Сформулировать третий закон Ньютона.
2.Применить закон Ньютона к канату и грузу.
3.На основании закона сделать вывод и определить силу, которая действует на канат со стороны груза.
Решение
Третий закон Ньютона формулируется так:
«Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны».
Математически он записывается так:
FA = –FB
Если на груз со стороны каната действует некоторая сила, то и груз действует на канат с этой силой, которая называется весом этого груза, или силой натяжения нити. Следовательно, груз действует на канат с силой 8∙103 Н.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22586
Мальчик медленно поднимает гирю, действуя на неё с силой 100 Н. Гиря действует на руку мальчика с силой:
а) больше 100 Н, направленной вниз
б) меньше 100 Н, направленной вверх
в) 100 Н, направленной вниз
г) 100 Н, направленной вверх
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж, иллюстрирующий ситуацию.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций.
5.Вычислить силу, с которой гиря действует на руку мальчика.
Решение
Запишем исходные данные: мальчик поднимает гирю вверх с силой F = 100 Н.
Сделаем рисунок. В данном случае рука мальчика выступает в роли подвеса. Так как мальчик поднимает гирю медленно, можно считать, что он поднимает ее равномерно (равнодействующая всех сил равна нулю). Выберем систему координат, направление оси которой совпадает с направлением движения руки и гири.
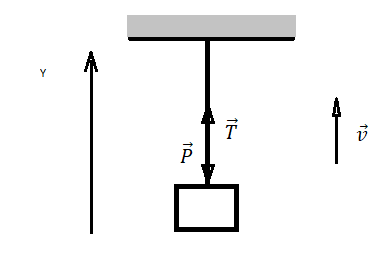
На руку (подвес) действуют только две силы. Поэтому второй закон Ньютона выглядит следующим образом:
P + T = 0
Запишем этот же закон в проекции на ось ОУ:
–P + T = 0
Отсюда:
P = T
Следовательно, на руку мальчика действует вес гири, который по модулю равен силе, с которой мальчик действует на эту гирю.
Внимание! Существует второй способ решения задачи через третий закон Ньютона. Согласно ему, тела действуют друг на друга с силами, равными по модулю, но противоположными по направлению.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.5k
Формула для измерения веса тела
Мы часто употребляем фразы наподобие: «Пачка конфет весит 250 грамм» или «я вешу 52 килограмма». Использование таких предложений происходит автоматический. Но что такое вес? Из чего он складывается и как его посчитать?
Для начала нужно понять, что неправильно говорить: «Этот предмет весит Х килограмм». В физике существует два разных понятия – масса и вес. Масса измеряется в килограммах, граммах, тонах и так далее, а вес тела рассчитывается в ньютонах. Поэтому, когда мы говорим, например, что мы весим 52 килограмма, мы на самом деле имеем в виду массу, а не вес.
Вес в физике
Масса – это мера инертности тела. Чем тело обладает большей инертностью, тем больше времени понадобится, чтобы придать ему скорость. Грубо говоря, чем выше значение массы, тем тяжелее сдвинуть предмет. В международной системе единиц массу измеряют в килограммах. Но её также измеряют и в других единицах, например;
- унция;
- фунт;
- стоун;
- американская тонна;
- английская тонна;
- грамм;
- миллиграмм и так далее.
Когда мы говорим один, два, три килограмма, мы сравниваем массу с эталонной массой (прообраз которой находится во Франции в МБМВ). Масса обозначается m.
Вес – это сила, которая действует на подвес или опору за счёт предмета, притягиваемого силой тяжести. Это векторная величина, а значит у него есть направление (как и у всех сил), в отличие от массы (скалярная величина). Направление всегда идёт в центр Земли (из-за силы тяжести). Например, если мы сидим на стуле, сиденье которого располагается параллельно Земле, то вектор силы направлен строго вниз. Вес обозначается P и рассчитывается в ньютонах [Н].
Если тело находится в движении или покое, то сила тяжести (Fтяж), действующая на тело, равна весу. Это справедливо, если движение происходит вдоль прямой линии относительно Земли, и оно имеет постоянную скорость. Вес действует на опору, а сила тяжести на само тело (которое располагается на опоре). Это разные величины, и независимо от того, что они равны в большинстве случаев, не стоит их путать.
Сила тяжести – это результат притяжения тела к земле, вес – воздействие тела на опору. Так как тело изгибает (деформирует) опору своим весом, возникает ещё одна сила, она называется сила упругости (Fупр). Третий закон Ньютона гласит, что тела взаимодействуют друг с другом с одинаковыми по модулю силами, но разными по вектору. Из этого следует, что для силы упругости должна быть противоположная сила, и эта она называется – сила реакции опоры и обозначается N.
По модулю |N|=|P|. Но так как эти силы разнонаправленные, то, раскрывая модуль, мы получим N= – P. Именно поэтому вес можно измерить динамометром, который состоит из пружинки и шкалы. Если подвесить груз на это устройство, пружинка растянется до определённой отметки на шкале.
Как измерить вес тела
Второй закон Ньютона гласит, что ускорение равно силе, делённой на массу. Таким образом, F=m*a. Так как Fтяж равна P (если тело находится в покое или движется по прямой (относительно Земли) с одинаковой скоростью), то и Р тела будет равняться произведению массы и ускорения (P=m*a).
Мы знаем, как найти массу, и знаем, что такое вес тела, осталось разобраться с ускорением. Ускорение – это физическая векторная величина, которая обозначает изменение скорости тела за единицу времени. Например, объект движется первую секунду со скоростью 4 м/с, а на второй секунде его скорость увеличивается до 8 м/с, значит, его ускорение равняется 2. По международной системе единиц ускорение рассчитывается в метрах на секунду в квадрате [м/с 2 ].
Если поместить тело в специальную среду, где будет отсутствовать сила сопротивления воздуха – вакуум, и убрать опору, то объект начнёт лететь равноускоренно. Название этого явления — ускорение свободного падения, которое обозначается g и рассчитывается в метрах на секунду в квадрате [м/с 2 ].
Интересно, что ускорение не зависит от массы тела, а значит если мы кинем листок бумажки и гирю на Земле в специальных условиях, при которых отсутствует воздух (вакуум), то эти предметы приземлятся в одно и то же время. Так как листок имеет большую площадь поверхности и относительно маленькую массу, то для того чтобы упасть, ему приходятся сталкиваться с большим сопротивлением воздуха. В вакууме такого не происходит, и поэтому перо, листок бумаги, гиря, пушечное ядро и другие предметы будут лететь с одной и той же скоростью и упадут в одно время (при условии, что они начнут лететь в одно и то же время, и их первоначальная скорость будет равняться нулю).
Так как Земля имеет форму геоида (или по-другому эллипсоида), а не идеального шара, то и ускорение свободного падения в разных участках Земли разное. Например, на экваторе оно равно 9,832 м/с 2 , а на полюсах 9,780 м/с 2 . Это происходит потому, что на некоторых участках Земли расстояние до ядра больше, а на некоторых меньше. Чем ближе объект находится к центру, тем сильнее он притягивается. Чем объект дальше, тем сила тяжести меньше. Обычно, в школе округляют это значение до 10, это делается для удобства расчётов. Если же необходимо измерить более точно (в инженерном или военном деле и так далее), то берут конкретные значения.
Таким образом, формула для расчёта веса телу будет выглядеть следующим образом P=m*g.
Примеры задач для расчёта веса тела
Первая задача. На стол положили груз массой 2 килограмма. Каков вес груза?
Для решения этой задачи нам понадобится формула по расчёту веса P=m*g. Мы знаем массу тела, а ускорение свободного падения примерно составляет 9,8 м/с 2 . Подставляем эти данные в формулу и получим P=2*9,8=19,6 Н. Ответ: 19,6 Н.
Вторая задача. На стол положили парафиновый шарик, объёмом 0,1 м 3 . Каков вес шарика?
Эту задачу необходимо решать в следующей последовательности;
- Для начала нам надо вспомнить формулу веса P=m*g. Ускорение нам известно – 9,8 м/с 2 . Осталось найти массу.
- Масса рассчитывается по формуле m=p*V, где p – это плотность, а V – объём. Плотность парафина можно посмотреть в таблице, объём нам известен.
- Необходимо подставить значения в формулу, для нахождения массы. m=900*0,1=90 кг.
- Теперь подставляем значения в первую формулу, для нахождения веса. P=90*9,9=882 Н.
Видео
В этом видео уроке разбирается тема – сила тяжести и вес тела.
Вес тела
О чем эта статья:
Невесомость: что это такое
Невесомость — это состояние, при котором тело не давит на опору или подвес.
Само слово «невесомость» как бы подсказывает нам, что веса здесь быть не должно. При этом непонятно, что с ним тогда происходит. Давайте разбираться.
Вес тела
Вес — это сила, с которой тело действует на опору или подвес. Измеряется вес, как и любая другая сила, в Ньютонах.
«Но погодите! Вес же измеряют в килограммах — я вот вешу 50»
Это не совсем верно. В быту мы часто подменяем понятие «масса» понятием «вес» и говорим: вес чемодана — десять килограммам. В физике это два совершенно разных понятия, которые при этом взаимосвязаны.
Если у вас неподалеку есть весы — приглашаем в эксперимент! Один нюанс: наша затея сработает именно с механическими весами, но не с электронными. Поехали!
Шаг 1. Если встать на весы ровно и не двигаться — ваш вес будет высчитываться по формуле:
P = mg
g — ускорение свободного падения [м/с 2 ]
На планете Земля g = 9,8 м/с 2
Здесь может возникнуть два возражения:
Это же сила тяжести, а не вес. Формула такая же!
На весах масса отображается в килограммах. И если я свою массу умножу на ускорение свободного падения, то явно получу число почти в 10 раз больше, чем показывают весы.
Точка приложения силы. Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Весы измеряют силу. Весы работают таким образом, что измеряют вес тела — силу, с которой мы на них действуем, а показывают — массу. Можно сделать вывод, что весы — это динамометр (прибор, измеряющий силу).
Шаг 2. Теперь пошалим и резко встанем на носочки! Стрелка резко отклонилась влево, а потом вернулась на место. Вы придали себе ускорение, направленное вверх — в то время, как ускорение свободного падения всегда направлено к центру Земли (вниз).
Теперь вес тела вычисляем по формуле:
P = m (g − a)
g — ускорение свободного падения [м/с 2 ]
a — ваше ускорение [м/с 2 ]
На планете Земля g = 9,8 м/с 2
Шаг 3. Последняя часть эксперимента — резко опуститься на пятки. Теперь вы сильнее давите на весы, потому что придали ускорение, направленное вниз. Стрелка весов отклонится вправо и вернется на место, когда вы придете в состояние покоя.
Формула веса примет вид:
P = m (g + a)
g — ускорение свободного падения [м/с 2 ]
a — ваше ускорение [м/с 2 ]
На планете Земля g = 9,8 м/с 2
Кстати, если ровно стоять на весах, но взвешиваться в лифте — все будет работать наоборот. Если лифт едет вверх, то он как будто давит весами на человека, стоящего на них, а это как раз ситуация с увеличением веса. А если вниз — весы как будто бы от вас «убегают», чтобы показать меньшее значение.
Этот случай мы можем описать через 2 закон Ньютона. Возьмем лифт, который едет вниз. Обозначим силы на рисунке.
N – сила реакции опоры [Н];
mg – сила тяжести [Н];
a – ускорение, с которым движется лифт [м/с 2 ].
При проецировании на ось y, направленную вниз, мы получаем:
А теперь нам понадобится третий закон Ньютона — по нему сила реакции опоры равна весу тела:
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Снова невесомость
Ну что, с весом разобрались. А теперь давайте сделаем так, чтобы его не стало и получилась та самая невесомость.
Чтобы привыкнуть к ощущению невесомости в космосе, космонавты тренируется в специальных самолетах-лабораториях:
Он взлетает и начинает просто падать, чтобы ускорение самолета было равно ускорению свободного падения. В этот момент, в формуле веса из g вычитается равное ему значение и получается 0:
P = m (g − a) = m (9,8 − 9,8) = 0
Вот мы и в невесомости!
Если они летят вокруг Земли, то да. Как писал Дуглас Адамс в книге «Автоспом по галактике»: «Летать просто. Нужно просто промахнуться мимо Земли».
Когда космический корабль обращается вокруг Земли, он просто пытается на нее упасть, но промахивается. Такой процесс происходит, когда корабль движется с первой космической скоростью, равной 7.9 км/с. Это та скорость, с которой корабль становится искусственным спутником Земли.
Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это минимальная скорость, с которой должно двигаться тело, чтобы оно могло без затрат дополнительной работы преодолеть влияние поля тяготения Земли, т. е. удалиться на бесконечно большое расстояние от Земли. А тело, которое двигается с третьей космической скоростью, и вовсе вылетит за пределы Солнечной системы. Такие дела. 🙂
Вес тела
теория по физике 🧲 динамика
Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.
Вес тела имеет электромагнитную природу (не путать с силой тяжести — она возникает между двумя телами и имеет гравитационную природу!). Обозначается P . Измеряется динамометром. Единица измерения — Н (Ньютон).
Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P ↑↓ N или P ↑↓ T .
Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:
Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:
Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.
Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.
Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:
P = mg = 16,38∙10 = 163,8 (Н)
Перегрузка
Перегрузка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности.
Перегрузка определяется отношением:
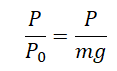
Перегрузка возникает, когда система, в которой находится тело, движется с ускорением.
Вес тела в движущейся равноускоренно системе
Вес тела в движущейся системе может быть больше или меньше веса того же тела в системе, которая находится в состоянии покоя:
- Если система движется равноускоренно в направлении ускорения свободного падения, вес тела меньше веса тела в неподвижной системе: при a ↑↑ g —P a ↑↓ g —P > P0.
- Если система движется с равномерной скоростью (ускорение равно нулю) в любом направлении по отношению к ускорению свободного падения, вес тела равен весу тела в неподвижной системе: при a = 0 —P = P0.
Применение законов Ньютона для определения веса тела
Опора или подвес неподвижны
Второй закон Ньютона в векторной форме:
N + m g = m a или T + m g = m a
Проекция на ось ОУ:
N – mg = 0 или T — mg = 0
Ускорение опоры направлено вверх
Второй закон Ньютона в векторной форме:
Проекция на ось ОУ:
P = N = ma + mg = m(a + g)
Ускорение опоры направлено вниз
Второй закон Ньютона в векторной форме:
Проекция на ось ОУ:
P = N = mg – ma = m(g – a)
Вершина выпуклого моста
Второй закон Ньютона в векторной форме:
Проекция на ось ОУ:
Нижняя точка вогнутого моста
Второй закон Ньютона в векторной форме:
Проекция на ось ОУ:
Полный оборот на подвесе
Второй закон Ньютона в векторной форме:
Проекция на ось ОУ в точке А:
Вес тела в точке А:
Проекция на ось ОУ в точке В:
Вес тела в точке В:
Важно! Центростремительное ускорение всегда направлено к центру окружности.
Пример №2. Автомобиль массой 1000 кг едет по выпуклому мосту с радиусом кривизны 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали невесомость?
Вес тела в верхней точке выпуклого моста равен:
Чтобы пассажиры почувствовали состояние невесомости, вес тела должен быть равен 0:
Масса не может быть нулевой, поэтому:
Значит, пассажиры в верхней точке моста почувствуют невесомость, если центростремительное ускорение будет равно ускорению свободного падения. Центростремительное ускорение определяется формулой:
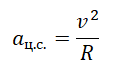
Отсюда скорость автомобиля в верхней точке моста должна быть равна:
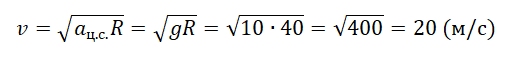
Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…
[spoiler title=”источники:”]
http://skysmart.ru/articles/physics/ves-tela
[/spoiler]
На предыдущих уроках мы узнали определение понятия силы, познакомились с силой тяжести и силой упругости.
Возможно, вы заметили, что рассматривая примеры и сравнивая тела с разными массами, мы избегали выражения “одно тело весит больше другого”. В повседневном жизни же мы часто используем подобные фразы, как и само слово “вес”.
На данном уроке мы узнаем о понятии веса со стороны физики.
Что такое вес?
Вспомним опыт, когда мы ставим тело (гирю) на опору (рисунок 1).
Мы уже говорили, что на гирю действует сила тяжести. Из-за этого начинает прогибаться доска — происходит ее деформация.
Возникает сила упругости, направленная вертикально вверх. Доска перестает прогибаться, когда сила тяжести и сила упругости уравновешивают друг друга.
Обратите внимание, что гиря и доска взаимодействуют друг с другом, но:
- Cила тяжести — это результат взаимодействия гири с Землей, а не с доской
- по всем изученным нами принципам должна быть еще одна сила, которая возникает со стороны гири
Подобная ситуация происходит в случае, если мы будем рассматривать тело, подвешенное на нити. Возникает некая сила, действующая на подвес.
Эта сила и называется весом тела.
Что называют весом тела?
Вес тела — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Характеристики веса
- Вес тела — это векторная физическая величина и обозначается буквой $vec{P}$
- Модуль веса тела обозначается буквой $P$
- Вес тела численно равен силе тяжести, если тело и опора/подвес неподвижны или движутся прямолинейно и равномерно.
$P=F_{тяж}$
- Вес тела приложен к опоре или подвесу и направлен перпендикулярно опоре или вдоль подвеса (рисунки 2, 3).
Сравните с изображением силы тяжести (рисунок 4). Следует помнить, что сила тяжести приложена к самому телу.
Вес как частный случай силы упругости
Когда мы ставим тело на опору — оно деформирует ее. Когда мы подвешиваем тело — оно деформирует подвес. Не всегда эта деформация видна как в наших предыдущих опытах.
Когда вы кладёте учебник на парту, что происходит? Учебник (тело) деформирует парту (опору). Но такая деформация не видна невооруженным глазом. Тем не менее, она существует. Если бы деформация не происходила, то не возникала бы сила упругости. Тогда ничего бы не препятствовало движению вашего учебника к самому центру Земли.
Так, парта в свою очередь деформирует учебник, что тоже незаметно.
Давайте рассмотрим опыт, где деформация тела будет заметна. Взгляните на рисунок 5.
У нас есть штатив и резиновый шнур длиной $l_0$ (рисунок 5, а). На шнур мы подвешиваем небольшой мешок с песком (рисунок 5, б).
Шнур растягивается и останавливается, когда сила тяжести становится равна возникшей в шнуре силе упругости. Длина шнура изменилась и стала равна $l$.
У нас провзаимодействовали два тела: шнур и мешок. Оба тела деформировались.
Теперь мы отрежем прикрепленный шнур (рисунок 5, в). Во время падения на мешок с песком действует только сила тяжести, он восстанавливает свою форму. Шнурок также восстанавливает свою форму.
Когда же мешок падает на рабочую поверхность (рисунок 5, г), то он снова деформируется. Теперь взаимодействует опора и тело.
В данном случае не видно, как деформируется опора, но, если бы мы подставили доску на брусьях, она бы прогнулась. Так мы наглядно показали, что при взаимодействии происходит деформация обоих тел.
Под действием опоры или подвеса происходит деформация тела. Опора сжимает нижнюю часть тела, а подвес растягивает его верхнюю часть.
Именно эта деформация тела вызывает появление в теле силы упругости. В данном случае сила упругости и будет весом тела.
Чем отличается вес тела от силы тяжести?
Вы уже знаете, что вес тела будет равен силе тяжести, если тело и опора/подвес неподвижны или движутся прямолинейно и равномерно. Также сила тяжести приложена к центру тела, а вес — к опоре или подвесу.
Но важнее помнить, из-за чего возникают эти две силы. Сила тяжести возникает из-за взаимодействия физического тела и Земли. А вес возникает в результате взаимодействия тела и опоры (подвеса). А это взаимодействие возникает тоже из-за взаимодействия тела и Земли. При этом тела деформируются, что приводит к возникновению силы упругости.
Определение Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.
Вес тела имеет электромагнитную природу (не путать с силой тяжести — она возникает между двумя телами и имеет гравитационную природу!). Обозначается P. Измеряется динамометром. Единица измерения — Н (Ньютон).
Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P↑↓N или P↑↓T.
Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:
P = T; P = N; P = Fупр.
Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:
P0 = Fтяж = mg
Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.
Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.
Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:
P = mg = 16,38∙10 = 163,8 (Н)
История понятия
Понятия тяжести и лёгкости в качестве неотъемлемых свойств физических тел упоминаются ещё древнегреческими философами. Платон описывал вес как естественную тенденцию предметов к поиску себе подобных. Для Аристотеля лёгкость была свойством в восстановлении порядка основных элементов: воздуха, земли, огня и воды. Архимед рассматривал вес как качество, противоположное плавучести. Первое контактное определение было дано Евклидом, описывающее величину как лёгкость одной вещи по сравнению с другой, измеряемую балансом.
Когда средневековые учёные обнаружили, что на практике скорость падающего предмета со временем возрастала. Они изменили концепцию веса для сохранения причинно-следственных связей между явлениями. Понятие было разделено для тел в состоянии покоя и находящихся в гравитационном падении.
Значительных результатов в теории добился Галилей, пришедший к выводу, что величина пропорциональна количеству вещества в объекте, а не скорости его движения, как предполагала Аристотелева физика. Открытие Ньютоном закона всемирного тяготения привело к принципиальному отделению веса от фундаментального свойства объектов, связанных с инерцией. Факторы окружающей среды и плавучесть учёный считал искажением условий измерения. Для подобных обстоятельств он ввёл термин кажущийся вес.
В XX веке ньютоновские концепции абсолютного времени и пространства были поставлены под сомнение работами Эйнштейна. Теория относительности поставила всех наблюдателей, движущихся и ускоряющихся, в разные условия. Это привело к двусмысленности относительно того, что именно подразумевается под массой, которая вместе с гравитационной силой стала по существу зависящей от системы отсчёта величиной.
Неоднозначности, порождённые относительностью, привели к серьёзным дебатам в педагогическом сообществе о том, как определять вес для учеников и что им должно называться. Выбор стал лежать между пониманием его как силы, вызванной гравитацией Земли, и контактным определением, вытекающим из акта взвешивания.
Единицы измерения веса в других системах единиц
Иногда в физике применяют систему единиц, называемую СГС (сантиметр, грамм, секунда). В этой системе единица длины – сантиметр (см), единица массы – грамм (г), единица времени секунда (с). В системе СГС единицу веса, как и любой силы, называют дина (обозначение: дин). 1 дин – это сила, которая сообщает телу массой 1 г ускорение, равное 1$frac<�см><�с^2>$. Дина в сравнении с ньютоном очень маленькая единица силы. Ньютон и дина соотносятся как:
При технических расчетах можно встретить еще одну единицу измерения веса, которую называют килограмм – сила (кгс). 1 кгс – это сила, с которой Земля действует на эталонную массу в один килограмм, притягивая ее.
[1Нapprox 0,10197162 кгс.]
В России килограмм-силу используют как внесистемную единицу измерения силы.
Получаем, дин, кгс – единицы измерения веса.
Различия с массой
Путаница в понимании того, чем отличается масса от веса, свойственна для людей, не изучающих физику подробно. Этому есть простое объяснение — как правило, эти термины используются в повседневной жизни взаимозаменяемо. В общем случае, если тело находится на поверхности земли и неподвижно, значение массы будет равно скаляру веса в килограммах. Таблица, проясняющая разницу между понятиями, выглядит так:
| Масса | Вес |
| Является свойством материи. Постоянна всегда. | Зависит от действия силы тяжести. |
| У материального объекта никогда не бывает равна нулю. | Может быть равен нулю при определённых условиях. |
| Не меняется в зависимости от местоположения. | Уменьшается или увеличивается в разных местах Земли или в зависимости от высоты над её поверхностью. |
| Является скалярной величиной. | Вектор с направлением к центру земли или к другому гравитационному центру. |
| Может быть измерена с помощью баланса | Измеряется с помощью пружинных весов. |
| Как правило, измеряется в граммах и килограммах. | Единица у силы и веса одна — Ньютон (обозначается как Н) |
Главное отличительное свойство массы заключается в том, что для классической динамики она является конкретной инвариантной величиной для каждого тела. Общая теория относительности описывает переход массы в энергию и наоборот.
Обычно численное значение между m и P на Земле строго пропорционально. На бытовом уровне чтобы узнать вес тела с известной массой, достаточно помнить, что объекты обычно весят в ньютонах приблизительно в 10 раз больше значения m в килограммах.
Вес в физике
Масса – это мера инертности тела. Чем тело обладает большей инертностью, тем больше времени понадобится, чтобы придать ему скорость. Грубо говоря, чем выше значение массы, тем тяжелее сдвинуть предмет. В международной системе единиц массу измеряют в килограммах. Но её также измеряют и в других единицах, например;
- унция;
- фунт;
- стоун;
- американская тонна;
- английская тонна;
- грамм;
- миллиграмм и так далее.
Когда мы говорим один, два, три килограмма, мы сравниваем массу с эталонной массой (прообраз которой находится во Франции в МБМВ). Масса обозначается m.
Способы измерения
Фактически вес можно измерить как силу реакции опоры на массу, появляющуюся в точке приложения. Величина возникновения этой силы по значению равна искомому P. Определить её можно с помощью пружинных весов. Поскольку сила тяжести, вызывающая фиксируемое отклонение на шкале, может варьироваться в разных местах, значения также будут отличаться. Для стандартизации измерительные приборы такого типа всегда калибруются на 9,80665 м/с2 в заводских условиях, а затем повторно в том месте, где будут использоваться.
Для измерения массы применяют рычажный механизм. Поскольку любые изменения в гравитации будут одинаково воздействовать на известные и неизвестные массы, балансный способ позволяет иметь в результате одинаковые значения в любом месте Земли. Весовые коэффициенты в этом случае калибруются и маркируются в единицах массы, поэтому балансировочный рычаг позволяет найти массу, сравнивая воздействие притяжения на искомый объект с воздействием на эталон.
При отсутствии гравитационного поля вдали от крупных астрономических тел, баланс рычага работать не будет, но, например, на Луне он покажет те же значения, что и на Земле. Некоторые подобные инструменты могут быть размечены в единицах веса, но, поскольку они калибруются на заводе-изготовителе для стандартной гравитации, то будут показывать P для условий, под которые они настроены.
Это значит, что рычажные весы не предназначены для измерения локальной силы тяжести, воздействующей на объект. Точный вес можно определить расчётным путём, умножив массу на значение локальной гравитации из соответствующих таблиц.
Ньютон – единица измерения веса в Международной системе единиц
В настоящее время в физике в большем масштабе, чем остальные, используют Международную систему единиц (СИ) в которой ньютон – единица измерения веса, как разновидности силы. Один ньютон (1Н) – это сила, сообщающая телу, имеющему массу в 1 килограмм, ускорение равное 1 метру, деленному на секунду в квадрате в направлении действия силы:
Ньютон не является основной единицей в СИ. С такой единицей как ньютон используют кратные и дольные единицы силы, применяя стандартные приставки системы СИ, например: $1кН=<10>^3Н;; 1нН=<10>^<-9>Н;; 1МН=<10>^6Н.$
И так, ньютон и $frac<�кгcdot м><�с^2>.$ – единицы измерения веса, как силы в системе СИ.
На других планетах
В отличие от массы, вес тела в разных местах варьируется в зависимости от изменения значения гравитационного ускорения. Величина силы притяжения на других планетах, как и на Земле, зависит не только от их массы, но и от того, насколько удалена поверхность от центра тяжести.
В таблице ниже приведены сравнительные гравитационные ускорения на других планетах, Солнце и Луне. Под поверхностью для газовых гигантов (Юпитер, Сатурн, Уран и Нептун) подразумеваются их внешние облачные слои, для Солнца — фотосфера. Значения в таблице указаны без учёта центробежного вращения и отражают фактическую гравитацию, наблюдаемую вблизи полюсов.
| Астрономический объект | Насколько гравитация превышает земную | Поверхностное ускорение м/с2 |
| Солнце | 27,9 | 274,1 |
| Меркурий | 0,377 | 3,703 |
| Венера | 0,9032 | 8,872 |
| Земной шар | 1 | 9,8226 |
| Луна | 0,1655 | 1,625 |
| Марс | 0,3895 | 3,728 |
| Юпитер | 2,64 | 25,93 |
| Сатурн | 1,139 | 11,19 |
| Уран | 0,917 | 9,01 |
| Нептун | 1,148 | 11,28 |
Для того чтобы получить собственный вес на другой планете, необходимо просто умножить его на число кратности из соответствующего столбика. Чем ближе к центру планеты делать замер, тем значение будет выше, и наоборот. Поэтому, несмотря на то что сила притяжения Юпитера из-за огромной массы в 316 раз превышает земную, вес на уровне облаков, из-за большой их удалённости от центра масс, выглядит не таким впечатляющим, как можно было бы ожидать.
Ещё один интересный эффект, называемый невесомостью, характерный не только для космоса. Его можно наблюдать при различных обстоятельствах и на Земле. Например, при свободном падении нет опоры, к которой была бы приложена сила, а значит вес будет равен нулю, несмотря на присутствие ускорения силы тяжести и массы.
Подобный феномен происходит с космонавтами Международной космической станции на орбите Земли. Фактически она всегда падает вместе со своими обитателями на поверхность планеты, поэтому её обитатели постоянно находятся в состоянии невесомости.
Таким образом, главное правило, объясняющее наблюдаемые феномены и позволяющее избежать путаницы с массой, выглядит так: значение P всегда измеряется с помощью контактных весов, помещённых между объектом и опорной поверхностью. Именно поэтому тело, размещённое на весах и падающее вместе с ними, не будет давить на прибор, а шкала, соответственно, покажет нулевое значение.
Примеры задач для расчёта веса тела
Первая задача. На стол положили груз массой 2 килограмма. Каков вес груза?
Для решения этой задачи нам понадобится формула по расчёту веса P=m*g. Мы знаем массу тела, а ускорение свободного падения примерно составляет 9,8 м/с 2 . Подставляем эти данные в формулу и получим P=2*9,8=19,6 Н. Ответ: 19,6 Н.
Вторая задача. На стол положили парафиновый шарик, объёмом 0,1 м 3 . Каков вес шарика?
Эту задачу необходимо решать в следующей последовательности;
- Для начала нам надо вспомнить формулу веса P=m*g. Ускорение нам известно – 9,8 м/с 2 . Осталось найти массу.
- Масса рассчитывается по формуле m=p*V, где p – это плотность, а V – объём. Плотность парафина можно посмотреть в таблице, объём нам известен.
- Необходимо подставить значения в формулу, для нахождения массы. m=900*0,1=90 кг.
- Теперь подставляем значения в первую формулу, для нахождения веса. P=90*9,9=882 Н.
Явление гравитации
Чтобы понять, что в физике означает g (в 7 классе общеобразовательных школ проходят эту тему), следует познакомиться с явлением гравитации. В конце XVII века Исаак Ньютон опубликовал свой знаменитый научный труд, в котором сформулировал основные положения механики. В этом труде особое место он выделил для так называемого закона Всемирного тяготения. Согласно нему все тела, которые обладают конечной массой, притягиваются друг к другу независимо от расстояния между ними. Сила притяжения между телами с массами m1, m2 вычисляется по следующей формуле:
F = G*m1*m2/r2.
Здесь G — универсальная гравитационная константа, r — расстояние между центрами масс тел в пространстве. Сила F называется гравитационным взаимодействием, которое, как и кулоновское, убывает с квадратом расстояния, однако в отличие от кулоновского гравитация носит только притягивающий характер.
Наше время
Сейчас люди практически не видят разницу массы и веса. Типичным примером этого является любая покупка в магазине, когда покупатель спрашивает у продавца информацию о весе продукта. С точки зрения науки, правильно было бы поинтересоваться его массой. Тем не менее на упаковках производитель указывает все как нужно.
Мы можем увидеть там такие надписи, как «масса нетто» (то есть масса чистого продукта) и «масса брутто» (масса продукта вместе с упаковкой). В результате этого масса и вес стали практически синонимами в потребительской сфере, и большинство людей искренне удивляются, когда кто-то пытается им доказать, что есть разница в массе и весе.
В настоящее время нет особых требований в том, чтобы каждый человек умел различать данные понятия. Скорее, это больше необходимо тем, кто занимается научной деятельностью.
Источник
Рассчитать вес по росту
Простой способ известный больше как формула Брокка. Упрощенная версия выглядит так:
- Для женщин: Идеальный вес = Рост (см) — 110
- Для мужчин: Идеальный вес = Рост (см) — 100
Пример: нормальный вес мужчины с ростом 180 см равен 80 кг, а женщины с ростом 170 см – 60 кг
Современный вариант этой же формулы выглядит немного иначе, но считается более точным:
- Для женщин: Идеальный вес = (Рост (см) — 110)*1,15
- Для мужчин: Идеальный вес = (Рост (см) — 100)*1,15
Пример: нормальный вес мужчины с ростом 180 см равен 92 кг, а женщины с ростом 170 см – 69 кг
Положим камень на горизонтальную крышку стола, стоящего на Земле (рис. 104). Поскольку ускорение камня относительно Земли равно пулю, то по второму закону Ньютона сумма действующих на него сил равна нулю. Следовательно, действие на камень силы тяжести m · g должно компенсироваться какими-то другими силами. Ясно, что под действием камня крышка стола деформируется. Поэтому со стороны стола на камень действует сила упругости. Если считать, что камень взаимодействует лишь с Землей и крышкой стола, то сила упругости должна уравновешивать силу тяжести: Fупр = -m · g. Эту силу упругости называют силой реакции опоры и обозначают латинской буквой N. Так как ускорение свободного падения направлено вертикально вниз, сила N направлена вертикально вверх – перпендикулярно поверхности крышки стола.
Поскольку крышка стола действует на камень, то по третьему закону Ньютона и камень действует на крышку стола силой P = -N (рис. 105). Эту силу называют весом.
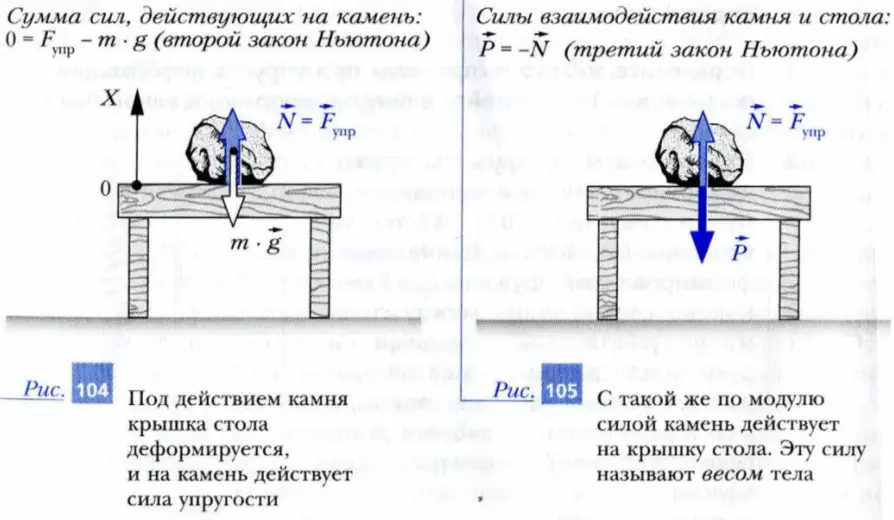
Весом тела называют силу, с которой это тело действует на подвес или опору, находясь относительно подвеса или опоры в неподвижном состоянии.
Ясно, что в рассмотренном случае вес камня равен силе тяжести: P = m · g. Это будет верно для любого тела, покоящегося на подвесе (опоре) относительно Земли (рис. 106). Очевидно, что в этом случае точка крепления подвеса (или опора) неподвижна относительно Земли.
Для тела, покоящегося на неподвижном относительно Земли подвесе (опоре), вес тела равен силе тяжести.
Вес тела также будет равен действующей на тело силе тяжести в случае, если тело и подвес (опора) движутся относительно Земли равномерно прямолинейно.
Если же тело и подвес (опора) движутся относительно Земли с ускорением так, что тело остается неподвижным относительно подвеса (опоры), то вес тела не будет равен силе тяжести.
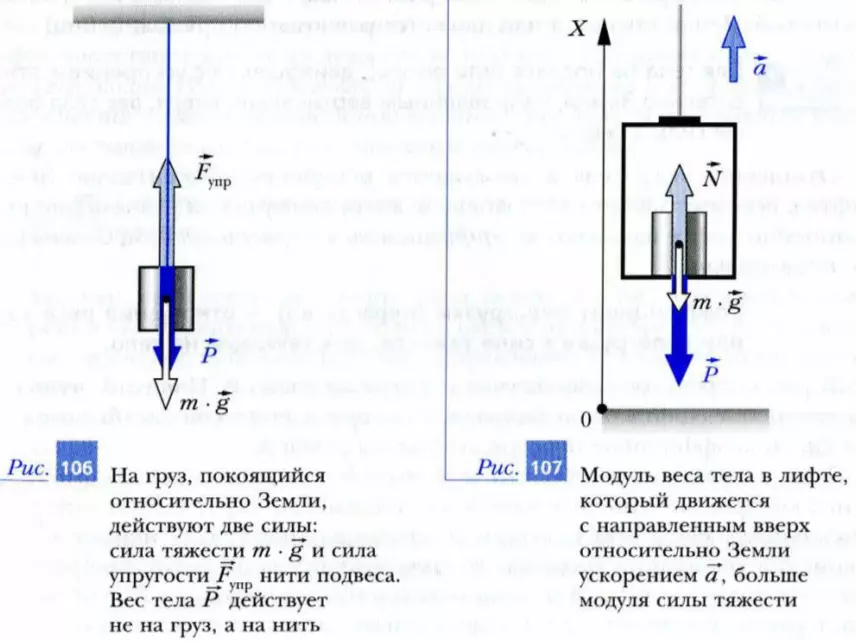
Рассмотрим пример. Пусть тело массой m лежит на полу лифта, ускорение a которого направлено вертикально вверх (рис. 107). Будем считать, что на тело действуют только сила тяжести m · g и сила реакции пола N. (Вес тела действует не на тело, а на опору – пол лифта.) В системе отсчета, неподвижной относительно Земли, тело на полу лифта движется вместе с лифтом с ускорением a. В соответствии со вторым законом Ньютона произведение массы тела на ускорение равно сумме всех действующих на тело сил. Поэтому: m · a = N – m · g.
Следовательно, N = m · a + m · g = m · (g + a). Значит, если лифт имеет ускорение, направленное вертикально вверх, то модуль силы N реакции пола будет больше модуля силы тяжести. В самом деле, сила реакции пола должна не только скомпенсировать действие силы тяжести, но и придать телу ускорение в положительном направлении оси X.
Сила N – это сила, с которой пол лифта действует на тело. По третьему закону Ньютона тело действует на пол с силой P, модуль которой равен модулю N, но направлена сила P в противоположную сторону. Эта сила является весом тела в движущемся лифте. Модуль этой силы P = N = m · (g + a). Таким образом, в лифте, движущемся с направленным вверх относительно Земли ускорением, модуль веса тела больше модуля силы тяжести.
Такое явление называют перегрузкой.
Например, пусть ускорение а лифта направлено вертикально вверх и его значение равно g, т. е. a = g. В этом случае модуль веса тела – силы, действующей на пол лифта, – будет равен P = m · (g + a) = m · (g + g) = 2m · g. То есть вес тела при этом будет в два раза больше, чем в лифте, который относительно Земли покоится или движется равномерно прямолинейно.
Для тела на подвесе (или опоре), движущемся с ускорением относительно Земли, направленным вертикально вверх, вес тела больше силы тяжести.
Отношение веса тела в движущемся ускоренно относительно Земли лифте к весу этого же тела в покоящемся или движущемся равномерно прямолинейно лифте называют коэффициентом перегрузки или, более кратко, перегрузкой.
Коэффициент перегрузки (перегрузка) – отношение веса тела при перегрузке к силе тяжести, действующей на тело.
В рассмотренном выше случае перегрузка равна 2. Понятно, что если бы ускорение лифта было направлено вверх и его значение было равно a = 2g, то коэффициент перегрузки был бы равен 3.
Теперь представим себе, что тело массой m лежит на полу лифта, ускорение которого a относительно Земли направлено вертикально вниз (противоположно оси X). Если модуль a ускорения лифта будет меньше модуля ускорения свободного падения, то сила реакции пола лифта по-прежнему будет направлена вверх, в положительном направлении оси X, а ее модуль будет равен N = m · (g – a). Следовательно, модуль веса тела будет равен P = N = m · (g – a), т. е. будет меньше модуля силы тяжести. Таким образом, тело будет давить на пол лифта с силой, модуль которой меньше модуля силы тяжести.
Это ощущение знакомо каждому, кто ездил на скоростном лифте или качался на больших качелях. При движении вниз из верхней точки вы чувствуете, что ваше давление на опору уменьшается. Если же ускорение опоры положительно (лифт и качели начинают подниматься), вас сильнее прижимает к опоре.
Если ускорение лифта относительно Земли будет направлено вниз и равно по модулю ускорению свободного падения (лифт свободно падает), то сила реакции пола станет равной нулю: N = m · (g – a) = m · (g – g) = 0. В этом случае пол лифта перестанет давить на лежащее на нем тело. Следовательно, согласно третьему закону Ньютона и тело не будет давить на пол лифта, совершая вместе с лифтом свободное падение. Вес тела станет равным нулю. Такое состояние называют состоянием невесомости.
Состояние, при котором вес тела равен нулю, называют невесомостью.
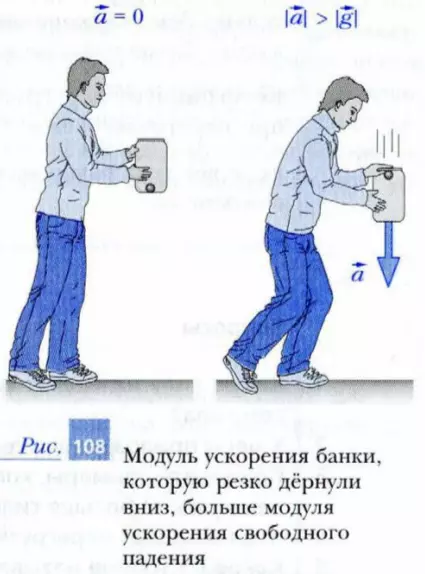
Наконец, если ускорение лифта, направленное к Земле, станет больше ускорения свободного падения, тело окажется прижатым к потолку лифта. В этом случае вес тела изменит свое направление. Состояние невесомости исчезнет. В этом можно легко убедиться, если резко дернуть вниз банку с находящимся в ней предметом, закрыв верх банки ладонью, как показано на рис. 108.
Итоги
Весом тела называют силу, с которой это тело действует на поднес или опору, находясь относительно подвеса или опоры в неподвижном состоянии.
Вес тела в лифте, движущемся с направленным вверх относительно Земли ускорением, по модулю больше модуля силы тяжести. Такое явление называют перегрузкой.
Коэффициент перегрузки (перегрузка) – отношение веса тела, при перегрузке к силе тяжести, действующей на это тело.
Если вес тела равен нулю, то такое состояние называют невесомостью.
Вопросы
- Какую силу называют силой реакции опоры? Что называют весом тела?
- К чему приложен вес тела?
- Приведите примеры, когда вес тела: а) равен силе тяжести; б) равен нулю; в) больше силы тяжести; г) меньше силы тяжести.
- Что называют перегрузкой?
- Какое состояние называют невесомостью?
Упражнения
- Семиклассник Сергей стоит на напольных весах в комнате. Стрелка прибора установилась напротив деления 50 кг. Определите модуль веса Сергея. Ответьте на остальные три вопроса об этой силе.
- Найдите перегрузку, испытываемую космонавтом, который находится в ракете, поднимающейся вертикально вверх с ускорением a = Зg.
- С какой силой действует космонавт массой m = 100 кг на ракету, указанную в упражнении 2? Как называется эта сила?
- Найдите вес космонавта массой m = 100 кг в ракете, которая: а) стоит неподвижно на пусковой установке; б) поднимается с ускорением a = 4g, направленным вертикально вверх.
- Определите модули сил, действующих на гирю массой m = 2 кг, которая висит неподвижно На легкой нити, прикрепленной к потолку комнаты. Чему равны модули силы упругости, действующей со стороны нити: а) на гирю; б) на потолок? Чему равен вес гири? Указание: для ответа на поставленные вопросы воспользуйтесь законами Ньютона.
- Найдите вес груза массой m = 5 кг, подвешенного на нити к потолку скоростного лифта, если: а) лифт равномерно поднимается; б) лифт равномерно опускается; в) поднимающийся вверх со скоростью v = 2 м/с лифт начал торможение с ускорением a = 2 м/с2; г) опускающийся вниз со скоростью v = 2 м/с лифт начал торможение с ускорением a = 2 м/с2; д) лифт начал движение вверх с ускорением a = 2 м/с2; е) лифт начал движение вниз с ускорением a = 2 м/с2.
