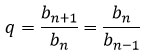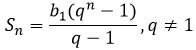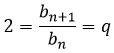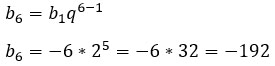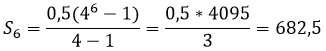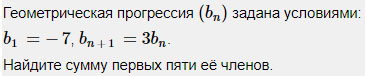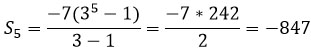Как найти модуль знаменателя геометрической прогрессии - Сайт, где вы сможете решить свои вопросы

Формула знаменателя геометрической прогрессии

ОПРЕДЕЛЕНИЕ

Геометрическая прогрессия представляет собой последовательность чисел, каждая из которых, начиная со второй, получается из предыдущей, умножая на то же число q, которое называется знаменателем прогрессии.

Пусть (
B=left{b_{1}, b_{2}, ldots, b_{n}, ldotsright}
) – геометрическая прогрессия, (
b_{n}
) – n-й член прогрессии, тогда знаменатель этой прогрессии может быть рассчитан по формуле:

(
q=frac{b_{n+1}}{b_{n}}
)

Если разность геометрической прогрессии (
mathrm{q}>1
), то прогрессия будет возрастать, если (
|q|<1
), то прогрессия уменьшается.

Примеры решения проблем

ПРИМЕР 1

Задача

Найти знаменатель геометрической прогрессии (
left(b_{n}right)
) , если (
b_{5}=-6, b_{7}=-54
)

Решение

Express (
b_{7}-b_{5}
) с использованием знаменателя прогрессии q:

(
b_{7}=b_{6} cdot q=left(b_{5} cdot qright) cdot q=b_{5} cdot q^{2}
)

отсюда

(
q^{2}=frac{b_{7}}{b_{5}}=frac{-54}{-6}=9 Rightarrow q=pm 3
)

Ответ (
q=pm 3
)

ПРИМЕР 2

Задача

состоит в том, чтобы найти знаменатель прогрессии. Геометрическая прогрессия определяется следующими соотношениями:

(
left{begin{array}{l}{b_{1}+b_{3}=50} \ {b_{2}+b_{4}=150}end{array}right.
)

Решение.

Выразите все члены прогрессии через первый член (
b_{2}=b_{1} q, b_{3}=b_{1} q^{2}, b_{4}=b_{1} q^{3}
) и знаменатель q:

(
left{begin{array}{l}{b_{1}+b_{1} q^{2}=50} \ {b_{1} q+b_{1} q^{3}=150}end{array}right.
)

Замените полученные выражения в данной системе:

(
frac{b_{1}+b_{1} q^{2}}{b_{1} q+b_{1} q^{3}}=frac{50}{150} Rightarrow frac{b_{1}+b_{1} q^{2}}{qleft(b_{1}+b_{1} q^{2}right)}=frac{1}{3} Rightarrow q=3
)

Мы делим первое уравнение на второе и выражаем знаменатель q:

(
frac{b_{1}+b_{1} q^{2}}{b_{1} q+b_{1} q^{3}}=frac{50}{150} Rightarrow frac{b_{1}+b_{1} q^{2}}{qleft(b_{1}+b_{1} q^{2}right)}=frac{1}{3} Rightarrow q=3
)

Ответ (
q=3
)

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 декабря 2022 года; проверки требуют 37 правок.

У этого термина существуют и другие значения, см. Прогрессия.

Геометри́ческая прогре́ссия — последовательность чисел $b_{1}$ , $b_{2}$ , $b_{3}$ , ldots (члены прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего члена умножением его на фиксированное число (знаменатель прогрессии). При этом ${displaystyle b_{1}neq 0,qneq 0;b_{n}=b_{n-1}q,nin mathbb {N} ,ngeqslant 2}$ ^[1].

Геометрическая прогрессия называется бесконечно убывающей^[2], если знаменатель прогрессии по абсолютной величине меньше единицы.

Произведением первых членов геометрической прогрессии ${displaystyle left{b_{n}right}}$ называется произведение от $b_{1}$ до b_n , то есть выражение вида ${displaystyle prod limits _{i=1}^{n}b_{i}=b_{1}cdot b_{2}cdot b_{3}cdot ldots cdot b_{n-2}cdot b_{n-1}cdot b_{n}.}$
Обозначение: $P_{n}$ .

Описание[править | править код]

Любой член геометрической прогрессии может быть вычислен по формуле

${displaystyle b_{n}=b_{1}q^{n-1}.}$

Если ${displaystyle b_{1}>0}$ и , прогрессия является возрастающей последовательностью, если , — убывающей последовательностью, а при q<0 — знакочередующейся^[3], при q=1 — стационарной (постоянной).

Своё название прогрессия получила по своему характеристическому свойству:

${displaystyle |b_{n}|={sqrt {b_{n-1}b_{n+1}}},}$

то есть модуль любого члена геометрической прогрессии, кроме первого, равен среднему геометрическому (среднему пропорциональному) двух рядом с ним стоящих членов^[4].

Примеры[править | править код]

Получение новых квадратов путём соединения середин сторон предыдущих квадратов

Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата^[5]^:8—9.
Геометрической является последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — геометрическая прогрессия со знаменателем 2 из тринадцати членов.
50; 25; 12,5; 6,25; 3,125; … — бесконечно убывающая геометрическая прогрессия со знаменателем 1/2.
4; 6; 9 — геометрическая прогрессия из трёх элементов со знаменателем 3/2.
, , , — стационарная геометрическая прогрессия со знаменателем 1 (и стационарная арифметическая прогрессия с разностью 0).
3; −6; 12; −24; 48; … — знакочередующаяся геометрическая прогрессия со знаменателем −2.
1; −1; 1; −1; 1; … — знакочередующаяся геометрическая прогрессия со знаменателем −1.

Свойства[править | править код]

Свойства знаменателя геометрической прогрессии[править | править код]

Знаменатель геометрической прогрессии можно найти по формулам:

${displaystyle q={dfrac {b_{n+1}}{b_{n}}}}$

Доказательство

По определению геометрической прогрессии.

${displaystyle q={sqrt[{n-k}]{dfrac {b_{n}}{b_{k}}}},{text{где }}k<n;;forall n,forall kin mathbb {N} .}$

Свойства членов геометрической прогрессии[править | править код]

Рекуррентное соотношение для геометрической прогрессии:

${displaystyle b_{n}=b_{n-1}cdot q}$

Доказательство

По определению геометрической прогрессии.

Формула общего (-го) члена:

${displaystyle b_{n}=b_{1}cdot q^{n-1}.}$

Обобщённая формула общего члена:

${displaystyle b_{n}=b_{k}cdot q^{n-k},{text{где }}k<n;;forall n,forall kin mathbb {N} .}$

Доказательство

${displaystyle b_{n}^{2}=b_{n}b_{n}=b_{1}q^{n-1}b_{1}q^{n-1}=b_{1}q^{n-1-i}b_{1}q^{n-1+i}=b_{n-i}b_{n+i}.}$

Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.

Доказательство

${displaystyle log(b_{n})=log(b_{1}q^{n-1})=log(b_{1})+(n-1)cdot log(q)}$
Формула общего члена арифметической прогрессии:
${displaystyle a_{n}=a_{1}+(n-1)cdot d}$ .
В нашем случае
$a_{1}=log(b_{1})$ ,
.

Доказательство

${displaystyle b_{n}^{2}=b_{n}b_{n}=b_{1}q^{n-1}b_{1}q^{n-1}=b_{1}q^{n-1-i}b_{1}q^{n-1+i}=b_{n-i}b_{n+i}.}$

Пусть ${displaystyle a_{k},a_{l},a_{m}}$ — соответственно -й, -й, -й члены геометрической прогрессии, где . Тогда для всякой такой тройки выполняется комплементарное свойство геометрической прогрессии, называемое тождеством геометрической прогрессии:

${displaystyle b_{k}^{l-m}cdot b_{l}^{m-k}cdot b_{m}^{k-l}=1.}$

Произведение членов геометрической прогрессии начиная с k-го члена, и заканчивая n-м членом, можно рассчитать по формуле

${displaystyle P_{k,n}={dfrac {P_{n}}{P_{k-1}}}.}$

Доказательство

${displaystyle P_{k,n}=prod _{i=k}^{n}b_{i}={frac {prod _{i=1}^{n}b_{i}}{prod _{j=1}^{k-1}b_{j}}}={frac {P_{n}}{P_{k-1}}}.}$

Сумма всех членов убывающей прогрессии:

, то ${displaystyle b_{n}to 0}$

при

, и

${displaystyle S_{n}to {frac {b_{1}}{1-q}}}$

при

Свойства суммы геометрической прогрессии[править | править код]

${displaystyle b_{n+1}=S_{n+1}-S_{n}}$
${displaystyle S_{n}=sigma _{n}cdot b_{1}b_{n}}$

где ${displaystyle sigma _{n}}$ — сумма обратных величин, т. е. ${displaystyle sigma _{n}={dfrac {1}{b_{1}}}+{dfrac {1}{b_{2}}}+cdots +{dfrac {1}{b_{n-1}}}+{dfrac {1}{b_{n}}}}$ .

Свойства произведения геометрической прогрессии[править | править код]

См. также[править | править код]

Арифметическая прогрессия
Арифметико-геометрическая прогрессия
Числа Фибоначчи
Показательная функция
Сумма ряда

Примечания[править | править код]

↑ Геометрическая прогрессия Архивная копия от 12 октября 2011 на Wayback Machine на mathematics.ru
↑ Это название, хотя и является общепринятым, неудачно, так как бесконечно убывающая геометрическая прогрессия является убывающей, только если и первый член, и знаменатель прогрессии положительны.
↑ Геометрическая прогрессия // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Если геометрическая прогрессия является конечной последовательностью, то её последний член таким свойством не обладает.
↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Mathesis, 1923. Архивная копия от 19 мая 2017 на Wayback Machine

Источник

Как найти знаменатель геометрической прогрессии

Согласно определению, геометрическая прогрессия – это последовательность неравных нулю чисел, каждое последующее из которых равно предыдущему, умноженному на некоторое постоянное число (знаменатель прогрессии). При этом в геометрической прогрессии не должно быть ни одного нуля, иначе вся последовательность «обнулятся», что противоречит определению. Чтобы найти знаменатель достаточно знать значения двух ее соседних членов. Однако, не всегда условия задачи бывают настолько простыми.

Вам понадобится

калькулятор

Инструкция

Разделите любой член прогрессии на предыдущий. Если значение предыдущего члена прогрессии неизвестно или неопределено (например, для первого члена прогрессии), то разделите на любой член последовательности значение последующего члена прогрессии.
Так как ни один член геометрической прогрессии не равен нулю, то при выполнении этой операции не должно возникнуть проблем.

Пример.
Пусть имеется последовательность чисел:

10, 30, 90, 270…

Требуется найти знаменатель геометрической прогрессии.
Решение:

1 вариант. Возьмем произвольный член прогрессии (например, 90) и разделим его на предыдущий (30): 90/30=3.

2 вариант. Возьмем любой член геометрической прогрессии (например, 10) и разделим на него последующий (30): 30/10=3.

Ответ: знаменатель геометрической прогрессии 10, 30, 90, 270… равен 3.

Если значения членов геометрической прогрессии заданы не явно, а в форме соотношений, то составьте и решите систему уравнений.
Пример.
Сумма первого и четвертого члена геометрической прогрессии равняется 400 (b1+b4=400), а сумма второго и пятого члена равняется 100 (b2+b5=100).

Требуется найти знаменатель прогрессии.
Решение:

Запишите условие задачи в виде системы уравнений:
b1+b4=400

b2+b5=100
Из определения геометрической прогрессии вытекает, что:

b2=b1*q

b4=b1*q^3

b5=b1*q^4, где q – общепринятое обозначение знаменателя геометрической прогрессии.
Подставив в систему уравнений значения членов прогрессии, получите:
b1+ b1*q^3=400

b1*q+ b1*q^4=100
После разложения на множители получается:
b1*(1+q^3)=400

b1*q(1+q^3)=100
Теперь разделите соответствующие части второго уравнения на первое:
[b1*q(1+q^3)] / [b1*(1+q^3)] = 100/400, откуда: q=1/4.

Если известна сумма нескольких членов геометрической прогрессии или сумма всех членов убывающей геометрической прогрессии, то для нахождения знаменателя прогрессии воспользуйтесь соответствующими формулами:
Sn = b1*(1-q^n)/(1-q), где Sn – сумма n первых членов геометрической прогрессии и
S = b1/(1-q), где S – сумма бесконечно убывающей геометрической прогрессии (сумма всех членов прогрессии со знаменателем меньшим единицы).
Пример.

Первый член убывающей геометрической прогрессии равен единице, а сумма всех ее членов равна двум.

Требуется определить знаменатель этой прогрессии.
Решение:

Подставьте данные из задачи в формулу. Получится:
2=1/(1-q), откуда – q=1/2.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

16
Июл 2013

Категория: Справочные материалы

Геометрическая прогрессия

2013-07-16
2021-06-28

А вы знаете удивительную легенду о зернах на шахматной доске? + показать

Определение

Геометрическая прогрессия — последовательность чисел (членов прогрессии) , в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии):

, где

Например, последовательность 1, 2, 4, 8, 16, … – геометрическая ()

Геометрическая прогрессия

Знаменатель геометрической прогрессии

$q=frac{b_{k+1}}{b_k}$ ,

Характеристическое свойство геометрической прогрессии

$b_n^2=b_{n-1}cdot b_{n+1}$ для

Последовательность является геометрической тогда и только тогда, когда для любого n > 1 выполняется указанное выше соотношение.

В частности, для геометрической прогрессии с положительными членами, верно: $b_n=sqrt{b_{n-1}cdot b_{n+1}}$

Формула n-го члена геометрической прогрессии

$b_n=b_1cdot q^{n-1}$

Сумма n первых членов геометрической прогрессии

$S_n=frac{b_1(q^n-1)}{q-1}$ , где

(если же , то )

Бесконечно убывающая геометрическая прогрессия

При , геометрическая прогрессия называется бесконечно убывающей. Суммой бесконечно убывающей геометрической прогрессии называется число $S=lim_{nto infty}S_n$ и $S=frac{b_1}{1-q}$

Посмотри это видео

Примеры

Пример 1. Последовательность {} –геометрическая прогрессия.

Найдите , если $b_6=-frac{1}{81}$ , $q=-frac{1}{9}.$

Решение: + показать

Приметр 2. Найдите знаменатель геометрической прогрессии {}, в которой $b_8=172,;b_{11}=2frac{11}{16}.$

Решение: + показать

Пример 3. Найдите девятый член геометрической прогрессии, если ее десятый член равен , а одиннадцатый член равен

Решение: + показать

Пример 4. Найдите сумму первых шести членов геометрической прогрессии

Решение: + показать

Пример 5. Найдите сумму первых пяти членов геометрической прогрессии {}, в которой $b_3=frac{1}{2},;b_5=2,;q>0.$

Решение: + показать

Пример 6. Представьте в виде обыкновенной дроби число

Решение: + показать

Пример 7. Найдите , если известно, что числа являются последовательными членами геометрической прогрессии (в указанном порядке).

Решение: + показать

Пример 8. Найдите знаменатель геометрической прогрессии, отношение суммы первых четырех членов которой, к сумме первых двух членов равно $frac{82}{81}.$

Решение: + показать

Пример 9. Между числами и вставьте три числа так, чтобы получилась геометрическая прогрессия

Решение: + показать

Вы можете пройти тест по теме «Геометрическая прогрессия»

Автор: egeMax |

комментариев 5

Печать страницы

Источник

Геометрическая прогрессия

Кусочек теории.

Геометрическая прогрессия – это последовательность чисел, не равных нулю, в которой каждый следующий член, начиная со второго, в одно и то же количество раз больше (или меньше) предыдущего.

Последовательность чисел 2; 4; 8; 16; 32; 64; … будет являться геометрической прогрессией, причем возрастающей, т.к. каждое следующее число больше предыдущего в 2 раза. В данном случае число 2 является знаменателем этой прогрессии.

Также геометрической прогрессией будет являться последовательность чисел 12; 6; 3; 1,5; 0,75; 0,375; … , причем убывающей, т.к. в ней числа уменьшаются в 2 раза. Но геометрическую прогрессию прежде всего связывают с умножением, поэтому правильнее сказать, что в последовательности числа увеличиваются в 0,5 раз. Здесь знаменателем будет число 0,5.

Знаменатель геометрической прогрессии обозначают буквой q. Если знаменатель не дан, то найти его можно делением текущего члена прогрессии на предыдущий:

Найти любой по счету член геометрической прогрессии можно, зная ее первый член и знаменатель. Запишем формулу n-ого члена:

Но необязательно знать именно первый член прогрессии. Пригодится может любое по счету число. Только тогда формула чутка изменится:

И держи третью формулу для нахождения n-ого члена геометрической прогрессии через предыдущий и последующий члены (правда по модулю)!

Помимо этих трех формул пригодится еще формула суммы:

Практика.

Задание 1.

Это задание можно решить без формул. Но если уж так хочется, то можно и по формулам, но мне вот не хочется)

Откинем пока минусы…

Если разделить 125 на 100, то мы увидим во сколько раз следующее число меньше предыдущего: в 1,25 раз. То же самое число получится, если 100 разделить на 80.

Найдем 4-ое число в этой последовательности: 80 : 1,25 = 64.

И 5-ое: 64 : 1,25 = 51,2.

Но не забываем, что знаки у чисел чередуются: четвертое число будет отрицательным, а пятое – положительным.

Ответ: 51,2.

Задание 2.