Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.
Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.
Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.
Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.
Путь
Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Вектор перемещения
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Рис. 1.1. Вектор перемещения и пройденный путь.
На рис. 1.1:
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
Правило сложения векторов
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).
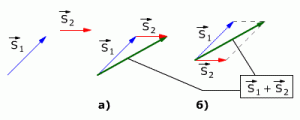
Рис. 1.2. Сложение векторов перемещений.
На рис 1.2 показаны правила сложения векторов S1 и S2:
а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма
Проекции вектора перемещения
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения 
(см.рис. 1.3).
Выберем ось ОХ так, чтобы вектор 
лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно Аx и Вx. Длина отрезка АxВx на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть
Sx = AxBx
ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор с проекцией вектора на какую-либо ось (например, Sx). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.
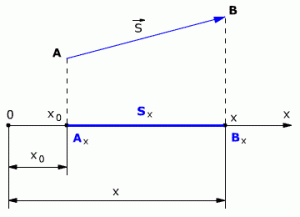
Рис. 1.3. Проекция вектора перемещения.
Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть
Sx = x – x0
Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:
Sy = y – y0 Sz = z – z0
Здесь x0, y0, z0 — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).
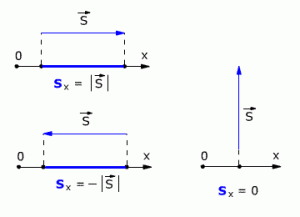
Рис. 1.4. Модули проекции вектора перемещения.
Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.
Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).
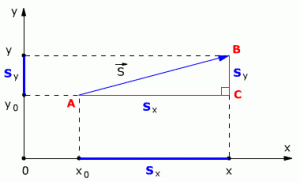
Рис. 1.5. Движение тела на плоскости.
Определим проекции вектора перемещения на осях ОХ и OY:
Sx = x – x0 Sy = y – y0
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как
АС = sx CB = sy
По теореме Пифагора
S2 = Sx2 + Sy2
Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.
Как найти модуль вектора перемещения
В кинематике для нахождения различных величин используются математические методы. В частности, чтобы найти модуль вектора перемещения, нужно применить формулу из векторной алгебры. В ней фигурируют координаты точек начала и конца вектора, т.е. первоначального и итогового положения тела.
Инструкция
Во время движения материальное тело меняет свое положение в пространстве. Его траектория может быть прямой линией или произвольной, ее длина составляет путь тела, но не расстояние, на которое оно переместилось. Эти две величины совпадают только в случае прямолинейного движения.
Итак, пусть тело совершило некоторое перемещение из точки А (х0, у0) в точку В (х, у). Чтобы найти модуль вектора перемещения, нужно вычислить длину вектора АВ. Начертите координатные оси и нанесите на них известные точки начального и конечного положения тела А и В.
Проведите отрезок из точки А в точку В, укажите направление. Опустите проекции его концов на оси и нанесите на графике параллельные и равные им отрезки, проходящие через рассматриваемые точки. Вы увидите, что на рисунке обозначился прямоугольный треугольник с катетами-проекциями и гипотенузой-перемещением.
По теореме Пифагора найдите длину гипотенузы. Этот метод широко применяется в векторной алгебре и носит название правила треугольника. Для начала запишите длины катетов, они равны разностям между соответствующими абсциссами и ординатами точек А и В:
ABx = x – x0 – проекция вектора на ось Ох;
ABy = y – y0 – его проекция на ось Оу.
Определите перемещение |AB|:
|AB| = √(ABx² + ABy²) = ((x – x0)² + (y – y0)²).
Для трехмерного пространства добавьте в формулу третью координату – аппликату z:
|AB| = √(ABx² + ABy² + ABz²) = ((x – x0)² + (y – y0)² + (z – z0)²).
Полученную формулу можно применять для любой траектории и типа движения. При этом величина перемещения обладает важным свойством. Она всегда меньше либо равна длине пути, в общем случае ее линия не совпадает с кривой траектории. Проекции – величины математические, могут быть как больше, так и меньше нуля. Однако это не имеет значения, поскольку в расчете они участвуют в четной степени.
Источники:
- модуль перемещения
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
С понятием пути вы уже неоднократно сталкивались. Познакомимся теперь с новым для вас понятием – перемещением, которое более информативно и полезно в физике, чем понятие пути.
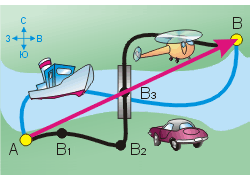
Допустим, из пункта А в пункт В на другом берегу реки нужно переправить груз. Это можно сделать на автомобиле через мост, на катере по реке или на вертолёте. В каждом из этих случаев путь, пройденный грузом, будет разным, но перемещение будет неизменным: из точки А в точку В.
Перемещением называют вектор, проведённый из начального положения тела в его конечное положение. Вектор перемещения показывает расстояние, на которое переместилось тело, и направление перемещения. Обратите внимание, что направление перемещения и направление движения – два разных понятия. Поясним это.
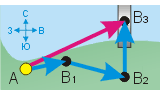
Рассмотрим, например, траекторию движения автомобиля от пункта А до середины моста. Обозначим промежуточные точки – В1, В2, В3 (см. рисунок). Вы видите, что на отрезке АВ1 автомобиль ехал на северо-восток (первая синяя стрелка), на отрезке В1В2 – на юго-восток (вторая синяя стрелка), а на отрезке В2В3 – на север (третья синяя стрелка). Итак, в момент проезда моста (точки В3) направление движения характеризовалось синим вектором В2В3, а направление перемещения – красным вектором АВ3.
Итак, перемещение тела – векторная величина, то есть имеющая пространственное направление и числовое значение (модуль). В отличие от перемещения, путь – скалярная величина, то есть имеющая только числовое значение (и не имеющая пространственного направления). Путь обозначают символом l, перемещение обозначают символом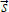 
(важно: со стрелочкой). Символом s без стрелочки обозначают модуль перемещения. Примечание: изображение любого вектора на чертеже (в виде стрелки) или упоминание его в тексте (в виде слова) делает необязательным наличие стрелочки над обозначением.
Почему в физике не ограничились понятием пути, а ввели более сложное (векторное) понятие перемещения? Зная модуль и направление перемещения, всегда можно сказать, где будет находиться тело (по отношению к своему начальному положению). Зная путь, положение тела определить нельзя. Например, зная лишь, что турист прошёл путь 7 км, мы ничего не можем сказать о том, где он сейчас находится.
Задача. В походе по равнине турист прошёл на север 3 км, затем повернул на восток и прошел ещё 4 км. На каком расстоянии от начальной точки маршрута он оказался? Начертите его перемещение.
Решение 1 – с измерениями линейкой и транспортиром.
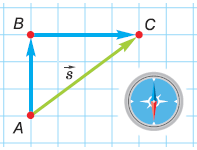
Перемещение – это вектор, соединяющий начальное и конечное положения тела. Начертим его на клетчатой бумаге в масштабе: 1 км – 1 см (чертёж справа). Измерив линейкой модуль построенного вектора, получим: 5 см. Согласно выбранному нами масштабу, модуль перемещения туриста равен 5 км. Но напомним: знать вектор – значит знать его модуль и направление. Поэтому, применив транспортир, определим: направление перемещения туриста составляет 53° с направлением на север (проверьте сами).
Решение 2 – без использования линейки и транспортира.
Поскольку угол между перемещениями туриста на север и на восток составляет 90°, применим теорему Пифагора и найдём длину гипотенузы, так как она одновременно является и модулем перемещения туриста:
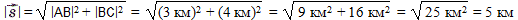
Как видите, это значение совпадает с полученным в первом решении. Теперь определим угол α между перемещением (гипотенузой) и направлением на север (прилежащим катетом треугольника):
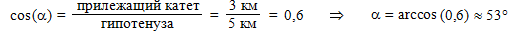
Итак, задача решена двумя способами с совпадающими ответами.
Скорость равномерного прямолинейного движения прямо пропорциональна перемещению тела и обратно пропорциональна значению времени этого перемещения.
v→=s→t.
Можно выразить перемещение из этой формулы, умножив обе части на значение времени: s→=v→⋅t.
О направлении векторов этих величин относительно друг друга можно судить, в частности, по уравнениям, записанным в векторной форме.
Проекция перемещения на ось (OX) рассчитывается по формуле
sx=vxt
, где (upsilon_x) — проекция скорости на ось (OX) принимает положительное значение, если направление перемещения совпадает с направлением оси (OX); принимает отрицательное значение, если перемещение противоположно направлено относительно оси (OX).
Если при решении задач направление движения не влияет на смысл условия и ход решения задачи, то направление векторных величин можно не учитывать. Тогда говорят о модулях величин, то есть их размере без учёта направления: (|vec{s}|=|vec{upsilon}|cdot t) можно заменить на s=vt.
При прямолинейном равномерном движении модуль перемещения равен пройденному пути: (|vec{s}|=s), если направление скорости совпадает с направлением вектора перемещения.
На рисунке представлена зависимость (v(t)) для равномерного движения.
Формула для расчета модуля перемещения: s=v1⋅t1.
Однако произведение v1⋅t1, т.е. скорости на промежуток времени, численно равно площади (S) закрашенной фигуры (в данном случае прямоугольника).
Это наблюдение позволяет сделать вывод; что при прямолинейном равномерном движении модуль перемещения численно равен площади прямоугольника, которые образуется между графиком скорости и осью времени. При этом необходимо учитывать моменты времени: начало наблюдения за объектом и конец наблюдения. В данном случае начало наблюдения соответствует точке (O,) а конец наблюдения — точке t1.
Можно говорить о равенстве пройденного пути и площади под графиком скорости.
|
Как найти модуль перемещения тела (формула)?
Общая формула для всех видов движения по которой можно найти модуль перемещения выглядит так. s = x-x0, где х0 – начальная координата, х – координата через промежуток времени, за которое совершено перемещение. Для более простых видов перемещения есть частные формулы. Для равномерного прямолинейного движения x = x0 + vt, где м – скорость тела. Для равноускоренного прямолинейного движения x = x0 + v0t + (a t^2)/2. система выбрала этот ответ лучшим
Zolotynka 6 месяцев назад Прежде чем писать/запоминать формулу, давайте разберемся, что представляет собой само понятие перемещения тела – это разница между двумя положениями объекта. Далее: это векторная величина, потому что у нее также есть направление – от начальной позиции к финальной. Формула перемещения выглядит следующим образом: Sx = x – x0. __ Перемещение не обязательно всегда положительно, оно также может быть нулевым или отрицательным. Знаете ответ? |
