Как найти мольную долю газа

Команда “Газы!” была объявлена еще две недели назад. И что?! Легкие задачи порешали и расслабились?! Или вы думаете, что задачи на газы касаются только 28-х заданий ЕГЭ?! Как бы не так! Если газов пока еще не было в 34-х заданиях, это ничего не значит! Задач на электролиз тоже не было в ЕГЭ до 2018 года. А потом как врезали, мама не горюй! Обязательно прочитайте мою статью “Тайны задач по химии? Тяжело в учении – легко в бою!”. В этой статье очень подробно рассказывается о новых фишках на электролиз. Статья вызвала шквал самых разных эмоций у преподавателей химии. До сих пор мне и пишут, и звонят, и благодарят, и бьются в конвульсиях. Просто цирк с конями, в котором я – зритель в первом ряду.

Однако, вернемся к нашим баранам, вернее, Газам. Я прошла через огонь и воду вступительных экзаменов и знаю точно – хочешь завалить абитуриента, дай ему задачу на Газы. Почитайте на досуге сборник задач И.Ю. Белавина. Я процитирую одну такую “мозгобойню”, чтобы вам жизнь медом не казалась. Попробуйте решить.

И.Ю. Белавин, 2005, задача 229

“Два из трех газов (сероводород, водород и кислород) смешали и получили газовую смесь, плотность которой оказалась равной плотности оставшегося газа. Полученную газовую смесь вместе с равным ей объемом третьего газа под давлением поместили в замкнутый сосуд емкостью 4 л, содержавший азот при н.у. и нагревали при 600 С до окончания химических реакций, затем постепенно охладили. Определите массы веществ, содержавшихся в сосуде после охлаждения, если плотность газовой смеси в сосуде перед нагреванием равнялась 9,25г/л. (Ответ: m(S) = 7,5 г, m(SO2) = 15 г, m(Н2О) = 9 г)”

Ну как, решили? Нет?! А ваши репетиторы?! Извините, это был риторический вопрос. Кстати, мои ученики, абитуриенты 2003-2008 гг. такие задачи щелкали, как семечки, на экзаменах во 2-й медицинский (теперь РНИМУ им. Н.И. Пирогова). Надеюсь, вам понятно, что 34-м задачам ЕГЭ еще есть куда усложняться, perfectio interminatus est (нет предела совершенству), с газами нужно работать, работать и работать. Поэтому команду “Газы!” отменять рано. Итак, поехали!

Сегодня мы поговорим о газовых смесях, затронем понятие плотности газа (абсолютной и относительной), средней молярной массы, решим задачи: определение средней молярной массы и плотности газа по компонентам смеси и наоборот.

• Газовая смесь – смесь отдельных газов НЕ вступающих между собой в химические реакции. К смесям газов относятся: воздух (состоит из азота, кислорода, углекислого газа, водяного пара и др.), природный газ (смесь предельных и непредельных углеводородов, оксида углерода, водорода, сероводорода, азота, кислорода, углекислого газа и др.), дымовые газы (содержат азот, углекислый газ, пары воды, сернистый газ и др.) и др.

• Объемная доля – отношение объема данного газа к общему объему смеси, показывает, какую часть общего объема смеси занимает данный газ, измеряется в долях единицы или в процентах.

• Мольная доля – отношение количества вещества данного газа к общему количеству вещества смеси газов, измеряется в долях единицы или в процентах.

• Плотность газа (абсолютная) – определяется как отношение массы газа к его объему, единица измерения (г/л). Физический смысл абсолютной плотности газа – масса 1 л, поэтому молярный объем газа (22,4 л при н.у. t° = 0°C, P = 1 атм) имеет массу, численно равную молярной массе.

• Относительная плотность газа (плотность одного газа по другому) – это отношение молярной массы данного газа к молярной массе того газа, по которому она находится

• Средняя молярная масса газа – рассчитывается на основе молярных масс составляющих эту смесь газов и их объемных долей

Настоятельно рекомендую запомнить среднюю молярную массу воздуха Мср(в) = 29 г/моль, в заданиях ЕГЭ часто встречается.

Обязательно посетите страницу моего сайта “Изучаем Х-ОбХ-04. Закон Авогадро. Следствия из закона Авогадро. Нормальные условия. Молярный объем газа. Абсолютная и относительная плотность газа. Закон объемных отношений” и сделайте конспекты по теории. Затем возьмите бумагу и ручку и решайте задачи вместе со мной.

ВАНГУЮ: чует мое сердце, что ЕГЭ по химии 2019 года устроит нам газовую атаку, а противогазы не выдаст!

Задача 1

Определить плотность по азоту газовой смеси, состоящей из 30% кислорода, 20% азота и 50% углекислого газа.

Задача 2

Вычислите плотность по водороду газовой смеси, содержащей 0,4 моль СО2, 0,2 моль азота и 1,4 моль кислорода.

Задача 3

5 л смеси азота и водорода имеют относительную плотность по водороду 12. Определить объем каждого газа в смеси.

Несколько задач со страницы моего сайта

Задача 4

Плотность по водороду пропан-бутановой смеси равна 23,5. Определите объемные доли пропана и бутана

Задача 5

Газообразный алкан объемом 8 л (н.у.) имеет массу 14,28 г. Чему равна его плотность по воздуху

Задача 6

Плотность паров альдегида по метану равна 2,75. Определите альдегид

Ну как? Пошло дело? Если туго, вернитесь к задачам и решайте их самостоятельно до тех пор, пока не щелкнет! А для стимуляции – десерт в виде еще одной задачи И.Ю. Белавина на газы. Наслаждайтесь ее решением самостоятельно!

И.Ю. Белавин, 2005, задача 202

“Сосуд емкостью 5,6 л при н.у. заполнили метаном, затем нагрели до высокой температуры, в результате чего произошло частичное разложение метана. Определите массу образовавшейся сажи, если известно, что после приведения к нормальным условиям объем полученной газовой смеси оказался в 1,6 раза больше объема исходного метана, эта газовая смесь обесцвечивает бромную воду и имеет плотность по воздуху 0,2931. (Ответ: m(C) = 0,6 г)”

Задачи И.Ю. Белавина – это крутой драйв! Попробуйте порешать, и вы откажетесь от просмотра любых ужастиков, поскольку запасетесь адреналином надолго! Но нам нужно спуститься на землю к ЕГЭ, простому и надежному, как первый советский трактор. Кстати, у меня в коллекции припасено немало сюрпризов с газовыми фишками, собранными за все годы работы и бережно хранимыми. Думаю, пришло время сказать им: “И снова здравствуйте!”, поскольку ЕГЭ с каждым годом становится “все чудесатее и чудесатее”. Но это уже совсем другая история. Читайте мои статьи – и вы подстелите соломку под свою ЕГЭшную попу.

Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии http://repetitor-him.ru. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Позвоните мне +7(903)186-74-55, приходите ко мне на курс, на бесплатные Мастер-классы “Решение задач по химии”. Я с удовольствием вам помогу.

Репетитор по химии и биологии кбн В.Богунова

При решении химических задач, при расчётах на работе, да и просто в жизни иногда приходится рассчитывать концентрации. Неважно, будет это школьная теоретическая задача, необходимость приготовить электролит для аккумулятора автомобиля, надобность узнать количество сахара для компота — все расчёты концентраций выполняются по известным формулам, которых не так много. Однако, с этим часто возникают трудности.

Прочитав эту статью, Вы научитесь легко рассчитывать концентрации веществ и при надобности играючи переводить одну концентрацию в другую. В статье приводятся примеры задач с решениями, а в конце приведём справочную табличку с формулами, которую можно распечатать и держать под рукой.

Массовая доля

Начнём с простого, но в то же время нужного способа выражения концентрации компонента в смеси — массовой доли.

Массовая доля есть отношение массы данного компонента к сумме масс всех компонентов. Обозначать её принято буквой w или ω (омега).

Рассчитывается массовая доля по формуле:

Large w_{i}=frac{m_{i}}{m}, ;;;;;(1)

где Large w_{i} — массовая доля компонента i в смеси,

Large m_{i} — масса этого компонента,

m — масса всей смеси.

И сразу разберём на примере:

Задача:

Зимой дороги посыпают песком с солью. Известно, что куча имеет массу 50 кг, и в неё всыпали 1 кг соли и перемешали. Найти массовую долю соли.

Решение:

Масса соли есть Large m_{i} по формуле выше. Масса всей смеси нам пока неизвестна, но найти её легко. Просуммируем массу песка и соли:

Large m = m_{п}+m_{с}= 50 кг + 1 кг = 51 кг

А теперь находим и массовую долю:

Large w_{с} = frac{m_{с}}{m} = 1 кг / 51 кг = 0.0196,

или умножаем на 100% и получаем 1.96%.

Ответ: 0.0196, или 1.96%.

Теперь решим что-то посложнее, и ближе к ЕГЭ.

Задача:

Смешали 200 г раствора глюкозы с массовой концентрацией 25% и 300 г раствора глюкозы с массовой концентрацией 10%. Найти массовую концентрацию полученного раствора, ответ округлить до целых.

Решение:

Обозначим первый и второй растворы соответственно Large m_{1} и Large m_{2}. Массу полученного после смешения раствора обозначим Large m и найдём:

Large m = m_{1} + m_{2} = 200 г + 300 г = 500 г

Массу самой глюкозы в первом и втором растворе обозначим Large m_{гл. 1} и Large m_{гл. 2}. По формуле (1) это будут наши массы компонентов. Массы растворов нам известны, их массовые концентрации тоже. Как найти массу компонента? Очень просто, находим неизвестное делимое умножением (и не забываем, что проценты — это сотые части):

Large m_{гл. 1} = w_{1}cdot m_{1} = 0.25 cdot 200 г = 50 г

Large m_{гл. 2} = w_{2}cdot m_{2} = 0.1 cdot 300 г = 30 г

Таким образом, общая масса глюкозы Large m_{гл}:

Large m_{гл} = m_{гл. 1} + m_{гл. 2} = 50 г + 30 г = 80 г.

Ответ: 80 г.

Задачи на смешение раствором с разными концентрациями одного вещества можно решать с помощью «конверта Пирсона».

Объёмная доля

Часто, когда мы имеем дело с жидкостями и газами, удобно оперировать их объёмами, а не массой. Поэтому, чтобы выражать долю какого-либо компонента в таких смесях (но и в твёрдых тоже вполне можно), пользуются понятием объёмной доли.

Объёмная доля компонента — отношение объёма компонента к сумме объёмов компонентов до смешивания. Объёмная доля измеряется в долях единицы или в процентах. Обычно обозначается греческой буквой φ (фи).

Рассчитывается объёмная доля по формуле:

Large phi_{B}=frac{V_{B}}{sum{V_{i}}}, ; ;;;; (2)

где Large phi_{B} — объёмная доля компонента B;

Large V_{B} — объём компонента B;

Large sum{V_{i}} — сумма объёмов всех компонентов.

Здесь важно понимать, что в формулу по возможности подставляем именно сумму объёмов всех компонентов, а не объём смеси, так как при смешивании некоторых жидкостей суммарный объём уменьшается. Так, если смешать литр воды и литр спирта, два литра аквавита мы не получим — будет примерно 1800 мл. В школьных задачах, как правило, это не так важно, но в уме держим и помним.

Задача:

Смешали 6 объёмов воды и 1 объём серной кислоты. Найти объёмную долю кислоты в полученном растворе.

Решение:

Так как объёмная доля — безразмерная величина, объёмы компонентов в условии задачи могут даваться в любых единицах — литрах, стаканах, баррелях, штофах, сексталях — главное, чтобы в одинаковых. Если не так — переводим одни в другие, если одинаковые — решаем. В нашем условии описаны просто некоторые «объёмы», их и подставляем.

Large phi_{H_{2}SO_{4}} = frac{V_{ H_{2}SO_{4} }} { V_{ H_{2}SO_{4}} + V_{H_{2}O}} = frac{1 : объём}{1 : объём + 6 : объёмов} = frac{1 : объём}{7 : объёмов} = 0.143, : или : 14.3%

Ответ: 14.3 %.

С газами всё обстоит немного интереснее — при не очень больших давлениях и температурах объёмная доля какого-либо газа в газовой смеси равна его мольной доле. (Ведь мы знаем, что молярный объём газов почти равен 22.4 л/моль).

Задача:

Мольная доля кислорода в сухом воздухе составляет 0.21. Найдите объёмную долю азота, если объёмная доля аргона составляет 1%.

Решение:

Внимательный читатель заметил, что мы написали о том, что объёмная и мольная доля для газов в смеси равны. Поэтому, объёмная доля кислорода равна также 0.21, или 21%. Найдём объёмную долю азота:

Large 100% – 21% – 1% = 78%.

Ответ: 78%.

Мольная доля

В тех случаях, когда нам известны количества веществ в смеси, мы можем выразить содержание того или иного компонента с помощью мольной доли.

Мольная доля — отношение количества молей данного компонента к общему количеству молей всех компонентов. Мольную долю выражают в долях единицы. ИЮПАК рекомендует обозначать мольную долю буквой x (а для газов — y).

Находят мольную долю по формуле:

Large x_{B} = frac{n_{B}}{sum{n_{i}}}, ;;;;;(3)

где Large x_{B} — мольная доля компонента B;

Large n_{B} — количество компонента B, моль;

Large sum{n_{i}} — сумма количеств всех компонентов.

Разберём на примере.

Задача:

При неизвестных условиях смешали 3 кг азота, 1 кг кислорода и 0.5 кг гелия. Найти мольную долю каждого компонента полученной газовой смеси.

Решение:

Сначала находим количество каждого из газов (моль):

Large n_{N_{2}} = frac{ m_{N_{2}}}{M_{N_{2}}} = frac {3000 : г}{28 : ^г/_{моль}} = 107.14 : моль

Large n_{O_{2}} = frac{ m_{O_{2}}}{M_{O_{2}}} = frac {1000 : г}{32 : ^г/_{моль}} = 31.25 : моль

Large n_{He} = frac{ m_{He}}{M_{He}} = frac {500 : г}{4 : ^г/_{моль}} = 125 : моль

Затем считаем сумму количеств:

Large sum {n} = 107.14 : моль + 31.25 : моль + 125 : моль = 263.39 : моль

И находим мольную долю каждого компонента:

Large y_{N_{2}} = frac {107.14 : моль}{263.39 : моль} = 0.4068, : или : 40.68 %;

Large y_{O_{2}} = frac {31.25 : моль}{263.39 : моль} = 0.1186, : или : 11.86 %;

Large y_{He} = frac {125 : моль}{263.39 : моль} = 0.4746, : или : 47.46 %;

Проверяем:

Large 40.68 % + 11.86 % + 47.46 % = 100%.

И радуемся правильному решению.

Ответ: 40.68%, 11.86% , 47.46%.

Молярность (молярная объёмная концентрация)

А сейчас рассмотрим, вероятно, самый часто встречающийся способ выражения концентрации — молярную концентрацию.

Молярная концентрация (молярность, мольность) — количество вещества (число молей) компонента в единице объёма смеси. Молярная концентрация в системе СИ измеряется в моль/м³, однако на практике её гораздо чаще выражают в моль/л или ммоль/л.

Также иногда говорят просто «молярность», и обозначают буквой М. Это значит, что, например, обозначение «0.5 М раствор соляной кислоты» следует понимать как «полумолярный раствор соляной кислоты», или 0.5 моль/л.

Обозначают молярную концентрацию буквой c (латинская «цэ»), или заключают в квадратные скобки вещество, концентрация которого указывается. Например, [Na⁺] — концентрация катионов натрия в моль/л. Кстати, слово «моль» в обозначениях не склоняют — 5 моль/л, 3 моль/л.

Рассчитывается молярная концентрация по формуле:

Large c_{B} = frac{n_{B}}{V} ; ; ;;; (4)

где Large n_{B} — количество вещества компонента B, моль;

Large V — общий объём смеси, л.

Разберём на примере.

Задача:

В пивную кружку зачем-то насыпали 24 г сахара и до краёв заполнили кипятком. А нам зачем-то нужно найти молярную концентрацию сахарозы в полученном сиропе. И кстати, дело происходило в Британии.

Решение:

Молекулярная масса сахарозы равна 342 (посчитайте, может мы ошиблись — C₁₂H₂₂O₁₁). Найдём количество вещества:

Large n_{сахарозы} = frac{24 : г}{342 : г/моль} = 0.0702 моль

Британская пинта (мера объёма такая) равна 0.568 л. Поэтому молярная концентрация находится так:

Large c_{сахарозы} = frac{0.0702 : моль}{0.568 : л} = 0.1236 моль/л

Ответ: 0.1236 моль/л.

Нормальная концентрация (молярная концентрация эквивалента, «нормальность»)

Нормальная концентрация — количество эквивалентов данного вещества в 1 литре смеси. Нормальную концентрацию выражают в моль-экв/л или г-экв/л (имеется в виду моль эквивалентов).

Обозначается нормальная концентрация как с_н, с_N, или даже c(f_eq B). Рассчитывается нормальная концентрация по формуле:

Large c_{N} = z cdot c_{B} = z cdot frac{n_{B}}{V}= frac{1}{f_{eq}} cdot frac {n_{B}}{V} ; ;;;; (5)

где Large n_{B} — количество вещества компонента В, моль;

V — общий объём смеси, л;

z — число эквивалентности (фактор эквивалентности Large f_{eq} = 1/z ).

Значение нормальной концентрации для растворов записывают как «н» или «N», а говорят «нормальность» или «нормальный». Например, раствор с концентрацией 0.25 н — четвертьнормальный раствор.

Разберём на примере.

Задача:

Рассчитать нормальность раствора объёмом 1 л, если в нём содержится 40 г перманганата калия. Раствор приготовили для последующего проведения реакции в нейтральной среде.

Решение:

В нейтральной среде перманганат калия восстанавливается до оксида марганца (IV). При этом в окислительно-восстановительной реакции 1 атом марганца принимает 3 электрона (проверьте на любой окислительно-восстановительной реакции перманганата калия с образованием оксида, расставив степени окисления), что означает, что число эквивалентности будет равно 3. Для расчёта концентрации по формуле (5) выше нам ещё не хватает количества вещества KMnO4. найдём его:

Large n_{KMnO_{4}}=frac{m _{KMnO_{4}}}{M _{KMnO_{4}} } = frac{40 : г}{158 г/моль}= 0.253 моль

Теперь считаем нормальную концентрацию:

Large c_{N_{KMnO_{4}}}= z cdot frac{n_{KMnO_{4}}}{V} = 3 cdot frac{0.253 : моль}{1 : л} = 0.759 моль-экв/л

Ответ: 0.759 моль-экв/л.

Таким образом, заметим важное на практике свойство — нормальная концентрация больше молярной в z раз.

Мы не будем рассматривать в данной статье особо экзотические способы выражения концентраций, о них вы можете почитать в литературе или интернете. Поэтому расскажем ещё об одном способе, и на нём остановимся — массовая концентрация.

Моляльная концентрация

Моляльная концентрация (моляльность, молярная весовая концентрация) — количество растворённого вещества (число моль) в 1000 г растворителя.

Измеряется моляльная концентрация в молях на кг. Как и с молярной концентрацией, иногда говорят «моляльность», то есть раствор с концентрацией 0.25 моль/кг можно назвать четвертьмоляльным.

Находится моляльная концентрация по формуле:

Large m_{B} = frac{n_{B}}{m_{A}}, ;;;;; (6)

где Large n_{B} — количество вещества компонента B, моль;

Large m_{A} — масса растворителя, кг.

Казалось бы, зачем нужна такая единица измерения для выражения концентрации? Так вот, у моляльной концентрации есть одно важное свойство — она не зависит от температуры, в отличие, например, от молярной. Подумайте, почему?

Массовая концентрация

Массовая концентрация — отношение массы растворённого вещества к объёму раствора. По рекомендации ИЮПАК, обозначается символом γ или ρ.

Находится массовая концентрация по формуле:

Large rho_{B}=frac{m_{B}}{V}, ;;;;; (7)

где Large m_{B} — масса растворенного вещества, г;

Large V — общий объём смеси, л.

В системе СИ выражается в кг/м³.

Разберём на примере.

Задача:

Рассчитать массовую концентрацию перманганата калия по условиям предыдущей задачи.

Решение:

Решение будет совсем простым. Считаем:

Large rho_{ KMnO_{4} }=frac{m_{ KMnO_{4} }}{V} =frac{40 : г}{1 : л} = 40 г/л.

Ответ: 40 г/л.

Также в аналитической химии пользуются понятием титра по растворенному веществу. Титр по растворенному веществу находится так же, как и массовая концентрация, но выражается в г/мл. Легко догадаться, что в задаче выше титр будет равен 0.04 г/мл (для этого надо умножить наш ответ на 0.001 мл/л, проверьте). Кстати, обозначается титр буквой Т.

А теперь, как обещали, табличка с формулами перевода одной концентрации в другую.

Таблица перевода одной концентрации в другую.

В таблице слева — ВО ЧТО переводим, сверху — ЧТО. Если стоит знак «=», то, естественно, эти величины равны.

	Массовая доля, large omega, %	Мольная доля, large x , %	Объёмная доля, large phi, %	Молярная концентрация, large c, моль/л	Нормальная концентрация, large c_{N} , моль-экв/л	Моляльная концентрация, large m, моль/кг	Массовая концентрация, large rho, г/л
Массовая доля, large omega, %	=	large omega_{B}=LARGE frac{x_{B} cdot M(B)}{sum x_{i} cdot M_{i}}	Для газов: omega = LARGE frac{phi_{A} cdot M(A)}{sum (M_{i} cdot phi_{i})}	large omega_{B}= LARGE frac{c_{B} cdot M(B)}{rho}	large omega_{B}=LARGE frac{c_{N} cdot M(B)}{rho cdot z}		large omega_{B}= LARGE frac{gamma_{B}}{rho}
Мольная доля, large x , %	large x_{B}=LARGE frac{frac{omega_{B}}{M(B)}}{sum frac{omega_{i}}{M_{i}}}	=				large x_{B}=LARGE frac{m_{B}}{m_{B}+frac{1}{M(A)}}
Объёмная доля, large phi, %	Для газов: large phi_{A}=LARGE frac{frac{omega_{A}}{M(A)}}{sum frac{omega_{i}}{M_{i}}}		=
Молярная концентрация, large c, моль/л	large c_{B}=LARGE frac{rho cdot omega_{B}}{M(B)}			=	large c_{B}=Large frac{c_{N}}{z}
Нормальная концентрация, large c_{N} , моль-экв/л	large c_{N}=LARGE frac{rho cdot omega_{B} cdot z}{M(B)}			large c_{N}=c_{B} cdot z	=
Моляльная концентрация, large m, моль/кг		large m_{B}=Large frac{x_{B}}{M(A)(1-x_{B})}				=
Массовая концентрация, large gamma, г/л	large gamma_{B}=rho cdot omega_{B}						=

Таблица будет пополняться.

Mole fraction is one of the ways to represent the concentration of the solution. It is defined as the number of molecules of component A divided by the total number of molecules of all the components in the solution. Let’s learn about the mole fraction its formula and examples in this article.

What is Mole Fraction?

Mole fraction is defined as,

Number of moles of component A in a mixture divided by the total number of moles of all the components in that mixture.

Mole fraction is one of the measurements of the concentration of the solution. The image given below tells the formula used to calculate the mole fraction.

The mole fraction is represented by the letter ‘X’. For example for a solution that has ‘a’ moles of solute and ‘b’ moles of the solvent the total moles in the solution is ‘a+b’. Now, the mole fraction of solute is X_solute = a / (a+b), similarly the mole fraction of solvent X_solvent  = b / (a+b). 

A Mole is a unit of measurement for measuring a larger number of substances such as molecules, atoms, and other particles in chemistry. One mole is equal to 6.02214076 × 10²³ values.

Mole Fraction Formula

The formula to calculate the mole fraction of any substance is discussed below in the article. Let’s take a solution in which two compounds compound A and compound B are mixed and the moles of compound A is n_A and the moles of compound B are n_B then,

Mole Fraction of A = Number of moles of A / (Number of moles of A + Number of moles of B)

X_A = n_A / (n_A+n_B)

Mole Fraction of B = Number of moles of B / (Number of moles of A + Number of moles of B)

X_B = n_B / (n_A+n_B)

Also, one of the most used properties of mole fraction is,

X_solute + X_solvent = 1

Proof:

Using Mole Fraction Formula

X_solute + X_solvent = a /(a+b) + b/(a+b)

                          = (a+b) / (a+b)

X_solute + X_solvent = 1

Now, by using the above formula

• X_solute = 1 – X_solvent
• X_solvent = 1 – X_solute

Unit of Mole Fraction

Mole fraction is a way of representing the concentration of the solution. It is the ratio of the moles of the solute or the mole of the solvent to the total moles of the solution. As we see it is a ratio of two similar quantities thus, it is a dimensionless quantity. 

So, Mole Fraction has no Unit.

Properties of Mole Fraction

Mole fraction is one the most important way for finding the concentration of the solution and it helps in studying the various properties of the solution. Some of the basic properties of Mole Fractions are,

• Mole fraction is independent of the temperature. Unlike other molar concentrations, mole fraction does not require knowledge of phase densities.
• The roles of ‘solvate’ and ‘solvent’ are reversible in a mole fraction as it is symmetric.
• For any Ideal gas mole fraction is defined as the ratio of the partial pressure of individual gas to the total pressure of the mixture.
• Finding the mole faction of the liquid solutions is difficult.

Advantages of Mole Fraction

The following are some of the advantages of using a mole fraction:

• Change in temperature has no effect on the mole fraction of the solution.
• Mole fraction in an ideal gas mixture is equal to the ratio of partial pressure to total pressure.
• Density of various phases is not required for finding the mole fraction of any solution.

Disadvantages of Mole Fraction

There are not many disadvantages of using mole fraction as the measure of the concentration of the solution. The only disadvantage of using mole fraction is that it cannot be used properly with liquid solutions.

Note:

• Sum of all the mole fractions in a solution is always one.

Read, More

• Molarity
• Normality
• Molality

Solved Examples on Mole Fraction

Example 1: If the molecular mass of CH₃OH is 39 and the molecular mass of H₂O is 27, what is the mole fraction of CH₃OH and H₂O in a solution made by dissolving 4.1 g of alcohol in 36 g of H₂O?

Answer:

Using the formula for moles,

Moles = wt(in gm) / molecular mass

Moles of H₂O = 36 / 27 
                      = 1.3 moles

Moles of CH₃OH = 4.1 / 39 
                           = 0.10 mole

Mole fraction of CH₃OH = 0.10 / (1.3 + 0.10)
                                      = 0.10 / 1.4

Mole fraction of CH₃OH = 0.0714

Now,

Mole fraction of H₂O = 1.3/(1.3+0.1)
                                 = 1.3/1.4

Mole fraction of  H₂O = 0.9286

Example 2: Calculate the mole fraction of each gas in a tank containing 2.5 × 10⁴ mol oxygen and 4.8 × 10⁴ mol helium.

Answer:

Number of moles of Helium = 4.8 × 10⁴

Number of moles of Oxygen = 2.5 × 10⁴

Since,

Mole Fraction of Helium = Number of moles of Helium / (Number of moles of Helium + Number of moles of Oxygen)

X_Helium = 4.8 × 10⁴ / (4.8 × 10⁴ + 2.5 × 10⁴)

            = 4.8 × 10⁴ / 7.3 × 10⁴

X_Helium = 0.6575

Mole Fraction of Oxygen = Number of moles of Oxygen / (Number of moles of Helium + Number of moles of Oxygen)

X_Oxygen = 2.5 × 10⁴ / (4.8 × 10⁴ + 2.5 × 10⁴)

            = 2.5 × 10⁴ / 7.3 × 10⁴

X_oxygen = 0.3424

Example 3: Calculate the acetone mole fraction in a solution of 6-mole benzene, 13 moles carbon tetrachloride, and 21 moles acetone.

Answer:

Moles of Benzene = 6

Moles of Carbon Tetrachloride = 13

Moles of Acetone = 21

Now,

Mole Fraction of Acetone = Moles of Acetone / (Moles of Benzene + Moles of Carbon Tetrachloride + Moles of Acetone)

X_acetone = 21 / (6+13+21)

X_acetone = 21 / 40

X_acetone = 0.525

Mole Fraction of Benzene = Moles of Benzene / (Moles of Benzene + Moles of Carbon Tetrachloride + Moles of Acetone)

X_benzene = 6 / (6+13+21)

X_benzene = 0.15

Mole Fraction of Carbon Tetrachloride = Moles of Carbon Tetrachloride / (Moles of Benzene + Moles of Carbon Tetrachloride + Moles of Acetone)

X_{carbon tetrachloride} = 6 / (6+13+21)

X_{carbon tetrachloride} = 0.15

Example 4: Calculate the mole fraction of solute, when the mole fraction of solvent is 0.23

Answer:

Since,

X_solute = 1 – X_solvent

X_solute = 1 – 0.23

X_solute = 0.77

Example 5: If the mole fraction of the solute is 0.64, determine the mole fraction of the solvent.

Answer:

Since,

X_solvent = 1 – X_solute

X_solvent = 1 – 0.64

X_solvent = 0.36

FAQs on Mole Fraction

Question 1: What is a mole fraction?

Answer:

Mole fraction is the ratio of the number of moles of the given solute to the total number of moles of the solution.

Question 2: Why do we use Mole Fraction?

Answer:

Mole fraction is the ratio of the number of moles of component A in the mixture to the total number of moles of the mixture. The mole fraction is useful because the ratio of the two components can be calculated if the mole fraction of each component is known and it does not changes with the temperature.

Question 3: What is the unit of mole fraction?

Answer:

Mole fraction is the ratio of two similar quantities so it is a unit less quantity.

Question 4: Is mole fraction temperature dependent concentration term?

Answer:

No, the mole fraction is not temperature dependent. So it is widely used when the temperature of the concentration changes rapidly.

Question 5: What is the relation between Mole Fraction and Molality?

Answer:

The relation between mole fraction and molality is discussed below,

Molality = (X_B × 1000) / (X_A × M_A)

where,
X_B is mole fraction of solute
X_A is mole fraction of solvent
M_A is mass of solvent

Last Updated :
13 Mar, 2023

Like Article

Save Article

Как известно, молекулы и атомы, которые составляют окружающие нас объекты, обладают очень маленькими размерами. Для проведения расчетов во время химических реакций, а также для анализа поведения смеси невзаимодействующих компонент в жидкостях и газах, используют понятие мольных долей. Что это такое, и как их можно применять для получения макроскопических физических величин смеси, рассматривается в данной статье.

Число Авогадро

В начале XX века, проводя эксперименты с газовыми смесями, французский ученый Жан Перрен измерил количество молекул H₂, которые содержатся в 1 грамме этого газа. Это количество оказалось огромной цифрой (6,022 * 10²³). Поскольку проводить расчеты с такими цифрами крайне неудобно, Перрин предложил название этой величине – число Авогадро. Это название было выбрано в честь итальянского ученого начала XIX века, Амедео Авогадро, который, так же как и Перрин, изучал смеси газов и даже смог сформулировать для них закон, который в настоящее время носит его фамилию.

Число Авогадро в настоящее время широко применяется при изучении различных веществ. Оно связывает макроскопические и микроскопические характеристики.

Количество вещества и молярная масса

В 60-е годы Международная палата мер и весов в систему физических единиц (СИ) ввела седьмую базовую единицу измерения. Ею стал моль. Моль показывает число элементов, которые составляют рассматриваемую систему. Один моль равен числу Авогадро.

Под молярной массой понимают вес одного моля данного вещества. Измеряется она в граммах на моль. Молярная масса является аддитивной величиной, то есть для ее определения для конкретного химического соединения необходимо сложить малярные массы химических элементов, которые составляют это соединение. Например, молярная масса метана (CH₄) равна:

M_CH4 = M_C + 4M_H = 12 + 4 * 1 = 16 г/моль.

То есть 1 моль молекул метана будет иметь массу 16 граммов.

Понятие о мольной доле

Чистые вещества редко встречаются в природе. Например, в воде всегда растворены различные примеси (соли); воздух нашей планеты – это смесь газов. Иными словами, любое вещество в жидком и газообразном состоянии представляет собой смесь различных элементов. Мольная доля – это величина, показывающая, какую часть в мольном эквиваленте занимает тот или иной компонент в смеси. Если количество вещества всей смеси обозначить как n, а количество вещества компонента i – как n_i, тогда можно записать следующее равенство:

x_i = n_i / n.

Здесь x_i – это мольная доля компонента i для данной смеси. Как видно, эта величина является безразмерной. Для всех компонентов смеси сумма их мольных долей формулой выражается такой:

∑_i(x_i) = 1.

Получить эту формулу не сложно. Для этого достаточно подставить в нее предыдущее выражение для x_i.

Атомные проценты

При решении задач по химии часто исходные величины даются в атомных процентах. Например, в смеси кислорода с водородом последний составляет 60 атомных %. Это означает, что из 10 молекул смеси 6 будут соответствовать водороду. Поскольку мольная доля – это отношение количества атомов компонента к их общему числу, то атомные проценты являются синонимом рассматриваемого понятия.

Перевод долей в атомные проценты осуществляется простым их увеличением на два порядка. Например, 0,21 мольная доля кислорода в воздухе соответствует 21 атомному %.

Идеальный газ

Понятие о мольных долях часто используют при решении задач с газовыми смесями. Большинство газов, находящихся в нормальных условиях (температура 300 К и давление 1 атм.) являются идеальными. Это означает, что атомы и молекулы, составляющие газ, находятся на большом расстоянии друг от друга и не взаимодействуют между собой.

Для идеальных газов справедливо следующее уравнение состояния:

P * V = n * R * T.

Здесь P, V и T – это три макроскопических термодинамических характеристики: давление, объем и температура соответственно. Величина R = 8,314 Дж/(К*моль) – это постоянная для всех газов, n – число частиц в молях, то есть количество вещества.

Уравнение состояния показывает, как будет изменяться одна из трех макроскопических характеристик газа (P, V или T), если зафиксировать вторую из них и изменять третью. Например, при постоянной температуре давление будет обратно пропорционально объему газа (закон Бойля-Мариотта).

Самое замечательное в записанной формуле заключается в том, что она не принимает во внимание химическую природу молекул и атомов газа, то есть является справедливой как для чистых газов, так и для их смесей.

Закон Дальтона и парциальное давление

Как рассчитать мольную долю газа в смеси? Для этого достаточно знать общее количество частиц и их число для рассматриваемого компонента. Однако можно поступить иначе.

Мольную долю газа в смеси можно найти, зная его парциальное давление. Под последним понимают давление, которое создал бы данный компонент газовой смеси, если имелась бы возможность убрать все остальные составляющие. Если обозначить парциальное давление i-го компонента как P_i, а давление всей смеси как P, тогда формула мольной доли для этого компонента примет вид:

x_i = P_i / P.

Поскольку сумма всех x_i равна единице, то можно записать следующее выражение:

∑_i(P_i / P) = 1, следовательно, ∑_i(P_i) = P.

Последнее равенство называется законом Дальтона, который так назван в честь британского ученого начала XIX века Джона Дальтона.

Закон парциального давления или закон Дальтона является прямым следствием из уравнения состояния для идеальных газов. Если атомы или молекулы в газе начинают взаимодействовать друг с другом (это происходит при высоких температурах и большом давлении), тогда закон Дальтона оказывается несправедлив. В последнем случае для расчета мольных долей компонентов необходимо пользоваться формулой через количество вещества, а не через парциальное давление.

Воздух как газовая смесь

Рассмотрев вопрос, как найти мольную долю компонента в смеси, решим следующую задачу: рассчитаем величины x_i и P_i для каждого компонента в воздухе.

Если рассматривать сухой воздух, то в его состав входят следующие 4 газовых компонента:

• азот (78,09 %);
• кислород (20,95 %);
• аргон (0,93 %);
• газ углекислый (0,04 %).

Из этих данных мольные доли для каждого газа вычислить очень просто. Для этого достаточно проценты представить в относительных величинах, как было сказано выше в статье. Тогда получаем:

x_N2 = 0,7809;

x_O2 = 0,2095;

x_Ar = 0,0093;

x_CO2 = 0,0004.

Парциальное давление этих компонент воздуха вычислим, учитывая, что атмосферное давление на высоте уровня моря равно 101 325 Па или 1 атм. Тогда получаем:

P_N2 = x_N2 * P = 0,7809 атм.;

P_O2 = x_O2 * P = 0,2095 атм.;

P_Ar = x_Ar * P = 0,0093 атм.;

P_CO2 = x_CO2 * P = 0,0004 атм.

Эти данные означают, что если убрать весь кислород и остальные газы из атмосферы, а оставить только азот, то давление упадет на 22 %.

Знание парциального давления кислорода играет жизненно важную роль для людей, которые погружаются под воду. Так, если оно составит меньше 0,16 атм., то человек моментально теряет сознание. Наоборот, превышение парциальным давлением кислорода отметки 1,6 атм. ведет к отравлению этим газом, которое сопровождается конвульсиями. Таким образом, безопасное парциальное давление кислорода для жизни человека должно лежать в пределах 0,16 – 1,6 атм.

Расчёт мольной доли (φ) вещества

Для характеристи состава многокомпонентной системы (смеси веществ или раствора) часто требуется определить мольную долю (φ) отдельного компонента в этой системе.

Мольная доля вещества – содержание вещества в смеси (растворе), выраженное отношением числа молей этого вещества к общему числу молей всех веществ, содержащихся в смеси.

Мольная доля φ(компонента) в смеси вычисляется по формуле:

φ(компонента) = ν(компонента) / сумма ν(компонентов смеси).

Задача 1. Какова мольная доля пропана в пропан-бутановой смеси, если его массовая доля в этой смеси составляет 75%?

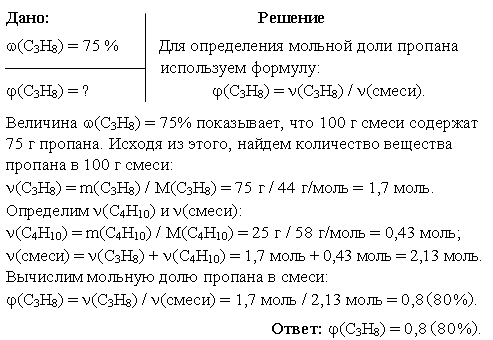
Задача 2. Синтетический каучук марки СКC-30 (сополимер бутадиена-1,3 и стирола) содержит 23,5% (по массе) звеньев стирола. Определите мольную долю звеньев бутадиена-1,3 в этом сополимере.

Решение
Сополимер бутадиена-1,3 и стирола образуется по схеме:

nCH₂=CH–CH=CH₂ + mCH₂=СН–C₆H₅ 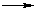[(–CH₂–CH=CH–CH₂–)_x(–CH₂–CH(C₆H₅)–)_y]_n+m

1 ≤ x << n;       1 ≤ y << m;

По условию задачи ω(–CH₂–CH(C₆H₅)–) = 23,5%, то есть 100 г сополимера содержат 23,5 г звеньев стирола C₈H₈ и 76,5 г бутадиеновых звеньев C₄H₆.
Найдём количество вещества C₄H₆ в 100 г сополимера:
ν(C₄H₆) = m(C₄H₆) / M(C₄H₆) = 76,5 г / 54 г/моль = 1,42 моль.
Определим количество вещества C₈H₈:
ν(C₈H₈) = m(C₈H₈) / M(C₈H₈) = 23,5 г / 104 г/моль = 0,22 моль.
Мольную долю звеньев бутадиена-1,3 рассчитаем по формуле:
φ(C₄H₆) = ν(C₄H₆) / [ν(C₄H₆) + ν(C₈H₈)] = 1,42 / 1,64 = 0,87 или 87%.

Ответ: φ(C₄H₆) = 0,87 (87%)