Как найти молярную долю смеси - Сайт, где вы сможете решить свои вопросы

Концентра́ция или до́ля компонента смеси — величина, количественно характеризующая содержание компонента относительно всей смеси. Терминология ИЮПАК под концентрацией компонента понимает четыре величины: соотношение молярного, или численного количества компонента, его массы, или объёма исключительно к объёму раствора^[1] (типичные единицы измерения — соответственно моль/л, л⁻¹, г/л, и безразмерная величина). Долей компонента ИЮПАК называют безразмерное соотношение одной из трёх однотипных величин — массы, объёма или количества вещества.^[2] Однако в обиходе термин «концентрация» могут применять и для долей, не являющихся объёмными долями, а также к соотношениям, не описанным ИЮПАК. Оба термина могут применяться к любым смесям, включая механические смеси, но наиболее часто применяются к растворам.

Можно выделить несколько типов математического описания: массовая концентрация, молярная концентрация, концентрация частиц и объемная концентрация^[3].

Эти стаканы, содержащие красный краситель, демонстрируют качественные изменения концентрации. Растворы слева более разбавлены, по сравнению с более концентрированными растворами справа.

Массовая доля[править | править код]

Массовая доля

определение	Массовая доля компонента — отношение массы данного компонента к сумме масс всех компонентов.
обозначение	— по рекомендациям ИЮПАК^[4]. — чаще в русскоязычной литературе. В технической литературе: — для массовой доли жидкой смеси — для массовой доли газовой смеси
единицы измерения	доли, %_масс (для выражения в %_масс следует умножить указанное выражение на 100 %)
формула	${displaystyle omega _{mathrm {B} }={frac {m_{mathrm {B} }}{m}}}$ где: ω_B — массовая доля компонента B m_B — масса компонента B; — общая масса всех компонентов смеси.

В бинарных растворах часто существует однозначная (функциональная) зависимость между плотностью раствора и его концентрацией (при данной температуре). Это даёт возможность определять на практике концентрации важных растворов с помощью денсиметра (спиртометра, сахариметра, лактометра). Некоторые ареометры проградуированы не в значениях плотности, а непосредственно концентрации раствора (спирта, жира в молоке, сахара). Следует учитывать, что для некоторых веществ кривая плотности раствора имеет максимум, в этом случае проводят два измерения: непосредственное, и при небольшом разбавлении раствора.

Часто для выражения концентрации (например, серной кислоты в электролите аккумуляторных батарей) пользуются просто их плотностью. Распространены ареометры (денсиметры, плотномеры), предназначенные для определения концентрации растворов веществ.

Объёмная доля[править | править код]

Объёмная доля

определение	Объёмная доля — отношение объёма компонента к сумме объёмов компонентов до смешивания.
обозначение	${displaystyle phi _{mathrm {B} }}$
единицы измерения	доли единицы, %_об (ИЮПАК не рекомендует добавлять дополнительные метки после знака %)
формула	${displaystyle phi _{mathrm {B} }={frac {V_{mathrm {B} }}{sum V_{i}}}}$ , где: ${displaystyle phi _{mathrm {B} }}$ — объёмная доля компонента B, V_B — объём компонента B; ${displaystyle sum V_{i}}$ — сумма объёмов всех компонентов до смешивания.

При смешивании жидкостей их суммарный объём может уменьшаться, поэтому не следует заменять сумму объёмов компонентов на объём смеси.

Как было указано выше, существуют ареометры, предназначенные для определения концентрации растворов определённых веществ. Такие ареометры проградуированы не в значениях плотности, а непосредственно концентрации раствора. Для распространённых растворов этилового спирта, концентрация которых обычно выражается в объёмных процентах, такие ареометры получили название спиртомеров или андрометров.

Молярность (молярная объёмная концентрация)[править | править код]

Молярная концентрация (молярность, мольность^[5])

определение	Молярность — количество вещества (число молей) компонента в единице объёма смеси.
обозначение	По рекомендации ИЮПАК, обозначается буквой или , где B — вещество, концентрация которого указывается.^[6]
единицы измерения	В системе СИ — моль/м³ На практике чаще — моль/л или ммоль/л. Также используют выражение «в молярности». Возможно другое обозначение молярной концентрации, которое принято обозначать М. Так, раствор с концентрацией 0,5 моль/л называют 0,5-молярным, записывают «0,5 M». Примечание: После числа пишут «моль», подобно тому, как после числа пишут «см», «кг» и т. п., не склоняя по падежам.
формула	${displaystyle {c_{mathrm {B} }}={frac {n_{mathrm {B} }}{V}}}$ , где: ${displaystyle n_{mathrm {B} }}$ — количество вещества компонента, моль; V — общий объём смеси, л

Нормальная концентрация (молярная концентрация эквивалента, «нормальность»)[править | править код]

Нормальная концентрация (молярная концентрация эквивалента, «нормальность»)

определение	Нормальная концентрация — количество эквивалентов данного вещества в 1 литре смеси.
обозначение	${displaystyle C_{N}(B)}$ , ${displaystyle C_{H}(B)}$ , ${displaystyle c(f_{eq}~mathrm {B} )}$
единицы измерения	Нормальную концентрацию выражают в моль-экв/л или г-экв/л (имеется в виду моль эквивалентов). Для записи концентрации таких растворов используют сокращения «н» или «N». Например, раствор, содержащий 0,1 моль-экв/л, называют децинормальным и записывают как 0,1 н.
формула	${displaystyle c(f_{eq}~mathrm {B} )=c{big (}(1/z)~mathrm {B} {big )}=zcdot c_{mathrm {B} }=zcdot {frac {n_{mathrm {B} }}{V}}={frac {1}{f_{eq}}}cdot {frac {n_{mathrm {B} }}{V}}}$ , где: ${displaystyle n_{mathrm {B} }}$ — количество вещества компонента, моль; — общий объём смеси, литров; — число эквивалентности (фактор эквивалентности $f_{{eq}}=1/z$ ).

Нормальная концентрация может отличаться в зависимости от реакции, в которой участвует вещество. Например, одномолярный раствор H₂SO₄ будет однонормальным, если он предназначается для реакции со щёлочью с образованием гидросульфата калия KHSO₄, и двухнормальным в реакции с образованием K₂SO₄.

Мольная (молярная) доля[править | править код]

Мольная (молярная) доля

определение	Мольная доля — отношение количества молей данного компонента к общему количеству молей всех компонентов.
обозначение	ИЮПАК рекомендует обозначать мольную долю буквой (а для газов — )^[7], также в литературе встречаются обозначения , .
единицы измерения	Доли единицы или %_мольн (ИЮПАК не рекомендует добавлять дополнительные метки после знака %)
формула	${displaystyle x_{mathrm {B} }={frac {n_{mathrm {B} }}{sum n_{i}}}}$ , где: ${displaystyle x_{mathrm {B} }}$ — мольная доля компонента B; ${displaystyle n_{mathrm {B} }}$ — количество компонента B, моль; $sum n_{i}$ — сумма количеств всех компонентов.

Мольная доля может использоваться, например, для количественного описания уровня загрязнений в воздухе, при этом её часто выражают в частях на миллион (ppm — от англ. parts per million). Однако, как и в случае с другими безразмерными величинами, во избежание путаницы, следует указывать величину, к которой относится указанное значение.

Моляльность (молярная весовая концентрация, моляльная концентрация)[править | править код]

Моляльная концентрация (моляльность,^[5] молярная весовая концентрация)

определение	Моляльная концентрация (моляльность,^[5] молярная весовая концентрация) — количество растворённого вещества (число моль) в 1000 г растворителя.
обозначение	Примечание: чтобы не путать с массой, в тех формулах где применяется моляльность, массу обозначают как
единицы измерения	моль/кг. Также распространено выражение в «моляльности». Так, раствор с концентрацией 0,5 моль/кг называют 0,5-мольным.
формула	${displaystyle {m_{mathrm {B} }}={frac {n_{mathrm {B} }}{m_{mathrm {A} }}}}$ , где: ${displaystyle n_{mathrm {B} }}$ — количество растворённого вещества, моль; ${displaystyle m_{mathrm {A} }}$ — масса растворителя, кг.

Следует обратить особое внимание, что, несмотря на сходство названий, молярная концентрация и моляльность — величины различные. Прежде всего, в отличие от молярной концентрации, при выражении концентрации в моляльности расчёт ведут на массу растворителя, а не на объём раствора. Моляльность, в отличие от молярной концентрации, не зависит от температуры.

Массовая концентрация (Титр)[править | править код]

Массовая концентрация (Титр)

определение	Массовая концентрация — отношение массы растворённого вещества к объёму раствора.
обозначение	или — по рекомендации ИЮПАК^[8]. — в аналитической химии
единицы измерения	доли, %_масс (для выражения в %_масс следует умножить указанное выражение на 100 %)
формула	${displaystyle rho _{mathrm {B} }={frac {m_{mathrm {B} }}{V}}}$ . где: ${displaystyle m_{mathrm {B} }}$ — масса растворённого вещества; — общий объём раствора;

В аналитической химии используется понятие титр по растворённому или по определяемому веществу (обозначается буквой ).

Концентрация частиц[править | править код]

определение	Концентрация частиц — отношение числа частиц N к объёму V, в котором они находятся
обозначение	— по рекомендации ИЮПАК^[9]. однако также часто встречается обозначение (не путать с количеством вещества).
единицы измерения	м⁻³ — в системе СИ, 1/л
формула	${displaystyle C_{mathrm {B} }={frac {N_{mathrm {B} }}{V}}={frac {n_{mathrm {B} }cdot N_{mathrm {A} }}{V}}=c_{mathrm {B} }cdot N_{mathrm {A} }}$ , где: ${displaystyle N_{mathrm {B} }}$ — количество частиц, — объём, ${displaystyle {ce {n_{mathrm {B} }}}}$ — количество вещества B, ${displaystyle N_{mathrm {A} }}$ — постоянная Авогадро, ${displaystyle c_{mathrm {B} }}$ — молярная концентрация B.

Весообъёмные (массо-объёмные) проценты[править | править код]

Иногда встречается использование так называемых «весообъёмных процентов»^[10], которые соответствуют массовой концентрации вещества, где единица измерения г/(100 мл) заменена на процент. Этот способ выражения используют, например, в спектрофотометрии, если неизвестна молярная масса вещества или если неизвестен состав смеси, а также по традиции в фармакопейном анализе.^[11] Стоит отметить, что поскольку масса и объём имеют разные размерности, использование процентов для их соотношения формально некорректно. Также международное бюро мер и весов^[12] и ИЮПАК^[13] не рекомендуют добавлять дополнительные метки (например «% (m/m)» для обозначения массовой доли) к единицам измерения.

Другие способы выражения концентрации[править | править код]

Существуют и другие, распространённые в определённых областях знаний или технологиях, методы выражения концентрации. Например, при приготовлении растворов кислот в лабораторной практике часто указывают, сколько объёмных частей воды приходится на одну объёмную часть концентрированной кислоты (например, 1:3). Иногда используют также отношение масс (отношение массы растворённого вещества к массе растворителя) и отношение объёмов (аналогично, отношение объёма растворяемого вещества к объёму растворителя).

Применимость способов выражения концентрации растворов, их свойства[править | править код]

В связи с тем, что моляльность, массовая доля, мольная доля не включают в себя значения объёмов, концентрация таких растворов остаётся неизменной при изменении температуры. Молярность, объёмная доля, титр, нормальность изменяются при изменении температуры, так как при этом изменяется плотность растворов. Именно моляльность используется в формулах повышения температуры кипения и понижения температуры замерзания растворов.

Разные виды выражения концентрации растворов применяются в разных сферах деятельности, в соответствии с удобством применения и приготовления растворов заданных концентраций. Так, титр раствора удобен в аналитической химии для волюмометрии (титриметрического анализа) и т. п.

Формулы перехода от одних выражений концентраций к другим[править | править код]

В зависимости от выбранной формулы погрешность конвертации колеблется от нуля до некоторого знака после запятой.

От молярности к нормальности[править | править код]

${displaystyle {c((1/z)~mathrm {B} )}={c_{mathrm {B} }}cdot {z}}$

где:

От молярности к титру[править | править код]

${displaystyle {T}={c_{mathrm {B} }}cdot {M}}$

где:

${displaystyle {c_{mathrm {B} }}}$ — молярная концентрация;
— молярная масса растворённого вещества.

Если молярная концентрация выражена в моль/л, а молярная масса — в г/моль, то для выражения ответа в г/мл его следует разделить на 1000 мл/л.

От массовой доли к молярности[править | править код]

${displaystyle c_{mathrm {B} }={frac {rho cdot omega _{mathrm {B} }}{M(mathrm {B} )}}}$

где:

Если плотность раствора выражена в г/мл, а молярная масса в г/моль, то для выражения ответа в моль/л выражение следует домножить на 1000 мл/л. Если массовая доля выражена в процентах, то выражение следует также разделить на 100 %.

От массовой доли к титру[править | править код]

где:

От моляльности к молярности[править | править код]

${displaystyle {c_{mathrm {B} }}=m_{mathrm {B} }{frac {mathrm {m} (A)}{V}}}$

где:

${displaystyle m_{mathrm {B} }}$ — моляльность,
— масса растворителя,
— суммарный объём раствора,

От моляльности к мольной доле[править | править код]

${displaystyle x_{mathrm {B} }={frac {m_{mathrm {B} }}{m_{mathrm {B} }+{frac {1}{M(mathrm {A} )}}}}}$

где:

${displaystyle m_{mathrm {B} }}$ — моляльность,
— молярная масса растворителя.

Если моляльность выражена в моль/кг, а молярная масса растворителя в г/моль, то единицу в формуле следует представить как 1000 г/кг, чтобы слагаемые в знаменателе имели одинаковые единицы измерения.

Сводная таблица[править | править код]

Формулы перехода от одних выражений концентраций к другим

			ω_B	φ_B	x_B	c_B	C_B	m_B	T_B
массовая доля	г/г	ω_B	${displaystyle omega _{mathrm {B} }={frac {mathrm {m} (B)}{mathrm {m} }}}$	${displaystyle omega _{mathrm {B} }=phi _{mathrm {B} }{frac {rho (B)}{rho }}}$	${displaystyle omega _{B}={frac {1}{{frac {M_{mathrm {A} }}{M_{mathrm {B} }}}({frac {1}{x_{mathrm {B} }}}-1)+1}}}$	${displaystyle omega _{B}={frac {M_{B}cdot c_{mathrm {B} }}{rho }}}$	${displaystyle omega _{B}={frac {M_{B}cdot c_{mathrm {B} }}{rho cdot N_{A}}}}$	${displaystyle omega _{mathrm {B} }={frac {m_{mathrm {B} }}{m_{mathrm {B} }+{frac {1}{M_{B}}}}}}$	${displaystyle omega _{B}={frac {T_{B}}{rho }}}$
объёмная доля	л/л	φ_B	${displaystyle phi _{mathrm {B} }={frac {omega _{B}}{rho (B)/rho }}}$	${displaystyle phi _{mathrm {B} }={frac {V_{mathrm {B} }}{V}}}$
мольная доля	моль/моль	x_B	${displaystyle x_{mathrm {B} }={frac {1}{{frac {M_{mathrm {B} }}{M_{mathrm {A} }}}({frac {1}{omega _{B}}}-1)+1}}}$		${displaystyle x_{mathrm {B} }={frac {n_{mathrm {B} }}{n}}}$	${displaystyle x_{mathrm {B} }={frac {c_{mathrm {B} }cdot V}{n}}}$		${displaystyle x_{mathrm {B} }={frac {m_{mathrm {B} }}{m_{mathrm {B} }+{frac {1}{M_{A}}}}}}$
молярность	моль/л	c_B	${displaystyle c_{mathrm {B} }={frac {rho cdot omega _{B}}{M_{B}}}}$		${displaystyle c_{mathrm {B} }={frac {x_{mathrm {B} }cdot n}{V}}}$	${displaystyle {c_{mathrm {B} }}={frac {n_{mathrm {B} }}{V}}}$		${displaystyle {c_{mathrm {B} }}=m_{mathrm {B} }{frac {mathrm {m} (A)}{V}}}$
нормальность	моль-экв/л	c((1/z) B)	${displaystyle c((1/z)~mathrm {B} )={frac {rho cdot omega _{B}}{M_{B}}}cdot z}$			${displaystyle {c((1/z)~mathrm {B} )}={c_{mathrm {B} }}cdot {z}}$
концентрация частиц	1/л	C_B	${displaystyle C_{mathrm {B} }={frac {rho cdot omega _{B}}{M_{B}}}cdot N_{A}}$			${displaystyle C_{mathrm {B} }=c_{mathrm {B} }cdot N_{mathrm {A} }}$	${displaystyle C_{mathrm {B} }={frac {N_{mathrm {B} }}{V}}}$
моляльность	моль/кг_р-ля	m_B	${displaystyle m_{mathrm {B} }={frac {omega _{B}}{M_{B}(1-omega _{B})}}}$					${displaystyle {m_{mathrm {B} }}={frac {n_{mathrm {B} }}{mathrm {m} (A)}}}$
титр	г/мл	T_B	${displaystyle {T_{B}}={rho }cdot {omega _{B}}}$			${displaystyle {T_{B}}={c_{mathrm {B} }}cdot {M}}$			${displaystyle T_{mathrm {B} }={frac {mathrm {m} (B)}{V}}}$

${displaystyle m_{mathrm {B} }}$ — моляльность вещества B,
— масса вещества B,
— масса растворителя,
— масса раствора,
$T_{B}$ — титр (массовая концентрация) B,
— плотность вещества B,
— плотность раствора,
— суммарный объём раствора,
${displaystyle N_{mathrm {A} }}$ — постоянная Авогадро,
${displaystyle N_{mathrm {B} }}$ — количество частиц вещества В,
${displaystyle n_{mathrm {B} }}$ — количество вещества В,
— количество раствора,
— молярная масса,

Примечания[править | править код]

↑ International Union of Pure and Applied Chemistry. concentration (англ.) // IUPAC Compendium of Chemical Terminology. — Research Triagle Park, NC: IUPAC. — ISBN 0967855098. — doi:10.1351/goldbook.C01222. Архивировано 20 июля 2018 года.
↑ International Union of Pure and Applied Chemistry. fraction (англ.) // IUPAC Compendium of Chemical Terminology. — Research Triagle Park, NC: IUPAC. — ISBN 0967855098. — doi:10.1351/goldbook.F02494. Архивировано 20 августа 2018 года.
↑ IUPAC Gold Book internet edition: «concentration».
↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book – mass fraction, w (англ.). goldbook.iupac.org. Дата обращения: 11 декабря 2018. Архивировано 13 декабря 2018 года.
↑ ¹ ² ³ Z. Sobecka, W. Choiński, P. Majorek. Dictionary of Chemistry and Chemical Technology: In Six Languages: English / German / Spanish / French / Polish / Russian. — Elsevier, 2013-09-24. — С. 641. — 1334 с. — ISBN 9781483284439.
↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book – amount concentration, c (англ.). goldbook.iupac.org. Дата обращения: 11 декабря 2018. Архивировано 21 декабря 2018 года.
↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book – amount fraction, x ( y for gaseous mixtures) (англ.). goldbook.iupac.org. Дата обращения: 11 декабря 2018. Архивировано 22 декабря 2018 года.
↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book – mass concentration, γ, ρ (англ.). goldbook.iupac.org. Дата обращения: 16 декабря 2018. Архивировано 7 декабря 2018 года.
↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book – number concentration, C,n (англ.). goldbook.iupac.org. Дата обращения: 11 декабря 2018. Архивировано 22 декабря 2018 года.
↑ Способы приготовления растворов на МедКурс. Ru. Дата обращения: 24 апреля 2012. Архивировано 29 октября 2012 года.
↑ Бернштейн И. Я., Каминский Ю. Л. Спектрофотометрический анализ в органической химии. — 2-е изд. — Ленинград: Химия, 1986. — с. 5
↑ The International System of Units (SI). www.bipm.org. Дата обращения: 23 декабря 2018. Архивировано из оригинала 14 августа 2017 года.
↑ Quantities, Units and Symbols in Physical Chemistry. www.iupac.org. Дата обращения: 23 декабря 2018. Архивировано из оригинала 20 декабря 2016 года.

Источник

Молярная доля – величина, которая характеризует отношение количества молей искомого вещества к общему количеству молей всех веществ, находящихся, например в растворе или смеси газов.

Как-же ее вычислить?

Для вычисления потребуется таблица Менделеева и калькулятор.

Этап 1.

Следует выписать формулы всех веществ и расчитать их молярные массы, используя таблицу Менделеева.

Пример:

Молярная масса воды (H20) равна 18. Почему? Атомная масса водорода (H) равна 1, а атомная масса кислорода (O) равна 16, соответственно 16+1+1=18.

Также, к примеру молярная масса оксида аллюминия (Al2O3) равна 27+27+16+16+16=102 (Атомная масса аллюминия 27, и как сказанно выше, кислорода 16).

Этап 2.

Теперь нужно определить количество молей каждого вещества. Для этого, массу вещества следует разделить на молярную массу.

Этап 3.

Теперь у нас есть сумма молей всех веществ (запишем, как Z) и количество молей искомого вещества (запишем, как n)

Формула для определения молярной доли X=n/Z, где X – искомая молярная доля, Z – сумма всех молей, n – моли искомого вещества.

Источник

При решении химических задач, при расчётах на работе, да и просто в жизни иногда приходится рассчитывать концентрации. Неважно, будет это школьная теоретическая задача, необходимость приготовить электролит для аккумулятора автомобиля, надобность узнать количество сахара для компота — все расчёты концентраций выполняются по известным формулам, которых не так много. Однако, с этим часто возникают трудности.

Прочитав эту статью, Вы научитесь легко рассчитывать концентрации веществ и при надобности играючи переводить одну концентрацию в другую. В статье приводятся примеры задач с решениями, а в конце приведём справочную табличку с формулами, которую можно распечатать и держать под рукой.

Массовая доля

Начнём с простого, но в то же время нужного способа выражения концентрации компонента в смеси — массовой доли.

Массовая доля есть отношение массы данного компонента к сумме масс всех компонентов. Обозначать её принято буквой w или ω (омега).

Рассчитывается массовая доля по формуле:

Large w_{i}=frac{m_{i}}{m}, ;;;;;(1)

где Large w_{i} — массовая доля компонента i в смеси,

Large m_{i} — масса этого компонента,

m — масса всей смеси.

И сразу разберём на примере:

Задача:

Зимой дороги посыпают песком с солью. Известно, что куча имеет массу 50 кг, и в неё всыпали 1 кг соли и перемешали. Найти массовую долю соли.

Решение:

Масса соли есть Large m_{i} по формуле выше. Масса всей смеси нам пока неизвестна, но найти её легко. Просуммируем массу песка и соли:

Large m = m_{п}+m_{с}= 50 кг + 1 кг = 51 кг

А теперь находим и массовую долю:

Large w_{с} = frac{m_{с}}{m} = 1 кг / 51 кг = 0.0196,

или умножаем на 100% и получаем 1.96%.

Ответ: 0.0196, или 1.96%.

Теперь решим что-то посложнее, и ближе к ЕГЭ.

Задача:

Смешали 200 г раствора глюкозы с массовой концентрацией 25% и 300 г раствора глюкозы с массовой концентрацией 10%. Найти массовую концентрацию полученного раствора, ответ округлить до целых.

Решение:

Обозначим первый и второй растворы соответственно Large m_{1} и Large m_{2}. Массу полученного после смешения раствора обозначим Large m и найдём:

Large m = m_{1} + m_{2} = 200 г + 300 г = 500 г

Массу самой глюкозы в первом и втором растворе обозначим Large m_{гл. 1} и Large m_{гл. 2}. По формуле (1) это будут наши массы компонентов. Массы растворов нам известны, их массовые концентрации тоже. Как найти массу компонента? Очень просто, находим неизвестное делимое умножением (и не забываем, что проценты — это сотые части):

Large m_{гл. 1} = w_{1}cdot m_{1} = 0.25 cdot 200 г = 50 г

Large m_{гл. 2} = w_{2}cdot m_{2} = 0.1 cdot 300 г = 30 г

Таким образом, общая масса глюкозы Large m_{гл}:

Large m_{гл} = m_{гл. 1} + m_{гл. 2} = 50 г + 30 г = 80 г.

Ответ: 80 г.

Задачи на смешение раствором с разными концентрациями одного вещества можно решать с помощью «конверта Пирсона».

Объёмная доля

Часто, когда мы имеем дело с жидкостями и газами, удобно оперировать их объёмами, а не массой. Поэтому, чтобы выражать долю какого-либо компонента в таких смесях (но и в твёрдых тоже вполне можно), пользуются понятием объёмной доли.

Объёмная доля компонента — отношение объёма компонента к сумме объёмов компонентов до смешивания. Объёмная доля измеряется в долях единицы или в процентах. Обычно обозначается греческой буквой φ (фи).

Рассчитывается объёмная доля по формуле:

Large phi_{B}=frac{V_{B}}{sum{V_{i}}}, ; ;;;; (2)

где Large phi_{B} — объёмная доля компонента B;

Large V_{B} — объём компонента B;

Large sum{V_{i}} — сумма объёмов всех компонентов.

Здесь важно понимать, что в формулу по возможности подставляем именно сумму объёмов всех компонентов, а не объём смеси, так как при смешивании некоторых жидкостей суммарный объём уменьшается. Так, если смешать литр воды и литр спирта, два литра аквавита мы не получим — будет примерно 1800 мл. В школьных задачах, как правило, это не так важно, но в уме держим и помним.

Задача:

Смешали 6 объёмов воды и 1 объём серной кислоты. Найти объёмную долю кислоты в полученном растворе.

Решение:

Так как объёмная доля — безразмерная величина, объёмы компонентов в условии задачи могут даваться в любых единицах — литрах, стаканах, баррелях, штофах, сексталях — главное, чтобы в одинаковых. Если не так — переводим одни в другие, если одинаковые — решаем. В нашем условии описаны просто некоторые «объёмы», их и подставляем.

Large phi_{H_{2}SO_{4}} = frac{V_{ H_{2}SO_{4} }} { V_{ H_{2}SO_{4}} + V_{H_{2}O}} = frac{1 : объём}{1 : объём + 6 : объёмов} = frac{1 : объём}{7 : объёмов} = 0.143, : или : 14.3%

Ответ: 14.3 %.

С газами всё обстоит немного интереснее — при не очень больших давлениях и температурах объёмная доля какого-либо газа в газовой смеси равна его мольной доле. (Ведь мы знаем, что молярный объём газов почти равен 22.4 л/моль).

Задача:

Мольная доля кислорода в сухом воздухе составляет 0.21. Найдите объёмную долю азота, если объёмная доля аргона составляет 1%.

Решение:

Внимательный читатель заметил, что мы написали о том, что объёмная и мольная доля для газов в смеси равны. Поэтому, объёмная доля кислорода равна также 0.21, или 21%. Найдём объёмную долю азота:

Large 100% – 21% – 1% = 78%.

Ответ: 78%.

Мольная доля

В тех случаях, когда нам известны количества веществ в смеси, мы можем выразить содержание того или иного компонента с помощью мольной доли.

Мольная доля — отношение количества молей данного компонента к общему количеству молей всех компонентов. Мольную долю выражают в долях единицы. ИЮПАК рекомендует обозначать мольную долю буквой x (а для газов — y).

Находят мольную долю по формуле:

Large x_{B} = frac{n_{B}}{sum{n_{i}}}, ;;;;;(3)

где Large x_{B} — мольная доля компонента B;

Large n_{B} — количество компонента B, моль;

Large sum{n_{i}} — сумма количеств всех компонентов.

Разберём на примере.

Задача:

При неизвестных условиях смешали 3 кг азота, 1 кг кислорода и 0.5 кг гелия. Найти мольную долю каждого компонента полученной газовой смеси.

Решение:

Сначала находим количество каждого из газов (моль):

Large n_{N_{2}} = frac{ m_{N_{2}}}{M_{N_{2}}} = frac {3000 : г}{28 : ^г/_{моль}} = 107.14 : моль

Large n_{O_{2}} = frac{ m_{O_{2}}}{M_{O_{2}}} = frac {1000 : г}{32 : ^г/_{моль}} = 31.25 : моль

Large n_{He} = frac{ m_{He}}{M_{He}} = frac {500 : г}{4 : ^г/_{моль}} = 125 : моль

Затем считаем сумму количеств:

Large sum {n} = 107.14 : моль + 31.25 : моль + 125 : моль = 263.39 : моль

И находим мольную долю каждого компонента:

Large y_{N_{2}} = frac {107.14 : моль}{263.39 : моль} = 0.4068, : или : 40.68 %;

Large y_{O_{2}} = frac {31.25 : моль}{263.39 : моль} = 0.1186, : или : 11.86 %;

Large y_{He} = frac {125 : моль}{263.39 : моль} = 0.4746, : или : 47.46 %;

Проверяем:

Large 40.68 % + 11.86 % + 47.46 % = 100%.

И радуемся правильному решению.

Ответ: 40.68%, 11.86% , 47.46%.

Молярность (молярная объёмная концентрация)

А сейчас рассмотрим, вероятно, самый часто встречающийся способ выражения концентрации — молярную концентрацию.

Молярная концентрация (молярность, мольность) — количество вещества (число молей) компонента в единице объёма смеси. Молярная концентрация в системе СИ измеряется в моль/м³, однако на практике её гораздо чаще выражают в моль/л или ммоль/л.

Также иногда говорят просто «молярность», и обозначают буквой М. Это значит, что, например, обозначение «0.5 М раствор соляной кислоты» следует понимать как «полумолярный раствор соляной кислоты», или 0.5 моль/л.

Обозначают молярную концентрацию буквой c (латинская «цэ»), или заключают в квадратные скобки вещество, концентрация которого указывается. Например, [Na⁺] — концентрация катионов натрия в моль/л. Кстати, слово «моль» в обозначениях не склоняют — 5 моль/л, 3 моль/л.

Рассчитывается молярная концентрация по формуле:

Large c_{B} = frac{n_{B}}{V} ; ; ;;; (4)

где Large n_{B} — количество вещества компонента B, моль;

Large V — общий объём смеси, л.

Разберём на примере.

Задача:

В пивную кружку зачем-то насыпали 24 г сахара и до краёв заполнили кипятком. А нам зачем-то нужно найти молярную концентрацию сахарозы в полученном сиропе. И кстати, дело происходило в Британии.

Решение:

Молекулярная масса сахарозы равна 342 (посчитайте, может мы ошиблись — C₁₂H₂₂O₁₁). Найдём количество вещества:

Large n_{сахарозы} = frac{24 : г}{342 : г/моль} = 0.0702 моль

Британская пинта (мера объёма такая) равна 0.568 л. Поэтому молярная концентрация находится так:

Large c_{сахарозы} = frac{0.0702 : моль}{0.568 : л} = 0.1236 моль/л

Ответ: 0.1236 моль/л.

Нормальная концентрация (молярная концентрация эквивалента, «нормальность»)

Нормальная концентрация — количество эквивалентов данного вещества в 1 литре смеси. Нормальную концентрацию выражают в моль-экв/л или г-экв/л (имеется в виду моль эквивалентов).

Обозначается нормальная концентрация как с_н, с_N, или даже c(f_eq B). Рассчитывается нормальная концентрация по формуле:

Large c_{N} = z cdot c_{B} = z cdot frac{n_{B}}{V}= frac{1}{f_{eq}} cdot frac {n_{B}}{V} ; ;;;; (5)

где Large n_{B} — количество вещества компонента В, моль;

V — общий объём смеси, л;

z — число эквивалентности (фактор эквивалентности Large f_{eq} = 1/z ).

Значение нормальной концентрации для растворов записывают как «н» или «N», а говорят «нормальность» или «нормальный». Например, раствор с концентрацией 0.25 н — четвертьнормальный раствор.

Разберём на примере.

Задача:

Рассчитать нормальность раствора объёмом 1 л, если в нём содержится 40 г перманганата калия. Раствор приготовили для последующего проведения реакции в нейтральной среде.

Решение:

В нейтральной среде перманганат калия восстанавливается до оксида марганца (IV). При этом в окислительно-восстановительной реакции 1 атом марганца принимает 3 электрона (проверьте на любой окислительно-восстановительной реакции перманганата калия с образованием оксида, расставив степени окисления), что означает, что число эквивалентности будет равно 3. Для расчёта концентрации по формуле (5) выше нам ещё не хватает количества вещества KMnO4. найдём его:

Large n_{KMnO_{4}}=frac{m _{KMnO_{4}}}{M _{KMnO_{4}} } = frac{40 : г}{158 г/моль}= 0.253 моль

Теперь считаем нормальную концентрацию:

Large c_{N_{KMnO_{4}}}= z cdot frac{n_{KMnO_{4}}}{V} = 3 cdot frac{0.253 : моль}{1 : л} = 0.759 моль-экв/л

Ответ: 0.759 моль-экв/л.

Таким образом, заметим важное на практике свойство — нормальная концентрация больше молярной в z раз.

Мы не будем рассматривать в данной статье особо экзотические способы выражения концентраций, о них вы можете почитать в литературе или интернете. Поэтому расскажем ещё об одном способе, и на нём остановимся — массовая концентрация.

Моляльная концентрация

Моляльная концентрация (моляльность, молярная весовая концентрация) — количество растворённого вещества (число моль) в 1000 г растворителя.

Измеряется моляльная концентрация в молях на кг. Как и с молярной концентрацией, иногда говорят «моляльность», то есть раствор с концентрацией 0.25 моль/кг можно назвать четвертьмоляльным.

Находится моляльная концентрация по формуле:

Large m_{B} = frac{n_{B}}{m_{A}}, ;;;;; (6)

где Large n_{B} — количество вещества компонента B, моль;

Large m_{A} — масса растворителя, кг.

Казалось бы, зачем нужна такая единица измерения для выражения концентрации? Так вот, у моляльной концентрации есть одно важное свойство — она не зависит от температуры, в отличие, например, от молярной. Подумайте, почему?

Массовая концентрация

Массовая концентрация — отношение массы растворённого вещества к объёму раствора. По рекомендации ИЮПАК, обозначается символом γ или ρ.

Находится массовая концентрация по формуле:

Large rho_{B}=frac{m_{B}}{V}, ;;;;; (7)

где Large m_{B} — масса растворенного вещества, г;

Large V — общий объём смеси, л.

В системе СИ выражается в кг/м³.

Разберём на примере.

Задача:

Рассчитать массовую концентрацию перманганата калия по условиям предыдущей задачи.

Решение:

Решение будет совсем простым. Считаем:

Large rho_{ KMnO_{4} }=frac{m_{ KMnO_{4} }}{V} =frac{40 : г}{1 : л} = 40 г/л.

Ответ: 40 г/л.

Также в аналитической химии пользуются понятием титра по растворенному веществу. Титр по растворенному веществу находится так же, как и массовая концентрация, но выражается в г/мл. Легко догадаться, что в задаче выше титр будет равен 0.04 г/мл (для этого надо умножить наш ответ на 0.001 мл/л, проверьте). Кстати, обозначается титр буквой Т.

А теперь, как обещали, табличка с формулами перевода одной концентрации в другую.

Таблица перевода одной концентрации в другую.

В таблице слева — ВО ЧТО переводим, сверху — ЧТО. Если стоит знак «=», то, естественно, эти величины равны.

	Массовая доля, large omega, %	Мольная доля, large x , %	Объёмная доля, large phi, %	Молярная концентрация, large c, моль/л	Нормальная концентрация, large c_{N} , моль-экв/л	Моляльная концентрация, large m, моль/кг	Массовая концентрация, large rho, г/л
Массовая доля, large omega, %	=	large omega_{B}=LARGE frac{x_{B} cdot M(B)}{sum x_{i} cdot M_{i}}	Для газов: omega = LARGE frac{phi_{A} cdot M(A)}{sum (M_{i} cdot phi_{i})}	large omega_{B}= LARGE frac{c_{B} cdot M(B)}{rho}	large omega_{B}=LARGE frac{c_{N} cdot M(B)}{rho cdot z}		large omega_{B}= LARGE frac{gamma_{B}}{rho}
Мольная доля, large x , %	large x_{B}=LARGE frac{frac{omega_{B}}{M(B)}}{sum frac{omega_{i}}{M_{i}}}	=				large x_{B}=LARGE frac{m_{B}}{m_{B}+frac{1}{M(A)}}
Объёмная доля, large phi, %	Для газов: large phi_{A}=LARGE frac{frac{omega_{A}}{M(A)}}{sum frac{omega_{i}}{M_{i}}}		=
Молярная концентрация, large c, моль/л	large c_{B}=LARGE frac{rho cdot omega_{B}}{M(B)}			=	large c_{B}=Large frac{c_{N}}{z}
Нормальная концентрация, large c_{N} , моль-экв/л	large c_{N}=LARGE frac{rho cdot omega_{B} cdot z}{M(B)}			large c_{N}=c_{B} cdot z	=
Моляльная концентрация, large m, моль/кг		large m_{B}=Large frac{x_{B}}{M(A)(1-x_{B})}				=
Массовая концентрация, large gamma, г/л	large gamma_{B}=rho cdot omega_{B}						=

Таблица будет пополняться.

Источник

From Wikipedia, the free encyclopedia

In chemistry, the mole fraction or molar fraction (x_i or χ_i) is defined as unit of the amount of a constituent (expressed in moles), n_i, divided by the total amount of all constituents in a mixture (also expressed in moles), n_tot.^[1] This expression is given below:

${displaystyle x_{i}={frac {n_{i}}{n_{mathrm {tot} }}}}$

The sum of all the mole fractions is equal to 1:

${displaystyle sum _{i=1}^{N}n_{i}=n_{mathrm {tot} }; sum _{i=1}^{N}x_{i}=1.}$

The same concept expressed with a denominator of 100 is the mole percent, molar percentage or molar proportion (mol%).

The mole fraction is also called the amount fraction.^[1] It is identical to the number fraction, which is defined as the number of molecules of a constituent N_i divided by the total number of all molecules N_tot. The mole fraction is sometimes denoted by the lowercase Greek letter χ (chi) instead of a Roman x.^[2]^[3] For mixtures of gases, IUPAC recommends the letter y.^[1]

The National Institute of Standards and Technology of the United States prefers the term amount-of-substance fraction over mole fraction because it does not contain the name of the unit mole.^[4]

Whereas mole fraction is a ratio of moles to moles, molar concentration is a quotient of moles to volume.

The mole fraction is one way of expressing the composition of a mixture with a dimensionless quantity; mass fraction (percentage by weight, wt%) and volume fraction (percentage by volume, vol%) are others.

Properties[edit]

Mole fraction is used very frequently in the construction of phase diagrams. It has a number of advantages:

it is not temperature dependent (as is molar concentration) and does not require knowledge of the densities of the phase(s) involved
a mixture of known mole fraction can be prepared by weighing off the appropriate masses of the constituents
the measure is symmetric: in the mole fractions x = 0.1 and x = 0.9, the roles of ‘solvent’ and ‘solute’ are reversed.
In a mixture of ideal gases, the mole fraction can be expressed as the ratio of partial pressure to total pressure of the mixture
In a ternary mixture one can express mole fractions of a component as functions of other components mole fraction and binary mole ratios:

${displaystyle {begin{aligned}x_{1}&={frac {1-x_{2}}{1+{frac {x_{3}}{x_{1}}}}}\[2pt]x_{3}&={frac {1-x_{2}}{1+{frac {x_{1}}{x_{3}}}}}end{aligned}}}$

Differential quotients can be formed at constant ratios like those above:

${displaystyle left({frac {partial x_{1}}{partial x_{2}}}right)_{frac {x_{1}}{x_{3}}}=-{frac {x_{1}}{1-x_{2}}}}$

${displaystyle left({frac {partial x_{3}}{partial x_{2}}}right)_{frac {x_{1}}{x_{3}}}=-{frac {x_{3}}{1-x_{2}}}}$

The ratios X, Y, and Z of mole fractions can be written for ternary and multicomponent systems:

${displaystyle {begin{aligned}X&={frac {x_{3}}{x_{1}+x_{3}}}\[2pt]Y&={frac {x_{3}}{x_{2}+x_{3}}}\[2pt]Z&={frac {x_{2}}{x_{1}+x_{2}}}end{aligned}}}$

These can be used for solving PDEs like:

${displaystyle left({frac {partial mu _{2}}{partial n_{1}}}right)_{n_{2},n_{3}}=left({frac {partial mu _{1}}{partial n_{2}}}right)_{n_{1},n_{3}}}$

${displaystyle left({frac {partial mu _{2}}{partial n_{1}}}right)_{n_{2},n_{3},n_{4},ldots ,n_{i}}=left({frac {partial mu _{1}}{partial n_{2}}}right)_{n_{1},n_{3},n_{4},ldots ,n_{i}}}$

This equality can be rearranged to have differential quotient of mole amounts or fractions on one side.

${displaystyle left({frac {partial mu _{2}}{partial mu _{1}}}right)_{n_{2},n_{3}}=-left({frac {partial n_{1}}{partial n_{2}}}right)_{mu _{1},n_{3}}=-left({frac {partial x_{1}}{partial x_{2}}}right)_{mu _{1},n_{3}}}$

${displaystyle left({frac {partial mu _{2}}{partial mu _{1}}}right)_{n_{2},n_{3},n_{4},ldots ,n_{i}}=-left({frac {partial n_{1}}{partial n_{2}}}right)_{mu _{1},n_{2},n_{4},ldots ,n_{i}}}$

Mole amounts can be eliminated by forming ratios:

${displaystyle left({frac {partial n_{1}}{partial n_{2}}}right)_{n_{3}}=left({frac {partial {frac {n_{1}}{n_{3}}}}{partial {frac {n_{2}}{n_{3}}}}}right)_{n_{3}}=left({frac {partial {frac {x_{1}}{x_{3}}}}{partial {frac {x_{2}}{x_{3}}}}}right)_{n_{3}}}$

Thus the ratio of chemical potentials becomes:

${displaystyle left({frac {partial mu _{2}}{partial mu _{1}}}right)_{frac {n_{2}}{n_{3}}}=-left({frac {partial {frac {x_{1}}{x_{3}}}}{partial {frac {x_{2}}{x_{3}}}}}right)_{mu _{1}}}$

Similarly the ratio for the multicomponents system becomes

${displaystyle left({frac {partial mu _{2}}{partial mu _{1}}}right)_{{frac {n_{2}}{n_{3}}},{frac {n_{3}}{n_{4}}},ldots ,{frac {n_{i-1}}{n_{i}}}}=-left({frac {partial {frac {x_{1}}{x_{3}}}}{partial {frac {x_{2}}{x_{3}}}}}right)_{mu _{1},{frac {n_{3}}{n_{4}}},ldots ,{frac {n_{i-1}}{n_{i}}}}}$

[edit]

Mass fraction[edit]

The mass fraction w_i can be calculated using the formula

${displaystyle w_{i}=x_{i}{frac {M_{i}}{bar {M}}}=x_{i}{frac {M_{i}}{sum _{j}x_{j}M_{j}}}}$

where M_i is the molar mass of the component i and M̄ is the average molar mass of the mixture.

Molar mixing ratio[edit]

The mixing of two pure components can be expressed introducing the amount or molar mixing ratio of them ${displaystyle r_{n}={frac {n_{2}}{n_{1}}}}$ . Then the mole fractions of the components will be:

${displaystyle {begin{aligned}x_{1}&={frac {1}{1+r_{n}}}\[2pt]x_{2}&={frac {r_{n}}{1+r_{n}}}end{aligned}}}$

The amount ratio equals the ratio of mole fractions of components:

${displaystyle {frac {n_{2}}{n_{1}}}={frac {x_{2}}{x_{1}}}}$

due to division of both numerator and denominator by the sum of molar amounts of components. This property has consequences for representations of phase diagrams using, for instance, ternary plots.

Mixing binary mixtures with a common component to form ternary mixtures[edit]

Mixing binary mixtures with a common component gives a ternary mixture with certain mixing ratios between the three components. These mixing ratios from the ternary and the corresponding mole fractions of the ternary mixture x₁₍₁₂₃₎, x₂₍₁₂₃₎, x₃₍₁₂₃₎ can be expressed as a function of several mixing ratios involved, the mixing ratios between the components of the binary mixtures and the mixing ratio of the binary mixtures to form the ternary one.

${displaystyle x_{1(123)}={frac {n_{(12)}x_{1(12)}+n_{13}x_{1(13)}}{n_{(12)}+n_{(13)}}}}$

Mole percentage[edit]

Multiplying mole fraction by 100 gives the mole percentage, also referred as amount/amount percent [abbreviated as (n/n)% or mol %].

Mass concentration[edit]

The conversion to and from mass concentration ρ_i is given by:

${displaystyle {begin{aligned}x_{i}&={frac {rho _{i}}{rho }}{frac {bar {M}}{M_{i}}}\[3pt]Leftrightarrow rho _{i}&=x_{i}rho {frac {M_{i}}{bar {M}}}end{aligned}}}$

where M̄ is the average molar mass of the mixture.

Molar concentration[edit]

The conversion to molar concentration c_i is given by:

${displaystyle {begin{aligned}c_{i}&=x_{i}c\[3pt]&={frac {x_{i}rho }{bar {M}}}={frac {x_{i}rho }{sum _{j}x_{j}M_{j}}}end{aligned}}}$

where M̄ is the average molar mass of the solution, c is the total molar concentration and ρ is the density of the solution.

Mass and molar mass[edit]

The mole fraction can be calculated from the masses m_i and molar masses M_i of the components:

${displaystyle x_{i}={frac {frac {m_{i}}{M_{i}}}{sum _{j}{frac {m_{j}}{M_{j}}}}}}$

Spatial variation and gradient[edit]

In a spatially non-uniform mixture, the mole fraction gradient triggers the phenomenon of diffusion.

References[edit]

^ ^a ^b ^c IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”) (1997). Online corrected version: (2006–) “amount fraction”. doi:10.1351/goldbook.A00296
^ Zumdahl, Steven S. (2008). Chemistry (8th ed.). Cengage Learning. p. 201. ISBN 978-0-547-12532-9.
^ Rickard, James N.; Spencer, George M.; Bodner, Lyman H. (2010). Chemistry: Structure and Dynamics (5th ed.). Hoboken, N.J.: Wiley. p. 357. ISBN 978-0-470-58711-9.
^ Thompson, A.; Taylor, B. N. (2 July 2009). “The NIST Guide for the use of the International System of Units”. National Institute of Standards and Technology. Retrieved 5 July 2014.

Источник

Расчёт мольной доли (φ) вещества

Для характеристи состава многокомпонентной системы (смеси веществ или раствора) часто требуется определить мольную долю (φ) отдельного компонента в этой системе.

Мольная доля вещества – содержание вещества в смеси (растворе), выраженное отношением числа молей этого вещества к общему числу молей всех веществ, содержащихся в смеси.

Мольная доля φ(компонента) в смеси вычисляется по формуле:

φ(компонента) = ν(компонента) / сумма ν(компонентов смеси).

Задача 1. Какова мольная доля пропана в пропан-бутановой смеси, если его массовая доля в этой смеси составляет 75%?

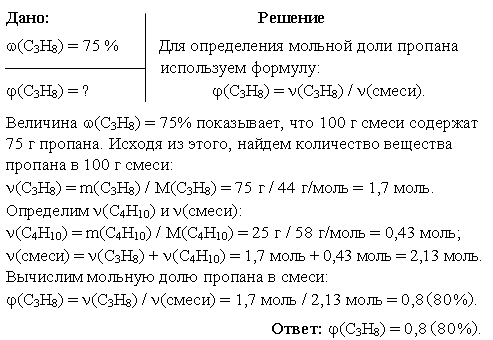
Задача 2. Синтетический каучук марки СКC-30 (сополимер бутадиена-1,3 и стирола) содержит 23,5% (по массе) звеньев стирола. Определите мольную долю звеньев бутадиена-1,3 в этом сополимере.

Решение
Сополимер бутадиена-1,3 и стирола образуется по схеме:

nCH₂=CH–CH=CH₂ + mCH₂=СН–C₆H₅ 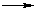[(–CH₂–CH=CH–CH₂–)_x(–CH₂–CH(C₆H₅)–)_y]_n+m

1 ≤ x << n; 1 ≤ y << m;

По условию задачи ω(–CH₂–CH(C₆H₅)–) = 23,5%, то есть 100 г сополимера содержат 23,5 г звеньев стирола C₈H₈ и 76,5 г бутадиеновых звеньев C₄H₆.
Найдём количество вещества C₄H₆ в 100 г сополимера:
ν(C₄H₆) = m(C₄H₆) / M(C₄H₆) = 76,5 г / 54 г/моль = 1,42 моль.
Определим количество вещества C₈H₈:
ν(C₈H₈) = m(C₈H₈) / M(C₈H₈) = 23,5 г / 104 г/моль = 0,22 моль.
Мольную долю звеньев бутадиена-1,3 рассчитаем по формуле:
φ(C₄H₆) = ν(C₄H₆) / [ν(C₄H₆) + ν(C₈H₈)] = 1,42 / 1,64 = 0,87 или 87%.

Ответ: φ(C₄H₆) = 0,87 (87%)

Источник

Массовая доля[править | править код]

Объёмная доля[править | править код]

Молярность (молярная объёмная концентрация)[править | править код]

Нормальная концентрация (молярная концентрация эквивалента, «нормальность»)[править | править код]

Мольная (молярная) доля[править | править код]

Моляльность (молярная весовая концентрация, моляльная концентрация)[править | править код]

Массовая концентрация (Титр)[править | править код]

Концентрация частиц[править | править код]

Весообъёмные (массо-объёмные) проценты[править | править код]

Другие способы выражения концентрации[править | править код]

Применимость способов выражения концентрации растворов, их свойства[править | править код]

Формулы перехода от одних выражений концентраций к другим[править | править код]

От молярности к нормальности[править | править код]

От молярности к титру[править | править код]

От массовой доли к молярности[править | править код]

От массовой доли к титру[править | править код]

От моляльности к молярности[править | править код]

От моляльности к мольной доле[править | править код]

Сводная таблица[править | править код]

Примечания[править | править код]

Массовая доля

Задача:

Решение:

Задача:

Решение:

Объёмная доля

Задача:

Решение:

Задача:

Решение:

Мольная доля

Задача:

Решение:

Молярность (молярная объёмная концентрация)

Задача:

Решение:

Нормальная концентрация (молярная концентрация эквивалента, «нормальность»)

Задача:

Решение:

Моляльная концентрация

Массовая концентрация

Задача:

Решение:

Таблица перевода одной концентрации в другую.

Properties[edit]

[edit]

Mass fraction[edit]

Molar mixing ratio[edit]

Mixing binary mixtures with a common component to form ternary mixtures[edit]

Mole percentage[edit]

Mass concentration[edit]

Molar concentration[edit]

Mass and molar mass[edit]

Spatial variation and gradient[edit]

References[edit]

Вам также может понравиться

Как найти время в питере

Как найти высоту клина

Как найти на окружности arctg

Добавить комментарий Отменить ответ