Как найти молярную электропроводность

Как найти молярную электропроводность

Молярная
электропроводность
(λ,
«ламбда»),
т. е.
электропроводность раствора, содержащего
1 моль электролита, помещенного между
параллельными электродами, расположенными
на расстоянии 1 м.

Молярная
электропроводность связана с удельной
электропроводностью следующим
соотношением:

,
[Ом-1м2моль-1] 

где с
– молярная концентрация раствора.

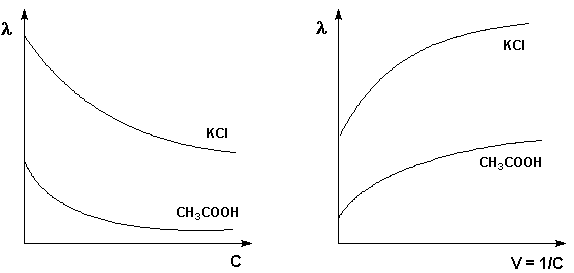
Молярная
электропроводность электролитов
увеличивается с уменьшением концентрации
(т.е. увеличением разведения раствора
V = 1/С), достигая некоторого максимального
значения
,
называемого молярной электропроводностью
при бесконечном разведении.

Рис.Зависимость молярнойРис. Зависимость
молярной
       
электропроводности от концентрации.           
электропроводности от разведения

Для слабого
электролита уменьшение молярной
электропроводности с увеличением
концентрации объясняется увеличением
степени диссоциации ()
с разбавлением раствора. Для сильного
электролита с уменьшением концентрации
ослабляется взаимодействие ионов между
собой, что увеличивает скорость их
движения и, следовательно, молярную
электропроводность раствора.

14. Подвижность ионов. Закон Кольрауша. Расчет степени и константы диссоциации.

Молярная
электропроводность связана с абсолютными
скоростями движения катионов и анионов
U+и U–:

             

Закон Ф. Кольрауша:

Молярная
электропроводность бесконечно
разбавленных растворов электролитов
является суммой подвижностей катиона
и анионаиданного
электролита:

Отсюда

 ,
      
.

Электролитическая
подвижность является важнейшей
характеристикой иона, отражающей его
участие в электропроводности раствора.

Полноту диссоциации
электролита можно оценить по степени
диссоциации α,

.

Величина степени
диссоциации зависит от природы
растворителя и растворенного вещества,
концентрации раствора и температуры.
По величине степени диссоциации
электролиты подразделяются на три
группы: сильные (α≥ 0.7), средней силы (0.3 <α< 0.7) и слабые (α≤ 0.3). К сильным электролитам относятся
почти все соли, большинство неорганических
кислот и щелочей; к слабым – все
органические кислоты, вода, NН4ОН,
Н2S и т.д. Электролитами средней
силы являются некоторые неорганические
кислоты: НF, НСN, Н3PO4.

Количественной
характеристикой силы электролита
является константа диссоциации К. Для
реакции

АВ = А++ В–,

константа
диссоциации равна

,
или

,

где с – концентрация
электролита.

15. Электродный потенциал. Формула Нернста.

При соприкосновении
металлической пластинки с полярным
растворителем (водой) либо раствором
электролита на границе электрод –
жидкость возникает двойной
электрический слой
(ДЭС) и возникает скачок потенциала,
называемый электродным потенциалом.

Величина электродного
потенциала металлического электрода
зависит от температуры и активности
(концентрации) иона металла в растворе,
в который опущен электрод. Математически
эта зависимость выражается уравнением
Нернста

    ,

где z – заряд иона,

–стандартный электродный
потенциал, равный потенциалу
электрода при активности иона металла,
равной 1 моль/л.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

From Wikipedia, the free encyclopedia

The molar conductivity of an electrolyte solution is defined as its conductivity divided by its molar concentration.[1][2]

{displaystyle Lambda _{text{m}}={frac {kappa }{c}},}

where:

κ is the measured conductivity (formerly known as specific conductance),[3]
c is the molar concentration of the electrolyte.

The SI unit of molar conductivity is siemens metres squared per mole (S m2 mol−1).[2] However, values are often quoted in S cm2 mol−1.[4] In these last units, the value of Λm may be understood as the conductance of a volume of solution between parallel plate electrodes one centimeter apart and of sufficient area so that the solution contains exactly one mole of electrolyte.[5]

Variation of molar conductivity with dilution[edit]

There are two types of electrolytes: strong and weak. Strong electrolytes usually undergo complete ionization, and therefore they have higher conductivity than weak electrolytes, which undergo only partial ionization. For strong electrolytes, such as salts, strong acids and strong bases, the molar conductivity depends only weakly on concentration. On dilution there is a regular increase in the molar conductivity of strong electrolyte, due to the decrease in solute–solute interaction. Based on experimental data Friedrich Kohlrausch (around the year 1900) proposed the non-linear law for strong electrolytes:

{displaystyle Lambda _{text{m}}=Lambda _{text{m}}^{circ }-K{sqrt {c}}=alpha f_{lambda }Lambda _{text{m}}^{circ },}

where

Λ∘
m is the molar conductivity at infinite dilution (or limiting molar conductivity), which can be determined by extrapolation of Λm as a function of √c,
K is the Kohlrausch coefficient, which depends mainly on the stoichiometry of the specific salt in solution,
α is the dissociation degree even for strong concentrated electrolytes,
fλ is the lambda factor for concentrated solutions.

This law is valid for low electrolyte concentrations only; it fits into the Debye–Hückel–Onsager equation.[6]

For weak electrolytes (i.e. incompletely dissociated electrolytes), however, the molar conductivity strongly depends on concentration: The more dilute a solution, the greater its molar conductivity, due to increased ionic dissociation. For example, acetic acid has a higher molar conductivity in dilute aqueous acetic acid than in concentrated acetic acid.

Kohlrausch’s law of independent migration of ions[edit]

Friedrich Kohlrausch in 1875–1879 established that to a high accuracy in dilute solutions, molar conductivity can be decomposed into contributions of the individual ions. This is known as Kohlrausch’s law of independent ionic migration.[7]
For any electrolyte AxBy, the limiting molar conductivity is expressed as x times the limiting molar conductivity of Ay+ and y times the limiting molar conductivity of Bx−.

{displaystyle Lambda _{text{m}}^{circ }=Sigma _{i}nu _{i}lambda _{i},}

where:

λi is the limiting molar ionic conductivity of ion i,
νi is the number of ions i in the formula unit of the electrolyte (e.g. 2 and 1 for Na+ and SO2−
4 in Na2SO4).

Kohlrausch’s evidence for this law was that the limiting molar conductivities of two electrolytes with two different cations and a common anion differ by an amount which is independent of the nature of the anion. For example, Λ0(KX) − Λ0(NaX) = 23.4 S cm2 mol−1 for X = Cl−, I− and 1/2 SO2−
4. This difference is ascribed to a difference in ionic conductivities between K+ and Na+. Similar regularities are found for two electrolytes with a common anion and two cations.[8]

Molar ionic conductivity[edit]

The molar ionic conductivity of each ionic species is proportional to its electrical mobility (μ), or drift velocity per unit electric field, according to the equation

{displaystyle lambda =zmu F}

where z is the ionic charge, and F is the Faraday constant.[9]

The limiting molar conductivity of a weak electrolyte cannot be determined reliably by extrapolation. Instead it can be expressed as a sum of ionic contributions, which can be evaluated from the limiting molar conductivities of strong electrolytes containing the same ions. For aqueous acetic acid as an example,[4]

{displaystyle {begin{aligned}Lambda _{text{m}}^{circ }({ce {CH3COOH}})&=lambda ({ce {CH3COO-}})+lambda ({ce {H+}})\&=Lambda _{text{m}}^{circ }({ce {CH3COONa}})+Lambda _{text{m}}^{circ }({ce {HCl}})-Lambda _{text{m}}^{circ }({ce {NaCl}}).end{aligned}}}

Values for each ion may be determined using measured ion transport numbers. For the cation:

{displaystyle lambda ^{+}=t_{+}cdot {frac {Lambda _{0}}{nu ^{+}}}}

and for the anion:

{displaystyle lambda ^{-}=t_{-}cdot {frac {Lambda _{0}}{nu ^{-}}}.}

Most monovalent ions in water have limiting molar ionic conductivities in the range of 40–80 S cm2 mol−1. For example:[4]

Cation λ, S cm2 mol−1
Li+ 38.6
Na+ 50.1
K+ 73.5
Ag+ 61.9
Anion λ, S cm2 mol−1
F− 55.4
Cl− 76.4
Br− 78.1
CH3COO− 40.9

The order of the values for alkali metals is surprising, since it shows that the smallest cation Li+ moves more slowly in a given electric field than Na+, which in turn moves more slowly than K+. This occurs because of the effect of solvation of water molecules: the smaller Li+ binds most strongly to about four water molecules so that the moving cation species is effectively Li(H
2O)+
4. The solvation is weaker for Na+ and still weaker for K+.[4] The increase in halogen ion mobility from F− to Cl− to Br− is also due to decreasing solvation.

Exceptionally high values are found for H+ (349.8 S cm2 mol−1) and OH− (198.6 S cm2 mol−1), which are explained by the Grotthuss proton-hopping mechanism for the movement of these ions.[4] The H+ also has a larger conductivity than other ions in alcohols, which have a hydroxyl group, but behaves more normally in other solvents, including liquid ammonia and nitrobenzene.[4]

For multivalent ions, it is usual to consider the conductivity divided by the equivalent ion concentration in terms of equivalents per litre, where 1 equivalent is the quantity of ions that have the same amount of electric charge as 1 mol of a monovalent ion: 1/2 mol Ca2+, 1/2 mol SO2−
4, 1/3 mol Al3+, 1/4 mol Fe(CN)4−
6, etc. This quotient can be called the equivalent conductivity, although IUPAC has recommended that use of this term be discontinued and the term molar conductivity be used for the values of conductivity divided by equivalent concentration.[10] If this convention is used, then the values are in the same range as monovalent ions, e.g. 59.5 S cm2 mol−1 for 1/2 Ca2+ and 80.0 S cm2 mol−1 for 1/2 SO2−
4.[4]

From the ionic molar conductivities of cations and anions, effective ionic radii can be calculated using the concept of Stokes radius. The values obtained for an ionic radius in solution calculated this way can be quite different from the ionic radius for the same ion in crystals, due to the effect of hydration in solution.

Applications[edit]

Ostwald’s law of dilution, which gives the dissociation constant of a weak electrolyte as a function of concentration, can be written in terms of molar conductivity. Thus, the pKa values of acids can be calculated by measuring the molar conductivity and extrapolating to zero concentration. Namely, pKa = p(K/1 mol/L) at the zero-concentration limit, where K is the dissociation constant from Ostwald’s law.

References[edit]

  1. ^ The best test preparation for the GRE Graduate Record Examination Chemistry Test. Published by the Research and Education Association, 2000, ISBN 0-87891-600-8. p. 149.
  2. ^ a b Atkins, P. W.; de Paula, J. (2006). Physical Chemistry (8th ed.). Oxford University Press. p. 762. ISBN 0198700725.
  3. ^ Conductivity, IUPAC Gold Book.
  4. ^ a b c d e f g Laidler K. J. and Meiser J. H., Physical Chemistry (Benjamin/Cummings 1982) p. 281–283. ISBN 0-8053-5682-7.
  5. ^ Laidler K. J. and Meiser J. H., Physical Chemistry (Benjamin/Cummings 1982) p. 256. ISBN 0-8053-5682-7.
  6. ^ Atkins, P. W. (2001). The Elements of Physical Chemistry. Oxford University Press. ISBN 0-19-879290-5.
  7. ^ Castellan, G. W. Physical Chemistry. Benjamin/Cummings, 1983.
  8. ^ Laidler K. J. and Meiser J. H., Physical Chemistry (Benjamin/Cummings 1982) p. 273. ISBN 0-8053-5682-7.
  9. ^ Atkins, P. W.; de Paula, J. (2006). Physical Chemistry (8th ed.). Oxford University Press. p. 766. ISBN 0198700725.
  10. ^ Yung Chi Wu and Paula A. Berezansky, Low Electrolytic Conductivity Standards, J. Res. Natl. Inst. Stand. Technol. 100, 521 (1995).
Источник

Макеты страниц

МОЛЯРНАЯ ПРОВОДИМОСТЬ

Электролитическая проводимость раствора зависит от концентрации в нем электролита. Поэтому принято выражать электролитическую проводимость раствора через его молярную проводимость А, определяемую соотношением

где — электролитическая проводимость раствора, с – концентрация раствора, выраженная в моль/дм3. Молярная проводимость измеряется в единицах

Пример

Раствор хлорида калия концентрации 0,20 моль/дм3 имеет при 298 К электролитическую проводимость См/см. Вычислим его молярную проводимость.

Решение

Пользуясь уравнением (3), находим

Поскольку то

Зависимость молярной проводимости от концентрации электролита

В общем случае молярная проводимость уменьшается при возрастании концентрации электролита. Конкретный характер этой зависимости различен для сильных и слабых электролитов.

Сильные электролиты. При низких концентрациях молярная проводимость сильного электролита оказывается пропорциональной квадратному корню из концентрации

Конкретный вид этой зависимости определяется эмпирическим уравнением, которое впервые сформулировал Кольрауш:

где – постоянная величина, а называется молярной проводимостью (электропроводностью) при бесконечном разбавлении, а иногда – предельной молярной проводимостью (электропроводностью). Таким образом,

Значение предельной проводимости для сильного электролита можно определить, построив график зависимости молярной проводимости от и экстраполируя его к точке . На рис. 10.3 показан такой график для раствора хлорида калия. Обратим внимание на то, что в области значений превышающих приблизительно график отклоняется от прямолинейного.

Слабые электролиты. Молярная проводимость растворов слабых электролитов значительно меньше, чем для растворов сильных электролитов. Дело в том, что

Рис. 10.3. Зависимость молярной проводимости от концентрации для растворов хлорида калия и уксусной кислоты.

Таблица 10.1. Молярные проводимости при бесконечном разбавлении для пар сильных электролитов с общим ионом

молярная проводимость раствора зависит от количества присутствующих в нем ионов. Слабые электролиты даже при низких концентрациях характеризуются малой степенью диссоциации. Но все же, когда концентрация слабого электролита становится очень Низкой, степень его ионизации резко возрастает. Это приводит к соответственному возрастанию молярной проводимости. На рис. 10.3 показан график зависимости молярной проводимости от квадратного корня из концентрации уксусной кислоты. Этот график имеет нелинейный характер и показывает, что слабые электролиты не подчиняются уравнению Кольрауша.

Ионная подвижность. В 1875 г. Кольрауш проводил сопоставление молярных проводимостей при бесконечном разбавлении для пары сильных электролитов, имеющих общие ионы. Он установил, что разность молярных проводимостей между членами каждой пары с общими ионами оказывается постоянной (табл. 10.1). На этом основании Кольрауш сформулировал закон аддитивности (независимости) ионных подвижностей, названный впоследствии его именем. Закон Кольрауша гласит, что молярная проводимость электролита при бесконечном разбавлении представляет собой сумму подвижностей ионов, образующих электролит, и что эти подвижности не зависят от других ионов.

Ионная подвижность связана с молярной проводимостью данного иона при бесконечном разбавлении. Для электролита состава 1:1 (иначе, для 1:1 – электролита) типа закон Кольрауша математически записывается так:

Здесь – ионная подвижность катиона, а – ионная подвижность аниона.

Ионная подвижность является мерой скорости, с которой данный ион перемещается через раствор. Вообще говоря, ионы с малыми ионными радиусами перемещаются медленнее, чем ионы с большими ионными радиусами. Это объясняется тем, что ион меньшего размера имеет более высокую плотность заряда и поэтому сильнее сольватируется растворителем (см. разд. 2.2). Его гидратная оболочка и, следовательно, его эффективный размер оказывается больше, чем у иона с большим ионным

радиусом. Большой эффективный заряд такого иона обусловливает его малую подвижность в растворе.

Двухзарядные или трехзарядные ионы, как правило, имеют более высокую ионную подвижность, чем однозарядные ионы. Исключение составляют ионы гидроксония и гидроксильные ионы которые имеют самые высокие ионные подвижности из всех ионов. Это объясняется быстрым переносом протонов между ионами в растворе.

Вычисление … для слабых электролитов

Если построить график зависимости молярной проводимости для слабого электролита от концентрации, получится кривая такого типа, как показано на рис. 10.3 для . Поскольку эта кривая не пересекается с вертикальной осью координат, нельзя определить Л” для слабого электролита экстраполяцией графика к нулевой концентрации. Однако эту величину можно найти, применяя к слабому электролиту закон Кольрауша об аддитивности ионных подвижностей для сильных электролитов.

Пример

Вычислим для уксусной кислоты, пользуясь следующими данными:

Решение

Уксусная кислота – слабый электролит. Соляная кислота, хлорид натрия и ацетат натрия – сильные электролиты. Применяя закон Кольрауша к сильным электролитам, находим

Для слабого электролита можно записать

Степень диссоциации

Выше было показано, что молярная проводимость электролита зависит от относительного количества ионов, присутствующих в растворе, а следовательно, от степени диссоциации электролита. Аррениус выдвинул предположение, что молярная проводимость электролита связана с его степенью диссоциации следующим соотношением:

При концентрациях, близких к нулю, т. е. при бесконечном разбавлении и, следовательно,

Рис. 10.4. Кондуктометрическое титрование.

Рис. 10.5. Кривые кондуктометрическо-го титрования сильной и слабой кислоты сильным основанием.

Уравнение (4) вместе с законом разбавления Оствальда (см. разд. 8.1) может использоваться для вычисления константы диссоциации слабого электролита по экспериментально установленным молярным проводимостям. Действительно, подставляя выражение (4) в выражение закона разбавления Оствальда

находим

Источник

Добавить комментарий